An Off-Line Error Compensation Method for Absolute Positioning Accuracy of Industrial Robots Based on Differential Evolution and Deep Belief Networks
Abstract
:1. Introduction
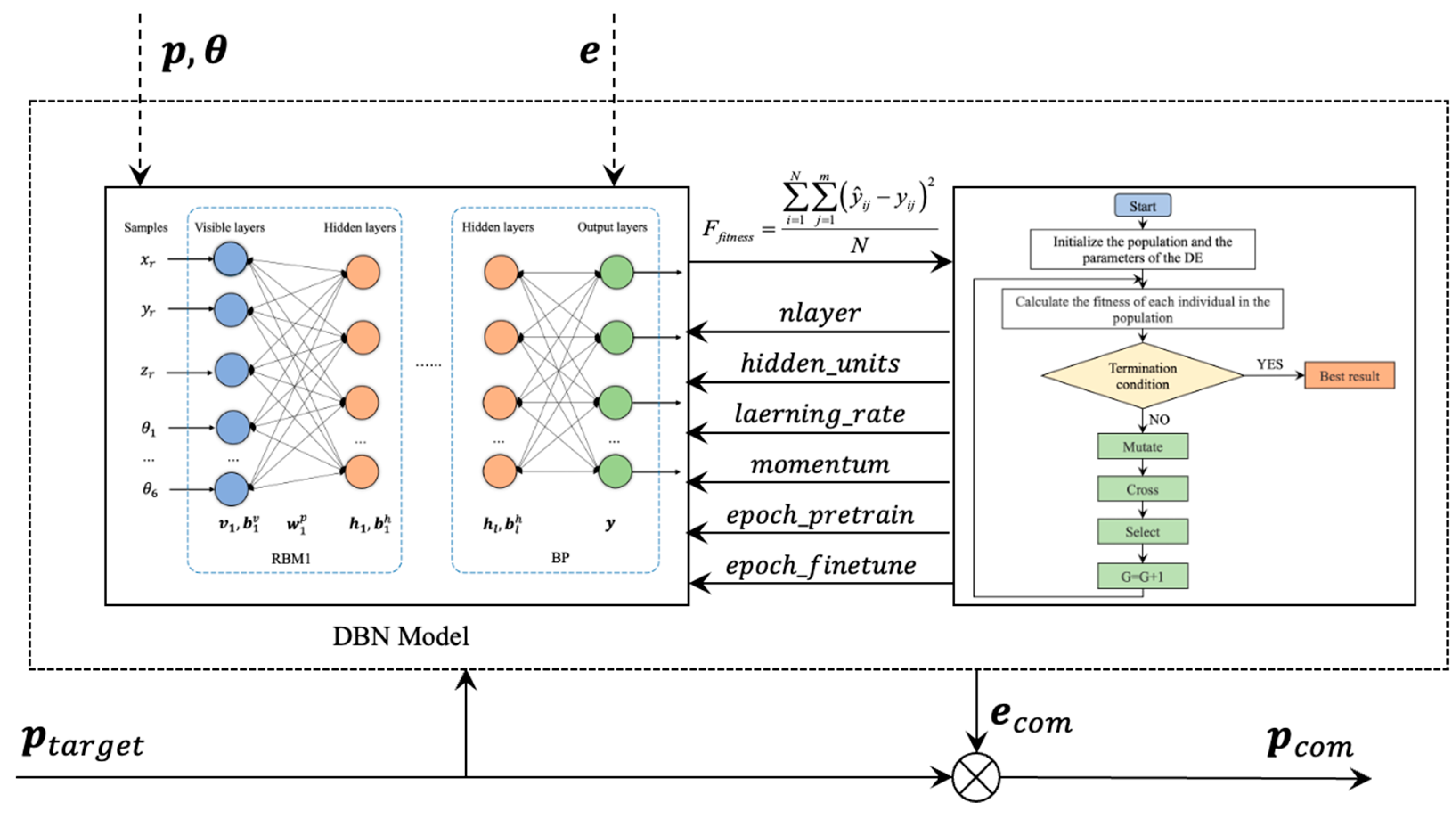
2. Robot Positioning Error Prediction Algorithm Based on DE and DBN
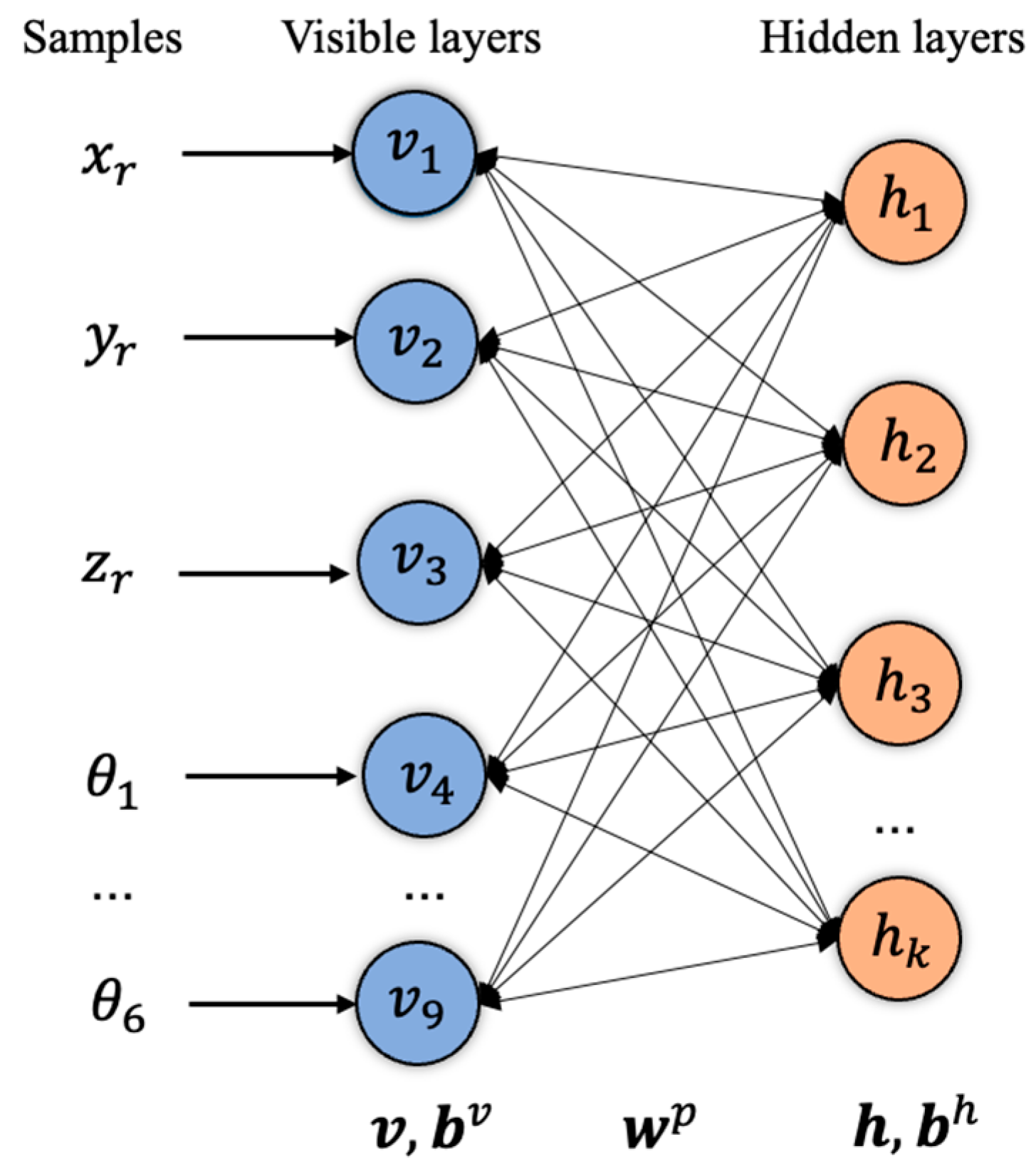
2.1. Principle of the DBN
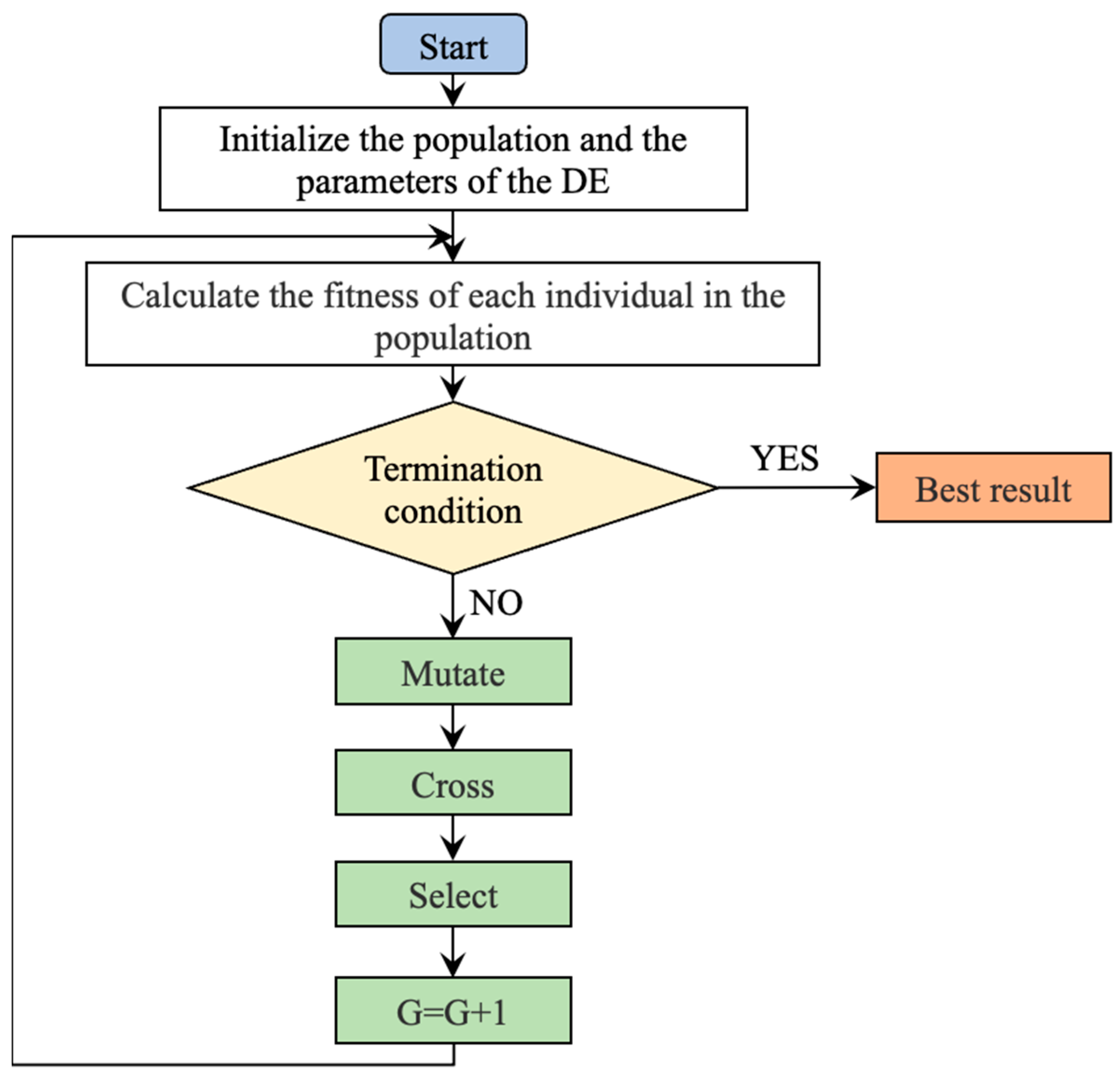
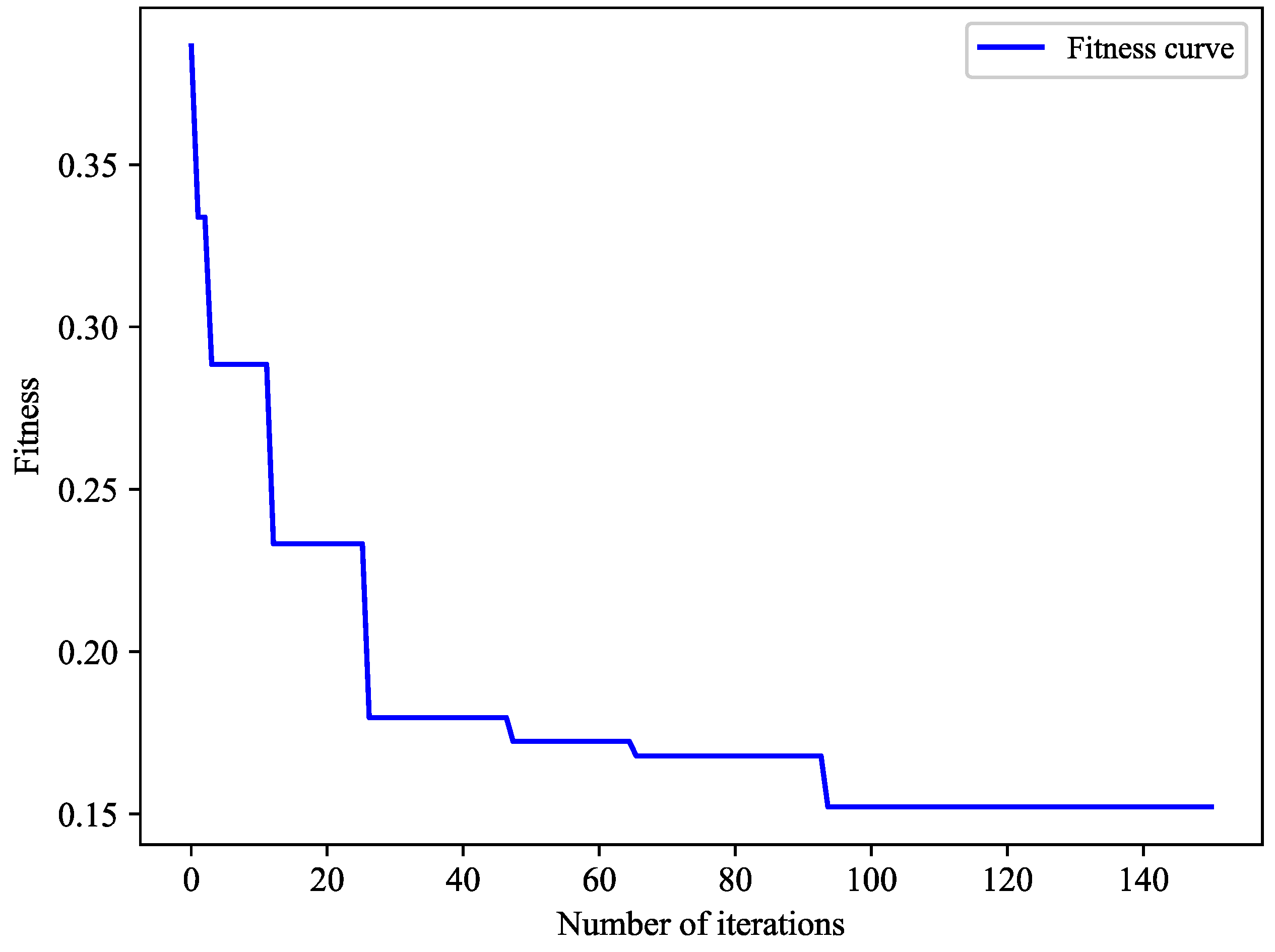
2.2. DBN Optimization Based on DE Algorithm
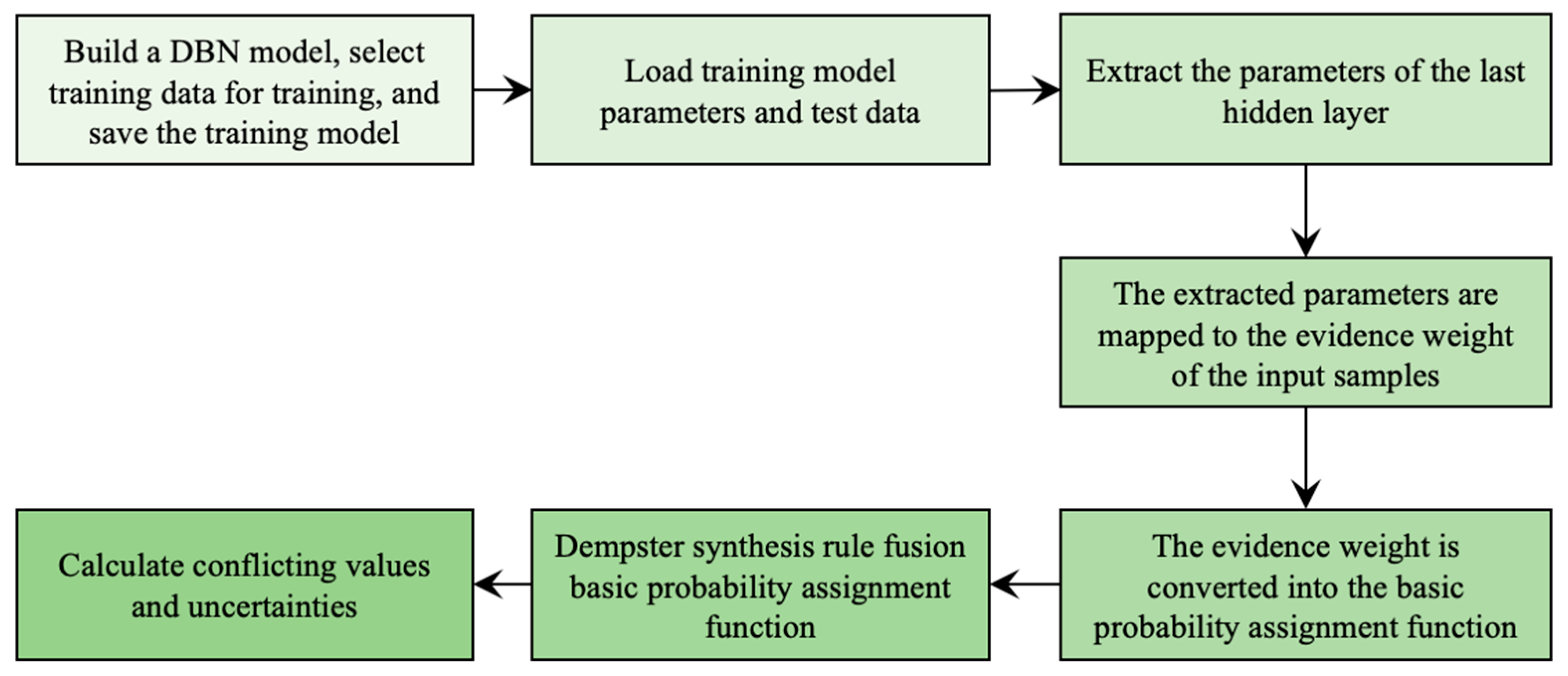
3. Supervised Predictive Optimization Based on Evidence Theory
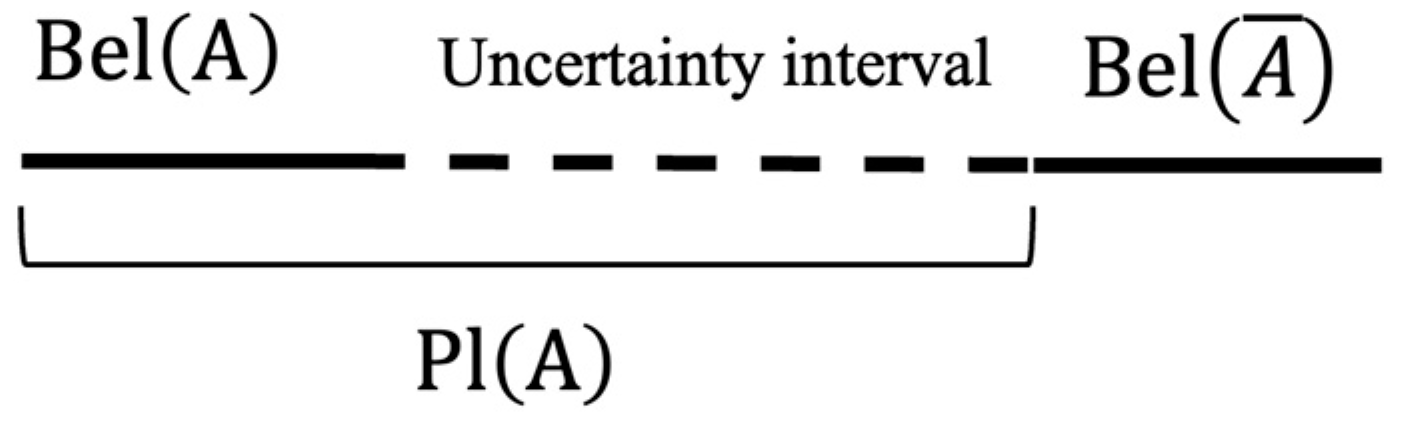
3.1. Evidence Theory
3.2. Optimization of Position Error Based on Evidence Theory
4. Experiments
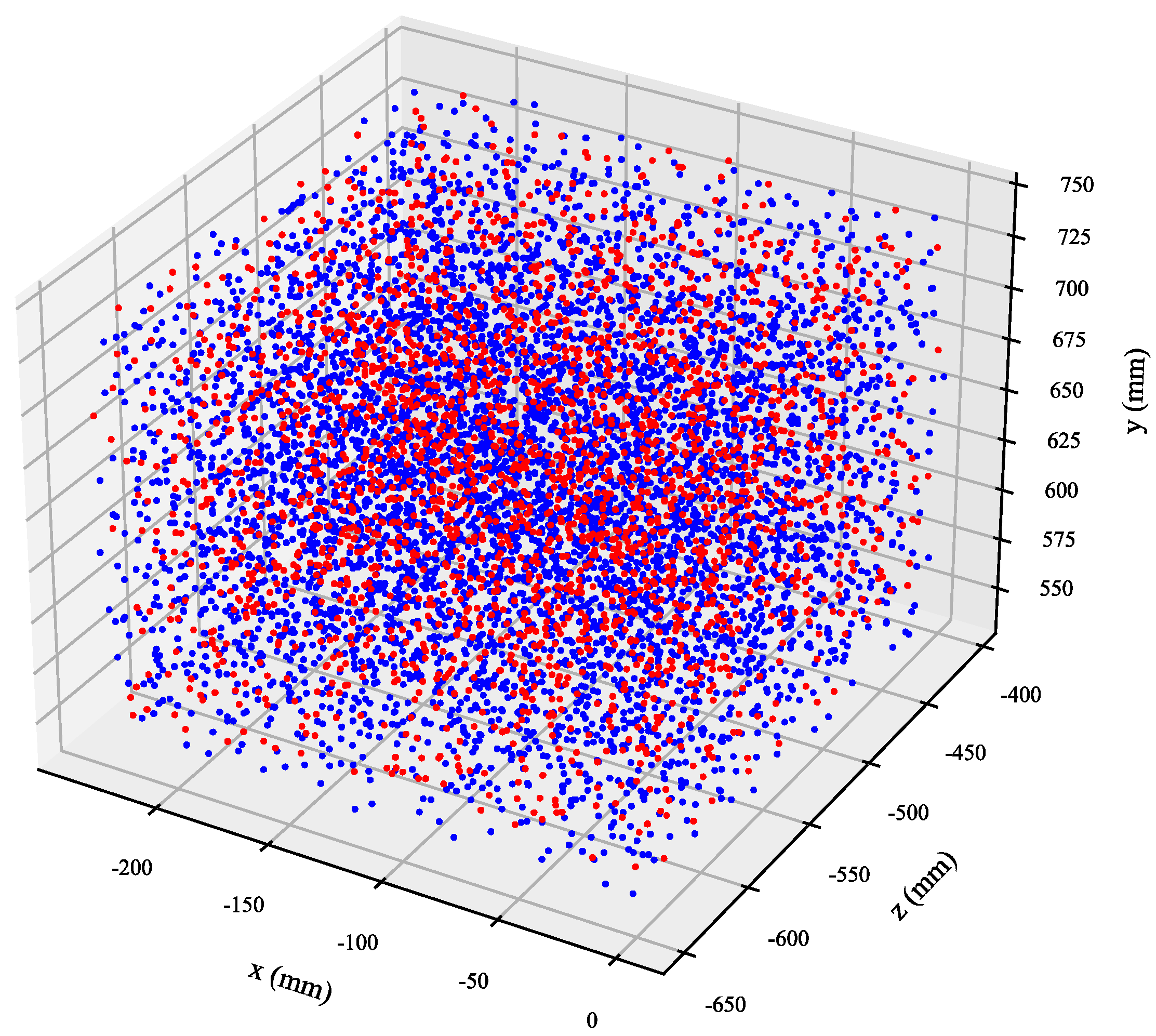
4.1. Experimental Setup and Data Collection
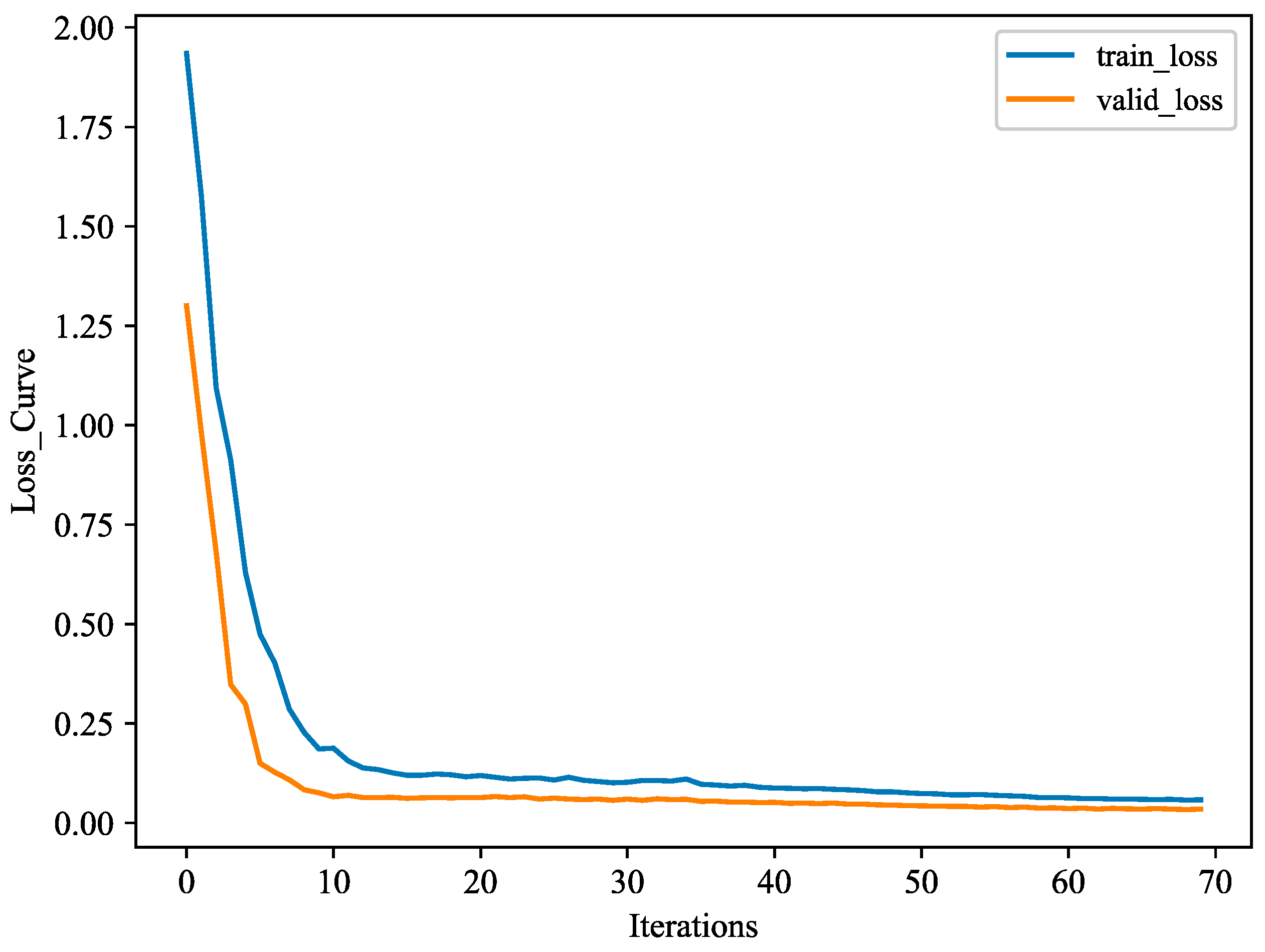
4.2. Model Training and Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mubarak, M.F.; Petraite, M. Industry 4.0 Technologies, Digital Trust and Technological Orientation: What Matters in Open Innovation? Technol. Forecast Soc. Chang. 2020, 161, 120332. [Google Scholar] [CrossRef]
- Papakostas, N.; Constantinescu, C.; Mourtzis, D. Novel Industry 4.0 Technologies and Applications. Appl. Sci. 2020, 10, 6498. [Google Scholar] [CrossRef]
- Jaskó, S.; Skrop, A.; Holczinger, T.; Chován, T.; Abonyi, J. Development of Manufacturing Execution Systems in Accordance with Industry 4.0 Requirements: A Review of Standard- and Ontology-Based Methodologies and Tools. Comput. Ind. 2020, 123, 103300. [Google Scholar] [CrossRef]
- Rosin, F.; Forget, P.; Lamouri, S.; Pellerin, R. Impacts of Industry 4.0 Technologies on Lean Principles. Int. J. Prod. Res. 2019, 58, 1644–1661. [Google Scholar] [CrossRef]
- Moosavi, J.; Bakhshi, J.; Martek, I. The Application of Industry 4.0 Technologies in Pandemic Management: Literature Review and Case Study. Healthc. Anal. 2021, 1, 100008. [Google Scholar] [CrossRef]
- Klerkx, L.; Rose, D. Dealing with the Game-Changing Technologies of Agriculture 4.0: How Do We Manage Diversity and Responsibility in Food System Transition Pathways? Glob. Food Sec. 2020, 24, 100347. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Khan, I.H.; Suman, R. Understanding the Potential Applications of Artificial Intelligence in Agriculture Sector. Adv. Agrochem. 2023, 2, 15–30. [Google Scholar] [CrossRef]
- Strong, R.; Wynn, J.T.; Lindner, J.R.; Palmer, K. Evaluating Brazilian Agriculturalists’ IoT Smart Agriculture Adoption Barriers: Understanding Stakeholder Salience Prior to Launching an Innovation. Sensors 2022, 22, 6833. [Google Scholar] [CrossRef]
- Ronaghi, M.; Ronaghi, M.H. Investigating the Impact of Economic, Political, and Social Factors on Augmented Reality Technology Acceptance in Agriculture (Livestock Farming) Sector in a Developing Country. Technol. Soc. 2021, 67, 101739. [Google Scholar] [CrossRef]
- Osinga, S.A.; Paudel, D.; Mouzakitis, S.A.; Athanasiadis, I.N. Big Data in Agriculture: Between Opportunity and Solution. Agric. Syst. 2022, 195, 103298. [Google Scholar] [CrossRef]
- Ahn, J.; Briers, G.; Baker, M.; Price, E.; Sohoulande Djebou, D.C.; Strong, R.; Piña, M.; Kibriya, S. Food Security and Agricultural Challenges in West-African Rural Communities: A Machine Learning Analysis. Int. J. Food Prop. 2022, 25, 827–844. [Google Scholar] [CrossRef]
- Zheng, T.; Ardolino, M.; Bacchetti, A.; Perona, M. The Applications of Industry 4.0 Technologies in Manufacturing Context: A Systematic Literature Review. Int. J. Prod. Res. 2021, 59, 1922–1954. [Google Scholar] [CrossRef]
- Frank, A.G.; Dalenogare, L.S.; Ayala, N.F. Industry 4.0 Technologies: Implementation Patterns in Manufacturing Companies. Int. J. Prod. Econ. 2019, 210, 15–26. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R. Substantial Capabilities of Robotics in Enhancing Industry 4.0 Implementation. Cogn. Robot. 2021, 1, 58–75. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, Y.; Yang, L.X.; Xiao, M.; Chen, S.Y. Robot Grinding System Trajectory Compensation Based on Co-Kriging Method and Constant-Force Control Based on Adaptive Iterative Algorithm. Int. J. Precis. Eng. Manuf. 2020, 21, 1637–1651. [Google Scholar] [CrossRef]
- Wang, W.; Tian, W.; Liao, W.; Li, B. Pose Accuracy Compensation of Mobile Industry Robot with Binocular Vision Measurement and Deep Belief Network. Optik 2021, 238, 166716. [Google Scholar] [CrossRef]
- Qi, J.; Chen, B.; Zhang, D. Compensation for Absolute Positioning Error of Industrial Robot Considering the Optimized Measurement Space. Int. J. Adv. Robot Syst. 2020, 17. [Google Scholar] [CrossRef]
- Kong, L.B.; Yu, Y. Precision Measurement and Compensation of Kinematic Errors for Industrial Robots Using Artifact and Machine Learning. Adv. Manuf. 2022, 10, 397–410. [Google Scholar] [CrossRef]
- Cao, C.T.; Do, V.P.; Lee, B.R. A Novel Indirect Calibration Approach for Robot Positioning Error Compensation Based on Neural Network and Hand-Eye Vision. Appl. Sci. 2019, 9, 1940. [Google Scholar] [CrossRef]
- Chen, D.; Yuan, P.; Wang, T.; Cai, Y.; Xue, L. A Compensation Method for Enhancing Aviation Drilling Robot Accuracy Based on Co-Kriging. Int. J. Precis. Eng. Manuf. 2018, 19, 1133–1142. [Google Scholar] [CrossRef]
- Chen, D.; Yuan, P.; Wang, T.; Ying, C.; Tang, H. A Compensation Method Based on Error Similarity and Error Correlation to Enhance the Position Accuracy of an Aviation Drilling Robot. Meas. Sci. Technol. 2018, 29, 085011. [Google Scholar] [CrossRef]
- Shen, N.Y.; Guo, Z.M.; Li, J.; Tong, L.; Zhu, K. A Practical Method of Improving Hole Position Accuracy in the Robotic Drilling Process. Int. J. Adv. Manuf. Technol. 2018, 96, 2973–2987. [Google Scholar] [CrossRef]
- Chen, D.; Wang, T.; Yuan, P.; Sun, N.; Tang, H. A Positional Error Compensation Method for Industrial Robots Combining Error Similarity and Radial Basis Function Neural Network. Meas. Sci. Technol. 2019, 30, 125010. [Google Scholar] [CrossRef]
- Wang, L.; Tang, Z.; Zhang, P.; Liu, X.; Wang, D.; Li, X. Double Extended Sliding Mode Observer-Based Synchronous Estimation of Total Inertia and Load Torque for PMSM-Driven Spindle-Tool Systems. IEEE Trans. Ind. Inf. 2022, 19, 8496–8507. [Google Scholar] [CrossRef]
- Fu, S.; Li, Y.; Zhang, M.; Hu, J.; Hua, F.; Tian, W. Robot Positioning Error Compensation Method Based on Deep Neural Network. J. Phys. Conf. Ser. 2020, 1487, 012045. [Google Scholar] [CrossRef]
- LI, B.; TIAN, W.; ZHANG, C.; HUA, F.; CUI, G.; LI, Y. Positioning Error Compensation of an Industrial Robot Using Neural Networks and Experimental Study. Chin. J. Aeronaut. 2022, 35, 346–360. [Google Scholar] [CrossRef]
- Wang, W.; Tian, W.; Liao, W.; Li, B.; Hu, J. Error Compensation of Industrial Robot Based on Deep Belief Network and Error Similarity. Robot Comput. Integr. Manuf. 2022, 73, 102220. [Google Scholar] [CrossRef]
- Qi, J.; Chen, B.; Zhang, D. A Calibration Method for Enhancing Robot Accuracy Through Integration of Kinematic Model and Spatial Interpolation Algorithm. J. Mech. Robot 2021, 13, 061013. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Algelany, S. High-Dimensional Chaotic Lorenz System: Numerical Treatment Using Changhee Polynomials of the Appell Type. Fractal. Fract. 2023, 7, 398. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Assiri, T.A.; Kallel, W. Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique. Symmetry 2023, 15, 931. [Google Scholar] [CrossRef]
- Khader, M.M.; Inc, M.; Adel, M.; Akinlar, M.A. Numerical Solutions to the Fractional-Order Wave Equation. Int. J. Mod. Phys. C 2023, 34, 2350067. [Google Scholar] [CrossRef]
- Adel, M.; Srivastava, H.M.; Khader, M.M. Implementation of an Accurate Method for the Analysis and Simulation of Electrical R-L Circuits. Math. Methods Appl. Sci. 2023, 46, 8362–8371. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Ahmad, H.; Assiri, T.A.; Adel, M.; Khader, M.M.; Ahmad, H.; Assiri, T.A. Approximate Analytical Solutions for the Blood Ethanol Concentration System and Predator-Prey Equations by Using Variational Iteration Method. AIMS Math. 2023, 8, 19083–19096. [Google Scholar] [CrossRef]
- Ibrahim, Y.F.; Abd El-Bar, S.E.; Khader, M.M.; Adel, M. Studying and Simulating the Fractional COVID-19 Model Using an Efficient Spectral Collocation Approach. Fractal. Fract. 2023, 7, 307. [Google Scholar] [CrossRef]
- Min, K.; Ni, F.; Chen, Z.; Liu, H.; Lee, C.-H. A Robot Positional Error Compensation Method Based on Improved Kriging Interpolation and Kronecker Products. IEEE Trans. Ind. Electron. 2023, 1–10. [Google Scholar] [CrossRef]
- Zhou, J.; Zheng, L.; Fan, W.; Zhang, X.; Cao, Y. Adaptive Hierarchical Positioning Error Compensation for Long-Term Service of Industrial Robots Based on Incremental Learning with Fixed-Length Memory Window and Incremental Model Reconstruction. Robot Comput. Integr. Manuf. 2023, 84, 102590. [Google Scholar] [CrossRef]
- Li, R.; Ding, N.; Zhao, Y.; Liu, H. Real-Time Trajectory Position Error Compensation Technology of Industrial Robot. Measurement 2023, 208, 112418. [Google Scholar] [CrossRef]
- Ma, S.; Deng, K.; Lu, Y.; Xu, X. Error Compensation Method of Industrial Robots Considering Non-Kinematic and Weak Rigid Base Errors. Precis. Eng. 2023, 82, 304–315. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Gao, S.; Xu, L.; Zhang, Y.; Pei, Z. Rolling Bearing Fault Diagnosis Based on SSA Optimized Self-Adaptive DBN. ISA Trans. 2022, 128, 485–502. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Yuan, X.; Yang, C.; Gui, W. A Novel Deep Learning Based Fault Diagnosis Approach for Chemical Process with Extended Deep Belief Network. ISA Trans. 2020, 96, 457–467. [Google Scholar] [CrossRef]
- Liu, J.; Wu, N.; Qiao, Y.; Li, Z. Short-Term Traffic Flow Forecasting Using Ensemble Approach Based on Deep Belief Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 404–417. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential Evolution: A Recent Review Based on State-of-the-Art Works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A Review of More than Two Decades of Research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An Improved Differential Evolution Algorithm and Its Application in Optimization Problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Khaparde, A.R.; Alassery, F.; Kumar, A.; Alotaibi, Y.; Khalaf, O.I.; Pillai, S.; Alghamdi, S. Differential Evolution Algorithm with Hierarchical Fair Competition Model. Intell. Autom. Soft Comput. 2022, 33, 1045–1062. [Google Scholar] [CrossRef]
- Fang, Z.; Roy, K.; Mares, J.; Sham, C.W.; Chen, B.; Lim, J.B.P. Deep Learning-Based Axial Capacity Prediction for Cold-Formed Steel Channel Sections Using Deep Belief Network. Structures 2021, 33, 2792–2802. [Google Scholar] [CrossRef]
- Tong, Z.; Xu, P.; Denœux, T. An Evidential Classifier Based on Dempster-Shafer Theory and Deep Learning. Neurocomputing 2021, 450, 275–293. [Google Scholar] [CrossRef]
- Du, Y.W.; Zhong, J.J. Generalized Combination Rule for Evidential Reasoning Approach and Dempster–Shafer Theory of Evidence. Inf. Sci. 2021, 547, 1201–1232. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W.; Wang, Z. Zero-Sum Polymatrix Games with Link Uncertainty: A Dempster-Shafer Theory Solution. Appl. Math. Comput. 2019, 340, 101–112. [Google Scholar] [CrossRef]
- Gudiyangada Nachappa, T.; Tavakkoli Piralilou, S.; Gholamnia, K.; Ghorbanzadeh, O.; Rahmati, O.; Blaschke, T. Flood Susceptibility Mapping with Machine Learning, Multi-Criteria Decision Analysis and Ensemble Using Dempster Shafer Theory. J. Hydrol. 2020, 590, 125275. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.; Li, Z.W.; Ding, L. Improved Fuzzy Bayesian Network-Based Risk Analysis with Interval-Valued Fuzzy Sets and D–S Evidence Theory. IEEE Trans. Fuzzy Syst. 2020, 28, 2063–2077. [Google Scholar] [CrossRef]
- Xiao, F. Generalization of Dempster–Shafer Theory: A Complex Mass Function. Appl. Intell. 2020, 50, 3266–3275. [Google Scholar] [CrossRef]
- Xiao, F. A New Divergence Measure for Belief Functions in D–S Evidence Theory for Multisensor Data Fusion. Inf. Sci. 2020, 514, 462–483. [Google Scholar] [CrossRef]
- Feng, R.; Xu, X.; Zhou, X.; Wan, J. A Trust Evaluation Algorithm for Wireless Sensor Networks Based on Node Behaviors and D-S Evidence Theory. Sensors 2011, 11, 1345–1360. [Google Scholar] [CrossRef]
- Wang, H.; Deng, X.; Jiang, W.; Geng, J. A New Belief Divergence Measure for Dempster–Shafer Theory Based on Belief and Plausibility Function and Its Application in Multi-Source Data Fusion. Eng. Appl. Artif. Intell. 2021, 97, 104030. [Google Scholar] [CrossRef]
- Slavkovic, N.; Zivanovic, S.; Kokotovic, B.; Dimic, Z.; Milutinovic, M. Simulation of Compensated Tool Path through Virtual Robot Machining Model. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 374. [Google Scholar] [CrossRef]






| Parameter | Symbol | Value |
|---|---|---|
| Dimensions of the objective function | n_dim | 9 |
| Maximum number of iterations | max_iter | 200 |
| Population size | size_pop | 30 |
| Mutation probability | prob_mut | 0.8 |
| Crossover probability | Crossp | 0.7 |
| Parameter | Symbol | Range |
|---|---|---|
| Number of hidden layers of DBN | nlayer | (1, 4) |
| Number of nodes in DBN hidden layer 1 | hidden_units [1] | (10, 101) |
| Number of nodes in DBN hidden layer 2 | hidden_units [2] | (10, 101) |
| Number of nodes in DBN hidden layer 3 | hidden_units [3] | (10, 101) |
| Number of nodes in DBN hidden layer 4 | hidden_units [4] | (10, 101) |
| Learning rate of DBN | learning_rate | (0.01, 1) |
| Momentum factor of DBN | momentum | (0.8, 1) |
| Iterations of RBM | epoch_pretrain | (1, 100) |
| Fine-tuning iterations of DBN | epoch_finetune | (1, 200) |
| Parameter | Symbol | Optimal Value |
|---|---|---|
| Number of hidden layers of DBN | nlayer | 4 |
| Number of nodes in DBN hidden layer 1 | hidden_units [1] | 7 |
| Number of nodes in DBN hidden layer 2 | hidden_units [2] | 56 |
| Number of nodes in DBN hidden layer 3 | hidden_units [3] | 62 |
| Number of nodes in DBN hidden layer 4 | hidden_units [4] | 56 |
| Learning rate of DBN | learning_rate | 0.9360 |
| Momentum factor of DBN | momentum | 0.9618 |
| Iterations of RBM | epoch_pretrain | 100 |
| Fine-tuning iterations of DBN | epoch_finetune | 70 |
| MSE | 0.0104 | 0.0017 | 0.0003 |
| RMSE | 0.1021 | 0.0412 | 0.0194 |
| MAPE | 0.1021 | 0.0412 | 0.0193 |
| MAE | 0.0824 | 0.0284 | 0.0900 |
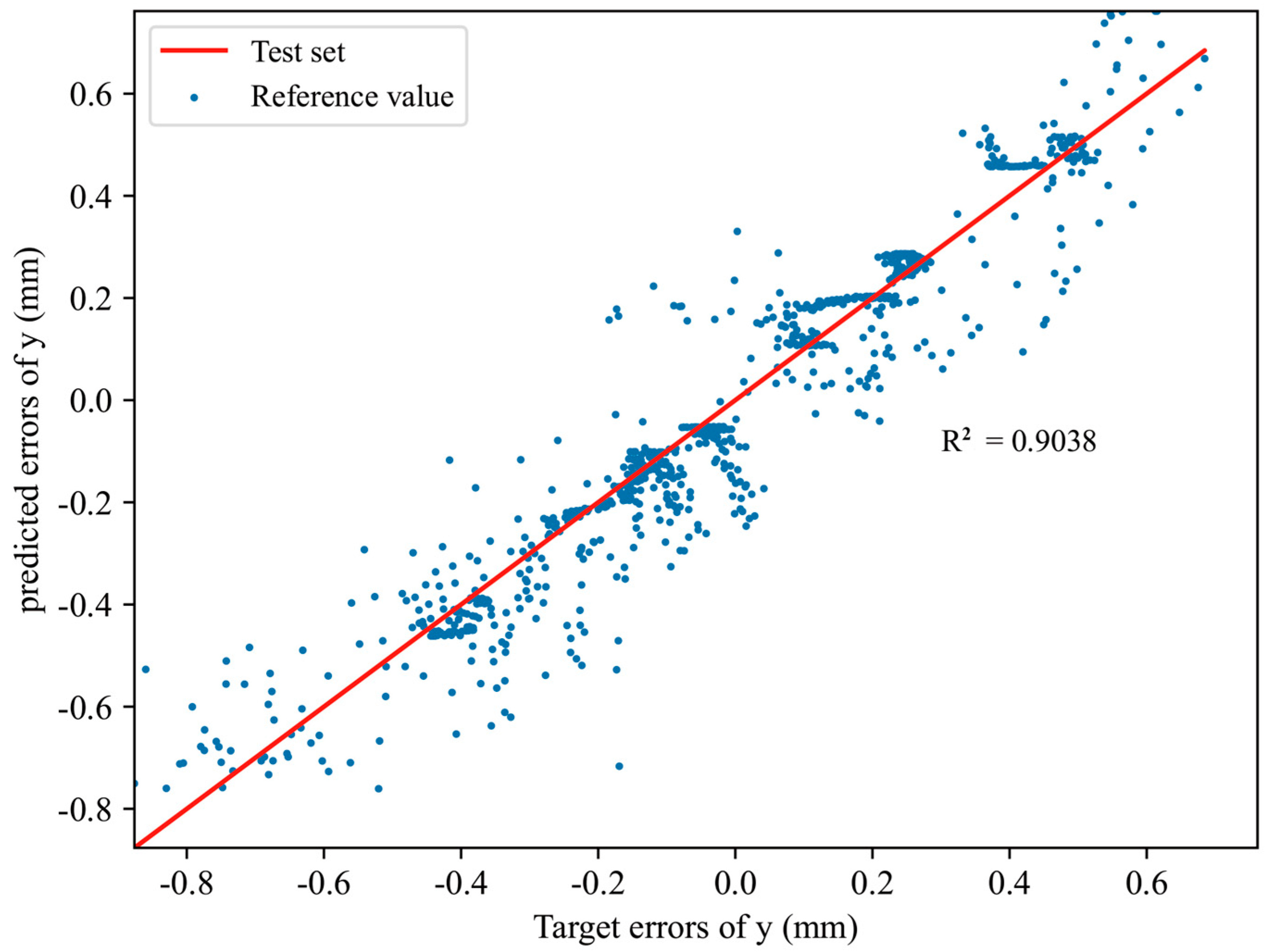
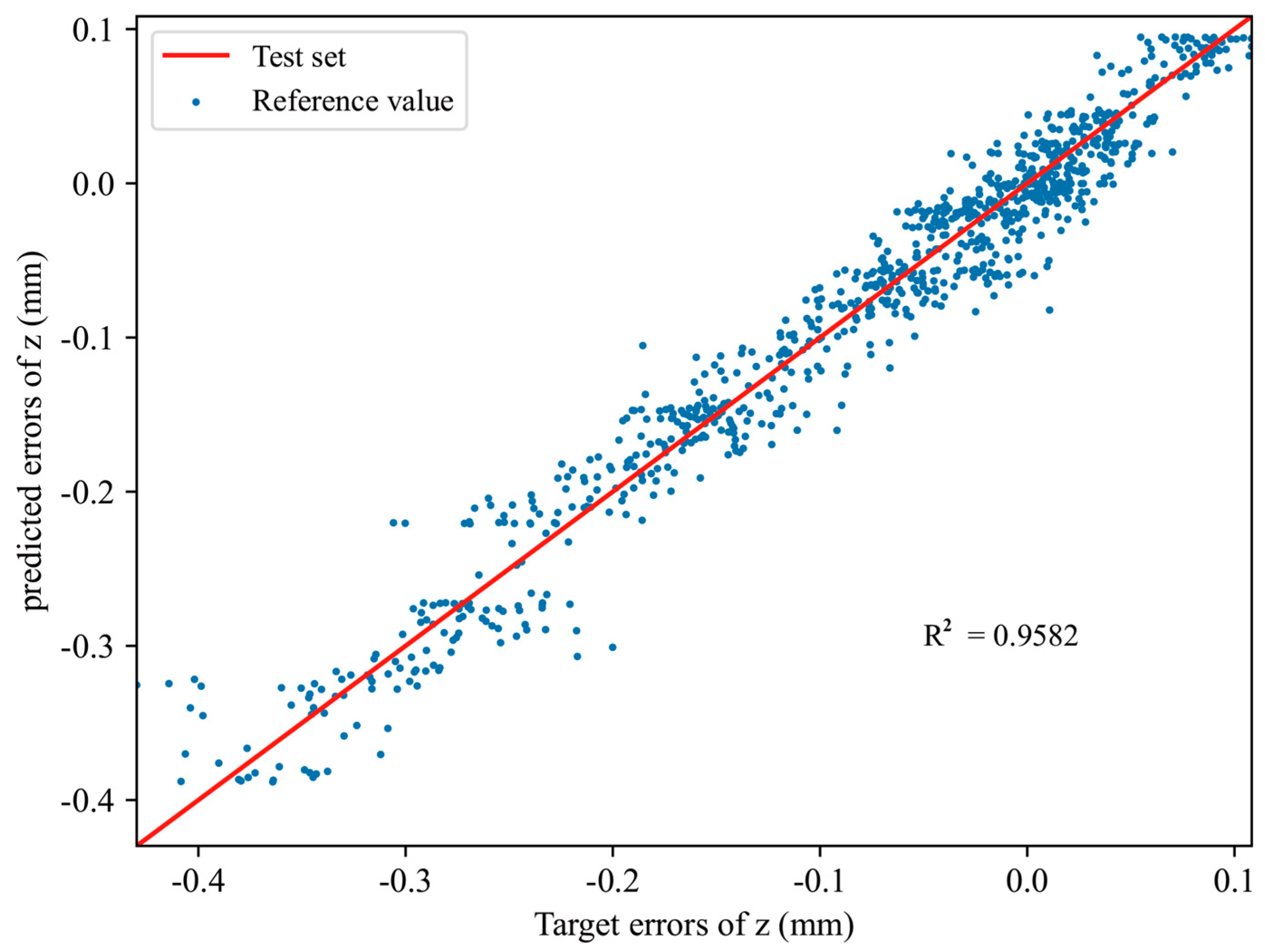
| R2 | 0.8701 | 0.9038 | 0.9582 |
| Error Range | Confidence | Percent Improvement | ||
|---|---|---|---|---|
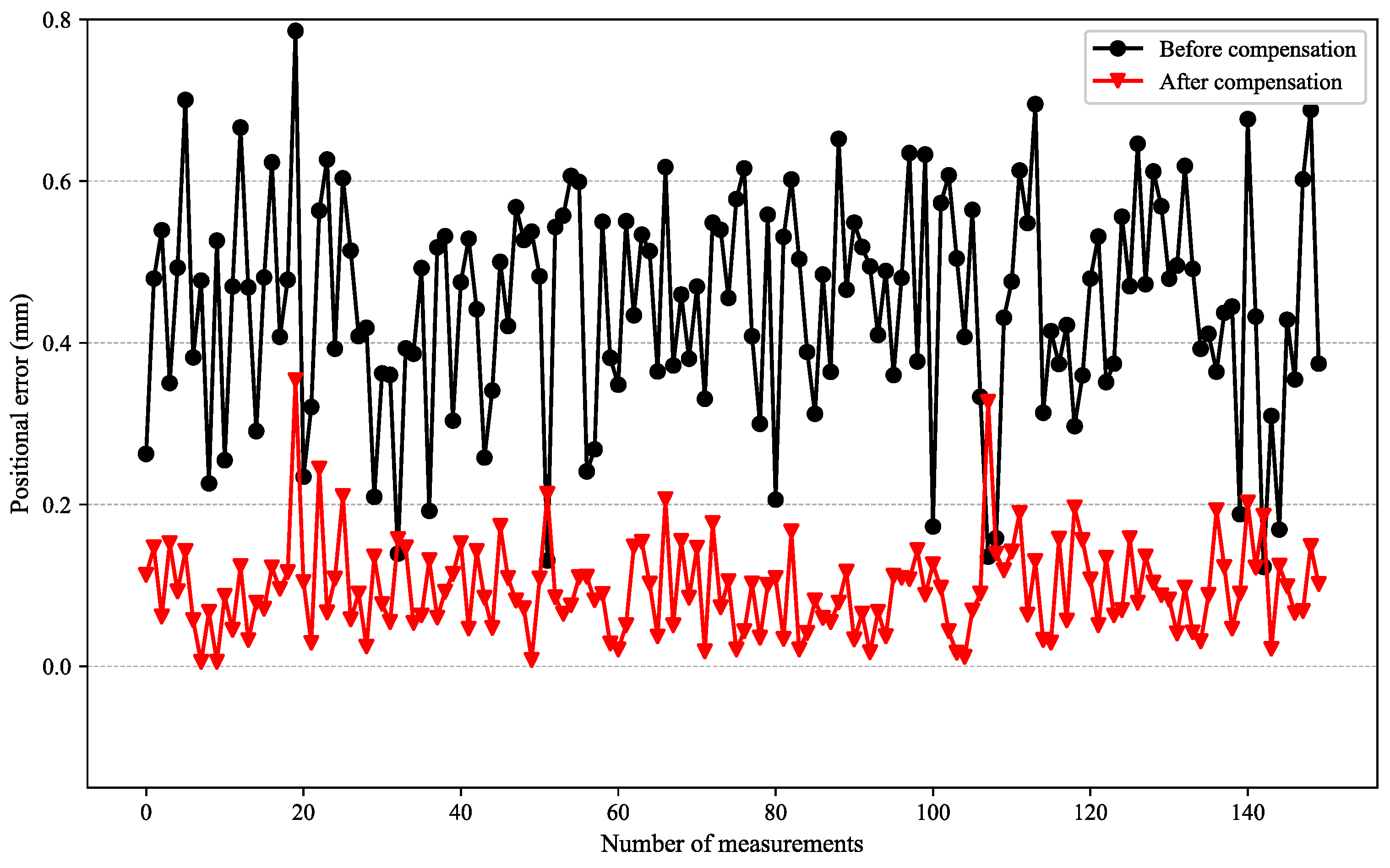
| error (mm) | Before | [−0.674, 0.773] | [−0.500, 0.345] | 65.56% |
| After | [−0.130, 0.368] | [−0.017, 0.017] | ||
| error (mm) | Before | [0.133, −0.559] | [−0.225, 0.063] | 55.22% |
| After | [0.108, −0.201] | [−0.047, 0.031] | ||
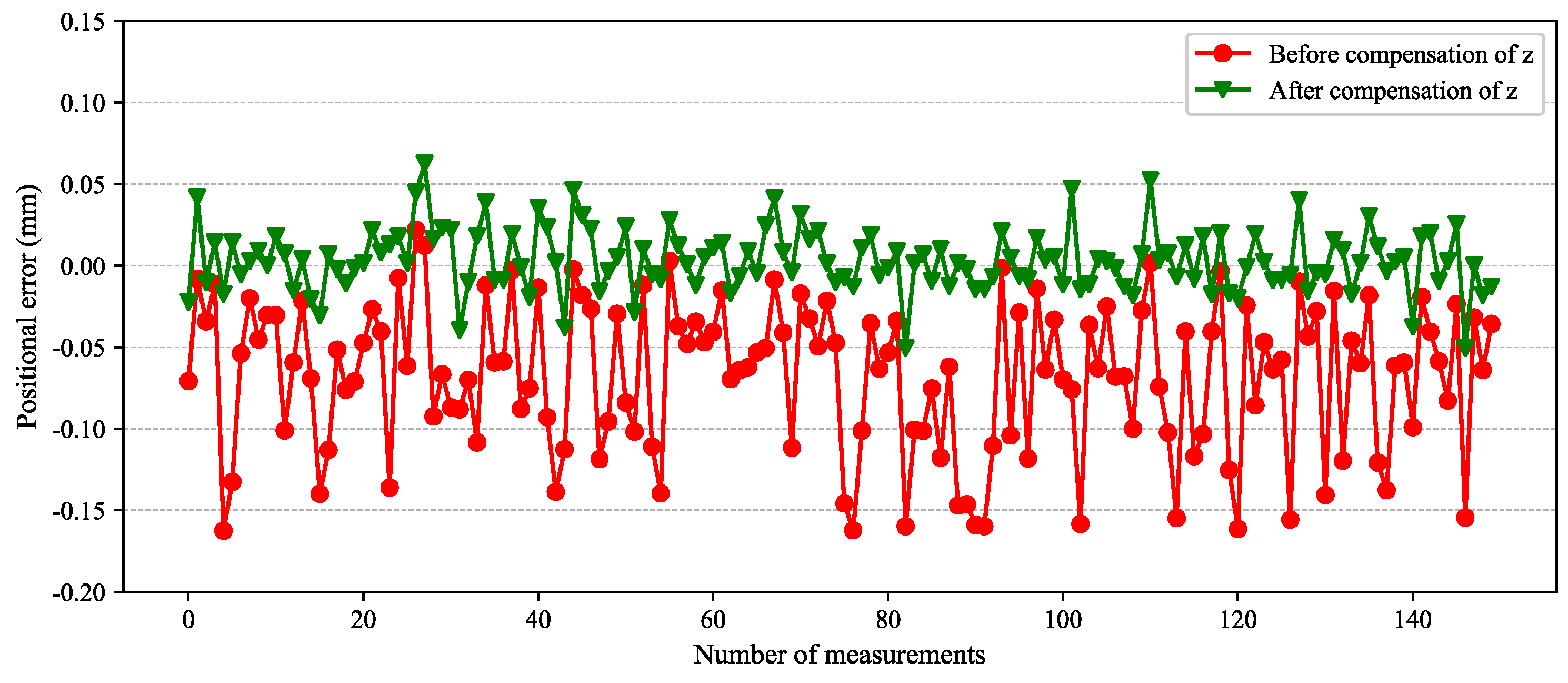
| error (mm) | Before | [0.003, −0.162] | [−0.115, −0.026] | 49.12% |
| After | [0.029, −0.054] | [−0.021, 0.009] |
| Error (mm) | Max | Min | Average |
|---|---|---|---|
| Uncompensated | 1.529 | 0.124 | 0.754 |
| GA-DNN | 0.965 | 0.017 | 0.284 |
| PSO-DNN | 0.519 | 0.172 | 0.333 |
| GPSO-DNN | 0.364 | 0.097 | 0.249 |
| PSO-DBN | 0.244 | Null | 0.110 |
| Uncompensated | 0.701 | 0.139 | 0.469 |
| DE-DBN | 0.255 | 0.006 | 0.083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Liu, H.; Chen, S.; Lan, J.; Qi, Q.; Xiao, W. An Off-Line Error Compensation Method for Absolute Positioning Accuracy of Industrial Robots Based on Differential Evolution and Deep Belief Networks. Electronics 2023, 12, 3718. https://doi.org/10.3390/electronics12173718
Tao Y, Liu H, Chen S, Lan J, Qi Q, Xiao W. An Off-Line Error Compensation Method for Absolute Positioning Accuracy of Industrial Robots Based on Differential Evolution and Deep Belief Networks. Electronics. 2023; 12(17):3718. https://doi.org/10.3390/electronics12173718
Chicago/Turabian StyleTao, Yong, Haitao Liu, Shuo Chen, Jiangbo Lan, Qi Qi, and Wenlei Xiao. 2023. "An Off-Line Error Compensation Method for Absolute Positioning Accuracy of Industrial Robots Based on Differential Evolution and Deep Belief Networks" Electronics 12, no. 17: 3718. https://doi.org/10.3390/electronics12173718
APA StyleTao, Y., Liu, H., Chen, S., Lan, J., Qi, Q., & Xiao, W. (2023). An Off-Line Error Compensation Method for Absolute Positioning Accuracy of Industrial Robots Based on Differential Evolution and Deep Belief Networks. Electronics, 12(17), 3718. https://doi.org/10.3390/electronics12173718






