Application of Improved Butterfly Optimization Algorithm in Mobile Robot Path Planning
Abstract
1. Introduction
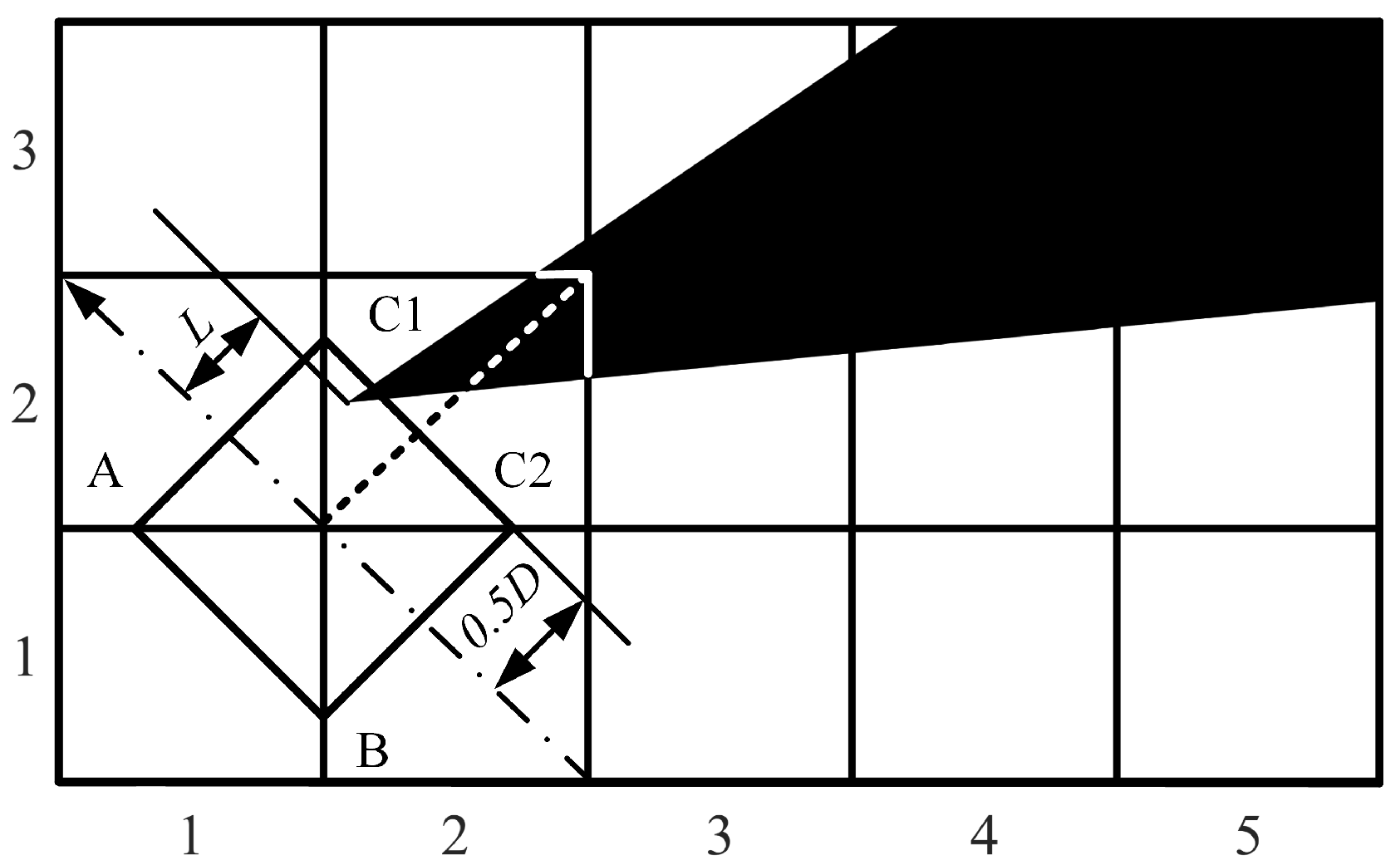
2. Environment Modeling
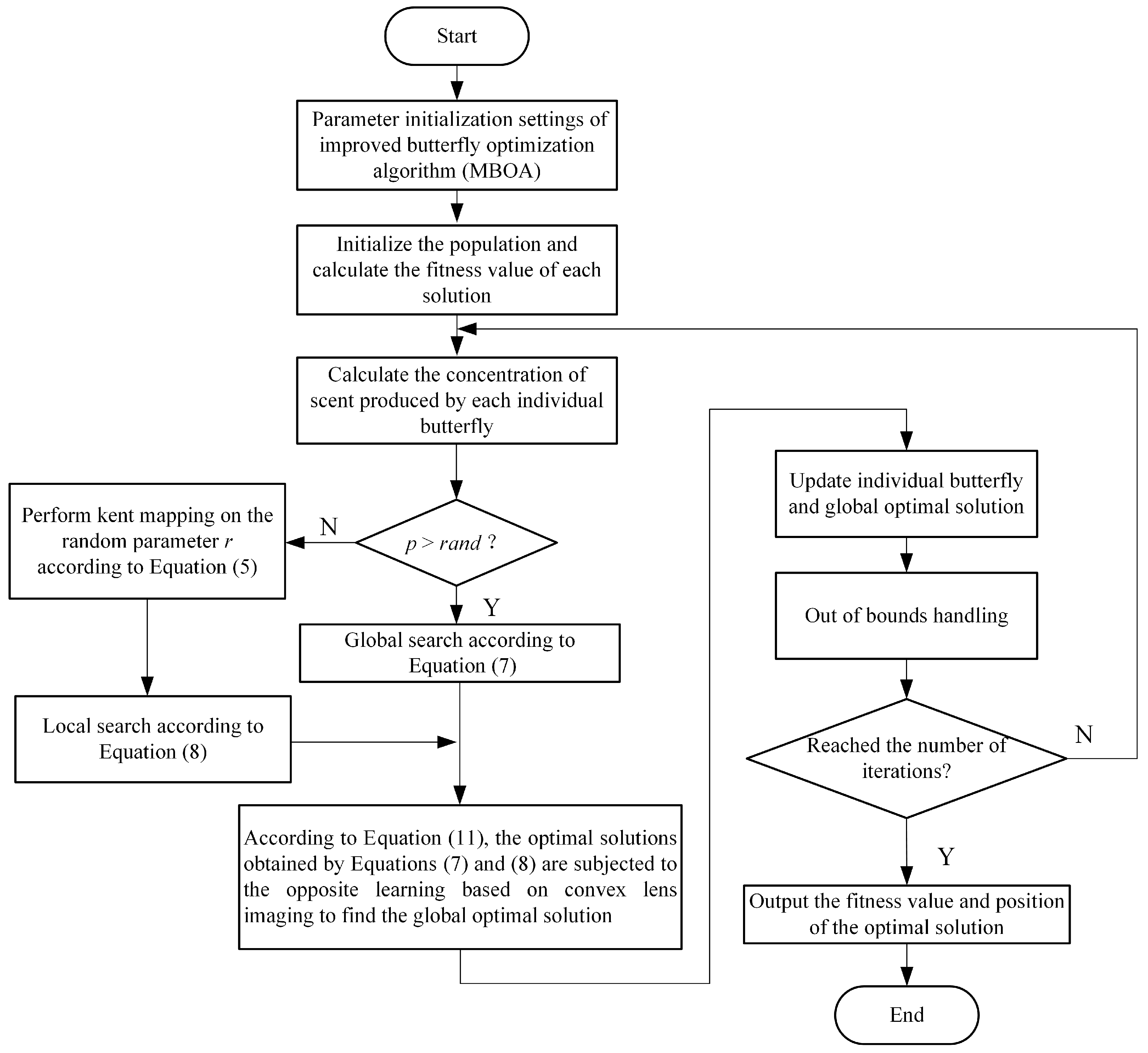
3. Improved Butterfly Optimization Algorithm
3.1. Kent Mapping
3.2. Adaptive Inertia Weights
3.3. Opposition-Based Learning Strategy Based on Convex Lens Imaging
3.4. Comparison of BOA with IBOA
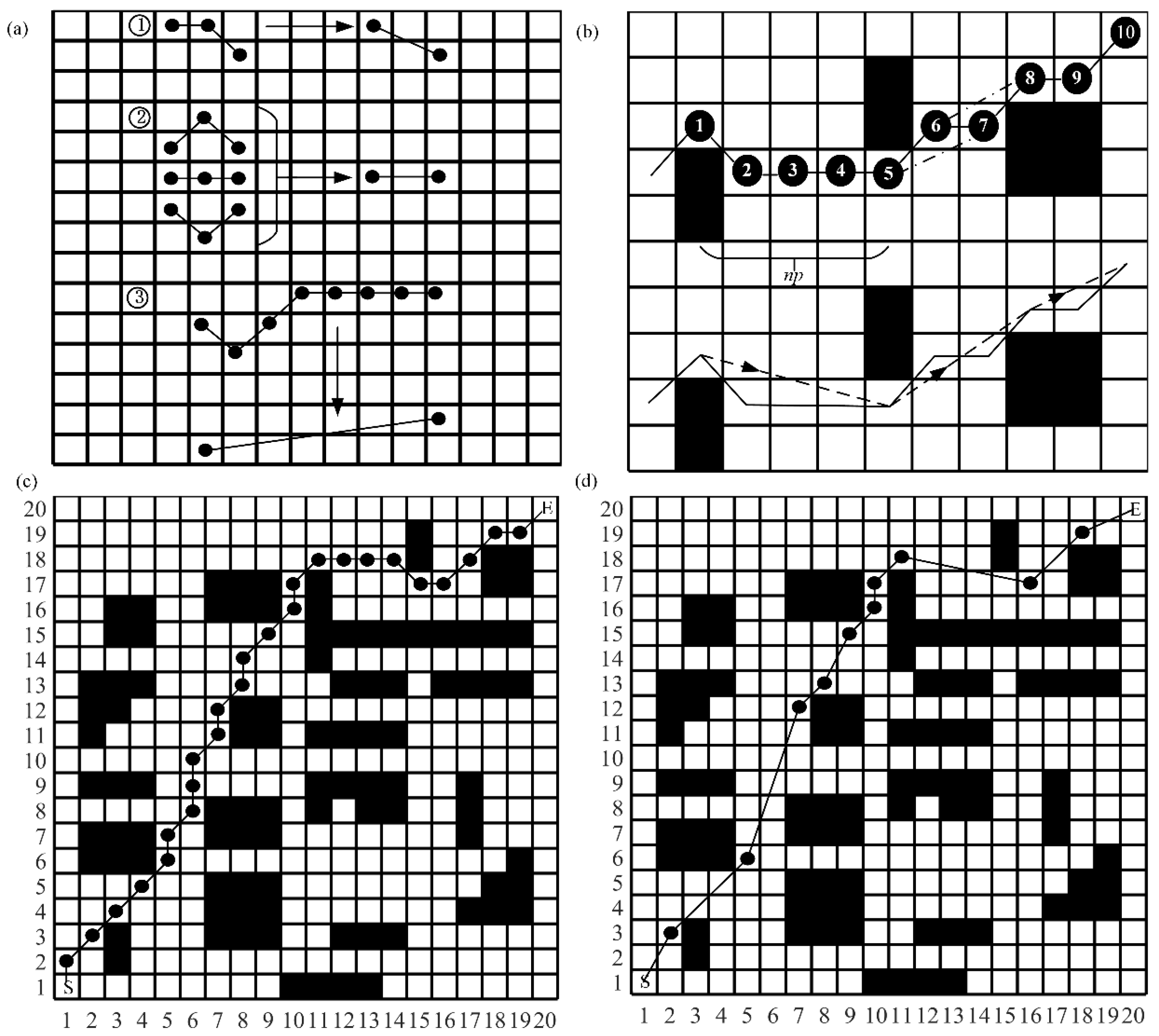
4. Path Planning Based on IBOA
4.1. Application of IBOA in Path Planning
4.2. Solution of Redundant Routes in Path Planning
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sathiya, V.; Chinnadurai, M. Evolutionary algorithms-based multi-objective optimal mobile robot trajectory planning. Robotica 2019, 37, 1363–1382. [Google Scholar] [CrossRef]
- Wang, J.; Meng, M.Q.H.; Khatib, O. Optimal motion planning for mobile robots. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2063–2073. [Google Scholar] [CrossRef]
- Li, K.; Hu, Q.; Liu, J. Path planning of mobile robot based on improved multiobjective genetic algorithm. Wirel. Commun. Mob. Comput. 2021, 2021, 8836615. (In Chinese) [Google Scholar] [CrossRef]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Chi, W.; Wang, C.; Wang, J.; Meng, M.Q.H. Risk-DTRRT-based optimal motion planning algorithm for mobile robots. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1271–1288. [Google Scholar] [CrossRef]
- Bozek, P.; Karavaev, Y.L.; Ardentov, A.A.; Yefremov, K.S. Neural network control of a wheeled mobile robot based on optimal trajectories. Int. J. Adv. Robot. Syst. 2020, 17, 172988142091607–172988142091616. [Google Scholar] [CrossRef]
- Zahid, T.; Kausar, Z.; Shah, M.F.; Saeed, M.T.; Pan, J. An intelligent hybrid control to enhance applicability of mobile robots in cluttered environments. IEEE Access 2021, 9, 50151–50162. [Google Scholar] [CrossRef]
- Alireza, M.; Vincent, D.; Tony, W. Experimental study of path planning problem using EMCOA for a holonomic mobile robot. J. Syst. Eng. Electron. 2021, 32, 1450–1462. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Li, X.; Liu, F.; He, Z.; Yao, Y.; Ruan, H.; Zhang, T. MPC-based high-speed trajectory tracking for 4WIS robot. ISA Trans. 2022, 123, 413–424. [Google Scholar] [CrossRef]
- Ali, H.; Gong, D.; Wang, M.; Dai, X. Path planning of mobile robot with improved ant colony algorithm and MDP to produce smooth trajectory in grid-based environment. Front. Neurorobot. 2020, 14, 44–56. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-Del-Pulgar, C.J.; García-Cerezo, A. Path planning for autonomous mobile robots: A review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Paikray, H.K.; Das, P.K.; Panda, S. Optimal multi-robot path planning using particle swarm optimization algorithm improved by sine and cosine algorithms. Arab. J. Sci. Eng. 2021, 46, 3357–3381. [Google Scholar] [CrossRef]
- Parque, V.; Miyashita, T. Smooth curve fitting of mobile robot trajectories using differential evolution. IEEE Access 2020, 8, 82855–82866. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, D. A new method on motion planning for mobile robots using jump point search and Bezier curves. Int. J. Adv. Robot. Syst. 2021, 18, 172988142110192–172988142110204. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A consolidated review of path planning and optimization techniques: Technical perspectives and future directions. Electronics 2021, 10, 2250–2287. [Google Scholar] [CrossRef]
- Muthukumaran, S.; Sivaramakrishnan, R. Optimal path planning for an autonomous mobile robot using dragonfly algorithm. Int. J. Simul. Model. 2019, 18, 397–407. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, L. Application of improved ant colony optimization in mobile robot trajectory planning. Math. Biosci. Eng. 2020, 17, 6756–6774. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wan, Y.; Wang, Y.; Guan, X.; Ren, W.; Li, G. Improved hybrid A* path planning method for spherical mobile robot based on pendulum. Int. J. Adv. Robot. Syst. 2021, 18, 172988142199295–172988142199308. [Google Scholar] [CrossRef]
- Zhou, H.; Xiong, H.L.; Liu, Y.; Tan, N.; Chen, L. Trajectory planning algorithm of UAV based on system positioning accuracy constraints. Electronics 2020, 9, 250–270. [Google Scholar] [CrossRef]
- Precup, R.; Voisan, E.; Petriu, E.M.; Tomescu, M.L.; David, R.; Szedlak-Stinean, A.; Roman, R. Grey wolf optimizer-based approaches to path planning and fuzzy logic-based tracking control for mobile robots. Int. J. Comput. Commun. Control 2020, 15, 1–17. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Zhou, Q.; Yuan, Z.Z. Research on the Digital Fountain Codes and Decodes Algorithm Based upon Kent Mapping. J. Syst. Sci. Math. Sci. 2011, 31, 731–741. (In Chinese) [Google Scholar]
- Falcó, A.; Hilario, L.; Montés, N.; Mora, M.C.; Nadal, E. A path planning algorithm for a dynamic environment based on proper generalized decomposition. Mathematics 2020, 8, 2245–2255. [Google Scholar] [CrossRef]
- Kim, H.; Kim, B.K. Energy-optimal transport trajectory planning and online trajectory modification for holonomic robots. Asian J. Control 2021, 23, 2185–2200. [Google Scholar] [CrossRef]
- Xu, L.; Fu, W.H.; Jiang, W.H.; Li, Z.T. Mobile robots path planning based on 16-directions 24-neighborhoods improved ant colony algorithm. Control Decis. 2021, 36, 1137–1146. (In Chinese) [Google Scholar]
- Wang, W.J.; Tao, Q.; Cao, Y.T.; Wang, X.H.; Zhang, X. Robot time-optimal trajectory planning based on improved cuckoo search algorithm. IEEE Access 2020, 8, 86923–86933. [Google Scholar] [CrossRef]
- He, Q.; Luo, S.H. Chimp optimization algorithm based on hybrid improvement strategy and its mechanical application. Control Des. 2021, 1–11. (In Chinese) [Google Scholar] [CrossRef]
- Yang, H.; Qi, J.; Miao, Y.; Sun, H.; Li, J. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization. IEEE Trans. Ind. Electron. 2019, 66, 8557–8566. [Google Scholar] [CrossRef]
- Muhammad, A.; Ali, M.A.H.; Turaev, S.; Shanono, I.H.; Hujainah, F.; Zubir, M.N.M.; Faiz, M.K.; Faizal, E.R.M.; Abdulghafor, R. Novel algorithm for mobile robot path planning in constrained environment. Comput. Mater. Continua. 2022, 71, 2697–2719. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, C.; Sun, P.; Liu, C. Safe and smooth motion planning for Mecanum-wheeled robot using improved RRT and cubic spline. Arab. J. Sci. Eng. 2020, 45, 3075–3090. [Google Scholar] [CrossRef]










| Function | V_no | Range | fmin |
|---|---|---|---|
| 100 | [−100, 100] | 0 | |
| 100 | [−100, 100] | 0 | |
| 100 | [−100, 100] | 0 | |
| 100 | [−5.12, 5.12] | 0 | |
| 100 | [−32, 32] | 0 | |
| 100 | [−600, 600] | 0 |
| F | BOA | IBOA | ||
|---|---|---|---|---|
| ave | std | ave | std | |
| F1 | 2.4432 × 10−5 | 2.5048 × 10−6 | 3.7334 × 10−9 | 1.74 × 10−9 |
| F2 | 0.0018123 | 0.00013418 | 9.406 × 10−7 | 4.6296 × 10−7 |
| F3 | 3.035 × 10−5 | 2.2703 × 10−6 | 3.9923 × 10−9 | 2.6031 × 10−9 |
| F4 | 2.2523 | 7.8826 | 1.8149 × 10−7 | 5.9147 × 10−7 |
| F5 | 0.036973 | 0.0036808 | 0.00012988 | 0.00027588 |
| F6 | 0.017841 | 0.0032376 | 9.0913 × 10−7 | 1.0834 × 10−6 |
| Value | IBOA | BOA | GA |
|---|---|---|---|
| Max | 31.7989898700000 | 36.6274170000000 | 36.9705627500000 |
| Min | 30.9705627500000 | 31.7989898700000 | 31.7989898700000 |
| Average | 31.7161471580000 | 33.7989898730000 | 33.1504617360000 |
| Median | 31.7989898700000 | 33.2132034400000 | 32.3847763100000 |
| Value | IBOA | BOA | GA |
|---|---|---|---|
| Max | 68.5269119345812 | 67.9411254969543 | 73.0121933088197 |
| Min | 63.8406204335659 | 65.5979797500000 | 65.8406204300000 |
| Average | 65.7778787337689 | 66.8766594032423 | 69.4440692218820 |
| Median | 65.8406204335659 | 66.7695526217004 | 69.6984848100000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, R.; Xiao, P.; Shu, D.; Sun, Y.; Jiang, M. Application of Improved Butterfly Optimization Algorithm in Mobile Robot Path Planning. Electronics 2023, 12, 3424. https://doi.org/10.3390/electronics12163424
Zhai R, Xiao P, Shu D, Sun Y, Jiang M. Application of Improved Butterfly Optimization Algorithm in Mobile Robot Path Planning. Electronics. 2023; 12(16):3424. https://doi.org/10.3390/electronics12163424
Chicago/Turabian StyleZhai, Rongjie, Ping Xiao, Da Shu, Yongjiu Sun, and Min Jiang. 2023. "Application of Improved Butterfly Optimization Algorithm in Mobile Robot Path Planning" Electronics 12, no. 16: 3424. https://doi.org/10.3390/electronics12163424
APA StyleZhai, R., Xiao, P., Shu, D., Sun, Y., & Jiang, M. (2023). Application of Improved Butterfly Optimization Algorithm in Mobile Robot Path Planning. Electronics, 12(16), 3424. https://doi.org/10.3390/electronics12163424





