Global Prescribed-Time Stabilization of Input-Quantized Nonlinear Systems via State-Scale Transformation

Abstract

The problem of global prescribed-time stabilization is reported in this paper for a kind of uncertain nonlinear system in power normal form. Compared with related work, the distinct characteristics of this study are that the system under consideration has an input-quantized actuator, and the prescribed time convergence of the system states is wanted. To meet these special requirements, a novel state-scaling transformation (SST) is firstly given to convert the prescribed-time stabilization of original systems to the asymptotic stabilization of the transformed one. Then, under the new framework of equivalent transformation, a quantized state feedback controller that ensures the achievement of the performance requirements is developed by using a power integrator (API) technique. Finally, the simulation results of a liquid-level system are provided to confirm the efficacy of the proposed approach.

1. Introduction

It is well known that all practical systems are inherently nonlinear systems because of the appearance of unmodel dynamics and disturbances. However, unlike linear systems it is very difficult or even impossible to find a unified solution to nonlinear systems due to the complexity of their structures. Fortunately, their special canonical structures can be exploited to obtain meaningful results. As a result, in the past decades researchers have began to focus on nonlinear systems with different special structures, such as strict-feedback nonlinear systems, pure-feedback nonlinear systems, and non-strict feedback nonlinear systems. Recently, power normal nonlinear systems (PNNSs) as a general structure of nonlinear dynamic systems have received lots of attention because of their significant values both in theory and practice [1,2]. But the general structure also leads to the control of PNNSs being challenging because of their distinctive feature of the non-existence and/or the lack of controllability/observability of the Jacobian linearization around the origin, which blocks the applications of commonly used methods such as backstepping and feedback linearization. Mainly thanks to the technique of adding a power integrator (API) [3], which develops the traditional backstepping technique by introducing the feedback-domination mechanism and contributes to a technological breakthrough in coping with such intrinsic obstacles, the asymptotic stabilizing/tracking control of PNNSs has made tremendous progress during an infinite time interval, for example, refer to [4,5,6,7,8,9,10,11,12] and the references therein.

On the other hand, to meet the practical needs the research on finite-time control has become popular recently because of the superior properties of the finite-time stable system, such as fast response, good robustness, and disturbance rejection. Especially, since the milestone work of the Lyapunov finite-time stability theorem was established in [13], many significant results have been obtained [14,15,16,17,18,19,20,21,22,23]. Note that the settling time functions achieved in the above-mentioned results depend on initial system conditions. This means that the settling time may increase to an unacceptable degree as the magnitude of initial conditions increases. To overcome this faultiness, Andrieu et al., in [24] put forward the notion of fixed-time stability, which requires that the upper bound of the associated settling time function exists regardless of the initial system conditions. Under the new framework of fixed-time stability, a great number of results have appeared to study the control designs of linear/nonlinear systems. Generally speaking, the existing methods of such fixed-time control designs can be classified into two kinds: one is the bi-limit homogeneous method [24,25], and the other is the Lyapunov-based method [25,26,27,28,29,30,31,32,33,34,35,36]. However, it is important to note that both two methods have some inherent shortcomings. Namely in the former, the upper bound of the settling time (UBST) function exists but is unknown, and in the latter, the UBST is bounded and adjustable, but it is difficult or even impossible to be prespecified discretionarily in line with requirements because the settling time function derived from the Lyapunov-based method currently relies on a few design parameters, whose choices are actually not easy to satisfy the pregiven settling time.

However, prespecifiable settling time is indeed expected by some practice applications, e.g., missile guidance [37]. This fact urges that prescribed/predefined-time control has become an active research topic [34,35,36,37,38,39,40,41]. Especially, drawing support from scaling the state by a function that grows unboundedly toward the terminal time, a computationally singular controller was given for prescribed-time stabilization (PTS) of Brunovsky systems in [42]. The extension of this technique was further refined in [43], where a novel state-scaling transformation (SST) was proposed to overcome the computationally singular problem and provided a solution to the problem of PTS for strict-feedback (switched) nonlinear systems. However, the powers of the studied systems are identically equal to 1 (i.e., $p_i=1$) required in [43], which certainly limits their application because many practical systems are described by PNNSs (refer to the typical example of liquid-level system given in Section 4). Moreover, another common drawback of the aforementioned results is that the effect of the quantized input is ignored.

As is known to all, most of the control tasks of modern engineering application are achieved based on network information transfer, which means that the actual control signals in such systems must be quantized to overcome the communication constraints including the limited data transmission rate of communication channels and their limited bandwidth. However, the application of quantizers inevitably introduces quantization errors, which seriously degrade the system’s performance and prevent the implementation of quantizers [44,45,46,47]. In addition, it should be mentioned that the appearance of quantized input nonlinearity will destroy system structure characteristics, and thus the existing methods cannot be directly applied. To date, few prescribed-time control techniques have been reported for the quantized nonlinear systems. Therefore, the following question naturally arises: For a PNNS with input quantization, is it possible to devise a controller to achieve its PTS? If possible, how can one design it?

This paper focuses on addressing the problem of global PTS for a kind of PNNSs with quantized input and giving an affirmative answer to the above question. The significant contributions are underlined as follows.

(i)

Fully taking into consideration the practical system requirements, both quantized input and prescribed-time convergence are included firstly in this paper.

(ii)

A novel SST is proposed to change the original PTS problem into the problem of asymptotic stabilization of the transformed one.

(iii)

Under a new homogeneous-like restricted condition on system growth, a systematic design method ensuring the achievement of the performance requirements is proposed by delicately utilizing the API technique.

(iv)

As an application of the proposed theoretical result, the problem of PTS with quantized input for a liquid-level system is solved.

Notations. The notations adopted in this paper are fairly standard. Specifically, for a vector $z={(z_1,\dots ,z_n)}^T\in {\mathbb{R}}^n$, denote ${\overline{z}}_j=(z_1,$$\dots ,z_j{)}^T\in {\mathbb{R}}^j$, $j=1,\dots ,n$, and the function ${\lceil z\rceil }^{\delta }$ is defined as ${\lceil z\rceil }^{\delta }=\mathrm{sign}\left(z\right){\left|z\right|}^{\delta }$ where the $\mathrm{sign}(·)$ is the signum function.

2. Problem Formulation and Preliminaries

2.1. Problem Formulation

Consider a HONS as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{z}}_1=d_1\left(t\right){⌈z_2⌉}^{q_1}+f_1\left(t,z_1\right),\hfill \\ {\dot{z}}_2=d_2\left(t\right){⌈z_3⌉}^{q_2}+f_2\left(t,{\overline{z}}_2\right),\hfill \\ ⋮\hfill \\ {\dot{z}}_{n-1}=d_{n-1}\left(t\right){⌈z_n⌉}^{q_{n-1}}+f_{n-1}\left(t,{\overline{z}}_{n-1}\right),\hfill \\ {\dot{z}}_n=d_n\left(t\right)Q\left(u\right)+f_n\left(t,{\overline{z}}_n\right),\hfill \end{array}\right.\end{array}$$

(1)

where ${\overline{z}}_i=(z_1,$$\dots ,z_i{)}^T\in {\mathbb{R}}^i$ is the system state (vector). $d_i\in \mathbb{R}$, $q_i\in {\mathbb{R}}^{+}$ (with $q_n=1$), $i=1,\dots ,n$ are the control coefficients and the power orders of the system, respectively. $f_i\in \mathbb{R}$ ($i=1,\dots ,n$) are uncertain continuous functions satisfying $f_i(t,0)=0$. $u\in \mathbb{R}$ is the control input to be designed, and Q denotes the mapping relationship between the designed control u and quantized input $Q\left(u\right)$, which is governed by $Q\left(u\right)\in \mathbb{R}$, which denotes the quantized input described by

$$Q\left(u\right)=Q_1\left(t\right)u+Q_2\left(t\right),$$

(2)

where

$$Q_1\left(t\right)=\left\{\begin{array}{ccc}1+{\vartheta }_1\delta ,\hfill & & {\displaystyle \left|u\right|\ge u_{min},}\\ 1,\hfill & & {\displaystyle \left|u\right|<u_{min},}\end{array}\right.$$

(3)

and

$$Q_2\left(t\right)=\left\{\begin{array}{ccc}0,\hfill & & {\displaystyle \left|u\right|\ge u_{min},}\\ {\vartheta }_2{u}_{min},\hfill & & {\displaystyle \left|u\right|<u_{min},}\end{array}\right.$$

(4)

where $0\le \delta <1$ and $u_{min}$ are known parameters and $-1\le {\vartheta }_j\le 1$, $j=1,2$ are unknown parameters of the quantizer (2).

Remark 1.

It is worth noting that many practical quantizers, such as logarithmic quantizer, hysteresis quantizer, and uniform quantizer, belong to the considered class described by (2). For instance, consider the logarithmic quantizer used in [44,45], which is modeled as

$$Q\left(u\right)=\left\{\begin{array}{ccc}{u}_j,\hfill & & {\displaystyle \frac{u_j}{1+\delta }<u\le \frac{u_j}{1-\delta },}\\ 0,\hfill & & {\displaystyle 0\le u<\frac{d}{1+\delta },}\\ -Q(-u),\hfill & & u<0,\end{array}\right.$$

(5)

where $u_j={\varsigma }^{1-j}d$ ($j=1,2,\dots$), with the parameters being selected to satisfy $d>0$ and $0<\varsigma <1$. $\delta =\frac{1-\varsigma }{1+\varsigma }$ determines the quantization density of $Q\left(u\right)$. $u_0=\frac{d}{1+\delta }$ determines the size of the dead zone for $Q\left(u\right)$.

Clearly, this quantizer is in the shape of (2) with ${\vartheta }_1=(Q\left(u\right)-u)/\left(\delta u\right)$ and $u_{min}=u_0$.

The aim of this paper is to present a quantized state feedback control mechanism that stabilizes system (1) within prescribed finite time under the following wild assumptions.

Assumption 1.

For $i=1,\dots ,n$, there are smooth functions ${\phi }_i\ge 0$ and a constant $\tau >0$ such that

$$\begin{array}{c}{\displaystyle |f_i(t,{\overline{z}}_i)|\le {\phi }_i\left({\overline{z}}_i\right)\sum _{j=1}^i{\left|z_j\right|}^{\frac{{\lambda }_i-\tau }{{\lambda }_j}},}\hfill \end{array}$$

(6)

where ${\lambda }_i$’s are recursively defined by

$$\begin{array}{c}{\lambda }_{n+1}=\tau ,q_i{\lambda }_{i+1}={\lambda }_i-\tau \ge 0,i=1,\dots ,n-1.\hfill \end{array}$$

(7)

Assumption 2.

There are (known) positive constants ${\underline{d}}_i$ and ${\overline{d}}_i$, $i=1,\dots ,n$ such that ${\underline{d}}_i\le d_i\left(t\right)\le {\overline{d}}_i$.

Remark 2.

Assumption 1 is a new type of condition of homogeneous-growth-like because in it ${\lambda }_i$’s are radically different from the conventional ones used in [4,5,6,7,8,9,10,11,12,15,16,17,18,19,20,21,22,23] where they are recursively defined by ${\lambda }_1=1,q_i{\lambda }_{i+1}={\lambda }_i-\tau \ge 0,i=1,\dots ,n$. In addition, it should be mentioned that it is reasonable in engineering practice to impose the control coefficients with the known boundedness in Assumption 2. Similar requirements can be found in the existing literature [21,22,23,32,33,46].

2.2. Preliminaries

Consider the nonlinear system

$$\begin{array}{c}\dot{z}=f(t,z),z\left(0\right)=z_0\in {\mathbb{R}}^n,\hfill \end{array}$$

(8)

where $f:\mathbb{R}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is continuous with respect to z and satisfies $f(t,0)=0$.

Definition 1

([26]). The origin of system (8) is globally finite-time stable if it is globally asymptotically stable and for any $z_0\in {\mathbb{R}}^n$, and a settling time function $T:{\mathbb{R}}^n\setminus \left\{0\right\}\to (0,\infty )$ exists such that each solution $z(t,z_0)$ of (8) satisfies $z(t,z_0)=0$, $\forall t\ge T\left(z_0\right)$.

Definition 2

([26]). The origin of system (8) is globally fixed-time stable if it is globally finite-time stable and the settling-time function $T\left(z_0\right)$ is bounded by a positive constant $\forall z_0\in \mathbb{R}$.

Definition 3.

The origin of system (8) is globally prescribed-time stable if it is globally fixed-time stable and for any prescribed finite time $T_c>0$ there is a tunable designing parameter $\vartheta \in \mathbb{R}$ such that $T\left(z_0\right)\le T_c$, $\forall z_0\in \mathbb{R}$.

Lemma 1

([4]). For any $x,y\in \mathbb{R}$, and a constant $a\ge 1$, one obtains (i) ${|x+y|}^a\le 2^{a-1}|x^a+y^a|$; (ii) $\left(\right|x|+{\left|y\right|)}^{1/a}\le {\left|x\right|}^{1/q}+{\left|y\right|}^{1/a}\le 2^{(a-1)/a}\left(\right|x|+{\left|y\right|)}^{1/a}$.

Lemma 2

([4]). If $c,d$ are positive constants, then for any real-valued function one obtains $\delta (u,v)>0$, ${\left|u\right|}^c{\left|v\right|}^d\le \frac{c}{c+d}{\delta (u,v)\left|u\right|}^{c+d}+\frac{d}{c+d}{\delta }^{-c/d}(u,v){\left|v\right|}^{c+d}$.

Lemma 3

([48]). Let $0<p\le 1$ and $a>0$ be constants. Then, for any $u,v\in \mathbb{R}$ there is ${|\lceil u\rceil }^{aq}-{\lceil v\rceil }^{ap}|\le 2^{1-p}{|{\lceil u\rceil }^a-{\lceil v\rceil }^a|}^p.$

3. Prescribed-Time Stabilization

In this section, we propose a constructive design mechanism of the state feedback controller, which can stabilize system (1) within any prescribed finite time $T_c>0$. The design consists of defining such a stabilizing controller as a piecewise one. Specially, when $t\in [0,T_c)$ we first design a non-autonomous controller to force the states tending to the origin regardless of initial conditions within $T_c$; thereafter, we design an autonomous controller to keep the states at the origin.

3.1. Controller Design of $t\in [0,T_c)$

Firstly, to shift the original PTS to the framework of asymptotic stabilization, the following novel coordinate transformation of state-scaling is introduced:

$$\begin{array}{c}{\zeta }_i={\Gamma }^{(1+c){\lambda }_i}{z}_i,i=1,\dots ,n,v={\Gamma }^{(1+c){\lambda }_{n+1}}Q\left(u\right),\hfill \end{array}$$

(9)

where v is the input of the transformed system and $c\ge (1/\tau )-1$ is a design constant and $\Gamma$ is defined as

$${\displaystyle \Gamma =\frac{T_c}{T_c-t}.}$$

(10)

Remark 3.

It is obvious that $\Gamma (·)$ is monotonically increasing on $[0,T_c)$ and satisfies $\Gamma \left(0\right)=1,\Gamma \left(T_c\right)=+\infty$.

From (9), system (1) is redescribed as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\zeta }}_1={\Gamma }^{(1+c)\tau }\left(d_1{⌈{\zeta }_2⌉}^{q_1}+g_1\left({\zeta }_1\right)\right),\hfill \\ {\dot{\zeta }}_2={\Gamma }^{(1+c)\tau }\left(d_2{⌈{\zeta }_3⌉}^{q_2}+g_2\left({\overline{\zeta }}_2\right)\right),\hfill \\ ⋮\hfill \\ {\dot{\zeta }}_{n-1}={\Gamma }^{(1+c)\tau }\left(d_{n-1}{⌈{\zeta }_n⌉}^{q_{n-1}}+g_{n-1}\left({\overline{\zeta }}_{n-1}\right)\right),\hfill \\ {\dot{\zeta }}_n={\Gamma }^{(1+c)\tau }\left(d_{n}Q\left(v\right)+g_n\left({\overline{\zeta }}_n\right)\right),\hfill \end{array}\right.\end{array}$$

(11)

where

$$\begin{array}{c}{\displaystyle g_i\left({\overline{\zeta }}_i\right)={\zeta }_i\frac{(1+c){\lambda }_i\dot{\Gamma }}{{\Gamma }^{1+(1+c)\tau }}+{\Gamma }^{(1+c)({\lambda }_i-\tau )}{f}_i\left({\overline{z}}_i\right),i=1,\dots ,n,}\hfill \end{array}$$

(12)

Proposition 1.

For $i=1,\dots ,n$, some smooth functions ${\overline{\phi }}_i\left({\overline{\zeta }}_i\right)\ge 0$ exist such that

$$\begin{array}{c}{\displaystyle |g_i\left({\overline{\zeta }}_i\right)|\le {\overline{\phi }}_i\left({\overline{\zeta }}_i\right)\sum _{j=1}^i{\left|{\zeta }_j\right|}^{\frac{{\lambda }_i-\tau }{{\lambda }_j}}.}\hfill \end{array}$$

(13)

Proof. 

See Appendix A. □

Next, a state feedback controller for the asymptotic stabilization of system (11) is designed for the case of $t\in [0,T_c)$ by employing the API technique.

Step 1. Take $\rho \ge {max}_{1\le i\le n}\left\{{\lambda }_i\right\}$ as a real number and the Lyapunov function $V_1$ for this step as

$$\begin{array}{c}{\displaystyle V_1=W_1={\int }_0^{{\zeta }_1}{⌈{\lceil s\rceil }^{\frac{\rho }{{\lambda }_1}}-0⌉}^{\frac{2\rho -{\lambda }_1}{\rho }}ds.}\hfill \end{array}$$

(14)

Applying Assumptions 1 and 2 and (13) produces

$$\begin{array}{c}{\displaystyle {\dot{V}}_1={\Gamma }^{(1+c)\tau }{\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}\left(d_1{\lceil {\zeta }_2\rceil }^{q_1}+g_1\right)}\hfill \\ {\displaystyle \le {\Gamma }^{(1+c)\tau }\left({\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}{d}_1{({\zeta }_2\rceil }^{q_1}-{\lceil {\zeta }_2^{*}\rceil }^{q_1})+d_1{\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}{\lceil {\zeta }_2^{*}\rceil }^{q_1}+{\left|{\pi }_1\right|}^{\frac{2\rho -{\lambda }_1}{\rho }}{\overline{\phi }}_1\right),}\hfill \end{array}$$

(15)

where ${\pi }_1={\lceil {\zeta }_1\rceil }^{\frac{\rho }{{\lambda }_1}}$, and ${\zeta }_2^{*}$ is the virtual controller of ${\zeta }_2$ to be specified.

Take the virtual controller ${\zeta }_2^{*}$ as

$$\begin{array}{c}{\displaystyle {\zeta }_2^{*}=-{\lceil {\pi }_1\rceil }^{\frac{{\lambda }_2}{\rho }}{\beta }_1^{\frac{{\lambda }_2}{\rho }}\left({\zeta }_1\right),}\hfill \end{array}$$

(16)

where

$$\begin{array}{c}{\displaystyle {\beta }_1\left({\zeta }_1\right)\ge {\left(\frac{n+{\overline{\phi }}_1}{{\underline{d}}_1}\right)}^{\frac{\rho }{q_1{\lambda }_2}},}\hfill \end{array}$$

(17)

is a smooth function. Then, by substituting (16) and (17) into (15), one obtains

$$\begin{array}{c}{\displaystyle {\dot{V}}_1\le -n{\Gamma }^{(1+c)\tau }{\left|{\pi }_1\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{d}_1{\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}\left({\lceil {\zeta }_2\rceil }^{q_1}-{\lceil {\zeta }_2^{*}\rceil }^{q_1}\right).}\hfill \end{array}$$

(18)

Step 2. Define ${\pi }_2={\lceil {\zeta }_2\rceil }^{\frac{\rho }{{\lambda }_2}}-{\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}$ and take the Lyapunov function $V_2=V_1+W_2$ with

$$\begin{array}{c}{\displaystyle W_2={\int }_{{\zeta }_2^{*}}^{{\zeta }_2}{⌈{\lceil s\rceil }^{\frac{\rho }{{\lambda }_2}}-{\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}⌉}^{\frac{2\rho -{\lambda }_2}{\rho }}ds.}\hfill \end{array}$$

(19)

From

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial W_2}{\partial {\zeta }_2}={\lceil {\pi }_2\rceil }^{\frac{2\rho -{\lambda }_2}{\rho }},}\hfill \\ {\displaystyle \frac{\partial W_2}{\partial {\zeta }_1}=-\frac{2\rho -{\lambda }_2}{\rho }\frac{\partial \left({\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}\right)}{\partial {\zeta }_1}\times {\int }_{{\zeta }_2^{*}}^{{\zeta }_2}{\left|{\lceil s\rceil }^{\frac{\rho }{{\lambda }_2}}-{⌈{\zeta }_2^{*}⌉}^{\frac{\rho }{{\lambda }_2}}\right|}^{\frac{\rho -{\lambda }_2}{\rho }}ds,}\hfill \end{array}\right.$$

(20)

a direct calculation gives

$$\begin{array}{ccc}{\displaystyle {\dot{V}}_2}\hfill & \le \hfill & -n{\Gamma }^{(1+c)\tau }{\left|{\pi }_1\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{d}_1{\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}\left({\lceil {\zeta }_2\rceil }^{q_1}-{\lceil {\zeta }_2^{*}\rceil }^{q_1}\right)\hfill \\ \hfill & \hfill & {\displaystyle +\frac{\partial W_2}{\partial {\zeta }_1}{\Gamma }^{(1+c)\tau }(d_1{\lceil {\zeta }_2\rceil }^{q_1}+g_1)+\frac{\partial W_2}{\partial {\zeta }_2}{\Gamma }^{(1+c)\tau }(d_2{\lceil {\zeta }_3\rceil }^{q_2}+g_2)}\hfill \\ \hfill & \le \hfill & -n{\Gamma }^{(1+c)\tau }{\left|{\pi }_1\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{d}_1{\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}\left({\lceil {\zeta }_2\rceil }^{q_1}-{\lceil {\zeta }_2^{*}\rceil }^{q_1}\right)\hfill \\ \hfill & \hfill & {\displaystyle +{\Gamma }^{(1+c)\tau }\left(\frac{\partial W_2}{\partial {\zeta }_1}(d_1{\lceil {\zeta }_2\rceil }^{q_1}+g_1)+d_2{\lceil {\pi }_2\rceil }^{\frac{2\rho -{\lambda }_2}{\rho }}\left({\lceil {\zeta }_3\rceil }^{q_2}-{\lceil {\zeta }_3^{*}\rceil }^{q_2}\right)\right.}\hfill \\ \hfill & \hfill & \left.+d_2{\lceil {\pi }_2\rceil }^{\frac{2\rho -{\lambda }_2}{\rho }}{\lceil {\zeta }_3^{*}\rceil }^{q_2}+{\lceil {\pi }_2\rceil }^{\frac{2\rho -{\lambda }_2}{\rho }}{g}_2\right),\hfill \end{array}$$

(21)

where ${\zeta }_3^{*}$ is the virtual controller of ${\zeta }_3$ to be designed later. To continue, the following estimates for some terms of (21) are needed.

First, based on the definitions of ${\pi }_j$ and ${\zeta }_j^{*}$ ($j=1,2$) and Lemma 3, one obtains

$$\begin{array}{ccc}{\displaystyle \left|{\lceil {\zeta }_2\rceil }^{q_1}-{\lceil {\zeta }_2^{*}\rceil }^{q_1}\right|}\hfill & =\hfill & \left|{\left({\lceil {\zeta }_2\rceil }^{\frac{\rho }{{\lambda }_2}}\right)}^{\frac{{\lambda }_2{q}_1}{\rho }}-{\left({\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}\right)}^{\frac{{\lambda }_2{q}_1}{\rho }}\right|\hfill \\ \hfill & \le \hfill & 2^{1-\frac{{\lambda }_2{q}_1}{\rho }}|{\lceil {\zeta }_2\rceil }^{\frac{\rho }{{\lambda }_2}}-{\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}{|}^{\frac{{\lambda }_2{q}_1}{\rho }}\hfill \\ \hfill & =\hfill & 2^{1-\frac{{\lambda }_2{q}_1}{\rho }}{\left|{\pi }_2\right|}^{\frac{{\lambda }_2{q}_1}{\rho }}.\hfill \end{array}$$

(22)

Thus, from (22), Assumption 2 and Lemma 2, it is obtained that

$$\begin{array}{ccc}{\displaystyle d_1{\lceil {\pi }_1\rceil }^{\frac{2\rho -{\lambda }_1}{\rho }}\left({\lceil {\zeta }_2\rceil }^{q_1}-{\lceil {\zeta }_2^{*}\rceil }^{q_1}\right)}\hfill & \le \hfill & {\displaystyle 2^{1-\frac{{\lambda }_2{q}_1}{\rho }}{\overline{d}}_1|{\pi }_1{|}^{\frac{2\rho -{\lambda }_1}{\rho }}{|{\pi }_2|}^{\frac{{\lambda }_2{q}_1}{\rho }}}\hfill \\ \hfill & \le \hfill & {\displaystyle \frac{1}{3}|{\pi }_1{|}^{\frac{2\rho -\tau }{\rho }}+{|{\pi }_2|}^{\frac{2\rho -\tau }{\rho }}{\varrho }_{21},}\hfill \end{array}$$

(23)

where ${\varrho }_{21}\ge 0$ is a smooth function.

Secondly, from (13) and Lemma 1, one obtains

$$\begin{array}{ccc}|g_2|\hfill & \le \hfill & {\displaystyle {\overline{\phi }}_2\left(|{\zeta }_1{|}^{\frac{{\lambda }_2-\tau }{{\lambda }_1}}+{|{\zeta }_2|}^{\frac{{\lambda }_2-\tau }{{\lambda }_2}}\right)}\hfill \\ \hfill & \le \hfill & {\displaystyle {\overline{\phi }}_2\left(|{\pi }_1{|}^{\frac{{\lambda }_2-\tau }{\rho }}+|{\pi }_2{|}^{\frac{{\lambda }_2-\tau }{\rho }}+{\beta }_1^{\frac{{\lambda }_2-\tau }{\rho }}{|{\pi }_1|}^{\frac{{\lambda }_2-\tau }{\rho }}\right)}\hfill \\ \hfill & \le \hfill & {\tilde{\phi }}_2\left(|{\pi }_1{|}^{\frac{{\lambda }_2-\tau }{\rho }}+{\left|{\pi }_2\right|}^{\frac{{\lambda }_2-\tau }{\rho }}\right),\hfill \end{array}$$

(24)

where ${\tilde{\phi }}_2\ge$ $\left(1+{\beta }_1^{\frac{{\lambda }_2-\tau }{\rho }}\right){\overline{\phi }}_2$ is a smooth function.

Using (24) and Lemma 2 yields

$$\begin{array}{ccc}{\lceil {\pi }_2\rceil }^{\frac{2\rho -{\lambda }_2}{\rho }}{g}_2\hfill & \le \hfill & {\lceil {\pi }_2\rceil }^{\frac{2\rho -{\lambda }_2}{\rho }}{\tilde{\phi }}_2({\left|{\pi }_1\right|}^{\frac{{\lambda }_2-\tau }{\rho }}+{\left|{\pi }_2\right|}^{\frac{{\lambda }_2-\tau }{\rho }})\hfill \\ \hfill & \le \hfill & \frac{1}{3}{\left|{\pi }_1\right|}^{\frac{2\rho -\tau }{\rho }}+{\left|{\pi }_2\right|}^{\frac{2\rho -\tau }{\rho }}{\varrho }_{22},\hfill \end{array}$$

(25)

where ${\varrho }_{22}\ge 0$ is a smooth function.

Finally, note that

$$\begin{array}{ccc}{\displaystyle \frac{2\rho -{\lambda }_2}{\rho }{\int }_{{\zeta }_2^{*}}^{{\zeta }_2}{\left|{\lceil s\rceil }^{\frac{\rho }{{\lambda }_2}}-{⌈{\zeta }_2^{*}⌉}^{\frac{\rho }{{\lambda }_2}}\right|}^{\frac{\rho -{\lambda }_2}{\rho }}ds}\hfill & \le \hfill & {\displaystyle \frac{2\rho -{\lambda }_2}{\rho }|{\pi }_2{|}^{\frac{\rho -{\lambda }_2}{\rho }}|{\zeta }_2-{\zeta }_2^{*}|}\hfill \\ \hfill & \le \hfill & {\displaystyle \frac{2\rho -{\lambda }_2}{\rho }{2}^{1-\frac{{\lambda }_2}{\rho }}\left|{\pi }_2\right|,}\hfill \end{array}$$

(26)

and

$$\begin{array}{ccc}{\displaystyle \left|\frac{\partial \left({\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}\right)}{\partial {\zeta }_1}\right|}\hfill & =\hfill & {\displaystyle \left|\frac{\partial \left({\beta }_1\lceil {\pi }_1\rceil \right)}{\partial {\zeta }_1}\right|}\hfill \\ \hfill & \le \hfill & {\displaystyle \left|\frac{\partial {\beta }_1}{\partial {\zeta }_1}\right||{\pi }_1|+\frac{\rho }{{\lambda }_1}{\beta }_1{\left|{\pi }_1\right|}^{\frac{\rho -{\lambda }_1}{\rho }}}\hfill \\ \hfill & \le \hfill & |{\pi }_1{|}^{\frac{\rho -{\lambda }_1}{\rho }}{\gamma }_2,\hfill \end{array}$$

(27)

where ${\gamma }_2\ge 0$ is a smooth function.

Therefore, on the basis of (24), (26), (27), and Lemma 2, one obtains

$${\displaystyle \begin{array}{ccc}\hfill & \hfill & {\displaystyle \frac{\partial W_2}{\partial {\zeta }_1}(d_1{\lceil {\zeta }_2\rceil }^{q_1}+g_1)}\hfill \\ \hfill & \le \hfill & \frac{2\rho -{\lambda }_2}{\rho }{\int }_{{\zeta }_2^{*}}^{{\zeta }_2}{\left|{\lceil s\rceil }^{\frac{\rho }{{\lambda }_2}}-{⌈{\zeta }_2^{*}⌉}^{\frac{\rho }{{\lambda }_2}}\right|}^{\frac{\rho -{\lambda }_2}{\rho }}ds\times \left|\frac{\partial \left({\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}}\right)}{\partial {\zeta }_1}\right|(d_1{\lceil {\zeta }_2\rceil }^{q_1}+g_1)\hfill \\ \hfill & \le \hfill & \frac{1}{3}|{\pi }_1{|}^{\frac{2\rho -\tau }{\rho }}+{\left|{\pi }_2\right|}^{\frac{2\rho -\tau }{\rho }}{\varrho }_{23},\hfill \end{array}}$$

(28)

where ${\varrho }_{23}\ge 0$ is a smooth function.

Substituting (23), (25), and (28) into (22) yields

$$\begin{array}{ccc}{\displaystyle {\dot{V}}_2}\hfill & \le \hfill & -(n-1){\Gamma }^{(1+c)\tau }|{\pi }_1{|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{d}_2{\lceil {\pi }_2\rceil }^{\frac{2\rho -r_2}{\rho }}\left({\lceil {\zeta }_3\rceil }^{q_2}-{\lceil {\zeta }_3^{*}\rceil }^{q_2}\right)\hfill \\ & & +{\Gamma }^{(1+c)\tau }(d_2\lceil {\pi }_2{\rceil }^{\frac{2\rho -r_2}{\rho }}{\lceil {\zeta }_3^{*}\rceil }^{q_2}+({\varrho }_{21}+{\varrho }_{22}+{\varrho }_{23}\left)\right|{\pi }_2{|}^{\frac{2\rho -\tau }{\rho }}).\hfill \end{array}$$

(29)

Then, one can design the virtual controller

$$\begin{array}{c}{\zeta }_3^{*}=-{\lceil {\pi }_2\rceil }^{\frac{{\lambda }_3}{\rho }}{\beta }_2^{\frac{{\lambda }_3}{\rho }}\left({\overline{\zeta }}_2\right),\hfill \end{array}$$

(30)

where the smooth function ${\beta }_2$ satisfies

$$\begin{array}{c}{\displaystyle {\beta }_2\left({\overline{\zeta }}_2\right)\ge {\left(\frac{n-1+{\varrho }_{21}+{\varrho }_{22}+{\varrho }_{23}}{{\underline{d}}_2}\right)}^{\frac{\rho }{q_2{\lambda }_3}},}\hfill \end{array}$$

(31)

such that

$$\begin{array}{ccc}{\displaystyle {\dot{V}}_2}\hfill & \le \hfill & -(n-1){\Gamma }^{(1+c)\tau }\left(|{\pi }_1{|}^{\frac{2\rho -\tau }{\rho }}+{|{\pi }_2|}^{\frac{2\rho -\tau }{\rho }}\right)+{\Gamma }^{(1+c)\tau }{d}_2{\lceil {\pi }_2\rceil }^{\frac{2\rho -r_2}{\rho }}\left({\lceil {\zeta }_3\rceil }^{q_2}-{\lceil {\zeta }_3^{*}\rceil }^{q_2}\right).\hfill \end{array}$$

(32)

Step i $(i=3,\dots ,n)$. The following proposition can be obtained in this step.

Proposition 2.

Suppose at step $i-1$, a $C^1$ Lyapunov function $V_{i-1}$ exists that is positive, definite, and proper, and a row of $C^0$ virtual controllers ${\zeta }_1^{*},\dots ,{\zeta }_i^{*}$ defined by

$$\begin{array}{cccccc}{\zeta }_1^{*}\hfill & =\hfill & 0,\hfill & {\pi }_1\hfill & =\hfill & {\lceil {\zeta }_1\rceil }^{\frac{\rho }{{\lambda }_1}}-{\lceil {\zeta }_1^{*}\rceil }^{\frac{\rho }{{\lambda }_1}},\hfill \\ {\zeta }_2^{*}\hfill & =\hfill & -{\lceil {\pi }_1\rceil }^{\frac{{\lambda }_2}{\rho }}{\beta }_1^{\frac{{\lambda }_2}{\rho }}\left({\zeta }_1\right),\hfill & {\pi }_2\hfill & =\hfill & {\lceil {\zeta }_2\rceil }^{\frac{\rho }{{\lambda }_2}}-{\lceil {\zeta }_2^{*}\rceil }^{\frac{\rho }{{\lambda }_2}},\hfill \\ \hfill & ⋮\hfill & \hfill & & ⋮\hfill & \\ {\zeta }_i^{*}\hfill & =\hfill & -{\lceil {\pi }_{i-1}\rceil }^{\frac{{\lambda }_i}{\rho }}{\beta }_{i-1}^{\frac{{\lambda }_i}{\rho }}\left({\overline{\zeta }}_{i-1}\right),\hfill & {\pi }_i\hfill & =\hfill & {\lceil {\zeta }_i\rceil }^{\frac{\rho }{{\lambda }_i}}-{\lceil {\zeta }_i^{*}\rceil }^{\frac{\rho }{{\lambda }_i}},\hfill \end{array}$$

(33)

with ${\beta }_1>0$, …, ${\beta }_{i-1}>0$ being smooth, such that

$$\begin{array}{c}{\displaystyle {\dot{V}}_{i-1}\le -(n-i+2){\Gamma }^{(1+c)\tau }\sum _{j=1}^{i-1}{\left|{\pi }_j\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{d}_{i-1}{\lceil {\pi }_{i-1}\rceil }^{\frac{2\rho -{\lambda }_{i-1}}{\rho }}({\lceil {\zeta }_i\rceil }^{q_{i-1}}-{\lceil {\zeta }_i^{*}\rceil }^{q_{i-1}}).}\hfill \end{array}$$

(34)

Then, the ith Lyapunov function $V_i=V_{i-1}+W_i$ with

$$\begin{array}{c}{\displaystyle W_i={\int }_{{\zeta }_i^{*}}^{{\zeta }_i}{⌈{\lceil s\rceil }^{\frac{\rho }{{\lambda }_i}}-{\lceil {\zeta }_i^{*}\rceil }^{\frac{\rho }{{\lambda }_i}}⌉}^{\frac{2\rho -{\lambda }_i}{\rho }}ds,}\hfill \end{array}$$

(35)

is $C^1$, positive, definite, and proper, and there is a $C^0$ state feedback controller

$$\begin{array}{c}{\zeta }_{i+1}^{*}=-{\beta }_i^{\frac{{\lambda }_{i+1}}{\rho }}\left({\overline{\zeta }}_i\right){\lceil {\pi }_i\rceil }^{\frac{{\lambda }_{i+1}}{\rho }},\hfill \end{array}$$

(36)

such that

$$\begin{array}{c}{\displaystyle {\dot{V}}_i\le -(n-i+1){\Gamma }^{(1+c)\tau }\sum _{j=1}^i{\left|{\pi }_j\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{d}_i{\lceil {\pi }_i\rceil }^{\frac{2\rho -r_i}{\rho }}({\lceil {\zeta }_{i+1}\rceil }^{q_i}-{\lceil {\zeta }_{i+1}^{*}\rceil }^{q_i}).}\hfill \end{array}$$

(37)

Proof. 

See the Appendix A. □

Step n. Selecting

$$\begin{array}{c}{\displaystyle V_n=\sum _{j=1}^n{W}_j=\sum _{j=1}^n{\int }_{{\zeta }_j^{*}}^{{\zeta }_j}{⌈{\lceil s\rceil }^{\frac{\rho }{{\lambda }_j}}-{\lceil {\zeta }_j^{*}\rceil }^{\frac{\rho }{{\lambda }_j}}⌉}^{\frac{2\rho -{\lambda }_j}{\rho }}ds,}\hfill \end{array}$$

(38)

the above inductive step indicates that a desired dead-zone output exists

$$\begin{array}{c}{\zeta }_{n+1}^{*}=-{\lceil {\pi }_n\rceil }^{\frac{{\lambda }_{n+1}}{\rho }}{\beta }_n^{\frac{{\lambda }_{n+1}}{\rho }}\left({\overline{\zeta }}_n\right),\hfill \end{array}$$

(39)

such that

$$\begin{array}{c}{\displaystyle {\dot{V}}_n\le -{\Gamma }^{(1+c)\tau }\sum _{j=1}^n{\left|{\pi }_j\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{(1+c)\tau }{\lceil {\pi }_n\rceil }^{\frac{2\rho -{\lambda }_n}{\rho }}\left(v-{\zeta }_{n+1}^{*}\right)}\hfill \\ {\displaystyle \le -{\Gamma }^{(1+c)\tau }\sum _{j=1}^n{\left|{\pi }_j\right|}^{\frac{2\rho -\tau }{\rho }}+{\Gamma }^{2(1+c)\tau }{\lceil {\pi }_n\rceil }^{\frac{2\rho -{\lambda }_n}{\rho }}\left(Q\left(u\right)-{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}\right).}\hfill \end{array}$$

(40)

Therefore, from (3) the state feedback control u is designed as

$$u=\left\{\begin{array}{ccc}{\displaystyle \left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}}{1-\overline{\delta }}+u_{min}\right),}\hfill & \hfill & {\zeta }_{n+1}^{*}>0,\hfill \\ 0,\hfill & \hfill & {\zeta }_{n+1}^{*}=0,\hfill \\ {\displaystyle \left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}}{1-\overline{\delta }}-u_{min}\right),}\hfill & \hfill & {\zeta }_{n+1}^{*}<0,\hfill \end{array}\right.$$

(41)

which renders

$$\begin{array}{c}\left(Q\left(u\right)-{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}\right)\hfill \\ {\displaystyle =\left\{\begin{array}{ccc}{\displaystyle \frac{Q\left(u\right)}{u}\left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}}{1-\delta }+u_{min}\right)-{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}>0,}\hfill & \hfill & {\zeta }_{n+1}^{*}>0,\hfill \\ 0,\hfill & \hfill & {\zeta }_{n+1}^{*}=0,\hfill \\ {\displaystyle \frac{Q\left(u\right)}{u}\left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}}{1-\delta }-u_{min}\right)-{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}<0,}\hfill & \hfill & {\zeta }_{n+1}^{*}<0.\hfill \end{array}\right.}\hfill \end{array}$$

(42)

By noting $-{\lceil {\pi }_n\rceil }^{\frac{2\rho -{\lambda }_n}{\rho }}{\zeta }_{n+1}^{*}\ge 0$, one obtains

$$\begin{array}{c}{\displaystyle {\dot{V}}_n\le -{\Gamma }^{(1+c)\tau }\sum _{j=1}^n|{\pi }_j{|}^{\frac{2\rho -\tau }{\rho }}\le -\sum _{j=1}^n{|{\pi }_j|}^{\frac{2\rho -\tau }{\rho }}.}\hfill \end{array}$$

(43)

Consequently, the following result is obtained.

Theorem 1.

For system (1) under Assumptions 1 and 2, the state feedback controller (41) consisting of (33) and (39) renders the states of the CLS convergent to zero within the prescribed finite time $T_c>0$.

Proof. 

Represents that property that the positive, definite, and proper properties of $V_n$ given in Proposition 2 together with (43) and Lemma Lemma 4.3 in [49] reveal that there are class ${\mathcal{K}}_{\infty }$ functions ${\eta }_1$, ${\eta }_2$ and ${\eta }_3$ such that

$$\begin{array}{c}{\eta }_1\left(\right|\zeta \left|\right)\le V_n\left(\zeta \right)\le {\eta }_2\left(\right|\zeta \left|\right),\end{array}$$

(44)

$$\begin{array}{c}{\displaystyle {\dot{V}}_n\le -{\eta }_3\left(\right|\zeta \left|\right),}\end{array}$$

(45)

which indicate that $\zeta \left(t\right)$ is asymptotically convergent and bounded on $[0,T_c)$.

On the other hand, the SST (9) gives

$$\begin{array}{c}{\displaystyle z_i\left(t\right)={\Gamma }^{-(1+c){\lambda }_i}{\zeta }_i\left(t\right)={\left(\frac{T_c-t}{T_c}\right)}^{(1+c){\lambda }_i}{\zeta }_i\left(t\right),i=1,\dots ,n.}\end{array}$$

(46)

Consequently, it further can be obtained that

$$\begin{array}{c}{\displaystyle \underset{t\to T_c}{lim}{z}_i\left(t\right)=\underset{t\to T_c}{lim}{\left(\frac{T_c-t}{T_c}\right)}^{(1+c){\lambda }_i}{\zeta }_i\left(t\right)=0,i=1,\dots ,n.}\end{array}$$

(47)

Therefore, the proof is completed. □

3.2. Controller Design for $t\in [T_c,+\infty )$ and Main Result

The state feedback controller that drives system states to zero in prescribed finite time $T_c>0$ has been designed in the above subsection. As a result, in this subsection we need only consider how to design a controller that the states reach and that is maintained at the origin for all $t\in [T_c,+\infty )$.

By the solution properties of existence and continuation, it is obtained that $z\left(T_c\right)=0$. Therefore, the control u can be simply selected as $u=0$, which, together with $f_i\left(0\right)=0$, guarantees $z\left(t\right)=0$ for any $t\in [T_c,+\infty )$ [43]. However, this choice will render that the CLS is sensitive to external disturbances. To avoid this, here we give an alternative solution for $t\in [T_c,+\infty )$. Observe that the original system (1) and the transformed system (11) have a similar structure except for the time-varying control coefficient ${\Gamma }^{(1+c)\tau }$. Therefore, by letting $\Gamma =1$, we can design a new controller u consisting of (33), (39) and (41) to keep the states at the origin for all $t\ge T_c$.

Till now, the control design of PTS for the system (1) is completed. Accordingly, the following theorem is given to sum up the main results of this paper.

Theorem 2.

Considering system (1) under Assumptions 1 and 2, if the state feedback controller

$$u=\left\{\begin{array}{ccc}{\displaystyle \left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}}{1-\delta }+u_0\right),}\hfill & \hfill & {\zeta }_{n+1}^{*}>0,\hfill \\ 0,\hfill & \hfill & {\zeta }_{n+1}^{*}=0,\hfill \\ {\displaystyle \left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_{n+1}^{*}}{1-\delta }-u_0\right),}\hfill & \hfill & {\zeta }_{n+1}^{*}<0,\hfill \end{array}\right.$$

(48)

with

$${\Gamma }_1=\left\{\begin{array}{ccc}{\displaystyle \frac{T_c}{T_c-t},}\hfill & \hfill & t\in [0,T_c),\hfill \\ {\displaystyle 1,}\hfill & \hfill & t\in [T_c,+\infty ),\hfill \end{array}\right.$$

(49)

$$\begin{array}{c}{\zeta }_{n+1}^{*}=-{\lceil {\pi }_n\rceil }^{\frac{{\lambda }_{n+1}}{\rho }}{\beta }_n^{\frac{{\lambda }_{n+1}}{\rho }}\left({\overline{\zeta }}_n\right),\hfill \end{array}$$

(50)

is applied, then the origin of the CLS is globally prescribed-time stable.

Proof. 

According to the properties of the monotonous growth of $\Gamma \left(t\right)=T_c/(T_c-t)$ and the asymptotical convergent of $\zeta \left(t\right)$ for all $t\in [0,T_c)$, one has

$$\begin{array}{c}\left|z\right(t\left)\right|\le \left|\zeta \right(t\left)\right|\le \left|\zeta \right(0\left)\right|=\left|z\right(0\left)\right|,\hfill \end{array}$$

(51)

which, together with $z\left(t\right)=0$ for any $t\in [T_c,+\infty )$, lead to

$$\begin{array}{c}\left|z\right(t\left)\right|\le \left|z\right(0\left)\right|,t\ge 0.\hfill \end{array}$$

(52)

That is to say, the origin of the CLS is globally Lyapunov stable. Furthermore, with the global prescribed-time convergent of the CLS in mind, this theorem is straightforwardly concluded from Definition 3. □

4. Simulation Example

To give an example of the utilization of the proposed control scheme, we consider a liquid-level system exhibited in Figure 1, the dynamics of which are represented by

$$\begin{array}{ccc}{C}_1{\dot{H}}_1\hfill & =\hfill & Q_1\hfill \\ C_2{\dot{H}}_2\hfill & =\hfill & Q-Q_1-Q_2\hfill \\ Q_1\hfill & =\hfill & \left\{\begin{array}{c}{k}_1\sqrt{2g|H_2-H_1|},H_2\ge H_1,\hfill \\ -k_1\sqrt{2g|H_2-H_1|},H_2<H_1,\hfill \end{array}\right.\hfill \\ Q_2\hfill & =\hfill & k_2\sqrt{2g{H}_2},\hfill \end{array}$$

(53)

where the physical meanings of system parameters are as

$H_i$	Liquid levels of tank i;
H	Steady-state liquid levels of two tanks;
$C_i$	Cross sections of tank i;
$k_1$	Cross sections of the inlet manual valves of tanks 1 and 2;
$k_2$	Cross sections of the right outlet manual valves of tank 2;
Q	Inflow rate of this system;
$Q_1$	Inflow rate from tank 2 to tank 1;
$Q_2$	Outflow rate of this system;
g	Gravitational acceleration.

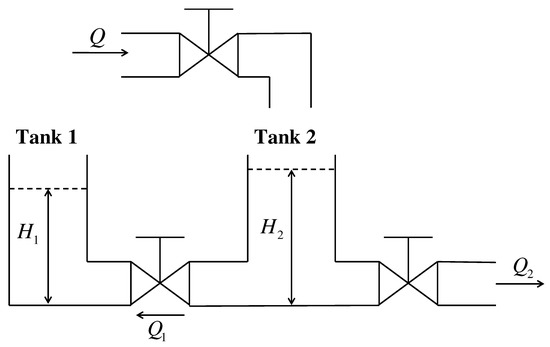
Figure 1. Schematic diagram of the liquid-level system.

By introducing the variable changes

$$\begin{array}{c}{\displaystyle z_1=H_1-H,z_2=H_2-H_1,u=\frac{Q}{C_2}-\frac{k_2\sqrt{2gH}}{C_2},}\hfill \end{array}$$

(54)

and taking the quantized input nonlinearity into account, the dynamics of (53) can be further modelled as

$$\begin{array}{c}{\dot{z}}_1=d_1{\lceil z_2\rceil }^{\frac{1}{2}},\hfill \\ {\dot{z}}_2=Q\left(u\right)+f_2\left({\overline{z}}_2\right),\hfill \end{array}$$

(55)

where $d_1=\frac{k_1\sqrt{2g}}{C_1}$ and $f_2\left({\overline{z}}_2\right)=-\frac{C_1}{C_2}{d}_1{\lceil z_2\rceil }^{\frac{1}{2}}-\frac{k_2\sqrt{2g}}{C_2}{\lceil z_1+z_2+H\rceil }^{\frac{1}{2}}+\frac{k_2\sqrt{2g}}{C_2}{\lceil H\rceil }^{\frac{1}{2}}$; Q denotes the quantized input nonlinearity described by (5). Based on Lemma 3, it is easily verified that

$$\begin{array}{ccc}|f_2|\hfill & \le \hfill & \frac{k_1\sqrt{2g}}{C_2}{|z_2|}^{\frac{1}{2}}+\frac{k_2\sqrt{2g}}{C_2}\left|{\lceil z_1+z_2+H\rceil }^{\frac{1}{2}}-{\lceil H\rceil }^{\frac{1}{2}}\right|\hfill \\ \hfill & \le \hfill & \frac{k_1\sqrt{2g}}{C_2}{|z_2|}^{\frac{1}{2}}+\frac{k_2\sqrt{2g}}{C_2}\left(|z_1{|}^{\frac{1}{2}}+{|z_2|}^{\frac{1}{2}}+H^{\frac{1}{2}}-H^{\frac{1}{2}}\right)\hfill \\ \hfill & \le \hfill & \frac{k_1\sqrt{2g}}{C_2}{|z_2|}^{\frac{1}{2}}+\frac{k_2\sqrt{2g}}{C_2}\left(|z_1{|}^{\frac{1}{2}}+{|z_2|}^{\frac{1}{2}}\right)\hfill \\ \hfill & \le \hfill & \frac{\sqrt{2g}}{C_2}(k_1+k_2)\left(|z_1{|}^{\frac{1}{2}}+{|z_2|}^{\frac{1}{2}}\right).\hfill \end{array}$$

(56)

That is, Assumption 1 is satisfied with ${\lambda }_3=\tau =1$ and ${\lambda }_1={\lambda }_2=2$, ${\phi }_2=\frac{\sqrt{2g}}{C_2}(k_1+k_2)$.

Introducing ${\zeta }_i={\Gamma }_1^{(1+c){\lambda }_i}{z}_i$, $i=1,2$ with

$${\Gamma }_1=\left\{\begin{array}{ccc}{\displaystyle \frac{T_c}{T_c-t},}\hfill & \hfill & t\in [0,T_c),\hfill \\ {\displaystyle 1,}\hfill & \hfill & t\in [T_c,+\infty ),\hfill \end{array}\right.$$

(57)

and taking $\rho =2$ and $c=0$, according to Theorem 2 one can design a state feedback controller

$$u=\left\{\begin{array}{ccc}{\displaystyle \left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_3^{*}}{1-\delta }+u_0\right),}\hfill & \hfill & {\zeta }_3^{*}>0,\hfill \\ 0,\hfill & \hfill & {\zeta }_3^{*}=0,\hfill \\ {\displaystyle \left(\frac{{\Gamma }^{-(1+c)\tau }{\zeta }_3^{*}}{1-\delta }-u_0\right),}\hfill & \hfill & {\zeta }_3^{*}<0,\hfill \end{array}\right.$$

(58)

$$\begin{array}{c}{\zeta }_3^{*}=-\left(0.1+{\varrho }_{21}+{\varrho }_{22}+{\varrho }_{23}\right){\lceil {\pi }_2\rceil }^{\frac{1}{2}},\hfill \end{array}$$

(59)

with ${\beta }_1=(1.1+\frac{2}{T_c}{(1+{\zeta }_1^2)}^{\frac{1}{2}})/d_1$ if $t\in [0,T_c)$ and ${\beta }_1=1.1/d_1$ if $t\in [T_c,+\infty )$, ${\pi }_2={\zeta }_2-{\zeta }_2^{*}$, ${\zeta }_2^{*}=-{\beta }_1{\zeta }_1^2$, ${\tilde{\phi }}_2=(1+{\beta }_1^{\frac{1}{2}})(1+c){\lambda }_2{\left|{\zeta }_2\right|}^{\tau /{\lambda }_2}/T_c+{\phi }_i$, ${\varrho }_{21}=3.7712d_1^{\frac{3}{2}}$, ${\varrho }_{22}=0.6667{\tilde{\phi }}_2^{\frac{3}{2}}+{\tilde{\phi }}_2$, ${\varrho }_{23}=|\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}{d}_1|+0.6667|\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}{|}^3{(d_1{\beta }_1^{\frac{1}{2}}+\frac{2}{T_c}{(1+{\zeta }_1^2)}^{\frac{1}{2}})}^3$, which can render the system (56) globally prescribed-time stable.

For the simplicity, select the system parameters as $H=100\mathrm{cm}$, $g=9.8\mathrm{m}/{\mathrm{s}}^2$, $C_1=C_2=\sqrt{2g}=4.427{\mathrm{cm}}^2$, $k_1=1{\mathrm{cm}}^2$, $k_2=0.25{\mathrm{cm}}^2$, $d=0.05$, and $\delta =0.2$ and the prescribed time as $T_c=4$ s. For different initial conditions (i) $(z_1\left(0\right),z_2\left(0\right))=(0.5,-1)$, (ii) $(z_1\left(0\right),z_2\left(0\right))=(5,-10)$, Figure 2, Figure 3, Figure 4 and Figure 5 are given to exhibit the responses of the CLS. It can be clearly seen that the convergence time of the system states stays below the prescribed time 4 s in spite of the initial value growing, which confirms the validity of the control scheme. As a result, the simulation results confirm the validity of the control scheme.

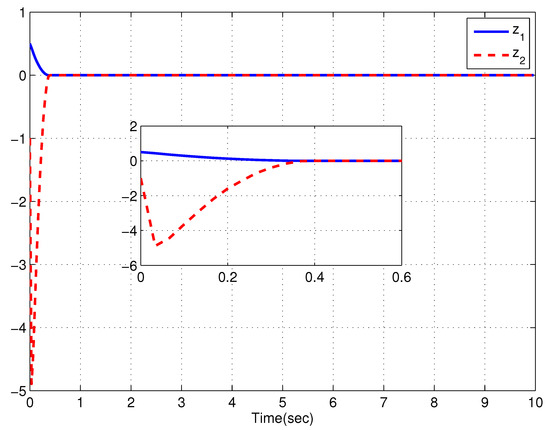
Figure 2. System states of case (i).

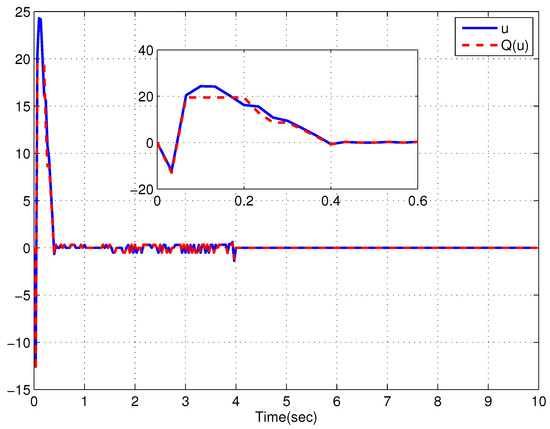
Figure 3. Dead-zone input and output of case (i).

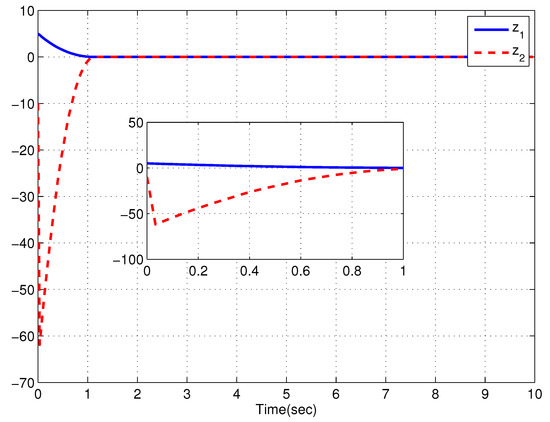
Figure 4. System states of case (ii).

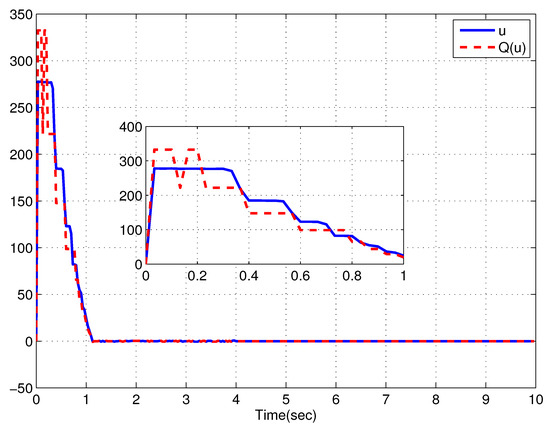
Figure 5. Dead-zone input and output of case (ii).

5. Conclusions

In this paper, the problem of prescribed-time state feedback stabilization has addressed a kind of PNNSs with quantized input nonlinearity. Based on a novel SST to translate the original problem of prescribed-time stabilization into the asymptotic stabilization of the transformed one, a constructive quantized control design procedure of state feedback is established with the aid of the API technique. A significant advantage of the presented scheme is that its settling time can be preset and is easy to adjust arbitrarily according to practical requirements. However, it is mentioned that the given controller is essentially based on the information of entire system states, and apparently the current method is unavailable to the case without such knowledge. Accordingly, knowing how to develop a control scheme for PNNSs only using partial state measurements [50] will be a topic of our future work. Moreover, the multi-agent systems [51] and cyber-physical systems [52,53] are very important systems that need to be studied, and thus exploring the application of the proposed method to such systems is also an interesting research topic.