A Rapidly Adaptive Collision Backoff Algorithm for Improving the Throughput in WLANs

Abstract

In the 802.11 protocol, the fundamental medium access mechanism is called Distributed Coordination Function (DCF). In DCF, before making any transmission attempt, the nodes count down a timer with a value randomly selected from the Contention Window (CW) size. If the transmitted packet is involved in a collision, the node increases the CW size in an attempt to reduce the collision rate. Conversely, if the packet is transmitted successfully, the node reduces the CW size in order to increase the frequency of the transmission attempts. The growth or reduction in the CW size has a critical effect on the network performance. Several backoff algorithms have been proposed to improve the system throughput. However, none of these methods enable the system to approach the theoretical maximum throughput possible under DCF. Accordingly, this study proposes the Rapidly Adaptive Collision Backoff (RACB) algorithm, in which the CW size is adjusted dynamically based on the collision rate, as analyzed by a mathematical model. Notably, RACB requires no knowledge of the number of nodes in the wireless network and is applicable to both lightly loaded and heavily loaded networks. The numerical results show that, by adjusting the CW size such that the collision rate is maintained at a value close to 0.1, RACB enables the system throughput to approach the maximum DCF throughput in wireless environments containing any number of nodes.

1. Introduction

The IEEE 802.11 [1,2,3,4] protocol is one of the most commonly deployed wireless access technologies around the world and provides a detailed specification of the Medium Access Control (MAC) layer and Physical Layer (PHY) of WLANs. The MAC specification defines two medium access coordination functions, namely the Point Coordination Function (PCF) and the Distributed Coordination Function (DCF). PCF is a centralized MAC protocol that supports collision-free and time-bounded services. By contrast, DCF is a contention-based scheme that employs the Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) protocol and the Binary Exponential Backoff (BEB) contention-resolution algorithm. In the IEEE 802.11 standard, DCF is the default medium access control method, while PCF is an optional function.

In a wireless network, collisions occur when two or more nodes transmit packets simultaneously. In order to avoid such collisions, DCF uses a random backoff period to force the nodes to defer their wireless channel access attempts for a short arbitrary period. In particular, the nodes randomly select a backoff period from the Contention Window (CW) size and then count this backoff period down before attempting to send their packets. During the countdown period, if another node transmits a packet, thereby causing the channel to become busy, the countdown process is frozen until the state of the channel returns to idle. The node then continues the countdown and attempts to transmit its packets once the counter reaches zero.

According to the discussions above, when the size of the CW is small, the average length of the backoff period is short. As a result, the waiting time before packet transmissions is also short. However, the probability of collisions is increased. Conversely, a larger CW size increases the waiting time before transmissions but reduces the collision probability. Accordingly, an appropriate setting of the CW size is essential for achieving an acceptable tradeoff between the channel collision rate and the waiting time before packet transmission.

In DCF, the variation in the CW size is determined by the BEB algorithm. More specifically, each time a node experiences a transmission collision, the size of the CW is doubled until it reaches the maximum value (CW_max) in order to reduce the probability of transmission collisions occurring again. By contrast, each time a packet is successfully transmitted, BEB restores the CW size to the minimum value (CW_min). However, in network environments containing a large number of nodes, all competing for the same wireless channel, such sudden large reductions in the CW size cause a severe degradation of the system throughput [5,6,7,8,9,10] since the shorter CW size results in a greater number of collisions after any successful transmission.

Song [11] attempted to resolve this problem using a modified backoff algorithm designated as Exponential Increase Exponential Decrease (EIED), in which the size of the CW was doubled after a collision (as in the original BEB scheme) but was only halved (rather than restored to the minimum value) after each successful transmission. Compared with BEB, EIED results in a significant improvement in the performance of the DCF mechanism in environments with a large number of contending nodes. However, in wireless networks containing many nodes, it is desirable to maintain the CW size as large as possible in order to avoid frequent collisions. Accordingly, Ye and Tseng [12] proposed an alternative backoff algorithm referred to as Linear Increase Linear Decrease (LILD), in which the CW size was increased and decreased linearly with an incremental step size of CW_min after each collision and successful transmission. Compared to BEB and EIED, the change in the CW size in LILD is more progressive, and, hence, LILD achieves a higher throughput than either BEB or EIED in networks containing a large number of nodes. However, EIED outperforms LILD in networks with a rapidly changing load due to the exponential change in the CW size. Accordingly, the present group [13] previously combined the respective advantages of EIED and LILD in a new backoff algorithm designated as Exponential-Linear Backoff Algorithm (ELBA). In the proposed algorithm, the channel was judged to be heavily loaded if the CW size exceeded a certain threshold value, and the size of the CW was adjusted linearly using the method prescribed in LILD. By contrast, when the CW size was smaller than this threshold value, the network was judged to be lightly loaded, and the CW size was adjusted exponentially, as in EIED. The experimental results showed that ELBA outperformed BEB, EIED and LILD under both light and heavy network loads.

Although the algorithms described above achieve better system throughput than DCF with BEB, their performance regarding system throughput is still not achieving theoretical maximum throughput [14]. According to the analysis results presented in [5,14], the optimal size of the CW varies with the number of nodes in the network. However, in practical networks, the individual nodes are unaware of the total number of nodes contending for the channel [15]. Thus, they are unable to determine the optimal CW size. Accordingly, the present study proposes a new backoff algorithm, referred to hereafter as the Rapidly Adaptive Collision Backoff (RACB) algorithm, which allows the system throughput to approach the maximum theoretical throughput in [14] with no knowledge of the number of wireless nodes in the network. In the proposed algorithm, the wireless nodes adjust the CW size directly based on their own observed collision rate, where the relationship between the optimal CW size and the collision rate is determined mathematically [5,14]. When the collision rate exceeds a certain threshold value, the nodes increase the CW size. By contrast, when the collision rate falls below the threshold value, the nodes reduce the CW size. Notably, the CW size is increased/decreased exponentially or linearly depending on the distance of the collision rate from the specified threshold value. Importantly, RACB enables the CW size to be adjusted adaptively in such a way that the system throughput approaches the maximum throughput without requiring any knowledge of the total number of nodes in the network.

The remainder of this paper is organized as follows. Section 2 introduces the basic operation of DCF and its related backoff algorithms. Section 3 analyzes the performance of DCF and examines the relationship between the maximum system throughput and the optimal CW size. Section 4 introduces the proposed RACB algorithm. Section 5 describes the experimental settings and presents the numerical results. Finally, Section 6 provides some brief concluding remarks and indicates the proposed direction of future research.

2. Background and Related Works

2.1. IEEE 802.11 DCF

Figure 1 [1] illustrates the basic operation of the CSMA/CA protocol in DCF. Before a wireless node transmits a new packet to the network, it first senses the activity of the channel. If the channel is sensed idle for an interval greater than the DIFS (Distributed Inter-frame Spacing), the node transmits the packet immediately. Conversely, if the channel is sensed busy, the node defers transmission until the end of the ongoing transmission. Once the channel becomes idle, the node initializes its backoff timer with a randomly selected backoff period with a duration greater than zero and less than the CW size. The node senses the channel as it waits and decrements the timer each time it senses the channel to remain idle for a DIFS. If the channel is still idle when the timer expires, the node transmits its packet. However, if another node starts to transmit during the countdown period, the node freezes its timer until the channel becomes idle for a DIFS once again, at which point it restarts the timer and transmits its packet once the timer expires.

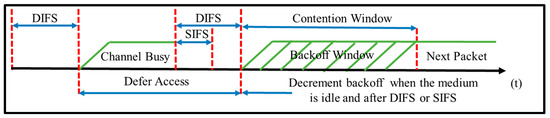
Figure 1. Operation of IEEE 802.11 DCF [1].

DCF adopts the BEB algorithm [1] to control the variation in the CW size. As shown in Figure 2 [1], the minimum value (CW_min) and maximum value (CW_max) of the CW size are set as 32 and 1024, respectively. In the first transmission attempt, BEB sets the CW equal to CW_min, and the node selects a random value for its backoff timer in the range of [0, CW_i−1]. Note that CW is the size of the contention window, CW_i is the current CW size and i is the number of failed transmission attempts thus far. After each unsuccessful transmission, CW is doubled, i.e., CW_i = 2 * CW_i−1 = 2ⁱ * CW_min, until it reaches the maximum value, CW_max = 2^m * CW_min. (Note that m is the maximum number of backoff stages in the BEB algorithm.) Once CW_i reaches CW_max, it remains at this value until a successful transmission occurs, at which point it is reset to CW_min.

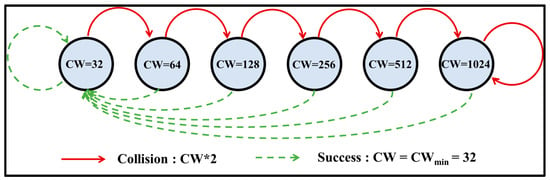
Figure 2. Markov chain model for BEB algorithm [1].

BEB is an asymmetric backoff algorithm; i.e., the CW size decreases drastically after a successful transmission. As a result, it causes a large number of collisions after any successful transmission, particularly in networks containing a large number of nodes, and degrades the system throughput accordingly [5].

2.2. Related Works

2.2.1. Exponential Increase Exponential Decrease (EIED)

Several modifications have been proposed to address the problems caused by the asymmetric nature of BEB [8,9,10,11,12,13]. For example, the Exponential Increase Exponential Decrease (EIED) method in [11] aims to reduce the CW size more slowly after successful transmissions by using an exponential reduction strategy. As shown in Figure 3 [11], the CW size is set initially to CW_min and is then doubled (CW_i = 2 * CW_i−1) after each unsuccessful transmission until the current CW reaches CW_max. The CW size is maintained at this value until a successful transmission occurs, at which point the current CW is halved (CW_i = CW_i−1/2). The CW size continues to be halved until it reaches CW_min, where it remains until an unsuccessful transition occurs.

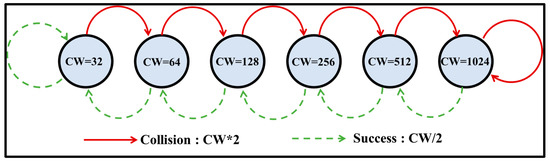
Figure 3. Markov chain model for EIED algorithm [11].

By decreasing the CW size exponentially rather than asymmetrically, EIED achieves a better DCF performance (i.e., a higher system throughput) than that obtained using BEB. For wireless networks containing a large number of wireless nodes, the CW size should be maintained as large as possible in order to avoid frequent collisions. However, the CW size may vary widely in EIED, particularly in networks with a large number of nodes. Consequently, EIED may be too sensitive to adapt to changes in the condition of the wireless network.

2.2.2. Linear Increase Linear Decrease (LILD)

The Linear Increase Linear Decrease (LILD) algorithm [12] aims to overcome this drawback of EIED by decreasing the CW size linearly rather than exponentially following a successful transmission. As shown in Figure 4, the CW size is set initially as CW_min. After each unsuccessful transmission, CW is incremented by CW_min (CW_i = CW_i−1 + CW_min) until it reaches CW_max. The CW is then decreased linearly by CW_min (CW_i = CW_i−1 − CW_min) each time a successful transmission occurs until it reaches CW_min.

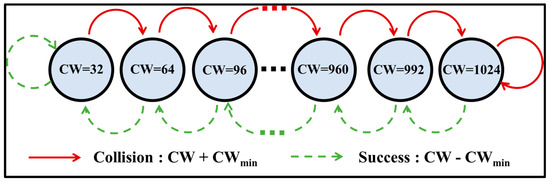
Figure 4. Markov chain model for LILD algorithm [12].

The CW size in LILD changes more slowly than in EIED and BEB, and, hence, LILD is better suited to networks with a large number of nodes. However, it is impractical for networks with variable loads because of the linear change in the CW size.

2.2.3. Exponential-Linear Backoff Algorithm (ELBA)

From the discussions above, EIED is suitable for networks with a light load, while LILD is more suitable for networks with a heavy load. Thus, the ELBA algorithm [13] aims to combine the respective advantages of EIED and LILD to improve the throughput in wireless networks with a variable load. In particular, ELBA sets a threshold referred to as the Contention Window Threshold, CW_Threshold, as an index against which to judge the network status. When the CW size is less than this threshold, the network load is assumed to be light, and the CW size is tuned exponentially as in EIED. By contrast, when the CW size is larger than this threshold value, the network is assumed to be heavily loaded, and the CW size is tuned linearly as in LILD. As shown in Figure 5, the CW size is initialized as CW_min. After each unsuccessful transmission, the CW is doubled (CW_i = CW_i−1 * 2) until it reaches CW_Threshold. After each subsequent unsuccessful transmission, the CW size is increased exponentially by CW_min (CW_i = CW_i−1 + CW_min) until it reaches CW_max. Following each successful transmission with the current CW size between CW_min and CW_Threshold, the CW is halved (CW_i = CW_i−1/2) until it reaches CW_min. By contrast, for current CW sizes in the range of CW_Threshold to CW_max, the CW is decreased exponentially by CW_min (CW_i = CW_i−1 − CW_min) until it reaches CW_Threshold.

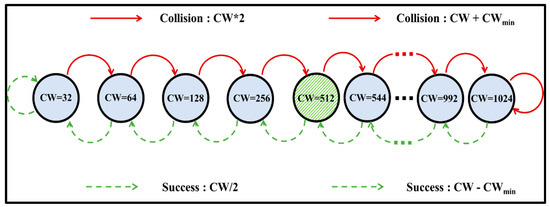
Figure 5. Markov chain model for ELBA algorithm [13].

In accordance with the IEEE 802.11 standard, ELBA sets CW_min and CW_max as 32 and 1024, respectively, and assigns the Contention Window Threshold as half of CW_max, i.e., 512. Notably, the adaptive approach of ELBA reduces the collision rate (and improves the system throughput) compared to BEB, EIED and LILD in both lightly loaded and heavily loaded networks.

2.3. Maximum Throughput in Wireless Networks

The authors in [14] devised an analytical model for maximizing the throughput in wireless networks by optimizing the CW size in accordance with the number of nodes (see Table 1). However, the model assumed that each node is able to determine the number of competing nodes in the network and can set the optimal CW accordingly, which is unreasonable in real-world wireless networks.

Table 1. Maximum throughput versus optimal CW size [14].

Number of Nodes	Optimal CW Size	Maximum Throughput
5	87	84.2361
10	184	83.7705
15	280	83.6218
20	377	83.5486

2.4. Contributions of Present Study

The present study proposes a Rapidly Adaptive Collision Backoff (RACB) algorithm for improving the system throughput over WLANs. RACB maximizes the system throughput by adjusting the CW size based on the collision rate of the nodes, where the relationship between the collision rate and the optimal CW size is described using a mathematical model. Notably, RACB requires no knowledge of the number of nodes in the wireless network and is applicable to both lightly loaded and heavily loaded networks.

3. Performance Analysis of DCF

3.1. Maximum System Throughput under DCF

In the present study, the throughput performance of DCF was investigated using a self-written simulator implemented in NS-2 tool [16]. The simulations commenced by examining the relationship between the maximum system throughput and the CW size in networks with different numbers of wireless nodes. In accordance with the IEEE 802.11 standard, the CW size was varied in the range of 32 to 1024. Furthermore, the network was assumed to contain 10, 20, 30, 40 or 50 nodes.

As shown in Figure 6, for all the simulated environments, the system throughput increases rapidly as the CW size first increases. However, at a certain optimal value of the CW size, the throughput saturates, or reduces slightly as a result of low channel utilization. For the smallest wireless network with 10 competing nodes, the maximum system throughput reaches 84.5% for a CW size of 160. For the network with 30 nodes, the maximum system throughput reduces slightly to 84% with an optimal CW size of 512. In Figure 6, the maximum system throughput of different number of nodes can be mapped to the different optimal CW size. The simulation results match the analysis in [14].

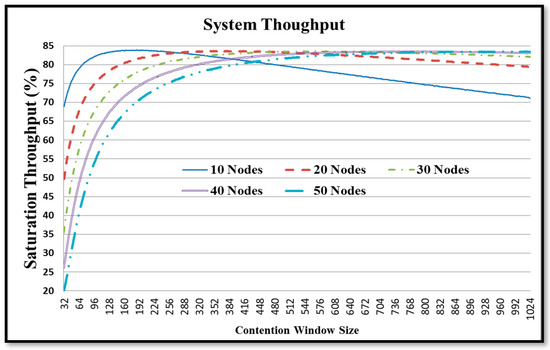
Figure 6. System throughput of DCF for different CW sizes.

Figure 7 shows the simulation results obtained for the variation in the saturation throughput with the number of network nodes under different backoff algorithms. As shown, ELBA outperforms DCF, EIED and LILD for all the considered networks. However, the system throughput still fails to meet the maximum value in [14] due to the non-optimal setting of the CW size. Moreover, as the number of nodes increases, the performance gap between ELBA and the maximum saturation throughput increases.

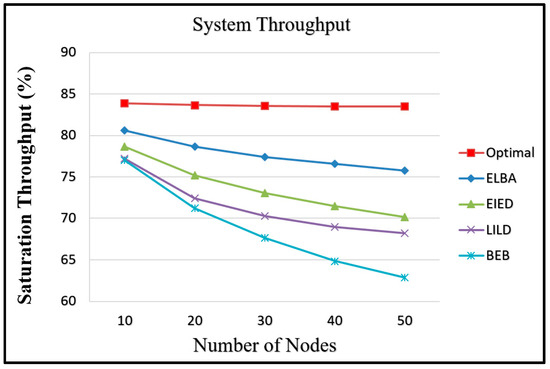
Figure 7. Saturation throughput of DCF under different backoff algorithms.

3.2. DCF Performance Analysis for Different CW Sizes

The optimal CW size, i.e., the CW size that achieves the maximum DCF throughput, can be obtained using the analytical model in [14]. However, as described in Section 2.3, this model is based on the unrealistic assumption that the nodes in the network are able to determine the number of competing nodes for the channel. Accordingly, the aim of the present study is to establish a more realistic approach for determining the optimal CW size. In practice, the throughput of wireless networks is closely related to the collision rate. Moreover, in backoff algorithms, the collision rate increases as the CW size reduces. Therefore, a further series of simulations was performed to investigate the relationship between the collision rate, the system throughput and the CW size in typical IEEE 802.11 environments with DCF. Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 show the corresponding results for networks containing 10, 20, 30, 40 and 50 nodes, respectively.

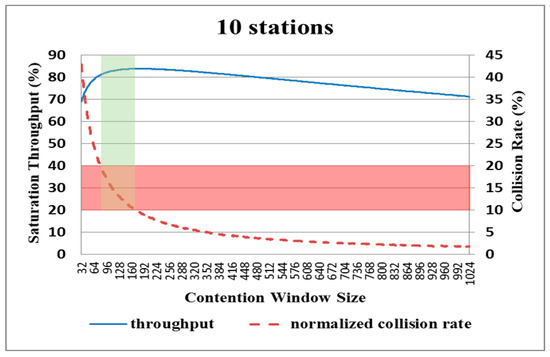
Figure 8. Variation in system throughput and collision rate with CW size for network with 10 nodes.

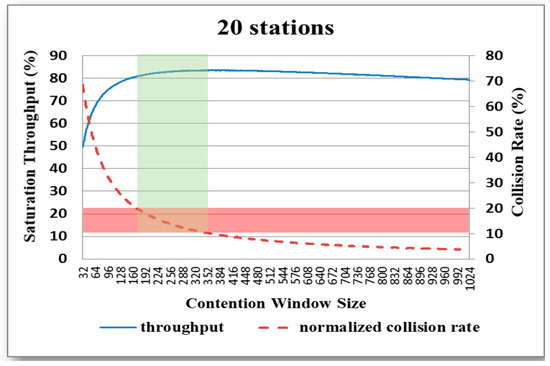
Figure 9. Variation in system throughput and collision rate with CW size for network with 20 nodes.

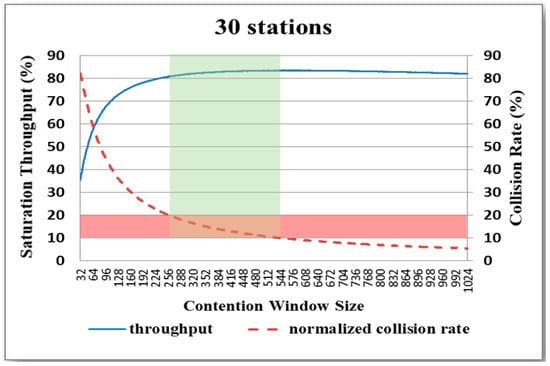
Figure 10. Variation in system throughput and collision rate with CW size for network with 30 nodes.

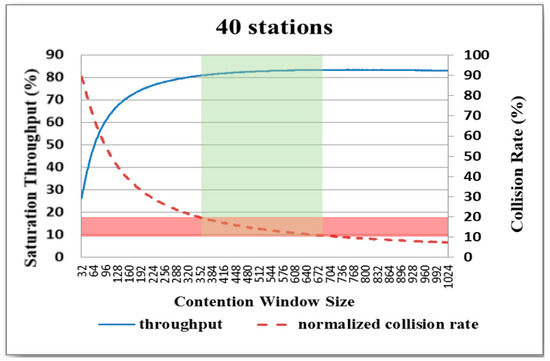
Figure 11. Variation in system throughput and collision rate with CW size for network with 40 nodes.

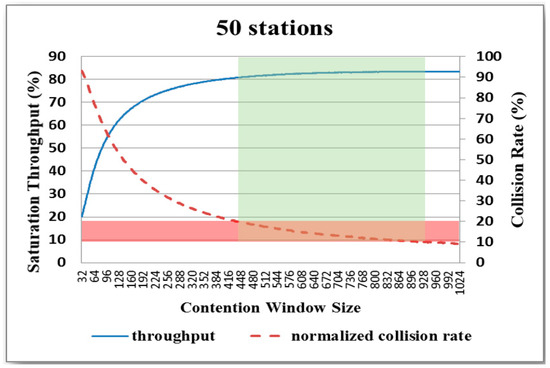
Figure 12. Variation in system throughput and collision rate with CW size for network with 50 nodes.

For each network, the collision rate decreases as the CW size increases. Thus, as described above in Figure 6, the system throughput generally improves with an increasing CW size, particularly as the CW size first increases. An inspection of Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 shows that, for each of the considered networks, the maximum system throughput occurs for collision rates in the range of 0.1–0.2. Importantly, in WLANs, each node is able to determine the collision rate for itself by counting the transmission results. Therefore, as described in the following section, the present study proposes a backoff algorithm in which the system throughput is maximized by controlling the CW size in such a way that the collision rate remains in the interval of 0.1–0.2.

4. Rapidly Adaptive Collision Backoff (RACB) Algorithm

4.1. Analytical Model for Relationship between Optimal CW Size and Collision Rate

To simplify the mathematical analysis, the following assumptions are undertaken: (1) the wireless network operates at saturation conditions; (2) the wireless channel is an error-free medium and (3) the hidden node problem does not exist. Table 2 summarizes the notations used in the mathematical analysis.

Table 2. Notations used in mathematical analysis.

Notations	Meaning
S	System throughput
PI	Probability of channel being idle
PS	Probability of successful transmission over wireless channel
PC	Probability of collision in wireless channel
$p_i$	Probability of node being idle
$p_s$	Probability of successful node transmission
$p_c$	Probability of collision node transmission
E[P]	Packet payload
$\sigma$	Slot time
TS	Average time for which channel is sensed busy due to successful transmission
TC	Average time for which channel is sensed busy due to collision
n	Number of nodes in network
$\tau$	Probability that node transmits
p	Probability of collision in wireless channel
m	Maximum number of backoff stages
CWi	Size of Contention Window after i collisions
bi,CWi−x	Probability that node is in certain state b after i collisions and remaining value of backoff timer is CWi−x

In the proposed model, the system throughput (S) is defined as

$$\mathrm{S}=\frac{\mathrm{p}\mathrm{a}\mathrm{y}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d} \mathrm{i}\mathrm{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{i}\mathrm{n} \mathrm{s}\mathrm{l}\mathrm{o}\mathrm{t} \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}}{\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{l}\mathrm{o}\mathrm{t} \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}}$$

(1)

In other words, S is defined as the fraction of time for which the channel is sensed busy due to the successful transmission of payload packets. S can be elaborated as follows:

$$\mathrm{S}=\frac{P_{S}E\left[P\right]}{P_I\sigma +{ P}_S{T}_S+P_C{T}_C}$$

(2)

where P_S is the probability of a successful transmission over the wireless channel, E[P] is the average packet payload size, T_S is the average time for which the channel is sensed busy due to a successful transmission and P_I is the probability that the channel is sensed idle. In addition, σ is the slot time, P_C is the probability of a channel collision and T_C is the average time for which the channel is sensed busy due to a collision.

T_S and T_C can be formulated as shown in Equation (3), where P* is the average length of the longest packet payload involved in a collision.

$$\left\{\begin{array}{c}{T}_S={PHY}_{hdr}+{MAC}_{hdr}+E\left[P\right]+SIFS+\delta +ACK+DIFS+\delta \\ T_C={PHY}_{hdr}+{MAC}_{hdr}+E\left[P*\right]+DIFS+\delta \end{array}\right.$$

(3)

In calculating the system throughput, the model assumes that the network contains n nodes and each node has a transmission probability of τ. The probability of none of the nodes transmitting over the wireless channel, P_I, is thus provided as

$$P_I={(1-\tau )}^n$$

(4)

Meanwhile, the probability P_S that only one of the n nodes transmits over the wireless channel, while the remaining n-1 nodes remain idle, can be described as

$$P_S=n\tau {(1-\tau )}^{n-1}$$

(5)

Finally, the probability P_C of more than one node attempting to transmit over the wireless channel at the same time is provided by

$$P_C=1-P_I-P_S=1-{(1-\tau )}^n-n\tau {(1-\tau )}^{n-1}$$

(6)

Probabilities P_I, P_S and P_c are calculated from the system perspective. From the node perspective, the equivalent probabilities are denoted as p_i, p_s and p_c, where p_i is the probability that the node is in an idle state (Equation (7)), p_s is the probability that the node achieves a successful transmission (Equation (8)) and p_c is the probability that the node transmission collides in the wireless channel (Equation (9)).

$$p_i=1-\tau$$

(7)

$$p_s={\tau (1-\tau )}^{n-1}$$

(8)

$$p_c=\tau {[1-(1-\tau )}^{n-1}]$$

(9)

In DCF, the size of the CW changes after each transmission attempt. The variation in the backoff window size is shown by the Markov chain model in Figure 13.

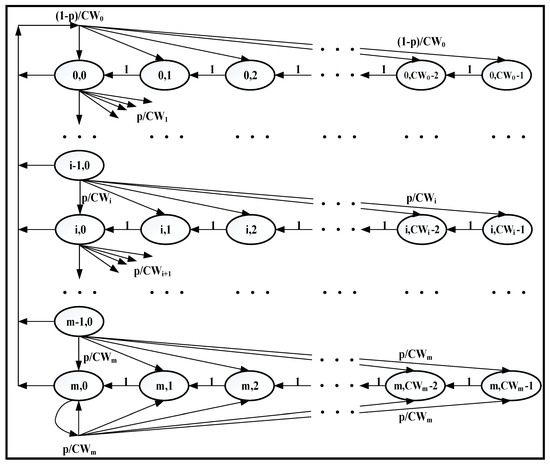
Figure 13. Markov chain model for variation in backoff window size in DCF [5].

In Figure 13, p is the collision probability, CW_i is the CW size after i collisions, m is the maximum number of backoff stages and bi, CW_i−x is the probability that the node is in a certain state b after i collisions and the remaining value of the backoff timer is CW_i−x. In other words, b_i,0 is the probability that the node is in state b after i collisions and the backoff timer is equal to zero. Mathematically, the probability b_i,k can be formulated as

$$\begin{gathered} b_{i-\mathrm{1,0}}\times p=b_{i,0}\to b_{i,0}=p^i\times b_{\mathrm{0,0}} 0<i<m \\ {b}_{m-\mathrm{1,0}}\times p=\left(1-p\right)b_{m,0}\to b_{m,0}=\frac{p^m}{1-p} b_{\mathrm{0,0}} \end{gathered}$$

(10)

Owing to the chain regularities, for each $\mathrm{k}\in (1,\mathrm{C}{W}_i-1)$, it follows that

$$b_{i,k}=\frac{{CW}_i-k}{{CW}_i}\times \left\{\begin{array}{c}\left(1-p\right){\sum }_j^m{b}_{j,0} i=0\\ p\times b_{i-\mathrm{1,0}} 0<i<m\\ p\times \left(b_{m-\mathrm{1,0}}+b_{m,0}\right) i=m\end{array}\right.$$

(11)

By combining Equation (10) and ${\sum }_{i=0}^m{b}_{i,0}=\frac{b_{\mathrm{0,0}}}{1-p}$, Equation (11) can be rewritten as

$$b_{i,k}=\frac{C{W}_i-k}{{CW}_i}{b}_{i,0} i\in \left(0,m\right), k\in (0,{CW}_i-1)$$

(12)

Furthermore, by combining Equations (10) and (12), $b_{i,k}$ can be expressed as a function of $b_{\mathrm{0,0}}$ and p as

$$\begin{array}{l}1={\sum }_{i=0}^m{\sum }_{k=0}^{{CW}_i-1}{b}_{i,k}={\sum }_{i=0}^m{b}_{i,0}{\sum }_{k=0}^{{CW}_i-1}\frac{C{W}_i-k}{C{W}_i}={\sum }_{i=0}^m{b}_{i,0}\frac{C{W}_i+1}{2} \\ =\frac{b_{\mathrm{0,0}}}{2}\left[CW\left({\sum }_{i=0}^{m-1}{\left(2p\right)}^i+\frac{{\left(2p\right)}^m}{1-p}\right)+\frac{1}{1-p}\right]\end{array}$$

(13)

Equation (13) can be simplified to

$$b_{\mathrm{0,0}}=\frac{2(1-2p)(1-p)}{\left(1-2p\right)\left(CW+1\right)+pCW(1-{\left(2p\right)}^m)}=\frac{2(1-p)}{\left(CW+1\right)+pCW(1-{\left(2p\right)}^m)}$$

(14)

The probability τ that a node transmits when the value of the backoff timer is equal to zero can be expressed as

$$\tau ={\sum }_{i=0}^m{b}_{i,0}=\frac{b_{\mathrm{0,0}}}{1-p}=\frac{2}{1+CW+pCW\left(1-{\left(2p\right)}^m\right)}$$

(15)

Taking the CW size as a constant value, Equation (15) can be simplified by setting m = 0 as

$$\tau =\frac{2}{1+\mathrm{C}W}$$

(16)

In other words, for a given value of CW, the transmission probability τ has a constant value. Accordingly, the relationship between the optimal CW size and the maximum system throughput for different numbers of nodes can be obtained as shown in Figure 14. Furthermore, from Equation (16), the relationships between the optimal CW size and the transmission probability, and the transmission probability and the collision rate, respectively, can be obtained as a function of the number of nodes in the network, as shown in Figure 15 and Figure 16.

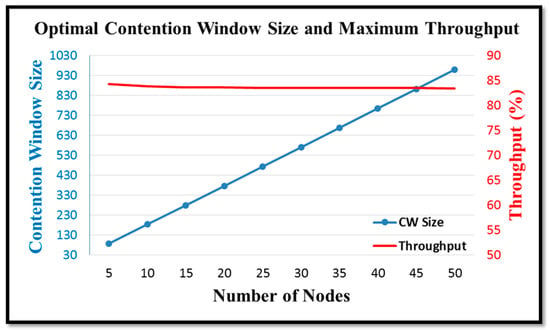
Figure 14. Relationship between optimal CW size and maximum throughput in networks with different numbers of nodes.

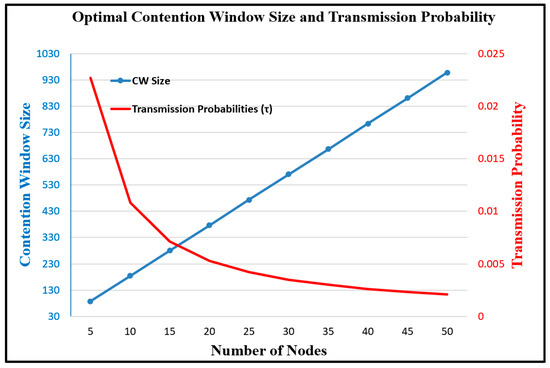
Figure 15. Relationship between optimal CW size and transmission probability in networks with different numbers of nodes.

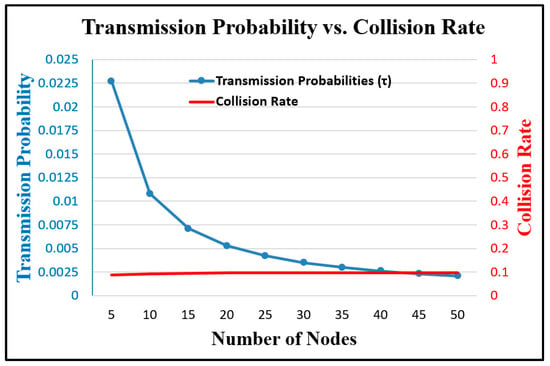
Figure 16. Relationship between transmission probability and collision rate in networks with different numbers of nodes.

Overall, the results presented in Figure 14, Figure 15 and Figure 16 show that the optimal CW size causes the collision rate to approach 0.1 for any number of nodes in the network. Therefore, by adjusting the CW size in such a way that the collision rate of the nodes remains close to 0.1, the system throughput approaches the maximum DCF throughput [14], irrespective of the size of the network.

4.2. CW Size Adjustment in Rapidly Adaptive Collision Backoff (RACB) Algorithm

As in all existing backoff algorithms [1,7,8,9,10,11,12,13], the RACB algorithm proposed in the present study adjusts the CW size after each transmission. However, while existing algorithms adjust the CW size based on the transmission outcome (i.e., success or collision), RACB adjusts the CW size based on the collision rate of the nodes.

RACB combines the respective advantages of EIED and LILD. In particular, as shown in Figure 17, when the collision rate is much higher or much lower than a specified index value, α, the CW size is adjusted exponentially such that the current collision rate of the node is rapidly restored to the target value (i.e., α = 0.1). Conversely, when the collision rate of the node falls between a high threshold value (${\alpha }_{threshold\_high}$) and a low threshold value (${\alpha }_{threshold\_low}$), the CW size is already close to the optimal value. Thus, the CW size is adjusted linearly (rather than exponentially) in order to maintain the collision rate within this interval and maximize the system throughput accordingly.

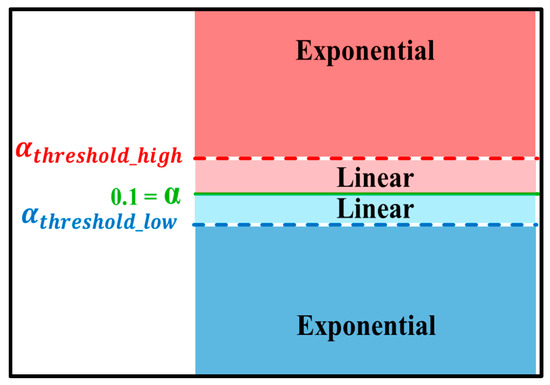
Figure 17. Variation in CW size in RACB algorithm.

The collision rate is a statistical value obtained after several transmissions. In other words, a collision rate of 0.1 indicates that one transmission failed within the past 10 transmissions. Consequently, to adjust the CW size, RACB adopts a Collision Rate Index (CRI) as the current collision rate. Let W_T be the weight of the current collision rate and ($(1-W_T)$) be the weight of the historical collision rate. The CRI is then formulated as

$${CRI}_T=\left(1-w_T\right)\times {CRI}_{T-1}+w_T\times collision$$

(17)

where collision is the transmission result and has a value of 0 for a successful transmission and 1 for a collision.

Figure 18 presents the pseudo code of the RACB algorithm. As shown, the CRI value is updated after each transmission. If CRI_T is higher than ${\alpha }_{threshold\_high}$, the CW size is doubled (CW_i = CW_i−1 * 2) until it reaches CW_max. By contrast, if CRI_T is lower than ${\alpha }_{threshold\_low}$, the CW size is halved (CW_i = CW_i−1/2) until it reaches CW_min. If CRI_T lies between ${\alpha }_{threshold\_high}$ and α, the CW size is increased by CW_min (CW_i = CW_i−1 + CW_min). Finally, if CRI_T lies between α and ${\alpha }_{threshold\_low}$, the CW is decreased by CW_min (CW_i = CW_i−1 − CW_min).

Figure 18. Pseudo code for Rapidly Adaptive Collision Backoff algorithm.

5. Performance Evaluation

5.1. Experimental Environment and Parameter Settings

The performance of the proposed RACB algorithm was compared with that of four existing backoff algorithms (DCF, EIED, LILD and ELBA). The simulations considered the wireless topology shown in Figure 19 with n nodes operating at saturation conditions in an error-free medium with no hidden node problem. The 802.11 WLAN (PHY: DSSS) parameters were assigned the same values as those used in [5] (Table 3).

Figure 19. Network topology.

Table 3. Simulation parameters.

Notations	Meaning
Packet Payload	8184 bits
MAC Header	272 bits
PHY Header	128 bits
ACK	112 bits + PHY Header
Channel Bit Rate	1 Mbit/s
Propagation Delay	1 μs
Slot Time	50 μs
SIFS	28 μs
DIFS	128 μs
CWmin	32
CWmax	1024
Simulation Time	300 s
Number of Nodes	10, 20, 30, 40, 50
α	0.1
wT	0.1
αthreshold_high	0.125
αthreshold_low	0.075

5.2. Numerical Results

Figure 20 and Figure 21 show the simulation results obtained for the variations in the collision rate and system throughput, respectively, with the number of nodes in the network under five different backoff algorithms (BEB, LILD, EIED, ELBA and RACB). Among the existing algorithms, ELBA achieves the lowest collision rate and the highest normalized throughput. However, the throughput still does not approach the ideal maximum value in [14] due to the non-optimality of the CW size.

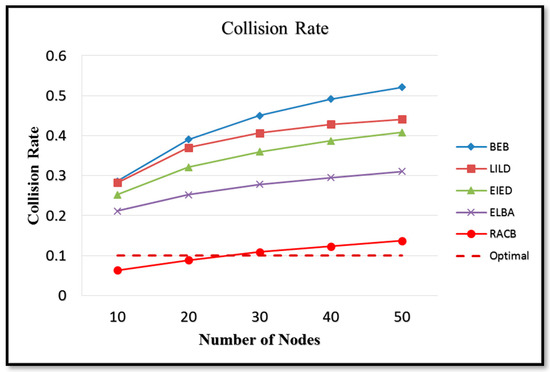
Figure 20. Variation in collision rate with number of nodes under different backoff algorithms.

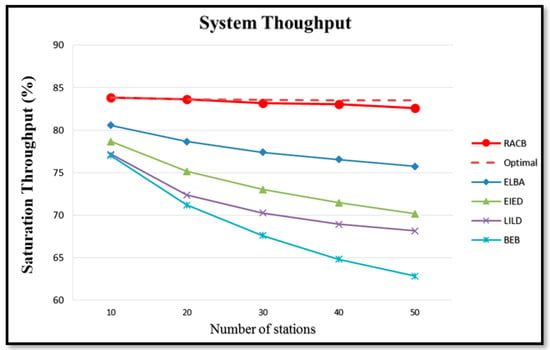
Figure 21. Variation in throughput with number of nodes under different backoff algorithms.

Among all the algorithms considered in Figure 20 and Figure 21, the RACB algorithm achieves the lowest collision rate and the maximum normalized throughput. For all values of n, the normalized throughput is close to the ideal maximum value. As a result, the effectiveness of the RACB algorithm in maximizing the system throughput by adjusting the CW size in such a way as to maintain a collision rate close to 0.1 is confirmed.

6. Conclusions

This study has derived a mathematical model to describe the relationship between the CW size and the collision rate in IEEE 802.11 wireless networks. It has been shown that the system throughput approaches the ideal maximum value for DCF when the collision rate of the network is close to 0.1. Accordingly, a Rapidly Adaptive Collision Backoff (RACB) algorithm has been proposed in which the CW size is adjusted after each transmission in such a way as to maintain the collision rate close to the ideal value of 0.1. Notably, the proposed algorithm can be deployed in both lightly loaded and heavily loaded networks and requires no knowledge of the number of nodes competing for the wireless channel. Furthermore, RACB combines the respective advantages of EIED and LILD in rapidly adjusting the CW size such that it remains close to the optimal size after each transmission. The numerical results have shown that RACB achieves a higher system throughput than the BEB, EIED, LILD and ELBA algorithms proposed in the literature. Future studies will explore the effects of the analytical model assumptions, namely an error-free medium and no hidden node problem, on the system throughput and collision rate [17,18,19,20,21,22,23,24,25,26,27,28,29].