Abstract
Recently, the broad learning system (BLS) has been widely developed in virtue of its excellent performance and high-computational efficiency. However, two deficiencies still exist in BLS and preclude its deployment in real applications. First, the standard BLS performs poorly in outlier environments because the least squares loss function it uses to train the network is sensitive to outliers. Second, the model structure of BLS is likely to be redundant since the hidden nodes in it are randomly generated. To address the above two issues, a new robust and compact BLS (RCBLS), based on M-estimator and sparsity regularization, is proposed in this paper. The RCBLS develops from the BLS model and maintains its excellent characteristics, but replaces the conventional least squares learning criterion with an M-estimator-based loss function that is less sensitive to outliers, in order to suppress the incorrect feedback of the model to outlier samples, and hence enhance its robustness in the presence of outliers. Meanwhile, the RCBLS imposes the sparsity-promoting -norm regularization instead of the common -norm regularization for model reduction. With the help of the row sparsity of -norm regularization, the unnecessary hidden nodes in RCBLS can be effectively picked out and removed from the network, thereby resulting in a more compact network. The theoretical analyses on outlier robustness, structural compactness and computational complexity of the proposed RCBLS model are provided. Finally, the validity of the RCBLS is verified by regression, time series prediction and image classification tasks. The experimental results demonstrate that the proposed RCBLS has stronger anti-outlier ability and more compact network structure than BLS and other representative algorithms.
1. Introduction
Over the past few years, deep learning has attracted considerable research interest in the field of artificial intelligence for its outstanding performance. However, deep learning methods also have some shortcomings, such as complicated network structures, time-consuming learning processes, poor interpretabilities, and so on. To alleviate this situation, Chen and Liu [1] recently proposed a novel neural network learning framework called the Broad Learning System (BLS). Unlike deep networks, BLS is built to construct neural networks via a broader application. In BLS, the original input data are first mapped into a group of feature spaces through feature learning. Then, the mapped features are further enhanced by nonlinear transformation. Finally, all the mapped and enhanced features are broadly concatenated and fed to the output layer, and the desired output weights are usually obtained by optimizing a regularized least squares (LS) problem. Compared with traditional deep learning methods, BLS has two distinct advantages [2]. First, drawing on the random learning theory of random vector functional link neural network [3], all the learning parameters used for feature mapping and feature enhancement in BLS are generated randomly and remain unchanged, then the output weights are the only model parameters that can be determined analytically, without iterative adjustments, thus making the learning process of BLS very efficient. Second, the model structure of BLS is very flexible, and it can be easily expanded to the incremental learning mode when there are new neural nodes or training samples. Plenty of experimental results on representative benchmarks and practical applications have demonstrated that BLS can learn thousands of times faster than traditional deep learning models, while obtaining a comparable or even better learning accuracy [1,4].
1.1. Related Work
Due to its strong generalization capability and superior learning efficiency, BLS has attracted extensive attentions from both academia and industry, and various improvements and expansions have been made to it [4]. As a novel neural network model, BLS has much room for network structure expansion, and many BLS-based structural variants have been constantly proposed, such as cascade BLS [5], deep cascade BLS [6], intergroup cascade BLS [7], stacked BLS [8], recurrent BLS and gated BLS [9,10], cascade BLS with dropout or dense connection [11], incremental multilayer BLS [12], etc. By introducing Takagi–Sugeno fuzzy systems into BLS, a new fuzzy BLS was established [13] and studied deeply [14,15,16,17,18]. Aiming at the imbalance learning problem, a kernel-based BLS [19] with a double kernel-mapping mechanism and an adaptive weighted BLS [20], with a density-based weight generation scheme, were put forward, respectively. To cope with datasets with a few labeled samples, the BLS was extended based on the manifold regularized sparse autoencoder method to develop a semi-supervised BLS [21]. To expand the capability of BLS in big data scenarios, a new hybrid recursive implementation of BLS was presented in [22]. In order to explain why BLS works well, the literature [23] has provided some theoretical interpretations of BLS from the perspective of the frequency domain. Recently, reinforcement learning has been widely introduced into BLS for performance improvement [24,25,26]. In addition, BLS and its variants have been widely applied to many practical applications, such as industrial intrusion detection [27], driver fatigue detection [28], disease detection [29,30,31], tropical cyclogenesis detection [32], intelligent fault diagnosis [33,34,35], license plate recognition [36], indoor fingerprint localization [37], air quality forecasting [38], photovoltaic power forecasting [39], stock price prediction [40], traffic flow prediction [41], machinery remaining useful life prediction [42], static voltage stability index prediction [43], time series prediction [44,45,46,47] and many others.
Although BLS has made great strides in many fields, it still suffers from the following two drawbacks. First, it lacks robustness to outliers. In standard BLS, the LS is taken as the default optimization criterion to train the model. The LS criterion can provide good performance in clean or Gaussian data environments, but it is very sensitive to outliers, which will severely degrade the performance of BLS when the training data are corrupted by outliers. To improve this situation, several robust versions of BLS have been proposed. In [48], three robust broad learning systems (RBLS) with different regularizers were developed to handle the data modeling with outliers contaminated. The core idea of RBLS is to use a -norm-based loss function as the optimization criterion for training, in order to improve the robustness of the models. In [49], several weighted penalty factor methods were applied to BLS to deal with outliers, and then the weighted BLS (WBLS) was put forward. By using the weighted penalty factor to constrain each sample’s contribution to modeling, the adverse effects of abnormal samples can be greatly reduced. Inspired by the robustness characteristic of correntropy, the maximum correntropy criterion (MCC) was adopted to train the BLS, generating a correntropy-based BLS (CBLS) [50]. Because of the intrinsic advantages of MCC, CBLS can achieve good performance in both outlier and noise-free environments. Additionally, a graph regularized robust broad learning system (GRBLS) [51] and a progressive ensemble kernel-based broad learning system (PEKB) [52] were recently proposed for noisy data classification. Though the above robust BLS variants are potential candidates when the training data contain outliers, they still have certain limitations. For instance, both RBLS and WBLS are primarily developed to handle single-output regression problems, but cannot cope with multi-output regression and multi-classification problems. Similarly, both GRBLS and PEKB are stinted on classification problems other than regression problems. As for CBLS, its robustness depends heavily on the kernel size, but how to determine this parameter is difficult under a lack of guidance. Therefore, the development of a more general robust BLS model remains to be further studied.
Another drawback of BLS is that its network structure may be redundant. As a kind of random neural network, BLS generates feature nodes and enhancement nodes by random projection. This randomness makes BLS very efficient in training. However, due to the instability and uncertainty of random projection, it is easy to produce redundant and irrelevant hidden nodes. These unnecessary hidden nodes not only increase the complexity of the BLS model and bring more computational overhead, but also degenerate its performance in turn due to overfitting. For this problem, targeted research work is insufficient. In [53], a new feature reduction layer based on sparse preservation projection was constructed and integrated into BLS to remove redundant or noisy information embedded in high-dimensional data, thus greatly improving the training efficiency and accuracy of large-scale multi-label classification. In [54], a joint regularization method was utilized to constrain the output weights of BLS for feature selection, in order to avoid the negative effects of feature redundancy and overfitting. Similarly, Miao et al. [55] applied a combined sparse regularization method to BLS to remove unnecessary feature information and thus boost classification performance. Nevertheless, these efforts are mainly focused on improving the performance of BLS for specific tasks through feature reduction [53] or feature selection [54,55], while research on the model structure simplification of BLS has not attracted enough attention. Therefore, how to pick out and eliminate the useless hidden nodes in BLS, in order to build a lightweight BLS model, is still an open problem to be solved.
1.2. Our Work
To address the above two concerns simultaneously, in this paper, we propose a novel, robust and compact broad learning system (RCBLS) for noisy data modeling. Different from the common BLS models that use LS as the Learning Criterion, the proposed RCBLS adopts a robust M-estimator-based loss function to train the model, in order to attenuate the adverse impacts of outliers and improve its anti-interference ability to outliers. Meanwhile, the RCBLS employs a new -norm regularization to replace the traditional -norm regularization for model reduction (the -norm and -norm are defined in Equations (1) and (2), respectively, in Section 2.1). As a sparsity promotion regularization method, the -norm regularization encourages row sparsity and can automatically compress the output weights corresponding to redundant hidden nodes to zero, which helps eliminate unnecessary hidden nodes and results in a more compact network. Extensive experiments on benchmark datasets are conducted to verify the effectiveness of the proposed method.
The key contributions of our work are as follows:
- A unified and general robust broad learning framework, called RCBLS, is proposed for noisy data regression and classification. By exploiting the robustness property of the M-estimator technique, different M-estimator functions such as Huber, Bisquare and Cauchy can be incorporated into RCBLS as optimization criterion to realize robust learning.
- Within this framework, the sparsity-promoting regularization with -norm is employed for model structure simplification. To the best of our knowledge, this is the first work that unifies the M-estimator and the sparse regularization into one single framework to build a robust and compact BLS model.
- An efficient optimization algorithm is devised to solve the RCBLS model. Additionally, the robustness, compactness and computational complexity of the proposed method are analyzed theoretically and verified empirically.
The rest of the paper is organized as follows. Section 2 provides the preliminaries of this paper. Section 3 presents the details of the proposed RCBLS. In Section 4, the robustness, compactness and computational complexity of RCBLS are analyzed theoretically. In Section 5, the performance of RCBLS is verified by multiple problems including regression, time series prediction and image classification. Finally, the conclusions and aims of future work are provided in Section 6.
2. Preliminaries
2.1. Notations
To ensure the readability and completeness of this work, we first summarize the notations used in the paper. Scalars are written in lowercase italics, vectors are written in lowercase boldface, and matrices are written in uppercase boldface. For matrix , its i-th row, j-th column are denoted by , respectively, and the (i, j) element of is declared as . The inverse matrix and transposed matrix of are denoted as and , respectively. The Frobenius norm (-norm) of is defined as
The -norm of is defined as
Here represents the -norm of the row vector , which is defined as .
2.2. BLS
BLS is an emerging neural network learning framework that has been proposed recently, and its typical structure is depicted in Figure 1. As the name implies, BLS is built in a broad sense rather than a deep manner, and the detailed establishment process is described below.
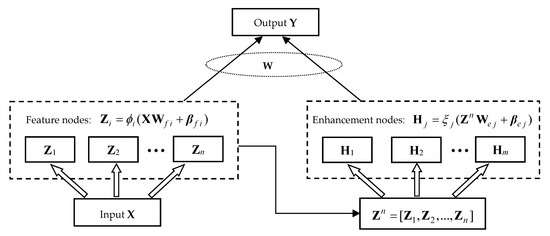
Figure 1.
Structure of BLS.
For a given training dataset , where N is the number of training samples, d is the dimension of the input , and c is the dimension of the output . First, the input data are mapped into n groups of random feature spaces in “feature nodes”:
where is usually a linear activation function for feature mapping, and are, respectively, the randomly generated weights and biases of the i-th feature mapping group, and p is the number of feature nodes in each group. Denote the concatenation of all the n groups of feature nodes as , and which are further transformed to generate m groups of enhancement features in the “enhancement nodes”:
where is usually a nonlinear activation function for feature enhancement, and are, respectively, the randomly generated weights and biases of the j-th enhancement group, and q is the number of enhancement nodes in each group. Similarly, denotes the concatenation of all the m groups of enhancement nodes.
Finally, all the feature and enhancement nodes are concatenated together and linked to the output layer; therefore, the BLS model can be expressed as:
where is a transformed feature representation of the original input X by feature mapping and feature enhancement, are the output weights between the hidden layer and output layer, and denotes the total number of feature and enhancement nodes. As mentioned above, all the feature nodes in and all the enhancement nodes in are randomly generated and stay the same, then the broad feature matrix is a constant matrix. Therefore, training a BLS is now reduced to finding a LS solution of the linear system . In standard BLS, the following objective function with -norm regularization is usually used to optimize :
where is the sum of squared training errors, which represents the loss, is the squared -norm of the network output weights, which acts as a regularizer, and λ is a regularization parameter to balance the two items and enhance the generalization ability of the model.
Then, setting the derivative of Equation (6), with respect to equal to zero, we finally obtain the optimal output weights as
where is an identity matrix.
3. The Proposed RCBLS
In this section, a novel, robust and compact broad learning system (RCBLS), combining M-estimator technique and sparse regularization method, is proposed. First, we present a unified learning framework of RCBLS. Next, an iterative optimization method is derived to solve the model, and then a complete RCBLS algorithm is summarized.
3.1. The RCBLS Model
As mentioned in Section 2.2, the standard BLS uses LS as the loss function, which aims to minimize the sum of squared training errors. That is, Equation (6) can be equivalently rewritten as
where is the residual between the actual observation and the network output corresponding to the i-th training sample. Although LS loss is a good choice in a clean data environment, it is very sensitive to outliers and prone to generate overfitting models, resulting in serious performance degradation of BLS in the presence of outliers. Intuitively, contaminated training samples, such as outliers, will produce large estimation errors, while the square operation used in LS may amplify them further, making the objective function highly biased and thus causing the learned model to be inaccurate. Therefore, employing robust metrics instead of the traditional LS criteria is more likely to overcome outliers and obtain robust BLS models.
In addition, due to the random generation rules of feature nodes and enhancement nodes, the obtained broad feature matrix in BLS may contain redundant and irrelevant components, especially when the number of feature nodes and enhancement nodes L is large. As shown in Equation (8), the general BLS model usually uses the -norm-based regularizer in the objective function for optimization. As a common choice, the -norm regularization is capable of avoiding overfitting and improving the generalization capability of the model, but it is powerless to eliminate redundancy. More specifically, by constraining with -norm, Equation (8) usually produces a dense solution for the output weights, in which all the values are discretely distributed in a non-zero form. This means that, for all the feature and enhancement nodes that connect the output weights, they play a certain role within the network and should be retained in the final BLS model. That is to say, the default -norm regularization is prone to train a large and redundant BLS model due to the non-zero output weights of the network. In contrast, sparse regularization methods tend to produce sparse solutions with partial components of zeros, which is conducive to eliminating unnecessary hidden nodes and improving the compactness of the BLS model.
Based on the above analysis, we introduce the M-estimator robust learning framework and -norm-based sparse regularization method into BLS, and propose a new RCBLS model, whose objective function can be formulated as
where is an M-estimator function, and denotes the -norm of a matrix, which is defined as Equation (2). Compared with the original BLS, the proposed RCBLS mainly has the following two improvements.
First, RCBLS adopts a robust M-estimator function to replace the traditional LS as a loss function. The M-estimator is one of the most popular approaches to combat outliers, and its basic idea is to use some mild piecewise functions as the fitness measure [56]. When the training residual is significantly large, its growth trend is more gentle than that of the LS estimator or even remains unchanged, in order to alleviate the adverse impacts of outlying residual errors. As a unified robust learning framework, a variety of M-estimators can be applied as , such as Huber, Bisquare, Cauchy, and their definitions and robustness analyses will be provided in Section 4.1.
Second, instead of using the common -norm regularization, a new -norm-based sparse regularizer is imposed in our RCBLS for generalization improvement, as well as structure simplification. As a sparsity promotion regularization method, the -norm regularization penalizes each row of as a whole and enforces sparsity among rows. Then, the derived solution is row sparse, in which many of the weight vectors are zero vectors. This means that the corresponding hidden nodes connecting zero weights are useless and can be deleted from the network, thus achieving a compact and lightweight network. A more detailed compactness analysis of RCBLS will be presented in Section 4.2.
3.2. Optimization of RCBLS
The objective function in Equation (9) is convex but non-smooth, so it cannot be solved analytically. Here, an efficient iterative optimization method based on augmented Lagrangian multiplier is devised to solve this problem. According to the KKT theorem, optimizing Equation (9) is equivalent to solving the following dual optimization problem:
where are the output weights to be solved, , in which are the residual errors corresponding to the i-th sample, , in which are the Lagrangian multipliers for the i-th equality constraint in Equation (9).
Taking the derivatives of in Equation (10), with respect to , , , respectively, and setting the derivatives to zero, we arrive at:
where is a diagonal matrix with the j-th diagonal element , that is
Since is a coefficient matrix corresponding to the derivation of the -norm regularization term, we call it the regularization matrix.
Defining
as the weight function, with respect to M-estimator , and letting , Equation (11) can be rewritten into the following matrix form:
where is the weight matrix.
Then, multiplying both sides of (14c) by , we obtain
Substitute Equation (14b) into Equation (14a), we have
Substitute Equation (16) into Equation (15), we have
Consequently, we obtain the analytic solution of output weights as
By comparing Equations (18) and (7), it can be seen that the main difference between RCBLS and BLS is that two matrices, the weight matrix and the regularization matrix , are added to the analytic solution of RCBLS. The essence of the weight matrix is to reversely assign different weights to each sample according to their training errors, in order to reduce the disturbances of outlier samples to the model. The regularization matrix is introduced as an auxiliary variable to solve the -norm optimization problem, in order to achieve a sparse solution.
In addition, we can observe from Equation (18) that the computing of relies on and , while and also depend on . So, it is impractical to calculate directly. In this work, we design an iterative method to solve this problem by computing , and alternately. More specifically, in each iteration, the values of and are first calculated with the current , then is updated based on the newly calculated and . The iteration process is repeated until reaching the maximum number of iterations. By incorporating the above iterative optimization process, Algorithm 1 describes the complete procedure of our RCBLS.
It is worth noting that in step 15 of the RCBLS algorithm, when , then the corresponding will tend to infinity. In this case, the proposed algorithm cannot be guaranteed to converge. So, in the implementation of our RCBLS, we regularize as , where is a very small constant to avoid the denominator being zero. It is easy to see that approximates when .
| Algorithm 1: Robust compact broad learning system (RCBLS) |
 |
4. Discussions
In this section, we theoretically analyze the outlier robustness, structural compactness and computational complexity of the proposed RCBLS.
4.1. Robustness Analysis
As stated in Section 3, the adoption of M-estimator and its corresponding weighting strategy is the key to ensure the strong robustness of RCBLS. The commonly used M-estimators mainly include Huber, Bisquare, Cauchy, etc. [56], and their cost functions, weight functions and default parameters are listed in Table 1. Next, we take Huber as an example for robustness analysis. For ease of interpretation, the typical curves of the cost function and weight function of Huber are depicted in Figure 2. From Table 1 and Figure 2, it can be analyzed that when the error e is less than or equal to the threshold k, it means that the current observation is a normal sample, then the cost function of Huber is equivalent to the ordinary LS function, and the corresponding weight of the sample is 1. On the other hand, when the error e is greater than k, it indicates that the current observation is likely to be an outlier. Then, a weight less than 1 is assigned to the sample, and the weight decreases monotonically with the increase of the error, that is, the larger the error, the smaller the weight. Through this reverse weighting strategy, large perturbations stemming from outliers can be effectively suppressed and the sensitivity of the model to outliers can be significantly reduced. The robustness analyses of other M-estimators are similar to that of the Huber, except for a slight difference in the weighting skills. Due to space limitation, we will not reiterate them here.

Table 1.
List of cost functions, weight functions and default parameters for three typical M-estimators.
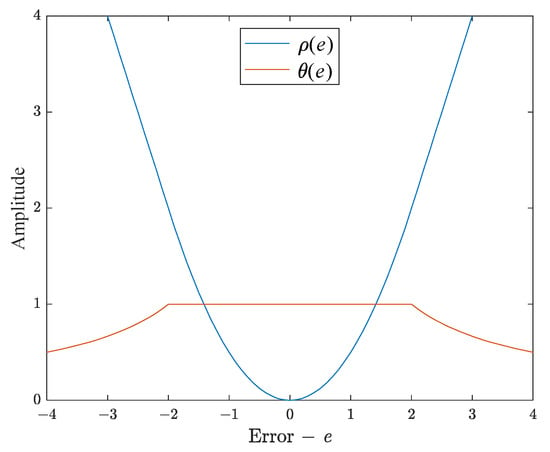
Figure 2.
Curves of cost function and weight function of Huber with k = 2.
From the perspective of robustness learning, the threshold k can be regarded as the tolerance degree of M-estimator function to outlier residuals, which has an important impact on the robustness and generalization performance of the RCBLS. A smaller value of k can produce stronger resistance to outliers, but it increases the probability of normal samples being misjudged as outliers, which makes the learning process insufficient. Conversely, a larger value of k increases the risk of outliers being misjudged as normal samples, resulting in inaccurate models. According to the robust statistics theory [57], the threshold k can be determined as
where tuning is an adjustment parameter, and its default values for three typical M-estimators are shown in Table 1; is the estimated standard deviation of the training errors, and a commonly used robust estimator of in outlier environment is provided as
where med(·) represents the median operation, and the constant value 0.6745 is introduced to make an unbiased estimator for Gaussian errors [57].
4.2. Compactness Analysis
The original BLS uses the random projection method to generate feature and enhancement nodes, which avoids the tedious training process and greatly reduces the computational cost, but at the same time makes the generated neural network model redundant. More specifically, because of the instability and uncertainty of random projection, the obtained broad feature matrix inevitably contains a certain number of redundant hidden nodes. However, since the -norm regularization used by default in BLS does not have sparsity, the resulting solution of the output weights is usually dense. That is to say, all the hidden nodes in , including redundant ones, are endowed with certain connection weights and should be retained in the network, which makes the structure of BLS very bloated.
As an improvement, the proposed RCBLS imposes a new sparse regularizer with -norm in the objective function to optimize the output weights. Since the introduced -norm regularization encourages row-level sparsity, the derived output weights matrix contains many zero rows. The row sparsity of the obtained is of great significance for further model reduction. First, from the perspective of network structure analysis, the row vector of represents the output weights between the i-th hidden node and all output nodes. Therefore, a of the zero vector means that all the connection weights from the current hidden node to each output node are zeros. Obviously, this hidden node and its out-going connections are unnecessary and can be removed from the network (highlighted in red in Figure 3a). In this way, a lightweight network with only necessary hidden nodes can be obtained. Moreover, the sparsity analysis and model reduction of RCBLS can also be explained from the perspective of model optimization. As discussed in Section 2.2, training a BLS model is equivalent to solving the linear system , where , . According to the rules of matrix multiplication, the elements in the i-th column of are multiplied by the elements in the i-th row of , respectively. That is, the i-th column of is corresponding to the i-th row of . Hence, for these zero rows, in , their corresponding columns (also known as the i-th hidden node) in are considered useless and can be deleted, and only the other columns in , corresponding to the non-zero rows of , are useful and should be preserved in the network. As an example, Figure 3b shows the model reduction process by setting N = 6, L = 5, c = 3. In this example, the first, third, and fifth rows in are zero rows. Therefore, we are able to remove the corresponding hidden nodes in the first, third and fifth columns in , in order to obtain a much simpler model. In summary, with the help of the row sparsity of the -norm regularization, our RCBLS is prone to generate a compact network with fewer hidden nodes.
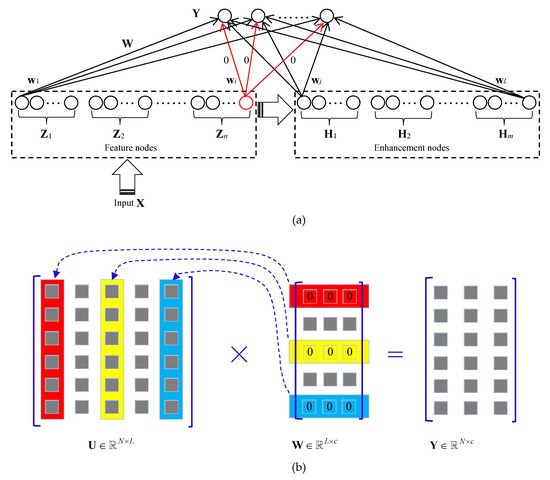
Figure 3.
Model reduction by sparse output weights. (a) From the perspective of network structure analysis. (b) From the perspective of model optimization.
4.3. Computational Complexity Analysis
Finally, we analyze the computational complexity of the proposed RCBLS. Using the same notations as in Algorithm 1, we simply set , , , , where N denotes the number of training samples, L denotes the total number of feature and enhancement nodes, and c denotes the dimension of training outputs. From Algorithm 1, we can see that the main computational overheads of RCBLS come from the calculations of the output weights in steps 11 and 16, while the computational costs of other steps are insignificant and negligible. In step 11, the complexity in calculating the initial is , where is the computational cost of the matrix inversion operation, and are the computational costs of three separate matrix multiplication operations. In general, , so the computational complexity in step 11 could be simplified as . In step 16, the complexity in calculating in each iteration is , where is the computational cost of matrix inversion operation, and are the computational costs of five separate matrix multiplication operations. For the same reason above, the computational complexity in step 16 could be simplified as . Hence, the overall computational complexity of RCBLS is , where t is the number of iterations. Empirical results in Section 5.5 will show that the convergence of RCBLS is fast and can converge to a stable value within only a few iterations, usually less than 10. Therefore, the computational efficiency of the proposed algorithm can be guaranteed in theory.
Compared to the original BLS with a computational complexity of , the added computational complexity of our RCBLS is , which is produced by iterative optimization calculations. Though the complexity of RCBLS is somewhat higher than that of the original BLS, it is acceptable to trade a little more computation time for the desired robustness improvement and structure simplification.
5. Experiments
In this section, extensive experiments, including regression, time series prediction and image classification, are carried out for performance evaluation. Since the proposed RCBLS is a unified robust learning framework based on M-estimator, three typical M-estimators, Huber, Bisquare and Cauchy, are selected for empirical research, and the corresponding algorithms are denoted as Huber-RCBLS, Bisquare-RCBLS and Cauchy-RCBLS, respectively. To demonstrate the effectiveness and superiority of the proposed algorithms, the experimental results of our RCBLS are compared with that of the original BLS [1], FBLS [13] and WBLS [49]. For regression and time series prediction problems, the root mean squared error (RMSE) is used to measure the performances of the algorithms. For image classification problems, the testing accuracy is adopted for performance evaluation. To make the experimental results more convincing, ten independent experimental runs are performed for each experiment, and the obtained experimental results are statistically analyzed and reported. Our experiments are conducted in the MATLAB R2016a software platform running on a laptop with a 2.9 GHZ CPU and 16 GB RAM, except for special explanations.
5.1. Robustness Evaluation on Regression Problems
We first evaluate the performances of RCBLS on six widely used regression datasets, which are detailed in Table 2. To assess the robustness of the methods, for each dataset, a certain proportion of training data are randomly selected and contaminated by outliers, while the testing data remain clean. Specifically, for the selected training sample (xi, yi), a random value between [ymin, ymax] is added to replace the corresponding output yi. In our study, the percentage of contaminated training samples to the total training samples is called the outlier level and denoted as R. In this experiment, four outlier levels are considered, i.e., R = 0%, 10%, 20% and 30%.

Table 2.
Specification of six regression datasets.
Six BLS-related algorithms, namely BLS, FBLS, WBLS, Huber-RCBLS, Bisquare-RCBLS and Cauchy-RCBLS, are used to model the contaminated datasets, and the experimental settings are as follows. For BLS, Huber-RCBLS, Bisquare-RCBLS and Cauchy-RCBLS, the common parameters to be set mainly include: the number of feature nodes per group p, feature nodes groups n, the number of enhancement nodes per group q, enhancement nodes groups m, and the regularization parameter λ. Referring to [1], we first set m = 1, and the other four parameters (p, n, q, λ) are determined by the grid search method, whose search spaces are {2, 4, …, 18, 20}, {2, 4, …, 18, 20}, {10, 20, …, 190, 200}, {10−10, 10−9, …, 104, 105}, respectively. Additionally, the maximum number of iterations tmax is uniformly set to 20 in our three RCBLS algorithms. For WBLS, since the feature mapping parameters p and n are not used, the key model parameters of this algorithm mainly include (q, λ), which are selected by grid search with the same search ranges as above. For FBLS, referring to [13], the key model parameters (Nr, Nt, Ne, λ) are decided by a similar grid search method, whose search spaces are {1, 2, …, 19, 20}, {1, 2, …, 9, 10}, {1, 2, …, 99, 100}, {10−10, 10−9, …, 104, 105}, respectively.
Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 report the experimental results of all comparison algorithms on six regression datasets with different outlier levels, including the optimal parameters, mean of training time, mean and standard deviation (SD) of testing RMSE. For the Parameters column, it corresponds to (p, n, q, λ) for BLS, Huber-RCBLS, Bisquare-RCBLS and Cauchy-RCBLS, (q, λ) for WBLS, (Nr, Nt, Ne, λ) for FBLS, in which the last value in parentheses denotes the power of the regularization parameter of the corresponding algorithm. That is, the real regularization parameter is (the same below). For the RMSE column, its best mean results for each dataset are shown in bold. The following results can be obtained from Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8:

Table 3.
Performance comparison of different algorithms on Abalone.

Table 4.
Performance comparison of different algorithms on Bodyfat.

Table 5.
Performance comparison of different algorithms on Housing.

Table 6.
Performance comparison of different algorithms on Mortgage.

Table 7.
Performance comparison of different algorithms on Strike.

Table 8.
Performance comparison of different algorithms on Weather Izmir.
- (1)
- When the training set does not contain outliers, i.e., R = 0%, the performances of all the six algorithms are basically equivalent. Especially on the Bodyfat, Mortgage and Strike, our RCBLS even achieves the smallest testing RMSE. This indicates that the proposed robust learning model is also suitable for clean data modeling in non-outlier environments.
- (2)
- When the training set contains outliers, the testing RMSE of BLS and FBLS increase rapidly with the increment of the outlier level, which indicates that these two algorithms are very sensitive to outliers. By contrast, as the outlier level increases, the testing RMSE of WBLS and the three RCBLS algorithms proposed in this paper only increase slightly, or even remain basically unchanged in some cases, showing their stronger resistance to outliers. But due to the abandonment of the feature mapping process, the performance of WBLS is not stable. For example, on the Bodyfat dataset, the testing RMSE of WBLS is much worse than our RCBLS. In addition, for all datasets at different outlier levels, except for the Abalone dataset under R = 10%, the optimal testing RMSE are all obtained by our RCBLS. From the above results, it can be concluded that our RCBLS performs best among all comparison algorithms in outlier environments.
- (3)
- By comparing the three proposed RCBLS algorithms, Huber-RCBLS, Bisquare-RCBLS and Cauchy-RCBLS, which incorporate different M-estimator functions, we can see that their learning performances are basically the same in most cases, and they can obtain the optimal results in different testing cases, respectively.
- (4)
- In terms of training time, due to the iterative optimization calculations in the learning process, our RCBLS algorithms take a little more training time than the original BLS, but their training times are usually only a few tenths of a second and still maintain a high learning efficiency.
To sum up, compared with other algorithms, our RCBLS can provide comparable performance in non-outlier environments and much better results in outlier environments without sacrificing much learning efficiency, showing good effectiveness and practicability for regression problems.
5.2. Robustness Evaluation on Time Series Prediction
In this section, four classical chaotic time series, Henon, Logistic, Lorenz and Rossler, are utilized to further verify the robustness of BLS, FBLS, WBLS and our RCBLS. The length of each time series is 2000, of which 1500 samples are used for training and 500 samples are used for prediction. For robustness evaluation, some outliers are added to the training set of each time series to replace the normal samples in order to construct the contaminated time series, while the testing set remains outlier-free. The manually added outliers are randomly generated between the minimum and maximum values of the corresponding training set.
Phase space reconstruction is a basic step in time series modeling and prediction, which is mainly used to reconstruct the input space and output space from the original time series. In our experiments, the phase space reconstruction parameters of each time series, namely, the embedding dimension and time delay, are empirically set as follows: four and one for Henon and Logistic, nine and one for Lorenz, one and five for Rossler, respectively. It should be noted that, different from the regression datasets in Section 5.1 where only the target output of the training samples contains outliers, in the reconstructed time series here, both the input and output of the training samples contain outliers. Apart from that, the experimental settings of each algorithm in this part are exactly the same as those in Section 5.1.
Table 9 shows the parameter settings and comparison results of different algorithms on the polluted time series. As can be seen from Table 9, for all four chaotic time series contaminated by outliers, the proposed RCBLS algorithms can always obtain the best or approximate best prediction results, in comparison with other competitive algorithms, showing stronger anti-outlier ability and robustness. In addition, the experimental results demonstrate that our RCBLS algorithms are also applicable and effective when both the input and output of the training samples contain outliers.

Table 9.
Performance comparison of different algorithms on contaminated time series.
5.3. Robustness Evaluation on Image Classification
In addition to regression and time series prediction, we further evaluate the effectiveness of our method for image classification problem in this section. The used benchmark here is the popular NORB dataset, which consists of 48,600 images of 50 different 3D toy objects belonging to five distinct categories: cars, trucks, airplanes, humans, and animals. Among them, half of the images are selected for training and testing, respectively. To test the robustness of RCBLS, the learning with corrupted labels is considered in this example. Following [58], we manually corrupt the original clean dataset by a noise transition matrix Q, where means that noisy label is flipped from clean label y. Specifically, a typical asymmetric structure called “pair flipping” is applied to construct Q:
where R is the outlier level to control the ratio of noisy labels. Here, R is selected from {30%, 40%, 45%} to test the performance of our RCBLS in extremely noisy environments.
Since WBLS is stinted on single-output regression tasks and cannot handle multi-classification problems, only the original BLS and FBLS are used here as comparison algorithms. Referring to [1], the common model parameters for BLS and RCBLS are set the same as (p, n, q) = (100, 10, 5000), and the regularization parameter λ is selected by the grid search method. For FBLS, in order to be fair, we first set the number of enhancement nodes to the same 5000, and the other parameters of the algorithm are determined by the grid search method. Moreover, since the original machine configuration is not capable of performing such a large-scale image classification task, all the algorithms are implemented on a workstation equipped with a 3.7 GHz CPU and 64 GB RAM.
Table 10 reports the comparison results of BLS, FBLS and RCBLS on Norb dataset at different outlier levels. As can be seen from Table 10, though our RCBLS algorithms require more training time in comparison with BLS, they are still more efficient than FBLS. In addition, under different outlier levels, our three RCBLS algorithms can always obtain significantly higher recognition accuracy than BLS and FBLS, and the higher the outlier level, the more obvious the advantage. For example, when R = 45%, the testing accuracy of Bisquare-RCBLS is 10.48% higher than the standard BLS and 10.07% higher than the FBLS. This experiment proves that the proposed RCBLS algorithms are also effective for classification problems with corrupted labels.

Table 10.
Performance comparison of BLS, FBLS and RCBLS on Norb with corrupted labels.
In fact, for the datasets used in the above three experiments, except for the time series datasets which are artificially generated, the regression datasets and the classification dataset are all datasets from the real world, and our method has achieved the expected results in all experiments. Therefore, it is reasonable to conclude that our method can function well and effectively in real world solutions.
5.4. Compactness Comparison
In this section we take Norb as an example for compactness comparison of our model structure. To better demonstrate the benefits of using -norm regularization in our RCBLS, the original BLS, with -norm regularization, is chosen as a typical representative for comparison. In this experiment, the parameter settings of BLS and RCBLS are exactly the same as in Table 10. That is, there are 1000 feature nodes and 5000 enhancement nodes in the networks. Accordingly, the size of the output weights to be solved in both BLS and RCBLS is 6000 × 5, here 5 denotes the number of classes in Norb. After training, we obtain the , and all weights under 10−3 in absolute value are set to 0.
Table 11 shows the model parameters and the corresponding compactness results of BLS and our three RCBLS on the Norb dataset. Since the network structure parameters (p, n, q) = (100, 10, 5000) are the same for all models, only the regularization parameters λ are given for brevity. In addition, here, we use Sparsity as a metric to measure the structural compactness of each model, which is measured as the proportion of all-zero rows in , or the percentage of the hidden nodes whose output weights are all zero with respect to the total number of hidden nodes in the network. From Table 11, we can draw the following two key conclusions. Firstly, our RCBLS model is more likely to generate sparse and compact networks than the original BLS. Since BLS adopts a non-sparse -norm regularization in the objective function for optimization, the obtained output weights are very dense, with a sparsity of 0% at different outlier levels. In contrast, by employing the -norm regularization, our RCBLS tends to produce row-sparse output weights, in which many row vectors are all zero. For example, when λ = 10−1, more than 70% of the output weight vectors in RCBLS are zero, which implies that most of the hidden nodes and their output connections are useless and can be removed from the network, thus greatly improving the compactness of the network structure. Secondly, the regularization parameter λ has great influence on the sparsity (compactness) of RCBLS. Specifically, the larger the λ, the higher the sparsity and the more compact the model.

Table 11.
Compactness comparison of BLS and RCBLS on Norb.
Further, we visualize the learned output weights matrices of BLS and RCBLS on the Norb dataset in Figure 4 for a more intuitive comparison of their sparsity and compactness. Since our three RCBLS all have similar sparsity behavior, here we just take Huber-RCBLS as a representative for demonstration. As previously mentioned, the size of in both BLS and Huber-RCBLS is 6000 × 5, which is too large to display clearly. So, for the sake of clarity, only a portion of from row 5901 to row 5950 is plotted in the figure, where the horizontal axis represents the row index and the vertical axis represents the corresponding weight vector (or row vector). As shown in Figure 4b, except for the three weight vectors at indexes 5909, 5919 and 5931, all other weight vectors of Huber-RCBLS are all zero, which is the so-called “row-sparsity”. This means that the corresponding hidden nodes with zero weights can be eliminated directly and then a more compact network can be achieved. As a contrast, Figure 4a shows that the weight vector of BLS is not sparse, and its values are scattered far away from zero, which is not applicable for model reduction.
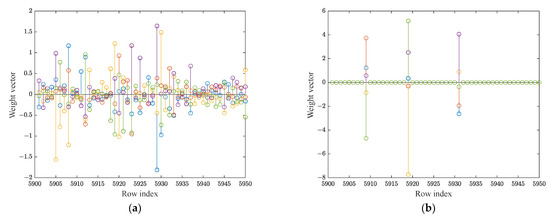
Figure 4.
The output weights matrix (part) of the learned classifier: (a) BLS, (b) Huber-RCBLS on the Norb dataset with 40% outlier level.
5.5. Convergence Demonstration
As described in Algorithm 1, several iterative calculations are required in RCBLS for optimizing the output weights. In order to visually illustrate the convergence behavior of RCBLS in the iterative learning process, we take the six regression datasets with 20% outlier level as examples and provide the corresponding convergence graphs, shown in Figure 5, where the horizontal axis represents the number of iterations and the vertical axis represents the corresponding testing RMSE. We can observe from the figures that on all the six datasets, the testing RMSE of the three RCBLS algorithms decrease rapidly during the first few iterations and then converge to a stable value after about 10 iterations. This proves the fast convergence speed and stable convergence result of the proposed method, and guarantees its efficiency and effectiveness in practical implementation.
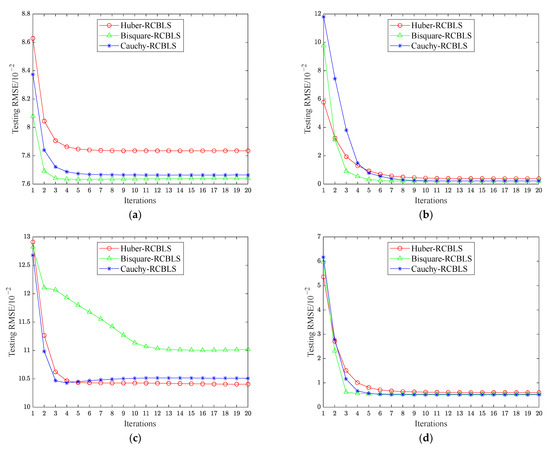
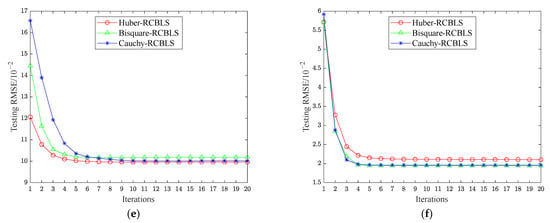
Figure 5.
Convergence behavior of RCBLS on (a) Abalone, (b) Bodyfat, (c) Housing, (d) Mortgage, (e) Strike, (f) Weather Izmir.
Compared with the original BLS, only one extra parameter is added in RCBLS, namely the maximum number of iterations . According to the above convergence results, the learning performance of RCBLS is insensitive to . In other words, can be chosen in a relatively loose range without affecting the learning performance of RCBLS. For example, for all the experimental datasets in this paper, in RCBLS is uniformly set to 20, and strong testing results are obtained. In fact, if we want to further reduce the training time of RCBLS, it is also feasible to set to a smaller value. In summary, the newly added parameter does not impair the usability of the proposed method.
6. Conclusions and Future Work
In this paper, a novel RCBLS model is proposed to improve the robustness and compactness of BLS. Compared with the original BLS model, the proposed RCBLS has two major innovations in terms of robust modeling and structure simplification. Firstly, our RCBLS uses the M-estimator-based robust learning framework instead of the traditional LS criterion as the loss function, in order to alleviate the negative impacts of outlier samples on the model and thus improve its robustness in the presence of outliers. Secondly, our RCBLS adopts the sparsity-promoted -norm regularization to replace the common -norm regularization for model reduction. With the assistance of the row sparsity of the -norm regularization, redundant hidden nodes in the network can be effectively distinguished and eliminated, thus generating a more compact network. Due to the introduction of M-estimator loss and -norm regularization in the objective function, the proposed model cannot be solved analytically, then an efficient iterative method based on augmented Lagrangian multiplier is derived to optimize it. In addition, solid theoretical analyses and diverse comparative experiments have confirmed the effectiveness and superiority of the proposed RCBLS model.
In contrast to existing robust BLS models which are designed only for a single type of learning task such as regression [48,49] or classification [51,52], and (or) require careful tuning of additional control parameters to achieve satisfactory performance [49,50], our RCBLS is a more general robust learning framework that can be widely applied to different situations, such as single/multiple output regression and binary/multi-class classification problems, without complicated parameter tuning. In addition, our RCBLS is equipped with a sparse and compact network structure, which is not available in other models. These distinct advantages guarantee that RCBLS has a good application prospect.
In future work, we plan to expand and apply the RCBLS to other practical fields, such as business performance evaluation and risk analysis [59,60], to further explore its application potential in real-world applications. In addition, we attempt to develop incremental versions of RCBLS to meet the needs of online or incremental learning.
Author Contributions
Conceptualization, W.G. and C.Z.; methodology, W.G.; software, X.Y.; validation, W.G. and Z.W.; resources, C.Z.; writing—original draft preparation, W.G.; writing—review and editing, W.G. and X.Y.; supervision, J.Y.; funding acquisition, W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National Natural Science Foundation of China (grant number 61603326) and the research fund of Jiangsu Provincial Key Constructive Laboratory for Big Data of Psychology and Cognitive Science (grant number 206660022).
Data Availability Statement
The data will be made available on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, C.L.P.; Liu, Z. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Chen, S.; Yuan, X. H-BLS: A hierarchical broad learning system with deep and sparse feature learning. Appl. Intell. 2023, 53, 153–168. [Google Scholar] [CrossRef]
- Igelnik, B.; Pao, Y.H. Stochastic choice of basis functions in adaptive function approximation and the functional-link net. IEEE Trans. Neural Netw. 1995, 6, 1320–1329. [Google Scholar] [CrossRef] [PubMed]
- Gong, X.R.; Zhang, T.; Chen, C.L.P.; Liu, Z.L. Research review for broad learning system: Algorithms, theory, and applications. IEEE Trans. Cybern. 2022, 52, 8922–8950. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Liu, Z.L.; Feng, S. Universal approximation capability of broad learning system and its structural variations. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1191–1204. [Google Scholar] [CrossRef]
- Ye, H.; Li, H.; Chen, C.L.P. Adaptive deep cascade broad learning system and its application in image denoising. IEEE Trans. Cybern. 2021, 51, 4450–4463. [Google Scholar] [CrossRef]
- Yi, J.; Huang, J.; Zhou, W.; Chen, G.; Zhao, M. Intergroup Cascade Broad Learning System with Optimized Parameters for Chaotic Time Series Prediction. IEEE Trans. Art. Intell. 2022, 3, 709–721. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, C.L.P.; Feng, S.; Feng, Q.; Zhang, T. Stacked broad learning system: From incremental flatted structure to deep model. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 209–222. [Google Scholar] [CrossRef]
- Du, J.; Vong, C.M.; Chen, C.L.P. Novel efficient RNN and LSTM-like architectures: Recurrent and gated broad learning systems and their applications for text classification. IEEE Trans. Cybern. 2021, 51, 1586–1597. [Google Scholar] [CrossRef]
- Mou, M.; Zhao, X.Q. Gated Broad Learning System Based on Deep Cascaded for Soft Sensor Modeling of Industrial Process. IEEE Trans. Instrum. Meas. 2022, 71, 2508811. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Lu, G.; Shen, P.; Bennamoun, M.; Shah, S.A.A.; Miao, Q.; Zhu, G.; Li, P.; Lu, X. Analysis and variants of broad learning system. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 334–344. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, C.; Zhang, J.; Guo, L.; Ding, L. Incremental Multilayer Broad Learning System with Stochastic Configuration Algorithm for Regression. IEEE Trans. Cogn. Dev. Syst. 2023, 15, 877–886. [Google Scholar] [CrossRef]
- Feng, S.; Chen, C.L.P. Fuzzy broad learning system: A novel neuro-fuzzy model for regression and classification. IEEE Trans. Cybern. 2020, 50, 414–424. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Sheng, B.; Li, P.; Chen, C.L.P. Multiview high dynamic range image synthesis using fuzzy broad learning system. IEEE Trans. Cybern. 2021, 51, 2735–2747. [Google Scholar] [CrossRef]
- Han, H.; Liu, Z.; Liu, H.; Qiao, J.; Chen, C.L.P. Type-2 fuzzy broad learning system. IEEE Trans. Cybern. 2022, 52, 10352–10363. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Chen, C.L.P.; Xu, L.; Liu, Z. On the accuracy-complexity tradeoff of fuzzy broad learning system. IEEE Trans. Fuzzy Syst. 2021, 29, 2963–2974. [Google Scholar] [CrossRef]
- Zou, W.; Xia, Y.; Dai, L. Fuzzy broad learning system based on accelerating amount. IEEE Trans. Fuzzy Syst. 2022, 30, 4017–4024. [Google Scholar] [CrossRef]
- Bai, K.; Zhu, X.; Wen, S.; Zhang, R.; Zhang, W. Broad learning based dynamic fuzzy inference system with adaptive structure and interpretable fuzzy rules. IEEE Trans. Fuzzy Syst. 2022, 30, 3270–3283. [Google Scholar] [CrossRef]
- Chen, W.X.; Yang, K.X.; Yu, Z.W.; Zhang, W.W. Double-kernel based class-specific broad learning system for multiclass imbalance learning. Knowl.-Based Syst. 2022, 253, 109535. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Chen, C.L.P.; Cao, W.; You, J.; Wong, H.S. Incremental weighted ensemble broad learning system for imbalanced data. IEEE Trans. Knowl. Data Eng. 2022, 34, 5809–5824. [Google Scholar] [CrossRef]
- Huang, S.L.; Liu, Z.; Jin, W.; Mu, Y. Broad learning system with manifold regularized sparse features for semi-supervised classification. Neurocomputing 2021, 463, 133–143. [Google Scholar] [CrossRef]
- Liu, D.; Baldi, S.; Yu, W.W.; Chen, C.L.P. A hybrid recursive implementation of broad learning with incremental features. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1650–1662. [Google Scholar] [CrossRef]
- Chen, G.Y.; Gan, M.; Chen, C.L.P.; Zhu, H.T.; Chen, L. Frequency principle in broad learning system. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6983–6989. [Google Scholar] [CrossRef]
- Mao, R.Q.; Cui, R.X.; Chen, C.L.P. Broad learning with reinforcement learning signal feedback: Theory and applications. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 2952–2964. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, Y.; Li, N.; Zhao, D.; Sun, Z.; Chen, C.L.P. BNAS: Efficient neural architecture search using broad scalable architecture. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5004–5018. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, Y.; Li, N.; Zhao, D. BNAS-v2: Memory-efficient and performance-collapse-prevented broad neural architecture search. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6259–6272. [Google Scholar] [CrossRef]
- Yang, K.X.; Shi, Y.F.; Yu, Z.W.; Yang, Q.M.; Sangaiah, A.K.; Zeng, H.Q. Stacked one-class broad learning system for intrusion detection in industry 4.0. IEEE Trans. Ind. Inf. 2023, 19, 251–260. [Google Scholar] [CrossRef]
- Yang, Y.X.; Gao, Z.K.; Li, Y.L.; Cai, Q.; Marwan, N.; Kurths, J. A complex network-based broad learning system for detecting driver fatigue from EEG signals. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5800–5808. [Google Scholar] [CrossRef]
- Pramanik, S.; Bhattacharjee, D.; Nasipuri, M.; Krejcar, O. LINPE-BL: A local descriptor and broad learning for identification of abnormal breast thermograms. IEEE Trans. Med. Imaging 2021, 40, 3919–3931. [Google Scholar] [CrossRef]
- Parhi, P.; Bisoi, R.; Dash, P.K. An improvised nature-inspired algorithm enfolded broad learning system for disease classification. Egypt. Inform. J. 2023, 24, 241–255. [Google Scholar] [CrossRef]
- Wu, G.H.; Duan, J.W. BLCov: A novel collaborative-competitive broad learning system for COVID-19 detection from radiology images. Eng. Appl. Artif. Intell. 2022, 115, 105323. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Yuen, K.V.; Yang, X.F.; Zhang, Y. Tropical Cyclogenesis Detection from Remotely Sensed Sea Surface Winds Using Graphical and Statistical Features-Based Broad Learning System. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4203815. [Google Scholar] [CrossRef]
- Zhong, D.X.; Liu, F.G. RF-OSFBLS: An RFID reader-fault-adaptive localization system based on online sequential fuzzy broad learning system. Neurocomputing 2020, 390, 28–39. [Google Scholar] [CrossRef]
- Mou, M.; Zhao, X.Q.; Liu, K.; Cao, S.Y.; Hui, Y.Y. A latent representation dual manifold regularization broad learning system with incremental learning capability for fault diagnosis. Meas. Sci. Technol. 2023, 34, 075005. [Google Scholar] [CrossRef]
- Fu, Y.; Cao, H.R.; Xuefeng, C.; Ding, J. Task-incremental broad learning system for multi-component intelligent fault diagnosis of machinery. Knowl.-Based Syst. 2022, 246, 108730. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Wang, B.S. Random-positioned license plate recognition using hybrid broad learning system and convolutional networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 444–456. [Google Scholar] [CrossRef]
- Wu, C.; Qiu, T.; Zhang, C.K.; Qu, W.Y.; Wu, D.O. Ensemble Strategy Utilizing a Broad Learning System for Indoor Fingerprint Localization. IEEE Internet Things J. 2022, 9, 3011–3022. [Google Scholar] [CrossRef]
- Zhan, C.J.; Jiang, W.; Lin, F.B.; Zhang, S.T.; Li, B. A decomposition-ensemble broad learning system for AQI forecasting. Neural Comput. Appl. 2022, 34, 18461–18472. [Google Scholar] [CrossRef]
- Zhou, N.; Xu, X.Y.; Yan, Z.; Shahidehpour, M. Spatio-Temporal Probabilistic Forecasting of Photovoltaic Power Based on Monotone Broad Learning System and Copula Theory. IEEE Trans. Sustain. Energy 2022, 13, 1874–1885. [Google Scholar] [CrossRef]
- Li, G.Z.; Zhang, A.N.; Zhang, Q.Z.; Wu, D.; Zhan, C.J. Pearson correlation coefficient-based performance enhancement of broad learning system for stock price prediction. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2413–2417. [Google Scholar] [CrossRef]
- Liu, D.; Baldi, S.; Yu, W.W.; Cao, J.D.; Huang, W. On training traffic predictors via broad learning structures: A benchmark study. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 749–758. [Google Scholar] [CrossRef]
- Cao, Y.D.; Jia, M.P.; Ding, P.; Zhao, X.L.; Ding, Y.F. Incremental Learning for Remaining Useful Life Prediction via Temporal Cascade Broad Learning System with Newly Acquired Data. IEEE Trans. Ind. Inf. 2023, 19, 6234–6245. [Google Scholar] [CrossRef]
- Yang, Y.D.; Huang, Q.; Li, P.J. Online prediction and correction control of static voltage stability index based on Broad Learning System. Expert Syst. Appl. 2022, 199, 117184. [Google Scholar] [CrossRef]
- Han, M.; Li, W.J.; Feng, S.B.; Qiu, T.; Chen, C.L.P. Maximum information exploitation using broad learning system for large-scale chaotic time-series prediction. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2320–2329. [Google Scholar] [CrossRef]
- Hu, J.; Wu, M.; Chen, L.F.; Zhou, K.L.; Zhang, P.; Pedrycz, W. Weighted kernel fuzzy C-means-based broad learning model for time-series prediction of carbon efficiency in iron ore sintering process. IEEE Trans. Cybern. 2022, 52, 4751–4763. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Xiong, L.; Yang, J. Multi-Attn BLS: Multi-head attention mechanism with broad learning system for chaotic time series prediction. Appl. Soft. Comput. 2023, 132, 109831. [Google Scholar] [CrossRef]
- Hu, X.; Wei, X.; Gao, Y.; Liu, H.F.; Zhu, L. Variational expectation maximization attention broad learning systems. Inf. Sci. 2022, 608, 597–612. [Google Scholar] [CrossRef]
- Jin, J.W.; Chen, C.L.P. Regularized robust broad learning system for uncertain data modeling. Neurocomputing 2018, 322, 58–69. [Google Scholar] [CrossRef]
- Chu, F.; Liang, T.; Chen, C.L.P.; Wang, X.; Ma, X. Weighted broad learning system and its application in nonlinear industrial process modeling. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3017–3031. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, B.; Wang, S.; Wang, W. Broad learning system based on maximum correntropy criterion. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3083–3097. [Google Scholar] [CrossRef]
- Jin, J.; Li, Y.; Chen, C.L.P. Pattern Classification with Corrupted Labeling via Robust Broad Learning System. IEEE Trans. Knowl. Data Eng. 2022, 34, 4959–4971. [Google Scholar] [CrossRef]
- Yu, Z.; Lan, K.; Liu, Z.; Han, G. Progressive Ensemble Kernel-Based Broad Learning System for Noisy Data Classification. IEEE Trans. Cybern. 2022, 52, 9656–9669. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.T.; Vong, C.M.; Chen, C.L.P.; Zhou, Y.M. Accurate and efficient large-scale multi-label learning with reduced feature broad learning system using label correlation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Jin, J.W.; Qin, Z.H.; Yu, D.X.; Li, Y.T.; Liang, J.; Chen, C.L.P. Regularized discriminative broad learning system for image classification. Knowl.-Based Syst. 2022, 251, 109306. [Google Scholar] [CrossRef]
- Miao, J.Y.; Yang, T.J.; Jin, J.W.; Sun, L.J.; Niu, L.F.; Shi, Y. Towards compact broad learning system by combined sparse regularization. Int. J. Inf. Technol. Decis. 2022, 21, 169–194. [Google Scholar] [CrossRef]
- de Menezes, D.Q.F.; Prata, D.M.; Secchi, A.R.; Pinto, J.C. A review on robust M-estimators for regression analysis. Comput. Chem. Eng. 2021, 147, 107254. [Google Scholar] [CrossRef]
- Tyler, D.E. Robust Statistics: Theory and Methods. J. Am. Stat. Assoc. 2008, 103, 888–889. [Google Scholar] [CrossRef]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS2018), Montréal, QC, Canada, 3–8 December 2018; pp. 8535–8545. [Google Scholar]
- Chang, V. Presenting Cloud Business Performance for Manufacturing Organizations. Inf. Syst. Front. 2020, 22, 59–75. [Google Scholar] [CrossRef]
- Chang, V.; Arunachalam, P.; Xu, Q.A.; Chong, P.L.; Psarros, C.; Li, J. Journey to SAP S/4HANA intelligent enterprise: Is there a risk in transitions? Int. J. Bus. Inf. Syst. 2023, 42, 503–541. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).