An Advanced Non-Interrupted Internal Calibration Model Based on Azimuth Modulation and Waveform Diversity for SAR Systems
Abstract
1. Introduction
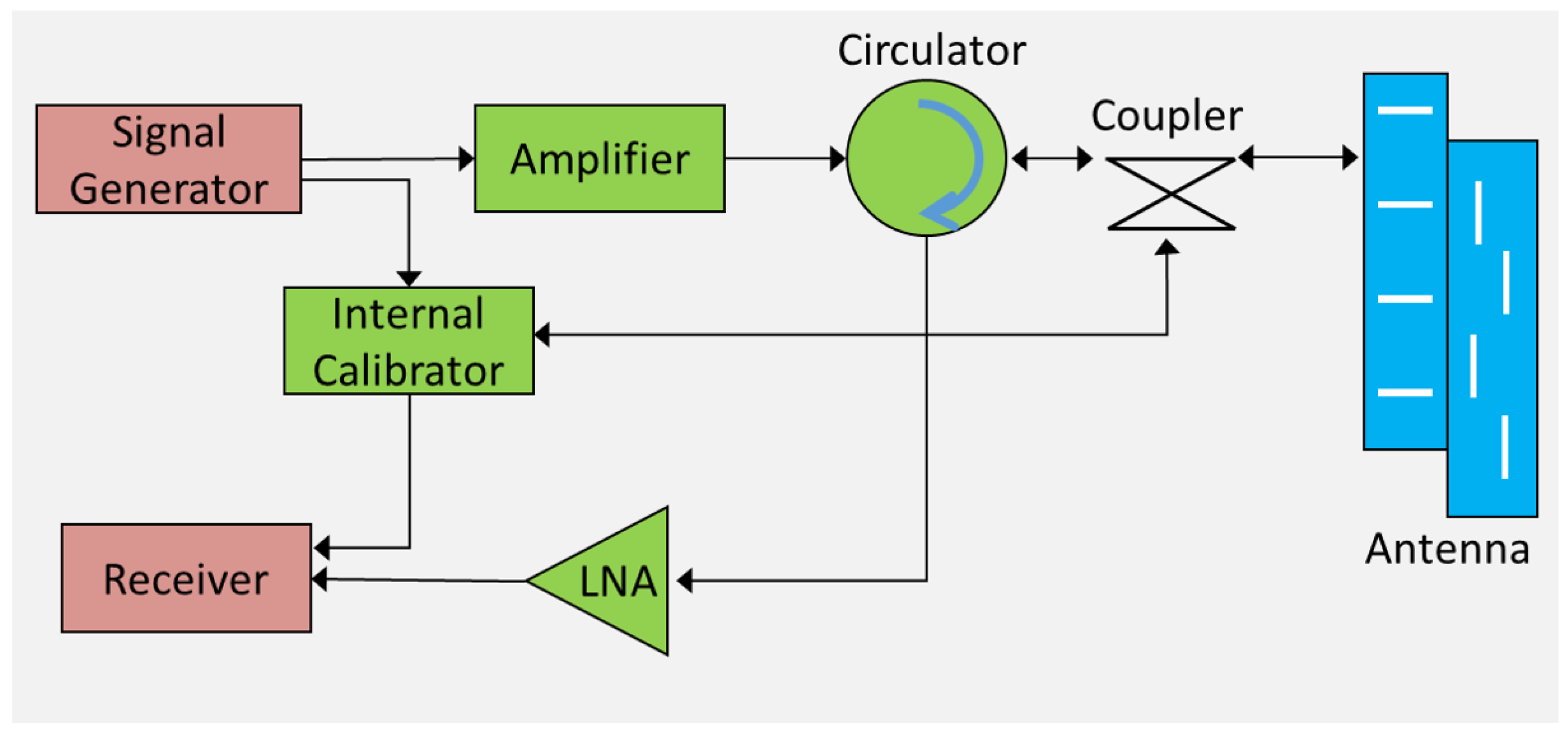
2. Principle of Internal Calibration
2.1. Transfer Function Derivation for Internal Calibration
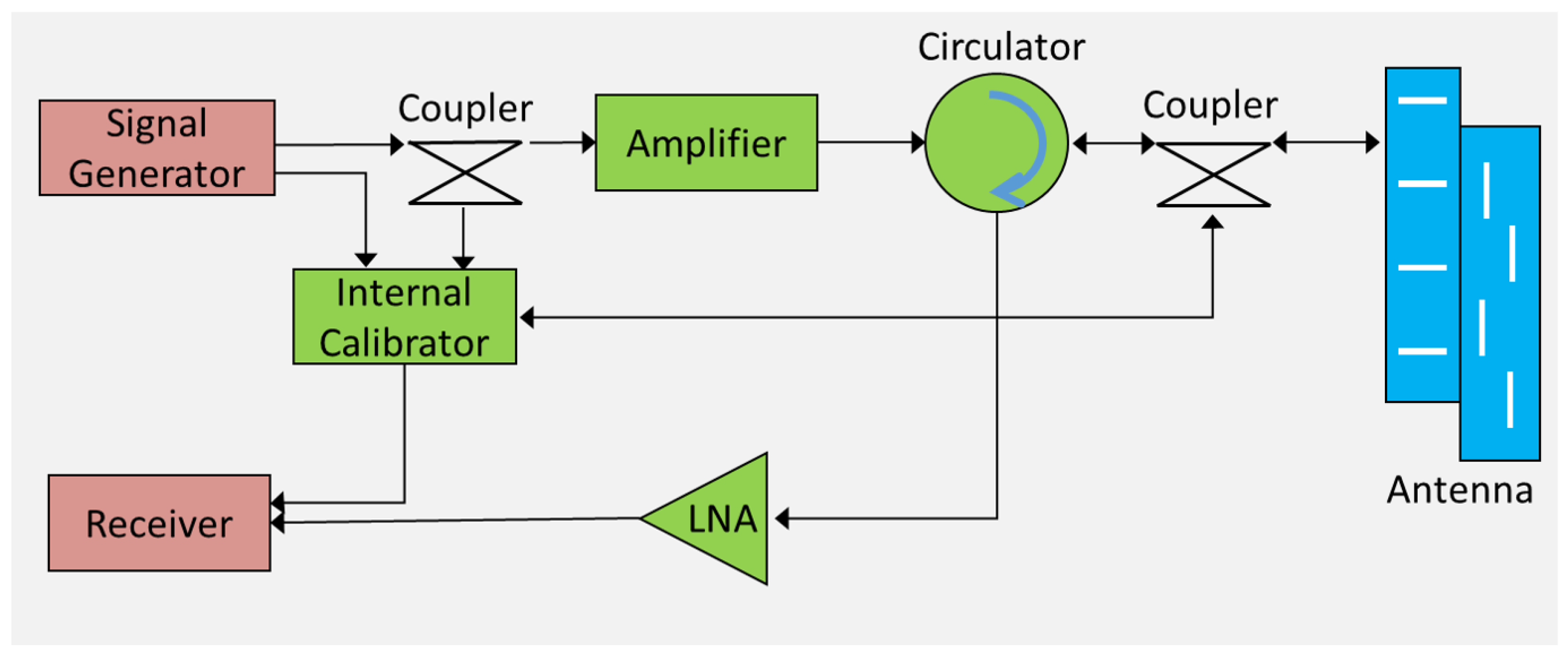
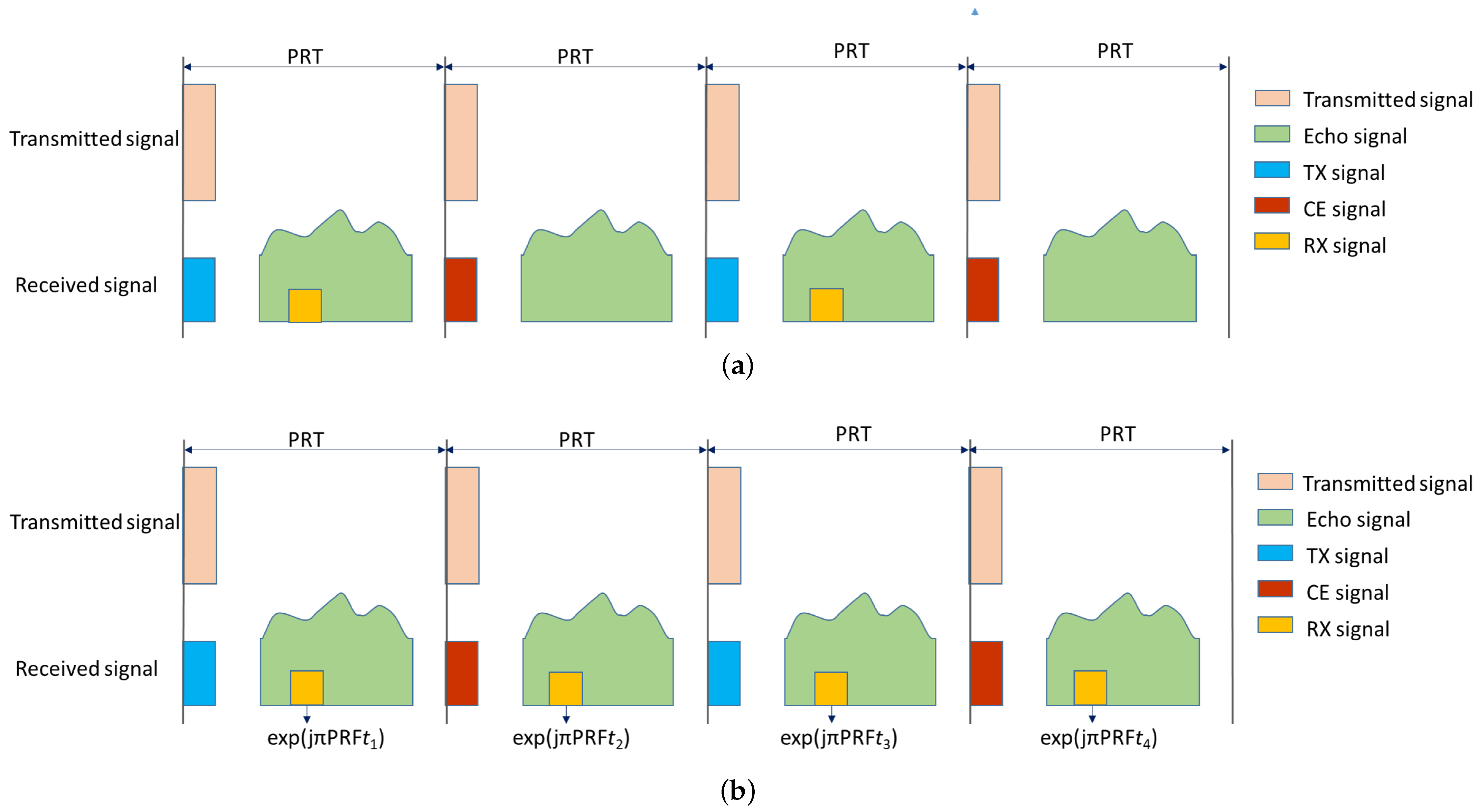
2.2. Non-Interrupted Internal Calibration Scheme [19]
3. Proposed Internal Calibration Model and Schemes
3.1. Non-Interrupted Internal Calibration Model
3.2. First Internal Calibration Scheme
3.2.1. Timing Diagram
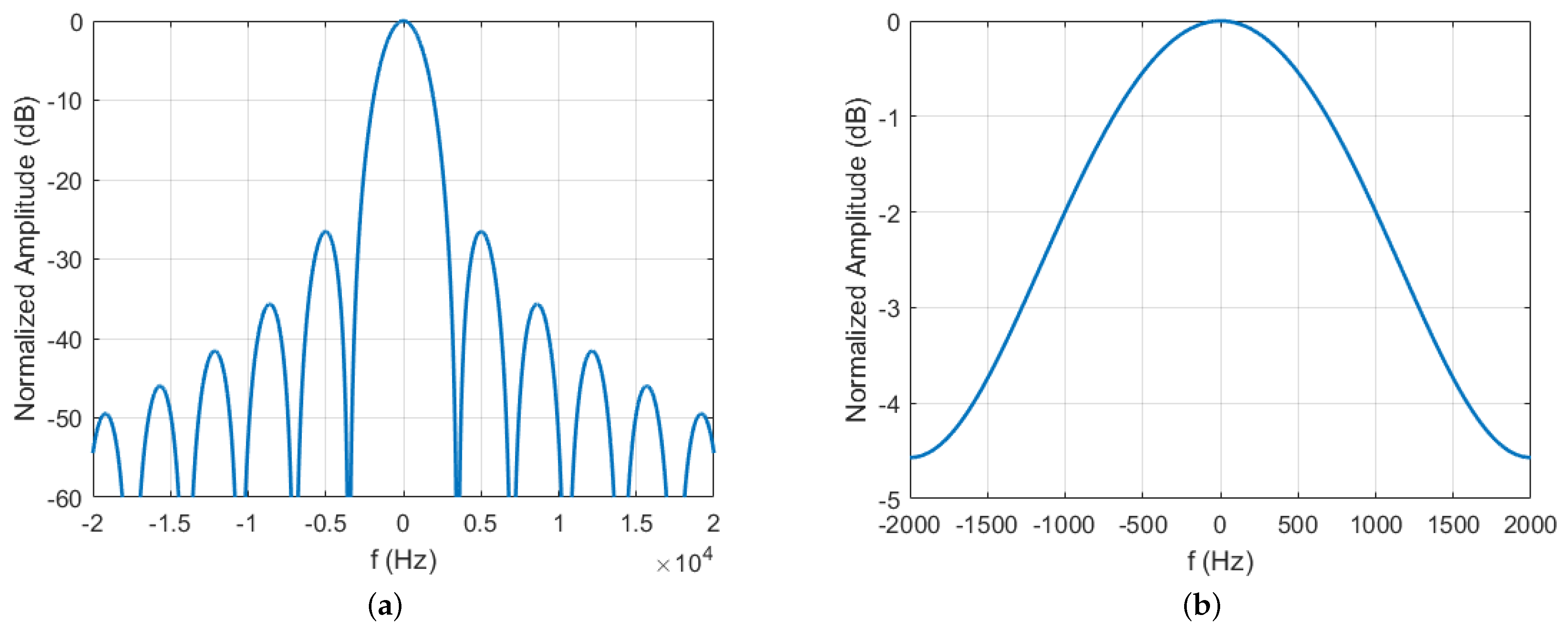
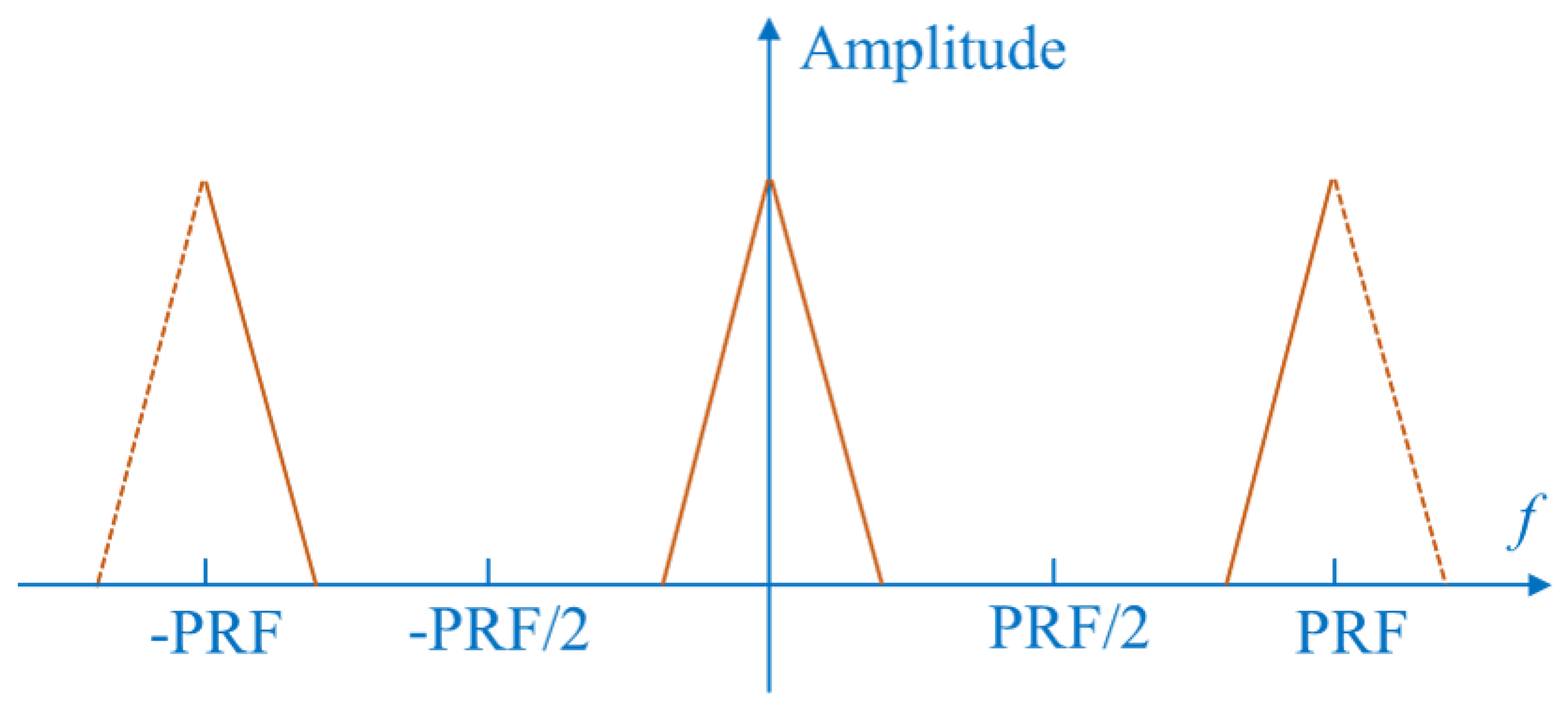
3.2.2. SNR Analysis and Processing Step
- step1:
- Range compression for signal.
- step2:
- After azimuth fast Fourier transform (FFT), the signal is extracted by a high pass filter.
- step3:
- Azimuth inverse FFT (IFFT) is carried out, then the signal is obtained via azimuth coherent integration every duration.
- step4:
- Obtain the compensation term and compensate for the echoes.
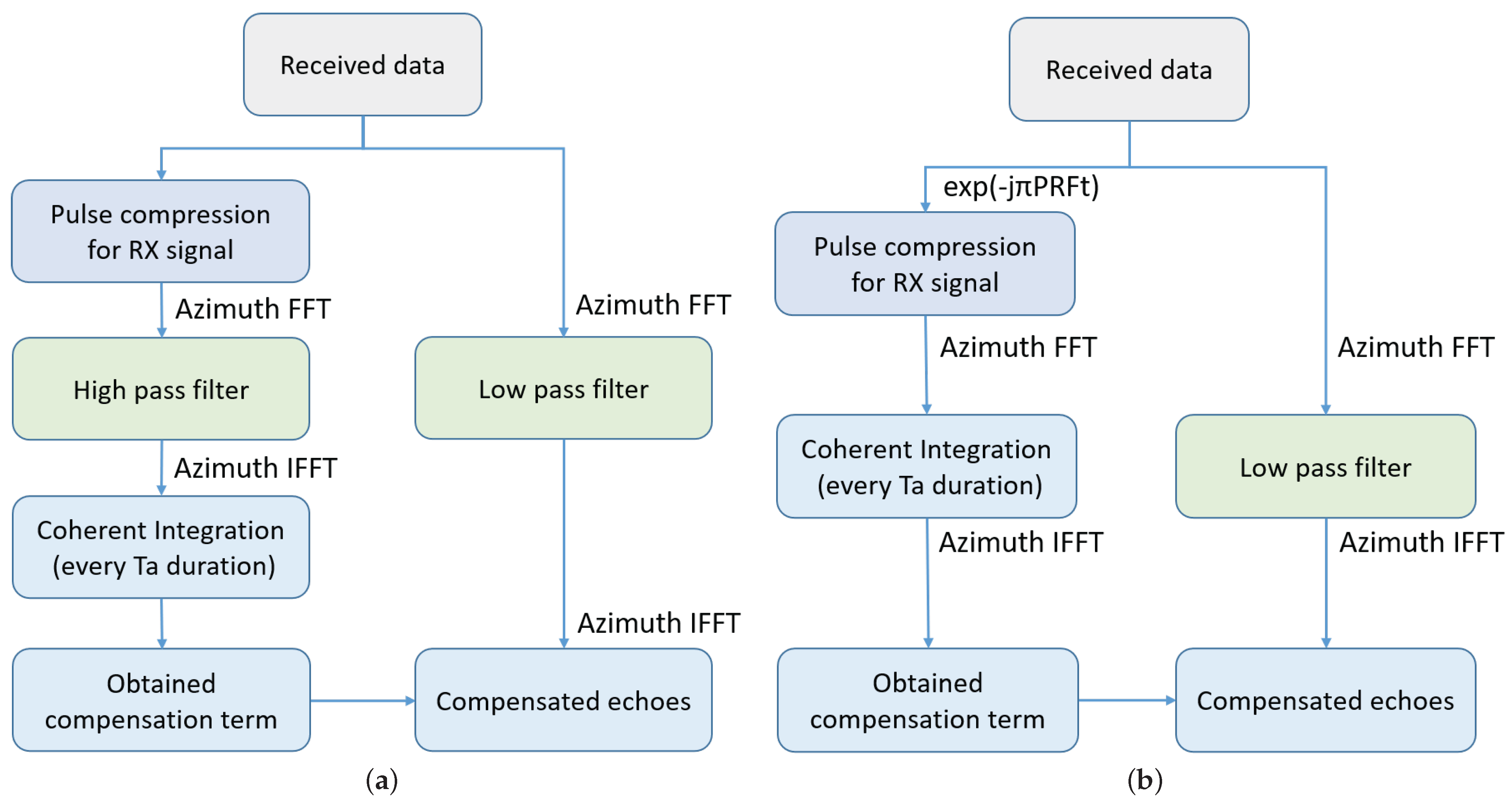
3.3. Second Internal Calibration Scheme
3.3.1. Timing Diagram
3.3.2. SNR Analysis and Processing Step
- step1:
- Multiply along the azimuth direction.
- step2:
- Range compression for signal.
- step3:
- Azimuth coherent integration every duration.
- step4:
- Obtain the compensation term and compensate for the echoes.
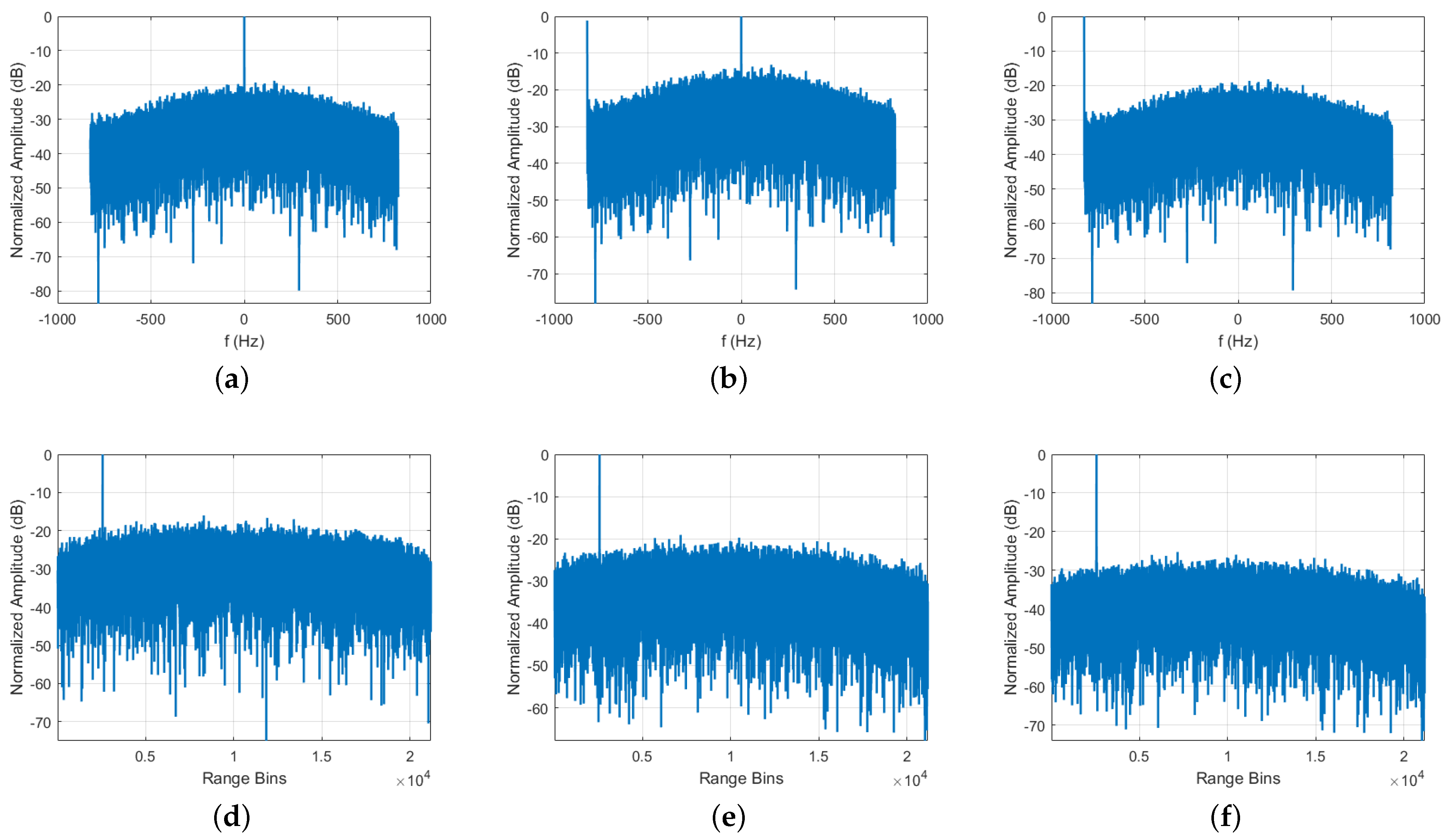
4. Simulation Experiment
4.1. SNR Analysis for Simulation Experiment
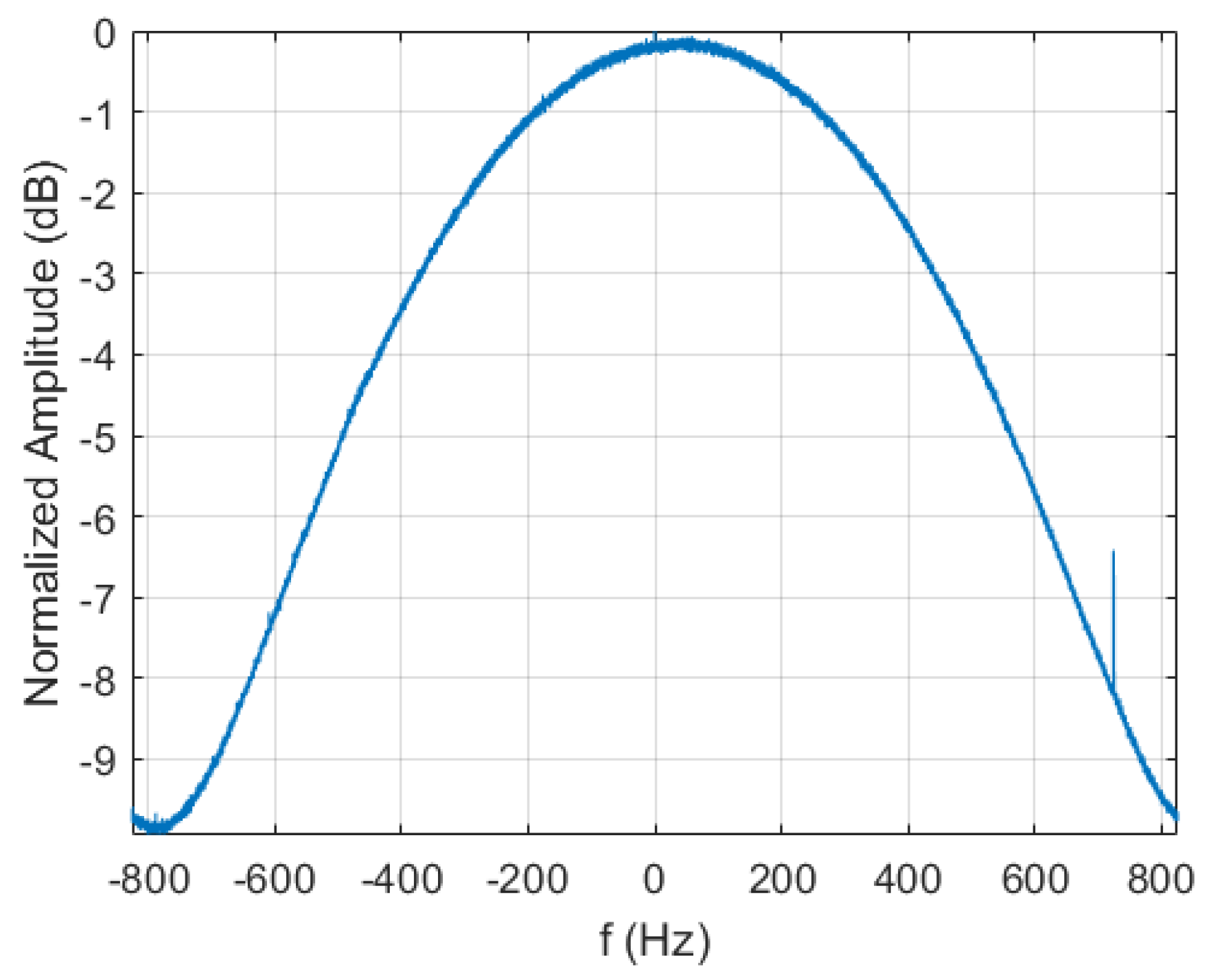
4.2. Experiment Using Sentinel-1 Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Theoretical Analysis for Upsampling Theory

References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A Tutorial on Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Freeman, A. SAR Calibration: An Overview. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1107–1121. [Google Scholar] [CrossRef]
- Schwerdt, M.; Schmidt, K.; Ramon, N.T.; Klenk, P.; Yaguemartinez, N.; Pratsiraola, P.; Zink, M.; Geudtner, D. Independent System Calibration of Sentinel-1B. Remote Sens. 2017, 9, 511. [Google Scholar] [CrossRef]
- Brautigam, B.; Schwerdt, M.; Bachmann, M. An Efficient Method for Performance Monitoring of Active Phased Array Antennas. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1236–1243. [Google Scholar] [CrossRef]
- Deng, Y.; Zheng, H.; Wang, R.; Feng, J.; Liu, Y. Internal Calibration for Stepped-Frequency Chirp SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1105–1109. [Google Scholar] [CrossRef]
- Wang, S.; Qi, H.; Yu, W. Polarimetric SAR Internal Calibration Scheme Based on T/R Module Orthogonal Phase Coding. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3969–3980. [Google Scholar] [CrossRef]
- Jager, M.; Scheiber, R.; Reigber, A. Robust, Model-Based External Calibration of Multi-Channel Airborne SAR Sensors Using Range Compressed Raw Data. Remote Sens. 2019, 11, 2674. [Google Scholar] [CrossRef]
- Schwerdt, M.; Brautigam, B.; Bachmann, M.; Doring, B.; Schrank, D.; Gonzalez, J.H. TerraSAR-X Calibration Results. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Friedrichshafen, Germany, 2–5 June 2008; Volume 2, pp. 205–208. [Google Scholar]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Zink, M.; Bamler, R. X-SAR Radiometric Calibration and Data Quality. IEEE Trans. Geosci. Remote Sens. 1995, 33, 840–847. [Google Scholar] [CrossRef]
- Wang, P.; Sun, H.; Yu, W. A Novel Wireless Internal Calibration Method of Spaceborne SAR. J. Radars 2018, 7, 35–46. [Google Scholar]
- Schied, E.; Rostan, F.; Oestergaard, A.; Traver, I.N.; Snoeij, P. The Sentinel-1 C-SAR Internal Calibration. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 341–343. [Google Scholar]
- Wang, X.; Wang, R.; Deng, Y.; Wang, P.; Li, N.; Yu, W.; Wang, W. Precise Calibration of Channel Imbalance for Very High Resolution SAR With Stepped Frequency. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4252–4261. [Google Scholar] [CrossRef]
- Younis, M.; Rommel, T.; de Almeida, F.; Huber, S.; Martone, M.; Villano, M.; Krieger, G. Investigations on the Internal Calibration of Multi-Channel SAR. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5386–5389. [Google Scholar]
- Zink, M.; Torres, R.; Buck, C.H.; Rosich, B.; Closa, J. Calibration and Early Results of the ASAR on ENVISAT. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 1, pp. 596–598. [Google Scholar]
- Schwerdt, M.; Hounam, D.; Alvarezperes, J.; Molkenthin, T. The Calibration Concept of TerraSAR-X: A Multiple-Mode, High-Resolution SAR. Can. J. Remote Sens. 2005, 31, 30–36. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, R.; Wang, P. Improved Phase-Encoding Calibration for Active Phased-Array Antennas of SAR. IEEE Geosci. Remote Sens. Lett. 2016, 13, 767–771. [Google Scholar] [CrossRef]
- Younis, M.; de Almeida, F.Q.; Huber, S.; Laux, C.; Krieger, G. An Internal Instrument Calibration Simulator for Multi-Channel SAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 9201–9204. [Google Scholar]
- Reimann, J.; Schwerdt, M. Technique for Concurrent Internal Calibration during Data Acquisition for SAR Systems. Remote Sens. 2020, 12, 1773. [Google Scholar] [CrossRef]
- Viet, H.T.; Minh, T.H. A Real-Time Internal Calibration Method for Radar Systems Using Digital Phase Array Antennas. In Proceedings of the Industrial Networks and Intelligent Systems: 7th EAI International Conference, INISCOM 2021, Hanoi, Vietnam, 22–23April 2021; Springer: Cham, Switzerland, 2021; pp. 88–103. [Google Scholar]
- Tran, V.H.; Hoang, M.T. Improving the Structure of a Signal Used for Real-Time Calibrating of the Receiving Channels of Digital Transceiver Modules in Digital Phased Antenna Arrays. J. Russ. Univ. Radioelectron. 2021, 24, 19–26. [Google Scholar]
- Brautigam, B.; Gonzalez, J.H.; Schwerdt, M.; Bachmann, M. TerraSAR-X Instrument Calibration Results and Extension for TanDEM-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 702–715. [Google Scholar] [CrossRef]
- Bordoni, F.; Younis, M.; Krieger, G. Ambiguity Suppression by Azimuth Phase Coding in Multichannel SAR Systems. IEEE Trans. Geosci. Remote Sens. 2011, 50, 617–629. [Google Scholar] [CrossRef]
- Natsuaki, R.; Sakar, N.; Yague-Martinez, N.; Pinheiro, M.; Prats-Iraola, P. Investigations on the Optimum Combination of Azimuth Phase Coding and Up-and Down-Chirp Modulation for Range Ambiguity Suppression. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2288–2291. [Google Scholar]
- Dall, J.; Kusk, A. Azimuth Phase Coding for Range Ambiguity Suppression in SAR. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1734–1737. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Schuchman, L. Dither Signals and Their Effect on Quantization Noise. IEEE Trans. Commun. 1964, 12, 162–165. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Nadir Echo Removal in Synthetic Aperture Radar via Waveform Diversity and Dual-Focus Postprocessing. IEEE Geosci. Remote Sens. Lett. 2018, 15, 719–723. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Jäger, M.; Moreira, A. Staggered SAR: Performance Analysis and Experiments With Real Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6617–6638. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Staggered SAR: High-Resolution Wide-Swath Imaging by Continuous PRI Variation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4462–4479. [Google Scholar] [CrossRef]
- Tan, L.; Jiang, J. Digital Signal Processing: Fundamentals and Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
| Azimuth Time | 0 | PRT | 2PRT | 3PRT | … | 2n · PRT | (2n + 1) · PRT |
|---|---|---|---|---|---|---|---|
| Scheme proposed in [19] | 1 | 1 | 1 | 1 | … | 1 | 1 |
| Proposed first scheme | 1 | 0 | 1 | 0 | … | 1 | 0 |
| Proposed second scheme | 1 | −1 | 1 | −1 | … | 1 | −1 |
| Parameter | Symbol | Value |
|---|---|---|
| Carrier frequency | 9.6 GHz | |
| Wavelength | 0.0312 m | |
| Velocity | V | 7000 m/s |
| Azimuth bandwidth | 3100 Hz | |
| Pulse repetition frequency | 4000 Hz | |
| Antenna length | 4 m | |
| Azimuth duration | 10 s | |
| Range pulse bandwidth | 80 MHz | |
| Range pulse width | 70 μs |
| Parameter | Symbol | Value |
|---|---|---|
| Carrier frequency | 5.405 GHz | |
| Pulse repetition frequency | 1650 Hz | |
| Azimuth duration | 15.3136 s | |
| Range pulse bandwidth | 50.6 MHz | |
| Sampling frequency | 56.3 MHz | |
| Range pulse width | 51.50 μs |
| Scheme | Image Disturbances | SNR of Signal | |||
|---|---|---|---|---|---|
| Mean | Max | ||||
| Scheme proposed in [19] | −31.7 dB | 0.0019 deg. | −18.4 dB | 360 deg. | 26.8 dB |
| Proposed first scheme | −34.4 dB | 0.0017 deg. | −19.6 dB | 360 deg. | 29.8 dB |
| Proposed second scheme | −35.8 dB | 0.0012 deg. | −20.5 dB | 360 deg. | 36.0 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, D.; Pang, X. An Advanced Non-Interrupted Internal Calibration Model Based on Azimuth Modulation and Waveform Diversity for SAR Systems. Electronics 2023, 12, 2677. https://doi.org/10.3390/electronics12122677
Liang D, Pang X. An Advanced Non-Interrupted Internal Calibration Model Based on Azimuth Modulation and Waveform Diversity for SAR Systems. Electronics. 2023; 12(12):2677. https://doi.org/10.3390/electronics12122677
Chicago/Turabian StyleLiang, Da, and Xiaoyu Pang. 2023. "An Advanced Non-Interrupted Internal Calibration Model Based on Azimuth Modulation and Waveform Diversity for SAR Systems" Electronics 12, no. 12: 2677. https://doi.org/10.3390/electronics12122677
APA StyleLiang, D., & Pang, X. (2023). An Advanced Non-Interrupted Internal Calibration Model Based on Azimuth Modulation and Waveform Diversity for SAR Systems. Electronics, 12(12), 2677. https://doi.org/10.3390/electronics12122677






