Ultra-Low-Power Compact Neuron Circuit with Tunable Spiking Frequency and High Robustness in 22 nm FDSOI
Abstract
:1. Introduction
2. FDSOI-Based LIF Neuron Circuit
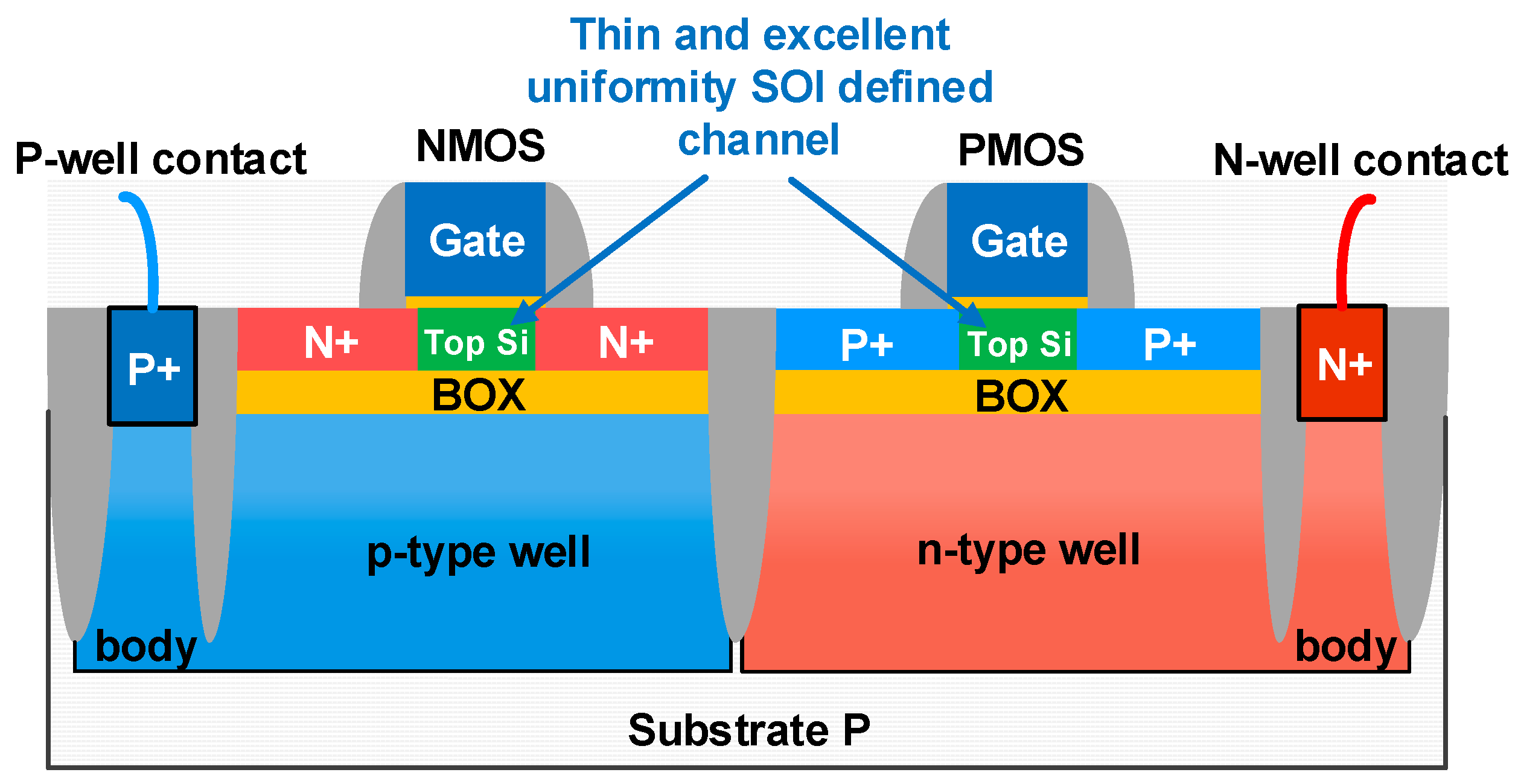
2.1. Advantages of FDSOI Technology in Neuron Circuit Design
2.2. Proposed Method
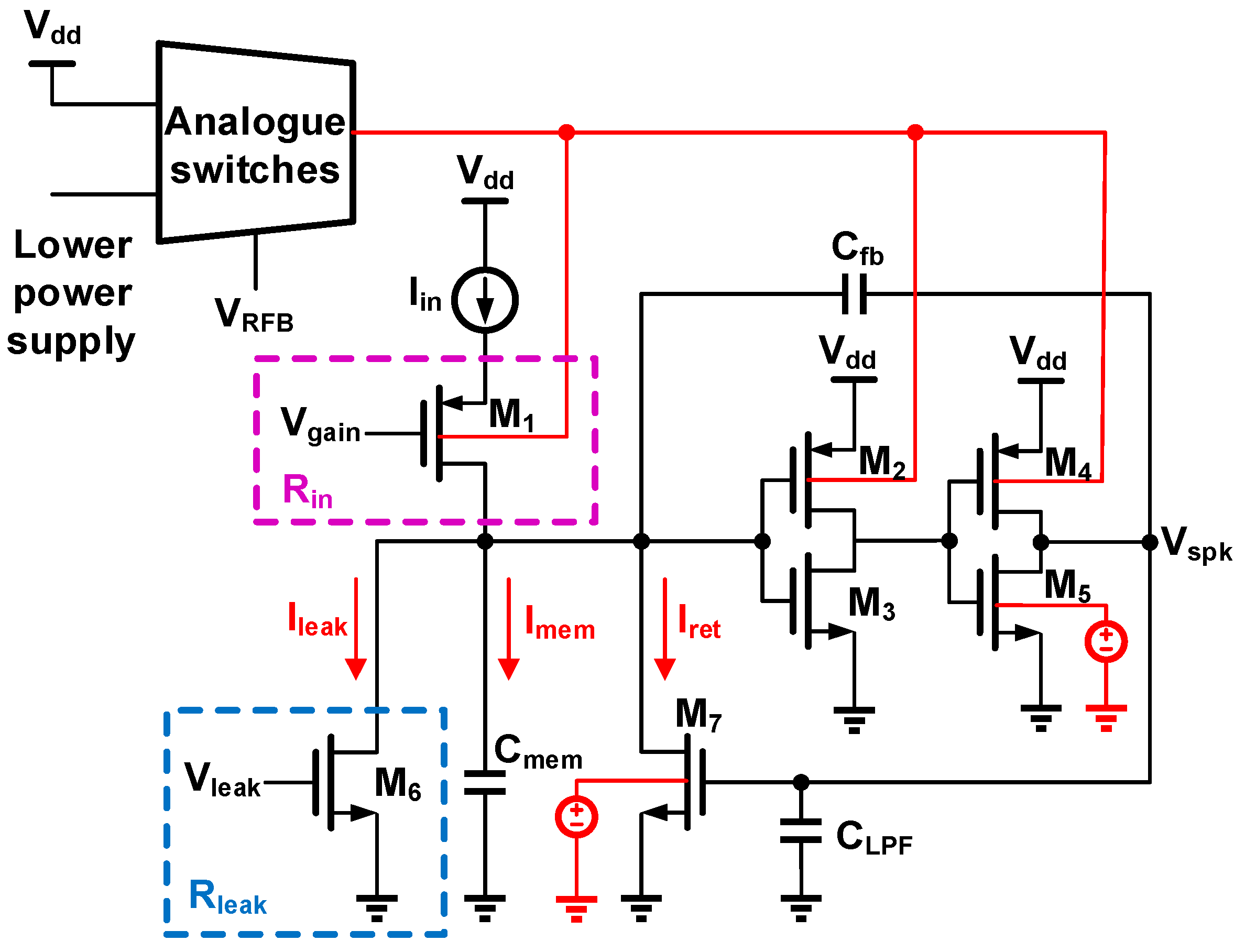
2.3. Proposed Subthreshold Neuron Circuit
3. Results
3.1. Neuron Circuit Post-Layout Simulation
3.2. Energy Per Spike
3.3. Monte Carlo Analysis
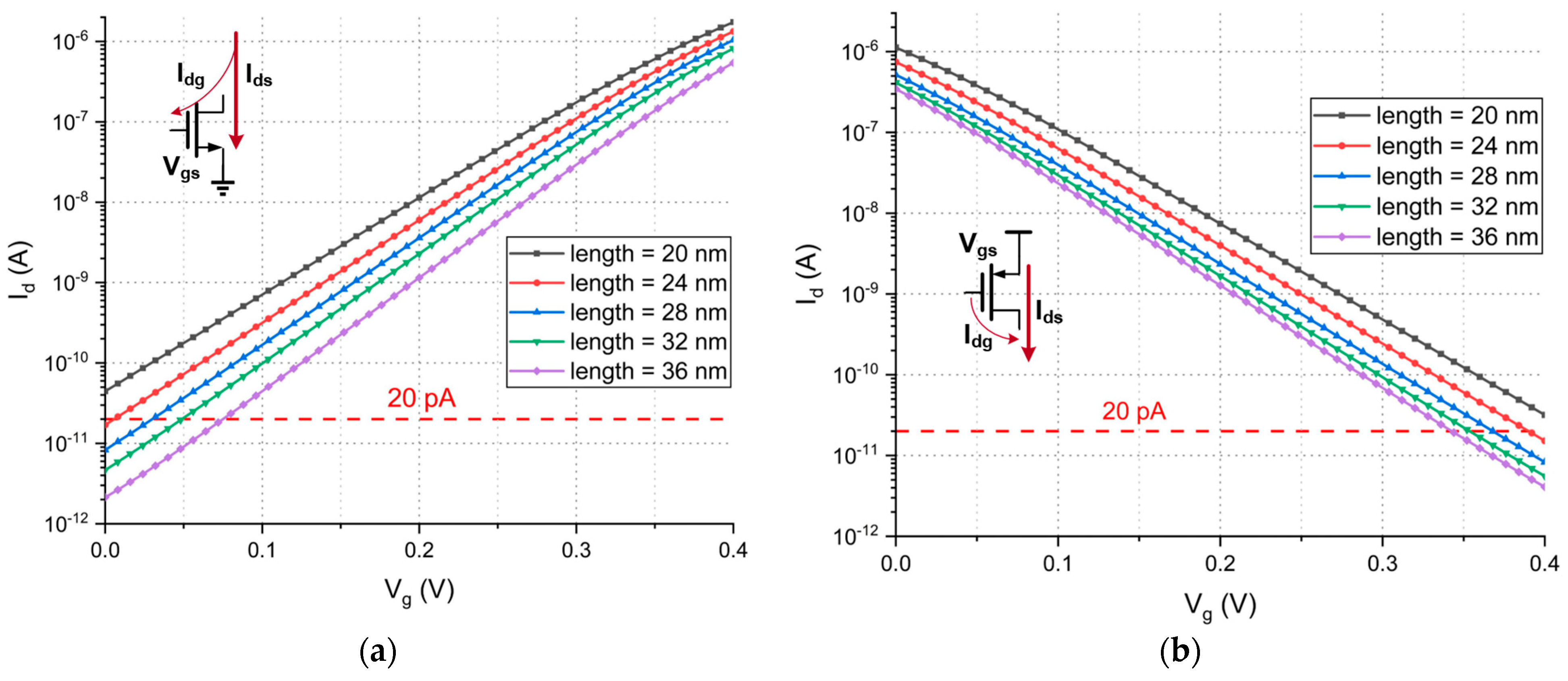
3.4. Process Robustness
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef]
- Sebastian, A.; Le Gallo, M.; Eleftheriou, E. Computational phase-change memory: Beyond von Neumann computing. J. Phys. D Appl. Phys. 2019, 52, 443002. [Google Scholar] [CrossRef]
- Grollier, J.; Querlioz, D.; Camsari, K.Y.; Everschor-Sitte, K.; Fukami, S.; Stiles, M.D. Neuromorphic spintronics. Nat. Electron. 2020, 3, 360–370. [Google Scholar] [CrossRef] [PubMed]
- Diehl, P.U.; Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 2015, 9, 99. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Srinivasan, G.; Panda, P.; Roy, K. Deep spiking convolutional neural network trained with unsupervised spike-timing-dependent plasticity. IEEE Trans. Cogn. Dev. Syst. 2018, 11, 384–394. [Google Scholar] [CrossRef]
- Zhao, C.; Hamedani, K.; Li, J.; Yi, Y. Analog spike-timing- dependent resistive crossbar design for brain inspired computing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 8, 38–50. [Google Scholar] [CrossRef]
- Thakur, C.S.; Molin, J.L.; Cauwenberghs, G.; Indiveri, G.; Kumar, K.; Qiao, N.; Schemmel, J.; Wang, R.; Chicca, E.; Hasler, J.O.; et al. Large-scale neuromorphic spiking array processors: A quest to mimic the brain. Front. Neurosci. 2018, 12, 891. [Google Scholar] [CrossRef]
- Wu, X.; Saxena, V.; Zhu, K. Homogeneous spiking neuromorphic system for real-world pattern recognition. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 254–266. [Google Scholar] [CrossRef] [Green Version]
- Indiveri, G.; Corradi, F.; Qiao, N. Neuromorphic architectures for spiking deep neural networks. In Proceedings of the Electron Devices Meeting (IEDM), 2015 IEEE International. IEEE, Washington, DC, USA, 7–9 December 2015; pp. 4.2.1–4.2.14. [Google Scholar] [CrossRef]
- Wijekoon, J.H.B.; Dudek, P. Spiking and bursting firing patterns of a compact VLSI cortical neuron circuit. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 1332–1337. [Google Scholar] [CrossRef]
- Papadimitriou, K.I.; Eliu, S.-C.; Eindiveri, G.; Drakakis, E.M. Neuromorphic log-domain silicon synapse circuits obey Bernoulli dynamics: A unifying tutorial analysis. Front. Neurosci. 2015, 8, 428. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, C.; Legat, J.-D.; Bol, D. A compact phenomenological digital neuron implementing the 20 Izhikevich behaviors. In Proceedings of the 2017 IEEE Biomedical Circuits and Systems Conference, Turin, Italy, 19–21 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Indiveri, G.; Stefanini, F.; Chicca, E. Spike-based learning with a generalized integrate and fire silicon neuron. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1951–1954. [Google Scholar] [CrossRef] [Green Version]
- Qiao, N.; Mostafa, H.; Corradi, F.; Osswald, M.; Stefanini, F.; Sumislawska, D.; Indiveri, G. A reconfigurable on-line learning spiking neuromorphic processor comprising 256 neurons and 128K synapses. Front. Neurosci. 2015, 9, 141. [Google Scholar] [CrossRef] [Green Version]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.-J.; et al. TrueNorth: Design and Tool Flow of a 65 mW 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Wu, X.; Saxena, V.; Zhu, K.; Balagopal, S. A CMOS spiking neuron for brain-inspired neural networks with resistive synapses and in situ learning. IEEE Trans. Circuits Syst. II Exp. Briefs 2015, 62, 1088–1092. [Google Scholar] [CrossRef] [Green Version]
- Kuang, Y.; Cui, X.; Zhong, Y.; Liu, K.; Zou, C.; Dai, Z.; Wang, Y.; Yu, D.; Huang, R. A 64K-neuron 64M-1b-synapse 2.64pJ/SOP neuromorphic chip with all memory on chip for spike-based models in 65nm CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2655–2659. [Google Scholar] [CrossRef]
- Cruz-Albrecht, J.M.; Yung, M.W.; Srinivasa, N. Energy-efcient neuron, synapse and STDP integrated circuits. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 246–256. [Google Scholar] [CrossRef]
- Nakada, K.; Asai, T.; Amemiya, Y. Analog CMOS implementation of a bursting oscillator with depressing synapse. In Proceedings of the 2004 Intelligent Sensors, Sensor Networks and Information Processing Conference, Melbourne, Australia, 14–17 December 2004; pp. 503–506. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lee, J.; Kim, Y.; Ayers, J.; Volkovskii, A.; Selverston, A.; Abarbanel, H.; Rabinovich, M. Low power real time electronic neuron VLSI design using subthreshold technique. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems, Vancouver, BC, Canada, 23–26 May 2004; Volume 4, pp. 744–747. [Google Scholar] [CrossRef]
- Folowosele, F.; Etienne-Cummings, R.; Hamilton, T.J. A CMOS switched capacitor implementation of the Mihalas-Niebur neuron. In Proceedings of the 2009 IEEE Biomedical Circuits and Systems Conference, Beijing, China, 26–28 November 2009; pp. 105–108. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [Green Version]
- Chicca, E.; Stefanini, F.; Bartolozzi, C.; Indiveri, G. Neuromorphic electronic circuits for building autonomous cognitive systems. Proc. IEEE 2014, 102, 1367–1388. [Google Scholar] [CrossRef] [Green Version]
- Livi, P.; Indiveri, G. A current-mode conductance-based silicon neuron for address-event neuromorphic systems. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 2898–2901. [Google Scholar] [CrossRef] [Green Version]
- van Schaik, A.; Jin, C.; McEwan, A.; Hamilton, T.J. A log- domain implementation of the Izhikevich neuron model. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 4253–4256. [Google Scholar] [CrossRef]
- Bartolozzi, C.; Mitra, S.; Indiveri, G. An ultra-low power current- mode filter for neuromorphic systems and biomedical signal processing. In Proceedings of the 2006 IEEE Biomedical Circuits and Systems Conference, London, UK, 29 November–1 December 2006; pp. 130–133. [Google Scholar] [CrossRef]
- Bee, X.E.; Fauzi, M.M.B.M.; Tan, P.B.Y. Modeling of MOSFET subthreshold swing mismatch with BSIM4 Model. In Proceedings of the IEEE International Conference on Semiconductor Electronics (ICSE), Kuala Lumpur, Malaysia, 17–19 August 2016; Volume 6, pp. 86–88. [Google Scholar] [CrossRef]
- Rajasekharan, D.; Kushwaha, P.; Chauhan, S.S.; Chauhan, Y.S. Non-boolean associative processing using FDSOI MOSFET-based inverter. IEEE Trans. Nanotechnol. 2018, 17, 1235–1243. [Google Scholar] [CrossRef]
- Carbon, A.; Philippe, J.-M.; Bichler, O.; Schmit, R.; Tain, B.; Briand, D.; Ventroux, N.; Paindavoine, M.; Brousse, O. PNeuro: A scalable energy-efficient programmable hardware accelerator for neural networks. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition, Dresden, Germany, 19–23 March 2018; pp. 1039–1044. [Google Scholar] [CrossRef]
- Schemmel, J.; Kriener, L.; Muller, P.; Meier, K. An accelerated analog neuromorphic hardware system emulating NMDA- and calcium-based non-linear dendrites. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2217–2226. [Google Scholar] [CrossRef] [Green Version]
- Mayr, C.; Partzsch, J.; Noack, M.; Hanzsche, S.; Scholze, S.; Hoppner, S.; Ellguth, G.; Schuffny, R. A biological-realtime neuromorphic system in 28 nm CMOS using low-leakage switched capacitor circuits. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 243–254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Folowosele, F.; Harrison, A.; Cassidy, A.; Andreou, A.G.; Etienne-Cummings, R.; Mihalas, S.; Niebur, E.; Hamilton, T.J. A switched capacitor implementation of the generalized linear integrate-and-fire neuron. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 2149–2152. [Google Scholar] [CrossRef]
- Bellec, G.; Salaj, D.; Subramoney, A.; Legenstein, R.; Maass, W. Long short-term memory and learning-to-learn in networks of spiking neurons. Adv. Neural Inf. Process. Syst. 2018, 31, 787–797. [Google Scholar]
- Le Guevel, L.; Billiot, G.; Paz, B.C.; Tagliaferri, M.L.V.; De Franceschi, S.; Maurand, R.; Cassé, M.; Zurita, M.; Sanquer, M.; Vinet, M.; et al. Low-power transimpedance amplifier for cryogenic integration with quantum devices. Appl. Phys. Rev. 2020, 7, 041407. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Chicca, E.; Indiveri, G. A recipe for creating ideal hybrid memristive-CMOS neuromorphic processing systems. Appl. Phys. Lett. 2020, 116, 120501. [Google Scholar] [CrossRef]
- Frenkel, C.; Lefebvre, M.; Legat, J.-D.; Bol, D. A 0.086-mm2 12.7-pJ/sop 64k-synapse 256-neuron online-learning digital spiking neuromorphic processor in 28-nm CMOS. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 145–158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bédécarrats, T.; Fenouillet-Béranger, C.; Cristoloveanu, S.; Galy, P. A BIMOS-based 2T1C analogue spiking neuron circuit integrated in 28 nm FD-SOI technology for neuromorphic application. Solid-State Electron. 2020, 168, 107717. [Google Scholar] [CrossRef]
- Cincon, V.; Vatajelu, E.I.; Anghel, L.; Galy, P. From 1.8V to 0.19V voltage bias on analog spiking neuron in 28nm UTBB FDSOI technology. In Proceedings of the 2020 Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon, Caen, France, 1–30 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Qiao, N.; Indiveri, G. Scaling mixed-signal neuromorphic processors to 28 nm FD-SOI technologies. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference, Shanghai, China, 17–19 October 2016; pp. 55–555. [Google Scholar] [CrossRef] [Green Version]
- Rubino, A.; Livanelioglu, C.; Qiao, N.; Payvand, M.; Indiveri, G. Ultra-low-power FDSOI neural circuits for extreme-edge neuromorphic intelligence. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 45–56. [Google Scholar] [CrossRef]












| Cmem | Cref | Cadp | |
|---|---|---|---|
| Value | 383 fF | 227 fF | 639 fF |
| Width | 9 µm | 9 µm | 15.5 µm |
| Length | 12 µm | 7 µm | 18 µm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, J.; Liu, Z.; Li, B.; Luo, J. Ultra-Low-Power Compact Neuron Circuit with Tunable Spiking Frequency and High Robustness in 22 nm FDSOI. Electronics 2023, 12, 2648. https://doi.org/10.3390/electronics12122648
Quan J, Liu Z, Li B, Luo J. Ultra-Low-Power Compact Neuron Circuit with Tunable Spiking Frequency and High Robustness in 22 nm FDSOI. Electronics. 2023; 12(12):2648. https://doi.org/10.3390/electronics12122648
Chicago/Turabian StyleQuan, Jiale, Zhen Liu, Bo Li, and Jiajun Luo. 2023. "Ultra-Low-Power Compact Neuron Circuit with Tunable Spiking Frequency and High Robustness in 22 nm FDSOI" Electronics 12, no. 12: 2648. https://doi.org/10.3390/electronics12122648
APA StyleQuan, J., Liu, Z., Li, B., & Luo, J. (2023). Ultra-Low-Power Compact Neuron Circuit with Tunable Spiking Frequency and High Robustness in 22 nm FDSOI. Electronics, 12(12), 2648. https://doi.org/10.3390/electronics12122648






