Hardware Implementation of an Approximate Simplified Piecewise Linear Spiking Neuron
Abstract
1. Introduction
2. Simplified Piecewise Linear Model
2.1. Original Piecewise Linear Spiking Neuron
2.2. Simplified Piecewise Linear Neuron Model
2.3. Verification of Dynamic Computational Characteristics
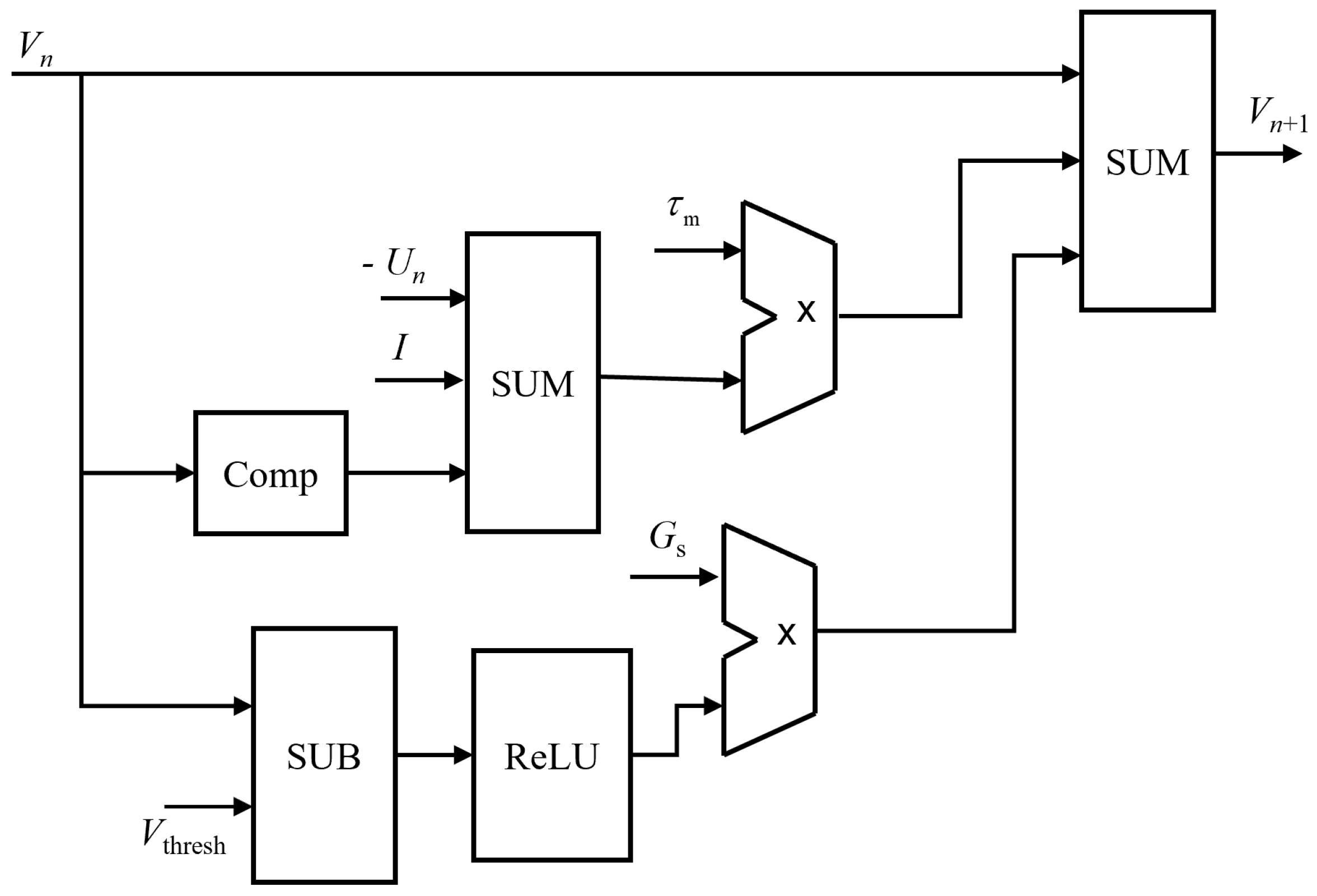
3. Hardware Implementation of the Approximate SPWL Model
- The V update module, which was used to calculate the change in membrane potential V. This module received input and feedback signals, and calculated the V change by combining the membrane potential update expression. The output of this module served as input to the spike generation logic;
- The U update module, which was used to calculate the recovery variable U of the membrane potential. The output of this module served as one of the inputs to the V update module;
- Spike generation logic, which was used to generate and recover spike signals. This module received the output signal of the V update module, and generated spike signals based on the set threshold; at the same time, it decided whether to adjust the threshold, based on control signals.
4. Results and Analysis
4.1. Hardware Synthesis and Test
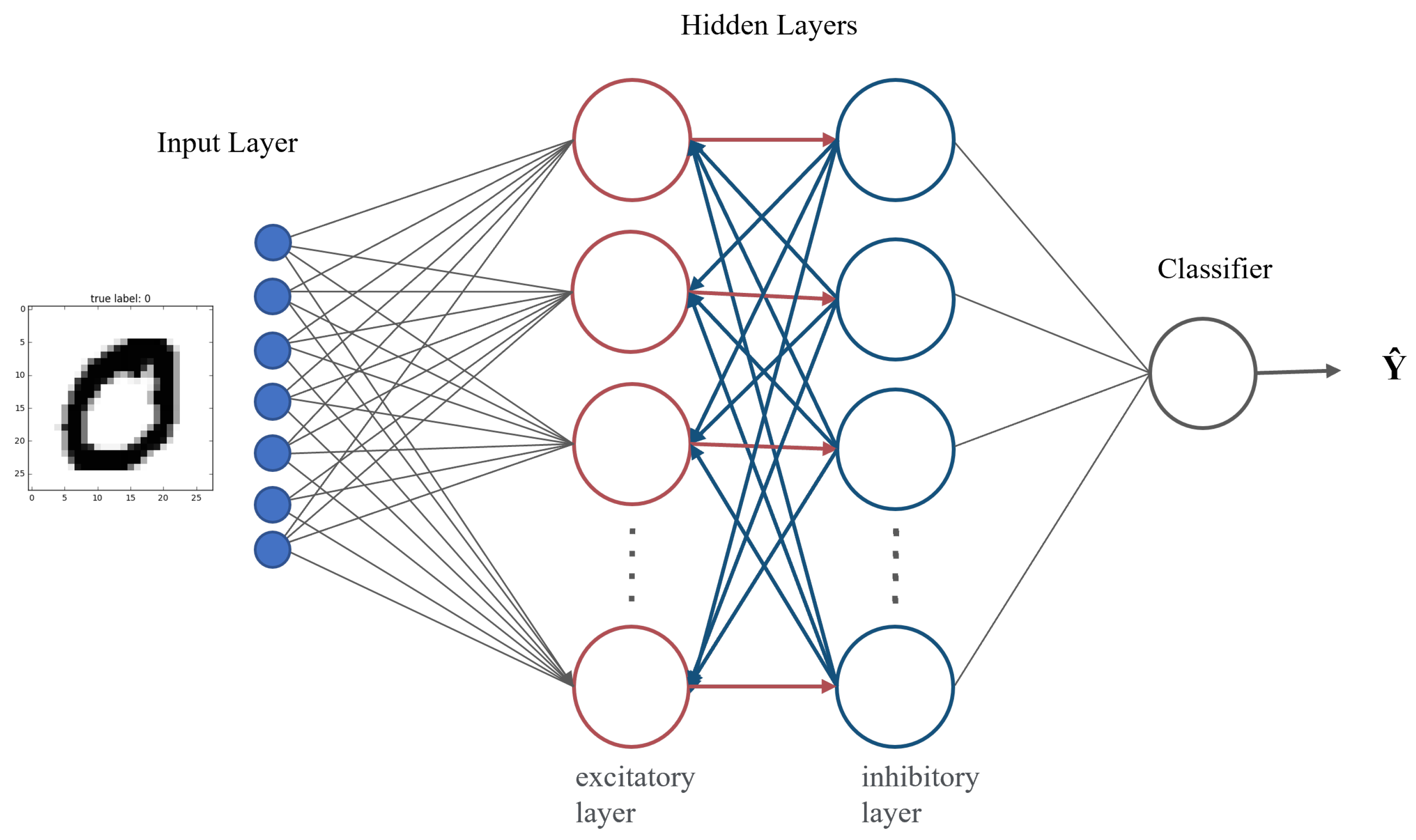
4.2. Application Test for the SPWL Neuron
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haghiri, S.; Ahmadi, A.; Saif, M. VLSI Implementable Neuron-Astrocyte Control Mechanism. Neurocomputing 2016, 214, 280–296. [Google Scholar] [CrossRef]
- Goaillard, J.M.; Moubarak, E.; Tapia, M.; Tell, F. Diversity of Axonal and Dendritic Contributions to Neuronal Output. Front. Cell. Neurosci. 2019, 13, 570. [Google Scholar] [CrossRef] [PubMed]
- Kirch, C.; Gollo, L.L. Spatially Resolved Dendritic Integration: Towards a Functional Classification of Neurons. PeerJ 2020, 8, e10250. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, S.C. Active Processing of Spatio-Temporal Input Patterns in Silicon Dendrites. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 307–318. [Google Scholar] [CrossRef]
- Xiang-hong, L.I.N.; Tian-wen, Z. Dynamical Properties of Piecewise Linear Spiking Neuron Model. Acta Electonica Sin. 2009, 37, 1270. [Google Scholar]
- Zang, Y.; Marder, E. Interactions among Diameter, Myelination, and the Na/K Pump Affect Axonal Resilience to High-Frequency Spiking. Proc. Natl. Acad. Sci. USA 2021, 118, e2105795118. [Google Scholar] [CrossRef] [PubMed]
- Zang, Y.; Marder, E. Neuronal Morphology Enhances Robustness to Perturbations of Channel Densities. Proc. Natl. Acad. Sci. USA 2023, 120, e2219049120. [Google Scholar] [CrossRef]
- Zang, Y.; Dieudonné, S.; Schutter, E.D. Voltage- and Branch-Specific Climbing Fiber Responses in Purkinje Cells. Cell Rep. 2018, 24, 1536–1549. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Gan, J.; Jonas, P. Fast-Spiking, Parvalbumin+ GABAergic Interneurons: From Cellular Design to Microcircuit Function. Science 2014, 345, 1255263. [Google Scholar] [CrossRef] [PubMed]
- Zang, Y.; Hong, S.; Schutter, E.D. Firing Rate-Dependent Phase Responses of Purkinje Cells Support Transient Oscillations. Elife 2020, 9, e60692. [Google Scholar] [CrossRef]
- Liu, H.; Wang, M.J.; Liu, M. SCPA: A Segemented Carry Prediction Approximate Adder Structure. IEICE Electron. Express 2021, 18, 20210335. [Google Scholar] [CrossRef]
- Liu, H.; Wang, M.; Yao, L.; Liu, M. A Piecewise Linear Mitchell Algorithm-Based Approximate Multiplier. Electronics 2022, 11, 1913. [Google Scholar] [CrossRef]
- FitzHugh, R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Izhikevich, E. Simple Model of Spiking Neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Grassia, F.; Levi, T.; Kohno, T.; Saïghi, S. Silicon Neuron: Digital Hardware Implementation of the Quartic Model. Artif. Life Robot. 2014, 19, 215–219. [Google Scholar] [CrossRef]
- Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian Learning through Spike-Timing-Dependent Synaptic Plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef]
- Song, S.; Abbott, L.F. Cortical Development and Remapping through Spike Timing-Dependent Plasticity. Neuron 2001, 32, 339–350. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Connor, J.A.; Walter, D.; McKown, R. Neural Repetitive Firing: Modifications of the Hodgkin-Huxley Axon Suggested by Experimental Results from Crustacean Axons. Biophys. J. 1977, 18, 81–102. [Google Scholar] [CrossRef]
- Morris, C.; Lecar, H. Voltage Oscillations in the Barnacle Giant Muscle Fiber. Biophys. J. 1981, 35, 193–213. [Google Scholar] [CrossRef]
- Hindmarsh, J.L.; Rose, R.M. A Model of Neuronal Bursting Using Three Coupled First Order Differential Equations. Proc. R. Soc. Lond. B Biol. Sci. 1984, 221, 87–102. [Google Scholar] [CrossRef]
- Stein, R.B. A theoretical analysis of neuronal variability. Biophys. J. 1965, 5, 173–194. [Google Scholar] [CrossRef]
- Ermentrout, G.B.; Kopell, N. Parabolic Bursting in an Excitable System Coupled with a Slow Oscillation. SIAM J. Appl. Math. 1986, 46, 233–253. [Google Scholar] [CrossRef]
- Fourcaud-Trocmé, N.; Hansel, D.; van Vreeswijk, C.; Brunel, N. How Spike Generation Mechanisms Determine the Neuronal Response to Fluctuating Inputs. J. Neurosci. 2003, 23, 11628–11640. [Google Scholar] [CrossRef]
- Brette, R.; Gerstner, W. Adaptive Exponential Integrate-and-Fire Model as an Effective Description of Neuronal Activity. J. Neurophysiol. 2005, 94, 3637–3642. [Google Scholar] [CrossRef] [PubMed]
- Nouri, M.; Hayati, M.; Serrano-Gotarredona, T.; Abbott, D. A Digital Neuromorphic Realization of the 2-D Wilson Neuron Model. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 136–140. [Google Scholar] [CrossRef]
- Haghiri, S.; Zahedi, A.; Naderi, A.; Ahmadi, A. Multiplierless Implementation of Noisy Izhikevich Neuron With Low-Cost Digital Design. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1422–1430. [Google Scholar] [CrossRef] [PubMed]
- Grassia, F.; Kohno, T.; Levi, T. Digital Hardware Implementation of a Stochastic Two-Dimensional Neuron Model. J. Physiol.-Paris 2016, 110, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, H.; Drakakise, E.M. An Efficient and Reconfigurable Synchronous Neuron Model. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 91–95. [Google Scholar] [CrossRef]
- Zang, Y.; Schutter, E.D. The Cellular Electrophysiological Properties Underlying Multiplexed Coding in Purkinje Cells. J. Neurosci. 2021, 41, 1850–1863. [Google Scholar] [CrossRef] [PubMed]
- Haghiri, S.; Ahmadi, A. A Novel Digital Realization of AdEx Neuron Model. IEEE Trans. Circuits Syst. II 2020, 67, 1444–1448. [Google Scholar] [CrossRef]
- Heidarpour, M.; Ahmadi, A.; Rashidzadeh, R. A CORDIC Based Digital Hardware For Adaptive Exponential Integrate and Fire Neuron. IEEE Trans. Circuits Syst. I 2016, 63, 1986–1996. [Google Scholar] [CrossRef]
- Gomar, S.; Ahmadi, A. Digital Multiplierless Implementation of Biological Adaptive-Exponential Neuron Model. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 1206–1219. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, B.; Huang, Z.; Liu, X.; He, S.; Li, Q.; Guo, D. Fractional Spiking Neuron: Fractional Leaky Integrate-and-Fire Circuit Described with Dendritic Fractal Model. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 1375–1386. [Google Scholar] [CrossRef] [PubMed]
- Leigh, A.J.; Mirhassani, M.; Muscedere, R. An Efficient Spiking Neuron Hardware System Based on the Hardware-Oriented Modified Izhikevich Neuron (HOMIN) Model. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3377–3381. [Google Scholar] [CrossRef]
- Pu, J.; Goh, W.L.; Nambiar, V.P.; Chong, Y.S.; Do, A.T. A Low-Cost High-Throughput Digital Design of Biorealistic Spiking Neuron. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1398–1402. [Google Scholar] [CrossRef]
- Amiri, M.; Nazari, S.; Faez, K. Digital Realization of the Proposed Linear Model of the Hodgkin-Huxley Neuron. Int. J. Circ. Theor. Appl. 2019, 47, 483–497. [Google Scholar] [CrossRef]
- Hassan, S.; Salama, K.N.; Mostafa, H. An Approximate Multiplier Based Hardware Implementation of the Izhikevich Model. In Proceedings of the 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 492–495. [Google Scholar] [CrossRef]


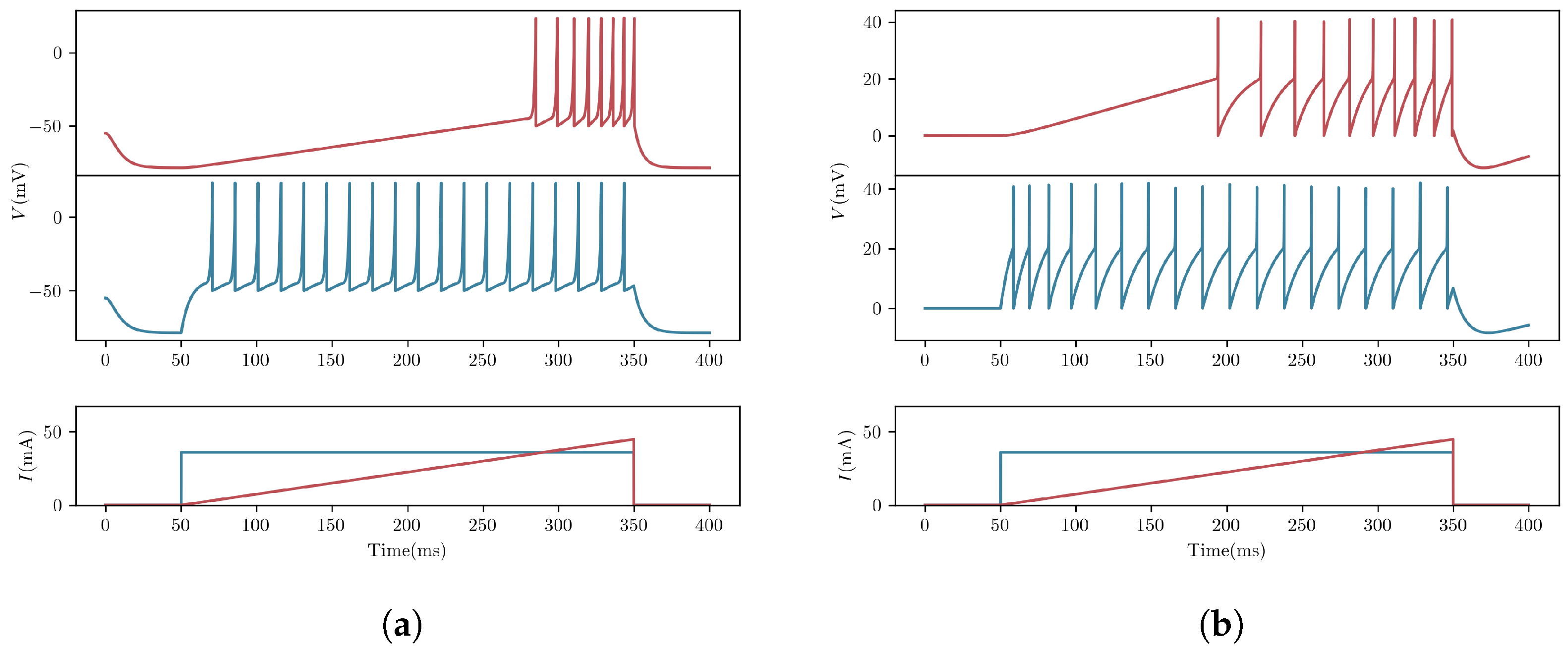







| Parameter | Details |
|---|---|
| V | Membrane potential of neurons. |
| U | Recovery variables, represents activated K current or inactivated Na current, and also achieves negative feedback regulation of V. |
| I | Synapse input current or external injection current. |
| Membrane time constant, which must satisfy . | |
| Resting potential, used with to describe the leakage of neuron. | |
| Spike generating threshold value. | |
| Spike conductance, whose unit is the leakage conductance (). | |
| Recovery time constant. | |
| k | Coupling strength between U and V. |
| Spike peak value. | |
| Difference of ion current before and after spike. |
| Neuron | Aera (μm2) | Power (mW) | Delay (ns) |
|---|---|---|---|
| FitzHugh–Nagumo [13] | 15,220.4 | 6.09 | 25.43 |
| Izhikevich [14] | 12,367.2 | 5.82 | 24.27 |
| Quartic [15] | 24,043.2 | 11.99 | 48.81 |
| Original PWL [5] | 9226.4 | 4.25 | 4.04 |
| SPWL-approx | 3999.6 | 0.90 | 1.55 |
| Label | Precision | Recall | F1-Score | Datasize |
|---|---|---|---|---|
| 0 | 0.97 | 0.97 | 0.97 | 980 |
| 1 | 0.97 | 0.97 | 0.97 | 1135 |
| 2 | 0.94 | 0.94 | 0.94 | 1032 |
| 3 | 0.93 | 0.94 | 0.94 | 1010 |
| 4 | 0.94 | 0.92 | 0.93 | 982 |
| 5 | 0.91 | 0.89 | 0.90 | 892 |
| 6 | 0.94 | 0.94 | 0.94 | 958 |
| 7 | 0.94 | 0.93 | 0.93 | 1028 |
| 8 | 0.90 | 0.91 | 0.91 | 974 |
| 9 | 0.92 | 0.94 | 0.93 | 1009 |
| average | 0.94 | 0.94 | 0.94 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, M.; Yao, L.; Liu, M. Hardware Implementation of an Approximate Simplified Piecewise Linear Spiking Neuron. Electronics 2023, 12, 2628. https://doi.org/10.3390/electronics12122628
Liu H, Wang M, Yao L, Liu M. Hardware Implementation of an Approximate Simplified Piecewise Linear Spiking Neuron. Electronics. 2023; 12(12):2628. https://doi.org/10.3390/electronics12122628
Chicago/Turabian StyleLiu, Hao, Mingjiang Wang, Longxin Yao, and Ming Liu. 2023. "Hardware Implementation of an Approximate Simplified Piecewise Linear Spiking Neuron" Electronics 12, no. 12: 2628. https://doi.org/10.3390/electronics12122628
APA StyleLiu, H., Wang, M., Yao, L., & Liu, M. (2023). Hardware Implementation of an Approximate Simplified Piecewise Linear Spiking Neuron. Electronics, 12(12), 2628. https://doi.org/10.3390/electronics12122628






