Abstract
It is very important to accurately identify the critical nodes of the power grid for its safe and stable operation. In this paper, a method for identifying the critical nodes of the power grid based on the improved entropy weight method (IEWM) is proposed, and the IEWM corrects issues with the information overlap between evaluation indices and inconsistency between the entropy weight (EW) and entropy value (EV). First, considering the power grid topology and operating conditions, structural factor evaluation indices and state factor evaluation indices are established. On this basis, the IEWM is used to assign weights to nodes with different voltage levels, which strengthens the consideration of node voltage levels in the identification method of critical nodes and makes the results more accurate and effective. Simulation experiments of IEEE 30-bus and IEEE 118-bus systems verify the accuracy of the critical node identification method proposed in this paper.
1. Introduction
With the expansion of the interregional interconnection degree of power grid and new energy connections, the structure of the power network becomes more complex. The uncertainty of power grid operation continues to increase, and frequent power outages cause serious economic losses and negative social impacts [1,2]. When the power grid fails, the critical nodes have a key role in the power grid, and may even cause the system to collapse gradually [3,4,5]. Therefore, it is important to precisely identify the critical nodes in the power grid to prevent power outages [6,7].
The evaluation results of critical nodes vary depending on the evaluation indices selected for the critical node evaluation of the power grid. Therefore, how to select appropriate and accurate evaluation indices is a major issue in evaluating critical nodes [8]. At present, the evaluation indices of power network critical nodes mainly come from the construction of power system topology and the analysis of power network characteristics. Therefore, many scholars have proposed a variety of methods for identifying critical nodes. Ref. [9] uses the link-based partitioning method to find the overlapping areas in the power grid and identifies the key nodes of the power grid using the betweenness centrality based on neighbor nodes (BCBNN) algorithm. In [3], a critical node evaluation method based on fixed control theory is proposed, which uses the minimum nonzero eigenvalue of the modified Laplace matrix. Ref. [10] develops an algorithmic procedure and mathematical method to evaluate the key and redundant nodes in the scaling network using the minimum dominant set (MDS) method. Methods for evaluating the importance of nodes in the power system in [3,9,10] are essentially based on the structural factor of the topology. Ref. [11] proposes evaluation indices such as electric dielectric number, transmission efficiency, spanning tree change rate, and so on. Based on the technique for order preference by similarity to an ideal solution (TOPSIS) method and the criteria importance through intercriteria correlation (CRITIC) method, a critical node identification method of power grid is established in [11]. In [12], the network topology is divided into three dimensions for analysis. Then, a multidimensional and multilayer node evaluation model based on the entropy weight method (EWM) is proposed in [12], considering the connection relationship between power grid and the communication network. To prevent cascading failures in power systems, [13] proposes a prediction method for key nodes and transmission lines in power grid, which includes two links—the historical data mining link and the prediction link. Ref. [14] uses the multi-objective optimization model to solve the problem of key node detection in the network and designs an adaptive local search strategy. From the perspective of network dynamics, Ref. [8] proposes a method to identify the key nodes of complex power systems, which is used to find the nodes that play an important role in the stability control and accurate monitoring of power grid. The construction of power system topology and the analysis of power network characteristics are crucial factors in assessing the importance of nodes in the power system.
In addition, the importance of power system nodes is closely related to the voltage level of grid nodes and the interaction between indices [15,16,17]. In [18], a critical node seeking method is proposed, which uses multiple voltage stability metrics. In [19], when the reactive power of all load nodes varies together, the change in the magnitude of the load node voltage is used to identify a set of weak nodes. The critical node identification methods in [18,19] fully prove the importance of node voltage level in identifying critical nodes. In [20], the structural factors and state factors of the power network are integrated and analyzed, and the static energy function model and the node structure vulnerability factor are built, without considering the influence of the node voltage level on the evaluation factors, and the interaction between factors. Although [21] considers the voltage level of the system and introduces the Tel entropy of the voltage growth ratio and the weighted power flow impact ratio to identify the critical nodes in the power system, it lacks the consideration of the structure of the power system.
To analyze the impact of node evaluation indices under different voltage levels, this paper proposes the improved entropy weight method (IEWM). The traditional EWM is a common weight allocation method, that is, the larger the difference between indices, the more information it contains and the smaller the entropy. Therefore, in comparison to the scaling method [22], which emphasizes overall differences, the EWM emphasizes local differences. This means that the index weight increases with the level difference between evaluation objects, leading to a greater impact on the evaluation results. However, there are two problems in the EWM. Firstly, when all entropy values used in the EWM are close to 1, even a small difference in the EV can lead to large changes in the EW. This can result in some indices being assigned weights that are not consistent with their importance, which can affect the accuracy of the final critical node identification result [23]. Secondly, the EWM does not consider the interaction between indices, which can reduce the accuracy of the analysis and lead to unreasonable results.
Therefore, this paper proposes a critical node identification method based on the IEWM, and the IEWM corrects the problems of information overlap between the evaluation indices and inconsistency between the EW and the EV. Firstly, considering the power grid topology and operating conditions, the evaluation indices of the power grid structure and state factors are established. Then, this paper proposes the IEWM, which is used to analyze the difference in the influence of the structure factor evaluation indices and state factor evaluation indices on the power system under different node voltage levels, and the weights are assigned to different evaluation indices, enhancing the consideration of node voltage level in the critical node identification method and improving the accuracy of identifying critical nodes. Finally, through the simulation experiments of the IEEE 30-bus system and IEEE 118-bus system, the accuracy of the recognition method in this paper is verified.
Generally, the main work of this paper can be summarized as follows.
- (1)
- This paper proposes an accurate and effective identification method for critical nodes using the IEWM;
- (2)
- To account for the construction of power system topology and the analysis of power network characteristics, this paper obtains several evaluation indices, including the electrical betweenness (), the electrical coupling (), the node power mobility (), the power supply weakness of the node (), and the node reactive power compensation degree (), and uses the independence weighting method to improve the EWM for reducing information overlap between these indices;
- (3)
- In the identification method, this paper proposes a method based on the IEWM to analyze the influence of node voltage on the evaluation index, enhancing the consideration of node voltage level of power grid in the identification method.
The framework of this article is organized as follows. Section 2 establishes the critical node evaluation indices. In Section 3, the IEWM is proposed and applied to the identification of power system critical nodes. Section 4 presents the simulation results of the IEEE 30-bus system and IEEE 118-bus system. Finally, Section 5 provides the conclusion of this paper.
2. Critical Node Evaluation Indices
2.1. Structural Factor Evaluation Indices
In the power grid, suppose that the topology model has n network nodes. The structural data set A is composed of the structural data for all nodes in the system.
For each node in the power system, there are numerous structural factor evaluation indices, such as , , and so on. These structural factor evaluation indices constitute the structural set of node i.
where:
where G is the set of generator nodes in the system, L is the set of load nodes in the system, is the actual output power of generator node r, is the actual load power absorbed by node s, is the electrical factor of node i, is the set of associated nodes of node i, is the current generated on branch ij after injecting a unit current source between node r and node s, and is the electrical distance between node i and node j [24], which is numerically equal to the voltage between node i and node j after injecting a unit current source from node i.
2.2. State Factor Evaluation Indices
For each node in the power system, there are many electric quantities, such as P, Q, and U, which reflect the state change in the node. The state data set B is composed of these state quantities.
The status factor evaluation indices include:
- (1)
- Node power mobility
Considering the difference in the generator output scenarios, this paper proposes as follows.
where is the base value of the power flow calculation capacity, and is the power injected into i by node j in scenario c, is the status factor of the generator operation, and the rated operation of generator is 1. is the set of associated nodes of node i. This index can reflect the ability of the node to transmit power. The larger , the greater the influence of the node in the transmission of the power system.
- (2)
- Node reactive power compensation degree
- (3)
- Power supply weakness of the node
Considering the limited power supply capacity of the line, this paper constructs .
where is the line set connected to node i, and is the variable representing the state of the line, which is 0 or 1. When the line is connected, the value of is 1. is the line capacity of line k. This index represents the energy transmission capacity of the node, and the greater the value, the greater the impact of the node on the power supply capacity of the power grid.
Overall, the state set of node i is constituted by the above state factor evaluation indices.
3. Critical Node Identification Method
3.1. The Improved Entropy Weight Method (IEWM)
In power networks, there is often information overlap between evaluation indices. The EWM does not eliminate the error caused by information overlap between evaluation indices when calculating EW. At the same time, the EWM has the problem of inconsistent information between EW and EV when EV approaches 1. Therefore, the EWM is an improvement.
Firstly, this paper introduces the independence weighting method to preprocess the data of EWM to reduce the information overlap between evaluation indices.
The data matrix C of the EWM is established by the structure data set A and the state data set B.
where is the normalized data of index j of node i. Matrix C is a data matrix containing n1 nodes and m evaluation indices.
Further, the complex correlation coefficient between the evaluation indices is calculated [25]:
where is the complex correlation coefficient of index j, represents the remaining matrix in the matrix after removing the column j, and is the average value of the matrix . If is larger, the linear relationship between index j and other indices is stronger and the overlapping information of index j is greater [26].
Further, the correction factor of index j is obtained as follows.
To reduce the information overlap between evaluation indices, this paper introduces the correction factor to the data matrix. The data matrix E of the IEWM is obtained:
where
Furthermore, the EV of the evaluation index j is calculated as follows.
where
With respect to the inconsistency between the EW and EV when the EV of EWM approaches 1 [27], this paper makes the following improvements.
where is the weight of index j, is the average of all entropy values not equal to 1, and is the weight correction, which represents raised to the power of 35.35. is used to reduce the inconsistency between the EW and EV when the EV of EWM approaches 1.
3.2. The Voltage Weighting Factor
The stability of the power system running is mainly affected by the state factor of the power system running. However, when the voltage level of the power system is high, the influence of the state factor of the power grid is reduced, and the structure factor of the power system is increased [16]. Therefore, the influence analysis of node structure factor and state factor evaluation indices under different voltage levels on the power system should be strengthened when evaluating critical nodes of power system.
Based on the above analysis, the structure factor and state factor evaluation indices should be assigned weights according to the node voltage level. Firstly, under different operating conditions, including load rate change, generator running state mutation, line fault, and so on, nodes are classified according to node voltage level based on the power flow results, and the IEWM is further used to analyze the data. If the data of n2 nodes are included under a certain voltage level, the matrix of this voltage level obtained from the structural data set A and the state data set B of n2 nodes is as follows.
where matrix is a data matrix containing five evaluation indices, namely, , , , , and . The data matrix of the IEWM is obtained according to the processing method of Equations (9)–(13), and the weight of index j of the IEWM under this voltage level is further obtained according to Equations (14)–(17).
Further, under this voltage level, the voltage weighting factor can be obtained according to the classification of node evaluation indices in this paper:
where is the set of state evaluation index , , and .
Further, the calculation of the node voltage weighting factor under different voltage levels is similar to the above calculation process. Taking the IEEE 118-bus system as an example, the voltage weighting factor under different voltage levels is shown in Table 1, where is the unit value of voltage scale.

Table 1.
Weighting factor of different node voltage levels.
For the power network, the voltage weighting factor can take into account the role of the state factor and the structure factor evaluation index of the power system, rather than simply linearly weighting the evaluation index of the system to fit the real power system characteristics.
3.3. The Combined Weight
In the power network, after the voltage weighting factor has been determined using the IEWM, the combined weight of node i is obtained using the combined weight method:
where is the structure value after the normalization of the structure factor evaluation index j of node i, and the evaluation indices of structure factors include and . is the status value of the status factor evaluation index k of node i after normalization processing, and the status factor evaluation indices include , , and . The greater the combined weight of node i, the greater the impact of the node on the continuous and stable operation of the power network. When node i ceases operation, the system is more likely to lose stability or even collapse.
3.4. Evaluation Process
Based on the above analysis, the evaluation process of critical nodes in this paper can be divided into the following steps.
In Figure 1, the identification process is divided into three parts with a total of eight steps. In part 1 (steps 1 to 3), the system to be evaluated is set up. In part 2 (steps 4 to 6), the structure data set A and the state data set B of the system to be evaluated are obtained mainly based on the system data, and the IEWM is used to obtain voltage weighting factor ρ. In part 3 (steps 7 to 8), the combined weight of node i is calculated and processed in descending order to obtain the critical nodes.
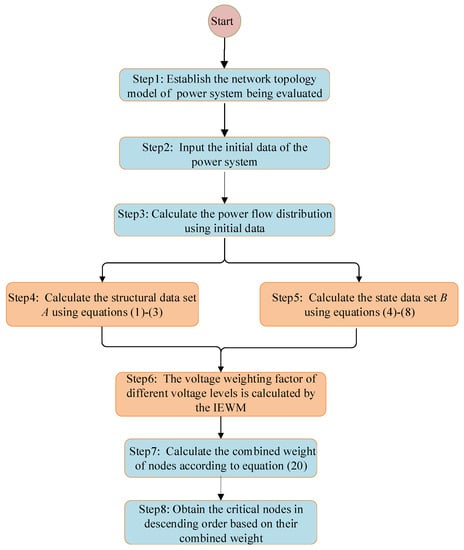
Figure 1.
Framework of critical node identification method.
3.5. Critical Node Verification Method
According to the above critical node evaluation method, the node evaluation result of the node system is obtained, and the node evaluation results are sorted to obtain the critical nodes of the power system. To explain the degree of influence of the identified critical nodes on the power network, this paper uses the node voltage status index [28] for comparison and verification analysis. The is as follows.
where is the voltage level of node j, is the injected power of node i in the power network, is the offset angle of node voltage, and is the imaginary part of admittance between node i and node j.
The voltage status index of each node in the power network is averaged to obtain the system voltage status index .
When the nodes of the power network are randomly attacked and quit operation, the connectivity state and power distribution of the power network change, which is reflected in the system voltage status index . Generally speaking, the smaller the average value of the system voltage status index of the whole system, the lower the stability of the system voltage, and the higher risk of system voltage collapse.
4. Simulation Results
4.1. IEEE 30-Bus System Simulation Experiment
4.1.1. IEEE 30-Bus System Critical Node Identification
This system is a standard IEEE 30-bus system. The system data are shown in [29], and the system topology diagram of the IEEE 30-bus system is shown in Figure 2.
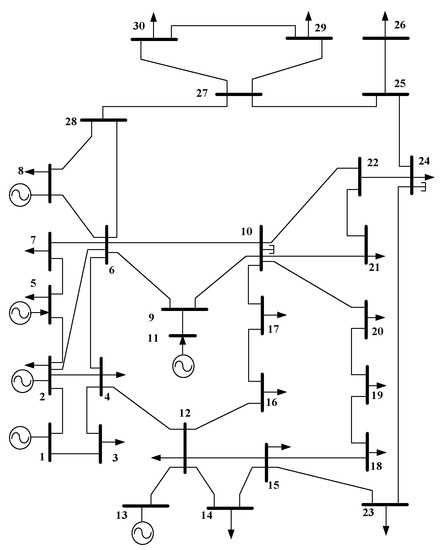
Figure 2.
Structure diagram of IEEE 30-bus system.
The simulation in this paper was performed on the MATLAB platform, and the accurate results of AC power flow calculation of the IEEE 30-bus system were achieved with the MATPOWER toolkit. According to the evaluation process shown in Figure 1, the , , , , and of each node are calculated. According to the simulation results in this paper, the exemplary data of the individual indicator are shown in Figure 3, which are the data after normalization according to Equation (9).
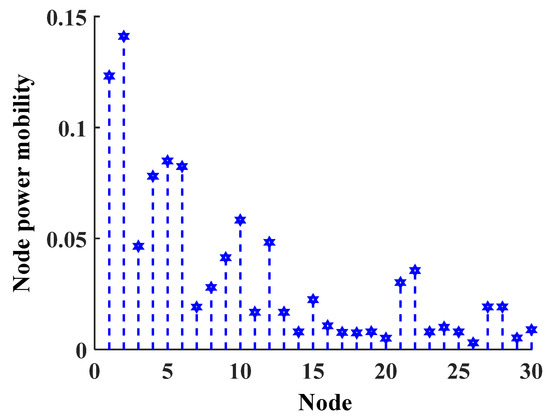
Figure 3.
Results of the calculation of .
To see the identification results of the method in this paper more directly, the ranking results of the top 15 nodes of the , , , , and are listed, as shown in Table 2.

Table 2.
Identification results of critical nodes of different evaluation indices in IEEE 30-bus system.
Further, according to Equations (10)–(20), the combined weight of each node of the IEEE 30-bus system is obtained, and the result is shown in Figure 4.
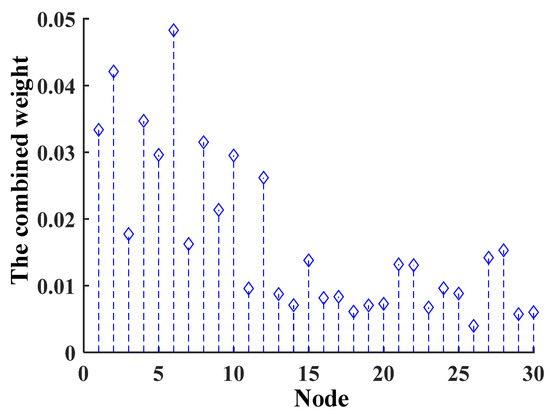
Figure 4.
The evaluation results of IEEE 30-bus system.
4.1.2. Comparison of Different Identification Methods
In [20], considering both state and structure characteristics, a comprehensive vulnerability index is proposed to accurately locate the weak nodes in the system. Based on the consideration of the system voltage level, Ref. [21] proposes a method for the identification of critical nodes in power grid by comprehensively considering the static voltage stability of nodes and the balance of branch transfer power flow distribution. Different from the identification methods in [20,21], this paper not only comprehensively considers the state and structural characteristics of the power system, but also uses IEWM to analyze the influence of the node voltage level on the state and structural characteristics. In order to verify the accuracy of the method in this paper, the evaluation results of the critical nodes in this paper were compared with the results in [20,21], and the top ten critical nodes were obtained, as shown in Table 3.

Table 3.
Comparison of the results of different identification methods.
By comparing the recognition results of [20,21], it can be seen that the recognition results of six nodes in this paper are the same as those in [20], and six nodes are the same as those in [21].
According to the IEEE 30-bus system structure diagram in Figure 2, most of the critical nodes evaluated by the method in this paper are generator nodes or intermediate nodes that undertake important transmission tasks in the network. According to the results identified in this paper, node 6 has the largest combined weight . In the IEEE 30-bus system, node 6 is the convergence of multiple lines, and is responsible for the transmission of energy from multiple generator nodes to load nodes. If node 6 is out of operation, the distance that the generator power must travel from nodes 5, 2, and 1 to load nodes 17, 18, and 19 is greatly increased. Therefore, the running state of node 6 is related to the energy transmission of the whole network, which has an important influence on the reliability of the system.
In order to further verify the accuracy of the identification method in this paper, three sets of simulation experiments were designed: Simulation experiments 1,2 and 3 were carried out attack simulation experiments on the first 10 nodes on the basis of the sorting results in [20,21] and this paper, respectively, to record the system voltage status index. Finally, the average value of the system voltage state index under multiple attacks in each experiment was calculated.
Generally speaking, the smaller the system voltage status index of the system, the worse the stability of the system and the greater the danger of system collapse. At the beginning of the attack simulation experiment, the system voltage status index of the IEEE 30-bus system was 0.9667. As can be seen from Figure 5, when the system was simulated according to different sorting results, the average value of the system voltage status index identified in this paper after the attack was 0.7597, and the average value of the system voltage status index in [20,21] was 0.7695 and 0.7634, respectively. According to the above simulation experiment results, the critical nodes identified by the method in this paper experienced a greater drop in the system voltage status index after the attack, which confirms the accuracy of the identification method in this paper.
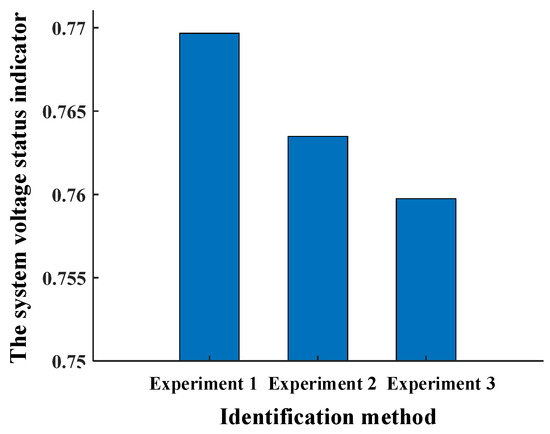
Figure 5.
Simulation experiment results of IEEE 30-bus system.
4.2. IEEE 118-Bus System Simulation Experiment
4.2.1. IEEE 118-Bus System Critical Node Identification
This system is a standard IEEE 118-bus system. The system data are shown in [30], and the system topology diagram is shown in Figure 6.
Figure 6.
Structure diagram of IEEE 118-bus system.
The simulation of the IEEE 118-bus system was performed on the MATLAB platform, and the accurate results of the AC power flow calculation of the IEEE 118-bus system were achieved with the MATPOWER toolkit. According to the evaluation process shown in Figure 1, the , , , , and of each node was calculated.
To see the identification results of the method in this paper more directly, the ranking results of the top 20 nodes of each index are listed, respectively, as shown in Table 4.

Table 4.
Identification results of critical nodes of different evaluation indices in IEEE 118-bus system.
The combined weight of the nodes was obtained in the IEEE 118-bus system according to Equation (20), and the results are shown in Figure 7. The larger the combined weight of a node, the more important the node is in the power system. The nodes with a large combined weight can be regarded as the critical nodes of the power network and need to be monitored during the operation of the power network.
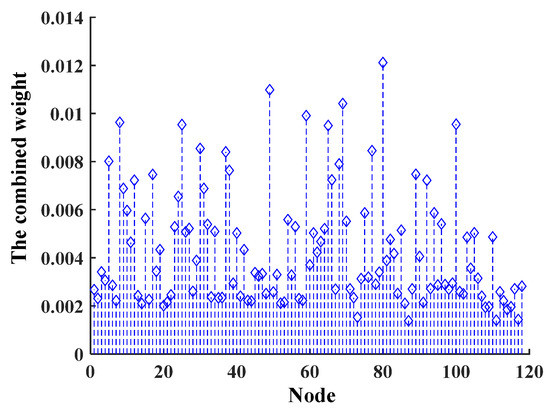
Figure 7.
The evaluation results of IEEE 118-bus system.
4.2.2. Comparison of Different Identification Methods
Ref. [2] proposes a weighted stochastic approach for link structure analysis (SALSA) algorithm to search critical node in electric power systems. Considering the load loss of the load node and the power generation of the power node, Ref. [7] introduces the electrical betweenness algorithm to measure the node vulnerability of the power system. From the perspective of power flow analysis, Ref. [15] proposes a node evaluation index based on the co-citation-hypertext-induced topic selection (MBCC-HITS) algorithm model. To verify the accuracy of the critical node identification results in the IEEE 118-bus system, this paper compares the evaluation results with those of the weighted-SALSA algorithm [2], the electrical betweenness algorithm [7], and the MBCC-HITS algorithm [15], as shown in Table 5.

Table 5.
Different identification results in IEEE 118-bus system.
To further verify the accuracy of the identification results in this paper, 10 groups of node random attack simulation experiments were conducted on the top 20 critical nodes with different identification results, shown in Table 5. Then, the system voltage status index was recorded after each group of attacks. At the same time, for comparative analysis, this paper conducted a random attack on the system: in the IEEE 118-bus system, we selected the same number of nodes for 10 groups of random attack simulation experiments and recorded the system voltage status index after each group of attacks. Simulation results are shown in Figure 8.
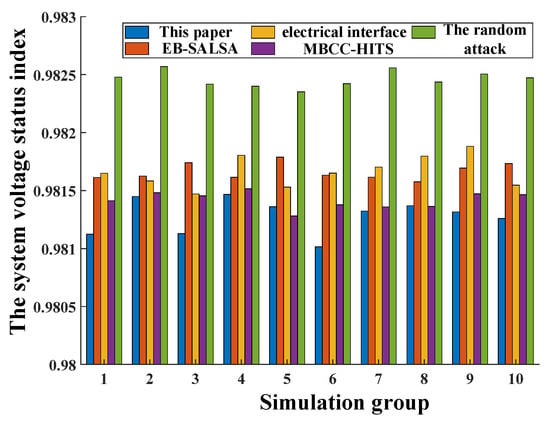
Figure 8.
Simulation experiment results of IEEE 118-bus system.
According to the comparison of simulation results in Figure 8, the drop in the system voltage status index of the evaluation results of this paper, the evaluation results of the EB-SALSA algorithm, the evaluation results of the electrical betweenness algorithm, and the evaluation results of the MBCC-HITS algorithm are all larger than the random attack. This proves that the identification methods in this paper, the EB-SALSA algorithm, the electrical betweenness algorithm, and the MBCC-HITS algorithm are all effective for the identification of critical nodes of the power system.
Meanwhile, according to Figure 6 and the data of the IEEE 118-bus system, most of the top 20 nodes identified in this paper are the nodes that undertake important transmission tasks in the IEEE 118-bus system or connect to important generators. Those nodes have a greater impact on network power flow, are more sensitive to power changes, and play a greater role in network energy transmission. The IEWM was used in this paper to comprehensively analyze the voltage level, structure factor evaluation indices, and state factor evaluation indices of the system to obtain the identification results of critical nodes. In the simulation experiment, the system voltage status index dropped more severely when attacked based on the evaluation results of this paper, which proves the accuracy of the identification method proposed in this paper. The real-life power grid is a complex network, and its characteristics are close to those of the IEEE 118-bus system. Therefore, the method is also effective for the real-life power grid.
By comparing Figure 5 and Figure 8, it can be seen that the IEEE 118-bus system has a relatively small range of system voltage status index drop after the attack compared with the IEEE 30-bus system, which indicates that with the increase in complexity of the power system, the power system is more robust.
5. Conclusions
In this paper, we proposed an accurate identification method for power systems. In Section 2, this paper established two types of evaluation indices according to the grid topology and operating conditions, which are the structural data set A and the state data set B. Then, in Section 3.1, this paper used the independence weighting method to optimize the data of the EWM to reduce the information overlap between indicators. At the same time, this paper further modified the entropy weight method, which solved the problem of the inconsistency between the EW and EV when the EV of the entropy method approaches 1. The IEWM was used in Section 3.2 to obtain the voltage weighting factor ρ, which was used to analyze the difference in the influence of the structure factor evaluation indices and state factor evaluation indices on the power system under different node voltage levels. The combined weight was obtained in Section 3.3, and thus, the critical nodes were obtained. Theoretical analysis and simulation experiments showed that:
- (1)
- Through the simulation and comparison experiment, the identification method in this paper was shown to have a high accuracy in the identification of critical nodes of the power system and to be able to identify the critical nodes of the power grid effectively. At the same time, through the simulation experiment, it was proven that with the increase in the complexity of the power system, the power system’s ability to resist attacks also becomes stronger.
- (2)
- This paper proposes the IEWM, which corrects issues with overlapping evaluation index information and inconsistency between the EW and the EV.
- (3)
- In the critical node evaluation process, a method based on the IEWM is proposed to analyze the influence of node voltage on the evaluation indices, which strengthens the consideration of the node voltage level in the critical node evaluation process.
Author Contributions
Conceptualization, L.Z.; methodology, G.L. and L.Z.; investigation, Z.K.; resources, G.L.; software, G.L.; validation, G.L.; funding acquisition, L.Z.; formal analysis, Z.K.; writing—original draft preparation, G.L.; visualization, Y.W.; supervision, L.Z., G.L. and Y.W.; writing—review and editing, L.Z. and Y.W.; project administration, Y.W. and Z.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used to support the research results of this paper are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jarmakiewicz, J.; Parobczak, K.; Maślanka, K. Cybersecurity protection for power grid control infrastructures. Int. J. Crit. Infrastruct. Prot. 2017, 18, 20–33. [Google Scholar] [CrossRef]
- Geng, J.; Piao, X.; Qu, Y.; Song, H.; Zheng, K. Method for finding the important nodes of an electrical power system based on weighted-SALSA algorithm. IET Gener. Transm. Distrib. 2019, 13, 4933–4941. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Xu, T.; Zhu, M.; He, Z. Evaluation of Critical Node Groups in Cyber-Physical Power Systems Based on Pinning Control Theory. IEEE Access 2022, 10, 48936–48947. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, X.; He, R.; Tian, M.; Zhang, Q. Identification of vital node in power grid based on importance evaluation matrix. High Volt. Eng. 2016, 42, 3347–3353. [Google Scholar]
- Abedi, A.; Romerio, F. Multi-period vulnerability analysis of power grids under multiple outages: An AC-based bilevel optimization approach. Int. J. Crit. Infrastruct. Prot. 2020, 30, 100365. [Google Scholar] [CrossRef]
- Lin, Z.; Wen, F.; Xue, Y. A restorative self-healing algorithm for transmission systems based on complex network theory. IEEE Trans. Smart Grid. 2016, 7, 2154–2162. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, B.-H.; Zhang, Z.; Yin, X.-G.; Wang, B. An electrical betweenness approach for vulnerability assessment of power grids considering the capacity of generators and load. Phys. A 2011, 390, 4692–4701. [Google Scholar] [CrossRef]
- Yang, D.-S.; Sun, Y.-H.; Zhou, B.-W.; Gao, X.-T.; Zhang, H.-G. Critical Nodes Identification of Complex Power Systems Based on Electric Cactus Structure. IEEE Syst. J. 2020, 14, 4477–4488. [Google Scholar] [CrossRef]
- Liu, F.; Xie, G.; Zhao, Z. Importance evaluation of power network nodes based on community division and characteristics of coupled network. Electr. Power Syst. Res. 2022, 209, 108015. [Google Scholar] [CrossRef]
- Nacher, J.C.; Akutsu, T. Analysis of critical and redundant nodes in controlling directed and undirected complex networks using dominating sets. J. Complex Netw. 2014, 2, 394–412. [Google Scholar] [CrossRef]
- Lin, G.; Mo, T. Critical Node Identification of Power Networks Based on TOPSIS and CRITIC Methods. High Volt. Eng. 2018, 44, 3383–3389. [Google Scholar]
- Zhao, M.; Wu, M.; Qiao, L.; An, Q.; Lu, S. Evaluation of Cross-Layer Network Vulnerability of Power Communication Network Based on Multi-Dimensional and Multi-Layer Node Importance Analysis. IEEE Access 2022, 10, 67181–67197. [Google Scholar]
- Geng, J.; Sun, X.; Li, F.; Wu, X. Prediction method of important nodes and transmission lines in power system transactive management. Electr. Power Syst. Res. 2022, 208, 107898. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, J.; Cheng, F.; Qiu, J.; Zhang, X. Multi-Objective Optimization of Critical Node Detection Based on Cascade Model in Complex Networks. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2052–2066. [Google Scholar] [CrossRef]
- Wang, H.; Shan, Z.; Ying, G.; Zhang, B.; Zou, G.; He, B. Evaluation method of node importance for power grid considering inflow and outflow power. J. Mod. Power Syst. Clean Energy 2017, 5, 696–703. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Y.; Li, H. Comprehensive vulnerability analysis of power system nodes considering energy margin and weighting factors. Electr. Power Autom. Equip. 2016, 36, 136–141. [Google Scholar]
- Sun, Y.; Cheng, K.; Xu, Q.; Li, D.; Li, Y. Identification of Weak Link for Active Distribution Network Considering Correlation of Photovoltaic Output. Autom. Electr. Power Syst. 2022, 46, 96–103. [Google Scholar]
- Adebayo, I.G.; Sun, Y. A Comparison of Voltage Stability Indices for Critical Node Identification in a Power System. In Proceedings of the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 21–23 January 2021. [Google Scholar]
- Yusuff, A.A.; Mosetlhe, T.C.; Ayodele, T.R. Power grid critical node identification based on singular value entropy and power grid flow distribution entropy. Electr. Power Syst. Res. 2021, 200, 107464. [Google Scholar] [CrossRef]
- Xu, H.; Li, H.; Zhao, X.; Huang, Z. Assessment on nodal comprehensive vulnerability based on operational state and network structure. Power Syst. Technol. 2014, 38, 731–735. [Google Scholar]
- Liu, M.; Liu, J.; Li, H.; Zhang, H.; Chen, Y.; Luo, Y. Identification of critical nodes of power grid considering voltage level. Electr. Power Autom. Equip. 2019, 39, 51–57. [Google Scholar]
- Yu, Z.; Chang, C.; Wang, W.; Mao, Q. Energy consumption assessment by AIA based time series scatter degree method. In Proceedings of the IEEE 2010 International Conference on Logistics Systems and Intelligent Management, Harbin, China, 9–10 January 2010. [Google Scholar]
- Li, Y.; Zhou, J. Modified entropy method and vague set based multi-objective flood control decision making approach. Water Resour. Power 2010, 28, 3235. [Google Scholar]
- Bompard, E.; Napoli, R.; Xue, F. Analysis of structural vulnerabilities in power transmission grids. Int. J. Crit. Infrastruct. Prot. 2009, 2, 5–12. [Google Scholar] [CrossRef]
- Li, Y.; Ma, W.; Zhang, Z.; Niu, G.; Wu, M.; Weng, Y. Energy Efficiency Evaluation of Multi-Energy Microgrid Based on Entropy-Independence-Gl Method. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference, Nanjing, China, 27–29 May 2022. [Google Scholar]
- Zhou, Y.; Li, X.; Qu, H. Node comprehensive vulnerability assessment of power grid based on anti-entropy-AHP quadratic programming combination weighting method. Electr. Power Autom. Equip. 2019, 39, 133–140. [Google Scholar]
- Ouyang, S.; Shi, Y. A New Improved Entropy Method and Its Application in Power Quality Evaluation. Autom. Electr. Power Syst. 2013, 37, 156–159. [Google Scholar] [CrossRef]
- Tan, Y.; Li, X.; Cai, Y.; Wang, C. Modeling cascading failures in power grid based on dynamic power flow and vulnerable line identification. Proc. CSEE 2015, 35, 615–622. [Google Scholar]
- Liu, B.; Li, Z.; Chen, X.; Huang, Y.; Liu, X. Recognition and Vulnerability Analysis of key Nodes in Power Grid Based on Complex Network Centrality. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 346–350. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, Y.; Wang, Y.; Ding, L.; Huang, T. Vulnerable Line Identification of Cascading Failure in Power Grid Based on New Electrical Betweenness. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 665–669. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).