Research on High-Quality Control Technology for Three-Phase PWM Rectifier
Abstract
:1. Introduction
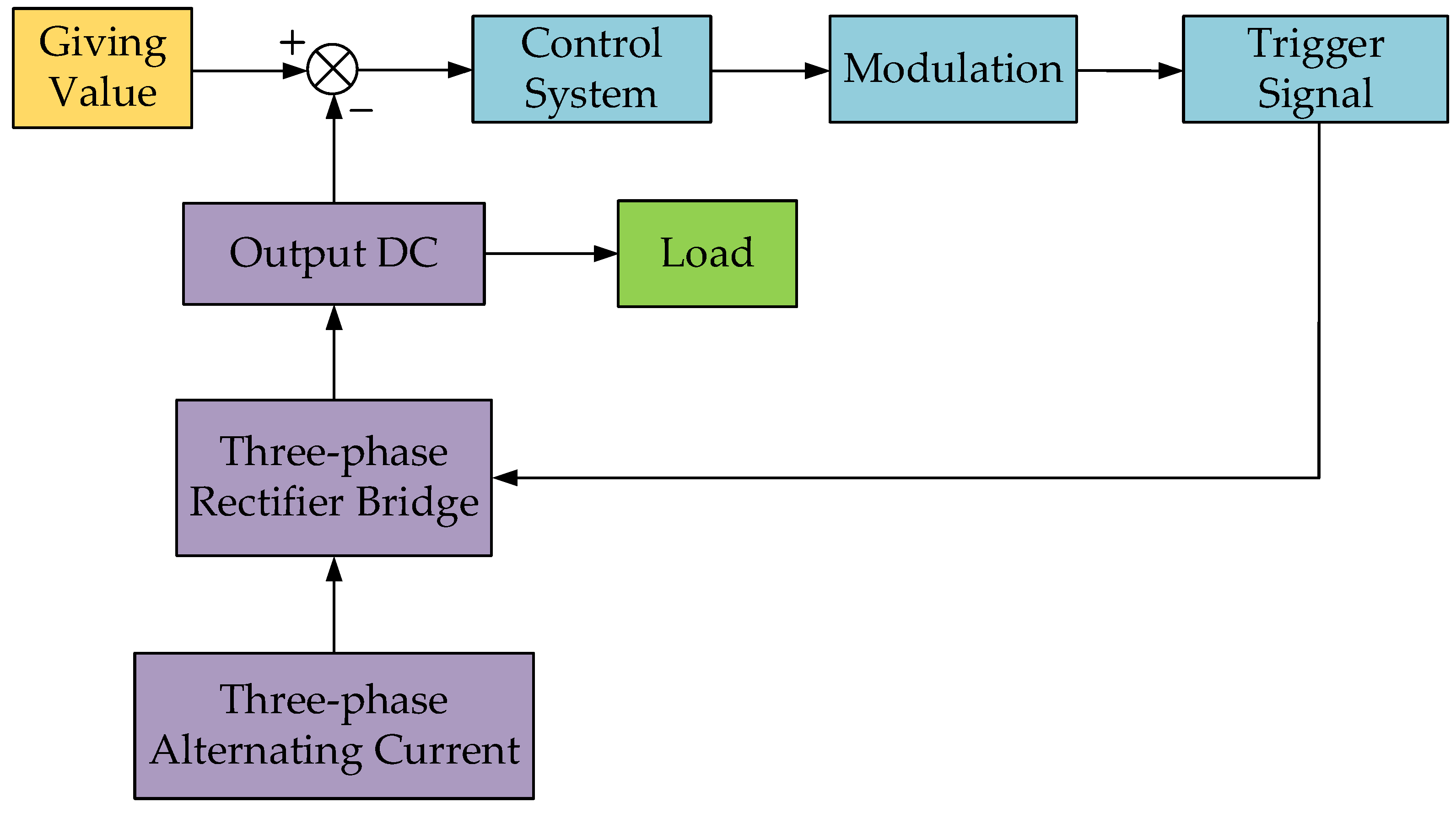
2. Mathematical Modeling of Three-Phase VSR
2.1. Coordinate Transformation and Establishment of the dq Model
2.1.1. Three-Phase Stationary Coordinate System to Two-Phase Stationary Coordinate System
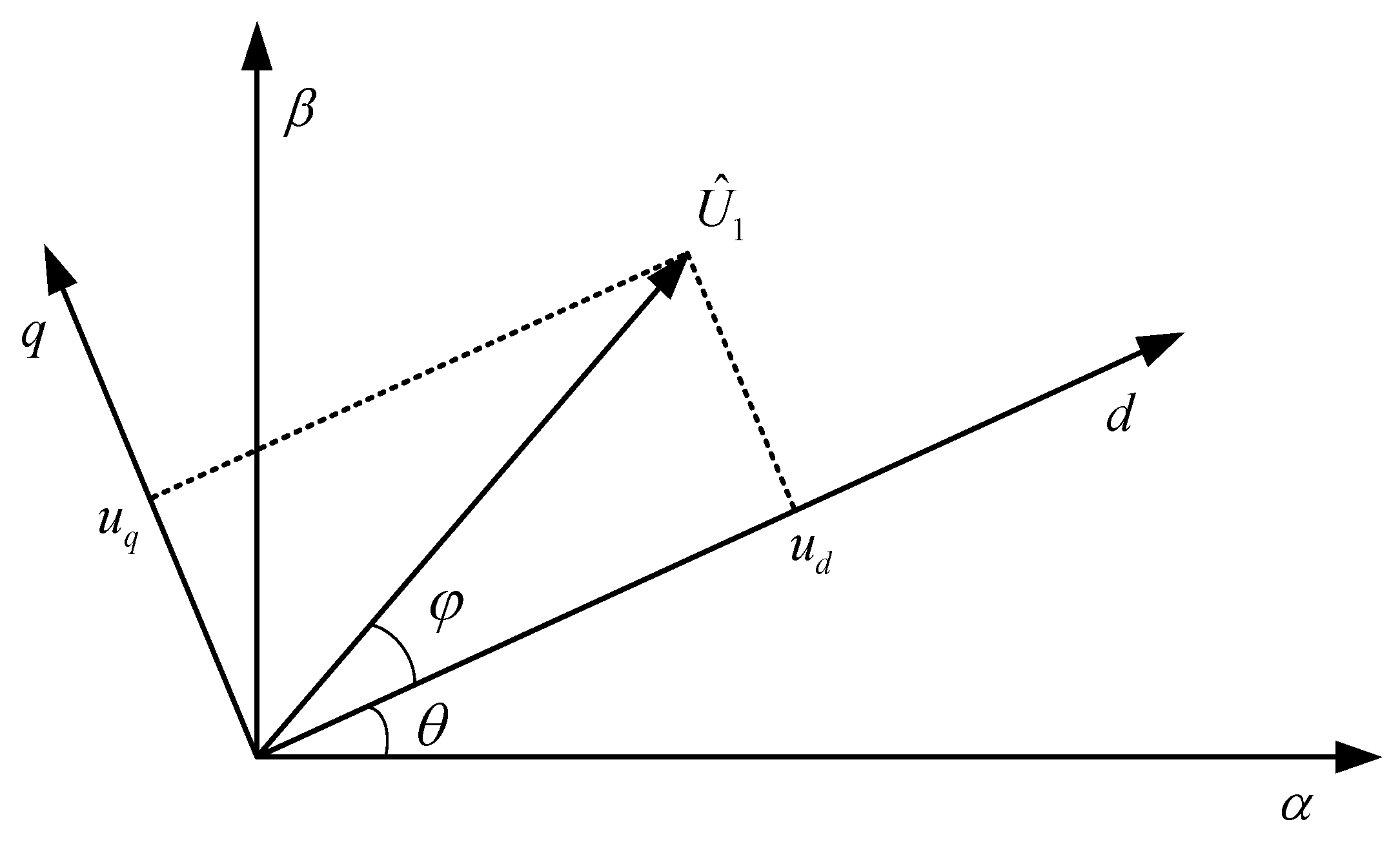
2.1.2. Two-Phase Stationary Coordinate System to Two-Phase Rotation Coordinate System
2.1.3. Three-Phase Stationary Coordinate System to Two-Phase Rotation Coordinate System
2.1.4. dq Model of Three-Phase VSR
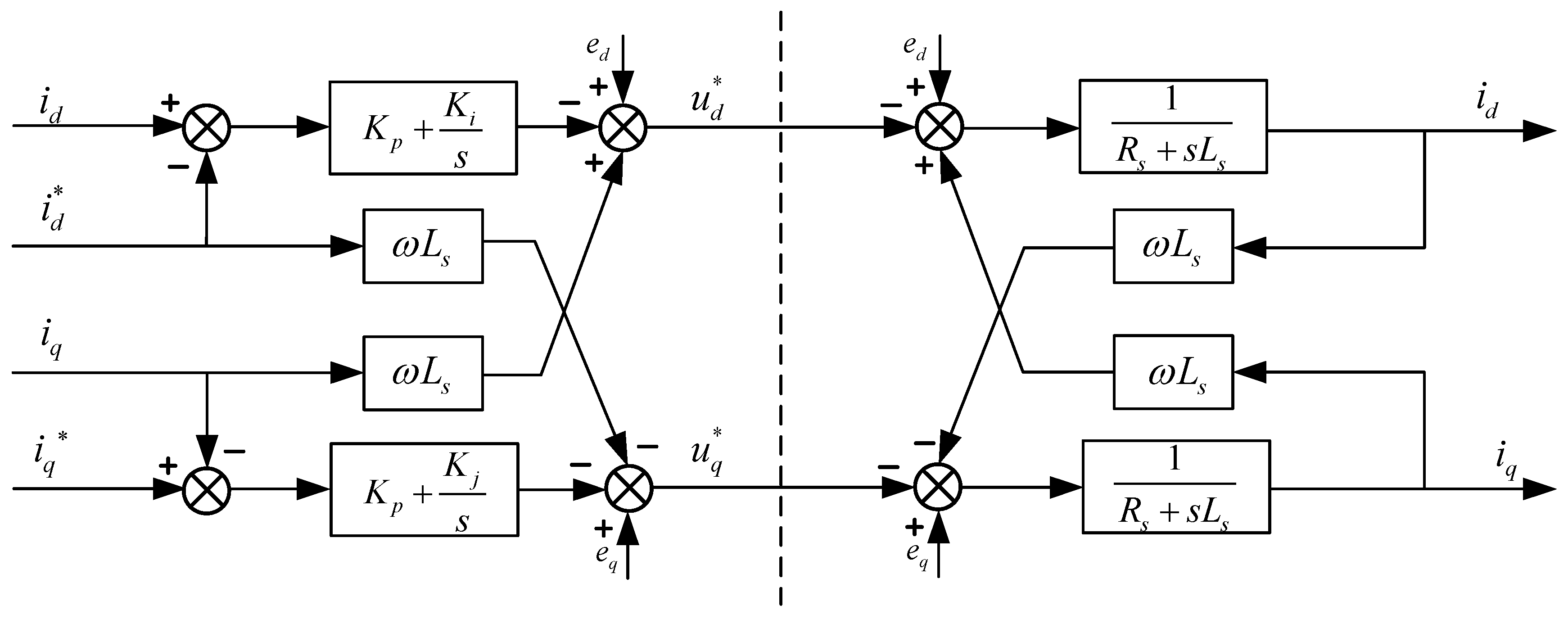
2.2. Controller Design
3. Simulation Analysis
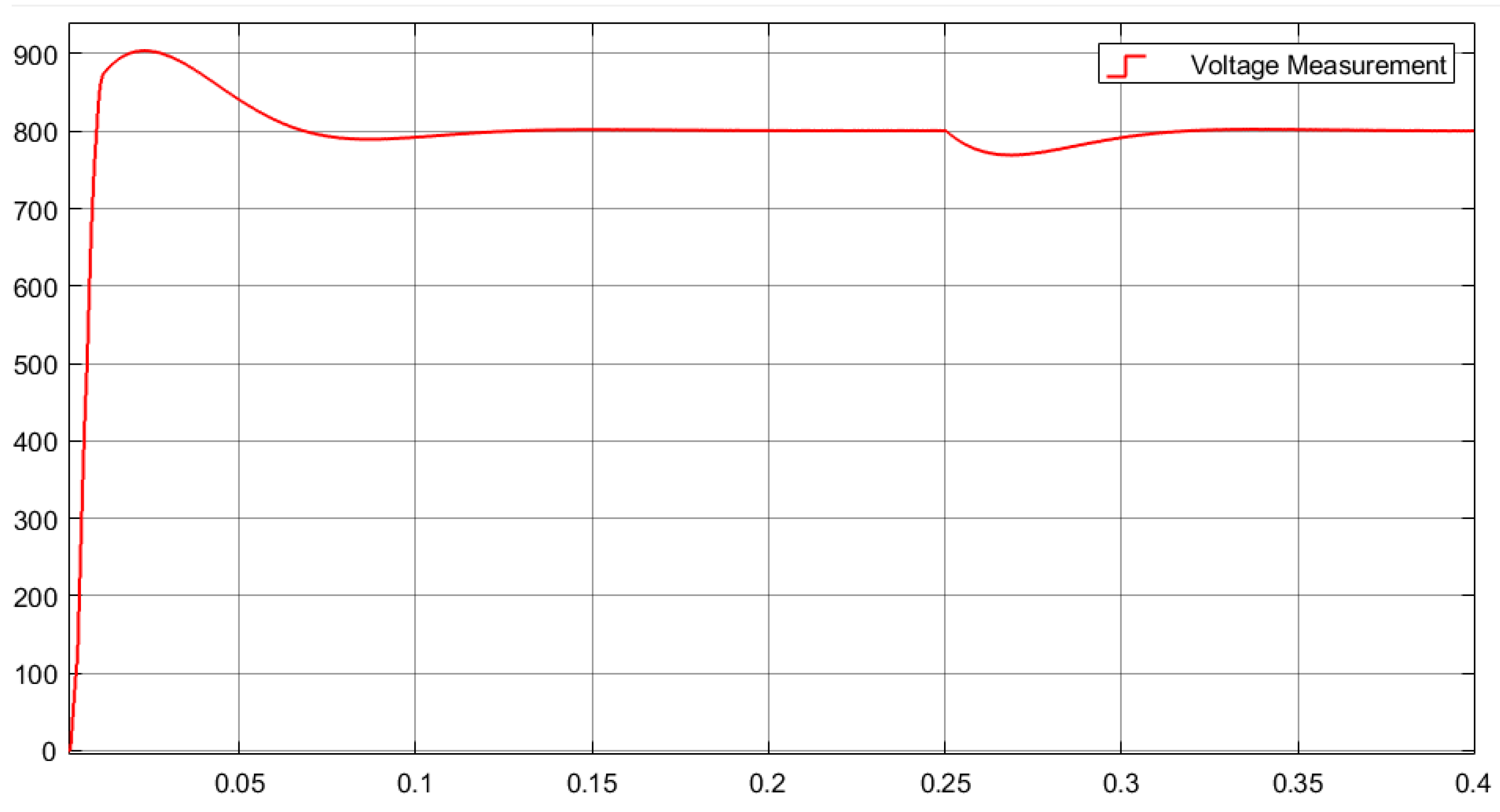
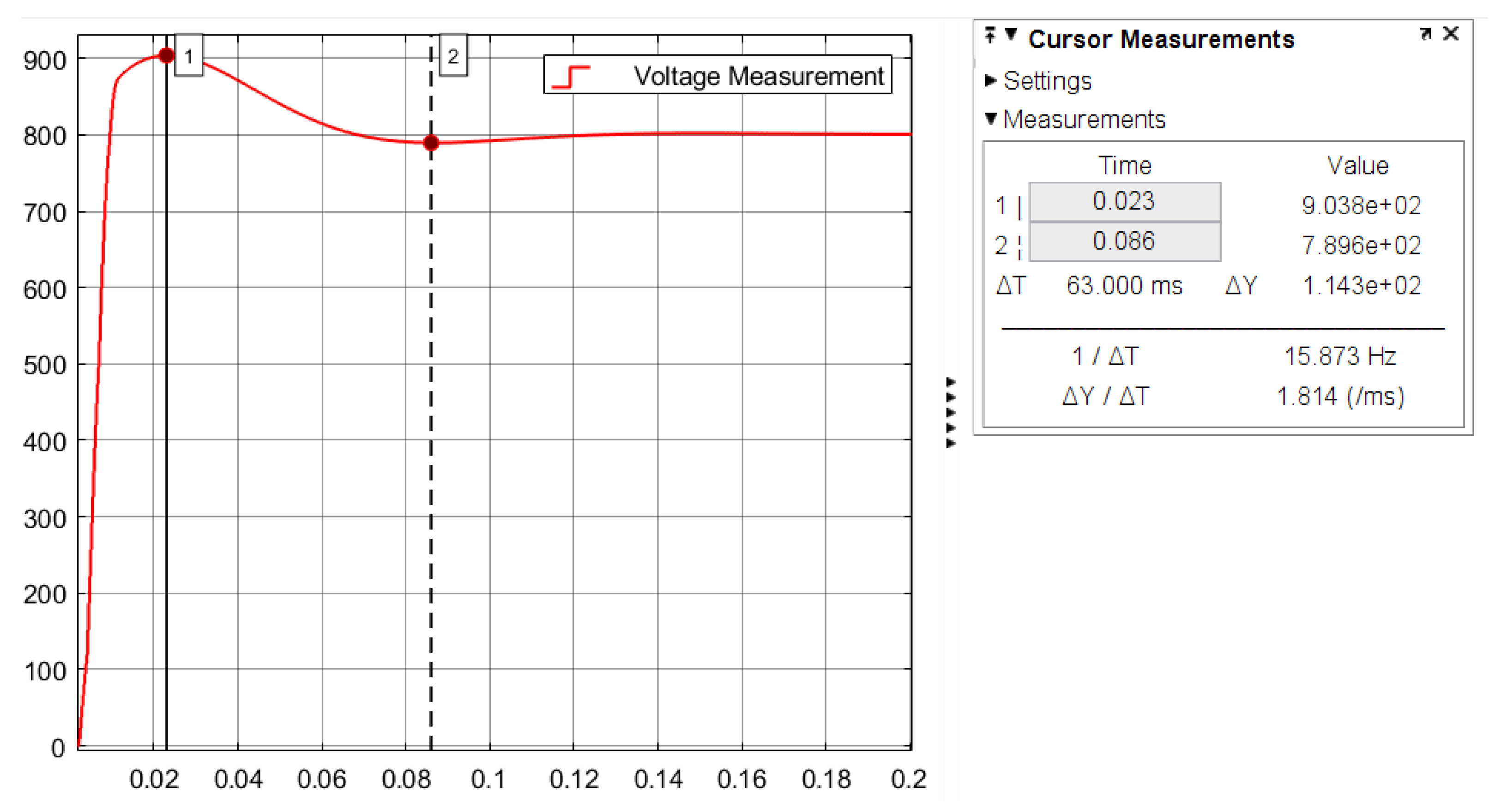
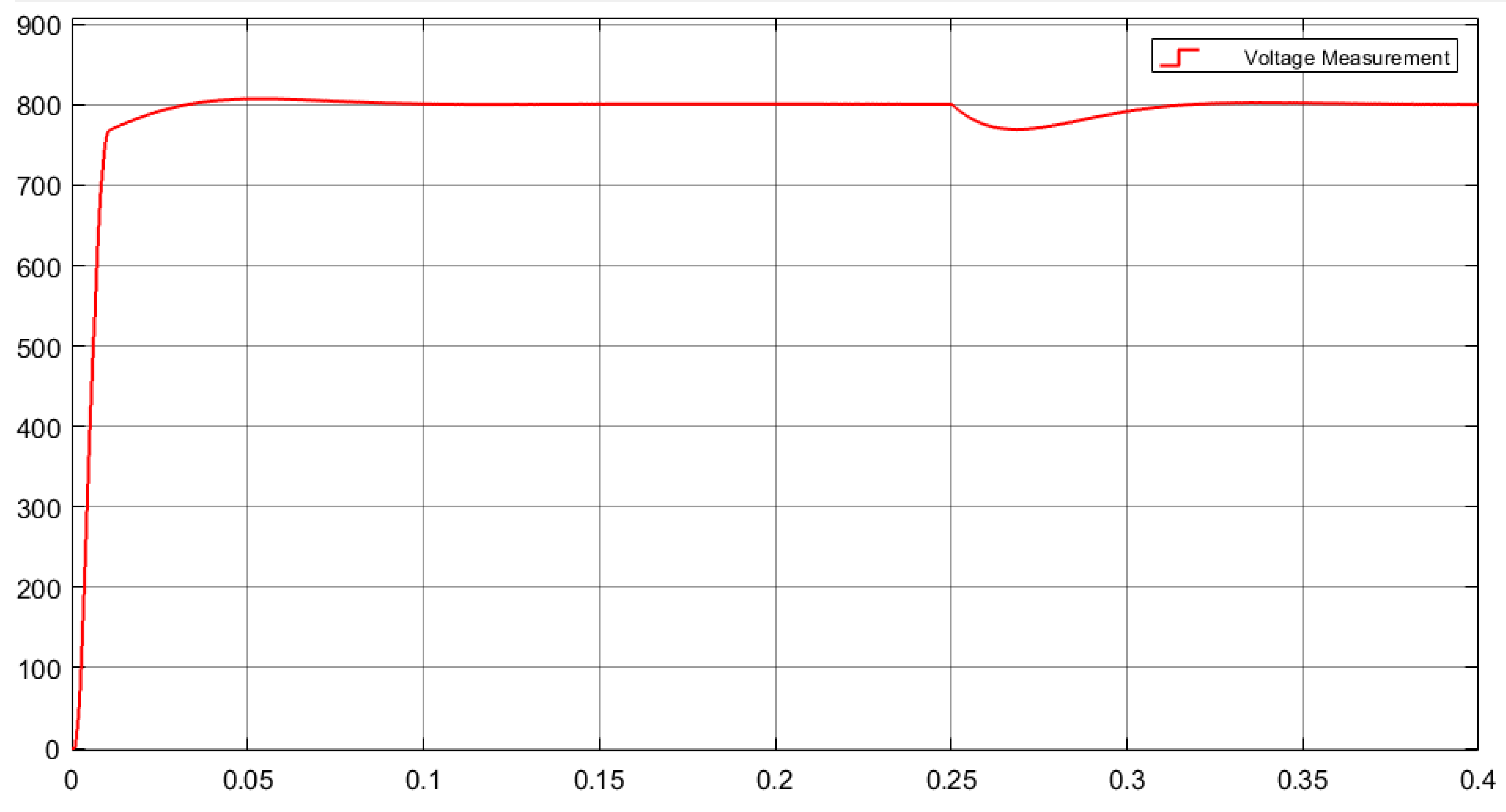
3.1. DC-Side Voltage Waveform
3.2. Analysis of Voltage and Current Waveform on the Grid-Side
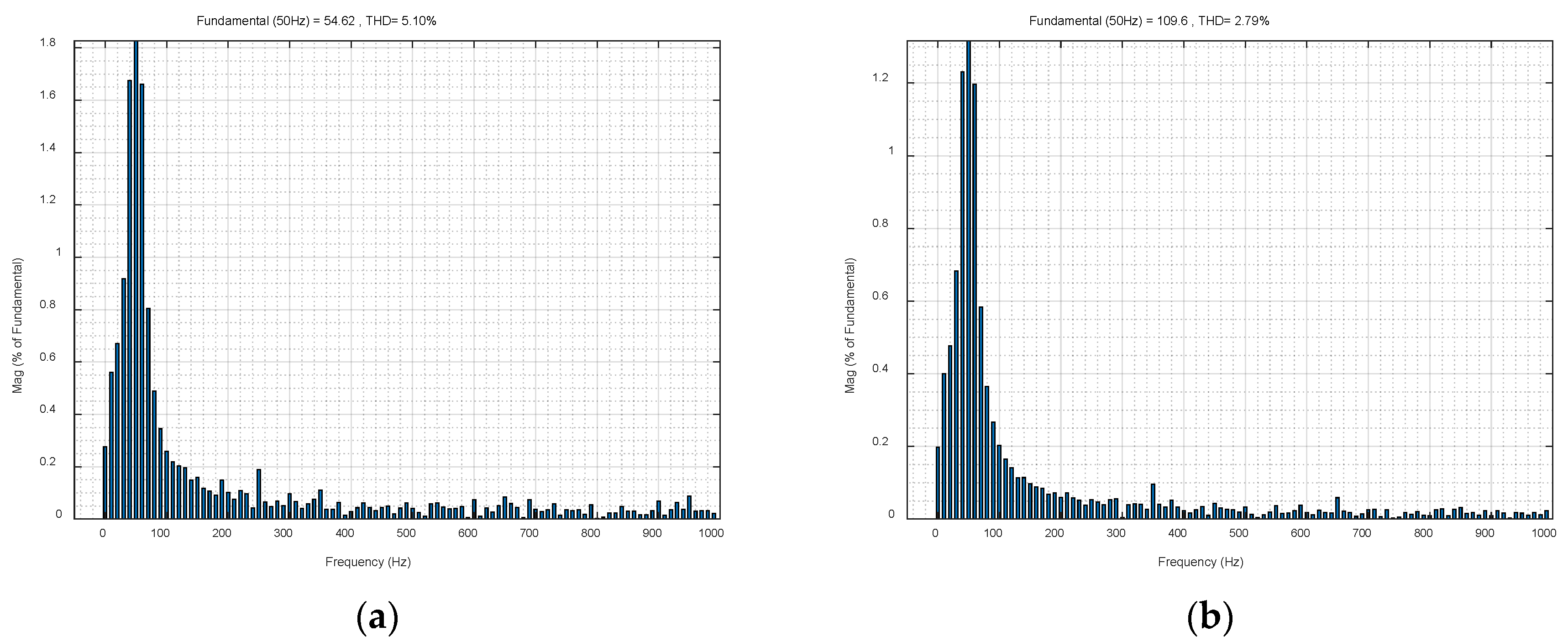
3.3. Analysis of Harmonic Content of Grid-Side Current
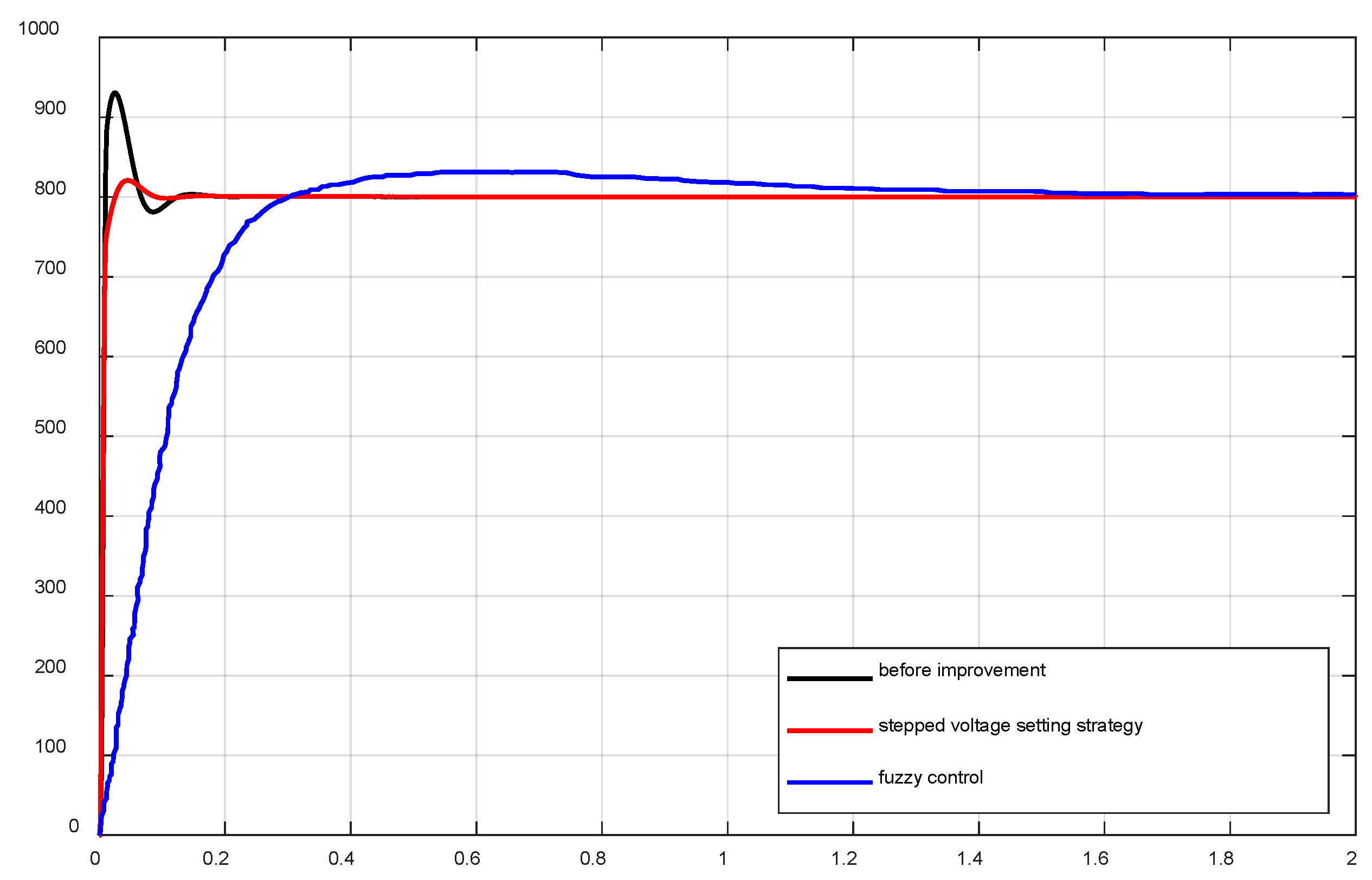
3.4. Control-Strategy Improvement
4. Conclusions
- (1)
- The control strategy has a short start-up time and good dynamic performance, and it can automatically and quickly track back to a given value when the load changes;
- (2)
- The control strategy can sinusoidize the network-side current, reduce the harmonic pollution on the network side, and operate in the state of unit-power factor;
- (3)
- The DC-side output-voltage overshoot was large at startup, and the simulation result was 12.88%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PWM | pulse width modulation |
| THD | total harmonic distortion |
| AC | alternating current |
| DC | direct current |
| VSR | voltage source rectifier |
| KVL | Kirchhoff’s voltage law |
| KCL | Kirchhoff’s current law |
| IGBT | insulated gate bipolar transistor |
| PID | proportional-integral-derivative |
| PI | proportional-integral |
| FFT | fast Fourier transform |
| PV | photovoltaic |
Appendix A
References
- Zhang, H.; Jin, R.; Zhao, Y.; Jiang, J.; Wang, A. Simulink Simulation Analysis of Single-phase Half Wave Controlled Rectifier under Different Load Conditions. Res. Explor. Lab. 2022, 41, 105–109. [Google Scholar]
- Cao, Y.; Shi, J.; Shi, X.; Liu, Y.; Liu, M. Exploration in One-Way Full-Wave Rectification Experiment Teaching Based on Analog Simulation. Mod. Inf. Technol. 2022, 6, 192–195. [Google Scholar]
- Wang, S.; Zhou, Y. Analysis on Active Power of a Three-phase Half-wave Controlled Rectifier with Resistor-Inductor Load in Intermittent State. Power Equip. 2017, 31, 240–244+249. [Google Scholar]
- Zhao, R.; He, Y.; Liu, Q. Research on Improvement of Anti-Disturbance Performance for Three-Phase PWM Rectifiers. Trans. China Electrotech. Soc. 2004, 19, 67–72. [Google Scholar]
- Zhang, L.; Zhao, J.; Shao, T.; Ma, R. Implement Waveform and Phase Control of Grid Side Current Based on PWM Rectifier. Available online: http://design.eccn.com/design_2022052709091520.htm2022/2023 (accessed on 27 May 2022).
- Abdollahi, R.; Gharehpetian, G.B.; Mohammadi, F.; Prakash, P.S. Multi-Pulse Rectifier Based on an Optimal Pulse Doubling Technique. Energies 2022, 15, 5567. [Google Scholar] [CrossRef]
- Corti, F.; Hassan Shehata, A.; Laudani, A.; Cardelli, E. Design and Comparison of the Performance of 12-Pulse Rectifiers for Aerospace Applications. Energies 2021, 14, 6312. [Google Scholar] [CrossRef]
- Li, T.; Gan, Y. Hybrid Modulated DCDC Boost Converter for Wearable Devices. Electronics 2022, 11, 3418. [Google Scholar] [CrossRef]
- Almutairi, A.; Sayed, K.; Albagami, N.; Abo-Khalil, A.G.; Saleeb, H. Multi-Port PWM DC-DC Power Converter for Renewable Energy Applications. Energies 2021, 14, 3490. [Google Scholar] [CrossRef]
- Fatma, M.; Hamid, M. PWM speed control of dc permanent magnet motor using a PIC18F4550 microcontroller. IOP Conf. Ser. Mater. Sci. Eng. 2019, 602, 012017. [Google Scholar] [CrossRef]
- Li, Y. Design of PWM Speed Regulation System for DC Motor Based on ARM. Eng. Test 2022, 62, 108–110. [Google Scholar]
- Koc, B.; Kist, S.; Hamada, A. Wireless Piezoelectric Motor Drive. Actuators 2023, 12, 136. [Google Scholar] [CrossRef]
- Surakasi, B.; Satish, R.; Pydi, B.; Kotb, H.; Shouran, M.; Abdul Samad, B. A NovelMethodology to Enhance the Smooth Running of the PM BLDC Motor Drive Using PWM-PWM Logic and Advance Angle Method. Machines 2023, 11, 41. [Google Scholar] [CrossRef]
- Venkatesan, M.; Rajamanickam, N.; Vishnuram, P.; Bajaj, M.; Blazek, V.; Prokop, L.; Misak, S. A Review of Compensation Topologies and Control Techniques of Bidirectional Wireless Power Transfer Systems for Electric Vehicle Applications. Energies 2022, 15, 7816. [Google Scholar] [CrossRef]
- Huang, R. The Research of the Application of the AC Charging System of Electric Vehicles in the New Energy Vehicle Technology Major. Auto Time 2023, 2, 113–115. [Google Scholar]
- Samavat, T.; Nazari, M.; Ghalehnoie, M.; Nasab, M.A.; Zand, M.; Sanjeevikumar, P.; Khan, B. A Comparative Analysis of the Mamdani and Sugeno Fuzzy Inference Systems for MPPT of an Islanded PV System. Int. J. Energy 2023, 2023, 7676113. [Google Scholar] [CrossRef]
- Ikeda, F.; Okamoto, M.; Hamasaki, K.; Yamada, H.; Tanaka, T. Constant DC-Capacitor Voltage-Control-Based Reactive Power Control Method of Bidirectional Battery Charger for EVs in Commercial Single-Phase Three-Wire Low-Voltage Feeders: Special Issue Paper. IEEJ J. Ind. Appl. 2021, 10, 761–769. [Google Scholar] [CrossRef]
- Rastgoo, S.; Mahdavi, Z.; Azimi Nasab, M.; Zand, M.; Padmanaban, S. Using an Intelligent Control Method for Electric Vehicle Charging in Microgrids. World Electr. Veh. J. 2022, 13, 222. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, X. PWM Rectifier and Its Control; China Machine Press: Beijing, China, 2003; pp. 3–5, 51–65. [Google Scholar]
- Pathak, P.K.; Yadav, A.K.; Tyagi, P. Design of Three Phase Grid Tied Solar Photovoltaic System Based on Three Phase VSI. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, F.J.; Sun, D.Y.; Duan, J.D. Diagnosis of single-phase open-line fault in three-phase PWM rectifier with LCL filter. IET Gener. Transm. Distrib. 2016, 10, 1410–1421. [Google Scholar] [CrossRef]
- Jiang, W.; Li, W.; She, Y. Control Strategy for PWM Rectifier Based on Feedback of the Energy Stored in Capacitor and Load Power Feed-Forward. Trans. China Electrotech. Soc. 2015, 30, 151–158. [Google Scholar]
- Cai, S.; Cao, H.; Liang, D.; Niu, R.; Jia, L.; Waseem, A. A three-phase voltage source PWM rectifier with strong DC Immunity based on model predictive control. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 7871–7876. [Google Scholar]
- Zhong, C.; Du, H.; Yang, M. Analysis of Starting Inrush Current of Three-phase Unity Power Factor VSR and Its Suppression. Power Electron. 2013, 47, 32–34. [Google Scholar]
- Zhang, X. Research on PWM Rectifier and Its Control Strategy. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2003. [Google Scholar]
- Lang, Y.; Xu, D.; Hadianamrei, S.; Ma, S. Improved feedforward control of three-phase voltage source PWM rectifier. Electr. Mach. Control. 2006, 10, 160–170. [Google Scholar]
- Huang, Q.; Tang, J.; Lin, L.; Liu, X.; Zhang, Y. Research on a kind of inner and outer loop decoupling control for three-phase voltage-source PWM rectifier. J. Shaoyang Univ. (Nat. Sci. Ed.) 2020, 17, 40–47. [Google Scholar]
- Li, D.; Shi, X. Simulation of Three·phase Voltage Source PWM Rectifier and Its Control Strategy. Control Inf. Technol. 2010, 3, 19–23. [Google Scholar]
- Zhou, Q.; Liang, H. The Design and Analysis of PI Regulator of Three-phase Voltage Source Rectifier. Power Electron. 2011, 45, 50–52. [Google Scholar]
- Zhu, Y.; Wang, Z.; Wang, C.; Zhu, Y.; Cao, X. A Novel Improved Coordinate Rotated Algorithm for PWM Rectifier THD Reduction. Electronics 2022, 11, 1435. [Google Scholar] [CrossRef]
- Yao, X.; Wang, X.; Feng, Z. Research on of Improvement of the Dynamic Ability for PWM Rectifier. Trans. China Electrotech. Soc. 2016, 31, 169–175. [Google Scholar]
- Jiang, L. Application of Fuzzy Control in Three-phase PWM Rectifier. J. Lanzhou Univ. Arts Sci. (Nat. Sci.) 2022, 36, 29–33. [Google Scholar]
- Yao, Q.; Zeng, G.; Huang, B.; Liu, J.; Wei, Y. Control strategy design of three-phase PWM rectifier based on variable universe fuzzy PI. Manuf. Autom. 2022, 44, 73–76. [Google Scholar]
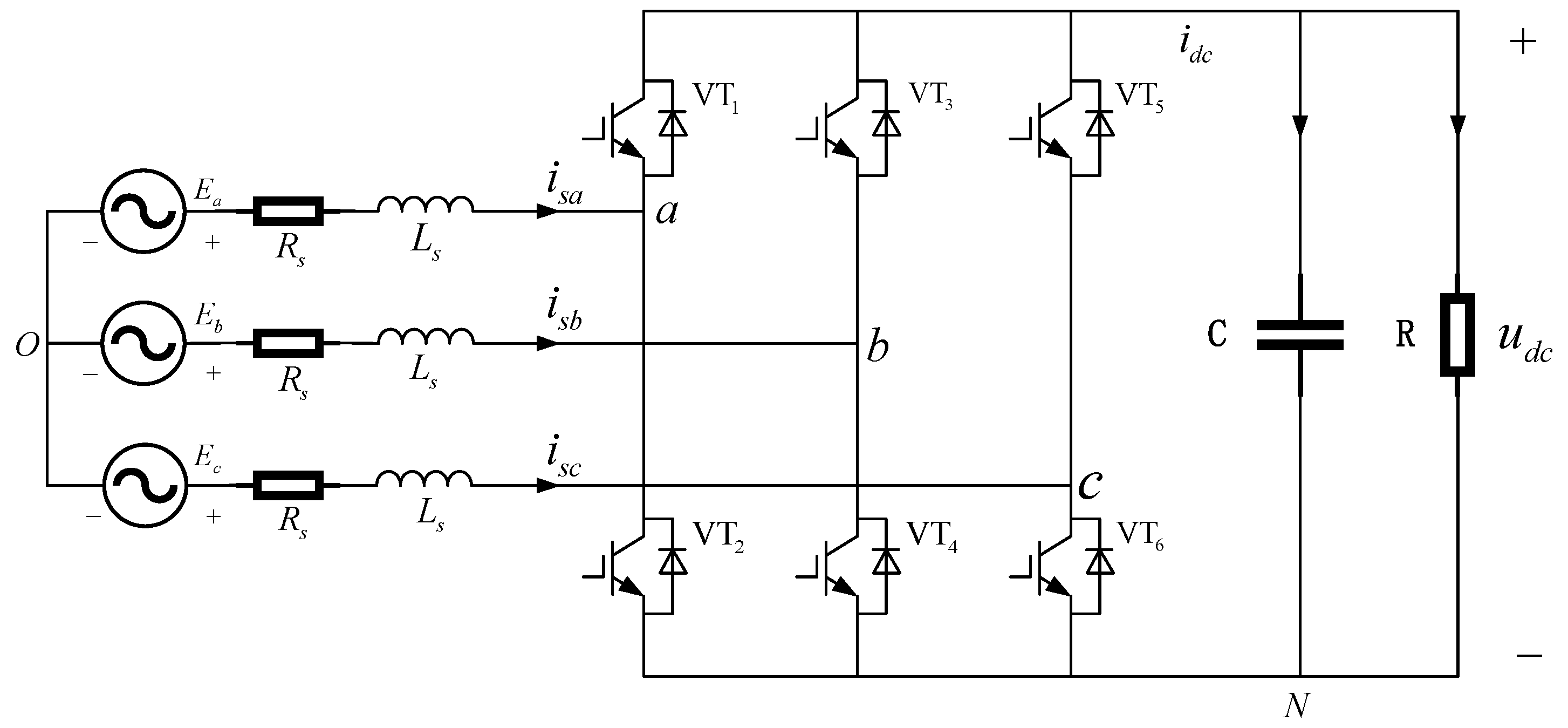





| Serial Number | Circuit Parameter | Value | Serial Number | Circuit Parameter | Value |
|---|---|---|---|---|---|
| 1 | Effective voltage value | 380 V | 6 | Voltage outer loop | 0.85 |
| 2 | Voltage frequency | 50 Hz | 7 | Voltage outer loop | 50 |
| 3 | 40 | 8 | Current inner loop | 10 | |
| 4 | 1 mH | 9 | Current inner loop | 25 | |
| 5 | DC-side capacitance | 6800 uF | 10 | Run time | 0.4 s |
| Serial Number | THD | Serial Number | THD | ||
|---|---|---|---|---|---|
| 1 | 10 | 1.86% | 5 | 30 | 5.10% |
| 2 | 15 | 2.79% | 6 | 35 | 5.66% |
| 3 | 20 | 3.58% | 7 | 40 | 6.48% |
| 4 | 25 | 4.02% | 8 | 50 | 8.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Song, J.; Yu, Y.; Xu, Q.; Zhou, X. Research on High-Quality Control Technology for Three-Phase PWM Rectifier. Electronics 2023, 12, 2417. https://doi.org/10.3390/electronics12112417
Zhou Z, Song J, Yu Y, Xu Q, Zhou X. Research on High-Quality Control Technology for Three-Phase PWM Rectifier. Electronics. 2023; 12(11):2417. https://doi.org/10.3390/electronics12112417
Chicago/Turabian StyleZhou, Zhiquan, Jiyu Song, Yanjun Yu, Qingrui Xu, and Xinhang Zhou. 2023. "Research on High-Quality Control Technology for Three-Phase PWM Rectifier" Electronics 12, no. 11: 2417. https://doi.org/10.3390/electronics12112417
APA StyleZhou, Z., Song, J., Yu, Y., Xu, Q., & Zhou, X. (2023). Research on High-Quality Control Technology for Three-Phase PWM Rectifier. Electronics, 12(11), 2417. https://doi.org/10.3390/electronics12112417






