Abstract
In this study, we propose three k-nearest neighbor (k-NN) optimization techniques for a distributed, in-memory-based, high-dimensional indexing method to speed up content-based image retrieval. The proposed techniques perform distributed, in-memory, high-dimensional indexing-based k-NN query optimization: a density-based optimization technique that performs k-NN optimization using data distribution; a cost-based optimization technique using query processing cost statistics; and a learning-based optimization technique using a deep learning model, based on query logs. The proposed techniques were implemented on Spark, which supports a master/slave model for large-scale distributed processing. We showed the superiority and validity of the proposed techniques through various performance evaluations, based on high-dimensional data.
1. Introduction
With the recent development of real-time image processing, technologies for object recognition and object retrieval in images extracted from real-time operating devices, such as closed-circuit television (CCTV), are being actively implemented [1,2,3,4,5,6,7]. These technologies can be used in various fields, such as crime prevention, monitoring systems, and analyzing traffic information.
Content-based image retrieval (CBIR) involves the retrieving of images by using features extracted from objects in video images. CBIR involves vectorizing the features extracted from images and determining the similarities between the vectors to retrieve similar images. In sum, CBIR is a way of retrieving images from a database. In CBIR, a user specifies a query image and obtains images from the database that are similar to the query. To find the most similar images, CBIR compares the content of the query image with the database images. Owing to the development of new technologies, such as artificial intelligence and machine learning, researchers have conducted studies into extracting various features from images [8,9,10,11]. Data becomes increasingly high-dimensional as the features provided by images become more varied. Therefore, similarity retrieval techniques that use high-dimensional data are needed to retrieve and compare similar images or objects. Additionally, the indexing structure for high-dimensional data similarity retrieval must be appropriately constructed, in accordance with the characteristics of high-dimensional data.
Nearest neighbor search (NNS) deals with the problem of finding the closest or most similar item to a given point. Closeness is typically expressed in terms of a dissimilarity function, such as Euclidean distance, Manhattan distance, and other distance metrics. Formally, the nearest-neighbor (NN) search problem is defined as follows: given a set S of points in a space M and a query point q ∈ M, find the closest point in S to q. k-NN search is a generalized NN problem. k-NN needs to find the k closest points.
Generally, in the distributed processing environment, a distributed k-NN query is processed as follows. First, each distributed node indexes data points. Depending on the indexing scheme, the k- NN query processing methodology is different. In general, when a k-NN query is inputted, all of the nodes are requested to process the k-NN query. Each node generates k closest data points and k data points generated in n nodes are merged. Finally, the result includes the k closest points to the query from the merged result.
Various studies have been conducted recently to address these problems [12,13,14,15,16,17]. A distributed, in-memory-based, high-dimensional indexing technique was proposed to efficiently perform image retrieval using high-dimensional feature data [12]. The authors of [12] utilized big data analysis platforms, such as Spark, to implement distributed, in-memory-based, high-dimensional indexing. In addition, the authors of [13] proposed an M-tree [13] indexing algorithm on Spark. Since all distributed servers participate in query processing [12], the load on all the servers can increase when there are many retrieval requests from users. In another study, a master/slave model for distributed index query processing was used to perform efficient image retrieval in airport video monitoring systems [14]. The researchers proposed a distributed MVP (multi-vantage-point) tree, which was based on the MVP tree. However, it had an inherent flaw: it was difficult to load large-scale, high-dimensional data into its memory. Moreover, backtracking operations frequently occurred when performing k-NN query processing in the tree. Backtracking is a commonly used algorithm for searching. When processing k-NN queries in a tree structure, it explores a specific node and returns to the parent node if there are no results. It generates query results by repeating this process. In another study, a distributed k-d tree [16] was proposed to enhance the performance of k-NN processing [15]. However, depending on the amount of distributed data, the height of the k-d tree could increase, which would increase the search time [15]. Using a k-d tree also results in frequent backtracking operations when performing k-NN processing [14].
Contrary to conventional hash functions [17], LSH (locality-sensitive hashing) aims to maximize hash collisions when indexing high-dimensional data. It stores similar data in the same bucket to improve the efficiency of the search and indexing. Using random vectors, LSH transforms high-dimensional data into low-dimensional bucket indexes. Following a query request, the system searches for the bucket that contains the query result using the query location, measures the actual distance between the data within the bucket, and performs k-NN query processing. However, in LSH, the k-NN results may include false positives, depending on the index creation parameters. More buckets can be searched to ensure accurate results; however, this increases the search cost because it requires distance comparisons among all the data in the adjacent buckets. Because k-NN query processing involves finding the closest k items, distance-based indexing is efficient as it can pre-calculate the distance values to the items and index them. In this paper, we used iDistance, which is a distance-based indexing method for efficient k-NN query processing.
The authors of [18] used a deep learning technique based on a combination of CNNs to classify images, and used RNNs to analyze natural language queries. They also used CNNs to take advantage of the deep learning technology in image content classification. The RNN model helps users to make search queries more efficiently. The authors of [19] identified occupied and vacant parking lots using a hybrid deep learning model. The model proposed in that study combined the superior features of CNNs and LSTM deep learning methods. The authors of [20] proposed a CBIR system that was based on multi deep neural networks, which combined convolutional neural networks (CNNs) and k-NN methodologies. The feature extraction of the user-supplied image was performed based on the CNNs, and the image similarity was calculated based on the k-NN methodologies in order to return a list of images. The authors of [21] compared the image retrieval of various machine learning models, such as SVMs (support vector machines), k-NNs, and CNNs.
In this paper, we propose k-NN optimization techniques that use a distributed, in-memory, index retrieval system structure, which can effectively retrieve large-scale, high-dimensional data. The proposed techniques were implemented on Spark to process large-scale data and to perform distributed index construction, using our research team’s previous study [17]. Spark is a multi-language engine for executing data engineering, data science, and machine learning on single-node machines or clusters. It utilizes in-memory caching and optimized query execution for fast analytic queries against data of any size. In our previous study, the k-NN query was converted into a simple range query owing to the index’s characteristics; therefore, k-NN query processing optimization was required. In this study, we proposed three techniques for k-NN query optimization: optimization, using the density of the feature data; cost-based optimization, which statistically stores and processes query processing costs; and DNN-based optimization, using machine learning. The validity and superiority of the proposed indexing and optimization techniques were verified using performance evaluations for each optimization technique. This study makes the following contributions to the field:
- A distributed indexing scheme for high-dimensional data: This study proposes a distributed, high-dimensional indexing scheme. The proposed scheme is a Spark-based, distributed indexing scheme for processing large, high-dimensional data efficiently.
- A distributed query allocation method: In order to perform efficient distributed processing, an efficient query allocation method is required. In this paper, we propose a distributed query allocation method based on query information.
- Three k-NN query optimization techniques: In this paper, we propose three optimization techniques for efficient k-NN query processing, based on a high-dimensional distributed index. We present three optimization techniques based on density, query processing costs, and deep learning using index information. We verified the validity of the proposed optimization techniques through performance evaluations.
The remainder of this paper is structured as follows. Section 2 explains the existing high-dimensional indexing methods and describes their problems. Section 3 describes the k-NN optimization techniques in the proposed distributed, high-dimensional indexing methods. Section 4 demonstrates the superiority of the proposed techniques through performance evaluations and compares the existing techniques with those proposed in this study. Finally, Section 5 reports on the conclusions of the study and future research directions.
2. Related Work
To efficiently perform CBIR, researchers have studied high-dimensional indexing techniques for retrieval, using the high-dimensional feature vectors of objects within images [12,13,14,15,16,22,23,24,25,26].
A method to address the challenges in quickly and efficiently indexing large-scale multimedia data was proposed in [12]. The proposed technique used Spark to build a distributed M-tree, enabling fast and cost-effective multimedia database retrieval. However, each node (or executor) in Spark did not have a specified indexing area and performed partitioning and indexing using the data partitioning policy. Consequently, the nodes were not filtered, because all of them must be visited when processing a k-NN query; therefore, when many queries occur, the load on all of the nodes increases, because they have to be visited when processing the queries. As a result, when the search is concentrated on a single node, the overall query processing time can be delayed until the result for that node is returned.
A new indexing method to address the scalability issue of k-d trees for k-NN query processing was proposed in [16]. The researchers constructed a distributed k-d tree to index multi-dimensional data, which is often used in this manner [16]. The distributed k-d tree consists of a global k-d tree and local k-d trees, which can serve as both masters and as slaves at each terminal node of the global k-d tree. The global k-d tree is used to divide the entire data area for processing, and local k-d trees are constructed for each partitioned area to build the index. The master/slave indexing structure is built and processed to perform distributed processing. Because the distributed k-d tree divides the area, it is easy to identify nodes that do not participate in query processing. Therefore, in [1], a filtering feature was added, which enabled more efficient query processing. However, a disadvantage of the k-d tree are the frequent backtracking operations. Moreover, because the distributed k-d tree is rebuilt as a set of local k-d trees, in addition to the global k-d tree, the query processing time increases as the tree height increases, depending on the data distribution.
A distributed MVP tree, distributed-MVP (D-MVP), was implemented to perform high-dimensional indexing for image retrieval in an airport video monitoring system [14]. The MVP tree is an improved version of the VP tree. To improve the effectiveness of later tree searches, the MVP tree divides the data using multiple partition points and stores them in each node. It also stores the distance to the partition points. The D-MVP tree uses a master/slave model for query processing, wherein the master node divides the area. The master monitors the overall system load and maintains balance. To avoid overloading a slave node, when input data are concentrated on it, the master node increases the height of the tree—a method called “hot spot load balancing”—to dynamically add partition areas. However, the M-tree family constantly calculates distances at higher nodes to find terminal nodes that can conduct query processing, which increases the load on the master node and delays the processing time in real-time query processing environments.
iDistance indexing [22] is a distance-based indexing technique that represents high-dimensional data as one-dimensional distances and indexes the data in a B+-tree [22,23]. The distance is calculated between the reference point and the corresponding data when they are displayed in the distance space. Key-values are generated in order of proximity to the reference point, and these key-values are indexed in the B+-tree. Because indexing is performed using only distance, the exact location of the object cannot be determined, and there is a possibility of generating the same key-value. Since iDistance adds a constant to the distance, there is almost no probability that one data point will be included in two reference points. However, if the distance exceeds the constant, an incorrect key-value may be generated. Therefore, an appropriate constant must be assigned. K-NN queries are converted to range queries for processing in iDistance because the index is the distance to the reference point. It is not possible to precisely locate all the data. The distance value between the query and reference points is calculated in order to compute the actual key-value to be inserted into the B+ tree, and only the data within the search range in which the k-NN query is converted is searched to generate the k-NN result. The search range converted to iDistance is initially set to 1% of the total index area, which may lead to frequent search range expansions. Therefore, an optimization technique is needed to convert these k-NN queries into range queries.
The authors of [24] proposed an optimization technique based on product quantization. They applied the optimization technique in different similarity search scenarios, such as brute-force, approximate, and compressed-domain. They also presented a near-optimal algorithmic layout for exact and approximate k-nearest neighbor searches on GPU.
The authors of [25] proposed a distributed image retrieval framework, based on location-sensitive hash (LSH) on Spark. A distributed, K-means-based bag of visual words (BoVW) algorithm and an LSH algorithm were proposed to build LSH index vectors on Spark in parallel. It performs a K-means-based BoVW distributed algorithm by extracting SIFT feature data point sets. However, it takes more than 95% of the time for the whole process of constructing the index, and the effect of clustering is very uncertain.
The authors of [26] proposed a fast CBIR system using Spark (CBIR-S), which targets large-scale images. It uses a memory-centric distributed storage system called Tachyon to enhance the write operation. It can speed up by using a parallel k-NN search method, which is based on the MapReduce model on Spark. In addition, it can exploit the cache method of the Spark framework.
A distributed, in-memory, high-dimensional indexing technique—which our research team previously proposed—was presented in [17]. It aims at efficient CBIR in large-scale, high-dimensional data, using a high-dimensional indexing technique with a master/slave structure. Additionally, Spark was used to build an index for high-dimensional vector data. A hybrid distributed high-dimensional index was implemented to address the issue of k-d trees and iDistance. Combining the advantages of both indexes, the overall structure consists of a master/slave structure, in which the master is responsible for data distribution and for selecting slaves for query processing, which reduces the system load. The slave nodes process the query and conduct the data indexing.
The k-NN algorithm has a wide range of uses because it finds k neighbors for a given value of k. However, it has a drawback: the processing cost increases proportionally to the amount of data or the number of dimensions. Several studies have been conducted to improve the throughput of k-NN [26,27,28].
The “jump method” was proposed to increase the speed of k-NN query processing [28]. To achieve this, the k-means algorithm is applied to the data, and clusters are generated using the formula proposed in the study. When the user provides a value for k, k centers are created, and the k-means algorithm allocates each data point to the nearest center.
Reference [29] overcomes the limitation of the original k-NN algorithm’s ignoring of the influence of the neighboring points, which directly affects localization accuracy. The researchers improved the indoor location identification using Wi-Fi-received, signal strength indicator (RSSI)-based fingerprints. The RSSI is highly dependent on the access point (AP) and the fingerprint learning stage, thus DNN is used in conventional k-NN to resolve this dependency. Additionally, DNN is used to classify fingerprint data sets. Then these possible locations in a certain class are classified by the improved k-NN algorithm to determine the final position. The improved k-NN is conducted by boosting the weights on K-nearest neighbors according to the number of matching AP.k-NN, and DNN were used to address the intrusion detection accuracy of existing intrusion detection systems [30]. Network attack data are classified by performing classification and labeling tasks on a “CICIDS-2017” dataset, which includes network attacks. The k-NN algorithm is used for machine learning, whereas DNN is used for deep learning, and the outputs of the two methods are then compared. A comparison with the general k-NN queries using the results demonstrates the superiority of DNN.
To perform efficient k-NN in a pre-built, high-dimensional index structure, an optimized k-NN query processing technique, which is tailored to the index structure, is required. This study investigates various k-NN optimization techniques for distributed, in-memory, high-dimensional indexes. The proposed techniques utilize deep learning models to optimize k-NN query processing performance. The proposed technique utilizes iDistance’s k-NN query processing method. iDistance converts a k-NN query into a range query and iteratively increases the scope of the search from 1% of the total index area until it finds k points. Here, a deep learning model was used to find a way to optimize the initial search area. We started with the idea that we can learn the initial search area based on many of the k-NN query processing logs that have been performed previously. In the query log, the query point information and k value information of the k-NN query were used as input features of deep learning, and the query processing result (final search area) was used as the correct answer data to perform weight learning of the DNN. This allows for optimal initial search values when a new k-NN query is entered, which is determined by iDistance as the initial search area, and query processing is performed.
3. Proposed Distributed, in-Memory, Index-Based k-NN Optimization Techniques
3.1. Overall Structure
This study proposes techniques to optimize the k-NN queries in pre-built, distributed, high-dimensional indexes. The proposed techniques included density-based optimization, which allocates different search ranges according to data density; cost-based optimization, which optimizes the search ranges using the statistical results of query processing; and deep-learning-based optimization, which predicts the optimal search range, depending on the query characteristics of using deep learning. To implement the proposed distributed, in-memory, index-based k-NN optimization techniques, we used an existing distributed in-memory index structure.
The existing index structure has a master/slave form, in which the master performs high-dimensional data area partitioning, while each slave performs indexing for the partitioned areas. Here, a distance-based index is used for high-dimensional data indexing. In distance-based indexing, data are converted to range queries for k-NN query processing, where the optimized search range must be determined. This study proposes optimization techniques to determine the initial search range.
Figure 1 shows the structure of k-NN query processing in the distributed, in-memory, high-dimensional index structure. As in our previous research, when the data were input, a distributed in-memory hybrid index, using k-d trees and iDistance, was built using Spark [17]. When processing a k-NN query, it was transformed into an optimized k-NN query by using the query location and k. Next, we allocated the query to each slave node for the distributed processing. This study proposed three k-NN query optimization techniques: density-based, cost-based, and DNN-based optimization.
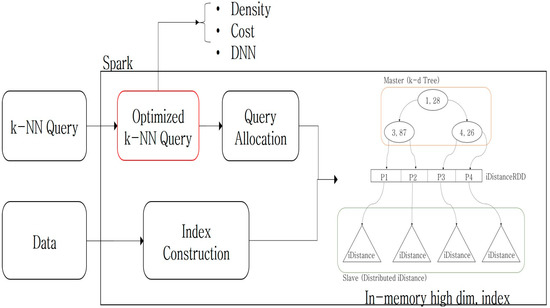
Figure 1.
Proposed k-NN processing procedure.
The data that were transformed into distance space had different densities depending on the data’s overall distribution. Therefore, transforming the search area according to the data density when performing k-NN queries can result in efficient query processing. This study proposed a density-based optimization technique to reflect the overall area distribution of the data. The density-based range value optimization technique calculated the initial search range value according to the k value, using the entire data area for processing. The density-based range optimization technique can reflect data density but not query processing statistics. The second proposed optimization technique optimizes the query expansion range using the number of query search attempts and candidates in the search range. The third proposed optimization technique uses a DNN model to derive a safe optimal range. A DNN model is a model with multiple hidden layers between the input and output layers. The depth of the DNN model has n layers, and the weight values were learned using the rectified linear unit (ReLU) [31] function between each layer. The query input data, k, and the query processing results were logged, and supervised learning was performed to optimize the k-NN queries. The k-NN query processing log was updated, and the learning model was periodically trained.
3.2. Distributed in-Memory Index Structure
Figure 2 shows the proposed distributed, in-memory, high-dimensional index structure. The proposed method performs k-NN query processing using the distributed, in-memory, high-dimensional indexing from our previous study. The previous study proposed distributed high-dimensional index structure by using k-d tree and iDistance, but it does not have optimized k-NN techniques. The proposed index structure uses Spark, a big data processing platform, to build the index in the distributed in-memory. It consists of a master—for query allocation and checking the query processing results—and several slaves—for the actual query processing and indexing. In Spark, the master node is configured on a driver node that manages the RDD (resilient distributed dataset). The slaves are configured on the worker nodes that store the actual RDD. The master node uses k-d-tree-based indexing to partition the index area allocated for each slave. The slave nodes construct iDistance indexing to store the actual data and process queries.
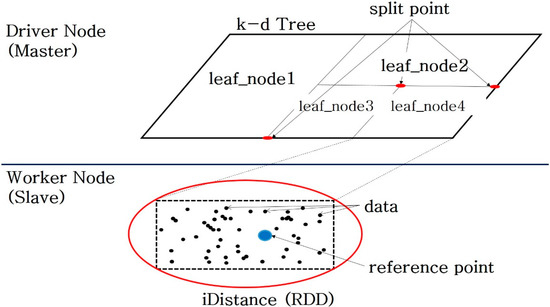
Figure 2.
Distributed in-memory high-dimensional index structure.
3.3. k-NN Query Processing Procedure
The k-NN queries are processed in the slave nodes, where the actual data are indexed. Because the slave nodes build the iDistance index, they perform the k-NN query processing in iDistance. The k-NN queries are converted into range queries, ready for processing in iDistance. The distance value between the query and the reference points is calculated. Next, we generate the search range by using this distance value, which is based on the B+ tree. This only performs the search action on the data within the search range. The search range converted in iDistance is simply set to 1% of the total index area. This study proposes three techniques to optimize the search area.
Figure 3 shows the k-NN query processing procedure using the proposed distributed in-memory index. The user’s query is input into the master node. The master node then calculates the optimal search range for the input k-NN query using the proposed optimized k-NN query processing technique. The optimized search range value is then passed to each slave node. The k-NN result value is then returned to the master node using the iDistance’s k-NN query processing technique. Next, the returned query results are merged to create the final result and are provided to the user. Since each slave node manages different data areas, it is not important to perform k-NN queries for the areas managed by the slaves that are not related to the current input query. Accordingly, different k values are allocated to each slave to process the queries.
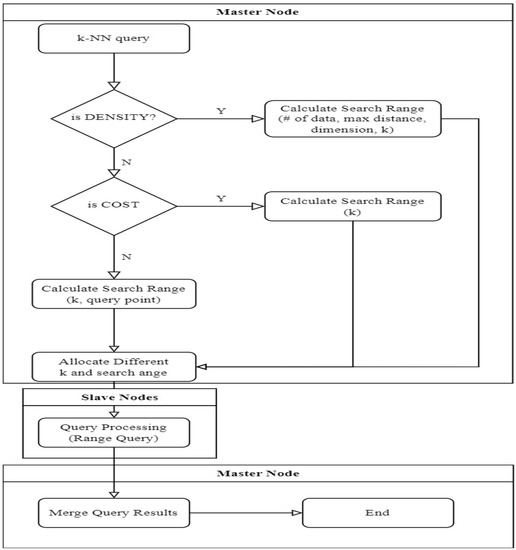
Figure 3.
k-NN query processing in the proposed technique.
Figure 4 shows the k-NN query processing procedure in iDistance. iDistance converts the data to distance information to manage it; therefore, it cannot process k-NN queries using distance information alone. This is because even the data points located at the same distance from the center of the k-NN query can be located in the opposite direction. Therefore, when a k-NN query is requested in iDistance, it is converted to a range query. The initial search range is set using the distance corresponding to 1% of the data area centered around the k-NN query location. If none of the k items are within the given range, then the area is expanded by 1%. The k-NN query is then repeated by expanding the search range. If the range contains k items, the k-NN query is terminated. The k items closest to the query are returned to the users. In this study, the master node converted the k-NN query into the optimal search range value. It was then passed to each slave node. The slave nodes then performed the range query by using the input search range. In iDistance, range queries are processed as follows: First, the distances between the query center point and all the reference points are calculated. Second, it checks whether the range query is included in the index area that each reference point manages. If the range query is included in an index area, the calculated distance value is calculated as a key-value, which the terminal node of the B+ tree manages. Third, the B+-tree search is performed by using the converted key-value. It calculates the actual distance values among all the pointers within the range and the searched data pointers. Finally, a set of the closest k pointers is created to perform the query processing.
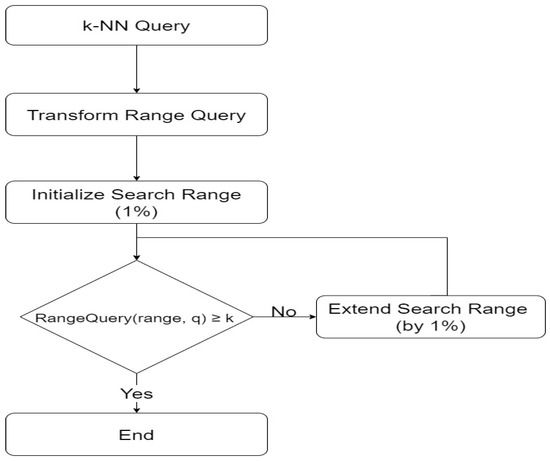
Figure 4.
k-NN query processing based on iDistance.
In k-NN queries, the nodes that are farther away have a lower probability of generating query results. Therefore, to reduce the number of candidate groups, different k values are assigned to the slave nodes depending on the distance between the query point and the nodes, as shown in Figure 5. The proposed method assigns higher k values to the nodes that are closer to the query point. To assign different k values, the minimum distance between the k-NN query and the search node is calculated. Different k values are assigned using this calculated distance. For example, calculations are performed and k values are assigned using the assumption that there is one data point for every search range value of ten. Slave node one, which covers the largest area, is allocated k = 10, so that it can find all ten data points. Because slave node two has a distance of 60 from the query point, it is allocated k = 4. Finally, slave node four, which covers the smallest area, has a distance of 70; therefore, it is allocated a value to find three data points. This technique can include different k values to reduce the search cost and shorten the time taken to derive the search results. In order to enable an efficiently distributed processing, we propose optimized k-NN models for determining the initial search range based on iDistance.
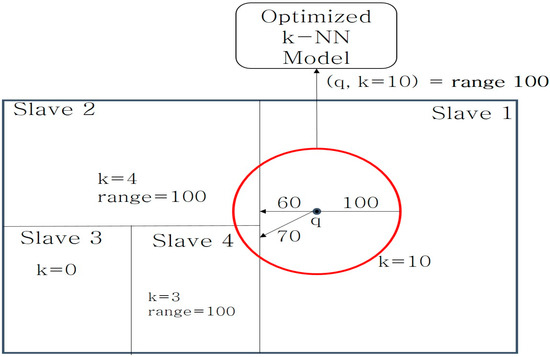
Figure 5.
Allocation of k values based on partitioned area.
3.4. k-NN Query Processing Optimization
iDistance is suitable for indexing high-dimensional data. However, it must convert a k-NN query into a range query to process the k-NN query. The initial search range value is set to 1% of the entire area. When tested, it caused frequent search area expansions and unnecessary repetitive searches. In order to address this issue, a k-NN query optimization technique was required to process the range queries according to the characteristics of the indexed data. In this paper, we proposed three query optimization techniques: setting the search area using the density of the indexed data area; optimizing the search area by statistically managing the cost of searching during the query processing; and calculating the optimal range value using the query location and k value, using a deep-learning-based optimization technique.
Algorithm 1 shows the proposed k-NN optimization algorithm. The query location, k, and the optimization methods (density-based, cost-based, and learning-based) were entered as inputs. The optimal range value for the query location and k were converted according to each optimization technique (Line 2). Next, to allocate different k values to all slave nodes, a new k was converted according to the range value, as shown in Figure 5 (Line 4). If the converted k was greater than zero, a range query was performed for that node (Line 6). The range query results were accumulated, the final query results were returned, and the algorithm was terminated.
| Algorithm 1. Optimized k-NN. | |
| Input: Query Point (qp), k of k-nn(k), Optimization Type(optType: DENSITY, COST, LEARNING) | |
| Output: Query Results | |
| 1: | results = {} |
| 2: | range = calculateQueryRange(qp, k, optType) |
| 3: | for slave in slaves do |
| 4: | dk = calculateDifferentK(qp, k, slave, range) |
| 5: | if dk > 0 then |
| 6: | results += processRangeQuery(qp, dk, slave, range) |
| 7: | else |
| 8: | not perform k-NN query |
| 9: | end for |
| 10: | return results |
3.4.1. Density-Based Optimization
The data transformed into distance space has different densities depending on the data’s overall distribution. Therefore, it is efficient to transform the search area when performing a k-NN query according to the data density. This study proposes a density-based optimization technique to reflect the overall area distribution of the data. Figure 6 shows the processing steps of the density-based optimization technique. In the offline stage, the density is calculated according to the data distribution. The average number of data points for each distance is also calculated. If there is two-dimensional data, when the maximum value of the data is (100, 100) and the minimum value is (0, 0), the maximum distance (approximately 141) of the area can be calculated using the Euclidean distance formula. In this scenario, if there are 100 data points in the area, the distribution of the data per range can be calculated using the area size and the number of data points. If the data are assumed to follow a standard normal distribution, a value of 100/141 = 0.7 can be obtained, and, using this, a value of 1.4 data points per range can be obtained. When a k-NN query occurs during the online stage, the optimal initial search range value is calculated using the formula (k value/number of data points per range), where the number of data points per range is calculated offline. For example, if k = 1, an initial search range value of (1/1.4) = 0.71 can be set, and if k = 2, an initial search range value of (2/1.4) = 1.42 can be calculated. A density-based initial search range calculation allows for the optimization of the initial search range for k-NN queries, according to the data density. The optimized range values are sent to each slave node to perform the query processing.
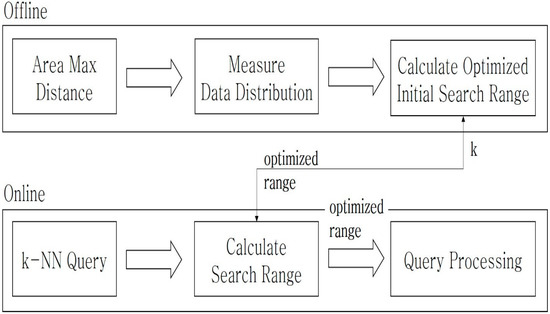
Figure 6.
Processing using density-based optimization.
Algorithm 2 shows an algorithm for calculating the query range. The query location, k, and the optimization techniques (density-based, cost-based, and learning-based) are entered as inputs, and the output is the optimized query range. The optimized range value is initially set to zero (Line 1). Under density-based optimization, the number of data points that can occur at each distance is calculated using the area’s data distribution and the maximum distance value (Line 3). The expected search range value is calculated according to the input value, k, using this value (Line 4). If another optimization method must be performed, the appropriate algorithm is implemented for each method (Lines 5–8). Cost-based optimization only utilizes k, whereas DNN-based optimization uses k and query positions. Finally, the optimal range value is returned, and the algorithm is terminated (Line 9).
| Algorithm 2. Calculation of the Query Range | |
| Input: Query Point (qp), k, optType: DENSITY, COST, LEARNING | |
| Output: Optimized Query Range | |
| 1: | search_range = 0 |
| 2: | if optType is DENSITY then |
| 3: | dpo = dataNum/maxDistance * dimension |
| 4: | search_range = k/dpo |
| 5: | elif optType = COST then |
| 6: | search_range = costBasedSearchRange(k) |
| 7: | else |
| 8: | search_range = DNNBasedSearchRange(qp, k) |
| 9: | return search_range |
3.4.2. Cost-Based Optimization
The density-based range optimization technique can reflect the data density but not the query processing statistics. The second optimization technique that we propose finds the query expansion range by using the statistics in the search result logs. Figure 7 shows the overall processing procedure of the k-NN optimization technique, using the query search cost. The query is processed using the initial search range of 1% in the existing iDistance, and then the increasing factor, α, and the decreasing factor, β, are used to optimize the initial search range of the same query. A series of calculations are performed using a threshold until it converges with the optimal range value. For example, when processing a 1-NN query, the query is processed using the existing search technique, and the statistical range value of 1-NN is set to the search range value (2%). If the same 1-NN is input again, the query is processed using the previously stored statistical range value (2%), and the query result is generated. Statistical range values are created and accumulated according to the k value through this, thereby converging the initial search range to a certain value. If there are two or more search iterations of the k-NN query, the increasing factor, α, is additionally applied to the statistical range value as many times as the search iterations. For example, if the search range value is increased twice in a 2% range search, then the next search range value is 2% * (2 * α). In the method of reflecting the number of search candidate groups in optimization checks and the number of search candidate groups, if the search range iterations end at the initially designated statistical search range (2%), then if the number of candidate groups is larger than the threshold (for example, the number of first 1-NN candidate groups is five), this means that more searches will be performed than were performed initially. The decreasing factor, β, reduces the statistical range value. Therefore, the statistical range value of the next 1-NN is 2% * β. The statistical range value converges to an appropriate value using the increasing and decreasing factors.
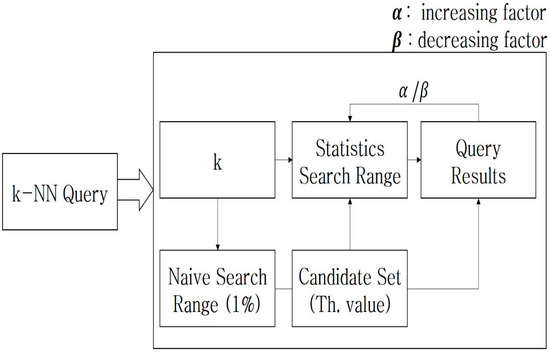
Figure 7.
Processing using cost-based optimization.
3.5. DNN-Based Optimization
The third optimization technique that we propose uses a DNN model, which has multiple hidden layers between the input and output layers. The depth of the DNN model has n layers, and the weight values are learned using the ReLU function between each layer. Figure 8 shows the overall processing procedure of the DNN-based k-NN optimization technique. During the offline stage, supervised learning is conducted using the optimal range of the query points, the search range, and the k values obtained through the pre-performing k-NN queries. The goal is to learn the mean squared error (MSE) in order to continuously reduce the error of the difference between the answer and the prediction sets. Learning is conducted using the logs of the k-NN query processing results. In the input layer, the number of neurons corresponding to each dimension of the query location (128 dimensions) is configured, and the k value is also used as an input value. The model is designed so that, after passing through n hidden layers, it ultimately predicts the search range value. Each hidden layer outputs the next layer’s input value using the learned weights and biases. The final output layer is composed of only one neuron because it must produce the optimal search range value for the k-NN query. The final search range values that are recorded in the query log are used as the answer set, and the differences between the predicted search range and the answer values are used to train the weights and biases of each hidden layer.
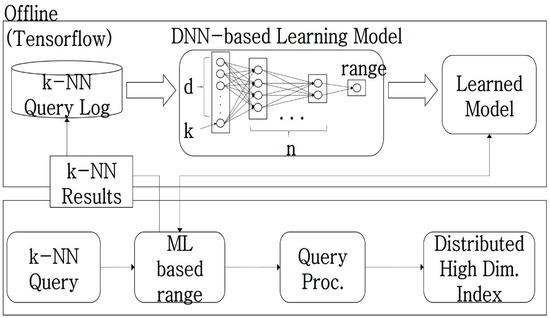
Figure 8.
Processing using DNN-based optimization.
To execute the DNN-based learning model, the k-NN query, Q, is transformed into a vector, with the form X = [dp0, dp1, … dpd, k]. The dpn represents the coordinate value corresponding to the n-th dimension. The k represents the number of target objects, k, to be found in the k-NN query. The hidden layers used in this study were structured as shown in Equations (1) and (2). The H denotes the hidden layer; each hidden layer is the result of the activation function, , applied to the sum of the previous hidden layer’s output value and the current hidden layer’s weight (W) and bias (b). In this study, we used ReLU for the activation function. The symbol l represents the number of hidden layers. The optimal number of hidden layers was derived using the performance evaluations in this study. The final hidden layer outputs the result value, , which is the predicted initial search range value for performing the k-NN search. The model is trained using the search range value, y, in the log that records the existing k-NN query processing results. The MSE error function for training the model is expressed using Equation (3), where M denotes the total number of queries recorded in the log, and ym denotes the search range value of the m-th k-NN query. Therefore, the error value is the accumulated difference between the predicted and actual search ranges divided by the number of queries. The learning model minimizes the MSE.
4. Performance Evaluations
This section demonstrates the validity of the proposed k-NN query processing optimization techniques through our performance evaluations. The optimal model was derived from a performance evaluation of the proposed DNN model, and the query processing time was compared with existing studies. The proposed techniques find k nearest data precisely when processing k-NN queries. That is, it achieves 100 % accuracy when processing k-NN queries. Therefore, we do not evaluate the accuracy of k-NN queries in the proposed techniques, but only the query processing time. Table 1 shows the performance evaluation environment. The distributed environment was implemented with four nodes, which consisted of an Intel(R) Core(TM) i5-6400, 2.7 GHz 4 Core processor (Santa Clara, CA, USA) and 48 GB of main memory. The evaluation was conducted using a total of eight partitions, with two partitions allocated to each server. The proposed techniques were implemented on Spark 2.3.1 (Apache Software Foundation, Wilmington, DE, USA). Additionally, the DNN model for machine-learning-based optimization was implemented by using TensorFlow 2.0.0 (Google, Mountain View, CA, USA).

Table 1.
Performance evaluation environment.
The feature data that can be distinguished for each image must be extracted for use in the query processing. Table 2 shows the experimental data’s features. The dataset consisted of the image features that were extracted using the scale-invariant feature transform (SIFT) [32] algorithm. The SIFT extracts the features invariant to the image’s size and rotation. The dimension of each data point can have values ranging between 0 and 255, and one data point represents the object features within a single image file. A dataset of one million 128-dimensional data points was used.

Table 2.
Experimental data features.
Figure 9 shows the distribution of all the data values. Comparing the distribution of the values from 0 to 255, out of 128 million data points, 21 million had a value of 0 (17% of the total), 7% had a value of 1, 4.8% had a value of 2, 3.8% had a value of 3, 3.2% had a value of 4, and 0.002% had values of 200–255. The performance evaluation used skewed data extracted by the SIFT algorithm.
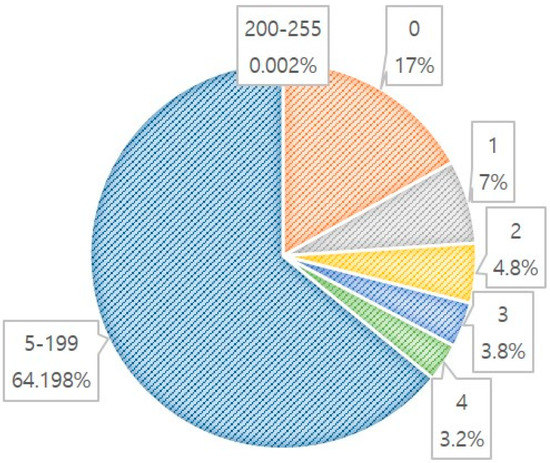
Figure 9.
Shape of data distribution.
To demonstrate the validity of the optimization technique using the DNN model, the MSE was evaluated in accordance with the DNN model depth. We created the model using TensorFlow, an open-source platform for machine learning, as the underlying platform. In total, 80% of the total data were used for training and 20% were used for validation. We used the Adam function, which is commonly used in DNN. Figure 10 shows the MSE according to the DNN model’s depth. As the depth value increased, the MSE decreased up until a depth of eight and, after that, it started to increase. This was confirmed as having been caused by overfitting—a problem in machine learning models.
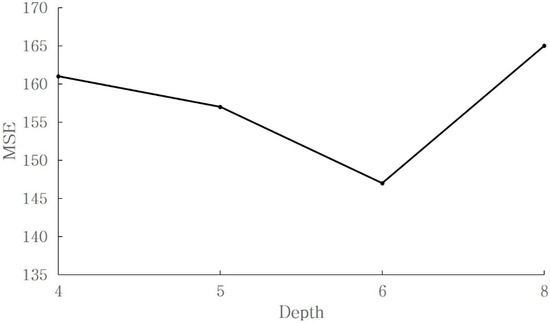
Figure 10.
MSE according to the DNN depth.
To avoid overfitting, we selected an appropriate depth using the results of previous experiments and conducted the training accordingly. Keras is an open-source library that serves a Python interface for artificial neural networks. It acts as an interface for the TensorFlow and offers various functions to optimize machine learning models. Figure 11 shows the MSE according to the optimization function. The depth of the DNN model was set to six. According to the performance evaluation results, Adamax [33] showed the smallest MSE value. Therefore, we conducted a performance evaluation using the Adamax optimization function, which demonstrated the best performance.
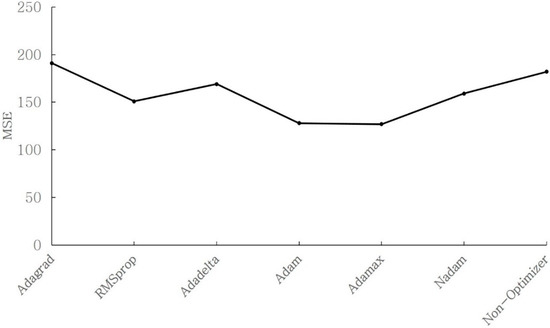
Figure 11.
MSE according to the optimization function.
In order to demonstrate the validity of the need for optimization, we evaluated the effectiveness of each optimization technique. We compared the existing iDistance technique with the three optimization techniques proposed in this study. The query processing time was compared after 100 queries had been performed. Figure 12 shows the performance comparison results of the k-NN query processing techniques. The x-axis represents the query number, which is the order in which the queries were input. The queries continued to be processed using the existing schemes, and the performance did not improve because there were no other methods for additional optimization. Therefore, they performed consistently from the beginning to the end. The proposed optimization techniques demonstrated performance changes as the queries were processed. Although the density-based optimization technique performed well in certain situations, it did not consistently perform well. It achieved good performance in areas in which the calculated density values matched. However, when the density values differed, it specified a considerably wide search range value. As the search range expanded, it increased the number of candidate sets. This resulted in a large distance calculation cost and a decrease in the query processing performance. The statistical optimization technique using query search cost had a search range increasing or decreasing factor. As shown in the graph, as the factor processed the queries, the performance improved and converged to a certain value. However, it was observed that it took some time for the value to converge. The DNN-based optimization technique using machine learning demonstrated consistently low processing costs from the beginning, compared with other techniques. The validity of the proposed k-NN optimization technique was proven using the performance evaluation results.
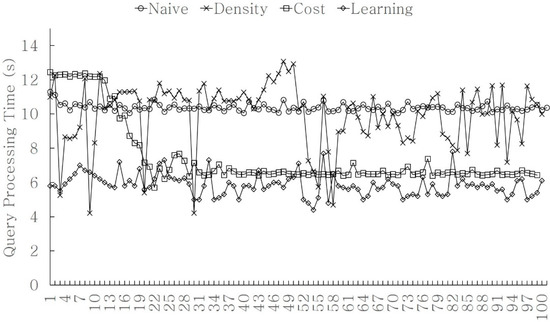
Figure 12.
Processing time by k-NN query processing method.
We compared the query processing time of the proposed optimization techniques and the existing distributed, high-dimensional indexing methods to verify their superiority. We selected the existing methods, such as the distributed k-d tree, the distributed iDistance, the sequential search, and the join-based k-NN. The distributed iDistance method was implemented on Spark. The sequential search was also implemented on Spark, where it searched and compared files sequentially using distributed processing. The join-based k-NN, which is a parallel CBIR system, was implemented on the Spark and Tachyon frameworks [26].
A performance evaluation was first conducted while we range queries were being processed. The range query parameters were as follows: The range was set to 50. We conducted 100 queries with 128-dimensional-feature data points. Figure 13 shows the range query processing time for each distributed high-dimensional indexing scheme. The sequential search showed consistent performance, regardless of the query, because it compared all data. The distributed k-d tree method showed the worst performance because it had to search both the global and local k-d trees, which resulted in high tree search costs and inferior performance, compared to the sequential search in tall trees, owing to the backtracking operations. The distributed iDistance method performed better than the sequential search, but worse than the proposed method. Since all of the nodes participate in the query, a master node that partitions data areas, such as the k-d tree, is lacking. Join k-NN performed better than the distributed k-d trees, but worse than the sequential search. Compared with the existing iDistance method, the proposed method performed better in reducing the processing time. In our method, the master node k-d tree limited the number of nodes participating in the query by partitioning areas. The proposed distributed, high-dimensional indexing scheme performed the best in terms of its range query processing time.
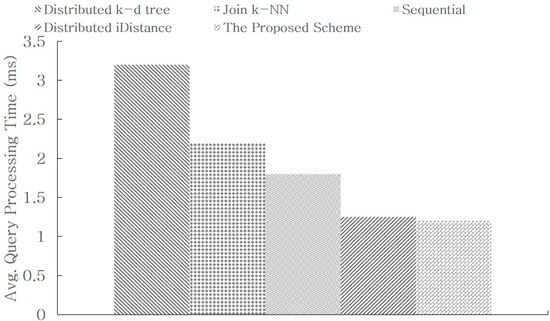
Figure 13.
Range query processing time according to the indexing method.
To evaluate the performance of k-NN queries, we set k to 100 and conducted the same 100 queries that we used in the range query evaluation. In particular, we compared the performances of the existing methods, the hybrid indexing method proposed by our research team, and a method that applies the three optimization techniques used for hybrid indexing. Figure 14 shows the k-NN query processing time with the indexing method. The sequential search had the worst performance because it requires extensive time to compare the distance for all the data and because it manages the k-nearest list using additional comparison operations. Although the distributed k-d tree method performed poorly in the range queries, it excelled in the k-NN queries. This is because it only finds the kth data in the local k-d tree and performs range retrieval using this, taking only as much time as a range query. However, as the k value increased, the distributed k-d tree method still struggled to find the kth data in the local k-d tree because of the excessive backtracking operations. The join k-NN technique is a state-of-the-art scheme, which exhibited very good performance for k-NN. However, it performed very badly during the range query evaluation. The distributed iDistance and the proposed techniques did not perform as effectively as the distributed k-d tree because they perform iterative range expansions and range searches to process k-NN queries and to find k items. Nevertheless, the distributed high-dimensional indexing method proposed in this study outperformed the existing distributed iDistance method. The reason for this was that the k-d tree in the master node pre-filters are areas that must not be retrieved by selecting nodes to participate in the query.
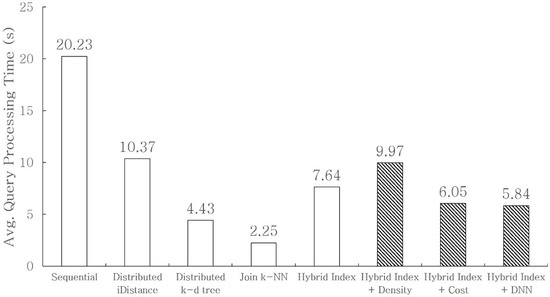
Figure 14.
k-NN query processing time, according to the indexing technique.
To evaluate the performance of the proposed density-based and DNN-based optimization techniques, we compared the changes in the difference in the search range values and the changes in k in the k-NN queries (Figure 15). The density-based optimization showed a linear increase in the difference between the actual and predicted search range values as k changed. When k was 100, the predicted search range value was more than 140% higher than the actual search area, resulting in frequent unnecessary searches. Conversely, the DNN-based optimization technique showed an average difference between the actual and predicted search range values of approximately 5.79%, demonstrating that it accurately predicted the actual search area. Moreover, contrary to the density-based technique, the performance of the DNN-based optimization technique was not significantly impacted by the changes in k, demonstrating that it is a more stable optimization technique.
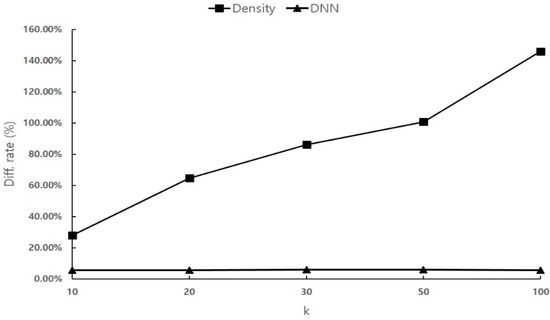
Figure 15.
Predicted search range values, according to k.
The performance evaluation results of the proposed k-NN optimization techniques showed the following: Density-based optimization techniques had different processing times depending on the density consistency. As a result, the average processing time was very unstable and the overall query processing performance was reduced. The cost-based optimization technique outperformed the density-based technique, but was worse than the distributed k-d tree. However, when comparing the range and k-NN queries, the proposed technique performed better, overall, because the distributed k-d tree took approximately three times as long to process the range queries. Finally, the method that applied machine learning optimization to the proposed technique outperformed the other optimization techniques. The machine-learning-based optimization technique demonstrated a stable query processing time, compared with the density-based optimization technique, and provided a more optimized query range in a faster time than the cost-based optimization technique. We demonstrated the superiority of our proposed high-dimensional indexing method, in terms of range and k-NN query processing times, using an overall performance evaluation.
The advantages of the proposed techniques in comparison with state-of-the-art technologies are as follows. First, the proposed techniques can improve the query processing time by filtering areas that do not need to be searched in advance in a distributed processing system structure. The existing techniques perform k-NN query processing through a distributed processing framework such as MapReduce [26]. Since they do not have any indices, unnecessary operations will be performed on all of the nodes. This results in a performance degradation of the overall system. Second, the query processing results of the proposed techniques only provide accurate results. The existing techniques provide approximate results to speed up search performance [24]. Third, various k-NN query optimization techniques have been proposed. When the proposed techniques apply to the real world system, they have the advantage of being able to find optimal performance by replacing optimization techniques. On the other hand, the limitations of the proposed techniques are as follows. First, we provide various optimization techniques to improve the performance of k-NN query processing. However, we do not show the “best” performance compared to the existing techniques. Second, there is the limitation that the proposed index and query processing techniques depends on a specific platform, such as Spark.
5. Conclusions
In this paper, we proposed three k-NN optimization techniques for a distributed, in-memory indexing method, which can efficiently retrieve large-scale, high-dimensional data. The proposed techniques were designed based on the density, cost, and DNN, and were implemented on Spark—a distributed in-memory processing platform—to process large-scale data. A distance-based index, iDistance, was used to efficiently manage high-dimensional values. The proposed techniques’ superiority in terms of range and k-NN query processing time was demonstrated through performance evaluations. The proposed techniques were tested in a cluster environment, which consisted of four servers. In the experiment, we used SIFT to extract the image features. The extracted features consisted of data points with 128 dimensions, which had values ranging from 0 to 255. The proposed techniques performed k-NN query processing based on distance-based, high-dimensional indexes. Therefore, since the k-NN query was only processed using distance information, we had to perform the calculation of the actual distance for the candidates. Therefore, when a significant number of candidate groups were generated, the query processing performance was poor. In the future, we will improve the query performance of the k-NN by making new optimizations. We also intend to conduct additional research on k-NN optimization in the future. Furthermore, we will devise an optimization model for distance-based indexes.
Author Contributions
Conceptualization, D.C., J.W., S.S., H.L., J.L., K.B. and J.Y.; methodology, D.C., J.W., H.L., J.L., K.B. and J.Y.; validation, D.C., J.W., S.S., H.L. and K.B.; formal analysis, D.C., J.W., S.S., H.L. and K.B.; writing—original draft preparation, D.C., J.W., J.L. and K.B.; writing—review and editing, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a National Research Foundation of Korea (NRF) grant, funded by the Korean Government (MSIT) (No. 2022R1A2B5B02002456); an Institute of Information and Communications Technology Planning and Evaluation (IITP) grant, funded by the Korean Government (MSIT) (No. 2014-3-00123, Development of High Performance Visual BigData Discovery Platform for Large-Scale Realtime Data Analysis); the MSIT (Ministry of Science and ICT), Korea, under the Grand Information Technology Research Center support program (IITP-2023-2020-0-01462), supervised by the IITP (Institute for Information and Communications Technology Planning and Evaluation); and the Cooperative Research Program for Agriculture Science and Technology Development (Project No. PJ016247012022), Rural Development Administration, Republic of Korea.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, Y.; Huang, J.; Schwing, A.G. VideoMatch: Matching based video object segmentation. Comput. Vis. ECCV 2018, 2018, 56–73. [Google Scholar] [CrossRef]
- Zhao, L.; He, Z.; Cao, W.; Zhao, D. Real-time moving object segmentation and classification from HEVC compressed surveillance video. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 1346–1357. [Google Scholar] [CrossRef]
- Joshi, K.A.; Thakore, D.G. A survey on moving object detection and tracking in video surveillance system. J. Soft Comput. Eng. 2012, 2, 44–48. [Google Scholar]
- Cheng, J.; Yuan, Y.; Li, Y.; Wang, J.; Wang, S. Learning to Segment Video Object With Accurate Boundaries. IEEE Trans. Multimed. 2020, 23, 3112–3123. [Google Scholar] [CrossRef]
- Matiolański, A.; Maksimova, A.; Dziech, A. CCTV object detection with fuzzy classification and image enhancement. Multimed. Tool. Appl. 2016, 75, 10513–10528. [Google Scholar] [CrossRef]
- Kakadiya, R.; Lemos, R.; Mangalan, S.; Pillai, M.; Nikam, S. AI based automatic robbery/theft detection using smart surveillance in banks. In Proceedings of the International Conference on Electronics, Communication and Aerospace Technology, Coimbatore, India, 12–14 June 2019; pp. 201–204. [Google Scholar] [CrossRef]
- Sukhia, K.N.; Riaz, M.M.; Ghafoor, A. Content-based retinal image retrieval. IET Image Process. 2019, 13, 1525–1534. [Google Scholar] [CrossRef]
- Yu, J.; Liu, H.; Zheng, X. Two-dimensional joint local and nonlocal discriminant analysis-based 2D image feature extraction for deep learning. Neural Comput. Applic. 2020, 32, 6009–6024. [Google Scholar] [CrossRef]
- Sharif, U.; Mehmood, Z.; Mahmood, T.; Javid, M.A.; Rehman, A.; Saba, T. Scene analysis and search using local features and support vector machine for effective content-based image retrieval. Artif. Intell. Rev. 2019, 52, 901–925. [Google Scholar] [CrossRef]
- Saritha, R.R.; Paul, V.; Kumar, P.G. Content based image retrieval using deep learning process. Cluster Comput. 2019, 22, 4187–4200. [Google Scholar] [CrossRef]
- Tadi Bani, N.T.; Fekri-Ershad, S. Content-based image retrieval based on combination of texture and colour information extracted in spatial and frequency domains. Electron. Libr. 2019, 37, 650–666. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, D.; Scott, G.; Uhlmann, J.; Shyu, C.R. In-memory distributed indexing for large-scale media data retrieval. In Proceedings of the International Symposium on Multimedia, Taichung, Taiwan, 11–13 December 2017; pp. 232–239. [Google Scholar] [CrossRef]
- Skopal, T.; Lokoč, J. New dynamic construction techniques for M-tree. J. Discrete Algor. 2009, 7, 62–77. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, W.; Tang, R.; Mao, J.; Luo, Q.; Li, C.; Wang, A. Distributed Indexes Design to Accelerate Similarity based Images Retrieval in Airport Video Monitoring Systems. In Proceedings of the International Conference on Fuzzy Systems and Knowledge Discovery, Zhangjiajie, China, 15–17 August 2015; pp. 1908–1912. [Google Scholar] [CrossRef]
- Patwary, M.M.A.; Satish, N.R.; Sundaram, N.; Liu, J.; Sadowski, P.J.; Racah, E.; Byna, S.; Tull, C.; Bhimji, W.; Prabhat; et al. PANDA: Extreme Scale Parallel k-Nearest Neighbor on Distributed Architectures. In Proceedings of the International Parallel and Distributed Processing Symposium, Chicago, IL, USA, 23–27 May 2016; pp. 494–503. [Google Scholar]
- Wei, H.; Du, Y.; Liang, F.; Zhou, C.; Liu, Z.; Yi, J.; Xu, K.; Wu, D. A k-d tree-based algorithm to parallelize kriging interpolation of big spatial data. GI Sci.Remote. Sens. 2015, 52, 40–57. [Google Scholar] [CrossRef]
- Lee, H.; Lee, H.; Wee, J.; Song, S.; Kang, T.; Choi, D.; Bok, K. Distance-based high-dimensional index structure for efficient query processing in spark environments. In Proceedings of the ICCC 2020, Busan, Korea, 12–14 November 2020; pp. 321–322. [Google Scholar]
- Yang, M.; He, D.; Fan, M.; Shi, B.; Xue, X.; Li, F.; Huang, J. Dolg: Single-stage image retrieval with deep orthogonal fusion of local and global features. In Proceedings of the IEEE/CVF International conference on Computer Vision, Montreal, BC, USA, 11–17 October 2021; pp. 11772–11781. [Google Scholar]
- Hung, B.T.; Chakrabarti, P. Parking lot occupancy detection using hybrid deep learning CNN-LSTM approach. In Proceedings of the 2nd International Conference on Artificial Intelligence: Advances and Applications: ICAIAA 2021, Jaipur, India, 27–28 March 2021; pp. 501–509. [Google Scholar]
- Hung, B.T.; Pramanik, S. Content-Based Image Retrieval using Multi Deep Neural Networks and K-Nearest Neighbor Approaches. 2023. Available online: https://www.researchgate.net/publication/368965259_Content-Based_Image_Retrieval_using_Multi_Deep_Neural_Networks_and_K-Nearest_Neighbor_Approaches (accessed on 10 March 2023).
- Yenigalla, S.C.; Srinivas Rao, K.; Ngangbam, P.S. Implementation of content-based image retrieval 3 using artificial neural networks 4. Hologr. Meets Adv. Manuf. 2023, 15, 10. [Google Scholar]
- Jagadish, H.V.; Ooi, B.C.; Tan, K.L.; Yu, C.; Zhang, R. iDistance: An Adaptive B+-tree based indexing method for nearest neighbor search. ACM Trans. Database Syst. 2005, 30, 364–397. [Google Scholar] [CrossRef]
- Huynh, C.V.; Huh, J.H. B+-Tree construction on massive Data with Hadoop. Cluster Comput. 2019, 22, 1011–1021. [Google Scholar]
- Johnson, J.; Douze, M.; Jégou, H. Billion-scale similarity search with gpus. IEEE Trans. Big Data 2019, 7, 535–547. [Google Scholar] [CrossRef]
- Hou, Z.; Huang, C.; Wu, J.; Liu, L. Distributed Image Retrieval Base on LSH Indexing on Spark. In Proceedings of the Big Data and Security: First International Conference, ICBDS 2019, Nanjing, China, 20–22 December 2019; pp. 429–441. [Google Scholar] [CrossRef]
- Mezzoudj, S.; Behloul, A.; Seghir, R.; Saadna, Y. A parallel content-based image retrieval system using spark and tachyon frameworks. J. King Saud. Univ. Comput. Inf. Sci. 2021, 33, 141–149. [Google Scholar] [CrossRef]
- Yan, Z.; Lin, Y.; Peng, L.; Zhang, W. Harmonia: A high throughput B+-tree for GPUs. In Proceedings of the ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, New York, NY, USA, 16–20 February 2019; pp. 133–144. [Google Scholar] [CrossRef]
- Vajda, S.; Santosh, K.C. A fast k-nearest neighbor classifier using unsupervised clustering. In Proceedings of the International Conference on Recent Trends in Image Processing and Pattern Recognition, Kingsville, TX, USA, 22–23 December 2022; Springer: Singapore, 2016. [Google Scholar]
- Dai, P.; Yang, Y.; Wang, M.; Yan, R. Combination of DNN and improved KNN for indoor location fingerprinting. Wirel. Commun. Mob. Comput. 2019, 2019, 4283857. [Google Scholar] [CrossRef]
- Atefi, K.; Hashim, H.; Kassim, M. Anomaly analysis for the classification purpose of intrusion detection system with K-nearest neighbors and deep neural network. In Proceedings of the IEEE 7th Conference on Systems, Process and Control (ICSPC), Melaka, Malaysia, 13–14 December 2019. [Google Scholar] [CrossRef]
- Hahnloser, R.H.R.; Sarpeshkar, R.; Mahowald, M.A.; Douglas, R.J.; Seung, H.S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 2000, 405, 947–951. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).