Dynamic Models with Sigmoid Corrections to Generation of an Achievable 4D-Trajectory for a UAV and Estimating Wind Disturbances

For an unmanned aerial vehicle (UAV) of an aircraft type, the problems of planning achievable trajectories as well as robust control under wind disturbances are considered. A computationally simple method for compiling a primary non-smooth 4D trajectory is proposed. Its segments connect the given waypoints and determine the desired average velocity in various sections. Instead of time-consuming methods of analytical smoothing of broken path joints using polynomials, a tracking differentiator with S-shaped smooth and limited sigmoid corrective actions is developed. This virtual dynamic model provides natural smoothing of the primary trajectory considering the design constraints on the velocity, acceleration, and thrust of the UAV. The tracking differentiator variables create an achievable trajectory and are used to synthesize the UAV tracking system. To compensate for the action of wind disturbances on the UAV, a disturbance observer is developed. It is a replica of the equations of the control plant model, which are directly affected by external uncontrolled disturbances. These algorithms also use sigmoid corrections. Unlike standard disturbances observers, this approach does not require the development of a dynamic model of external disturbances and does not assume their smoothness. 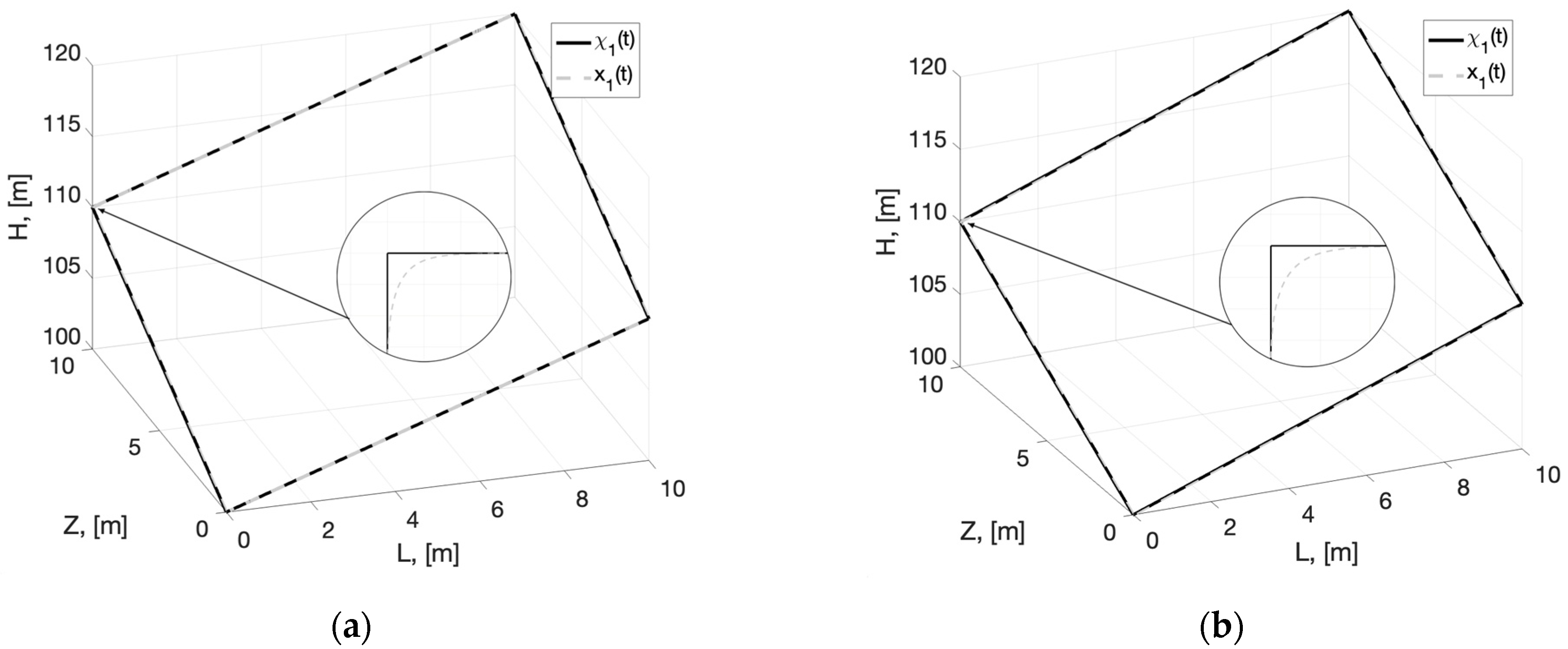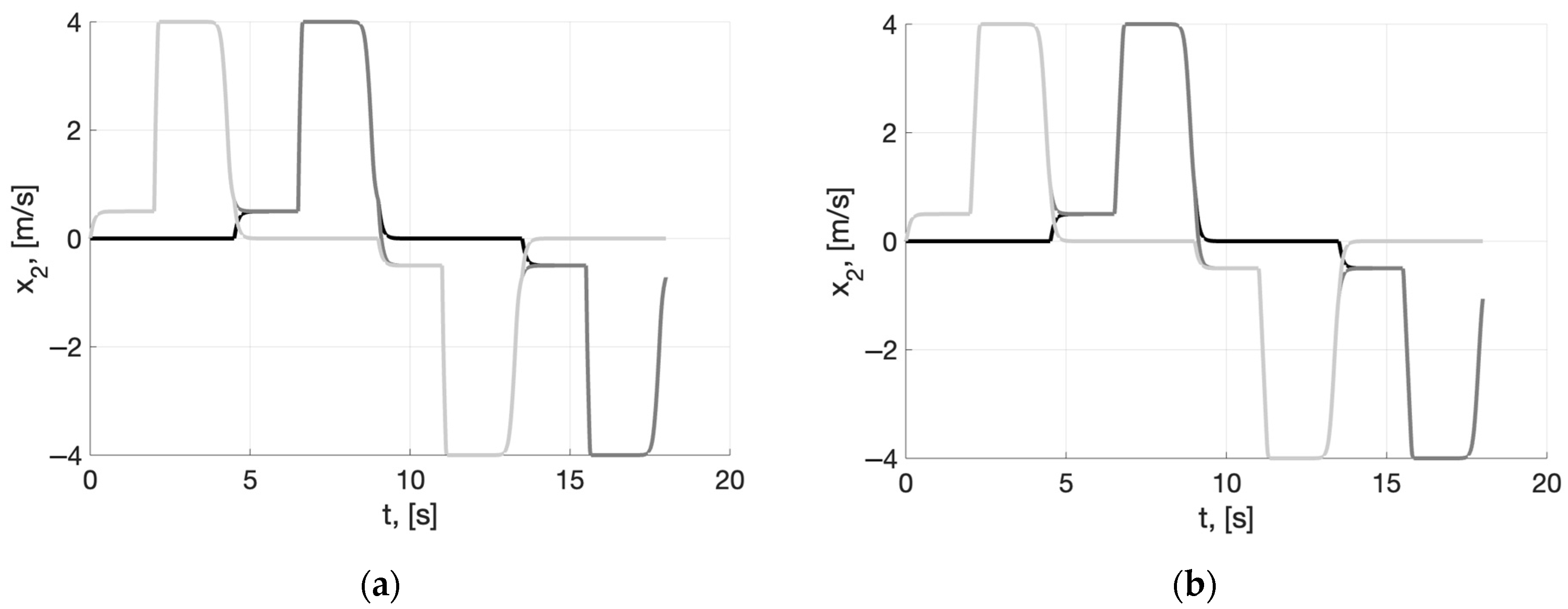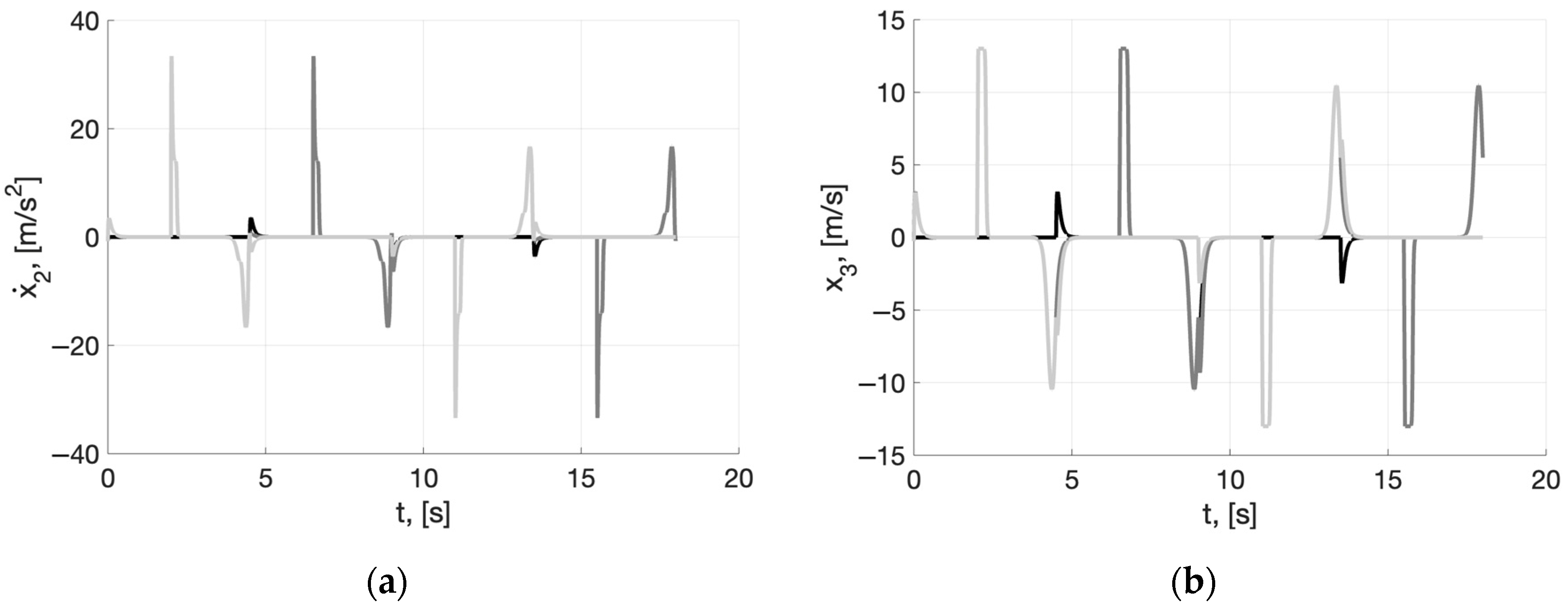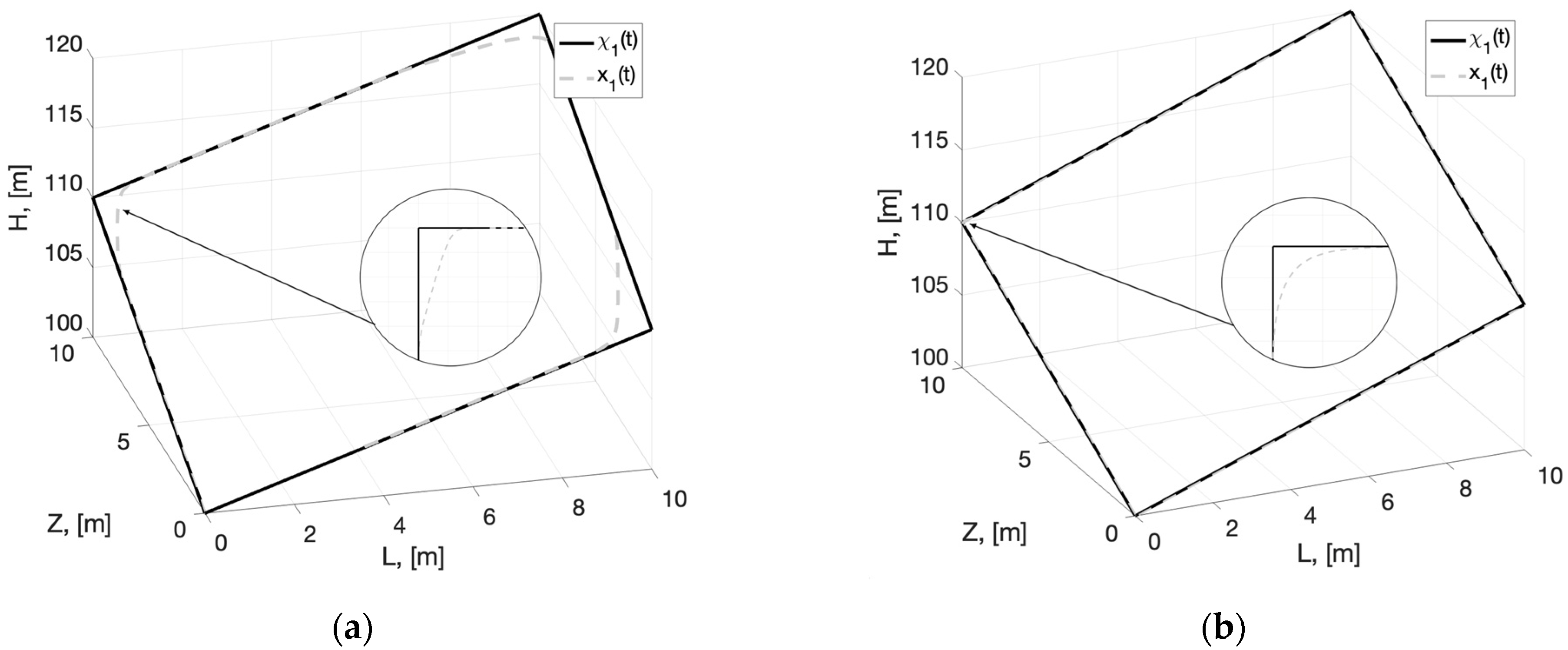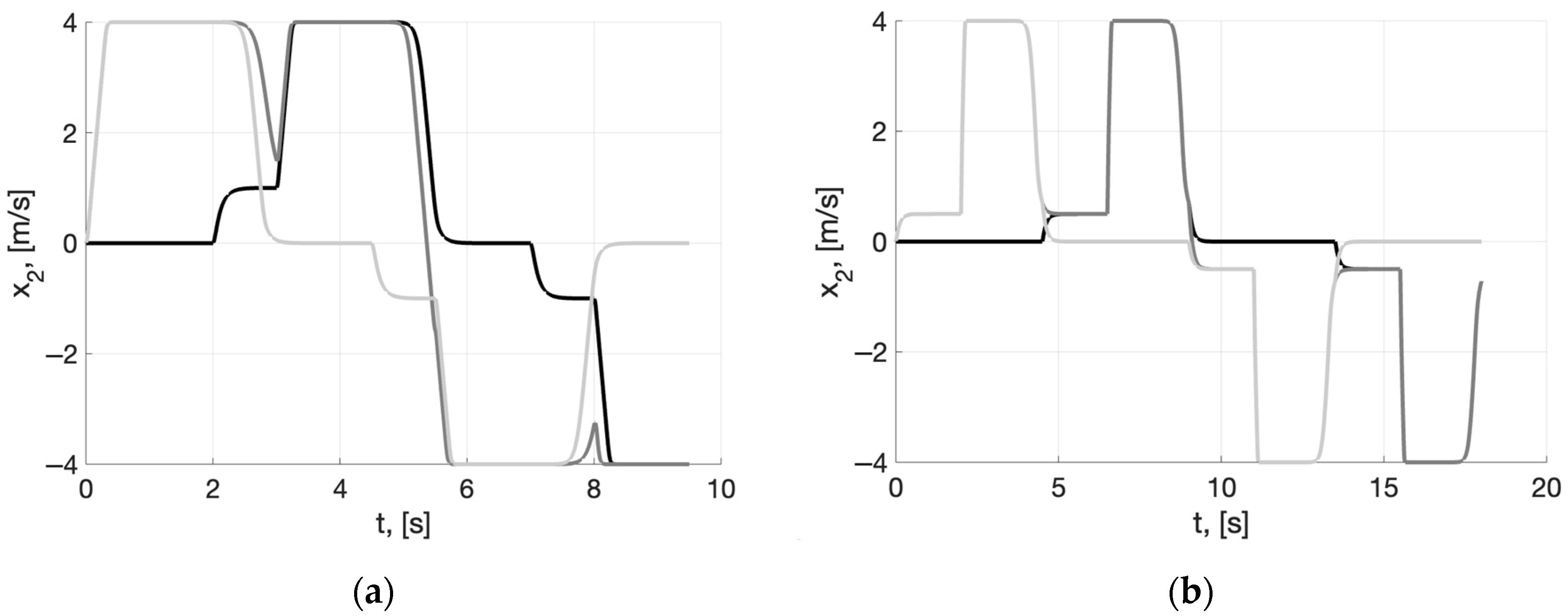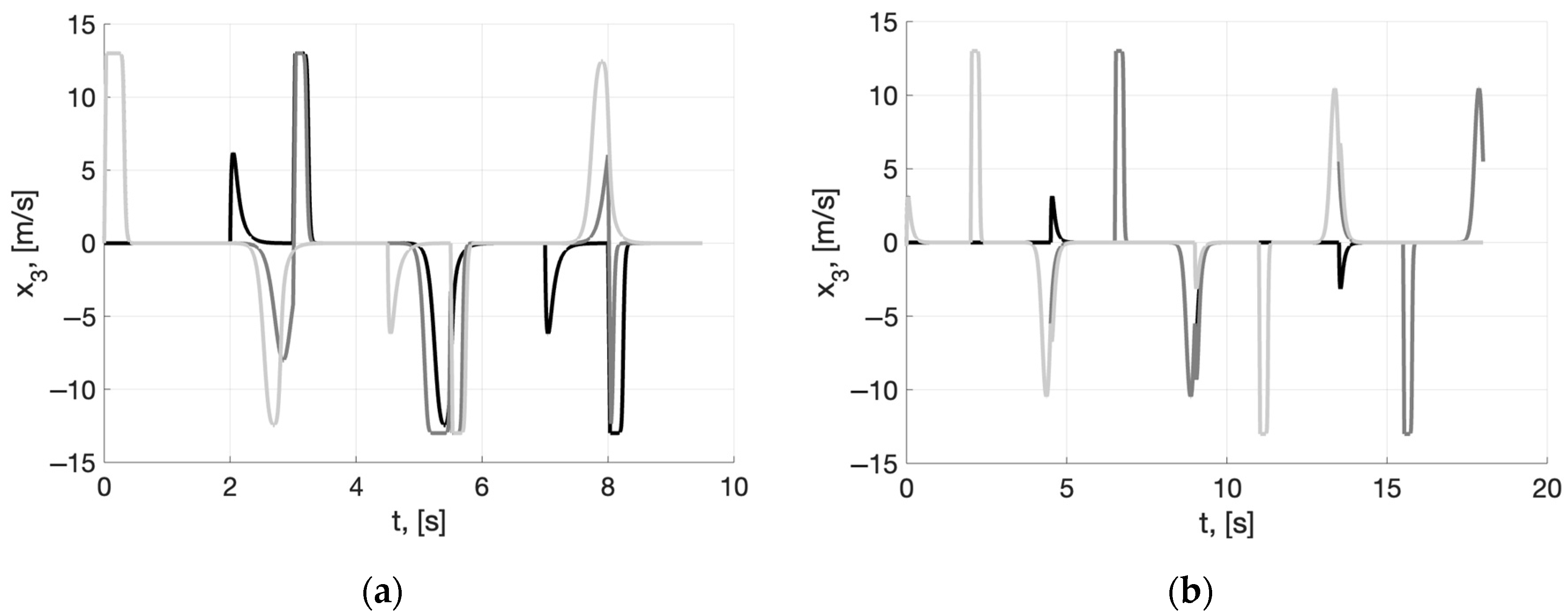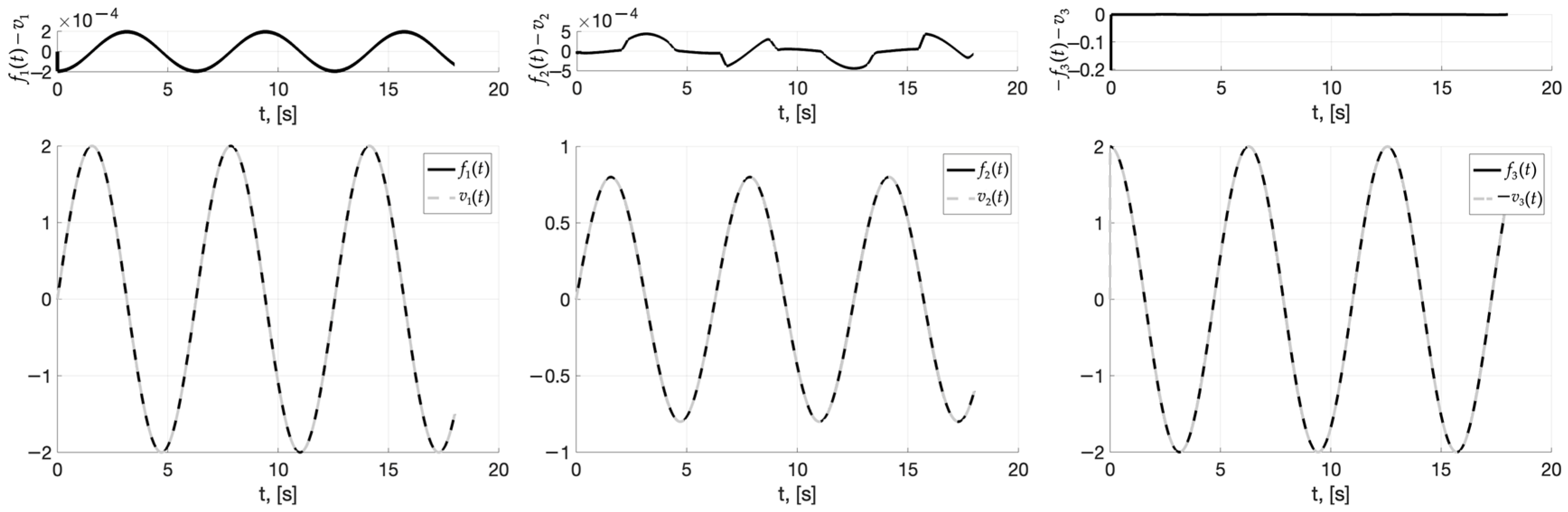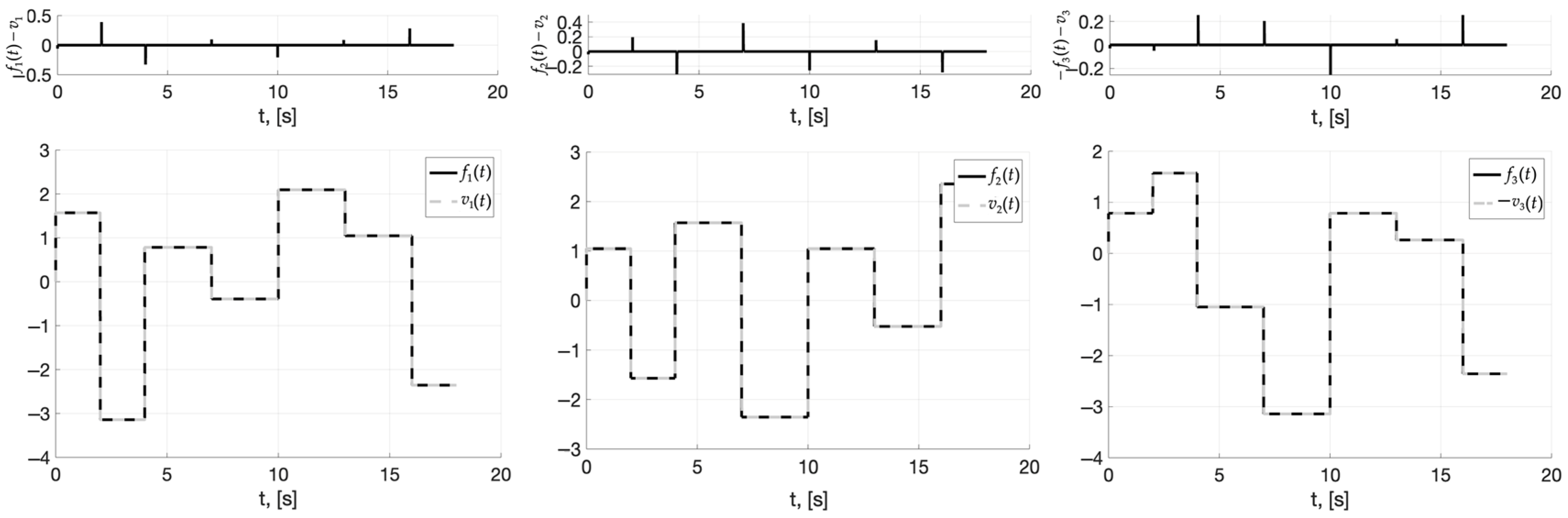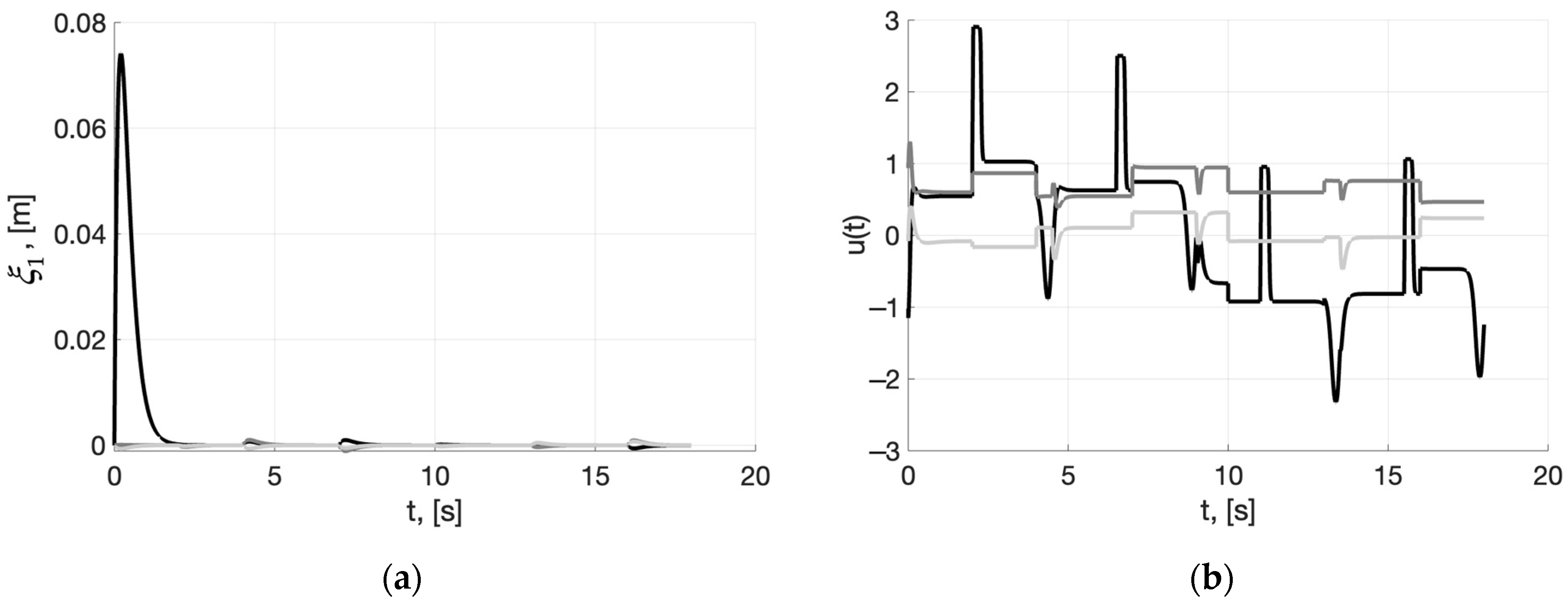The effectiveness of the developed algorithms was confirmed by numerical simulation.