Optical Solitons for a Concatenation Model by Trial Equation Approach
Abstract
1. Introduction
Governing Model
2. Trial Equation Method
3. Mathematical Analysis
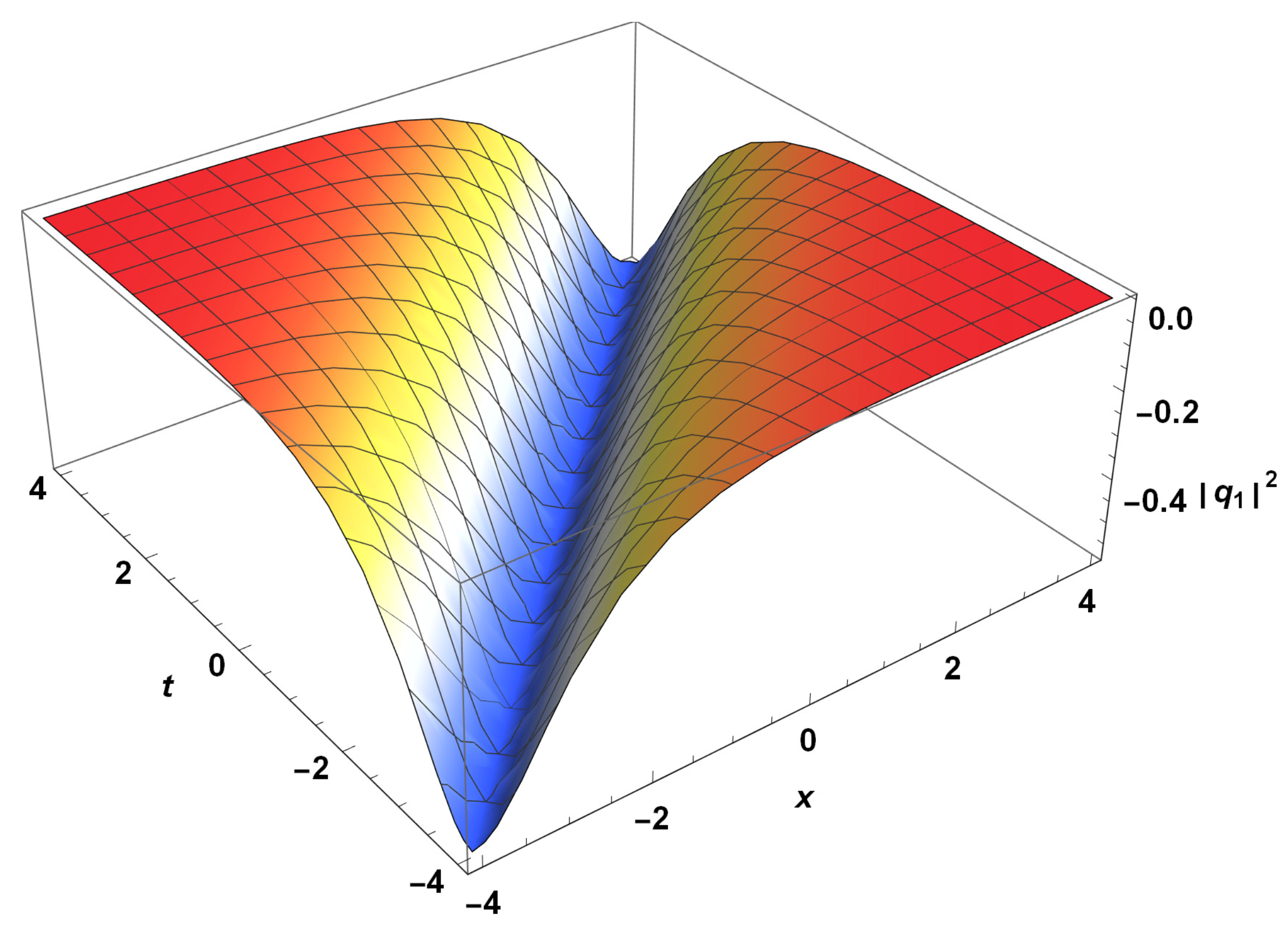
4. Exact Solutions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ankiewicz, A.; Akhmediev, N. Higher-order integrable evolution equation and its soliton solutions. Phys. Lett. A 2014, 378, 358–361. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Wang, Y.; Wabnitz, S.; Akhmediev, N. Extended nonlinear Schrödinger equation with higher-order odd and even terms and its rogue wave solutions. Phys. Rev. E 2014, 89, 012907. [Google Scholar] [CrossRef] [PubMed]
- Triki, H.; Sun, Y.; Zhou, Q.; Biswas, A.; Yıldırım, Y.; Alshehri, H.M. Dark solitary pulses and moving fronts in an optical medium with the higher-order dispersive and nonlinear effects. Chaos Solitons Fractals 2022, 164, 112622. [Google Scholar] [CrossRef]
- Biswas, A.; Vega-Guzman, J.; Kara, A.H.; Khan, S.; Triki, H.; Gonzalez-Gaxiola, O.; Moraru, L.; Georgescu, P.L.; Alghamdi, A.A. Optical solitons and conservation laws for the concatenation model: Undetermined coefficients and multipliers approach. Optik, 2022; Submitted. [Google Scholar]
- Kudryashov, N.A.; Biswas, A.; Borodina, A.G.; Yıldırım, Y.; Alshehri, H. Painlevé analysis and optical solitons for a concatenated model. Optik 2022, 272, 170255. [Google Scholar] [CrossRef]
- Biswas, A.; Milovic, D.; Edwards, M. Mathematical Theory of Dispersion-Managed Optical Solitons; Springer: New York, NY, USA, 2010. [Google Scholar]
- Ekici, M. Stationary optical solitons with complex Ginzburg–Landau equation having nonlinear chromatic dispersion and Kudryashov’s refractive index structures. Phys. Lett. A 2022, 440, 128146. [Google Scholar] [CrossRef]
- Ekici, M. Stationary optical solitons with Kudryashov’s quintuple power law nonlinearity by extended Jacobi’s elliptic function expansion. J. Nonlinear Opt. Phys. Mater. 2023, 32, 2350008. [Google Scholar] [CrossRef]
- Sonmezoglu, A. Stationary optical solitons having Kudryashov’s quintuple power law nonlinearity by extended G/G-expansion. Optik 2022, 253, 168521. [Google Scholar] [CrossRef]
- Gonzalez-Gaxiola, O.; Biswas, A.; Moraru, L.; Alghamdi, A.A. Dispersive optical solitons with Schrödinger-Hirota equation by Laplace-Adomian decomposition approach. Optik, 2022; Submitted. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.-Y.; Biswas, A.; Yıldırım, Y.; Moraru, L.; Moldovanu, S.; Alshehri, H.M. Optical Solitons for a Concatenation Model by Trial Equation Approach. Electronics 2023, 12, 19. https://doi.org/10.3390/electronics12010019
Wang M-Y, Biswas A, Yıldırım Y, Moraru L, Moldovanu S, Alshehri HM. Optical Solitons for a Concatenation Model by Trial Equation Approach. Electronics. 2023; 12(1):19. https://doi.org/10.3390/electronics12010019
Chicago/Turabian StyleWang, Ming-Yue, Anjan Biswas, Yakup Yıldırım, Luminita Moraru, Simona Moldovanu, and Hashim M. Alshehri. 2023. "Optical Solitons for a Concatenation Model by Trial Equation Approach" Electronics 12, no. 1: 19. https://doi.org/10.3390/electronics12010019
APA StyleWang, M.-Y., Biswas, A., Yıldırım, Y., Moraru, L., Moldovanu, S., & Alshehri, H. M. (2023). Optical Solitons for a Concatenation Model by Trial Equation Approach. Electronics, 12(1), 19. https://doi.org/10.3390/electronics12010019








