Abstract
In the past decade, the application of deep reinforcement learning (DRL) in portfolio management has attracted extensive attention. However, most classical RL algorithms do not consider the exogenous and noise of financial time series data, which may lead to treacherous trading decisions. To address this issue, we propose a novel anti-risk portfolio trading method based on deep reinforcement learning (DRL). It consists of a stacked sparse denoising autoencoder (SSDAE) network and an actor–critic based reinforcement learning (RL) agent. SSDAE will carry out off-line training first, while the decoder will used for on-line feature extraction in each state. The SSDAE network is used for the noise resistance training of financial data. The actor–critic algorithm we use is advantage actor–critic (A2C) and consists of two networks: the actor network learns and implements an investment policy, which is then evaluated by the critic network to determine the best action plan by continuously redistributing various portfolio assets, taking Sharp ratio as the optimization function. Through extensive experiments, the results show that our proposed method is effective and superior to the Dow Jones Industrial Average index (DJIA), several variants of our proposed method, and a state-of-the-art (SOTA) method.
1. Introduction
Portfolio trading aims to allocate resources in a way that maximizes returns while minimizing risk. Many prior studies have employed reinforcement learning (RL) algorithms to address a variety of stock trading problems and have proved both the potential and promising results of deep reinforcement learning (DRL) in financial markets [1,2,3,4,5].
RL combines the tasks of “forecasting” and “portfolio construction” into one integration step so as to closely combine the machine learning problem with the objectives of investors. The process that traders use to invest in stocks to maximize profits is the same as how the RL agents interact with the environment to obtain rewards and maximize the cumulative reward. RL can also easily consider important constraints such as transaction cost [6], market liquidity, and investors’ risk aversion.
However, the existing methods have some common limitations. When confronted with a complex market environment, agents frequently struggle to find the optimal strategy. Li [7] has proved that using feature preprocessing in a trading algorithm can obtain higher transaction performance. More crucially, the stock market will be influenced by political, economic, and natural disasters (such as COVID-19); in other words, the stock market has externalities, and the impact of external shocks will cause the stock price to rise or fall abnormally.
In this paper, we employed the autoencoder (AE) network in the RL framework. AE has been used for noise resistance training in many fields to improve robustness. Qi et al. [8] proposed a robust stacked autoencoder (R-SAE) based on maximal correntropy criteria (MCC). The proposed method outperforms other machine learning methods on the MNIST benchmark dataset in noise-proof ability. Li et al. [9] introduced a deep sparse autoencoder with lossless and nonnegative constraints, which increases the model’s robustness and the performance of anti-interference. Therefore, we propose a novel anti-risk portfolio trading system based on DRL. The trading system consists of a stacked sparse denoising autoencoder (SSDAE) and an actor–critic based RL agent. The noise resistance training is performed on the financial data to extract the robust features, and the actor–critic algorithm is based on advantage actor–critic (A2C) and consists of two networks in which the actor network learns and implements the investment policy, which is then evaluated by the critic network to determine the best action plan by continuously redistributing various portfolio assets to maximize the expected return on investment. All the sample data for this study were collected from Yahoo Finance. We tested our method on 24 Dow Jones stocks with sufficient liquidity by comparing different state preprocessing methods. Experimental results show that the proposed method is effective and better than a SOTA algorithm. The contributions of this work are three-fold: (1). we propose a state preprocessing network that employs SSDAE to perform anti-noise training on stock data to extract the robustness features so as to improve the robustness of agent transaction decision making; (2). we have performed extensive experiments to test the performance of our proposed method and demonstrate that it outperforms other state preprocessing methods, such as PCA&DWT [7], LSTM-AE [10], RSAE, Dow Jones Industrial Average index (DJIA), and a SOTA method [11]; and (3). the experimental results show that our proposed method performs better in balancing benefits and risks and demonstrates the importance of state preprocessing in reinforcement learning trading.
2. Preliminary
2.1. Problem Setup
We formulate the portfolio trading process as a generalized Markov decision process (MDP), and the stock market state was reconstructed using the autoencoder technology. MDP is defined as the tuple , where is the state space, is the action space, represents the probability of selecting action from to the next state , and represents the direct reward of taking action at state s and arriving at the new state . The goal of RL agent is to maximize the cumulative income while controlling the transaction cost and risk cost.
The goal was to find an optimal policy :
where indicates the distribution of state–action pairs that the RL agent will encounter under the control of policy .
For each policy , you can define its corresponding Q-value function:
2.1.1. State Space
The state space of our trading environment consisted of four parts []. Each letter is defined as follows:
- ∈ :available balance at current time step t.
- ∈ : shares owned of each stock at current time step t.
- ∈ : close price of each stock at current time step t.
- ∈ : encoding features at current time step t.
2.1.2. Action Space
The agent’s job in the portfolio trading problem is to figure out how much of each stock to buy and sell. We do not enable investors to short assets in our action space; we do not allow investors to borrow assets and then return them in the future; we do not allow investors to borrow assets and then return them in the future. For a single stock, our action space was defined as , where k and −k represent the number of shares we can buy and sell, and . is a predefined parameter that sets the maximum number of shares for each buying action; the action space was normalized to , which also means that our action space was continuous, and after the action selection of each state, we executed the sell action first and then the buy and hold action.
2.1.3. Reward Function
The reward function is the change in portfolio value caused by action in states and .
where denotes the portfolio values at t + 1 and t, respectively. The portfolio value is the total stock value plus the balance, and is the transaction cost.
The reward function can also be set directly to the trade return [12,13], as follows:
where represents the realized logarithmic rate of the trade return in a period of time t, and the length of the period is s.
Each deal entails transaction charges, which come in a variety of forms and are charged differently by different brokers. We assume our transaction cost is . We also use the existing financial technical indicators to trade off the return and risk, such as the Sharpe ratio [1,14,15].
where is the excess return in a period of trading; is the standard deviation of the daily trade return multiplied by 2521/2 (252 is the approximate number of trading days in a year and is the frequently used factor in the financial field), ; is the risk-free rate of return; and is the daily return.
2.2. Trading mode
Assuming that we have $1 million and trade in D stocks, each stock in the portfolio will be bought gradually, and the remaining funds after daily trading will be the balance b.
The trading environment assumptions are:
- The trading volume of the agent is very small compared to the size of the whole market, so the agent’s trades do not affect the state transition of the market environment.
- The liquidity of the market is high enough that the orders can be rapidly executed at the close price.
- The transaction cost is a fixed proportion of the trade volume of the day.
3. Methodology
In this section, we present how we depicted stock markets, an overview of SSDAE, and an optimized method of DRL.
3.1. Depiction of Stock Markets
The stock market has the characteristics of a complex description, being non-stationary, and low signal–to–noise ratio. The key issue in stock trading is to grasp the correct trading moment and perform the correct trading behavior according to the market situation. As for the stock market, the commonly employed data is regular sequences, such as open price, close price, high price, low price, and volume (OHCLV) data. In order to fully describe the market, we added financial technical indicators. The technical indicators are very close to the market, respond quickly to the short-term changes of the market, and are intuitive and clear. The technical indicators that are currently popular in the stock market can be classified into five categories: moving averages, volatility, trend, momentum, and volume. Our initial features consisted of 11 + 5 features selected from the above five categories, as well as OHCLV data. Table 1 shows all the technical indicators we used.

Table 1.
Summary of financial technical indicators.
Simple moving average (SMA) is a fundamental technical indicator that is defined as
where represents the close data over a given time period and n represents the time span.
The exponential moving average (EMA) is a trend-following indicator that emphasizes recent data above historical data. It is defined as an exponentially decreasing weighted moving average as
The moving average convergence divergence (MACD) is an indicator that indicates the difference between a long-term moving average and a short-term moving average. This indicator keeps the advantages of moving averages while also avoiding the generation of erroneous trade signals. MACD can be expressed as follows:
where DEA is the arithmetic mean of DIF over the time span. and EMA is defined in Equation (7).
The Williams percentage range (WPR) is a dynamic technical indicator to judge whether the market is overbought/oversold. WPR is very similar to the random oscillator. The only difference is that the scale of WPR is from top to bottom, while the random oscillator has internal smoothing.
where and represent the maximum value of the highest price and the minimum value of the lowest price in the past n time intervals, respectively.
The relative intensity index (RSI) is a price-following oscillator:
where represents the upward price change at time t, and represents the downward price change at time t.
The commodity channel index (CCI) measures the deviation between commodity prices and their average statistical prices. The higher the index, the higher the price than the average. The lower the price, the lower the average price.
where TP (typical price) represents the typical price, and its calculation formula is ; represents the highest price at time t; represents the lowest price at time t; MD (mean deviation) is the average deviation of TPl and represents the trading volume at time t.
The on-balance volume (OBV) is to quantify the trading volume, make a trend line, cooperate with the stock price trend line, and speculate on the market atmosphere from the change of price and the increase or decrease of trading volume.
where represents the trading volume at time t.
The awesome oscillator (AO) calculates the difference between the simple moving average of phase 34 and phase 5. The simple moving average used is not calculated using the closing price but using the midpoint of each line. The AO is usually used to identify trends or predict possible reversals.
where MEP is median price, and the formula is MEP = (high + low)/2
The force index (FI) is used to indicate the strength of an upward or downward trend. The index measures the strength of bull potential at each increase and bear potential at each decrease.
The true strength index (TSI) is a technical momentum oscillator used to identify trends and reversals. The indicator may be useful for determining overbought and oversold conditions, indicating potential trend direction changes via centerline or signal line crossovers and warning of trend weakness through divergence.
where , r is usually set to 25, and s is set to (12).
3.2. Overview of SSDAE
Raw financial data can only indicate patterns or characteristics of market dynamics to a limited extent, so it is not ideal for direct input to RL agents. However, putting all price data and technical indicators into the state space will lead to complex design and delay. Delay is a key factor in algorithmic trading. Most studies simplify the state space by using only OHCLV data [14]. A better solution is to reduce the dimension through the feature extraction method. Therefore, we propose using an autoencoder network to extract features from raw financial data and encoder features with robustness information. Figure 1 depicts the SSDAE autoencoder network’s structure. indicates the input data of the ith node, and indicates the input data of the kth node of the Nth hidden layer. The arrow in the network represents the connection weight between two adjacent layer nodes.
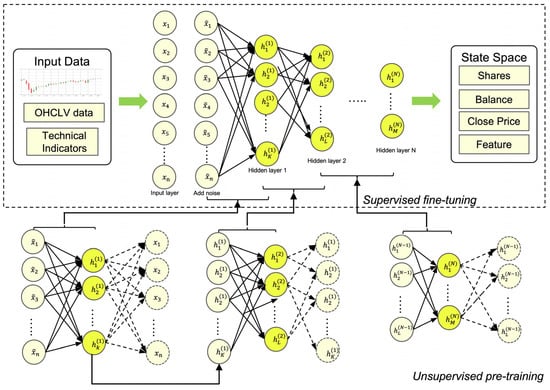
Figure 1.
The structure of SSDAE autoencoder network.
3.2.1. Sparse Denoising Autoencoder (SDAE)
Considering that the stock market is also influenced by external factors such as social networks, politics, and natural disasters (such as COVID-19); in order to make RL agents more robust after training, we naturally introduced denoising autoencoder (DAE)) [15] and sparse autoencoder (SAE) to reconstruct original financial data, the first to eliminate accidental events and the second to minimize external factors.
The Autoencoder (AE) [16] is a type of unsupervised machine learning; the AE can be regarded as a three-layer neural network. The feedforward functions of the AE can be defined as follows:
where is the activation function. In this paper, we use the sigmoid function ; W is the weight matrix; b is the bias vector; and , , , and are initialized with random values.
The AE only relies on the strategy of minimizing reconstruction errors for network training, which may cause the network to learn only the copy of the original input. Considering that the stock market is also influenced by external factors such as social networks, politics, and natural disasters (such as COVID-19), in order to make RL agents more robust after training, we naturally introduced a denoising autoencoder (DAE)) [15] and sparse autoencoder (SAE) to reconstruct original financial data; the first is to eliminate accidental events, and the second is to minimize external factors.
Based on the AE, DAE adds noise to the input layer data (randomly zeroing the input layer nodes) to make the whole encoder network more robust. It passes on the original input vector to noise processing result . The random selection unit was forcibly set to 0 according to a certain proportion, and then used the data , so as to train better anti-noise ability.
The SAE adds conditional restrictions on the AE, . The network units were randomly activated to prevent the encoder from working with a low reconstruction error at each point, which also makes the whole encoder network more robust. is the sparsity parameter (generally a smaller value close to 0). In order to achieve this limitation, the objective function introduced an additional penalty factor, namely relative entropy (Kullback–Leibler divergence), which is a method to measure the difference between two distributions. The principle is shown in:
where KL is expressed in , is the relative entropy between two Bernoulli random variables with mean value. When , , and the size of KL increases with the difference between and increasing monotonically; and when approaches 0 or 1, the relative entropy becomes infinite, so minimizing the penalty factor can make approach .
Given the raw financial training data set , where and denotes the total number of training samples, the SDAE was trained by a backpropagation algorithm to minimize the following sparsity regularized reconstruction loss function:
where is the sparsity term parameter, and λ is the weight decay term parameter.
3.2.2. Stacked Sparse Denoising Autoencoders (SSDAE)
To enhance the learning ability of the autoencoder network, the method of increasing the number of network layers was generally adopted. The error back propagation algorithm was used in the majority of our existing shallow neural networks, including ordinal autoencoder networks. When the number of layers is increased, the propagation error decreases, and the gradient disappearance problem becomes more frequent. This issue was avoided by using a stacked autoencoder. Figure 1 shows the SSDAE network structure of N hidden layers. At present, the SSDAE network still adopts the greedy layer-by-layer training method [16], which mitigates the step dispersion phenomena to a certain extent. That is, the first hidden layer is pre-trained. Then, the output of the first layer is used to pre-train the second layer. This procedure is repeated for the remaining layers. After all layers have been pre-trained, the network used for encoding in each layer is erased, leaving only the decoding network of each layer. Then, using the BP algorithm, all layers are fine-tuned until the network’s ideal parameters are reached. The SSDAE network converts the original input into the nth layer’s extracted features. The SSDAE network’s loss function during the fine-tuning stage is as follows:
where is the weight of the lth layer in the SSDAE. The sparsity term was omitted because the pretrained weights were employed as regularization to our network.
Considering that some studies have focused on the accuracy of AE-predicted and -reconstructed financial sequence data [17,18,19,20,21], and the effectiveness of feature extraction can only be judged according to the results of strategy performance, we ignored the accuracy verification of AE reconstruction data in this paper.
3.3. Optimization via Reinforcement Learning—Advantage Actor–Critic Learning
There are currently only a handful of quantitative studies that employ the actor–critic algorithm. The authors of [11] conducted a comparison of three actor–critical algorithms: proximal policy optimization (PPO), advantage actor critical (A2C), and deep deterministic policy gradient (DDPG). Experimental results indicated that A2C outperforms other algorithms. As a result, this paper employed A2C and implemented it using stable-baselines3 [22]. The framework of our proposed model is described in Figure 2.
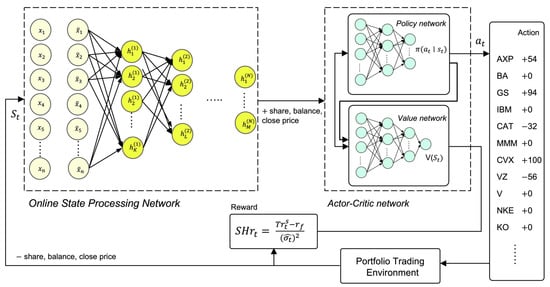
Figure 2.
Overview of the proposed model.
The A2C algorithm [23] proposed by OpenAI is the synchronous variant of Google’s Asynchronous Advantage Actor Critic (A3C) algorithm [24]. It has been demonstrated that A2C performs similarly to A3C but with less implementation and execution complexity. The A2C is different from other actor–critic algorithms in that it improves the policy gradient updates. A2C uses the advantage function instead of the original return in the critical network, which can be used as an indicator to measure the quality of the selected action value and the average value of all actions. In addition to estimating the advantage function, the critic network also calculates the value function. This means that by evaluating how excellent an action is and how good it can be at the same time, the policy network’s large variance is decreased, and the model becomes more robust. In large batch sizes, synchronous gradient updates are more cost-effective, faster, and superior. The A2C’s stability properties make it ideal for stock trading.
We updated our policy based on the value function:
where is the policy network. is the advantage function and can be written as
where is the value expectation of the executor network in a certain state, is the maximum value obtained by selecting action a in a certain state, , and updated policy . The following is evidence of strategy improvement:
According to the greedy strategy of , the new strategy obtained by updating all states must make each state’s value equal to or greater than its value before the update. As demonstrated above, the strategy of RL must be improved after each round of renewal.
4. Experiments
4.1. Dataset Descriptions
We provide a summary of a real-world datasets of our experiments in Table 2. All the data used in this work is available on Yahoo Finance and Google Finance.

Table 2.
Training, validation, and test sets.
4.2. Evaluation Metrics
We used six performance measurement metrics to evaluate the back test results:
- Cumulative return (CR): is the total amount earned by an RL agent during the trading period, excluding transaction costs.
- Maximum drawdown (MDD) [25]: refers to the maximum loss percentage from peak to trough during the trading period.
- Sharp ratio (SR): Sharp ratio [26] is used to measure the rate of return that trading strategies can achieve when confronted with a unit of risk. It is the most commonly used mainstream standardized metric for evaluating portfolio strategies’ performance. Equation (5) has illustrated the calculating formula.
- Calmar ratio (CMR): Calmar ratio [27] is used to measure the risk by using the concept of MDD.
- Alpha: Alpha value is used to measure the excess return obtained by the model relative to the benchmark within the trading range. The greater the alpha value, the more capable it is of generating additional returns in comparison to the benchmark. The calculation process of alpha value is shown in:where is the yield of the model, is the beta value of the model, and is the yield of the benchmark strategy.
- Beta: Beta value is an indicator used to assess the systemic risk of the model relative to the benchmark. If the beta value is greater than one, the volatility of the model is greater than the benchmark; if the beta value is less than one, the volatility of the model is less than the benchmark; and if the beta value is equal to one, the volatility of the model is the same as that of the benchmark. The computation method is illustrated below:where is the covariance, and is the variance of the benchmark strategy.
CR and alpha values are to evaluate the profitability of RL agent separately; MDD and beta values are used to measure the ability of risk control; SR is a risk adjusted return, which can consider the performance, comprehensive income, and risk of the strategy.
4.3. Experimental Details
Our stock portfolio trading environment was based on OpenAI gym [28]. In order to better test the anti-risk performance of strategies, we chose to test the time set, including the time period of the COVID-19 outbreak. Finally, the parameters that needed to be set in advance are summarized in Table 3 and Table 4. To prevent inadequate learning such as local minimum and overfitting, dropout and gradient were applied.

Table 3.
Summary of RL agent’s parameters.

Table 4.
Summary of SSDAE parameters.
4.4. Discussion of Comparison Methods
It was also difficult to compare the results of our proposed method with other studies due to the difference in transaction variety, mode, environment, and RL algorithm. All comparative methods are trained and traded under the same trading environment, trading rules, and parameters. For comparison with our proposed model, in addition to the DJIA index, we selected an advanced portfolio management strategy from the current literature to compare the performance that was an open-source method that does not use feature extraction and improves performance by integrating multiple agents [11]. We also implemented several variants or simplified versions of SSDAE to investigate the roles of several key components: we chose RSAE [29], which lacked a sparse and denoise network compared with our proposed method; LSTM-AE [10], a method of extracting time series information for financial series; and a machine learning method using PCA and wavelet denoising technology [7].
4.5. Results and Analysis
As shown in Figure 3 and Table 5, the SSDAE agent performs best in all measurement indicators. It was observed that our proposed method outperforms the DJIA index and the SOTA method without state preprocessing in all measurement indicators. This demonstrates the advanced nature of our proposed method in RL trading algorithm. Compared with the variants (LSTM-AE, PCA&DWT) or simplified version (RSAE), our method shows that it does better in balancing benefits and risks: In terms of CR and Alpha, the SSDAE agent outperforms other state preprocessing approaches, hitting 88.5% (CR) and 0.28 (alpha). In the beta values and MDD (%), they reached 0.69 and −21.7, respectively. Finally, from the perspective of comprehensive income and risk, there is no doubt that SSDAE agent performs best in terms of SR and CMR, which are 1.37 and 1.71 respectively.
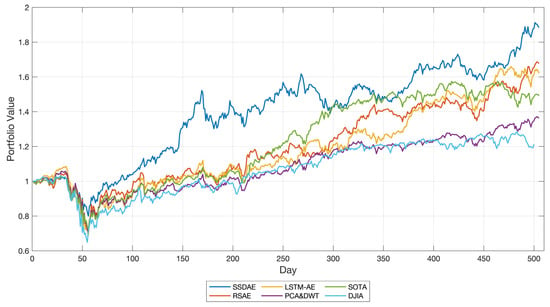
Figure 3.
The cumulative wealth on DJIA.

Table 5.
The results in different RL methods.
The most significant feature of our proposed method was the risk control ability compared with other methods. This shows that extracting robust features from anti-noise training can improve the anti-risk ability of trading strategy. The same as the conclusion of the research on the prediction of financial sequences using an autoencoder method [30], our experiment also found that the use of autoencoder technology can reduce the noise of the features of stock markets. In general, noise resistance training is very important for the RL trading system.
5. Conclusions
In this paper, according to the characteristics of the exogenous nature, complexity, and noise of financial time series data, we proposed an anti-risk portfolio trading system based on DRL. It consists of an SSDAE autoencoder and an advantage actor–critic based RL agent. By comparing the trading performances of different state preprocessing methods, including two variants methods, a simplified version, a SOTA method, and the benchmark DJIA, we found that the impact of anti-noise training on the trading strategy trained by RL agent is positive and promising. Results also illustrate the importance of state preprocessing in reinforcement learning. The advantages of the proposed method are its expansibility, applicability, flexibility, and speed to train, but its interpretability needs further discussion. We will explore using better risk measurement tools such as value-at-risk [31] and conditional-value-at-risk [32] to design newly effective reward functions and, considering the excessive trading volume of the strategy, optimize the transaction cost in the trading process, which is also an issue that needs attention.
Author Contributions
Conceptualization, Formal Analysis, Data Analysis, Data Interpretation, Literature Search, Software, Methodology, and Writing—Original draft, H.Y.; Developed the contextualization of the state of the art, Conceptualization, Funding Acquisition, and Project Administration, J.L.; Resources, Supervision, Validation, and Writing—review and editing, D.T.; Literature Search, Investigation, Writing—review and editing, Proofreading, and Visualization, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [the National Social Science Foundation of China] grant number [18BGL224] and the APC was funded by [the National Social Science Foundation of China] grant number [18BGL224].
Data Availability Statement
The stock price and trading volume data that support the findings of this study are available from Yahoo Finance [32].
Acknowledgments
We acknowledge the financial support from the National Social Science Foundation of China (18BGL224).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Almahdi, S.; Yang, S.Y. An Adaptive Portfolio Trading System: A Risk-Return Portfolio Optimization Using Recurrent Reinforcement Learning with Expected Maximum Drawdown. Expert Syst. Appl. 2017, 87, 267–279. [Google Scholar] [CrossRef]
- Bertoluzzo, F.; Corazza, M. Testing Different Reinforcement Learning Configurations for Financial Trading: Introduction and Applications. Procedia Econ. Financ. 2012, 3, 68–77. [Google Scholar] [CrossRef]
- Deng, Y.; Bao, F.; Kong, Y.; Ren, Z.; Dai, Q. Deep Direct Reinforcement Learning for Financial Signal Representation and Trading. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 653–664. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.G. Reinforcement Learning in Financial Markets—A Survey; FAU Discussion Papers in Economics: Erlangen, Germany, 2018. [Google Scholar]
- Jiang, Z.; Liang, J. Cryptocurrency Portfolio Management with Deep Reinforcement Learning. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; IEEE: New York, NY, USA, 2017; pp. 905–913. [Google Scholar]
- Zhang, Y.; Zhao, P.; Li, B.; Wu, Q.; Huang, J.; Tan, M. Cost-Sensitive Portfolio Selection via Deep Reinforcement Learning. IEEE Trans. Knowl. Data Eng. 2020, 34, 236–248. [Google Scholar] [CrossRef] [Green Version]
- Li, L. An Automated Portfolio Trading System with Feature Preprocessing and Recurrent Reinforcement Learning. arXiv 2021, arXiv:2110.05299. [Google Scholar]
- Qi, Y.; Wang, Y.; Zheng, X.; Wu, Z. Robust Feature Learning by Stacked Autoencoder with Maximum Correntropy Criterion. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; IEEE: New York, NY, USA, 2014; pp. 6716–6720. [Google Scholar]
- Li, W.; Shang, Z.; Gao, M.; Qian, S.; Zhang, B.; Zhang, J. A Novel Deep Autoencoder and Hyperparametric Adaptive Learning for Imbalance Intelligent Fault Diagnosis of Rotating Machinery. Eng. Appl. Artif. Intell. 2021, 102, 104279. [Google Scholar] [CrossRef]
- Jung, G.; Choi, S.-Y. Forecasting Foreign Exchange Volatility Using Deep Learning Autoencoder-LSTM Techniques. Complexity 2021, 2021, 6647534. [Google Scholar] [CrossRef]
- Yang, H.; Liu, X.-Y.; Zhong, S.; Walid, A. Deep Reinforcement Learning for Automated Stock Trading: An Ensemble Strategy. In Proceedings of the First ACM International Conference on AI in Finance, New York, NY, USA, 15–16 October 2020; pp. 1–8. [Google Scholar]
- García-Galicia, M.; Carsteanu, A.A.; Clempner, J.B. Continuous-Time Reinforcement Learning Approach for Portfolio Management with Time Penalization. Expert Syst. Appl. 2019, 129, 27–36. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, Y.; Ye, D.; Zhao, P.; Tan, M. Relation-Aware Transformer for Portfolio Policy Learning. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 4647–4653. [Google Scholar]
- Théate, T.; Ernst, D. An Application of Deep Reinforcement Learning to Algorithmic Trading. Expert Syst. Appl. 2021, 173, 114632. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and Composing Robust Features with Denoising Autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, D.K.; Parida, A.K.; Khuntia, S.S. Financial Market Prediction under Deep Learning Framework Using Auto Encoder and Kernel Extreme Learning Machine. Appl. Soft Comput. 2021, 99, 106898. [Google Scholar] [CrossRef]
- Bi, Q.; Yan, H.; Chen, C.; Su, Q. An Integrated Machine Learning Framework for Stock Price Prediction. In Proceedings of the China Conference on Information Retrieval, Xi’an, China, 14–16 August 2020; Springer: Cham, Switzerland, 2020; pp. 99–110. [Google Scholar]
- Bao, W.; Yue, J.; Rao, Y. A Deep Learning Framework for Financial Time Series Using Stacked Autoencoders and Long-Short Term Memory. PLoS ONE 2017, 12, e0180944. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Chhim, L.; Zheng, B.; Nojima, Y. Stacked Deep Learning Structure with Bidirectional Long-Short Term Memory for Stock Market Prediction. In Proceedings of the International Conference on Neural Computing for Advanced Applications, Shenzhen, China, 3–5 July 2020; Springer: Singapore, 2020; pp. 447–460. [Google Scholar]
- Gündüz, H. Stock Market Prediction with Stacked Autoencoder Based Feature Reduction. In Proceedings of the 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; IEEE: New York, NY, USA, 2020; pp. 1–4. [Google Scholar]
- Ross, S.; Mineiro, P.; Langford, J. Normalized Online Learning. arXiv 2013, arXiv:1305.6646. [Google Scholar]
- Zhang, Y.; Clavera, I.; Tsai, B.; Abbeel, P. Asynchronous Methods for Model-Based Reinforcement Learning. arXiv 2019, arXiv:1910.12453. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Magdon-Ismail, M.; Atiya, A.F. Maximum Drawdown. Risk Mag. 2004, 17, 99–102. [Google Scholar]
- Sharpe, W.F. Mutual Fund Performance. J. Bus. 1966, 39, 119–138. [Google Scholar] [CrossRef]
- Young, T.W. Calmar Ratio: A Smoother Tool. Futures 1991, 20, 40. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Soleymani, F.; Paquet, E. Financial Portfolio Optimization with Online Deep Reinforcement Learning and Restricted Stacked Autoencoder—DeepBreath. Expert Syst. Appl. 2020, 156, 113456. [Google Scholar] [CrossRef]
- Sun, H.; Rong, W.; Zhang, J.; Liang, Q.; Xiong, Z. Stacked Denoising Autoencoder Based Stock Market Trend Prediction via K-Nearest Neighbour Data Selection. In Proceedings of the International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017; Springer: Cham, Switzerland, 2017; pp. 882–892. [Google Scholar]
- Jorion, P. Value at Risk: The New Benchmark for Managing Financial Risk; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Conditional Value-at-Risk for General Loss Distributions. J. Bank. Financ. 2002, 6, 1443–1471. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).