Numerical Solutions of a Differential System Considering a Pure Hybrid Fuzzy Neutral Delay Theory
Abstract
:1. Introduction
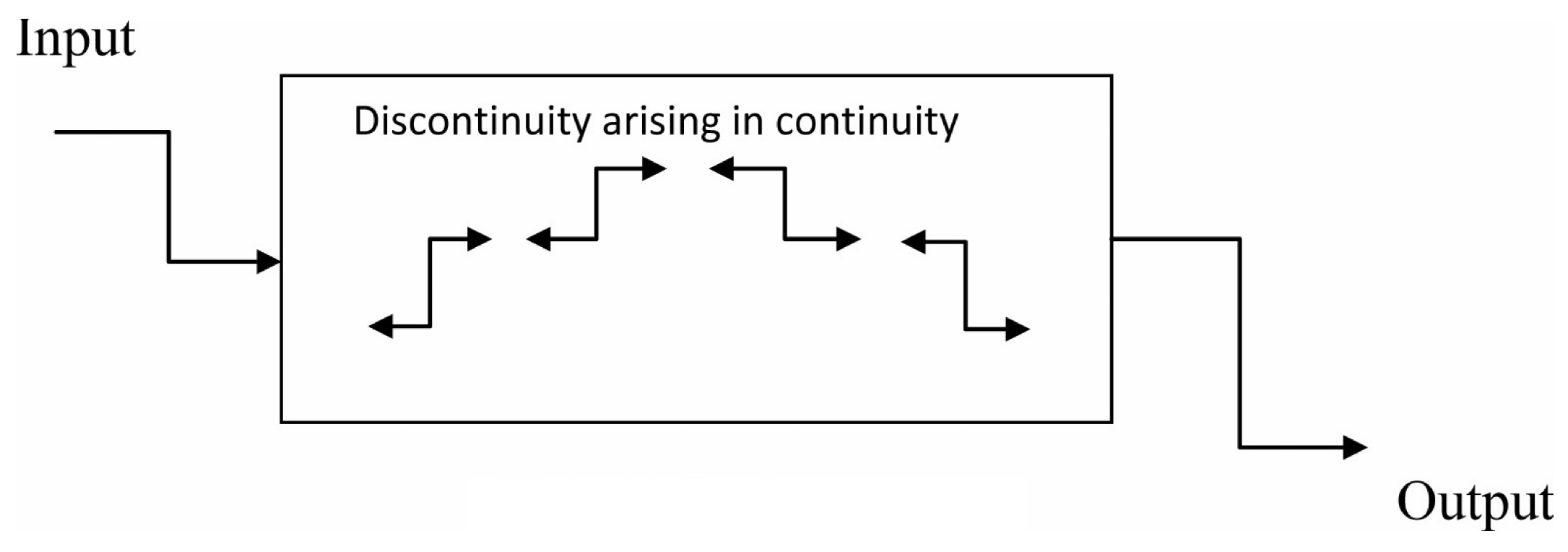
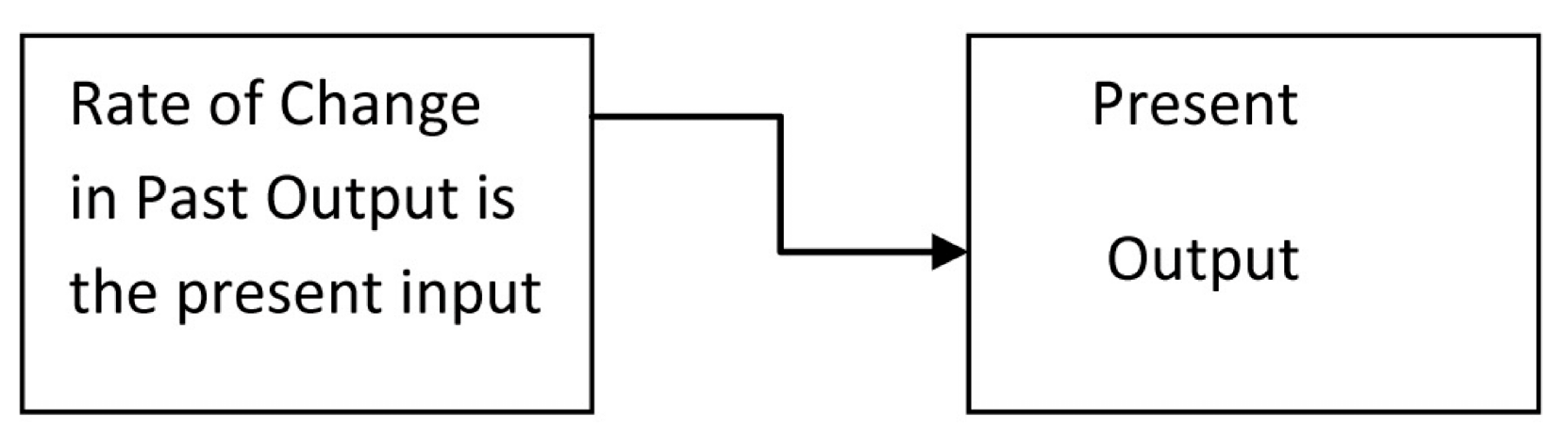
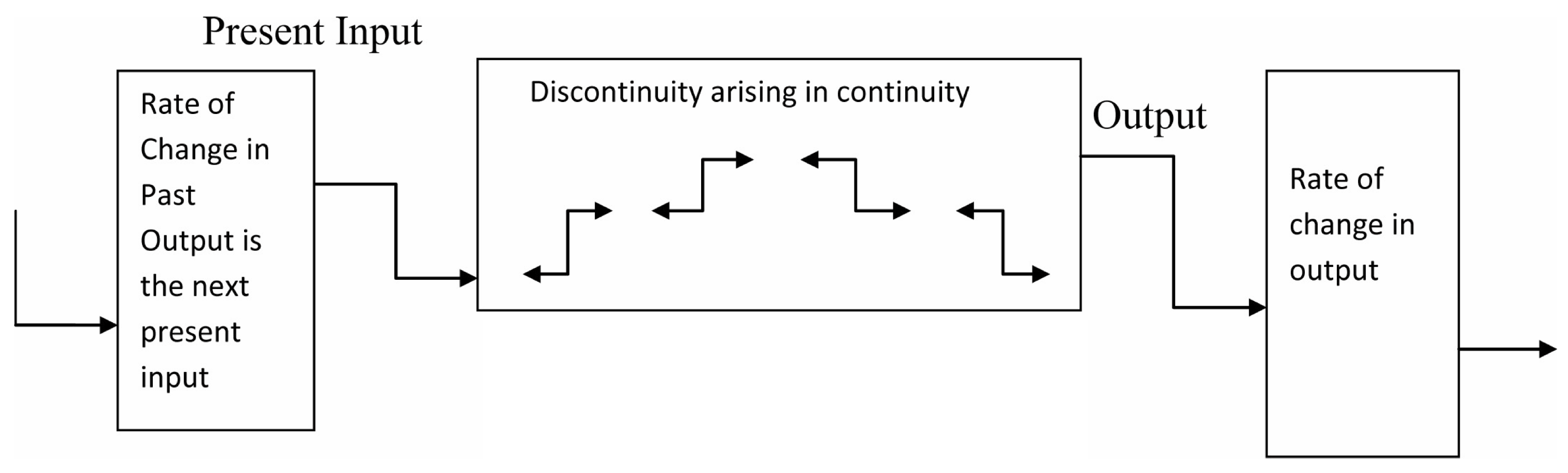
2. Hybrid Fuzzy Neutral Delay Differential Equations
3. The RK-4 Method and Pure Hybrid Fuzzy Neutral Delay Differential Equations
4. Numerical Example
5. Results, Discussion and Conclusions
- We developed hybrid fuzzy neutral delay differential equations and pure hybrid fuzzy neutral delay differential equations as governing equations for new systems based on fuzzy differential equations.
- Many authors have extended the fuzzy differential equations so far to include fuzzy hybrid differential equations and fuzzy delay differential equations. However, in this study, the fuzzy differential equations are extended to combinations of hybrid and delay differential equations, particularly neutral delay differential equations.
- The theoretical details were applied to a numerical example, and both analytical and numerical solutions were found. In this way, we generalized the approximate solutions algebraically.
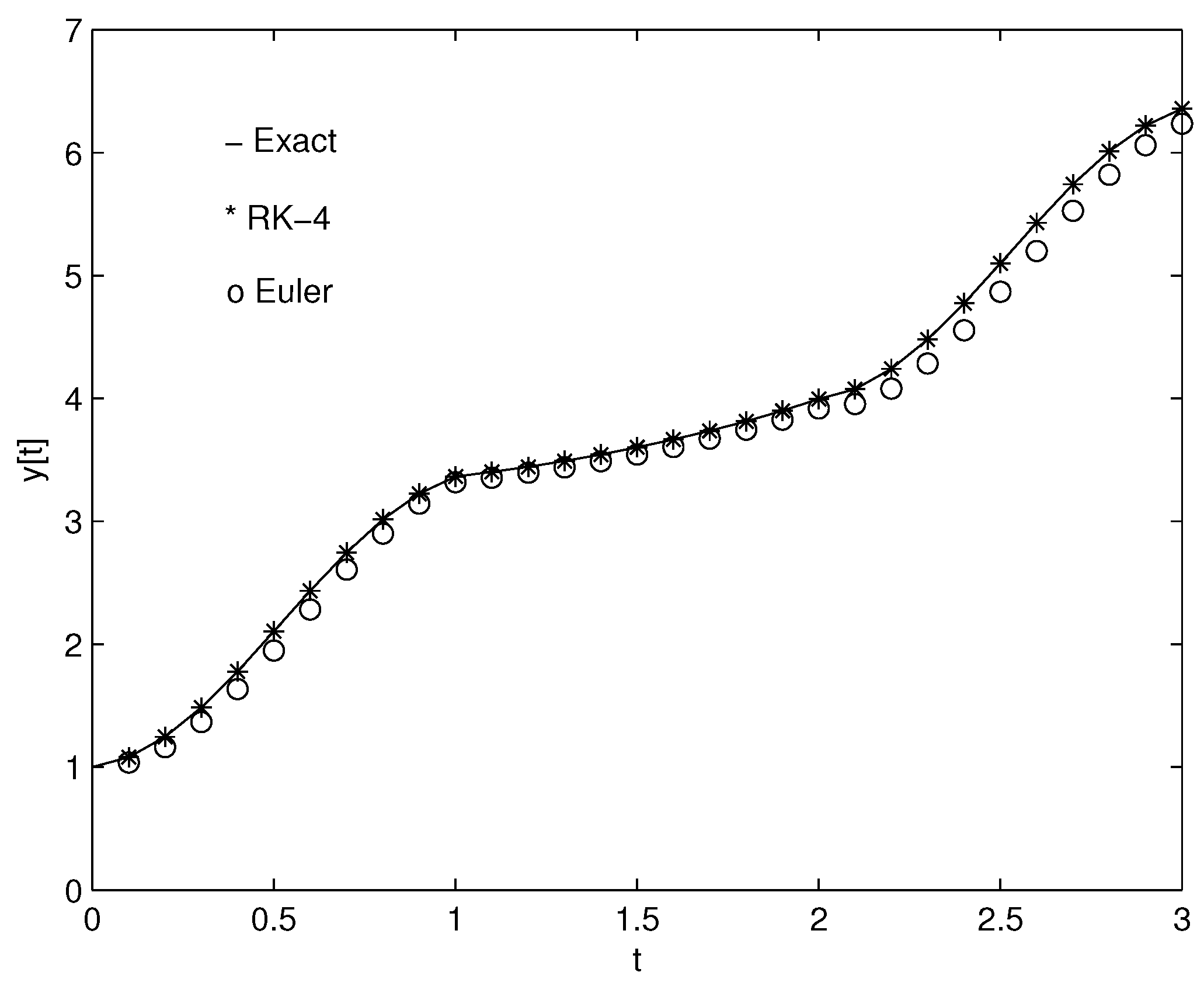
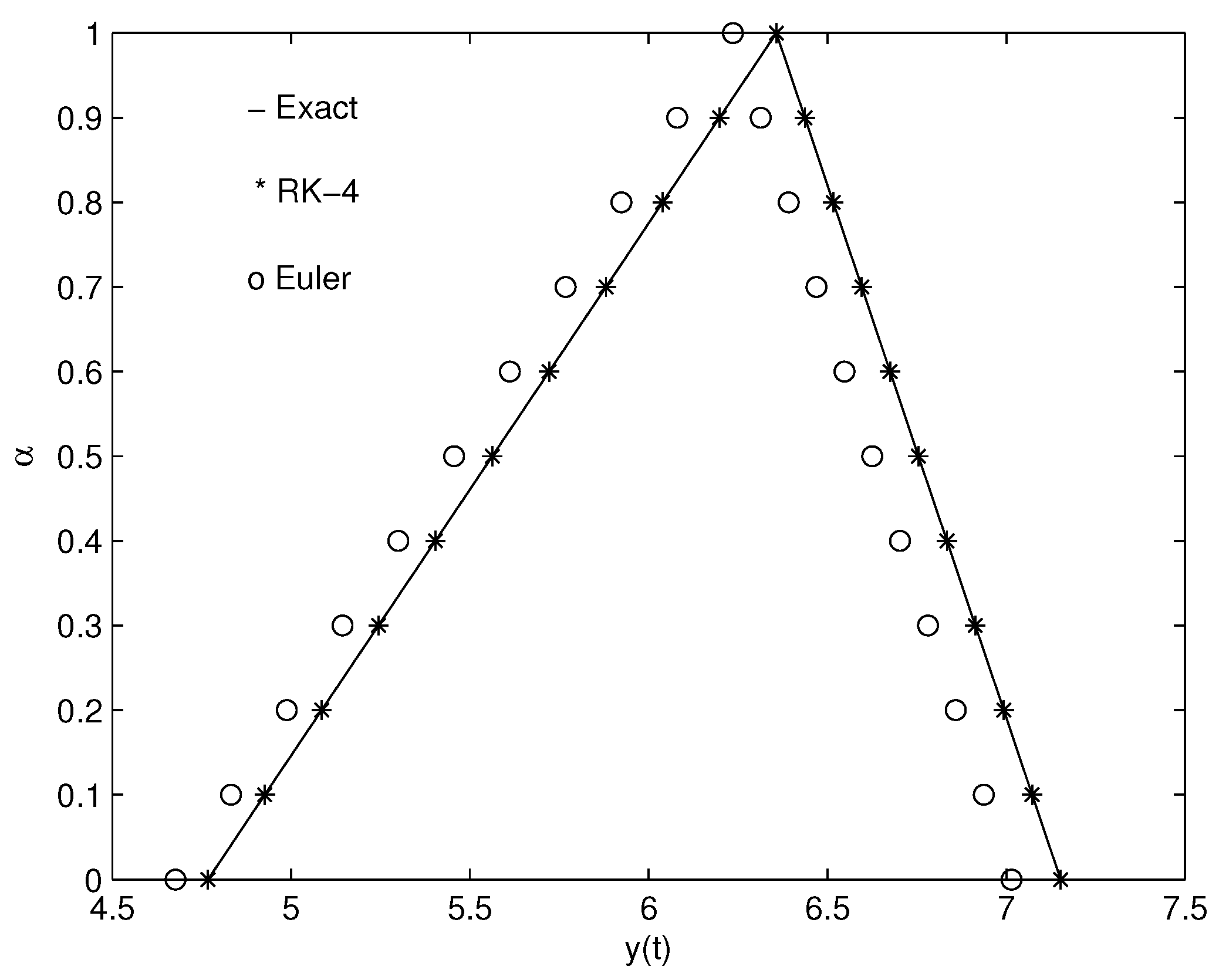
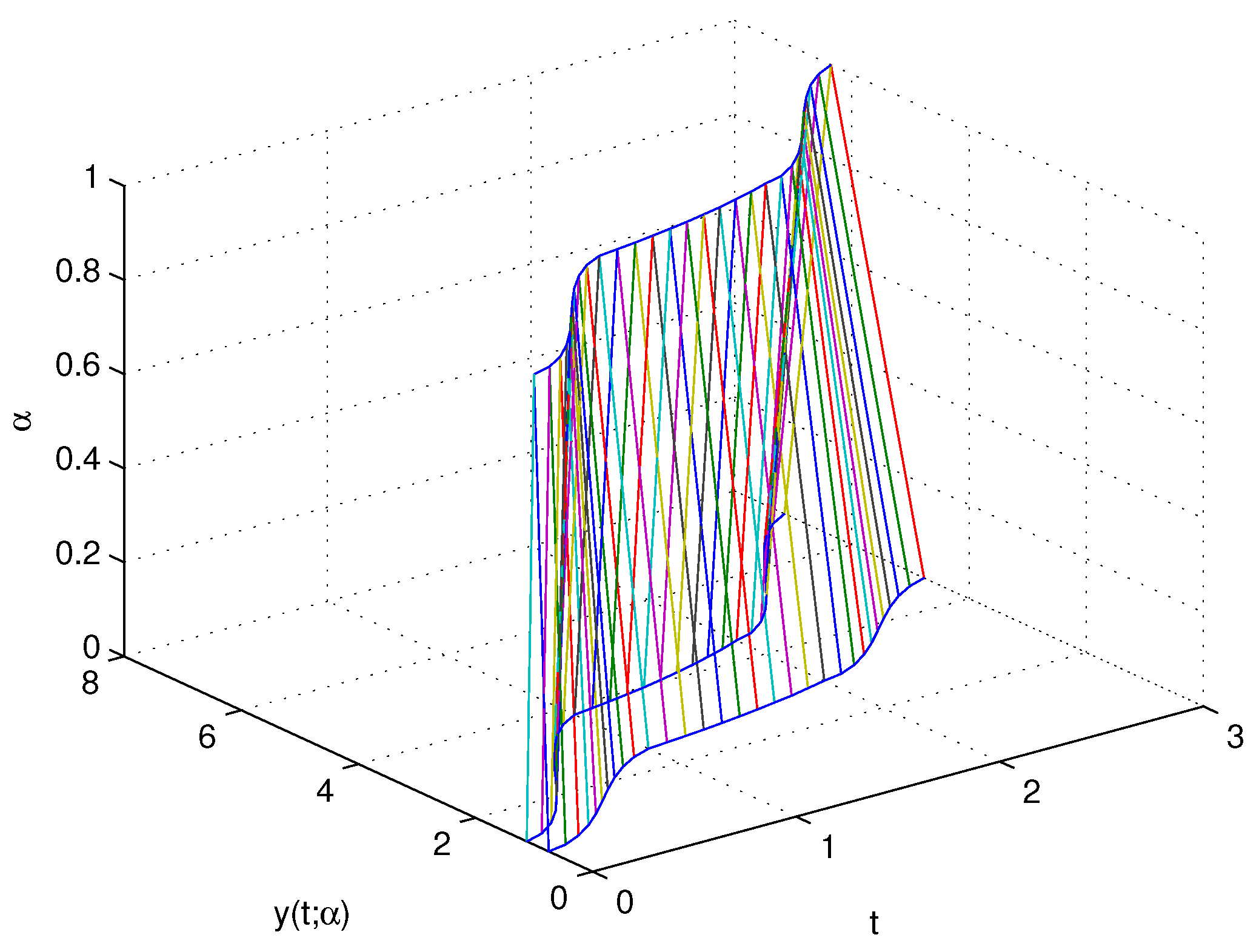
- Though it is dealing with fuzzy solutions, it is enough to provide fuzzy plots. Nevertheless, we provided both non-fuzzy and fuzzy types of solutions. In both the non-fuzzy and fuzzy types of solutions, the coincidence of the exact and approximate solutions was shown graphically. For different values of t, the fuzzy valued plots were provided.
- The most important part of the paper involved using the Runge–Kutta method for solving non-pure (that is, including ) hybrid fuzzy neutral delay differential equations, which we employed to solve a pure form of it (that is, without ).
- We evaluated analytical solutions to the problem that we offered in the study, even though we dealt with numerical answers. The numerical solutions obtained by means of the fourth-order Runge–Kutta method were generalized and mentioned in the problem. Thus, when increasing the order to solve a different problem, the readers themselves can find the numerical solution. For the numerical results, we compared the numerical solutions obtained by means of the fourth-order Runge–Kutta and Euler methods with the exact solutions.
- Note that the fourth-order Runge–Kutta method gives better accuracy than the Euler method. Nonetheless, we compared the result with the Euler method to establish that the system obeys even the lower order methods.
- Though it is a more complicated form of a fuzzy differential equation, we also provided a numerical example to verify the theoretical results.
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, J.; Li, S.; Liu, Y.; Dong, H. A hybrid method for the fault diagnosis of onboard traction transformers. Electronics 2022, 11, 762. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Taghieh, A.; Aly, A.A.; Felemban, B.F.; Althobaiti, A.; Mohammadzadeh, A.; Bartoszewicz, A. A hybrid predictive type-3 fuzzy control for time-delay multi-agent systems. Electronics 2021, 11, 63. [Google Scholar] [CrossRef]
- Doumari, S.A.; Givi, H.; Dehghani, M.; Montazeri, Z.; Leiva, V.; Guerrero, J.M. A new two-stage algorithm for solving optimization problems. Entropy 2021, 23, 491. [Google Scholar] [CrossRef]
- Couri, L.; Ospina, R.; da Silva, G.; Leiva, V.; Figueroa-Zuniga, J. A study on computational algorithms in the estimation of parameters for a class of beta regression models. Mathematics 2022, 10, 299. [Google Scholar] [CrossRef]
- Goetschel, R.; Voxman, W. Elementary fuzzy calculus. Fuzzy Sets Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Allahviranloo, T. Numerical Solution of fuzzy differential equation by Runge-Kutta method. Nonlinear Stud. 2004, 11, 117–129. [Google Scholar] [CrossRef] [Green Version]
- Pereira, A.; Campos, V.; Roveda, J.; Santana, F.; de Medeiros, F. Convergence analysis of an elitist non-homogeneous genetic algorithm with crossover/mutation probabilities adjusted by a fuzzy controller. Chil. J. Stat. 2018, 9, 19–32. [Google Scholar]
- Abbasbandy, S.; Allahviranloo, T. Numerical solution of fuzzy differential equation. Math. Comput. Appl. 2002, 7, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Abbasbandy, S.; Allahviranloo, T. Numerical solution of fuzzy differential equation by Taylor method. J. Comput. Methods Appl. Math. 2002, 2, 113–124. [Google Scholar] [CrossRef]
- Chang, S.L.; Zadeh, L.A. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybern. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Towards fuzzy differential calculus. Differ. Fuzzy Sets Syst. 1982, 8, 225–233. [Google Scholar] [CrossRef]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Ma, M.; Friedman, M.; Kandel, A. Numerical solutions of fuzzy differential equations. Fuzzy Sets Syst. 1999, 105, 133–138. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Pederson, S.; Sambandham, M. The Runge-Kutta method for hybrid fuzzy differential equations. Nonlinear Anal. Hybrid Syst. 2008, 2, 626–634. [Google Scholar] [CrossRef]
- Pederson, S.; Sambandham, M. Numerical Solution of hybrid fuzzy differential equation IVPs by a characterization theorem. Inf. Sci. 2009, 179, 319–328. [Google Scholar] [CrossRef]
- Sambandham, M. Perturbed Lyapunov-like functions and hybrid fuzzy differential equations. Int. J. Hybrid Syst. 2002, 2, 23–34. [Google Scholar]
- Najeeb, S.; Rawi, A.L.; Kadhim Salih, R.; Ali Mohammed, A. Numerical solution of Nth order linear delay differential equation using Runge-Kutta method. Salama Sci. J. 2006, 3, 140–146. [Google Scholar]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford Press: Oxford, UK, 2003. [Google Scholar]
- Jayakumar, T.; Parivallal, A.; Bharathi, D.P. Numerical solutions of fuzzy delay differential equations by fourth order Runge-Kutta Method. Adv. Fuzzy Sets Syst. 2016, 21, 135–161. [Google Scholar] [CrossRef]
- Bharathi, D.P.; Jayakumar, T.; Vinoth, S. Numerical solution of fuzzy pure multiple retarded delay differential equations. Int. J. Res. Advent Technol. 2018, 6, 3693–3698. [Google Scholar]
- Bharathi, D.P.; Jayakumar, T.; Vinoth, S. Numerical solution of fuzzy pure multiple neutral delay differential equations. Int. J. Adv. Sci. Res. Manag. 2019, 4, 172–178. [Google Scholar]
- Bharathi, D.P.; Jayakumar, T.; Vinoth, S. Numerical solution of fuzzy mixed delay differential equations via Runge-Kutta method of order four. Int. J. Appl. Eng. Res. 2019, 14, 70–74. [Google Scholar]
- Bharathi, D.P.; Jayakumar, T.; Vinoth, S. Numerical solution of fuzzy neutral delay differential equations an application of Runge-Kutta method of order four via Runge-Kutta method of order four. J. Emerg. Technol. Innov. Res. 2019, 6, 765–768. [Google Scholar]
- Wang, Q.; Chen, H.; Yuan, C. A note on exponential stability for numerical solution of neutral stochastic functional differential equations. Mathematics 2022, 10, 6. [Google Scholar] [CrossRef]
- Hyder, A.A.; Soliman, A.H. Analytical manner for abundant stochastic wave solutions of extended KdV equation with conformable differential operators. Math. Methods Appl. Sci. 2022, in press. [CrossRef]
- Hyder, A.A.; Soliman, A.H. An extended Kudryashov technique for solving stochastic nonlinear models with generalized conformable derivatives. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105730. [Google Scholar] [CrossRef]
- Hyder, A.A. White noise theory and general improved Kudryashov method for stochastic nonlinear evolution equations with conformable derivatives. Adv. Differ. Equ. 2020, 2020, 236. [Google Scholar] [CrossRef]
- Gao, S.; Hu, J. Numerical method of highly nonlinear and nonautonomous neutral stochastic differential delay equations with Markovian switching. Adv. Differ. Equ. 2020, 2020, 688. [Google Scholar] [CrossRef]
- Cabezas, X.; Martin-Barreiro, C.; Garcia, S.; Delgado, E.; Leiva, V. A two-stage location problem with order solved using a Lagrangian algorithm and stochastic programming for a potential use in COVID-19 vaccination based on sensor-related data. Sensors 2021, 21, 5352. [Google Scholar] [CrossRef]
- Zeidabadi, F.A.; Dehghani, M.; Trojovsky, P.; Hublovsky, S.; Leiva, V.; Dhiman, G. Archery algorithm: A novel stochastic optimization algorithm for solving optimization problems. Comput. Mater. Contin. 2022, 72, 399–416. [Google Scholar] [CrossRef]
- Baleanu, D.; Asad, J.H.; Jajarmi, A. New aspects of the motion of a particle in a circular cavity. Proc. Rom. Acad. A 2018, 19, 361–367. [Google Scholar]
- Baleau, D.; Sajjadi, S.S.; Jajarmi, A.; Asad, J.H. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur. Phys. J. Plus 2019, 134, 2–10. [Google Scholar]
- Baleanu, D.; Asad, J.H.; Jajarmi, A. The fractional model of spring pendulum: New features within different kernels. Proc. Rom. Acad. A 2018, 19, 1–8. [Google Scholar]
- Jajarmi, A.; Baleanu, D.; Sajjadi, S.S.; Asad, J.H. A new feature of the fractional Euler Lagrange equations for a coupled oscillator using a nonsingular operator approach. Front. Phys. 2019, 7, 196. [Google Scholar] [CrossRef] [Green Version]
| Approximate | Exact | |||
|---|---|---|---|---|
| 0.0 | 4.76804606005959 | 7.15206909008938 | 4.76803919566105 | 7.15205879349158 |
| 0.1 | 4.92698092872824 | 7.07260165575506 | 4.92697383551642 | 7.07259147356389 |
| 0.2 | 5.08591579739689 | 6.99313422142073 | 5.08590847537179 | 6.99312415363621 |
| 0.3 | 5.24485066606555 | 6.91366678708640 | 5.24484311522715 | 6.91365683370852 |
| 0.4 | 5.40378553473420 | 6.83419935275208 | 5.40377775508252 | 6.83418951378084 |
| 0.5 | 5.56272040340285 | 6.75473191841775 | 5.56271239493789 | 6.75472219385315 |
| 0.6 | 5.72165527207151 | 6.67526448408342 | 5.72164703479326 | 6.67525487392547 |
| 0.7 | 5.88059014074016 | 6.59579704974910 | 5.88058167464863 | 6.59578755399779 |
| 0.8 | 6.03952500940881 | 6.51632961541477 | 6.03951631450400 | 6.51632023407010 |
| 0.9 | 6.19845987807746 | 6.43686218108044 | 6.19845095435937 | 6.43685291414242 |
| 1.0 | 6.35739474674612 | 6.35739474674612 | 6.35738559421473 | 6.35738559421473 |
| Approximate | Exact | |||
|---|---|---|---|---|
| 0.0 | 4.676726124815156 | 7.015089187222735 | 4.76803919566105 | 7.15205879349158 |
| 0.1 | 4.832616995642328 | 6.937143751809149 | 4.92697383551642 | 7.07259147356389 |
| 0.2 | 4.988507866469501 | 6.859198316395563 | 5.08590847537179 | 6.99312415363621 |
| 0.3 | 5.144398737296671 | 6.781252880981976 | 5.24484311522715 | 6.91365683370852 |
| 0.4 | 5.300289608123844 | 6.703307445568391 | 5.40377775508252 | 6.83418951378084 |
| 0.5 | 5.456180478951015 | 6.625362010154805 | 5.56271239493789 | 6.75472219385315 |
| 0.6 | 5.612071349778188 | 6.547416574741219 | 5.72164703479326 | 6.67525487392547 |
| 0.7 | 5.767962220605360 | 6.469471139327633 | 5.88058167464863 | 6.59578755399779 |
| 0.8 | 5.923853091432531 | 6.391525703914047 | 6.03951631450400 | 6.51632023407010 |
| 0.9 | 6.079743962259703 | 6.313580268500461 | 6.19845095435937 | 6.43685291414242 |
| 1.0 | 6.235634833086875 | 6.235634833086875 | 6.35738559421473 | 6.35738559421473 |
| RK-4 Method | Euler Method | |||
|---|---|---|---|---|
| 0.0 | 0.000006864 | 0.000010297 | 0.091313071 | 0.136969606 |
| 0.1 | 0.000007093 | 0.000010182 | 0.094356840 | 0.135447722 |
| 0.2 | 0.000007322 | 0.000010068 | 0.097400609 | 0.133925837 |
| 0.3 | 0.000007551 | 0.000009953 | 0.100444378 | 0.132403953 |
| 0.4 | 0.000007780 | 0.000009839 | 0.103488147 | 0.130882068 |
| 0.5 | 0.000008008 | 0.000009725 | 0.106531916 | 0.129360184 |
| 0.6 | 0.000008237 | 0.000009610 | 0.109575685 | 0.127838299 |
| 0.7 | 0.000008466 | 0.000009496 | 0.112619454 | 0.126316415 |
| 0.8 | 0.000008695 | 0.000009381 | 0.115663223 | 0.124794530 |
| 0.9 | 0.000008924 | 0.000009267 | 0.118706992 | 0.123272646 |
| 1.0 | 0.000009153 | 0.000009153 | 0.121750761 | 0.121750761 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhandapani, P.B.; Thippan, J.; Martin-Barreiro, C.; Leiva, V.; Chesneau, C. Numerical Solutions of a Differential System Considering a Pure Hybrid Fuzzy Neutral Delay Theory. Electronics 2022, 11, 1478. https://doi.org/10.3390/electronics11091478
Dhandapani PB, Thippan J, Martin-Barreiro C, Leiva V, Chesneau C. Numerical Solutions of a Differential System Considering a Pure Hybrid Fuzzy Neutral Delay Theory. Electronics. 2022; 11(9):1478. https://doi.org/10.3390/electronics11091478
Chicago/Turabian StyleDhandapani, Prasantha Bharathi, Jayakumar Thippan, Carlos Martin-Barreiro, Víctor Leiva, and Christophe Chesneau. 2022. "Numerical Solutions of a Differential System Considering a Pure Hybrid Fuzzy Neutral Delay Theory" Electronics 11, no. 9: 1478. https://doi.org/10.3390/electronics11091478
APA StyleDhandapani, P. B., Thippan, J., Martin-Barreiro, C., Leiva, V., & Chesneau, C. (2022). Numerical Solutions of a Differential System Considering a Pure Hybrid Fuzzy Neutral Delay Theory. Electronics, 11(9), 1478. https://doi.org/10.3390/electronics11091478









