Resource-Efficient Hardware Implementation of Perspective Transformation Based on Central Projection

Abstract

Perspective correction of images is an important preprocessing task in computer vision applications, which can resolve distortions caused by shooting angles, etc. This paper proposes a hardware implementation of perspective transformation based on central projection, which is simpler than the homography transformation method. In particular, it does not need to solve complex equations, thus no software assistance is required. The design can be flexibly configured with different degrees of parallelism to meet different speed requirements. Implemented on the Xilinx Zynq-7000 platform, 2893 Look-up Tables (LUTs) are required when the parallelism is one, and it can process a 20 Hz video with a resolution of 640 × 480 in real time. When the parallelism is eight, it can process 157 Hz video and requires 11,223 LUTs. The proposed design can well meet the actual needs.

1. Introduction

With the development of science and technology, the applications of images and videos in daily life are more and more extensive. However, due to the shooting angle and other issues, there are often deviations between the captured image and the real image, including perspective distortion [1] and barrel distortion [2]. Barrel distortion can be corrected by adding optical lenses [3] or using mathematical algorithms [4]. The perspective distortion is greatly affected by the shooting angle and shooting distance, and the degree of distortion of the captured picture is uncertain; thus, mathematical algorithms are often used to compensate. This paper mainly discusses the perspective transformation of images.

The perspective transformation of images has a wide range of application scenarios. In [1,5], the technology is used for license plate recognition, and the license plate image with perspective distortion is corrected into a rectangle, which increases the accuracy of license plate recognition. The method of perspective transformation is applied to the projector in [6,7,8,9,10,11,12,13,14] to solve the problem of distortion of the projected image caused by the poor placement of the projector. In [15], applying it to the field of architectural engineering imaging measurement is beneficial to better record the important features and functions of the building. In addition, perspective transformation can also be used for the correction of various types of text images; for example, Refs. [16,17] are used for the correction of Chinese and English documents, respectively. This also has some hardware design: Ref. [18] complete the Application Specific Integrated Circuit (ASIC) design to address the optical distortion and perspective distortion present in the microscopic system. Moreover, Refs. [19,20,21] are all implemented on the Field Programmable Gate Array (FPGA), which are used to generate the Bird’s-Eye View (BEV), correction of input video from two cameras, and obstacle detection, respectively.

The transformation of the image includes two parts, coordinate transformation and image interpolation. Coordinate transformation usually uses homography transformation and linear average stretching. The linear average stretch is corrected according to the difference between the representative points of the image before and after the transformation, and its variable range is limited. In comparison, the homography transformation is more widely used. In the papers mentioned above, Refs. [9,18] use linear average stretching, and [1,5,6,7,8,10,11,12,13,14,15,16,17,19,20,21] use homography transformation. However, the homography transformation requires the use of a transformation matrix, but the transformation matrix contains eight unknowns, and its solution is very complicated. Most of the existing schemes use a pure software approach to achieve homography transformation [1,5,6,7,8,10,11,12,13,14,15,16,17]. In addition, a small number of papers present a solution to implement the homography transformation in hardware [19,20,21], but they all require software assistance to calculate the transformation matrix. This paper proposes a hardware design of perspective transformation based on central projection. It does not need to calculate the transformation matrix or software-assisted calculation, and the hardware can independently perform various basic transformations of the image.

The coordinates of the pixel points in the perspective view obtained by coordinate transformation are not necessarily integers. At this time, to calculate the pixel value of the point, an interpolation algorithm is required. Common interpolation algorithms in image processing include the nearest neighbor interpolation [22], linear interpolation [23], bilinear interpolation [24], bicubic interpolation [25] and spline interpolation [26]. The nearest neighbor interpolation is the simplest interpolation algorithm, which directly uses the pixel value of the integer point closest to the current point as the pixel value of the current point. Linear interpolation is an interpolation algorithm widely used in mathematical calculations and computer graphics, which makes full use of the information of other nearby pixels. A more accurate image can be recovered, but a division operation is required, and the resource occupancy and time required are worse than the nearest neighbor interpolation. Both bilinear interpolation and bicubic interpolation are developed on the basis of linear interpolation, and are suitable for image processing with high precision requirements. Relatively speaking, the images obtained by using these two algorithms will be clearer, but the calculation is more complicated, and the hardware implementation is not friendly. Spline interpolation can get a finer picture than bilinear interpolation and bicubic interpolation in some specific cases, but it is also computationally complex. The hardware structure proposed in this paper is compatible with any of the above-mentioned interpolation algorithms, but considering the low resource occupation and real-time performance, this paper only discusses and designs the nearest neighbor interpolation.

In more detail, this paper has made the following contributions:

• The transformation method of the central projection has been improved, and two variable parameters have been added, so that it can achieve a similar effect to the homography transformation.
• The hardware design of perspective transformation based on the central projection transformation is proposed. Compared with the most used homography transformation, it is simpler, and the hardware does all the calculations.
• It has excellent compatibility. According to actual application scenarios, the calculation speed and required resources can be flexibly adjusted by increasing or decreasing the number of pixel calculation modules. When the degree of parallelism is one, it requires 2893 Look-up Tables (LUTs), which can process $640\times 480$ resolution video at 20 Hz, and when the degree of parallelism is eight, it is 11,223 LUTs, which can process 157 Hz video streams.
• The design of this paper is more practical; it can complete many image transformations, such as scaling, translation, tilt correction, BEV and rotation. The specific change implementation methods have been given.

The rest of the paper is organized as follows: Section 2 describes the perspective transformation method based on central projection and nearest neighbor interpolation, the specific hardware design is described in Section 3, the results and discussions are in Section 4, and the conclusion is in Section 5.

2. Perspective Transformation and Interpolation Algorithm

To realize the correction of the image more easily, this paper directly performs the perspective transformation of the image according to the geometric relationship of the image before and after the central projection [27,28].

2.1. Perspective Transformation Based on Central Projection

Assuming that there is a light source S and an arbitrary quadrilateral $\mathit{Q}$, a rectangle $\mathit{R}$ is obtained under the projection of the light source S. A schematic diagram is shown in Figure 1.

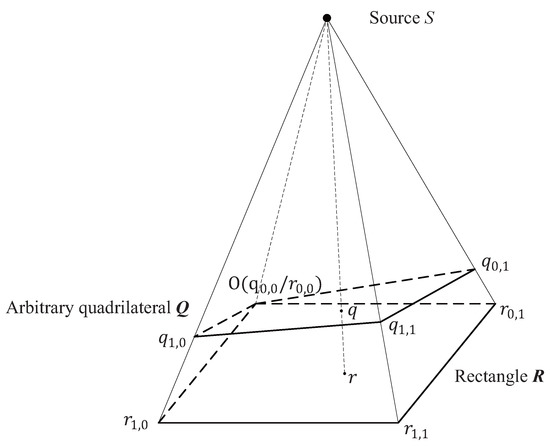
Figure 1. Schematic diagram of the center projection.

It can be observed that each point in the mapped image $\mathit{R}$ can find its corresponding point in the original image $\mathit{Q}$. In order to calculate the value of the pixel in the transformed image, the best way is to find the mapping relationship from $\mathit{Q}$ to $\mathit{R}$.

To simplify the calculation, it is assumed that the four vertices $r_{0,0}$, $r_{0,1}$, $r_{1,0}$ and $r_{1,1}$ of $\mathit{R}$ are represented in the three-dimensional coordinate system as $(0,0,0)$, $(0,1,0)$, $(1,0,0)$ and $(1,1,0)$, respectively. Since the concern is the coefficient of the linear combination of vectors $\overrightarrow{O{r}_{0,1}}$ and $\overrightarrow{O{r}_{1,0}}$ at any point r in the quadrilateral $\mathit{R}$, such a representation does not affect the final result. Any point r in the quadrilateral $\mathit{R}$ can be expressed as

$$\overrightarrow{Or}=x_0\overrightarrow{O{r}_{1,0}}+x_1\overrightarrow{O{r}_{0,1}},$$

(1)

where $x_0$ and $x_1$ are the coefficients of the linear combination of vectors, independent of the coordinate system.

Similarly, any point q in the original quadrilateral $\mathit{Q}$ can be expressed as

$$\overrightarrow{Oq}=y_0\overrightarrow{O{q}_{1,0}}+y_1\overrightarrow{O{q}_{0,1}},$$

(2)

where $y_0$ and $y_1$ are the coefficients of the linear combination of vectors.

The four vertices in the original image $\mathit{Q}$ are coplanar, so satisfy

$$\overrightarrow{O{q}_{1,1}}=a_0\overrightarrow{O{q}_{1,0}}+a_1\overrightarrow{O{q}_{0,1}},$$

(3)

where $a_0$ and $a_1$ are the coefficients of the linear combination of vectors, and the values of both are constants for a given quadrilateral.

In addition, r can also be expressed as

$$\overrightarrow{Or}=\overrightarrow{OS}+t\overrightarrow{Sq},$$

(4)

where t is the multiplication coefficient.

Thus, according to the relationship between the four vertices of the image before and after transformation, four equations can be obtained,

$$\left\{\begin{array}{c}\overrightarrow{O{r}_{0,0}}=(0,0,0)=\overrightarrow{OS}+t_0\overrightarrow{S{q}_{0,0}}=(1-t_0)\overrightarrow{OS}+t_0\overrightarrow{O{q}_{0,0}}\hfill \\ \overrightarrow{O{r}_{0,1}}=(0,1,0)=\overrightarrow{OS}+t_1\overrightarrow{S{q}_{0,1}}=(1-t_1)\overrightarrow{OS}+t_1\overrightarrow{O{q}_{0,1}}\hfill \\ \overrightarrow{O{r}_{1,0}}=(1,0,0)=\overrightarrow{OS}+t_2\overrightarrow{S{q}_{1,0}}=(1-t_2)\overrightarrow{OS}+t_2\overrightarrow{O{q}_{1,0}}\hfill \\ \overrightarrow{O{r}_{1,1}}=(1,1,0)=\overrightarrow{OS}+t_3\overrightarrow{S{q}_{1,1}}=(1-t_3)\overrightarrow{OS}+t_3\overrightarrow{O{q}_{1,1}}\hfill \end{array},\right.$$

(5)

where $t_0$, $t_1$, $t_2$ and $t_3$ are multiplication coefficients.

Since $q_{0,0}$ and $r_{0,0}$ coincide at point O, $t_0=1$. Multiply the left and right sides of Equation (5) by the normal vector of the plane $\mathit{Q}$ and solve it to obtain

$$t_3=t_1+t_2-1.$$

(6)

From Equations (3), (5) and (6), it can be solved

$$\left\{\begin{array}{c}{t}_0=1\hfill \\ t_1=\frac{a_0}{a_0+a_1-1}\hfill \\ t_2=\frac{a_1}{a_0+a_1-1}\hfill \\ t_3=\frac{1}{a_0+a_1-1}\hfill \end{array}.\right.$$

(7)

Substituting Equations (1) and (2) into Equation (4), we obtain

$$x_0\overrightarrow{O{r}_{1,0}}+x_1\overrightarrow{O{r}_{0,1}}=\overrightarrow{Or}=\overrightarrow{OS}+t(y_0\overrightarrow{O{q}_{1,0}}+y_1\overrightarrow{O{q}_{0,1}}-\overrightarrow{OS}).$$

(8)

Bring Equations (5) and (7) into Equation (8),

$$(1-\frac{t{y}_0(1-t_2)}{t_2}-\frac{t{y}_1(1-t_1)}{t_1}-t)\overrightarrow{OS}+(\frac{t{y}_0}{t_2}-x_0)\overrightarrow{O{r}_{1,0}}+(\frac{t{y}_1}{t_1}-x_1)\overrightarrow{O{r}_{0,1}}=(0,0,0).$$

(9)

Because $\overrightarrow{OS}$, $\overrightarrow{O{r}_{1,0}}$ and $\overrightarrow{O{r}_{0,1}}$ are linearly independent, their coefficients are all 0, so

$$(y_0,y_1)=\frac{(a_0{x}_0,a_1{x}_1)}{(a_0+a_1-1)+(1-a_1)x_0+(1-a_0)x_1}.$$

(10)

Knowing the pixel coordinates $(x_0,x_1)$ in the transformed image, the corresponding pixel coordinates $(y_0,y_1)$ in the original image can be calculated from Equation (10). Combined with a reasonable interpolation algorithm, we can restore the transformed image from the original image.

The central projection transformation can be used to correct the distorted image into a rectangle or to perform geometric transformations such as the rotation of the original image, in order to preserve the background outside the distorted subject in the original image and adjust the size of the transformed image. On the one hand, $(x_0,x_1)$ and $(y_0,y_1)$ in Equation (10) can take negative values, which makes the possible pixel values of image $\mathit{Q}$ and $\mathit{R}$ extend outward, and the transformed image can retain the background. On the other hand, parameters $k_w$ and $k_h$ are introduced to control the size of the transformed image $\mathit{R}$, and the values of $k_w$ and $k_h$ need to be less than $0.5$. Assuming that the width of the transformed image is W, the height is H, and the position of the pixel in the image is $(h_r,w_r)$, then the formula for calculating $(x_0,x_1)$ of this point is

$$\left\{\begin{array}{c}{x}_0=(h_r-H\times k_h)/(H\times (1-2\times k_h))\hfill \\ x_1=(w_r-W\times k_w)/(W\times (1-2\times k_w))\hfill \end{array}.\right.$$

(11)

2.2. Nearest Neighbor Interpolation

The nearest neighbor interpolation is the simplest interpolation algorithm. This method is used to search for the nearest integer pixel point to the current pixel point, and directly use the pixel value of this point as the current point pixel value. The advantage of this method is that the hardware implementation is simple.

3. The Hardware Implementation

The structure proposed in this paper is suitable for images of different sizes, and only needs to change $h_r$, $w_r$, H and W in Equation (11) for images of different sizes. Next, an image with the size of $640\times 480$ in $RGB565$ format will be used as an example to introduce the specific design.

The overall hardware structure is shown in Figure 2. Described by Verilog HDL language, it adopts fixed-point arithmetic, and retains nine decimal places during the calculation. First, the pixels in the original image are stored in the memory in the order from left to right and top to bottom, and the memory can be Block Random Access Memory (BRAM), Double Data Rate (DDR) or other memory. Second, according to the input coordinates of the four vertices, $a_0$ and $a_1$ are calculated by Equation (3), and the vertex coordinates can be the vertices of the distorted subject or the manually inputted coordinates. Third, determine the parallelism. The parallelism of this paper refers to the number of groups of $y_0$ and $y_1$ calculation modules and interpolation modules, and the parallelism of n means that there are n groups participating in the computation at the same time. As the parallelism increases, the throughput of the design increases and the required hardware resources also increase; for every doubling of the parallelism, the throughput basically doubles. This method can meet the needs of different application scenarios. To complete the calculation correctly, at least one group is required, and the maximum number of groups cannot exceed the number of clock cycles required by the $y_0$ and $y_1$ calculation modules and the interpolation module. This is because it is necessary to ensure that the generation time difference of the addresses of two adjacent valid pixel points is greater than or equal to one clock cycle. Fourth, the pixel positions in the transformed image are sequentially assigned to the parallel $y_0$ and $y_1$ calculation modules; use Equation (11) to obtain $x_0$ and $x_1$, and then use Equation (10) to obtain $y_0$ and $y_1$. Finally, use an interpolation algorithm to calculate the coordinates of the pixel closest to the point, and then read the pixel value from memory. In the specific hardware design, we also use some techniques to reduce the hardware cost [29,30], including optimizing the calculation process to reduce the number of adders and multipliers, as well as multiplexing the dividers that require large resources; the specific optimization will be introduced in detail below.

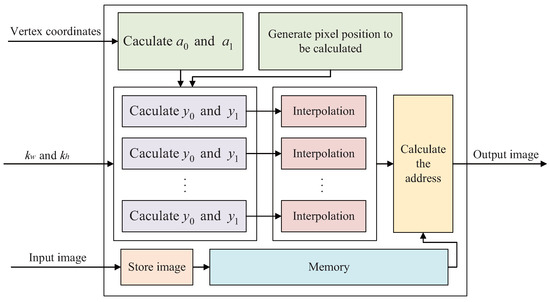
Figure 2. The overall hardware structure of perspective transformation.

3.1. Caculate $a_0$ and $a_1$

The values of $a_0$ and $a_1$ are determined by Equation (3), assuming that the $\overrightarrow{O{q}_{1,0}}$ direction is the x axis, and the $\overrightarrow{O{q}_{0,1}}$ direction is the y axis. The coordinates of the four points $q_{0,0}$, $q_{0,1}$, $q_{1,0}$ and $q_{1,1}$ are expressed as $(c_{1x},c_{1y})$, $(c_{2x},c_{2y})$, $(c_{3x},c_{3y})$ and $(c_{4x},c_{4y})$ respectively, then

$$\left\{\begin{array}{c}(c_{4x}-c_{1x})=a_0(c_{3x}-c_{1x})+a_1(c_{2x}-c_{1x})\hfill \\ (c_{4y}-c_{1y})=a_0(c_{3y}-c_{1y})+a_1(c_{2y}-c_{1y})\hfill \end{array}.\right.$$

(12)

Let $x_{10}=c_{3x}-c_{1x}$, $y_{10}=c_{3y}-c_{1y}$, $x_{01}=c_{2x}-c_{1x}$, $y_{01}=c_{2y}-c_{1y}$, $x_{11}=c_{4x}-c_{1x}$, $y_{11}=c_{4y}-c_{1y}$, then it can be solved by Equation (12)

$$\left\{\begin{array}{c}{a}_0=\frac{y_{01}{x}_{11}-x_{01}{y}_{11}}{y_{01}{x}_{10}-x_{01}{y}_{10}}\hfill \\ a_1=\frac{x_{10}{y}_{11}-y_{10}{x}_{11}}{y_{01}{x}_{11}-x_{01}{y}_{11}}\hfill \end{array}.\right.$$

(13)

From Equations (12) and (13), directly calculating $a_0$ and $a_1$ from four vertex coordinate values requires 8 multipliers, 10 subtractors and 2 dividers. In order to reduce the hardware cost, on the one hand, the calculation process can be optimized. It is noted that the denominators of the two formulas in Equation (13) are the same, so two multipliers and one subtractor can be reduced. On the other hand, the values of $a_0$ and $a_1$ only need to be calculated once when performing a perspective transformation on an image, and the latency has little impact on throughput. Therefore, the method of time division multiplexing is used to calculate the two divisions separately and share a divider. The optimized design is shown in Figure 3, which only needs six multipliers, nine subtractors and one divider to complete the calculation of $a_0$ and $a_1$.

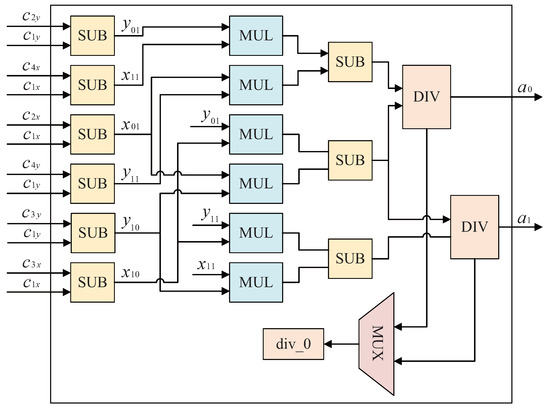
Figure 3. Hardware structure for calculating $a_0$ and $a_1$.

3.2. Generate the Pixel Position to Be Calculated

This module is used to generate the x and y axis coordinates of the pixel to be calculated and the enable signal, and complete the scheduled work. Taking the parallel calculation of two groups of $y_0$ and $y_1$ calculation modules and interpolation modules as an example, the timing diagram is shown in Figure 4.

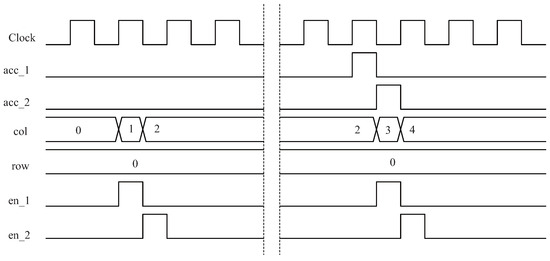
Figure 4. Timing diagram when there are two sets of $y_0$ and $y_1$ calculation modules and interpolation modules.

In the Figure 4, $acc\text{\_}1$ and $acc\text{\_}2$ are inputs, which are the output enable of the interpolation module, and the high is valid, which means that an interpolation operation is completed. $col$ and $row$ are outputs, representing the column and row information of the pixel, respectively. $en\text{\_}1$ and $en\text{\_}2$ are outputs, which represent the input enable signals of the first and second $y_0$ and $y_1$ calculation modules, respectively. At the beginning, $en\text{\_}1$ and $en\text{\_}2$ were pulled high, one after another, and the two $y_0$ and $y_1$ calculation modules started to work successively. After the two successively complete the calculation of pixel points, $acc\text{\_}1$ and $acc\text{\_}2$ are pulled high, then the values of $row$ and $col$ increase, and at the same time, a new round of calculation is enabled again until the complete image is calculated.

3.3. Caculate $y_0$ and $y_1$

To calculate the values of $y_0$ and $y_1$, first obtain $x_0$ and $x_1$ from Equation (11), and then calculate Equation (10). The hardware structure for calculating $x_0$ is shown in Figure 5, and the same structure can also be used to calculate $x_1$. According to Equation (11), a division operation is required for each calculation of $x_0$ and $x_1$, and the delay of the divider is very high. For a certain $k_h$ and $k_w$, the denominator is a fixed value, so in the first operation, the denominator is calculated and its reciprocal is stored in the register. Then, the subsequent calculations can change the division operation into a multiplication operation, which is represented by a dotted line.

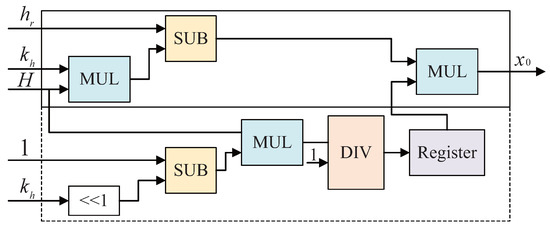
Figure 5. Hardware structure for calculating $x_0$; the dashed part is run only once.

The hardware structure for calculating $y_0$ and $y_1$ is shown in Figure 6. It is worth noting that the bit width of the divider used in Figure 6 is the same as that of the divider used in Figure 5, and both used the same time division multiplexing technique as in Figure 3. $x_0$ and $y_0$ share a divider, and $x_1$ and $y_1$ share a divider; thus, the structures shown in Figure 5 and Figure 6 use a total of two dividers. The values of $y_0$ and $y_1$ are calculated from Equation (10). To increase the operating frequency, avoid executing too much combinational logic in a single clock cycle when calculating the denominator of Equation (10). Therefore, when calculating $a_0+a_1-1$ and $(a_0+a_1-1)+(1-a_1)x_0+(1-a_0)x_1$, two additions are distributed over two clock cycles, and one addition operation is performed in each clock cycle.

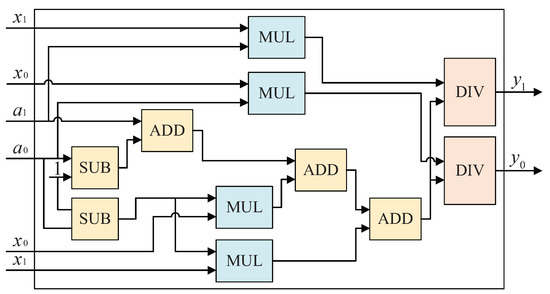
Figure 6. Hardware structure for calculating $y_0$ and $y_1$.

3.4. Interpolation

After obtaining the values of $y_0$ and $y_1$, it is necessary to use Equation (2) to calculate the real coordinates of the pixel in the original image, and then use the interpolation algorithm to obtain the pixel value; a simple and efficient nearest neighbor interpolation is used in this paper. Let the coordinates of the corresponding point q in the original image be $(q_x,q_y)$, by Equation (2)

$$\left\{\begin{array}{c}{q}_x=y_0(c_{3x}-c_{1x})+y_1(c_{2x}-c_{1x})+c_{1x}\hfill \\ q_y=y_0(c_{3y}-c_{1y})+y_1(c_{2y}-c_{1y})+c_{1y}\hfill \end{array}.\right.$$

(14)

The hardware structure is shown in Figure 7. First, use Equation (14) to calculate $q_x$ and $q_y$ in parallel. Note at this step that the values of $(c_{3x}-c_{1x})$, $(c_{2x}-c_{1x})$, $(c_{3y}-c_{1y})$ and $(c_{2y}-c_{1y})$ have been calculated in the structure shown in Figure 3, as $x_{10}$, $x_{01}$, $y_{10}$ and $y_{01}$, respectively. Therefore, the register can be used for buffering, and it is input as a known value when calculating Equation (14), which can reduce four subtractions. The coordinates at this time are not necessarily integers. It is necessary to use an interpolation algorithm to replace its value with the value of the nearest pixel. The value of the pixel on which side it should take is determined according to rounding, so the position of the nearest pixel is related to the value of the fractional part of $q_x$ and $q_y$. Take out the fractional part of $q_x$ and compare it with $0.5$. If it is greater than or equal to $0.5$, the x-axis coordinate of the nearest pixel is the integer part of $q_x+1$, otherwise it is the integer part of $q_x$. The calculation method of the y-axis coordinate is the same.

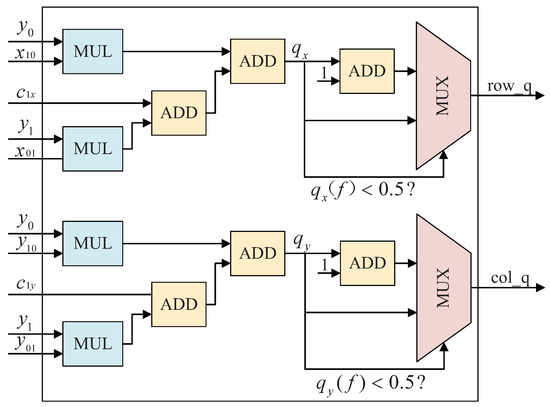
Figure 7. Calculate the coordinates of the nearest pixel using an interpolation algorithm. $q_x\left(f\right)$ represents the fractional part of $q_x$, $q_y\left(f\right)$ represents the fractional part of $q_y$, $row\text{\_}q$ and $col\text{\_}q$ represent the x-axis and y-axis coordinates of the closest pixel, respectively.

3.5. Calculate the Address

To take out the value of the nearest pixel, it is also necessary to calculate its address in the memory. For the original image with a size of $640\times 480$,

$$addr=row\text{\_}q\times 640+col\text{\_}q,$$

(15)

then, the pixel value of the address is taken out from the memory, and this value is the pixel value of the transformed image.

3.6. Timing Diagram of the Overall Structure

Time diagrams can be a good representation of how each module works and its time dependencies [31,32]. In each of the above modules, the structure shown in Figure 3 is only calculated once for an image, and its delay has little effect on the overall calculation speed. In order to ensure the accuracy, the divider of this module is 32 bits wide, so the overall delay is 67 cycles. The bit width of the divider in Figure 5 and Figure 6 is 24 bits, so the delay of the structure in Figure 5 is 27 cycles in the first calculation, and 3 cycles in subsequent calculations, and the delay of the structure of Figure 6 is 28 cycles. The structure shown in Figure 7 has a delay of four cycles. Taking the parallelism of eight as an example, the timing diagram of calculating an image in this design is shown in Figure 8.

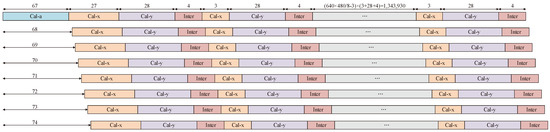
Figure 8. Timing diagram when parallelism is eight. Among them, Cal-a represents calculating $a_0$ and $a_1$ using the structure in Figure 3, Cal-x represents calculating $x_0$ and $x_1$ using the structure in Figure 5, Cal-y represents calculating $y_0$ and $y_1$ using the structure in Figure 6, and Inter represents the interpolation algorithm using the structure in Figure 7.

4. Results and Discussion

The proposed design was packaged as an Intellectual Property (IP) core for testing. On the one hand, the functional verification is carried out, and the achievable functions are introduced and verified using the FPGA development board. On the other hand, the performance of the design of this paper is compared with the existing scheme, including hardware resources and processing speed.

4.1. Functional Verification

First, simulate the hardware circuit to verify the correctness of its function. The original image is converted into a binary file and then input to the hardware circuit. After the simulation is completed, the output binary file is converted into an image, and stitched together with the original image to demonstrate the features of the design in this paper. Then, use the FPGA development board to verify the correctness of the circuit to prove its practicability under real conditions.

4.1.1. Features

Depending on the input, the design of this paper can perform different functions, including scaling, translation, tilt correction, rotation and BEV.

(1)

Scaling

Adjust the value of $k_h$ and $k_w$ to change the size of the transformed image. When their value is greater than 0, it is reduced, and when it is less than 0, it is enlarged. Generally, $k_h=k_w$, otherwise it will cause the picture ratio to be out of balance. The zoom in and zoom out of the picture are shown in Figure 9.

Figure 9. Scaling of the image. (a) is the original image, (b) is the enlarged image, set $k_h=k_w=-0.5$, (c) is the reduced image, and set $k_h=k_w=0.2$.

(2)

Translation

The translation of the image can be achieved by adjusting the coordinates of the four vertices of the original image. Because the original image and the transformed image are relative to each other, if the x axis coordinates of the four vertex coordinates of the original image are increased at the same time, the transformed image will move upward, and if it is reduced, the image will move downward. As the y coordinate increases, the image moves to the left, otherwise it moves to the right. Set $k_h=k_w=0.2$, first increase the x axis coordinates of the four vertices of the original image by 50, and then decrease the y axis coordinates by 100. The transformed images are shown in Figure 10.

Figure 10. Translation of the image. (a) Is the original image, (b) is the transformed image obtained by increasing the x axis coordinate of the original image vertex by 50 and (c) is the transformed image obtained by reducing the y axis coordinate by 100 on the basis of (b).

(3)

Tilt correction

Due to the shooting angle, the black and white grid in the original image is distorted. Input the coordinates of the four vertices of the distorted object in turn, and select the appropriate $k_h$ and $k_w$ values to correct them. Set $k_h=k_w=0$ and $k_h=k_w=0.2$, respectively, and the converted images are shown in Figure 11. It can be observed that when $k_h=k_w=0$, the corrected image has only the target subject and no background, which loses some image elements and does not conform to human habits. After adding $k_h$ and $k_w$, the corrected image can be adjusted more flexibly.

Figure 11. Correction of the image. (a) Is the original image, (b) is the corrected image when $k_h=k_w=0$ and (c) is the corrected image when $k_h=k_w=0.2$.

(4)

BEV

The method of generating BEV is the same as that of tilt correction. It is necessary to input the coordinates of the four vertices of the target to be transformed and select the appropriate values of $k_h$ and $k_w$. The results of BEV are shown in Figure 12.

Figure 12. BEV of the image. (a) Is the original image, (b) is the BEV when $k_h=k_w=0$ and (c) is the BEV when $k_h=k_w=0.2$.

(5) Rotation

The design also implements image rotation by entering specific vertex coordinates of the original image. The size of the image is $640\times 480$, so the vertex coordinates of the rotated image are $(0,0)$, $(0,640)$, $(480,0)$ and $(480,640)$. Assuming that the angle of image rotation is $\theta$, the schematic diagram of rotation is shown in Figure 13, where $\phi =arctan(4/3)$.

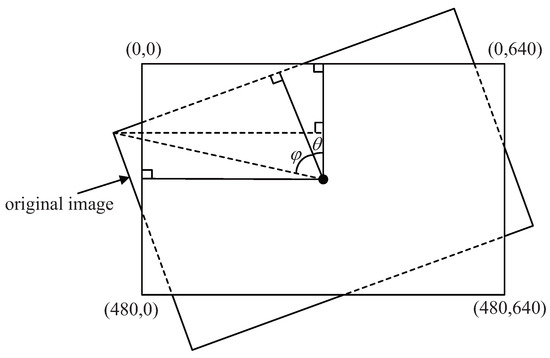
Figure 13. Schematic diagram of image rotation.

Then, the formula for calculating the coordinates of the original image can be obtained,

$$\left\{\begin{array}{c}{c}_{1x}=240-400cos(\phi +\theta )\hfill \\ c_{1y}=320-400sin(\phi +\theta )\hfill \\ c_{2x}=240-400cos(\phi -\theta )\hfill \\ c_{2y}=320+400sin(\phi -\theta )\hfill \\ c_{3x}=240+400cos(\phi -\theta )\hfill \\ c_{3y}=320-400sin(\phi -\theta )\hfill \\ c_{4x}=240+400cos(\phi +\theta )\hfill \\ c_{4y}=320+400sin(\phi +\theta )\hfill \end{array}.\right.$$

(16)

In order to test the design proposed in this paper, an external test circuit is built to implement Equation (16), which uses a Look-up table to store all possible data in the Read Only Memory (ROM). Set the precision of the rotation angle to 1° and its value range to [−179,180], then a total of $8\times 360=2880$ data needs to be stored. These data are stored in ROM as a 12-bit signed number, which requires 54K BRAMs on the FPGA. The eight data corresponding to each angle are stored in the ROM from top to bottom in the order of Equation (16). The address of the first data are

$$add{r}_1=(angle+179)\times 8,$$

(17)

where $angle$ is the angle value to be rotated, and the addresses of other data can be obtained by successively accumulating.

Set the rotation angles to 30° and −135°, respectively, $k_h=k_w=0.1$, and input the coordinates obtained in the Look-up Table into the design of this paper. The results are shown in Figure 14.

Figure 14. Rotation of the image. (a) Is the original image, (b) is the image rotated by 30° and (c) is the image rotated by −135°.

4.1.2. Verify on FPGA

The design of this paper is verified on the FPGA, as shown in Figure 15. In this test environment, the real-time video can be processed, the OV5640 camera is used to capture the image, the DDR is used to cache the image, and the original video and the processed video can be displayed on the screen through the High Definition Multimedia Interface (HDMI) at the same time. In addition, the system is connected with the notebook computer through the Universal Asynchronous Receiver/Transmitter (UART), and the whole system can be controlled by the control terminal running on the notebook computer. The experimental results demonstrate that the design can correct images with perspective distortion in real time.

Figure 15. Test environment for the proposed design.

4.2. Analysis of Performance

The proposed design has greater flexibility. The parallel operation of multiple $y_0$ and $y_1$ calculation modules can be realized by simply modifying the pixel scheduling module. With the increase in the degree of parallelism, the calculation speed increases obviously, and the required resources increase at the same time. We analyzed the performance of 1-way parallel and 8-way parallel, called $Design\text{\_}1$ and $Design\text{\_}8$, respectively, and compared with the existing schemes, as shown in Table 1.

In [18], the input image is divided into grids, then the image is corrected in the grid. Moreover, the hardware design scheme is given, which can solve the optical distortion and perspective distortion to a certain extent. The homography transformation method is used in [19,20,21], which needs to be realized by matrix multiplication, and different transformation matrices can realize different perspective transformations. The result obtained by this method is more in line with the observation habits of the human eye, but the solution of the transformation matrix needs to solve the 8-variable linear equation system, which is extremely difficult for hardware. Thus, they all use software to solve the transformation matrix first, and then use hardware to calculate the corrected image. Specifically, ref. [19] supports video stream input in the Video Graphic Array (VGA) format, and generates the required BEV. In [20], the video stream of 30 frames in Full High Definition (FHD) format is supported, and the parameters are calculated by the software and then passed to the hardware module to realize the correction of the pictures captured by the two cameras. A BEV can be generated and used for obstacle detection using [21]. Compared with the existing design, the design of this paper uses the central projection to realize the perspective transformation, which is in line with the habit of the human eye, and does not introduce complex calculations; thus, the overall required resources are few and no software calculation is required. At the same time, the structure can also flexibly choose the degree of parallelism to achieve different computing speeds. $Design\text{\_}1$ can process 20 frames of VGA video, and $Design\text{\_}8$ can process 157 frames of VGA video. The required resources are also smaller than [18]. The hardware resources required at the same speed are basically the same as [19,20,21], but all calculations are completely implemented by hardware, which is a great advantage.

Table 1. Comparison of the performance of different hardware implementations.

Design	[18]	[19]	[20]	[21]	$\mathit{Design}\text{\_}1$	$\mathit{Design}\text{\_}8$
Function	OD 1 and PT 2	BEV	PT	BEV/PT	BEV/PT	BEV/PT
WSRCP 3	No	Yes	Yes	Yes	No	No
Platform	ASIC	Zynq-7000	Stratix III	Virtex 6	Zynq-7000	Zynq-7000
LUTs	30,000	2280	6987	2983	2893	11,223
Registers	- 4	-	7922	5684	1376	5821
BRAM	-	4	-	0	0	0
DSP	-	37	128	9	8	64
Video Resolution	HD 5 (FHD 6)	VGA 7	FHD	VGA	VGA	VGA
Maximum frequency	140 MHz	100 MHz	74.25 MHz	-	215.8 MHz	212.2 MHz
Maximum frame rate	60 Hz	-	30 Hz	30 Hz	20 Hz	157 Hz

¹ OD: Optical Distortion. ² PT: Perspective Transformation. ³ WSRCP: Whether Software is Required to Calculate Parameters. ⁴ -: Not given in the paper. ⁵ HD: High Definition, the resolution is 1366 × 768. ⁶ FHD: the resolution is 1920 × 1080. ⁷ VGA: the resolution is 640 × 480.

Table 1. Comparison of the performance of different hardware implementations.

Design	[18]	[19]	[20]	[21]	$\mathit{Design}\text{\_}1$	$\mathit{Design}\text{\_}8$
Function	OD 1 and PT 2	BEV	PT	BEV/PT	BEV/PT	BEV/PT
WSRCP 3	No	Yes	Yes	Yes	No	No
Platform	ASIC	Zynq-7000	Stratix III	Virtex 6	Zynq-7000	Zynq-7000
LUTs	30,000	2280	6987	2983	2893	11,223
Registers	- 4	-	7922	5684	1376	5821
BRAM	-	4	-	0	0	0
DSP	-	37	128	9	8	64
Video Resolution	HD 5 (FHD 6)	VGA 7	FHD	VGA	VGA	VGA
Maximum frequency	140 MHz	100 MHz	74.25 MHz	-	215.8 MHz	212.2 MHz
Maximum frame rate	60 Hz	-	30 Hz	30 Hz	20 Hz	157 Hz

¹ OD: Optical Distortion. ² PT: Perspective Transformation. ³ WSRCP: Whether Software is Required to Calculate Parameters. ⁴ -: Not given in the paper. ⁵ HD: High Definition, the resolution is 1366 × 768. ⁶ FHD: the resolution is 1920 × 1080. ⁷ VGA: the resolution is 640 × 480.

5. Conclusions

This paper presents a hardware design for perspective transformation that can be used to process images in real time. First, a perspective transformation method based on a central projection is given, which is also optimized for better hardware implementation. Then, its hardware design structure is proposed, taking many measures to minimize resource consumption and reduce latency. In order to adapt to more situations, a flexible and configurable hardware structure is designed, which can adapt to different degrees of parallelism to improve the processing speed. Finally, the features of the design are presented and compared with existing hardware designs for perspective correction. The design of this paper has obvious advantages in computational complexity because it does not require solving complex equations, and can perform operations such as scaling, translation, tilt correction, BEV, and rotation of the image. In addition, the design can process the images captured by the camera in real time: $Design\text{\_}1$ and $Design\text{\_}8$ can process 20 Hz and 157 Hz video with a resolution of $640\times 480$, respectively.

Future improvements will be to complete the ASIC design, while continuing to optimize resources and speed, and apply it to computer vision processing systems.