An Algorithm to Predict E-Bike Power Consumption Based on Planned Routes

Abstract

E-bikes, i.e., bikes equipped with a small electrical engine, are becoming increasingly widespread, thanks to their positive contribution to mobility and sustainability. A key component of an e-bike is the battery that feeds the drive unit: clearly, the higher the capacity of the battery, the longer the distances that the biker will cover under engine support. On the negative side, the additional weight incurred by the electric components is likely to ruin the riding experience in case the battery runs out of power. For this reason, an integrated hardware-software system that provides accurate information about the remaining range is essential, especially for older or “not-in-shape” bikers. Many e-bikes systems are already equipped with a small control unit that displays useful information, such as speed, instantaneous power consumption, and estimated range as well. Existing approaches rely on machine learning techniques applied to collected data, or even on the remaining battery capacity and the assistance level required by the drive unit. They do not consider crucial aspects of the planned route, in particular the difference in altitude, the combined weight of bike and biker, and road conditions. In this paper, we propose a mathematical model implemented in an application to compute battery consumption, and hence the presumed remaining range, in a more accurate way. Our application relies on external sources to compute the route and the elevation data of a number of intermediate points. We present the mathematical model on which our application is based, we show the implemented application in shape of an app, and we report the results of the experiments.

1. Introduction

E-bikes are bikes equipped with a small electrical engine that supports the bikers in their effort without substituting them in pedaling. They are widely appreciated and are becoming increasingly widespread as they have turned out to be useful not only for the single biker, but also to the environment because of their positive contribution to mobility and sustainability [1].

An e-bike is very similar to a regular bike, but the key difference is the presence of an engine fed by a battery. Clearly, the higher the capacity of the battery the longer the distances that the biker will cover exploiting the engine support. In fact, it is well-known that, to manyBattery Electric Vehicles (BEV) users, the fear of the insufficient battery charge causes a state of real discomfort, known as “range anxiety” [2]. As it happens, e-bikes are more properly hybrid vehicles because the driver can always count on his/her muscle strength. However, without the support of the drive unit, (s)he has to significantly produce more effort due to the weight of the e-bike, which is considerably higher than that of a regular bicycle. This circumstance can completely ruin the riding experience.

To support e-bikers in deciding the distance they can cover, many e-bikes are equipped with a small control unit that displays useful information, such as speed and instantaneous power consumption, and provides an estimation of the remaining distance that can be supported by the engine. Of course, the more this information is accurate, the best is the support to the bikers, especially for older or “not-in-shape” bikers.

Unfortunately, the computation of the range information in current small control units only depends on the bare remaining battery capacity and the assistance level(in e-bikes, the biker can choose “how much” the engine assists her/his pedaling effort by a multiplier factor; this is called “assistance level”) required from the drive unit. This limitation is because such a computation is easy and can be implemented even in simple control units. However, this choice neglects crucial aspects of the planned route (see [3] for an in-depth critique of this aspect), in particular the difference in altitude, the combined weight of bike and biker, and road conditions. For instance, the same remaining battery capacity can lead to different distances in a flat street or in a hill road.

In this paper, we have tackled the problem of estimating battery consumption along a pre-calculated (planned) route. Basing on the classical power model (see, e.g., [4,5,6], we have designed an algorithm for calculating the predicted battery discharge that takes into account various physical parameters and we have developed a (prototype) mobile application that is able to suggest the user the driving options (i.e., assistance level, gear, speed) for the actual power consumption to match the expected levels).

The application is designed to interact with the user as little as possible. General information needed by the algorithm, such as the characteristics of the bicycle (i.e., engine and battery) and of the biker (weight, good/bad shape, maximum effort/cadence sustainable) are requested only when customizing the application.

For the additional information required to feed the mathematical model of power consumption, we adopt different strategies. With regard to the gradient and rolling resistance components, relevant data (i.e., altitude, paved or unpaved surface) are acquired by mapping GPS position onto OpenStreetMap (https://www.openstreetmap.org, last accessed on 18 March 2022) data. The most difficult part of the model involves the computation of the air resistance component, which demands for the determination of air density and wind intensity. There are at least two possible approaches. One possibility is to use the sensors available in the smartphone (humidity and pressure if available). The second option is to acquire data from nearby meteo stations, as already done by a number of mobile apps.

We observe that modern e-bikes are equipped with a number of sensors (speed, cadence, torque, battery temperature) that gather and send data to the control unit. Sensed data, as well as other useful information, such as the current battery charge and the value of the odometer, can in principle be exchanged also with the smartphone. However, decoding the protocol used by the manufacturers is by no means easy and may require dedicated hardware. Here, we adopt the second alternative mentioned above but we set as a goal for further development a “purely software” solution, that we will briefly describe in the Concluding remarks section, based on machine learning techniques (in part inspired by [7]).

To the best of our knowledge, very few works have previously addressed the same problem. In all the cases we have reviewed, the setting was significantly different, along at least one of the three dimensions: goal, approach, and scope (see

Table 1. Related work summary.

Ref.	BEV	Goal	Approach	Scope
[7]	E-bike	Forecast in a given area	Machine learning	Waterloo University area
[8]	Car	Real-world driving energy consumptions	Analytical model of power losses + linear regression	General
[3]	Car	Better range estimation algorithms	Battery model/Control Theory model	Map data
[9]	Car	Reduce anxiety	Remote control with warning messages (state of charge, min-cost route, etc.)	Position based
[10]	Car	Impact of driving style on range	Measurements only	Pre-defined short urban-rural road roads
[11]	Car	Future power requirement	Physical and history based power model	Downloaded road map
[12]	E-bike	Range prediction	Mixed: Bayesian update of deterministic initial estimates	Urban mobility system
[13]	E-bike	Off-line forecast	N/A	Biker and road situations

). In particular, for the few works that address the range estimation problem for e-bikes, the emphasis is on city routes in the context of daily commuting and/or sustainable urban mobility. Our goal instead is to provide information to the biker on the battery consumption in the case of new (and not necessarily urban) routes in a context of cycle tourism. In this scenario, the biker is not able to refer to his/her previous experience to assess whether the current battery level will be sufficient to complete the tour (as it is instead likely to happen in the case of a more or less regular commute).

In the following section, we analyze the literature that we consider relevant to our work. We preliminary observe, however, that ours and the (very few) papers that address the problem of range estimation in e-bikes differ in the respective objectives in the first place. While we focus on tourist cycle routes, characterized by mixed elevation profiles, the works examined in the literature focus essentially on urban commuting (also with the aim of integrating e-bikes with other sustainable means of transport) mainly characterized by flat profiles.

1.1. Related Work

There is a fairly large body of studies that aim at devising accurate algorithms for predicting the driving range of purely electric vehicles, often termed BEV (Battery Electric Vehicles). However, the majority of these works address the range estimation problem for electric cars (see, e.g., [3,8,9,10,11,14]), while very few of them explicitly deal with e-bikes [7,12]. It can be argued that, besides other obvious motivations, a reason for the minor interest in the range of e-bikes is that these are actually hybrid vehicles, which can move (with the muscle force impressed on the pedals) even in case of completely discharged battery. In spite of this, as already outlined in the introductory section, there are a number of other reasons for investigating the range prediction problems also in case of e-bikes.

As the starting point, we can observe that almost all modern e-bikes are equipped with a display unit that shows, in addition to a number of trip data such as speed and distance covered, also the status of battery charge and the corresponding expected remaining range. The latter is however an average value that typically depends only on (and varies with) the currently selected assistance level.

Making a step further, some manufacturers provide online applications for determining the range that can be covered by e-bikes with fully charged batteries. Such applications are in principle much more accurate as they take a large number of elements into account that can influence the duration of the battery. For example, in case of Bosch, in addition to the particular engine and the battery characteristics, the application also takes into account data related to the biker (weight, of course, but also preferred cadence and maximum admissible intensity of effort), road and environmental conditions (presence of climbs, wind intensity, etc.) [13]. In our model, we make use of almost all of these data as well. The main difference with the online applications is that in the latter the range is estimated regardless of the actual planned route.

In Table 1, we report a summary of the related work we have analyzed. For each work we report whether it addresses cars or e-bikes, which is the goal, on which approach it is based, and which is the scope.

One of the few studies that seem relevant to our work is described in [7]. The authors made use of data obtained in the context of the WeBike project of the University of Waterloo [15]. To a fleet of identical e-bikes, they added GPS equipped smartphones and appropriate sensors which were capable of “sampling” position and charge level of the battery. They then organized the data collected from each biker participating in the project (student or university employee) into segments, each one characterized by an appropriate length and a corresponding battery consumption. Then, according to two different models, the authors used the resulting data to make range predictions along trips resulting from the composition of individual segments.

For the first model, they simply determined the average consumption of a trip and, starting from this, they estimated the e-bike range up to the completely discharged battery. The second model was more elaborate and involved calculating the residual charge at the trip destination (supposed to be known). For each segment composing the trip, the model predicted the battery consumption as a linear function of four variables whose value could be determined: from the GPS tracks (speed), from an on-board sensor (battery temperature) or from the data present in the OpenStreetMap maps (road surface and number of stop signs/traffic lights). The unknown coefficients on each section were then determined by applying least-squares linear regression using a portion of the collected segment data as the training set.

The good results obtained in part depend on the following two conditions which do not apply in general, and certainly not to our work. First of all, as pointed out by the authors, the environment where the experimentation took place was essentially a flat landscape. In our experience, in situations where very little assistance is required from the engine unit, the accuracy of the range indications in the (even simple) displays supplied by the manufacturer is already quite high. The state of affairs is rather different in case of hilly or mountain roads; here the differences in strength/fitness among bikers can lead to very different requests to the engine, with really important consequences on the battery discharge and on the covered range.

Secondly, the routes traveled by the participants in the experiment were mainly linked to urban commuting. This made it possible to compose trips using a number of well-known segments (the ones whose data were collected beforehand). However, it is reasonable to expect that, under these circumstance, the biker him/herself will soon be able to know what to expect from his/her bike in terms of performance and range, without external help. The problem always arises when working in new and often unique situations.

In general, however, even simple machine learning techniques (such as the one used in [7]) can be useful to tune the range forecasts according to the biker’s characteristics, i.e., speed and assistance required. This is a solution adopted in some of the works we have cited for the range prediction of BEV cars. In particular, in [11], the authors use a physical power model similar to the one we adopt here. They partition the parameters required by the model in three groups. Those in the first group (C1) are static parameters and include, for instance, the frontal area of the car but also its drag coefficient. These can be considered constant values, which only depend on the vehicle under analysis. The second group (C2) includes dynamic but (relatively) easy to predict parameters. These are essentially the parameters related to the road (slope and rolling resistance) and can be obtained by a pre-downloaded map. The last group (C3) includes dynamic parameters that are difficult to predict and include speed and acceleration. The coefficients of the latter in the physical model are precisely those that, in [11], are estimated using linear regression.

We note that, in our case, the range of speed values for which the engine provides assistance is quite limited. Below 10 Km/h it is even difficult to balance a bike while for the upper bound there are quite strict rules (25 Km/h in Europe, 20 Mi/h in the U.S.). This is important since the power consumed varies with the cube of speed and the strict range helps in narrowing the predictions as well. In any case, this is a parameter whose average value can be determined by history and included in a machine learning model, together with the assistance levels typically required by the biker. The latter is equally difficult to anticipate but plays a significant role in the resulting power drain.

The other study which is relevant to our research is described in [12]. The goal of that paper is to describe the “development of a mobile application oriented to the integration of the e-bike in the mobility process”. This again is a different objective with respect to ours. Nonetheless, range prediction is one of the features made available through the application and this is clearly relevant to us. The approach described in [12] is probabilistic, based on the Naive Bayes (NB) classifier. Starting from a deterministic estimate of the range, which makes use of some readily available information (initial level of battery charge, bike and engine type), the classifier updates the estimate using posterior probabilities. As an example, one such probability is that the average speed was x Km/h given an observed variation of $\Delta R$ Km with respect to the range measured deterministically. Other probabilities involve level of charge, weight of biker, and accumulated altitude. These posterior probabilities are in turn approximated using previously collected profile data.

The peculiarity of this approach is that it does not make use of any complex mathematical model for power consumption, with its corresponding difficulties of accurately measuring some required parameter. As in case of [7], the application context of this work is however urban and the observations made above are still valid. Moreover, with respect to the time of writing of [12], the typical capacity of batteries is significantly higher, easily reaching 500 Wh and even more. This means that a urban round trip is hardly sufficient to drain all the available power.

We conclude this section by pointing out that there are other works that deal with different aspects connected with the spread of e-bikes, from both the technological and of social impact viewpoints. From a more strictly technical perspective, the studies that can impact on the autonomy of an e-bike are interesting for us, even if they do not directly deal with the issue of range estimation. For an up-to-date study we refer the interested reader to the work of Arango et al. [16] and to the references contained therein.

1.2. Organization of the Paper

This paper is organized as follows. Starting from the limitations presented in Section 1.1, we propose a mathematical model of the computation of the remaining distance (Section 2). Then, we describe the application that implements the proposed mathematical model (Section 3) and the results of its exploitation (Section 4). We discuss the results achieved and point out some future work (Section 5). Finally, Section 6 concludes the paper.

2. Materials and Methods

A needed premise to our work is that the proposed mathematical model requires several parameters. Some are simple to find while others can be difficult. We tackle this issue in two ways: first, we enable the choice among different e-bike models, each of which defines all the e-bikes parameters (i.e., the biker must know only the name of his/her e-bike); second, we provide some default values that can be exploited when the actual values are not known.

2.1. Mathematical Model for Power Consumption

In this section we describe the ideal model considered that accounts for the (instantaneous) power $P=P\left(t\right)$ consumed by an e-bike. We stress the fact that the e-bikes we consider in this paper are strictly pedelecs. The drive unit of a pedelec does not deliver any power unless the rider also does. Hence, the equations that we report below describe the power consumed by the combined bike-human system.

To compute P, we must determine the forces opposing the motion, and this in turn reduces to evaluate the impact of road slope, friction and air resistance. Indeed, following, e.g., [5], we can express P as the sum of three contributions:

$$P=P_s+P_f+P_r$$

which we now consider in more details.

• A mass m body placed on a surface with slope s is subject to the gradient resistance force

  $$F_s=g·m·s$$

  (1)

  where g is the gravity acceleration, $g\approx$ 9.81 m/s. Moving the body uphill at speed v consumes power $P_s=F_s·v$.
• If the body is an e-bike, the rolling resistance force is proportional to the total load $w=m·g$ on the wheels

  $$F_f=C_r·m·g$$
  If we always assume optimal tyre pressure, we can consider the factor $C_r$ a constant depending on the bike characteristics only. Then, if the e-bike moves at speed v, the instant power drained due to friction is $P_f=C_r·m·g·v$.
• The force due to air resistance is proportional to the air density $\rho$, the frontal area A exposed by the vehicle (including the rider, in case of a bike) and the square of speed:

  $$F_r=\frac{1}{2}{C}_d·\rho ·A·v^2$$

  where the so-called drag coefficient $C_d$ is usually determined experimentally, as it accounts for very complex dependencies. Once more, if the e-bike moves at speed v, the power consumed due to air resistance is $P_r=\frac{1}{2}{C}_d·\rho ·A·v^3$.

Integrating the above formulas along the given route, even for a piecewise constant speed function, is clearly out of question because there does not seem to be any reasonable way for the biker to accurately measure some of the required parameters, and it would be just as unreasonable to ask him/her to provide them to the app.

In the attempt to simplify the computation, yet providing a good approximation, we limit our approach to bituminous surfaces, e.g., asphalt. For this type of terrain, and optimally inflated tyres, typical values for the the rolling resistance coefficient $C_r$ range from 0.001 and 0.002 (for this and other parameters’ estimation, see [5,6]).

Other simplifying assumptions that appears adequate regard the A and $C_d$ parameters, whose values we assume be fixed along the entire route. Following [5,17] we set average values A = 0.5 m${}^2$ and $C_d=0.7$.

The density value $\rho$ depends on some physical parameters—pressure P, temperature T, and relative humidity H—that in principle can be available to the app. An increasing number of devices have pressure sensors but in general the app can determine reasonable approximations by querying local meteo stations, as a number of specialized apps already do. Once these parameters have been acquired, the density value can be calculated using known formulas (see, for example, [18]).

In order to compute the gradient resistance force we divide the route into sections where we assume the slope is constant. For a given section $S_i$, we consider the departure and arrival altitudes, $H_i$ and $H_f$, respectively, the length ℓ of the section and calculate the average slope using the formula;

$$s=\mathrm{tg}\arcsin \frac{H_f-H_i}{\ell }$$

Actually, note that even for a very steep road (say 10%), the approximation $s\approx \frac{H_f-H_i}{\ell }$ is adequate. In addition, if $s\le 0$ we assume $F_s=0$, otherwise use (1). Note that, in all the above equations, the mass m includes bike, biker, clothes, and possible luggage.

2.2. Computing Power Consumption to Achieve Rider’s Goals

In this section we describe the algorithm we have designed to compute the battery consumption which depends on some additional contraints posed by the user, either implicitly or explicity. The algorithm makes use of the model described in Section 2.1 to compute the expected battery discharge. However, the model is not sufficient to make a reasonable guess. The actual power consumded depends significantly on the assistance level required from the drive unit. A very steep section is like to “force” any biker to ask for maximum assistance but in general the level depends on personal chracteristics, such as the biker being or not being in fit.

With respect to a classic car navigation system, our algorithm thus requires at least an indication of the maximum effort the rider is willing to make (and letting the drive unit do the rest). This can be provided to the app either quantitatively, by specifying a precise Watt value, but also by indicating a level on a qualitative scale, such as low, medium, or high effort. Note that assuming that the user be able to provide a numeric value is not unrealistic here. After all, an e-bike equipped with torque and cadence sensors (which is the case, for instance, for all mid-drive e-bikes) allows the control unit to display the instantaneous power consumed by the biker. After a while, bike riders can then get a grasp on what means to “push”, say, 100 rather than 200 Watts on the pedals.

A second costraint is the maximum power deliverable by the drive unit. Denote it by P. European regulations prescribe $P=0.25$ Kilowatts. However, this is a requirement on the nominal power, i.e., the power the engine is able to deliver continuously without overheating. The peak power is usually significantly higher. A system equipped with typical 15 Ah/36 V battery and controller can provide up to $0.54$ Kilowatts. Our experience with various different units (including Bosh Performance CX, Yamaha PW SE, and Specialized 1.3) is that, if the wheather conditions are not extreme, peak power is a better option to set as the value of P.

A final implicit constraint is speed, which is again severely limited in many european countries. More precisely, by law the engine of an e-bike must not deliver any power when the speed exceeds 25 Km/h (20 Mph in the U.S.). In our current implementation the algorithm tries to maximize speed (and thus reduce time) subject to the maximum effort constraint.

In what follows, we consider a generic e-bike system (i.e., engine and controller) with k levels of assistance. Essentially all commercial systems assign suggestive names to each level (e.g, Eco, Turbo, Sport, etc.) but the point is that they correspond to fractions of the muscle power provided by the biker. For instance, Yamaha PW series systems provide four assistance levels, namely ECO+, ECO, Standard, and High. These correspond, respectively, to numeric values 0.5, 1, 1.9, and 2.8 with the following meaning: for each Watt provided by muscle power, the engine adds 0.5 Watts in ECO+ mode, 1 Watt in ECO mode and so on. In our algorithm we refer to the k levels as $a_1,\dots ,a_k$, in increasing numeric value. In addition, for ease of description, we assume two additional levels, namely $a_0=0$ and $a_{k+1}=\infty$.

Let M denote the maximum human effort (in Watts) set by the biker, P the maximum power that the engine can deliver without overheating, and $S=(S_1,S_2,\dots ,S_n)$ the subdivision of the route into sections. In addition, we let $v_{max}$ denote the maximum allowed speed and $v_{min}$ refer to a minimum acceptable/maintainable speed.

We first present our pseudo-code to estimate the Watt-hours to complete a given section. The output given by algorithm GetWH is actually the pair of values $(W_m,W_b)$, where $W_m$ is the “muscle” power estimate while $W_b$ is the minimum power required from the drive unit of the e-bike. The core of the algorithm is clearly the application of the mathematical model to a prescribed speed value.

GetWH($v,i,M$)

• Using the model for power consumption, compute $W=W\left(v\right)$, the number of Watt-hours required to complete section $S_i$ at speed v.
• Let ℓ be the length of $S_i$.
• Set ${\displaystyle t=\frac{\ell }{v}}$.
• Partition W as the sum $W_M+W_B$, where $W_M=tM$ is the human contribution and $W_B$ is clearly “the rest”, i.e., the energy required from the drive unit.
• Return $W_M,W_B$.

The pseudo-code for the main algorithm follows. For each section $S_i$, TourSchedule first checks that $S_i$ can be complete with the available power $W_m+W_b$, i.e., muscles plus engine. If not, the algorithm emits a warning message and skips to the next section. Otherwise, starting from the admissible max speed, it finds the minimum assistance level $a_j$ that makes it feasible and continues with decreasing speed until $a_j\ne a_{k+1}$. The preliminary check guarantees that a viable speed exists for which this is possible.

Note also that (for simplicity) in the pseudo-code we assume that the input (i.e., electrical) power and the mechanical power at the wheels coincide. This amounts to assuming efficiency 1, which is clearly unrealistic. Efficiency depends on the RPMs, but while the exact efficiency curve varies from engine to engine, its overall shape exhibits broad similarities. The efficiency rises up to about 60–70 RPMs (considering gear reductions), then describes a sort of plateau up to about 90–100 RPMs, with values around 0.75–0.8, and then decreases very rapidly. We use these values for the test setup (see Section 4).

TourSchedule($S=(S_1,S_2,\dots ,S_n),M$)

• Set $W_{TOT}=0$ and $A=\left[\right]$
• For $i=1,2,\dots ,n$

  (a)

  (Feasibility check) $W_m,W_b=\mathtt{GetWH}(v_{min},i,M)$

  (b)

  If $W_b>P$

  • Append $a_{k+1}$ to A
  • Emit a warning message for section $S_i$
  • Continue to next section

  (c)

  Set $v=\max \_\mathrm{speed}$ (i.e., 25 Km/h)

  (d)

  $W_m,W_b=\mathtt{GetWH}(v,i,M)$.

  (e)

  Find assistance level $a_j$ such that $a_j{W}_m\ge W_b>a_{j-1}{W}_m$.

  (f)

  If $a_j=a_{k+1}$ reduce speed by $\delta$, i.e., set $v=v-\delta$, and go to step 2.4

  (g)

  Append $a_j$ to A and set $W_{tot}=W_{tot}+a_j{W}_m$

  (h)

  Optionally determine the shift that better suits the desired cadence.

• Return $W_{tot},A$ (and optionally the sequence of gear shifts)

The time complexity of the algorithm is upper bounded by $c·\max \_\mathrm{speed}·k$, for some constant c. This quadratic complexity is by no means a problem given the typical values of k (number of assistance levels) and the limits on $\max \_\mathrm{speed}$. In any case, the cost could be reduced by introducing a logarithmic search for both speed and assistance levels.

2.3. External Services

As mentioned, in our work we have exploited external services to retrieve information about the path. In particular, we used:

• the OSMDroid (https://osmdroid.github.io/osmdroid/, last accessed on 18 March 2022) library to implement the map visualization in a fully functional and open source alternative to the one that uses Google Maps as default;
• the OpenTopoData (https://www.opentopodata.org, last accessed on 18 March 2022) API to retrieve altitude information of single geographical points;
• the OSMBonusPack (https://github.com/MKergall/osmbonuspack, last accessed on 18 March 2022) library to implement routing and directions;
• the OpenStreetMap Nominatim (https://nominatim.org, last accessed on 18 March 2022) API to request location information about a geographical positions.

3. Implementation

This section describes the developed application (as a smartphone app) that implements proposed the mathematical model previously described, by means of a typical use case.

First of all, the application needs the user to enter her/his data (height, weight and experience level, this last one can also be customized by specifying exactly the user’s power and cadence limits) and her/his preferences (preferred level of effort) as shown in Figure 1a.

It is also required the selection of the owned e-bike model (Figure 1b); if the model is not present in the list, it is possible to set a personalized one (filling in all its characteristics from those relating to the bicycle itself to those of the electronic system as displayed in the Figure 1c, including the e-bike assistance levels).

The data required for a personalized bicycle are:

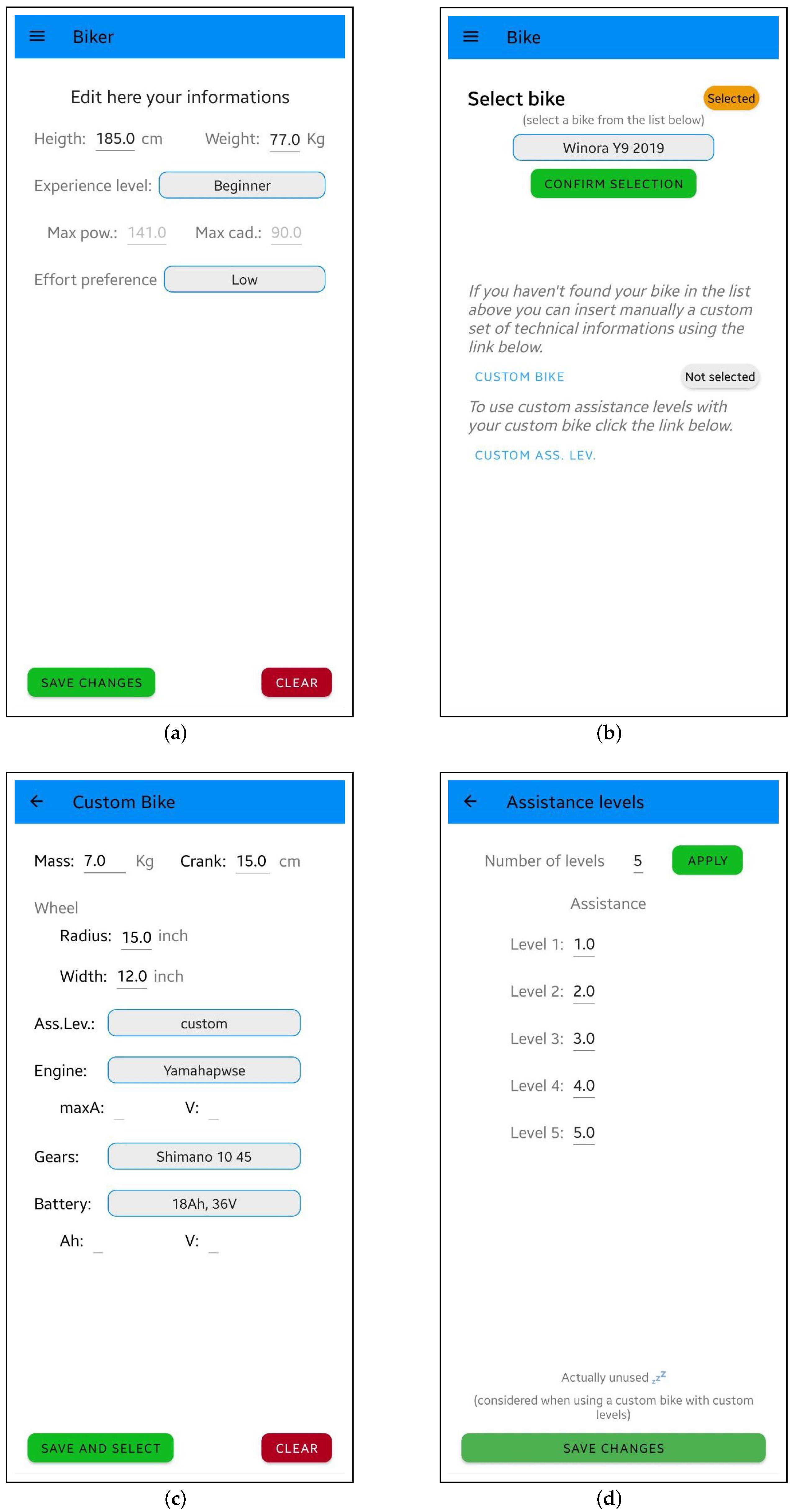
• the mass in kg;
• the length of the pedal in cm;
• the wheel specifying both the radius and the width in inches;
• the mounted motor selected from those available by default or it can be configured by specifying the maximum amperage and voltage;
• the gearbox by selecting the configuration from those available;
• the battery, selected from those available in the system, or configured by specifying amperage and voltage;
• the assistance levels selected from the predefined ones or they can be set in a personalized way in a specific section of the application (Figure 1d).

After filling in the data necessary to use the application, the user is able to use the two main functions:

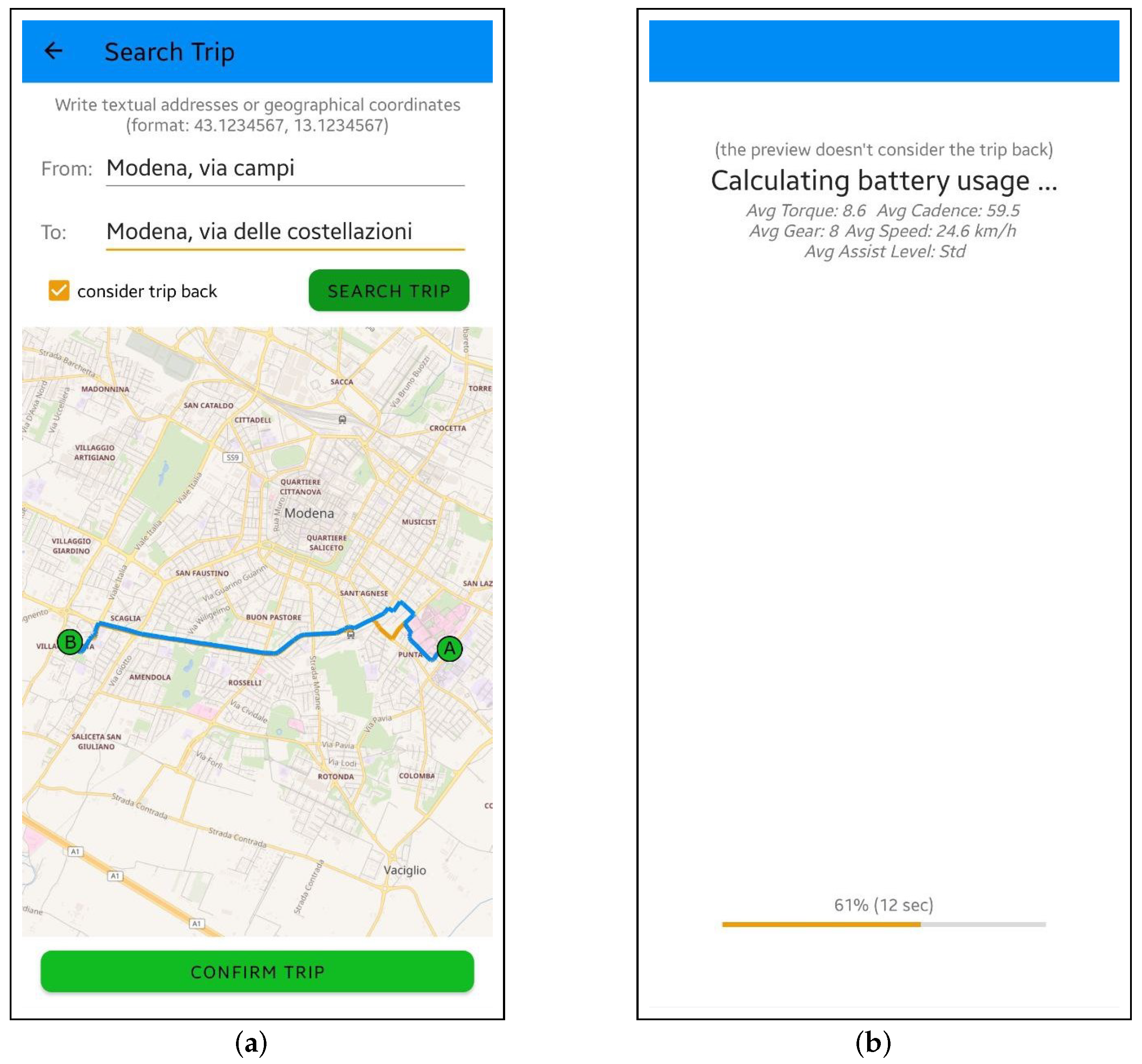
• search for a route, defining a starting point and a destination point for the e-bike ride (in this case it is possible to include the return to the starting point, see Figure 2a);
• search for a circuit, defining a sequence of locations that will represent a polygon to be covered with the e-bike (it is possible to reorder the sequence by holding a location and positioning it where preferred).

In both cases it is possible to interact with the map (Figure 3a) to get more information; when the biker is sure that (s)he has set the route correctly (s)he can start the calculation of the forecasts which may take some time (unfortunately it’s a limitation due to the API used in the project to find the data regarding the height of each geographical point, see Figure 2b).

Once the calculation is complete, it will be possible to view the results in three separate sections:

• a map (Figure 3a) that allows the biker to view the points of interest of our route highlighting any problems with the route (sections considered impossible with the current configurations);
• a page that shows the average details of our track (Figure 3b) for both the outward and return journeys respectively (data such as overall length, average torque, average cadence, battery consumption and so on);
• the list of navigation instructions (Figure 3c) to follow with the computed data relating to each section of the route (data such as the length of the section, the recommended gear, the recommended level of assistance and so on).

The biker can save the results of the forecasts in order to be able to retrieve them at a later time (adapting them, in that case, to a different configuration of preferences); it is also possible to start a navigation mode in real time along the traced path following a series of checkpoints.

The navigation mode is available both for circuits and for round trip routes; in this last case the distinction between the two navigations is made letting the user choose which of the two to follow.

4. Results

We performed experiments using two E-bikes with different drive units:

• A Specialized Turbo Vado 5.0 (2020 model), mounting a Specialized 1.3 engine and equipped with a 604 Wh battery. Using the Mission Control App it is possible to tune the three available assistance levels, often termed as Eco, Trail, and Turbo. The default (preset) numerical values for the three levels are 1.3, 2.9, and 3.8, respectively, which we left unchanged for the experiments. The peak (electrical) power of the engine is approximately 560 W while the torque reaches the remarkable maximum of 90 Nm.
• A Pegasus Premio 10 Lite (2021 model), powered by a 4th Gen. Bosch Performance Line CX and a 625 Wh battery. The four assistance levels (Eco, Tour, Sport, and Turbo) adds 0.6, 1.4, 2.4, and 3.4 times the muscle power provided by the biker, respectively. The engine’s peak electrical power amounts to 600 W with 75 Nm max torque.

We performed two sets of experiments, with slightly different aims. As the model at the moment does not include the contribution of wind, we waited for days with no wind to perform the rides. In addition, in the setup we prescribed cadence in the range where the engine provides almost constant efficiency, above 75%. This is because, due to gear reduction ratio, on mid drives this is kept close to the cadence where also the majority of bikers are efficient, namely 60 to 100 RPMs [19].

In the first set, we used the Turbo Vado e-bike whose display has a very fine-grained scale for measuring the residual battery charge. We carried out two tests: the first one on an entirely flat urban route of 7 Km, which we repeated twice; the second test on an extra-urban route of 22 Km, including an uphill stretch of one kilometer, as well as other ups and downs of shorter length. In the first case, we required more effort from the engine, declaring little propensity for effort. The consumption forecast by our application, with Trail assistance level, was 14% of charge and proved to be precise within the accuracy of the measuring instrument (i.e., 1% of battery capacity and relative error not greater than seven percent). For the extra-urban route we have instead declared a moderate propensity to efforts, which lead the application to suggest the use of the Eco level only. The expected battery charge reduction was around 20% of full capacity while that measured by the Specialized display was 18%, with a relative error of about ten percent.

The results are summarized in

Table 2. First set summary with Specialized Turbo Vado 5.0 2020 (legend: AL is Assist Level, BC is Battery Consumption, RE is Relative Error).

Test	Conditions	Forecast	Results
1	Low biker effort, flat urban (14 Km)	AL Trial, BC 14%	accurate (RE not greater than 7%)
2	Moderate biker effort, extra urban (22 Km)	AL Eco, BC 20%	18% (RE about 10%)

.

In the second set of experiments we used the Pegasus e-bike, with the efficient Bosch drive unit. To measure battery charge, the supplied Intuvia display has a very coarse-grain analogical scale, composed of only five marks, presumably corresponding to 20% of charge level each. However, the display also shows the remaining range, which is ultimately the information that the biker needs. The value highlighted by the display clearly depends on the assistance level currently selected.

We only describe one test with the Bosch-powered e-bike, which we performed on a mixed urban and suburban circuit of 14 Km, which we repeated twice. Our application prescribed the Tour level and expected a final charge 72% full. In addition, at startup, the expected remaining range highlighted by the Intuvia display was of 110 Km. At the end of the first round, the range was reduced to only 102 Km, while at the end of the whole test it showed a remaining autonomy of 88 Km. As we expected, and as already pointed out, such range information is of little help. It appeared quite obvious that the displayed value depended heavily on the energy demand of the last few kilometers (if not of the last few hundred meters). During the first round, the value had dropped to 93 Km and then went back up to 116 Km.

At the end of the test, the Intuvia display still showed full marks for the battery charge, which we interpreted as “at least” 80% full, instead of the 72% estimated by our application. A simple computation would thus lead to expect at least a range of 140 Km under Tour (1.3) assistance, which would be quite surprising. For instance, the online range assistant by Bosch, with a bike/biker setup very close to that of our application, prescribes only 103 Km for flat routes (and ours was not completely flat). The results are therefore still uncertain, which clearly need further investigations.

The results are summarized in

Table 3. Second set summary with Pegasus Premio 10 Lite (legend: AL is Assist Level, BC is Battery Consumption).

Test	Conditions	Forecast	Results
1	Mixed urban and suburban (14 Km × 2, tot. 28 Km)	AL Tour, BC 28%	uncertain, probably ≤20%

.

5. Discussion

Our tests pointed out a twofold situations. For the Turbo Vado e-bike, the forecast was very close to the actual battery consumption, with an error of 1%, which is very low and can be due to different reasons difficult to manage in a precise way (e.g., the precise number of decelerations/accelerations due to traffic, traffic lights, roundabouts, etc.). For the Pegasus e-bike, apparently, our application did not perform any better than the Intuvia display, obtaining a difference between the forecasted remaining battery energy (72%) and the displayed one (80%) that is not very large but neither small. Of course, we say “apparently” because the fact that the display of Intuvia is based on (coarse-grained) marks and not on percentage with 1 unit of resolution, does not help in having precise comparisons. In addition, as already pointed out, it is by no means obvious that the full battery capacity is measured uniformly across the five marks of the gauge.

Even if a more accurate way of testing our application is needed, from the above-presented preliminary results our approach seems to be sound. The forecasted battery consumption turns out to be close to the actual battery consumption, providing the biker with a useful tool to plan her/his trips. As mentioned, the difference between the forecast and the actual capacity can be due to the coarse-grained information reported by the bikes’ displays and to the difficulty to have an accurate estimation of the battery capacity at the end of the test. Also the environment condition can influence the bike consumption; for instance, even if we tested the application during a non-windy day, some wind can have influenced the results. Nevertheless, we state that our findings are relevant, support the proposed model, and point out an interesting directions.

Future Work

With regard to future work, we sketch some directions, some aimed at overcoming the previously mentioned limitations. First, a wireless connection between the application and the bike can enable the communication of the status of the bike components in order to improve the computation; this could be enacted by means of a Bluetooth connection, which is available in most e-bikes; this could be a first step towards the integration of our application in the e-bike device. Second, the algorithm could take into consideration more parameters retrieved from an online service, for instance the wind direction and strength. Third, a very challenging aspect is to apply our approach to mountain e-bikes, i.e., bikes that ride off-road; of course, the computation is much more complex because the ground can vary in a very different way and the battery consumption as well. In general, we aim at performing more tests of our application in order to better validate the proposed model.

6. Conclusions

E-bikes are spreading more and more, and this call for an appropriate support for bikers. In particular, in this paper we have focused on the computation of the battery power consumption given a path. We have proposed a mathematical model that takes several parameters into consideration. We have implemented it in an application that can be customized by setting the bike and the biker characteristics and that the bikers can use to compute the battery consumption given a path as input.

Our proposal differs from others for three main reasons:

• Goal: our proposal aims at providing a forecast of the battery consumption given a whatever path, while other proposals focus on known paths, for instance to support bike sharing;
• Approach: our proposal relies on a mathematical model without the need of existing data, while others rely on machine learning techniques and data collected in previous tours;
• Scope: our proposal lets the biker choose a whatever path, while others consider the usual path or predefined paths, often only urban paths.

Our tests have shown that the application computation reflects the actual power consumption reported by the bike display at the end of the trip.