1. Introduction
Network-based data processing has attracted considerable attention due to recent advancements in reconfigurable computing, allowing complex and complete systems to be efficiently implemented and deployed in embedded applications. Field-Programmable Gate Arrays (FPGA) have been used to support parallel algorithm for decades, but it was a tight integration of reconfigurable logic with hard processing cores (both general purpose cores and graphics processing units) as well as latest advances in high-level synthesis tools that awoke more interest in network-based parallel data processing.
Network-based processing algorithms are characterized by a network of nodes, connected in a mesh so that data are processed by a number of nodes in parallel. Connecting processing units in a mesh/torus/fat tree is explored in many supercomputers, including IBM Summit [
1], Sunway TaihuLight [
2], and Fugaku [
3]. Supercomputing capabilities are definitely required in modern data centers but are not suitable for embedded systems due to constraints such as size, portability, power, and cost. The design of efficient embedded systems therefore involves different optimization criteria. Embedded systems have dedicated functions and can be optimized for particular operations in terms of execution time, existing real-time constraints, cost, and power consumption [
4].
FPGA have become more common as a core technology used to build electronic embedded systems. Moreover, Programmable Systems-on-Chip (PSoC) integrate reconfigurable logic with hardcore general-purpose and graphics-processing units, embedded memory blocks, high-performance interfaces, and specific-processing units (such as Digital Signal Processing (DSP) blocks) becoming complete, versatile, and programmable systems on a chip, steadily displacing general purpose processors and ASICs (Application-Specific Integrated Circuits). There are many reports of successful implementation of high-performance systems with FPGAs/PSoCs [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22].
In this paper, we intend to survey and classify one particular type of such systems that involve network-based data processing. The survey is based on the previous author’s work, summarizing different contributions and comparing them with alternatives. Three types of networks are analyzed:
- -
sorting networks;
- -
searching networks;
- -
counting networks.
The benefits and limitations of the proposed methods and architectures are demonstrated through examples from data processing and data mining, instrumentation, communications and other areas. With this work, we intend to review the recent research activity in the field and give recommendation for future network-based designs.
The remainder of this paper is organized as follows. Different types of data processing networks are characterized in
Section 2. Various hardware implementation approaches are reviewed in
Section 3. Advantages and drawbacks are identified and summarized in
Section 4. Conclusion and recommendations are given in
Section 5.
2. Networks for Data Processing
This section characterizes three selected types of data processing networks, which are suitable to parallel implementation in reconfigurable hardware.
2.1. Sorting Networks
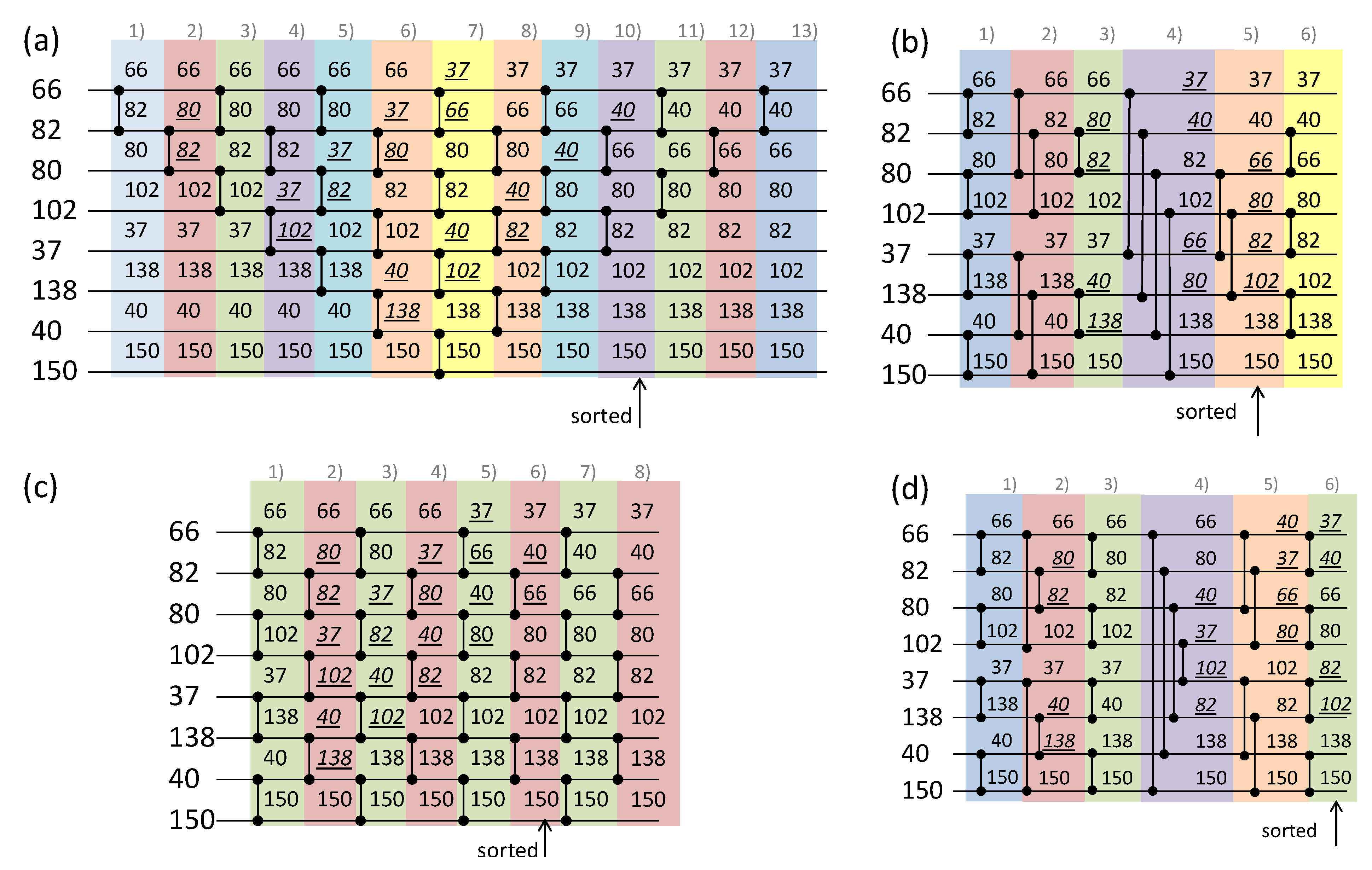
As the name indicates, the main objective of a sorting network is to sort data. A sorting network consists of two-input comparators and wires. Input data are applied in parallel to the input wires (on the left of a sorting network) and propagate to outputs (to the right) being repositioned by comparators located at specific locations and connecting pairs of wires. In case of ascending sort, a comparator swaps the values if and only if the top wire’s value is greater than the bottom wire’s value. The specific comparator locations are defined by the applied sorting algorithm. Several comparators may operate in parallel provided they are not connected to the same wires. For example,
Figure 1a illustrates a bubble-sort sorting network for 8 integer input data (a comparator is represented as a pair of two dots connected by a short vertical line using the widely known Knuth notation
![Electronics 11 01029 i001]()
). When a comparator swaps data items, these are underlined and shown in italics.
A sorting network can be characterized by a series of parameters such as the number of input data N, the width of input data M, the number of required comparators C(N), and the number of levels L(N). All the comparators that do function independently of each other (i.e., in parallel) are assigned to the same level. The sorting network from
Figure 1a has the following parameters: N = 8, C(N) = N × (N − 1)/2 = 28, L(N) = 2 × N − 3 = 13 (all the levels are numbered at the top of
Figure 1a and highlighted by distinct background colors). The first seven levels of comparators will “sink” the largest input value to the bottom wire and the remaining will “push” the smallest input value to the top sorting also all the intermediate values. As the bubble sort is known as a nonefficient algorithm (average performance is O(N
2) in terms of the number of comparisons), the bubble-sorting network inherits the same characteristic.
Other, more efficient sorting networks have been proposed, the most known of which are Batcher even–odd merge sort, even–odd transition sort, and bitonic merge sort [
23] (see
Figure 1b–d). The principal characteristics of the presented sorting networks are summarized in
Table 1. These characteristics give the first-level indication of the cost and efficiency of the respective networks. The smaller the value C(N) (the number of required comparators), the less hardware resources would be needed for implementation. The smaller the value L(N), the less is the network delay and the greater the throughput. Taking into account these parameters, even–odd merge and bitonic merge network should be more suitable for hardware implementation, but this is not always the case due to the following reasons:
- (1)
The number of comparators grows exponentially with the number of inputs N in all the network types. For any interesting number of N (at least several thousands), the demanded hardware resources become prohibitive.
- (2)
The even–odd merge and bitonic merge networks are not regular, therefore it is not easy to design parameterizable circuits that could be created for any value of N. Even-odd transition networks are definitely the most regular and therefore easily parameterizable for any value of N.
- (3)
The networks are “hardwired” in a sense that even if all the data appear to be sorted, these have to propagate through the remaining comparators until the results could be read from the outputs. This situation is illustrated in
Figure 1 with a “sorted” label.
- (4)
Even-odd transition networks can be seen as a good example of iterative circuit with a main module composed of two comparator lines (and two levels: green and red in
Figure 1c). The full network is just a replication of N/2 equal modules. Therefore, the function of this N/2-module iterative circuit can be performed by a sequential circuit that uses just one copy of the module but requires N/2 clock cycles to obtain the result. This is a very good example of space/time trade-off in digital design as it becomes possible to drastically reduce the number of comparators (alleviating much the resources problem) at the cost of only a slight increase in the processing time (basically, register setup and propagation times multiplied by N/2).
2.2. Searching Networks
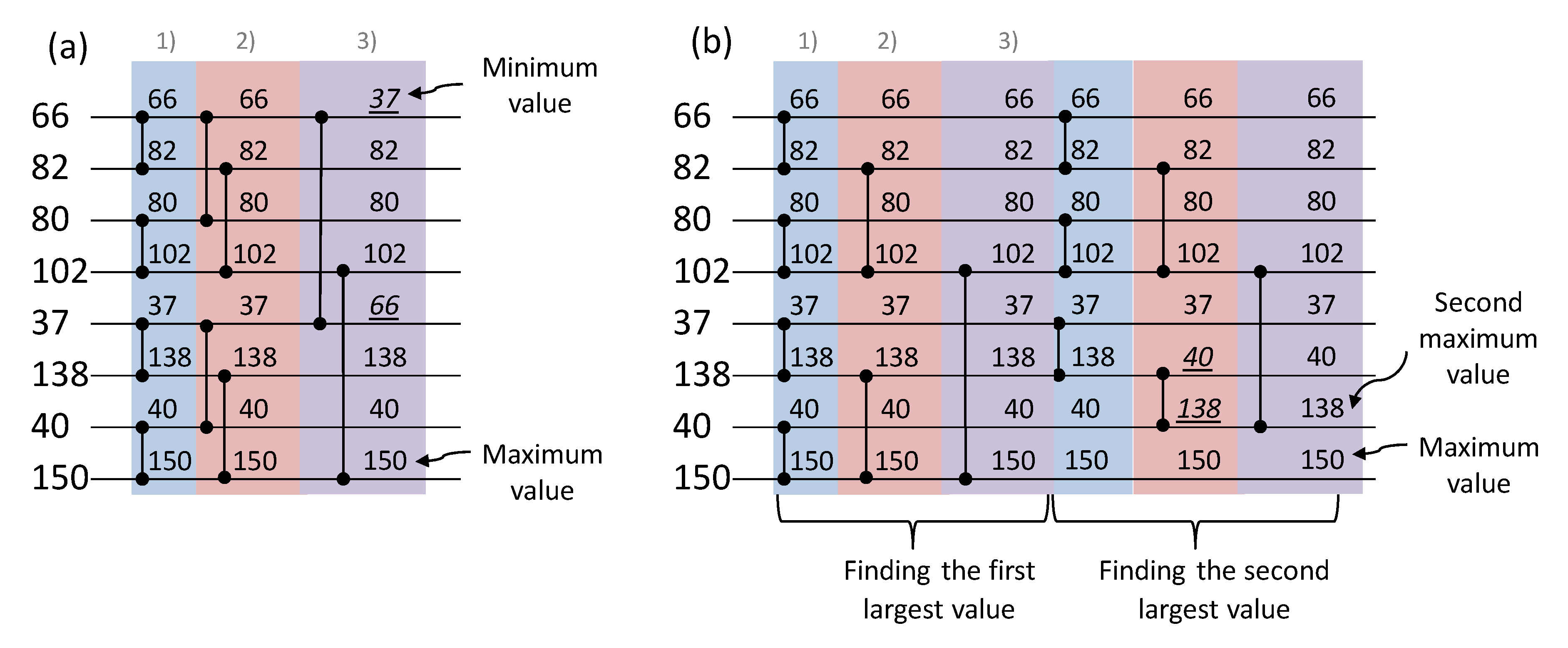
A searching network permits a single (of a couple of) maximum/minimum value(s) to be found in a set of N data items. Obviously, a sorting network could be used to realize this task (with the maximum and the minimum values available at the bottom and the top network’s output wires), but that would be a waste of time and resources. So, more efficient parallel solutions do exist and an example is given in
Figure 2 [
23]. Here, comparators are organized in different levels and connected so that: (1) firstly, maximum/minimum values are identified in all consecutive pairs of input values; (2) then all minimum and all maximum values are considered as two new subsets and the first point is repeated for each of them iteratively until only two values are left, one maximum and one minimum. The key parameters of a searching network are the same as that of a sorting network: N = 8, M, C(N), and L(N). L(N) =
, thus searching is completed in three steps, and the network requires C(N) =
comparators. Different levels are highlighted in
Figure 2 by distinct background colors.
The problem of discovering two smallest (or greatest) values looks similar but is more complex than discovering only the minimum (maximum) [
24]. However, the same parallel comparator network can be adapted to solve this new task. In particular, after finding the first smallest (or greatest) value, the search for the second smallest (greatest) value could be continued in a similar manner, but processing N − 1 remaining data items (see
Figure 2b).
Variations of the basic searching networks contribute to solving other more complicated tasks such as finding the most frequent value or a set of the most frequent values above a given threshold [
25].
2.3. Counting Networks
Counting networks do count specific values at the inputs. Probably, the most known counting networks are used to calculate the Hamming weight (the number of nonzero elements) of an input binary vector [
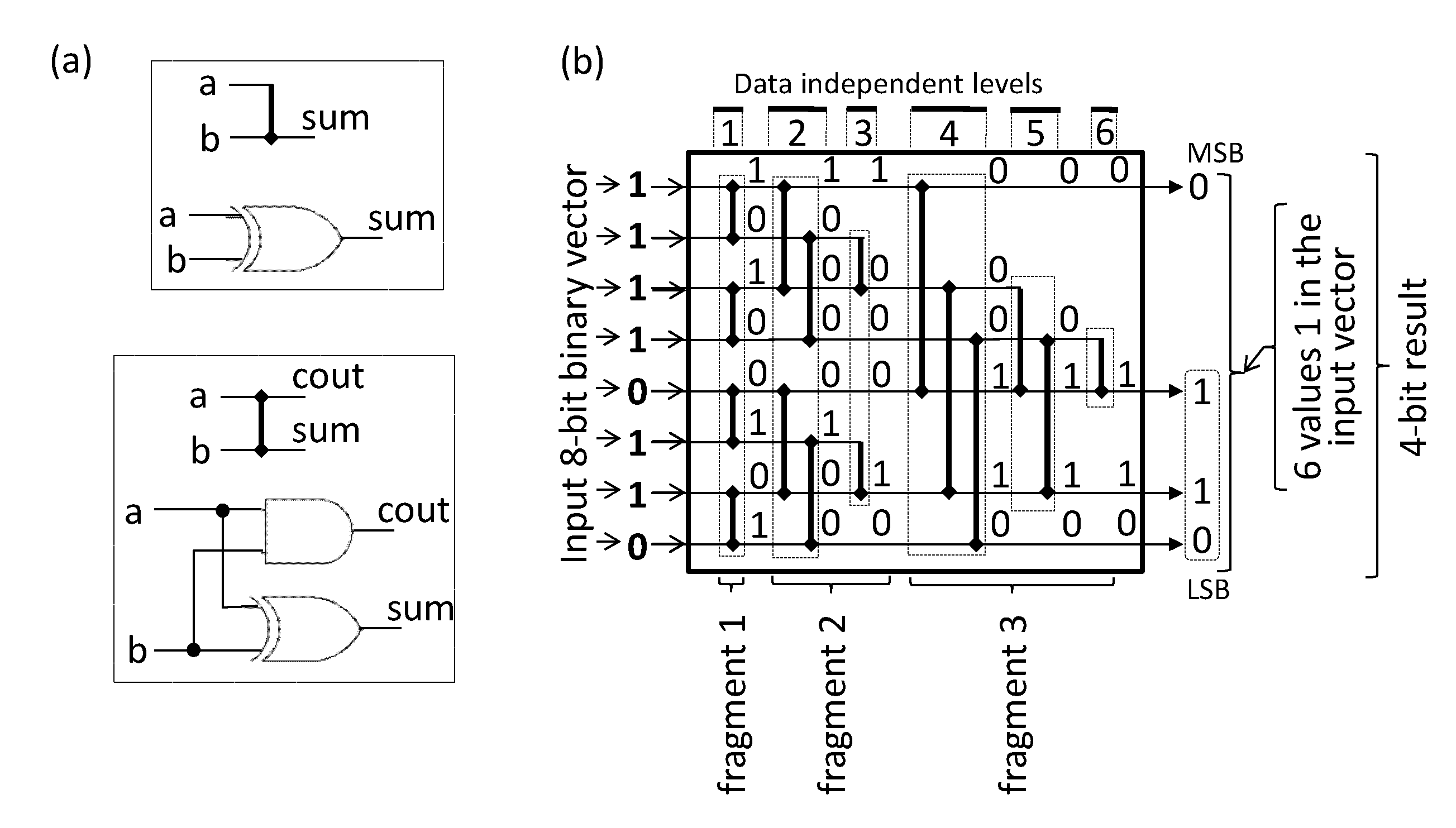
26]. Unlike the networks described above, counting networks do not use conventional comparators and, instead of them, recur to either half-adders or XOR gates (see
Figure 3a, where these elements are represented with rhomb-ended lines
![Electronics 11 01029 i002]()
and
![Electronics 11 01029 i003]()
, respectively).
Figure 3b gives an example of a counting network for a vector with M = 8 bits. The fragments of the network are composed of one or more levels and each fragment i = 1, 2, …,
, calculates the Hamming weights of 2
i-bit binary vectors. For example, fragment 1 calculates the Hamming weights in four (M/2
1) 2-bit vectors, which are 11, 11, 01, and 10; fragment 2 calculates the Hamming weights in two (M/2
2) 4-bit vectors: 1111 and 0110; and, finally, the last fragment, 3, calculates the Hamming weight in a single (M/2
3) 8-bit vector: 11110110, producing the result 0110
2 (6 in decimal). The total number of levels (including data-independent components) in the network is L(M) = 6. For a general value of M = 2
f, the counting network has the following parameters:
the number of components (half-adders or XOR gates) at any fragment i = 1, 2, …, f is ;
the total number of components in the network is C(M) = ;
the number of levels .
3. Implementations of Parallel Networks in Reconfigurable Hardware
As it was illustrated in the previous section, various basic components (such as comparators or half-adders) belonging to the same network level can operate in parallel since they manipulate independent data. Therefore, such networks are very well suited to implementation in reconfigurable hardware, provided the number of components and levels can easily be customized to particular network parameters N and M. In this section, various implementation approaches will be analyzed and their advantages and pitfalls identified.
3.1. Implementations of Sorting Networks
Sorting is a very demanded operation in various fields, therefore a lot of research had directed toward optimizing executing this task. Sorting accelerators are often used in a very large number of systems beginning from simple embedded systems processing data received from sensors and ending with complex multichip-distributed computing systems that can be found in such areas as medical instrumentation, machine-tool control, communications, industrial networks, vehicles, agriculture, monitoring motorways, etc. [
25].
The first efficient implementations of sorting networks in FPGA have been reported 10–15 years ago, when the logic capacity of programmable devices has reached sufficient levels to compete with general-purpose and application-specific processing systems for solving computationally intensive problems. For example, Mueller et al. [
27,
28] exploit the reconfigurability of FPGAs at runtime by reprogramming the chip for individual workloads, achieving high resource utilization and implementing data and task parallelism [
27]. Their implementations and experiments are targeted towards a Virtex-5 FPGA available on the Xilinx ML510 development board and running at 100 MHz. The authors analyzed bitonic and even-odd merge sorting networks and came to the conclusion that despite requiring more comparators, bitonic merge sorters are preferred because both the number of concurrent comparators for each level is constant (equal to N/2) and the delay for all signal paths is equal. For the selected bitonic merge network type, three alternative circuits have been studied: combinational (no clock), synchronous (exploring trade-off between the latency and clock frequency), and fully pipelined (allowing a new input data set to be applied every clock cycle). The authors did all the initial experiments, permitting to estimate approximately resources that would be required for instantiating a single M = 32-bit two-input comparator. That work permitted to conclude that the used Virtex-5 FX130T chip could accommodate just 1024 32-bit comparators. The implemented sorters were able to process up to N = 2
p=6 = 64 data items. The overall conclusion is that only small data subsets can be sorted in parallel in an FPGA-based accelerator therefore some software-based merger would make sense. When merging the sorted by the accelerator subsets in software, the speedup decreases with the increase of the data set size. The explanation is that the ratio between the work done by software (the CPU—Central Processing Unit) to work done in parallel in the accelerator decreases. Though no high speed-ups have been achieved over a CPU, the works [
27,
28] provide the important step towards incorporating the capabilities of FPGAs into parallel data processing engines.
Zuluaga et al. [
29] affirm that sorting networks offer great performance but are prohibitively expensive for large data sets and propose tools to automatically generate a large set of candidate designs, which would lead to hardware implementations of sorting networks with reduced area, which are optimized for latency or throughput. A Domain-Specific Language (DSL) is introduced that permits different sorting networks to be represented. The designed DSL compiler generates Verilog Register-Transfer Level (RTL) descriptions for each desired design. To reduce the area cost, the suggested generator explores the regularity of the sorting networks to “fold” them by reusing sorting elements and constructing a variety of sequential datapaths. The resulting circuits are called “sorting networks with streaming reuse”. Experiments have been targeted to the Xilinx Virtex-6 XC6VLX760 FPGA using M = 16-bit input data. The authors report that the circuit with maximum reuse, which recurs to only one sorter, and the lowest throughput could be fit in the employed FPGA for N = 2
19, M = 16.
Sklyarov et al. [
30,
31,
32] performed analysis of different sorting networks and concluded that even–odd transition networks are among the most regular and easily scalable. As the
Table 1 confirms, even–odd transition networks are often characterized as considerably slower and more resource consuming comparing with even–odd merge and bitonic merge networks. However, the regularity of the even–odd transition networks permits simple iterative circuits to be designed with a main module composed of just two vertical comparator lines, as explained in
Section 2.1. Since the reused core module is identical for every pair of network’s levels, no multiplexers or complex interconnections are required, which would definitely be needed for bitonic merge and even–odd merge networks, leading to increasing propagation delays and decreasing throughput. A feedback N × M-bit register is inserted before a pair of vertical comparator lines and different levels are activated sequentially, still using many parallel comparison operations at each level. Initially N data items are copied in parallel to the register. Thus, there are N multiplexers at the register inputs taking data from outside (before processing) and from the second vertical line of comparators (during processing). Hardware resources are obviously decreased from N × (N − 1)/2 (see
Table 1) to N − 1 comparators. The resulting circuits are easily scalable to any N and the respective parameterizable VHDL specifications are given in [
25]. The overall throughput should be decreased as besides of executing the required by the network comparison operations, the register’s delay slows down the sorting. This is however not true because in practice the number of paths through the vertical levels of comparators is decreased when comparing to hardwired combinational sorting networks. This is because usually (not taking into account the worst case) the data become sorted at some stage earlier than passing through all the network’s levels (this situation is illustrated in
Figure 1 with the “sorted” label). The sequential sorter takes advantage of this fact and stops sorting as soon as at any stage no swaps in the vertical comparator lines are detected. Experiments realized on the Xilinx Zynq xc7z020 PSoC prove that no performance degradation is identified and the resources are reduced significantly, allowing constructing sorting circuits for N = 512/M = 32 [
31]. The authors also called attention to the fact that although very interesting throughputs could be demonstrated by sorting networks themselves, such theoretical throughputs are not achievable in practice because of communication overheads. Indeed, initial data need to be supplied to the sorter (ideally, in parallel) and the results have to be taken from the sorter. So, trying to increase the number of sortable in parallel elements might be useless if there is no sufficient bandwidth to supply these elements to the sorter. To alleviate this problem, a communication-time sorter has been proposed in [
32] that is based on the network from [
30] permitting to find minimum and maximum values and enables data sorting to be completely overlapped in time with data transfers so that sorting is completed as soon as the last data item is received. Sorting subsets in an FPGA-based hardware accelerator and merging in software running on a hard processor in a Zynq PSoC has also been explored in [
32].
Najafi et al. propose a more area-efficient sorting network in [
33], which relies on unary processing. The idea is to encode every data item by a sequence of values ‘1’ followed by a sequence of values ‘0’ in a stream of 0’s and 1’s, such that the value is defined by the fraction of 1’s in the stream. Such an encoding permits to substitute conventional comparators by AND and OR gates. The authors report significant area reductions compared to traditional binary encoding but at the same time additional overhead is incurred by both conversion units which are required to encode the data from the binary to the stream format and a much longer operation time due to performing the operation on 2
M-bit long streams.
Norollah et al. [
34] suggest a multidimensional data sorter relying on matrix-based sorting suitable for real-time systems. The main achievements of the proposal are reducing the required resources and increasing memory efficiency, while experiencing a small negative impact on the execution time. Firstly, the authors propose organizing N input data in
matrix and activating
sorting networks to sort all the data. At each phase (out of six phases), each sorting network sorts its assigned either row or column items independently. Then, three-dimensional matrices are explored, leading to reduced resources but increasing the required number of sorting phases. Experiments executed on XC7VX485T FPGA of Virtex-7 family proved that the number of Look-Up Tables (LUTs) indeed dropped significantly when compared to a conventional bitonic merge sorting network, but the number of registers was increased (due to embedding a pipeline stage between each level in the network).
Srivastava et al. [
35] tried to solve the slow throughput problem in the merge sort and proposed a merge sort-based hybrid design where the final few levels in the merge sort network are replaced with “folded” bitonic merge networks. The authors tried to mix merge and bitonic sorting networks in attempt to alleviate their drawbacks. Thus, at the initial steps of the suggested sorting network merge sorting structure is employed, while the final steps recur to the bitonic method to increase parallelism. The experiments executed on the XC7VX690T FPGA confirm improving the throughput and reducing memory consumption.
Besides of the briefly characterized key works, other reports of efficient implementation of sorting networks in FPGA are recorded in the literature [
36,
37,
38,
39].
3.2. Implementations of Searching Networks
Searching networks are frequently employed in data mining, searching, and database applications, where only top query outputs that score the most with respect to a given search key may need further processing [
40]. Searching for a single maximum/minimum value is a straightforward implementation of the network from
Figure 2a. To locate two largest (or smallest) values, the network from
Figure 2b could be used.
Sklyarov et al. report the results of such implementation in [
25,
30], considering two possible approaches: combinational and sequential. For the combinational implementation, the respective parameterizable VHDL specification is given in [
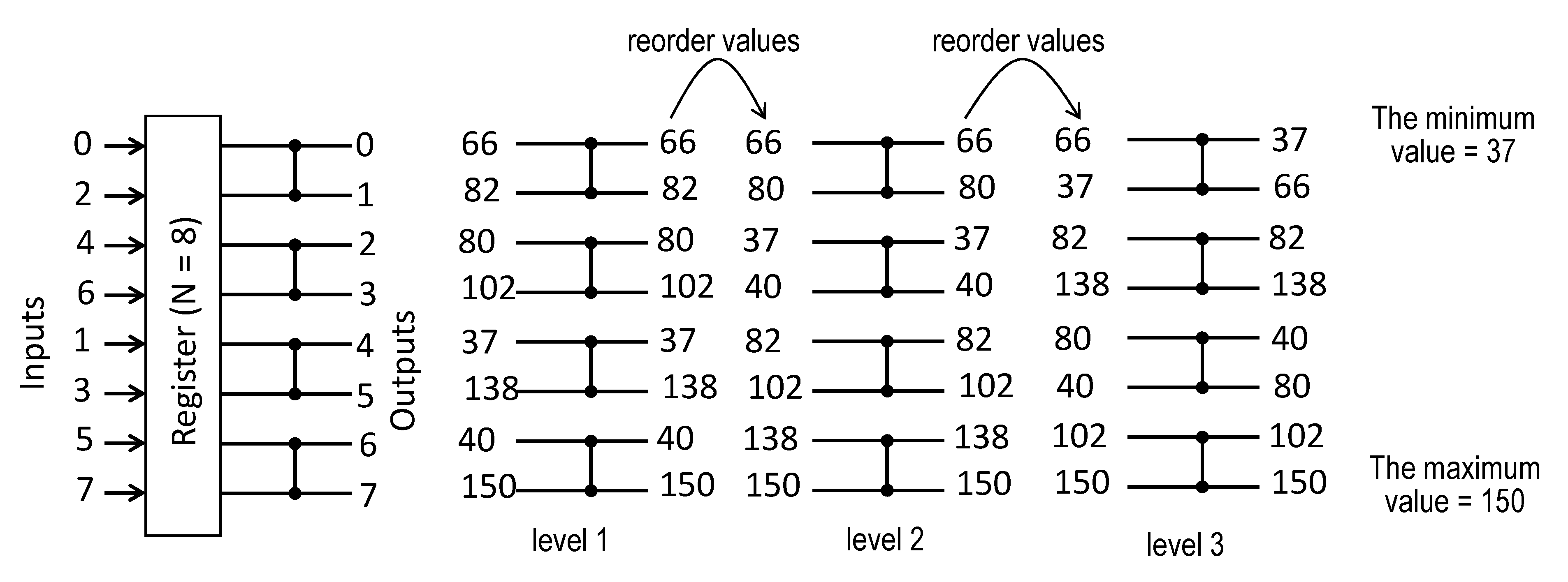
25]. In the sequential circuit, illustrated in
Figure 4 for N = 8, a register is sequentially reused between the levels of comparators. The circuit is constructed such that even N/2 outputs 0, 2, 4, 6 of levels 1, 2 are connected with the upper N/2 inputs of the next levels 2, 3, respectively, and odd N/2 outputs 1, 3, 5, 7 of levels 1, 2 are connected with the lower N/2 inputs of the next levels 2, 3. Thus, outputs 0, 1, …, 7 depicted on the right-hand side of the register in
Figure 4 are fed back to the register’s inputs so that the lower input line is connected with the output 7, the line above the lower line is connected with the output 5, etc. Comparison of the networks in
Figure 2a and
Figure 4 suggests that any level in
Figure 2a executes a similar operation to the respective iteration in
Figure 4. Outputs after the first iteration in
Figure 4 are the same as the outputs of the first level in
Figure 2a. Subsequent iterations give similar results as the respective level in
Figure 2a, but the values are reordered as described above. Such sequential implementation permits the required hardware resources to be reduced. While the network in
Figure 2 uses C(N) =
comparators, the circuit in
Figure 4 functions with just
comparators. The implementation in
Figure 4 is regular, easily scalable for any N, and does not involve complex multiplexing schemes. The minimum and maximum values are found in L(N) =
clock cycles. The results of experiments reported in [
25] show that the throughput of the networks in
Figure 2a and
Figure 4 is almost the same.
When two maximum/minimum values have to be identified, the networks from
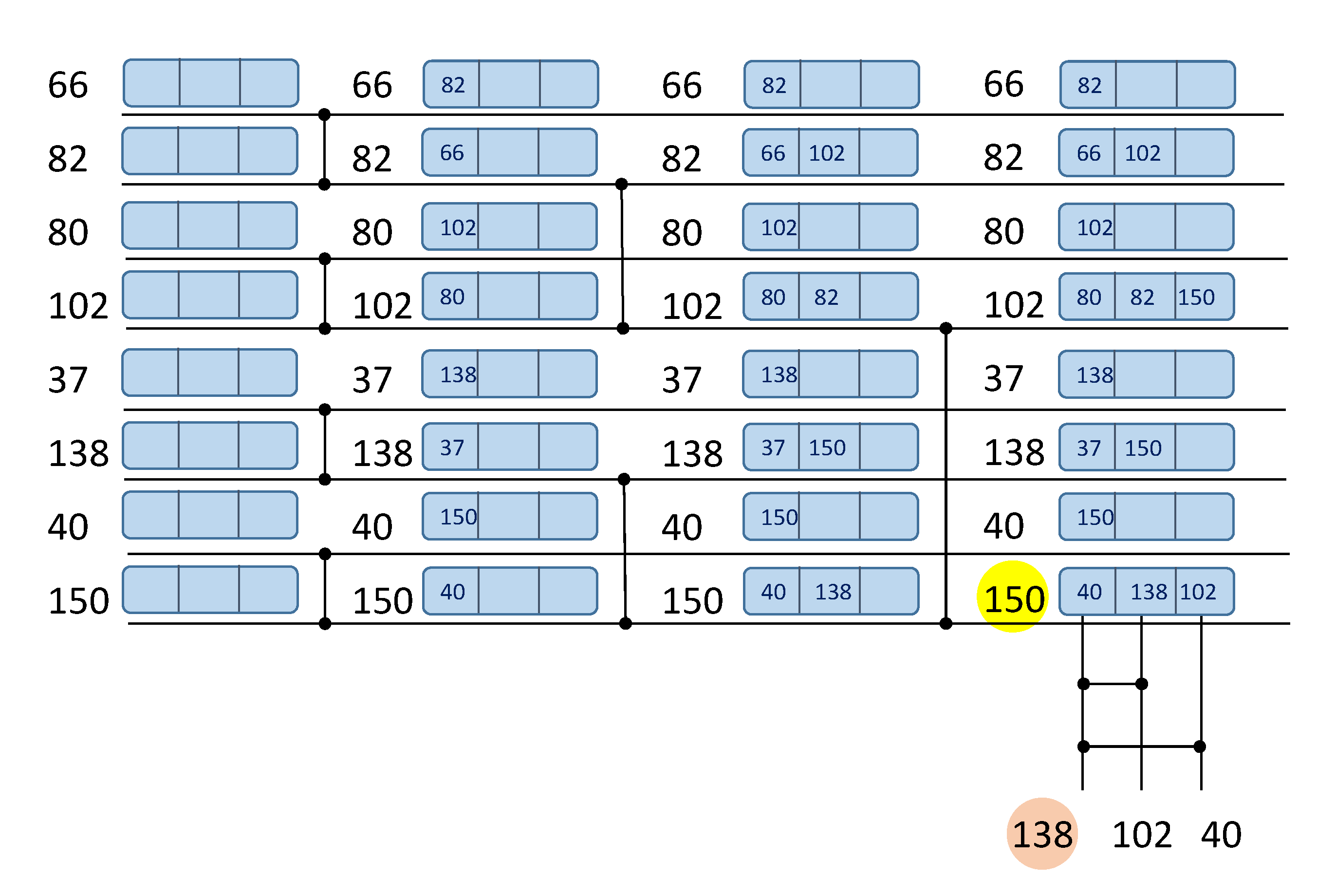
Figure 2b can be implemented as is. Wey et al. [
24] suggest that the number of comparators in
Figure 2b could be reduced if keeping track of the compared data items at each level. The respective algorithm for N = 8 (and the same data set as in
Figure 2b) is illustrated in
Figure 5. Here, each data element requires a small memory, keeping at most L(N) data items. After every comparison operation, these memories need to be updated for the involved data items. For example, in the first level of comparators (the left-hand side of
Figure 5), the first comparator analyzes the data items 66 and 82. Consequently, the value 82 is written to item 66 memory and the value 66 is written to item 82 memory. After executing all L(N) comparator levels the largest data item (150) can be read from the bottom horizontal line, as before. However, to find the second largest value (138) just L(N) − 1 = 2 additional comparators are required that would only analyze data values recorded in the memory of 150 (i.e., data values 40, 138, and 102 in the example of
Figure 5). As the result, the required number of comparators is reduced to: C(N) = N + L(N) − 2. For big values of N the resources (number of comparators) are diminished considerably, but additional memory requirements as well as memory management introduce an overhead. The authors also explore a tree structure search approach in [
24] and conclude that while this approach achieves higher speed performance, it requires a greater number of comparisons.
The bit-searching approach proposed by Tzimpragos et al. in [
41] allows several minimum or maximum values to be found. Here, the search is not based on comparisons between the elements of a dataset. Instead of this, the items’ bits are scanned from MSB (Most Significant Bit) to LSB (Least Significant Bit) with the aid of filters constructed from FPGA LUTs. This scheme works very well for small data items (whose number of bits M ≤ 3–4) but is not efficiently scalable for greater values of M. The authors report that for M > 4, the previous, described above approaches are less resource-consuming. A positive aspect of this solution is that the number of needed stages does not increase with the input size N.
3.3. Implementations of Counting Networks
Counting networks can be used efficiently for calculating the Hamming weight (HW) of binary vectors. This operation has many practical applications, such as binarized neural networks, cryptography, telecommunications, cheminformatics, bioinformatics and others [
42]. Besides simply counting the HW, certain applications require the HW to be compared to either a fixed threshold or to the HW of another binary vector (possibly of a different length). The respective network-based implementations will be briefly characterized below.
Pedroni proposes a network-based Hamming weight comparator circuit in [
43] relying on a triangular bit sorter circuit composed of M × (M − 1)/2 nodes with two gates (AND and OR) per node. The bit sorter sorts all the bits on the input binary vector. Then, if an output j, j = 1, 2, …, M is equal to 1, it indicates that the input vector has HW equal to or greater than j. The author gives a complete parametrizable VHDL code, allowing the design to be tested on an FPGA and also reports the results of implementation on the EPF10K20C240 FPGA.
Piestrak has improved on the previous results using sorting networks of lower time and cost complexities and suggested combinational digital comparators built using multioutput threshold circuits [
44]. The complexity and latency estimation is executed but no hardware implementation details are provided.
Parhami also addresses the problem of Hamming weight comparators and proposes efficient circuits based on accumulative and up/down parallel counters in [
45]. First, the author suggests using a network of parallel counters, adding the sum of M increment signals to a stored count (which has
bits). The HW count part of the design consists of a tree of increasingly wider ripple-carry adders. A fixed-threshold HW comparator is obtained if the arithmetic negation of the threshold k, that is, −k, is placed in the count register at start. Then it is only necessary to check whether the final count result is positive or negative. In the up-down parallel counters, the inputs are interpreted as signed count signals (increments and decrements), each encoded in 2 bits. These permit the comparison of the HWs of two vectors of the same length (one vector ‘1’ bits are considered to be positive values +1 and another vector ‘1’ bits are considered to be negative values −1). The author also presented a detailed cost and latency theoretical analysis of the previous three designs, concluding that his proposal exhibits better characteristics. No hardware implementation results are however reported.
Sklyarov et al. [
25,
26] suggest hardware circuits based on counting networks presented in
Figure 3. Several types of counting networks are analyzed and compared, such as pure combinational, partially sequential with reusable fragments, and pipelined. HW comparators are also proposed one of which is based on carry-network blocks from [
45] and the other one recurs to LUTs. A single LUT(n,1), i.e., a LUT with n inputs and 1 output, can be configured to support any threshold k < 2
n. It is also suggested how to deal with k >> 2
n. The proposed designs are not based on sorting networks, leading to more modest hardware resources. This is because, in contrast to sorting networks, the number of the used basic components in counting networks is incrementally reduced as data move from left to right (see
Figure 3). Thus, albeit the number of levels is the same (when compared to the number of levels in the best sorting networks), due to incrementally reduced complexity at each level, counting networks can be employed for a significantly greater value of M than sorting networks (within the same target hardware constraints). The authors report the results of experiments on two FPGA/PSoC-based prototyping boards: the Atlys with the Xilinx Spartan-6 FPGA and ZedBoard with the Xilinx Zynq including Artix-7 FPGA that prove that the proposed counting networks outperform the previous parallel counter-based designs. It is also illustrated that counting networks can be mapped efficiently to DSP slices that are available as standard components in modern FPGAs.
LUT-based circuits are explored in [
46] where firstly, two optimized LUT-based designs that permit the Hamming weight to be determined for M = 8 and M = 36 are suggested. The Hamming weight for M > 36 can be calculated in a tree-based structure. A combination of counting networks, LUT- and DSP- based circuits is proposed in [
47]. It is noticed that LUT-based circuits and counting networks are the fastest solutions for small values of M (M ≤ 128 bits). The result for bigger vectors (M >> 128) is produced as a combinational sum (executed in either DPS slices or in a circuit built from logical slices [
47]) of the HWs of the sub-vectors.
Networks of LUTs are further explored in [
48,
49].
A Hamming distance processing element is presented in [
48] by Pilz et al. The implementation is inspired by the LUT-based Hamming weight counter [
46]. Therefore, the calculation is performed in a generic adder tree structure, which is adjusted to any value M. The first tree stage was optimized specifically for Xilinx 7-series FPGAs and uses 6-input LUTs. The next tree stages implement a usual adder tree, adding two previous results together and transmitting the newly produced result to the subsequent tree stage iteratively, until the final result is calculated. Pipeline registers are inserted between all tree stages. Based on the suggested processing elements, a generic system architecture is proposed for binary string comparisons, implemented on a Virtex UltraScale+ FPGA. The system is adaptable to different values of M and the authors have demonstrated high throughput for streaming data.
A LUT-efficient compressor architecture for performing HW count operation is described by Umuroglu et al. in [
49] to be used in matrix multiplications of variable precision. The authors noticed that a HW count unit built as a tree of LUTs and adders would require a large number of logic resources and many stages to pipeline the adder tree. Therefore, they suggested applying a carry-free bit heap compression executing a carry-save addition with parallel full adders. Only the last addition phase does require carry propagation. This work is similar to parallel counters from [
45].
Rasoulinezhad et al. state in [
50] that modern FPGA LUT-based architectures are not well suited to implementation of compressor trees (which can be considered parallel counters with explicit carry-in and carry-out signals to be connected to adjacent compressors in the same stage) and suggest that existing FPGA logic elements (basically, LUTs) should be extended with a 6-input XOR gate. The authors demonstrate that the proposed modifications improve compressor tree synthesis using generalized parallel counters.
4. Advantages and Drawbacks
Sorting, searching, and counting are definitely important operations in a wide range of applications. Some of those applications require high-speed processing; therefore, hardware accelerators are often implemented to meet performance requirements. As reported in the previous section, reconfigurable hardware is a good implementation platform for different types of data-processing networks because it can be customized easily to different networks’ parameters (such as the data width M and data items number N). Actually, the characteristics of accelerator units vary greatly in the number N and width M of inputs that they can process. For example, certain filters require just a dozen or two of inputs, while image processing applications work with several tens of inputs; this number increases significantly when we move to video processing or database applications. That is why almost all reviewed implementations try to increase the number N of inputs that could be processed in a single chip.
Latency, area, and throughput have been used as the key metrics for performance evaluation. In reconfigurable hardware various area/speed trade-offs can naturally be explored by registering and pipelining intermediate results between networks’ levels. This opportunity has been analyzed in almost all of the reviewed works and the general conclusion is that pipelining, despite introducing certain overhead (increasing latency), is definitely required to reduce the networks’ complexity (area) and to be able to increase both the value N and the network throughput. In addition, a combinational data processing network (in particular, a sorting network) always takes the same number of levels (i.e., the same latency) to produce the result. As it has already been noted, traversing all the network’s levels is not always necessary as the data may be already processed (sorted) at some earlier network stages. Thus, the network depth should be adaptable to particular problem instance characteristics. This opportunity is explored in some of the proposed solutions where processing stops as soon as no data swaps are executed at a particular network level. This is only achievable in a sequential circuit that uses just one copy of a module of parallel elements whose outputs are connected to its proper inputs though a feedback register. It should be noted that this technique is not applicable to searching and counting networks.
FPGA are able to provide high energy efficiency by exploiting low-level fine-grained parallelism through customizing data paths to the requirements of a specific algorithm/application. Thus, FPGA-based hardware accelerators are suitable to low-cost low-power embedded systems.
Many designs try to explore specific FPGA features such as embedded DSP slices and direct programming and interconnecting of FPGA LUTs. This requires the detailed knowledge and experience with the target FPGA architecture. Although the achievable performance gains are interesting, unfortunately, this approach is not particularly scalable and is very error prone. Therefore, the authors, instead of determining and filling LUT contents manually, develop auxiliary software tools capable of generating constants for LUTs. Debugging such circuits is, however, a tedious task and the scalability problem is not solved easily.
More recent reconfigurable platforms combine on a single chip high-capacity programmable logic (FPGA) and state-of-the-art general-purpose processors. Such architectures permit to experiment with software–hardware codesign, where a part of the system is implemented in a highly optimized parallel processing unit and another part in software running on a traditional processor. For data processing networks, high-level parallelism can be applied directly, leading to hardware implementations that are potentially faster than relevant software functions running in general-purpose processors. However, it is well known that software is much more flexible and portable. In addition, hardware accelerators are subject to a number of (primarily resource) constraints. For example, searching and sorting networks can be mapped to FPGAs for data sets not exceeding several thousands of items. In software, designers/programmers are able to cope with complexity in a much easier manner than in hardware. Thus, new solutions should be explored trying to combine flexibility and maintainability of software with the speed and predictability of hardware, which can be achieved in hardware/software codesign. Usually, the designers recur to programmable systems-on-chip, incorporating a standard processor coupled with reconfigurable logic with high-performance interfaces connecting both parts of the chip. Software and hardware programming of such devices is directly supported by the respective vendor’s integrated design tools.
It is interesting to observe that almost all reviewed works recur to low level hardware designs (usually in VHDL/Verilog or in a specially developed language whose specifications are later automatically translated to standard HDL (Hardware Description Language) RTL descriptions). Very few works have experimented with standard High-Level Synthesis (HLS) tools. It is a pity, because although HDLs allow the creation of high-performance and resource-optimized circuits, whose development time is not extremely long, higher-level specification languages are easier to learn and often do not require such detailed knowledge of the target FPGA architecture. Therefore, HLS tools are much more accessible to algorithm and system designers compared to tools that only accept HDLs. Obviously, very platform-specific features, such as direct programing of DSP slices and LUTs, are out of reach of designers using HLS tools, but ease to learn, ease to change and maintain, and shorter development time are definitely advantages of this technology. Moreover, the verification and debug efforts are reduced drastically, because the simulation could be executed at higher abstraction levels, running much faster than at RTL level and allowing design errors to be located and fixed in a much simpler way. In addition, different software/hardware partitioning boundaries may more easily be tested and the respective area/performance trade-offs evaluated. Thus, we expect that HLS will be applied more intensively in future implementations of networks for data processing.
It is straightforward to map data-processing networks onto hardware using cascaded elements (such as comparators or half-adders) if all the input data are available concurrently. However, for large data sets, this simple approach is not technically feasible due to high routing complexity, area consumption, as well as limited I/O bandwidth. Frequently, the designers implementing data-processing networks in hardware report the ideal throughput, assuming that all inputs are readily available and ignoring any communication overheads. It is, however, known that communication overheads are often the main bottleneck in system performance, not allowing the theoretical throughput to be achieved in practice. To solve this problem, designs have been proposed that allow processing to be overlapped in time with data transfers.
5. Conclusions
This paper reviews the recent advances in data processing in reconfigurable hardware with the aid of parallel networks connecting simple processing elements (such as comparators and half-adders) in certain patterns. In particular, sorting, searching, and counting networks have been analyzed with the most influential contributions being briefly characterized. It has been shown that although very appreciable results have already been achieved, with various authors proving the benefits of reconfigurable hardware implementations compared to software solutions, more work is still required in particular in the scope of exploring high-level synthesis potential and reducing the communication bottleneck, which is currently the main limiting factor of the majority of the designs. Different proposals have been carried out to mitigate the bandwidth limitation, such as communication-time data processing [
32] and a data compression mechanism [
51].
Besides this, the authors do usually compare the performance of their accelerators with that of software running on an (either soft or hard) embedded processor. This permits reporting appreciable speed-ups that, however, are frequently nullified if a comparison would be done with a high-speed general-purpose (not embedded) processor. This is not a limitation however, since data processing is frequently required in embedded systems that do need to process information received from sensors and have hard real-time constraints. Here, low power and predictability might be more important that the processing speed itself. Overall, the proposed designs are very suitable for embedded systems working with limited value of N and are not too appropriate for real big data applications.
Due to area and bandwidth limitations, we believe that future solutions will explore more software–hardware codesign, trying to combine the benefits of fast parallel processing in hardware with the flexibility and ease of debug and development of software.
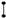 ). When a comparator swaps data items, these are underlined and shown in italics.
). When a comparator swaps data items, these are underlined and shown in italics.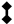 and
and 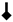 , respectively). Figure 3b gives an example of a counting network for a vector with M = 8 bits. The fragments of the network are composed of one or more levels and each fragment i = 1, 2, …,, calculates the Hamming weights of 2i-bit binary vectors. For example, fragment 1 calculates the Hamming weights in four (M/21) 2-bit vectors, which are 11, 11, 01, and 10; fragment 2 calculates the Hamming weights in two (M/22) 4-bit vectors: 1111 and 0110; and, finally, the last fragment, 3, calculates the Hamming weight in a single (M/23) 8-bit vector: 11110110, producing the result 01102 (6 in decimal). The total number of levels (including data-independent components) in the network is L(M) = 6. For a general value of M = 2f, the counting network has the following parameters:
, respectively). Figure 3b gives an example of a counting network for a vector with M = 8 bits. The fragments of the network are composed of one or more levels and each fragment i = 1, 2, …,, calculates the Hamming weights of 2i-bit binary vectors. For example, fragment 1 calculates the Hamming weights in four (M/21) 2-bit vectors, which are 11, 11, 01, and 10; fragment 2 calculates the Hamming weights in two (M/22) 4-bit vectors: 1111 and 0110; and, finally, the last fragment, 3, calculates the Hamming weight in a single (M/23) 8-bit vector: 11110110, producing the result 01102 (6 in decimal). The total number of levels (including data-independent components) in the network is L(M) = 6. For a general value of M = 2f, the counting network has the following parameters: