Deformable MEMS with Fringing Field: Models, Uniqueness Conditions and Membrane Profile Recovering
Abstract
:1. Introduction to The Problem
- To evaluate how the effect due to the fringing field affects the electrostatic force in the device, obtaining an increase for the total electrostatic force ;
- To achieve a new uniqueness condition of the solution for (1), which depends on the electromechanical properties of the membrane and the real parameter that weights the effects due to the fringing field;
- Starting from the uniqueness condition obtained in the previous item, obtaining a new, unique condition ensuring both existence and uniqueness for (1), which depend on both the electromechanical properties of the membrane and the real parameter that weights the effects due to the fringing field;
- To recover the membrane profile by means of numerical techniques consolidated in the literature, which represent the most suitable techniques for the numerical solution of second-order elliptic semi-linear differential models. These techniques (based on shooting procedures, Keller box schemes and Lobatto formulas) have been implemented in MatLab® R2019a running on an Intel Core 2 CPU at 1.45 GHz, comparing their performances as real parameters that weight the effect due to the varying fringing field, in order to achieve suitable ranges for the membrane material’s electromechanical properties that ensure convergence (even with ghost solutions); and
- Finally, to obtain the important link between the mechanical properties of the material constituting the membrane and the electrical operating parameters of the device without ghost solutions (which is interesting for industrial applications).
2. A Brief Description of the 1D Electrostatic MEMS Device
2.1. The Device Functioning as an Actuator
2.2. The Device Functioning as a Sensor
3. The Mathematical Model Governing the Behavior of the Device
3.1. From the Electrostatic MEMS Device with Two Parallel Metallic Plates to the 1D Electrostatic Membrane MEMS Device
3.2. The Fringing Field Problem and the Pelesko–Driscoll Theory
3.3. On the Local Proportionality between and the Curvature of the Membrane
3.4. On Possible Limitations for , , and
4. Some Advantages and Disadvantages of the Model
5. On the Existence of At Least One Solution: A Well Known Result
6. A New Algebraic Condition Ensuring the Uniqueness of the Solution
- If ,otherwise, if
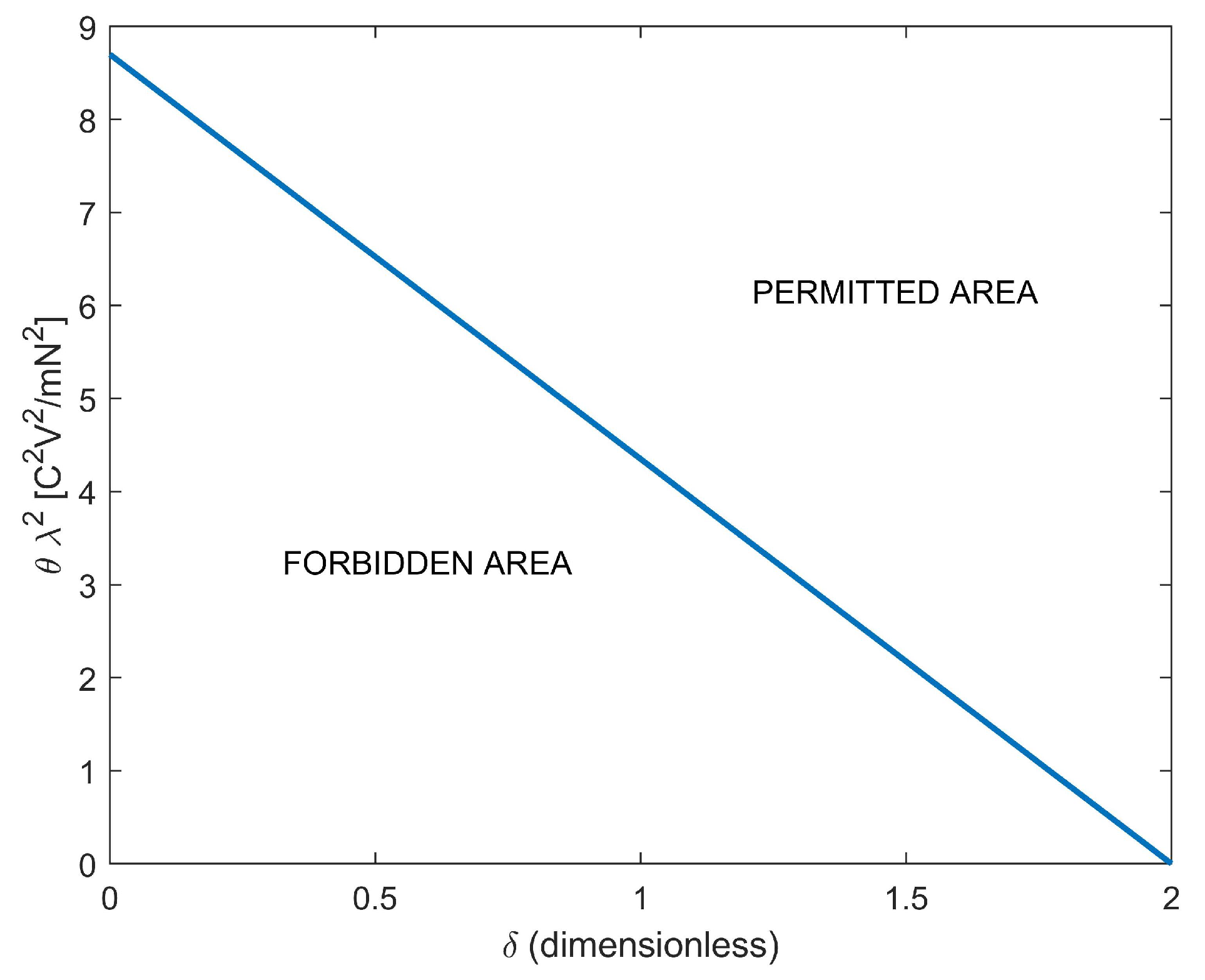
7. A New Algebraic Condition Ensuring Both Existence and Uniqueness
8. How the Fringing Field Affects the Electrostatic Force in the Device
9. Numerical Approaches
9.1. A Useful Transformation of the Model under Study
9.2. Shooting Procedure
9.3. A Brief Description of the Keller Box Scheme
9.4. Concerning III/IV-Stage Lobatto IIIa Formulas
10. Numerical Results
10.1. A New Limitation for
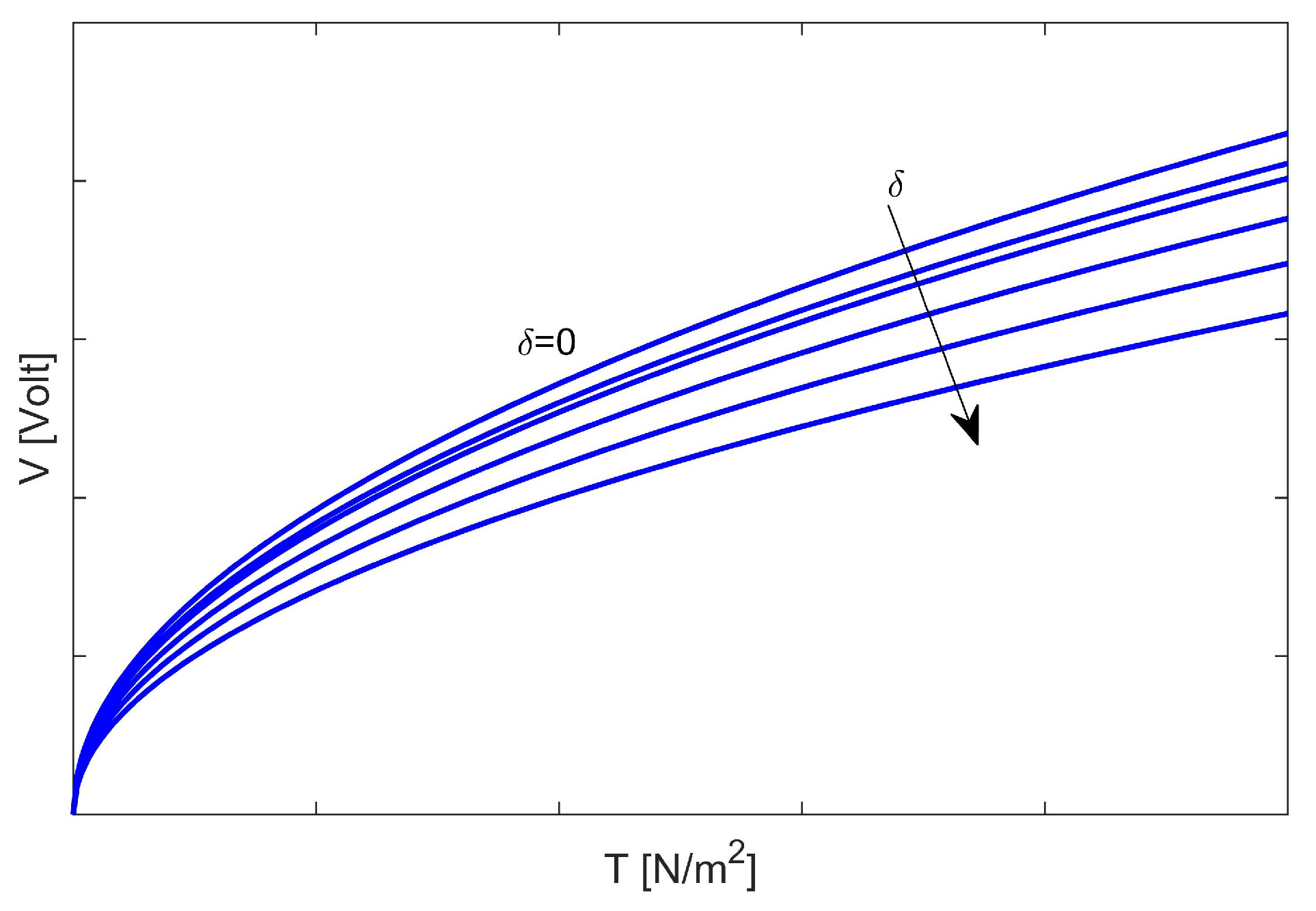
10.2. A New External to Overcome the Inertia of the Membrane
10.3. On the Possible Presence of Ghost Solutions and the Convergence of the Numerical Procedures
11. On the Limitation for and a Reliable Value of to Overcome the Membrane Inertia
12. On the Influence of Electromechanical Properties on the Proposed Procedure
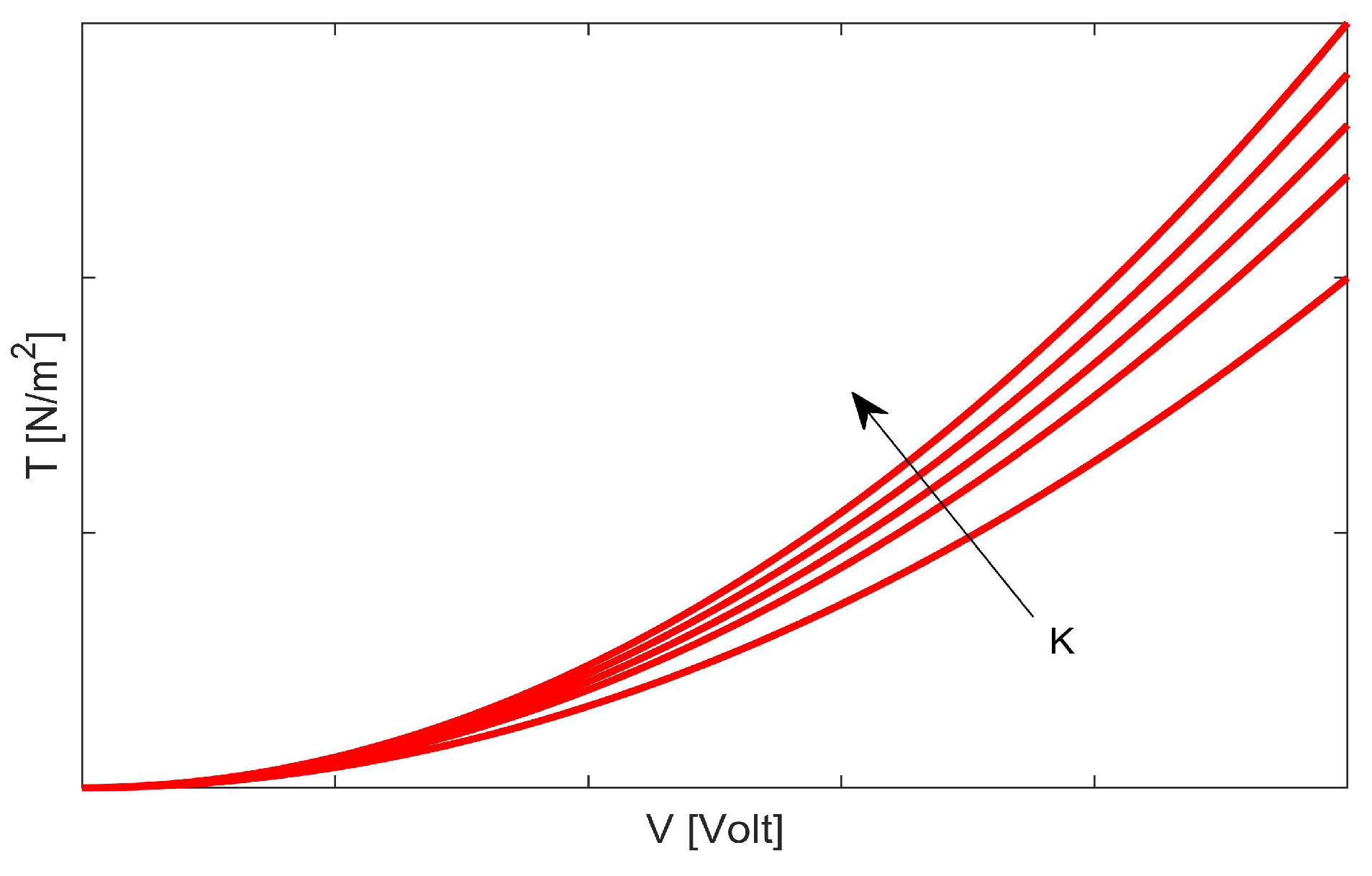
- Both recovering the membrane profile numerically and obtaining the limitations for T and for V strongly depend on the electromechanical properties of the material constituting the membrane. In fact, the prevailing presence of throughout the procedure highlights this dependence. In particular, we have seen how the presence in the denominator of in the starting analytical model influences and therefore the concavity of the membrane profile, in the sense that the greater (i.e., the greater T) the lower the concavity of the membrane. From the physical point of view, this translates into the fact that the higher the T, the greater the mechanical resistance that the membrane offers to deformation.
- On the other hand, as confirmed by (29), the higher the T (i.e., with values less than ) the lower the H, so it is confirmed that more resistant membranes will cause deformations that are more contained to the edges.
- Moreover, as it should be, also strongly influences the conditions of existence and uniqueness of the solution for the model under study (see (35)).
- It is worth underlining the fact that the proposed procedure is based on numerical techniques of which the convergences depend exclusively on . In other words, it is the electromechanical properties of the membrane material that “manage” the convergences of the numerical techniques used and ensure that the membrane profile obtained does not represent a ghost solution, regardless of the value of the parameter that weights the effect due to the fringing field, though obviously within the range of its possible values, (see (127)).
- Furthermore, (139) highlights how the electromechanical properties of the material constituting the membrane once again influence the choice of T. In other words, having chosen the intended use of the device (that is, choosing an external V to apply), directly affects the value of T. Vice versa, having selected a specific value of T (that is, having chosen the material of which the membrane must be constituted), from (139), it is possible to establish the intended use of the device.
- It is worth noting that from derives an important link between (which is the parameter that weighs the effects due to the fringing field) and the ratio . In fact, based on (126), and taking into account (12), it easily follows that:in whichandwith . In other words, after one has fixed the length L of the device and the material constituting the membrane (that is, once T is fixed), explicitly depends on , as evidenced by (144). Thus, as confirmed by the experimental facts, the higher the ratio (i.e., L/d 1), the less the effects due to the fringing field will be. However, in the current state of modeling, as it is one-dimensional, we can say nothing about the dependence of on the ratio , where w is the width of the device. We arrive at the same conclusions starting from (135).
13. Destinations of Use of the Device Studied
14. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MEMS | microelectromechanical systems |
| x | spatial abscissa ((m)) |
| profile of the membrane ((m)) | |
| bounded domain | |
| electrostatic field ((V/m)) | |
| critical security distance ([m]) | |
| real positive parameter that weights the effect due to the fringing field (dimensionless) | |
| d | distance between the parallel plates ((m)) |
| L | length of the MEMS ((m)) |
| V | external electric voltage applied ((V)) |
| permittivity of the free space ((C2/Nm3)) | |
| electrostatic pressure ((N/m2)) | |
| electrostatic force ((N)) | |
| T | mechanical tension of the membrane at rest ((N/m2)) |
| density ((kg/m3)) | |
| D | stiffness coefficient ((N/m)) |
| p | mechanical pressure ((N/m2)) |
| electrostatic capacitance ((F)) | |
| k, | coefficients of proportionality (dimensionless) |
| self-stretching coefficient (dimensionless) | |
| coefficient of stretching energy (dimensionless) | |
| stretching parameter (dimensionless) | |
| bounded functions which carries the dielectric properties of the material constituting the membrane (dimensionless) | |
| parameter depending on the electrostatic capacitance (dimensionless) | |
| capacitor belonging to the control circuit ((F)) | |
| drop-voltage ([C2V2/mN2]) | |
| real parameter that weights the effects due to the fringing field (dimensionless) | |
| Pelesko–Driskoll fringing function | |
| coefficient of proportionality (dimensionless) | |
| geometric curvature of the membrane ((m−1)) | |
| function of proportionality (dimensionless) | |
| electromechanical properties of the material constituting the membrane (C2V2/mN2) | |
| H | (dimensionless) |
| real positive parameter (dimensionless) | |
| fringing field ([V/m]) |
References
- Pelesko, J.A.; Bernstein, D.H. Modeling MEMS and NEMS; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 1998. [Google Scholar]
- Gad-el-Hak, M. Design and Fabrication; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2006. [Google Scholar]
- Ghodssi, R.; Lin, P. MEMS Materials and Processes Handbook; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Younis, M.I.; Nayfeh, A.H. A Study of the Nonlinear Response of a Resonant Microbeam to an Electric Actuation. Nonlinear Dyn. 2003, 31, 91–117. [Google Scholar] [CrossRef]
- Morabito, F.C. Independent Component Anaysis and Feature Extraction Techniques for NDT Data. Mater. Eval. 2000, 58, 85–92. [Google Scholar]
- Greco, A.; Costantino, D.; Morabito, F.C.; Versaci, M. A Morlet Wavelet Classification Technique for ICA Filtered sEMG Experimental Data. Modeling and Simulation of MEMS Components: Challenges and Possible Solutions, Micromachining Techinques for Fabrication of Micro and Nano Structures, Portland, OR, USA, 20–24 July 2003; pp. 166–171. [Google Scholar]
- Gad-el-Hak, M. Modeling and Simulation of MEMS Components: Challenges and Possible Solutions, Micromachining Techinques for Fabrication of Micro and Nano Structures; Springer Nature: Singapore, 2012. [Google Scholar]
- De Holiveira Hansen Noble, R.; Mária, M.; Romans, S.; Jost, A.; Steffen, C.; Tim, R.; Bernhard, W.; Wolfgang, B.; Stefan, M. Magnetic Fils for Electromagnetic Actuation in MEMS Switches. Microsyst. Technol. 2018, 24, 529–551. [Google Scholar]
- Zhu, J. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2020, 11, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, Z.; Chang, Y.; Ma, Y.; Shih, K.; Dong, B.; Lee, C. Leveraging of MEMS Technologies for Optical Metamaterials Applications. Adv. Opt. Mater. 2019, 8, 1900653. [Google Scholar] [CrossRef]
- Lee, S.; Chen, C.; Deshp, V.V.; Lee, G.H.; Lee, I.; Lekas, M. Electrically Integrated SU-8 Clamped Graphene Drum Resonators for Strain Engineering. Appl. Phys. Lett. 2013, 102, 153101. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Smith, A.D.; Forsberg, F.; Wagner, S.; Schröder, S.; Akbari, S.S.A.; Fischer, A.C.; Villanueva, L.G.; Östling, M.; Lemme, M.C.; et al. Manufaccture and Characterization of Graphene Membranes with Suspended Silicon Proof Masses for MEMS and NEMS Applications. Microsyst. Nanoeng. 2020, 102, 17. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Venkatachalam, S.; Zhou, R.; Xu, H.; Pokharel, A.; Fefferman, A. High-Q Silicon Nitride Drum Resonators Strongly Coupled. Nano Lett. 2021, 21, 5738–5744. [Google Scholar] [CrossRef]
- Phan, A.; Truong, P.; Schade, C.; Joslin, K.; Talke, F. Analytical Modeling of an Implantable Opto-Mechanical Pressure Sensor to Study Long Term Drift. In Proceedings of the ASME 2020 29th Conference on Information Storage and Processing Systems, Virtual, 24–25 June 2020; p. V001T06A003. [Google Scholar]
- Yen, Y.K.; Chiu, C.Y. A CNOS-MEMS-Based Membrane-Bridge Nanomechanical Sensors for Small Molecule Detection. Sci. Rep. 2020, 10, 5237. [Google Scholar] [CrossRef]
- Ma, T.; Cao, H.; Shen, C. A Temperature Error Parallel Processing Model for MEMS Gyroscope based on a Novel Fusion Algorithm. Electronics 2020, 9, 499. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Watkins, C.; Xie, H. MEMS Mirrors for LiDAR: A Review. Micromachines 2020, 11, 456. [Google Scholar] [CrossRef] [PubMed]
- Javaher, H.; Ghanati, P.; Azizi, S. A Case Study on the Numerical Solution and Reduced Order Model of MEMS. Sens. Imaging 2018, 19, 153–169. [Google Scholar] [CrossRef]
- Versaci, M.; Jannelli, A.; Morabito, F.C.; Angiulli, G. MEMS Device considering the Effect of the Fringing Field. Sensors 2021, 21, 5237. [Google Scholar] [CrossRef]
- Hashimoto, K.; Shiotani, T.; Mitsuya, H.; Chang, K.C. MEMS Vibrational Power Generator for Bridge Slab and Pier Health Monitoring. Appl. Sci. 2020, 10, 8258. [Google Scholar] [CrossRef]
- Versaci, M.; Di Barba, P.; Morabito, F.C. Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review. Membranes 2020, 10, 361. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, B. Research on a CMOS-MEMS Infrared Sensor with Reduced Graphene Oxide. Sensors 2020, 20, 4007. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane MEMS Device with Fringing Field. Comput. Appl. Math. 2021, 40, 87. [Google Scholar] [CrossRef]
- Versaci, M.; Di Barba, P. Deformable MEMS with Fringing Field: A New Uniqueness Condition for Identifying the Electrode Profile. In Proceedings of the 20th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering, Lodz/Cracow, Poland, 20–23 September 2021. [Google Scholar]
- Versaci, M.; Jannelli, A.; Angiulli, G. Electrostatic Micro-Electro-Mechanical-Systems (MEMS) Devices: A Comparison Among Numerical Techniques for Recovering the Membrane Profile. IEEE Access 2020, 8, 125874–125886. [Google Scholar] [CrossRef]
- Pelesko, J.A.; Driscoll, T.A. The Effect of the Small-Aspect-Ratio Approximation on Canonical Electrostatic MEMS Models. J. Eng. Math. 2005, 53, 239–252. [Google Scholar] [CrossRef] [Green Version]
- Cassani, D.; Ghoussoub, N. On a Fourth Order Elliptic Problem with a Singular Nonlinearity. Adv. Nonlinear Stud. 2011, 9, 189–209. [Google Scholar] [CrossRef]
- Jonassen, N. Electrostatics; Springer: Singapore, 2014. [Google Scholar]
- Bayley, P.B.; Shampine, L.F.; Waltman, P.E. Nonlinear Two Points Boundary Value Problems; Academic Press: London, UK, 1969. [Google Scholar]
- Kress, R. Numerical Analysis; Springer: New York, NY, USA, 1998. [Google Scholar]
- Versaci, M.; Di Barba, P.; Morabito, F.C. MEMS With fringing Field: Curvature-Dependent Electrostatic Field and Numerical Techniques for Recovering the Membrane Profile. Comput. Appl. Math. 2021, 40, 128. [Google Scholar] [CrossRef]

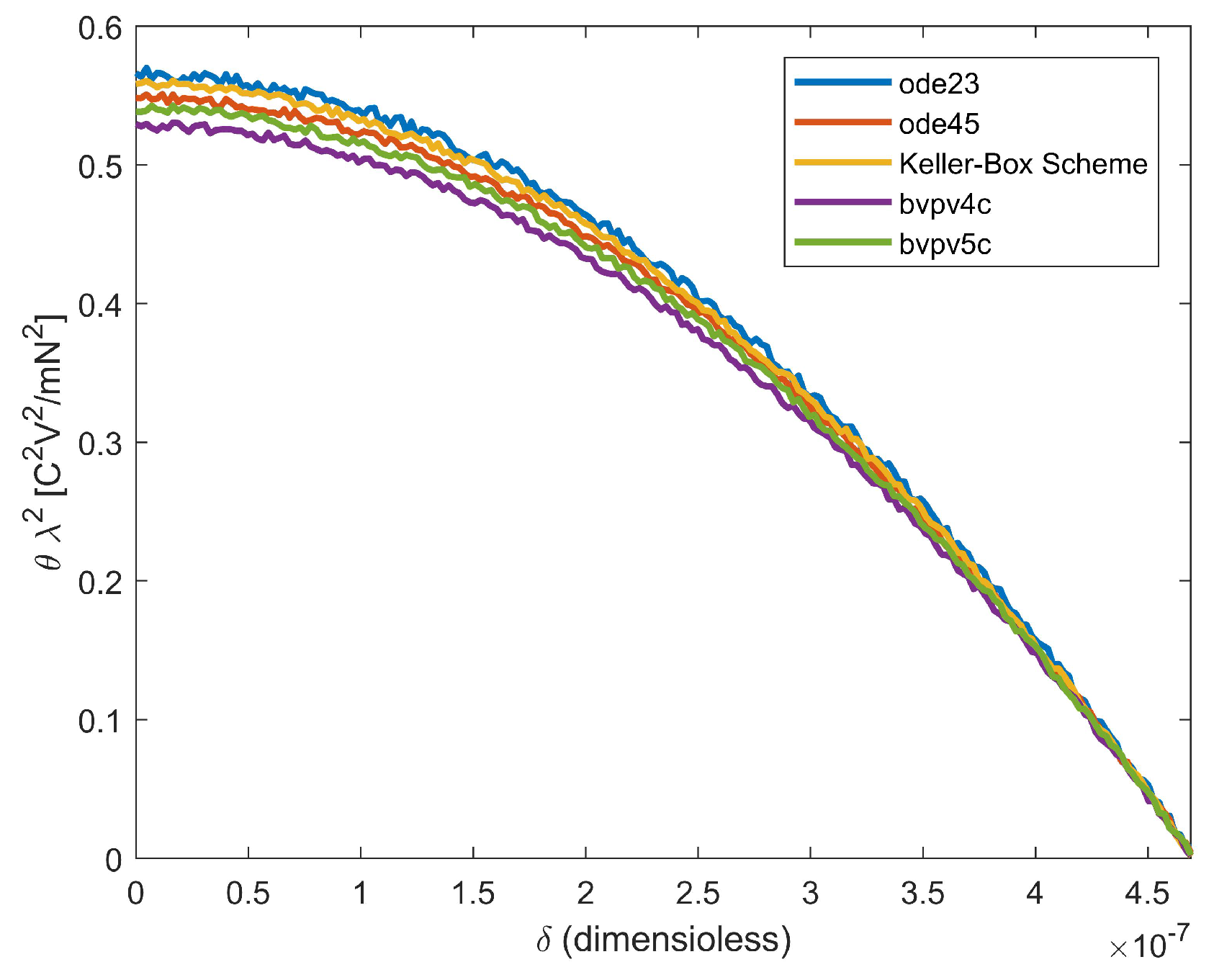

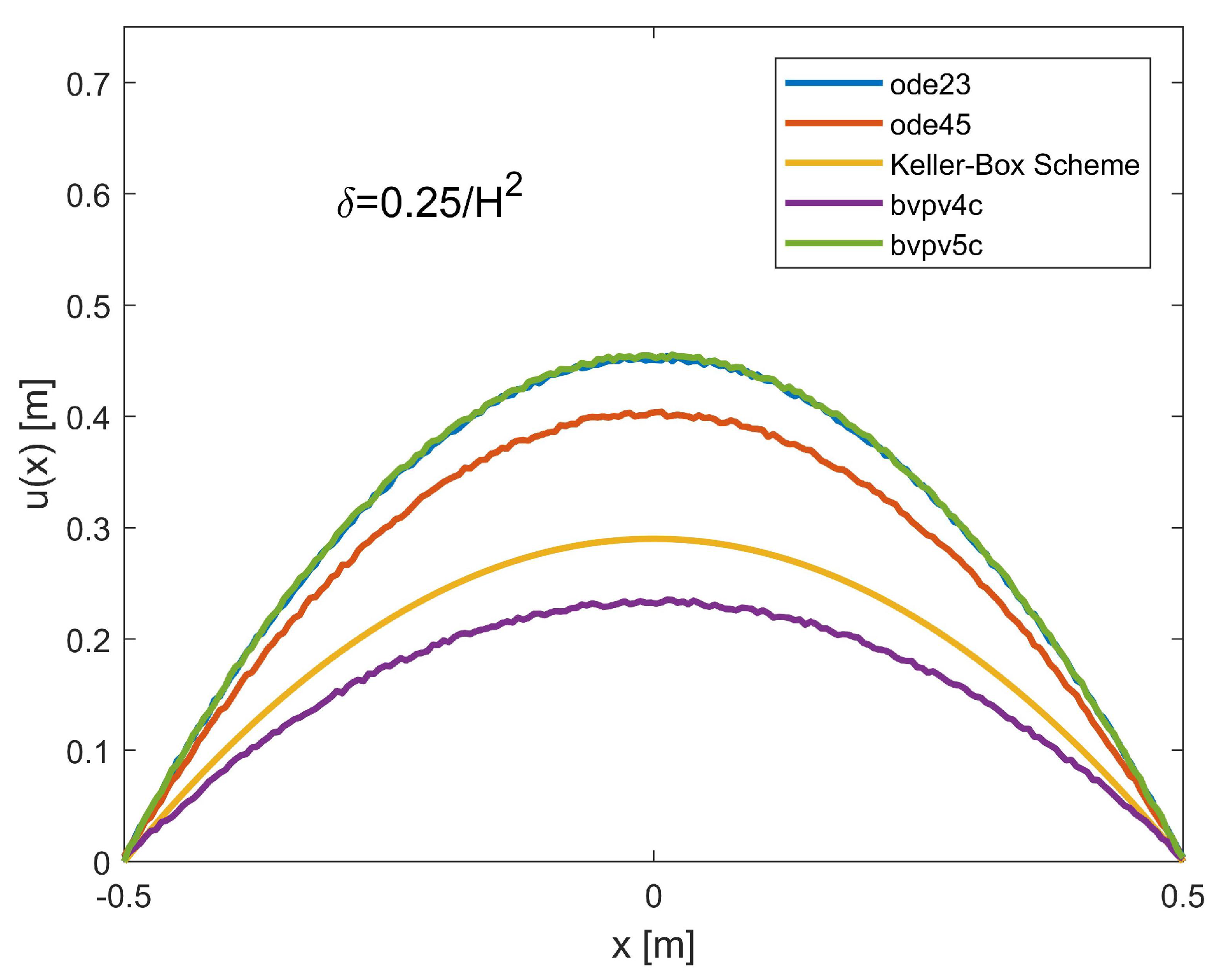
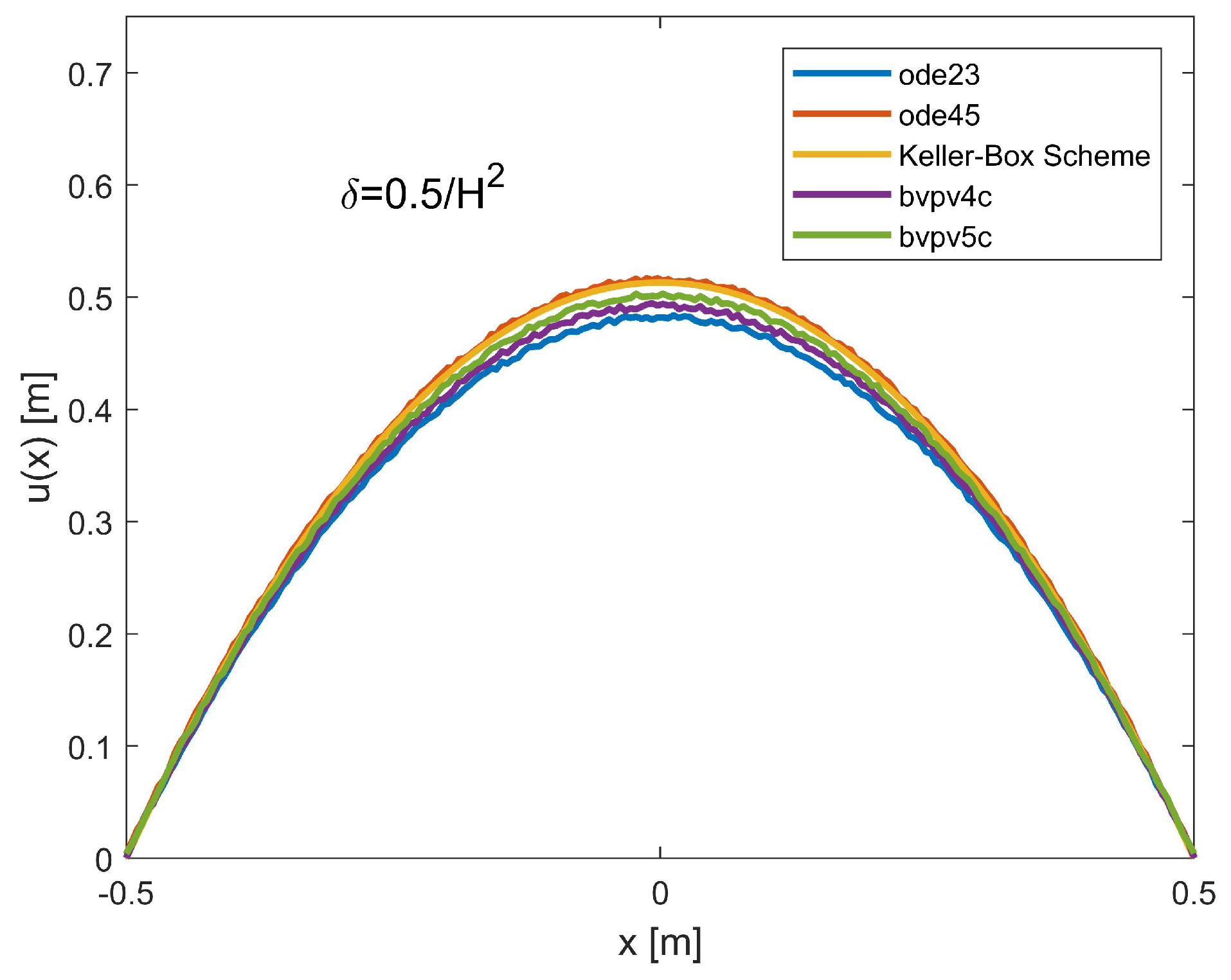
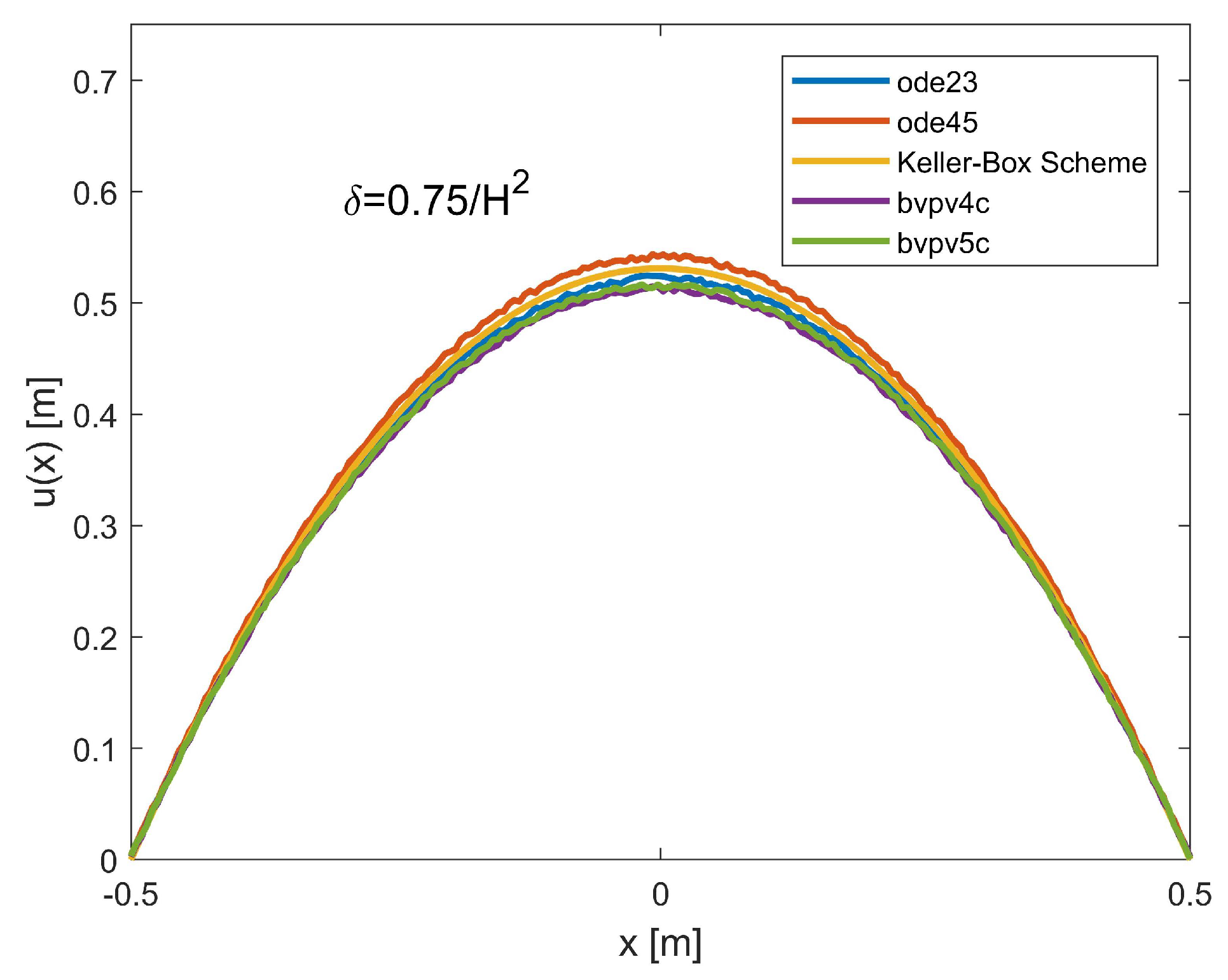

| Shooting (ode 23) | Shooting (ode 45) | Keller-Box Scheme | III-Stage Lobatto IIIa (bpv4c) | IV-Stage Lobatto IIIa (bpv5c) | |
|---|---|---|---|---|---|
| 0 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Versaci, M.; Di Barba, P. Deformable MEMS with Fringing Field: Models, Uniqueness Conditions and Membrane Profile Recovering. Electronics 2022, 11, 798. https://doi.org/10.3390/electronics11050798
Versaci M, Di Barba P. Deformable MEMS with Fringing Field: Models, Uniqueness Conditions and Membrane Profile Recovering. Electronics. 2022; 11(5):798. https://doi.org/10.3390/electronics11050798
Chicago/Turabian StyleVersaci, Mario, and Paolo Di Barba. 2022. "Deformable MEMS with Fringing Field: Models, Uniqueness Conditions and Membrane Profile Recovering" Electronics 11, no. 5: 798. https://doi.org/10.3390/electronics11050798
APA StyleVersaci, M., & Di Barba, P. (2022). Deformable MEMS with Fringing Field: Models, Uniqueness Conditions and Membrane Profile Recovering. Electronics, 11(5), 798. https://doi.org/10.3390/electronics11050798







