Abstract
In recent times, Microgrids (MG) have emerged as solution approach to establishing resilient power systems. However, the integration of Renewable Energy Resources (RERs) comes with a high degree of uncertainties due to heavy dependency on weather conditions. Hence, improper modeling of these uncertainties can have adverse effects on the performance of the microgrid operations. Due to this effect, more advanced algorithms need to be explored to create stability in MGs’. The Model Predictive Control (MPC) technique has gained sound recognition due to its flexibility in executing controls and speed of processors. Thus, in this review paper, the superiority of MPC to several techniques used to model uncertainties is presented for both grid-connected and islanded system. It highlights the features, strengths and incompetencies of several modeling methods for MPCs and some of its variants regarding handling of uncertainties in MGs. This survey article will help researchers and model developers to come up with more robust model predictive control algorithms and techniques to cope with the changing nature of modern energy systems, especially with the increasing level of RERs penetration.
1. Introduction
Due to increased technological advancement, there has been a drastic increase in the demand for global energy. This demand has been geared towards not only making energy globally available but also to ensure an adequate and reliable supply of power devoid of interruptions. The role of the United Nations in trying to make energy accessible and sustainable for all, including the Paris Agreement, which has led to a great investment and hence increased thirst for clean, reliable, and sustainable power supply [1]. The traditional system of power supply has not been in conjunction with the above global consent as it uses fossil fuels to produce power which is one of the main sources of carbon emission, hence negatively impacting the environment. The global desire to produce clean energy has been backed up with improved technologies that have re-branded the ideology of the energy sector from being completely fossil fuel-based to a mixture of both renewable energy-based Distributed Energy Resources (DERs) and clean-burning fossil fuel-based generators.
The continuous use of fossil fuels in the conventional power system has posed a serious threat to the oil and gas reserves and it has been verified that in the next couple of years most of these non-replenishable natural occurring energy resources will be completely depleted. To heal the globe of this situation, global renewable energy markets have evolved massively within the last few decades [2,3]. DERs comprise Renewable Energy Resources (RERs), conventional generators, thermoelectrics, Energy Storage Systems (ESSs), and sufficient ancillary facilities for effective energy supply management and control. RERs (wind, solar biomass, geothermal, etc.) are resources that are harnessed from nature and has the ability to replenish themselves. However, they tend to be limited in flow and amount at any given period of time. A conventional generator uses either propane, gasoline, or diesel to supply electricity via the alternator. Thermoelectric devices produce electricity based on temperature differences while energy storage systems store energy produced at a certain period and use them at a later period to avoid mismatch between demand and supply. RERs are majorly introduced into the conventional power systems to reduce the environmental pollution effects of burning fossil fuels and to produce clean energy that is more environmentally-friendly. Although many countries are adopting the applications of green technologies, however, some major world leaders are still reliant on fossil fuels due to policies and regulations. If renewable energy or green technology is to replace fossil fuels which are the major source of carbon emission in power generation, there must be lucrative and result-oriented based proposals to convince the regulatory bodies and other market players in the fossil fuel business so that a competitive and enabling environment can be created for all [2,3,4]. Both the global renewable energy transition and growth capacity by continent are shown in Figure 1 and Figure 2 [4].
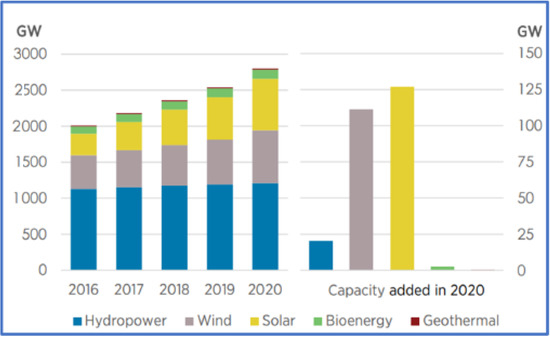
Figure 1.
Global renewable energy transition [4].
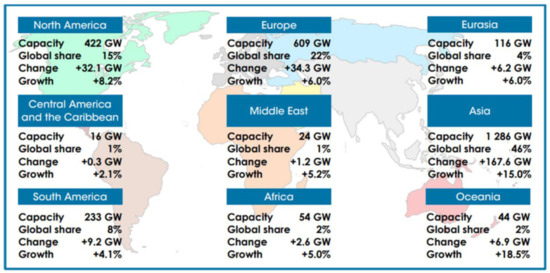
Figure 2.
Renewable Energy Resources (RERs) growth capacity in gigawatt (GW) by continent [4].
Apart from the environmental sustainability benefit of DERs development, there are credible technical benefits in terms of loss reduction, reducing the cost of energy transmission, voltage profile improvement, etc. One significant concept for effective DERs deployment is the concept of Microgrids (MGs) [5,6,7,8]. The definition of MG depends on individual particular views: The DERs planning point of view differs from the control perspective and MG can also be defined based on each DER important characteristics. Firstly, MG can be defined as an integration of DERs and loads, and secondly, MG can be defined as a controllable entity that can operate in either grid-connected or islanded mode. According to the International Council of Large Electrical Systems (CIGRE), MGs are defined as low voltage distribution networks consisting of interconnected loads (controllable and critical) and DERs that can work either as a single or multi-controllable unit being connected to a grid network or islanded [9].
A typical MG consists of RERs like solar PV, wind turbines, fuel cells, Combined Heat and Power units (CHP), solar thermal units, hydropower, and conventional power sources like diesel generators and gas turbines. About 34 percent of the world’s MG establishment can be found in the United States due to the aging energy system being heavily reliant on fossil fuels. MGs have replaced the fossil system for security and reliability. The Asia Pacific takes about 40 percent of the total world MG capacity [9]. Since the world is moving towards getting reliable and sustainable power supply, MGs must be capable of effectively and efficiently supplying power. Many modern control techniques have evolved to help MGs successfully achieve their goals. Control techniques help MGs to deliver the required power due to the intermittencies that emerge from renewable energies. Model predictive control has been recognized immensely over the recent decade due to its ability to handle and process multiple disturbances that stem from RERs.
Motivation of the Study and Research Gap
Without a doubt, the high penetration of RESs into MGs has helped to reduce environmental problems and financial situations of power systems; it, however, comes with a huge negative repercussion. Their availability depends on climatic conditions (rainy/cloudy or sunny days) making them very unpredictable and unreliable. This intermittency has created huge uncertainties in MG operations like voltage and frequency regulations, increased faults, and difficult protection strategies. Hence, maintaining MG system stability, reliability and protection become a challenging issue and a crucial area of research focus. Power stability issues are very low in conventional large power systems compared to small low voltage power systems (MGs) owning to the fact that large systems have a self-stabilizing effect from the frictional force inherent, which is not the case for a small decentralized power system [9]. However, in low voltage decentralized power systems like MGs, the need for system control is very huge due to the numerous instability issues that accompanied the intermittent nature of the RERs. Predictive control in large power systems is very difficult due to large constraints and complex computational analyses but forecasting of RERs and loads is better and cheap compared to small low voltage systems where the accuracy of the forecast results tend to be of poor quality if the process is said to be executed [10]. These uncertainties have created a dynamic environment, making MGs operation very difficult and requiring advanced control techniques to solve stability issues.
Many advanced computational control techniques have been carried out to deal with uncertainties or to model uncertainties in MG operations but few have had satisfactory results in predicting or forecasting demand and RERs [10,11,12,13,14,15,16,17,18,19,20,21,22,23] and if they do, a majority do not compensate for errors in the prediction or forecasting process [13,14]. This gap has created a lot of disturbances in MG operations. Some renowned approaches have been used to model these disturbances which involve assigning probabilities distributions to solve uncertainty issues but the results have not been quite successful in handling the uncertainties due to the computational burden of generated scenarios [14,24,25,26,27,28]. Other optimization approaches have also had an average degree of success in handling these uncertainties due to the conservativeness of the result [29,30,31,32]. Another major issue is the idea of using groups of uncertainty sets for different uncertainty cases [24,33,34,35] instead of using a general or comprehensive uncertainty treatment. This will however lead to the introduction of certain parameters or variables to control the sensitivity of the optimization process [36,37,38,39].
Few research works have entirely considered all necessary uncertainties; the majority of those that claim to include all uncertainties could be on either “all demand” or “all supply” without considering all uncertainties in both demand and supply [11,40]. Error in the forecasting of loads and RESs is very prominent among these control techniques [10,41]. There is however a need for more reliable and accurate control algorithm(s) that can measure uncertainties in MGs. Hence, one of the key control techniques that have gained an enormous reputation in MG operations is Model Predictive Control Algorithm (MPC). MPC can handle Multiple Inputs and Multiple Outputs systems (MIMO). The advantage of its application is that it is a multivariable controller that controls the output simultaneously by taking into account all the in-fractions between system variables [42,43,44,45,46,47,48,49,50]. The speed of the processor enables it to handle multiple complex problems while taking into account the disturbances created in the system. These features make MPC controllers more superior to other control techniques as seen in Table 1.

Table 1.
Comparison between MPC, stochastic, and robust optimization techniques.
MGs have also been exposed to cyber and communication threats over the recent decade due to natural- and human-induced activities. Many control strategies have been developed to ensure the resilience of MGs to physical, cyber, and communication delays and threats but the idea of developing metrics to quantify their resilience has been a difficult task [51,52]. Other control techniques proved to have a computational burden in trying to address issues of communication and cyberattacks [53]. Model predictive controllers have manifested better control effects compared to traditional proportional integral derivative (PID) controllers in responding to communication delays since the length of communication delay affects the MGs stability [48,54,55].
The main research direction is to present a comparative review on MPC-controlled and other uncertainty modeling techniques of microgrid systems. The review considers the various uncertainties (voltage profile enhancement, power quality improvement, transmission losses, and frequency stability) as a whole instead of individual capabilities. This is professed in both grid-connected and islanded microgrid modes. The organization of the remaining paper is as follows: Section 2 presents the basic architecture of MG in terms of both operations and control. Section 3 presents the basic operating principles and concepts of MPC. Section 4 discusses recent applications of MPC to both grid-connected and islanded microgrids design. Section 5 gives an overview of MPC superiority in MG management and the paper is concluded in Section 6.
2. Microgrid Architecture
Several factors have to be considered in establishing a MG, such as the geographical location, financial availability as MG construction requires huge initial capital investments, load demand, and historical knowledge of the existing electrical system of such environment [56]. Hence, for a MG to effectively and efficiently deliver the required power for consumption, the design architecture must support both the operational and control patterns. A typical MG configuration consists of DERs, storage systems, and standard communication and control systems as seen in Figure 3 below. Depending on the purpose of establishment, it can be either grid-connected or islanded and the point of changing from one mode to another is the point of common coupling. The situations of the energy market and availability of RESs initiate the idea of power trading with the main grid and the consideration of the energy storage systems for uninterrupted power supply. Microgrid tends to engage in power trading in two facets: (a) When the available energy supply from the Distributed Energy Resources (DERs) are in excess and (b) when the grid cost of electricity is cheaper than the generation from the DERs. Instead of curtailing the excess energy produced, especially from RERs, it is better to sell to the grid. In addition, the price of electricity from the grid should be monitored to know the periods of lowest tariffs. This power trading improves both the financial and resilient characteristics of the microgrid. The local and central controllers tend to help in shifting the mode of the MGs with the help of power electronics devices [2,3]. Conventional large power systems have used AC configuration owning to the fact that the AC system exhibits an inherent characteristic that supports the characteristic of fossil fuel-driven generators. This makes stability issues a low priority compared to small power systems (MGs) that have huge instability issues. This concept gave birth to the DC MG system where power electronics devices are predominantly used to eradicate issues of stability, reliability, and protection from uncertainties created by RESs. Many other MGs have used hybrid systems where both AC and DC systems are used. The hybrid MG is depicted in Figure 4 below.
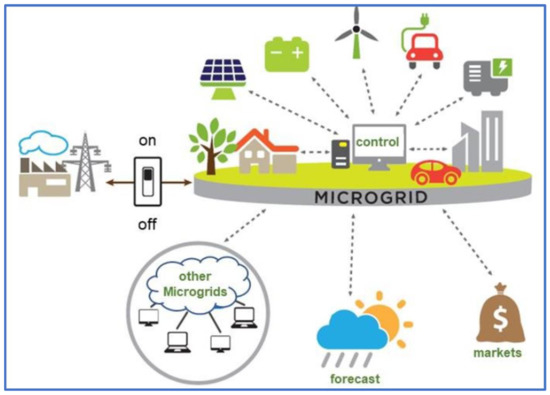
Figure 3.
A typical MG architecture [2].
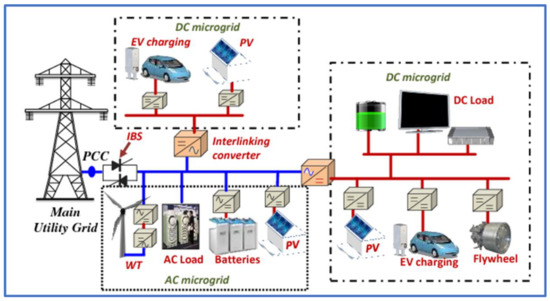
Figure 4.
Hybrid MG architecture [3].
3. MPC Operating Concept and Control Strategy
The idea of MPC dated as far back as the 1970s as it was then centered mainly in process industries. Due to its ability to solve problems of complex dynamic systems, its concept has been widely used in other areas of research, especially in power systems optimization. It is a universal control algorithm that houses a wide range of control tools. It has been one of the main control algorithms because of several inherent characteristics; it can process information of complex systems in the shortest duration (seconds), it can handle systems with multivariable cases, has the tendency of introducing a feedforward control to take responsibility for measurable disturbances, and is very useful when future references are known [57,58]. It has a fast processor with a large memory that solves an online optimization problem at each time step. The control strategy of an MPC is based on the fact that it uses the model of a system to predict what exactly the future outcome will be over a prediction horizon. It then predicts a set of future outcomes from prior historical data based on reference to a particular cost function given by the equation below:
where:
- = reference trajectory;
- = predicted value for variable;
- = variable;
- = weighting factor;
- i = number of variables.
At a particular sampling point or time k, the algorithm executes a set of input values that gives a predicted outcome. Only the first sampling of input is implemented moving the supposed horizon where a new optimal plan will take responsibility for disturbances acting or have acted on the system [59]. The optimization algorithm is repeated at time k + 1 using new measures or estimates, establishing a feedback mechanism which is seen in Figure 5 [60].
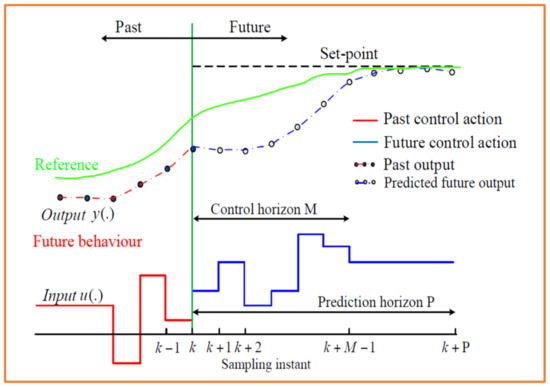
Figure 5.
MPC control strategy [37].
The success of the strategy depends on the structure of the MPC algorithm as seen in Figure 6 [37]. The efficiency of an MPC strategy depends on the process model and optimizer. A model with good prediction characteristics can lead to a good performance of the controller. Based on both historical and available data, the process model captures the dynamics of the system and predicts control outcomes or actions [37] in line with a reference trajectory. The optimizer provides the control mechanism for the algorithm. Both the cost function and constraints available are being controlled by the optimizer. The optimizer ensures that the optimization cost function is analyzed to satisfy the objective function of the optimization problem without violating the necessary constraints acting on the system, and it has the ability to track the errors made in the predictions by the model of the system to avoid forecast errors.
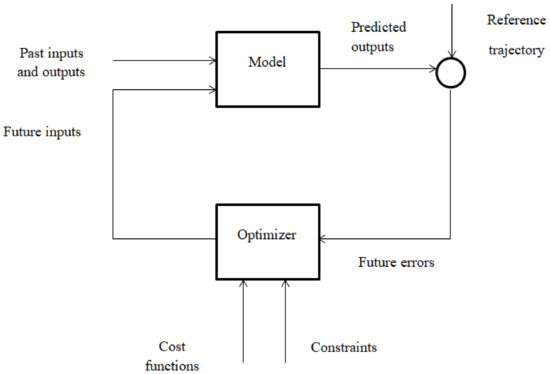
Figure 6.
Basic structure of MPC.
4. MPC-MG Operations
Managing the optimal planning of a microgrid is a very difficult task due to the fact that they are small decentralized low voltage systems with small demand and a high rate of disturbances from intense penetration of RERs. MPC has been applied to both grid-connected and isolated MG systems to help deal with several parameters as seen in Figure 7. Many scholarly works have been done to minimize the operating cost or maximize the revenue generation of microgrids but accurately implementing the mentioned objectives has been difficult due to numerous factors. These factors could be as a result of the intermittency posed by nature (weather conditions), error in trying to predict the situation of nature, and the computational complexities that are associated with optimizing the situation to get an optimal plan. According to [61], there are two standard methods or approaches used to solve the problem of uncertainty in MGs: Reactive approach and preventive approach.
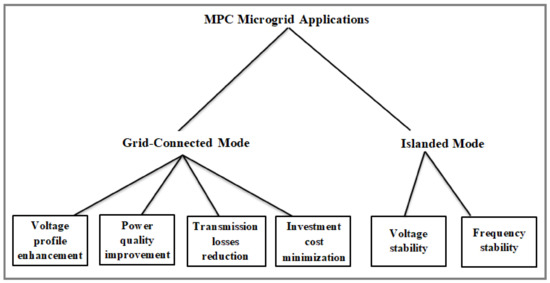
Figure 7.
MPC solution approach to MG operations.
The reactive method depends on a priori information or historical or predefined deterministic data (MPC and rolling horizon approaches) and the preventive method depends on scenario generations (stochastic and robust optimizations). Majority of both the reactive and preventive optimization techniques carried out in MGs are centered on grid-connected systems compared to isolated MGs [62]. The preventive approaches have proven to be ineffective and not reliable for uncertainty considerations.
The stochastic optimization approach requires assigning probabilities for scenario generations, which is sometimes computationally demanding with the static assumption of uncertainty. The robust optimization becomes over-conservative for measurements and requires different algorithms for different uncertainty sets. This is not the case of MPC; it works on inputs of a system considering the internal dynamics to give or predict an output by capturing forecast error to compensate for unforeseen initial forecasting, making it ideal for uncertainty consideration [63,64,65]. A comparison between MPC and preventive optimizations is given in Table 1.
Many times, MPC has been combined with either of the two preventive methods to prevent or reduce uncertainties in many scholarly articles. When MPC is combined with stochastic optimization to give the Stochastic Model Predictive Control (SMPC), the stochastic scenarios are used to execute the optimization process by assigning probabilities without much or totally considering the disturbances in the process. The MPC technique helps to reduce the computational time and takes account of the uncertainties without assuming by implementing a feedback scenario where compensation is done to eradicate the external influences of the integration of renewable technologies.
Thus, combining model predictive control with robust optimization gives a better result compared to robust optimization because instead of employing different algorithms which require time and more expertise, MPC does a single consideration of all the uncertainties or disturbances acting on the system. The optimizer in the MPC algorithm has the ability to trace errors made by the process model in predicting future outputs based on the dynamics of the system. Conservatism is highly reduced by the action of the MPC compensation process.
4.1. MPC for Grid-Connected MG Applications
More work of MPC applications to MG is centered on grid-connected systems than isolated systems because the cost of implementing measurements, automation, forecasting, and information processing is very small compared with the derived economic benefits as opposed to isolated systems [10]. Accuracy of the forecast of load and RERs is of better quality in grid-connected systems. Decentralizing power systems through the establishment of MGs has led to an increase in demand and accessibility of energy but comes with uncertainties of demand and RERs.
Barrios et al. proposed an MPC approach for unit commitment in MG in the presence of high uncertainties associated with demand and RESs [66]. A particular type of energy market is considered so that the MG can provide the required demand of load and RERs. An MPC technique is applied at every time step to cover demand regarding uncertainties introduced due to prediction. The main objective of the MPC technique adopted in the work is to reduce the operational cost. Two conditions are considered in the study, which is the conventional unit commitment and unit commitment based on MPC. Prediction errors increased the operation cost of the conventional system but a reduced cost is seen for the MPC unit commitment due to the feedback mechanism.
Parisio et al. proposed that the decentralization of the power system has led to an increase in energy demand and therefore requires new methodologies to model a smart grid environment [67]. The work is focused on minimizing overall MG operational costs to match predicted demand for a certain day by obeying the complex constraints. Four different strategies are considered, which are heuristics, Mixed-Integer Linear Programming (MILP), MILP-MPC, and benchmark. It is supposed that the demand for load and RERs are known with certainty. The proposed MILP-MPC gives less violation because of the feedback mechanism introduced by the MPC, giving a result closed to the benchmark. The cost function is given as:
subject to:
where:
- = disturbances vectors;
- = assumed to be known over prediction horizon for ;
- = independent of objective function;
- = column vectors;
- = time step.
Xie and IIic proposed an MPC algorithm to dispatch all the available resources to supply fluctuating loads at a minimum cost due to consideration of the prediction model [68]. The output of the controllable units is adjusted to compensate for uncertainties. Kou et al. [69] proposed a Stochastic Model Predictive Control (SMPC) approach that works in a two-layer step. The top layer ensures that there is a balance of power in the system and the bottom layer considers the uncertainties emerging from both supply and demand ends. The main objective of the proposed approach is to ensure optimal power scheduling with total consideration of disturbances acting on the system. The special attribute associated with this proposed approach is the consideration of all uncertainties from both demand and supply sides. The uncertainties from wind generation and PEV charging both have different distribution characteristics but the MPC controller in the system handles both uncertainties simultaneously instead of treating them as separate uncertainty sets.
Despite MPC’s ability to compensate for disturbances in the RERs system, some violations have been experienced in scheduling optimal resources. In order to mitigate, these violations, forecasting errors have to be taken into consideration. Y. Zhang et al. proposed an MPC approach, considering forecasting uncertainties and forecast errors of load, wind, PV, and electricity price [70]. The work incorporated stochastic analysis where scenarios are generated to approximate forecast errors and uncertainties. The objective is to minimize operation costs. Three different states of the art approaches are compared to the proposed stochastic MPC; a Deterministic Day Ahead programming (D-DA), a Stochastic Day Ahead programming (S-DA), and Deterministic Standard MPC (D-MPC). Simulation results show that S-MPC yields the lowest cost compared to D-MPC. This is because both S-DA and D-DA are open-loop systems where optimization takes place only at the beginning of the scheduling. Both D-MPC and S-MPC are closed-loop where optimization is executed once for each time step. S-MPC considers all uncertainties affecting the system while D-MPC assumes that the system is stable with known demand and no disturbance.
Gulin et al. proposed an approach of a power flow optimization in a Direct Current (DC) MG that accounts for predictions uncertainty [71]. Unlike other methods of uncertainty consideration, here a chance-constrained method is used to account for power prediction uncertainties. The work is done on the idea of allowing violations of constraints in line with predefined probability levels, allowing the utility grid to compensate for error(s) on the prediction horizon. Two different approaches are used to deliver a minimum cost; D-MPC and S-MPC. D-MPC did not account for uncertainties while S-MPC accounted for uncertainties and gives a lower cost by allowing a tradeoff between constraints being violated and prospect. Both approaches are defined below.
D-MPC scheme is defines as:
Subject to:
S-MPC scheme is defined as:
Subject to:
where:
- J = Economic criterion;
- u = Linear function;
- = Optimization control sequence;
- = Initial storage state;
- = Minimum grid availability, grid availability at time instant k, and maximum grid availability.
Dao et al. proposed a hierarchical and distributed MPC approach for the energy management of a microgrid. The main objective of the proposed approach is to provide an economic management framework to maximize the benefits of the system. In order to ensure that forecast errors are taken into consideration and that uncertainties are effectively and efficiently handled to enhance maximum benefits, a negotiation activity or process is carried out between the hierarchical and distributed MPC algorithms to compensate for forecast errors within the system [72]. Gambino et al. proposed an economic dispatch problem for an integrated microgrid (heat and electricity generation). The main objective of the proposed approach is to optimally dispatch resources so as to minimize the overall cost of the microgrid. Microgrids that normally incorporate dual derivatives, as the case of combined heat and power to solve economic dispatch problems, are prone to uncertainties from loads, energy prices, and weather forecasts. A feedback mechanism generated by the MPC controller compensates for uncertainties associated with time-varying loads, energy prices, and RERs power outputs [73].
Bella et al. proposed a hierarchical MPC (two-layer control system) control scheme that constitutes of dynamic decoupled subsystems. The main objective of the approach is to optimally share resources among the various subsystems so as to satisfy the overall demand and account for disturbances acting on the system [74]. Scheduling takes place in the upper layer and each subsystem is adjusted or designed in a way that at any time instance, an independent control action can be executed from the internal request or a neighboring subsystem based on the MPC. At the end of every time step, the supervisor checks the system for either a deficit or excess demand in each subsystem. A compensation activity is initiated by the supervisor in the subsystem(s) that exhibit shortages due to disturbances or uncertainties so as to ensure the overall system demand is achieved.
The majority of researchers have focused on exogenous factors or external factors (customer loads, wind speed, PV, and price profile) in considering uncertainty measurements with few works or no work being done considering endogenous factors (types of equipment, and storage). Prodan and Zio proposed a predictive control framework that takes into account uncertainties modeling. The work is focused on including internal (state) dynamics and structural properties of the individual components of RESs (solar and wind, on-site storage) which may change (stochastically) due to degradation, failure, and aging effects. By considering both factors, the operating cost of the system can be reduced [75]. Nassouron et al. proposed an MPC approach for an economic dispatch problem considering heterogeneous systems (system with different computational applications) [76]. Owning to the fact that several heterogeneous generators and storage elements are used in the approach, the dispatch problem cannot be solved using classical optimization methods due to the differences in characteristics of the generators and storage elements. Two techniques are used to optimally schedule the resources: MPC tracking and Economic MPC (EMPC). The Economic MPC yields a better cost compared to the tracking MPC. Table 2 shows the summary of recent approaches of MPC applications to grid-connected systems.

Table 2.
Summary of recent MPC applications to grid-connected systems.
From Table 2, it is evident that the introduction of MPC, either as an independent operation or a combination of MPC and other modeling techniques gives a better and desirable outcome of handling the various uncertainties compared to the various preventive techniques. The table presents a summary of different objectives and uncertainty handling strategies but what is more unique is the capability of MPC to model the disturbances and achieve the desired goals. This explanation is also applicable to Table 3 in the case of islanded systems.

Table 3.
Summary of recent MPC applications to islanded systems.
4.2. MPC for Isolated MG Applications
Many utility companies and government-sponsored electric power systems have been implementing or providing incentives or demand-side management opportunities for their customers to establish on-site Distributed Generators (DGs) and energy storage systems to increase the number of isolated MGs in the supply of power. However, these efforts have proven to be quite expensive or not cost-effective at all. Hence, several research efforts have been devoted and are continuously being devoted to achieving the cost-effective operation of the isolated microgrid.
Parissio et al. proposed an MPC approach for energy management of multiple residential MGs having DERs, electrical storage systems with both thermal, and electrical loads [92]. The objective of the proposed MPC approach is to reduce energy costs and improve customers’ comfort through a demand-side management scheme. An optimal plan is computed to compensate for imbalances affecting the system based on the weather forecast. The demand-side management scheme can help customers to know when to have an affordable cost of uninterruptable power.
Most of the works in predictive algorithms have considered favorable conditions (where generation is greater than demand). According to [93], a nonlinear MPC algorithm is developed or proposed for an Energy Management System (EMS) of an isolated MG with DERs in which automated load shedding of non-critical loads is done when the system foresees power imbalances that could affect the stability of the MG. This predictive algorithm is proposed to identify upcoming generation problems when MG is operating in an islanded mode. The objective is to predict and manage constraints in states and control signals. Hans et al. proposed a control technique that can give better prediction accuracy while minimizing cost. Comparison is presented between an open-loop minimax approach and closed-loop minimax MPC approach considering the worst-case cost evaluation in trying to get better prediction accuracy and uncertainty handling [94]. The open-loop system gives a very conservative solution because it did not implement a feedback mechanism. The closed-loop Minimax MPC strategy however employed the theory of paramterization (choosing parameters) of future inputs on the predicted disturbance leading to accurate predictions and lower cost. This is due to the presence of the MPC strategy that normally uses a predefined input to make accurate future predictions.
Gu et al., proposed an MPC technique for Combined Cooling, Heat, and Power microgrid (CCHP) with feedback correction to reduce running cost and handle uncertainties [95]. A two-stage optimization approach is executed in this work of which the first stage is based on forecasting the required load and renewable energies integration. The second stage focuses on compensating for the error in the prediction process. The MPC ensures that forecast is repeated for every time interval to get accurate data to be in line with rapid changes that take place in load and RERs demand. If, however, there is a disturbance in the system due to inaccurate forecasting, a feedback correction is done to eliminate the disturbance.
Deterministic unit commitments have proven inappropriate for island MGs because their small scale demands are hard to predict and RERs generation is highly variable. Y. Zhang et al., proposed a Robust Model Predictive Control (RMPC) approach to solve the operating cost of an islanded MG by minimizing cost [57]. The work states that of recent times, both chance-constrained and scenario-based stochastic optimization methods have been used to minimize MG cost. It has however, been concluded that these two methods involve high or huge computational burden and uncertain parameters and forecast errors are not accurately accounted for and as a result, have posed a high negative impact on MG cost.
However, another method is the robust optimization used to solve an optimal scheduling problem with uncertain parameters. The conservativeness of this approach is a huge concern for cost minimization by MG operators. In this proposed RMPC approach, an MPC is introduced to reduce the conservativeness of the RO due to the rolling up manner and feedback mechanism that it exhibits. Two control strategies are considered in the approach used; a conventional 2-stage RO and RMPC-based optimization. The results for the cost function of RMPC is lower than the conventional two-stage RO since a feedback control action is generated to consider the forecast uncertainties. This is justified by the RO cost function with the uncertainty budget given below.
subject to:
where:
- = auxiliary variables.
Sach et al. proposed a stochastic model predictive control approach for a rural isolated microgrid. The main focus or objective of the proposition is the development of an advanced control technique to improve robustness towards predictions error and uncertainties acting on the system. For normal MPC operation, a control technique is implemented for a one-time step and subsequent control actions rely on the dignity of the previous time step [96]. This proposed stochastic MPC considers the probability of a constraint violation over several time steps. A probability distribution approach based on the stochasticity of the load and renewables is used to compensate for the disturbances on the system. Jaboulay et al. proposed a controlled algorithm based on MPC with the objective of minimizing operation cost and maintaining power balance in the system [97]. The controller takes into account the physical constraints of the system while scheduling the required resources. Instead of making a few decisions as opposed to other control techniques for every time step, the MPC takes multiple decisions for every updated forecast because it can handle multiple inputs and outputs. Scenarios are run in parallel on a semi-physical platform to compensate for uncertainties.
According to [10], the cost of forecast service and power quality using automation is very high in isolated systems compared to grid-connected systems. Zhang et al. proposed an EMS for multi-isolated MGs connected by a centralized system to minimize the overall cost of the EMS [47]. An MPC technique is introduced with the intent of considering or reducing the impacts of forecast errors of the load and RERs, hence reducing overall cost. Berkel et al. proposed a hierarchical MPC for a smart MG to solve the power stability issue. Two (2) levels of management are presented where the first level solves the frequency issue and the second level solves the cost function. The objective of the hierarchical MPC is to make accurate predictions of load and RERs by rejecting disturbances from penetration and to handle constraints to guarantee stability and performance of the smart MG [9]. The summary of recent approaches of MPC applications to isolated systems is shown in Table 3 below.
5. Superiority of MPC in Microgrid Designs and Operational Management
Various problems encountered in the operations of both grid-connected and isolated microgrid systems, as described in Table 2 and Table 3 above, are in actual situations quite challenging to manage. However, the introduction of MPC has helped achieve a better system design, which considerably reduces the operation cost. As a summary of the various operation problems discussed above, the following highlights show the MPC’s superiority:
- In grid-connected microgrids, the prediction of energy market situations is achieved more accurately in terms of the load demand and generation dynamics, especially in the face of the uncertainties introduced by RERs. In isolated microgrids, operating in favorable conditions or deterministic conditions, where demand is known with certainty, is not possible because of the unpredictable nature of RERs. The effectiveness of MPC in tracking the disturbances and uncertainties has led to an increase in the desired operational benefits under these two conditions.
- In hybrid systems with thermal generators, a conventional unit commitment operation cannot accurately predict the output of RERs, which increases the effective operational cost. MPC introduction has, however, helped to achieve better control of prediction errors by the effects of its superior feedback mechanisms. In standalone systems and hybrid systems, MPC encourages multiple residential microgrids to interact effectively. It enhances efficient Peer-to-Peer (p2p) energy trading by cognizant of the differences in the energy needs and energy produced by connected parties known as the ‘Prosumers’ [114].
- Stochastic approaches do not give reliable performances when it comes to forecasting and forecast errors; combining MPC with this operation condition yields improved results in the desired outputs. The MPC exhibits superior performances compared to other options by considering both external and internal factors while solving uncertainty issues.
Below are also the limitations of MPC:
- One of the biggest challenges of MPC applications is that, it relies on historical information to predict the future. For newly-established energy systems (grid-connected or islanded), the application of MPC looks extremely difficult or impossible.
- MPC applications require high modeling expertise which comes with a high cost.
- The quality and accuracy of the predictive model plays a significant role in the control process. Having a balanced trade-off between the model accuracy and calculation complexity is a serious challenge.
- Another key issue in MPC is the design of the sampling interval. This interval determines the performance of the model. A better performance can be achieved considering small sampling time intervals. This will however reduce computational burden and economy of scale.
6. Conclusions
Recently microgrids have emerged as an approach to make energy easily available to global demand. This is more prominent to areas that are remote or inaccessible for grid connections. However, the presence of RERs tend to make the operation of the MG environment very uncertain due to the various disturbances that erupt from their penetrations. The advancement in technology has produced numerous modeling techniques to handle the uncertainties associated with the penetration effects. Various modeling techniques to model uncertainties in microgrids are presented in this review exercise but the results show that there are still deficiencies in the control process. Due to the speed of the processor along with its ability to adapt to several applications, it has now become a preferential control technique. A review of two classifications of modeling uncertainties (proactive and preventive) are presented in this review. The merits and demerits of each of the classifications were presented, showing the superiority of a proactive approach (MPC and rolling horizon) to preventative (stochastic and robust).
This review is limited to only the modeling of power availability from DERs, especially RERs in the MG environment. Future work could be focused on a specific uncertainty like voltage or frequency control, faults detection, or other protection control objectives.
Author Contributions
K.V.K. conceptualized and prepared original draft; O.B.A. provided resource, edited the manuscript and provided funding; M.E.L. provided resource and editing; Y.S. validated and provided funding; T.S. supervised. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abujarad, S.Y.; Mustafa, M.; Jamian, J. Recent approaches of unit commitment in the presence of intermittent renewable energy resources: A review. Renew. Sustain. Energy Rev. 2017, 70, 215–223. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Kumar, K.P.; Saravanan, B. Recent techniques to model uncertainties in power generation from renewable energy sources and loads in microgrids—A review. Renew. Sustain. Energy Rev. 2017, 71, 348–358. [Google Scholar] [CrossRef]
- Agency, I.R.E.N.A. Renewable Capacity Highlights. 2021. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2021/ (accessed on 15 December 2021).
- Parag, Y.; Ainspan, M. Sustainable microgrids: Economic, environmental and social costs and benefits of microgrid deployment. Energy Sustain. Dev. 2019, 52, 72–81. [Google Scholar] [CrossRef]
- Anestis, A.; Georgios, V. Economic benefits of Smart Microgrids with penetration of DER and mCHP units for non-interconnected islands. Renew. Energy 2019, 142, 478–486. [Google Scholar] [CrossRef]
- Astriani, Y.; Shafiullah, G.; Anda, M.; Hilal, H. Techno-economic Evaluation of Utilizing a Small-Scale Microgrid. Energy Procedia 2019, 158, 3131–3137. [Google Scholar] [CrossRef]
- Basu, A.K.; Chowdhury, S.; Chowdhury, S.; Paul, S. Microgrids: Energy management by strategic deployment of DERs—A comprehensive survey. Renew. Sustain. Energy Rev. 2011, 15, 4348–4356. [Google Scholar] [CrossRef]
- Berkel, F.; Görges, D.; Liu, S. Load-frequency control, economic dispatch and unit commitment in smart microgrids based on hierarchical model predictive control. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 2326–2333. [Google Scholar] [CrossRef]
- Mazzola, S.; Vergara, C.; Astolfi, M.; Li, V.; Perez-Arriaga, I.; Macchi, E. Assessing the value of forecast-based dispatch in the operation of off-grid rural microgrids. Renew. Energy 2017, 108, 116–125. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khambadkone, A.M.; Khosravi, A. A computational framework for uncertainty integration in stochastic unit commitment with intermittent renewable energy sources. Appl. Energy 2015, 152, 71–82. [Google Scholar] [CrossRef]
- Alharbi, W.; Bhattacharya, K. Accommodating High Levels of Renewable Generation in Remote Microgrids under Uncertainty. In Proceedings of the 2014 IEEE Electrical Power and Energy Conference, Calgary, AB, Canada, 12–14 November 2014; pp. 60–64. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.; Kim, H. Robust Optimal Operation of AC/DC Hybrid Microgrids Under Market Price Uncertainties. IEEE Access 2018, 6, 2654–2667. [Google Scholar] [CrossRef]
- Mazidi, M.; Rezaei, N.; Ghaderi, A. Simultaneous power and heat scheduling of microgrids considering operational uncertainties: A new stochastic p-robust optimization approach. Energy 2019, 185, 239–253. [Google Scholar] [CrossRef]
- Kong, X.; Liu, D.; Wang, C.; Sun, F.; Li, S. Optimal operation strategy for interconnected microgrids in market environment considering uncertainty. Appl. Energy 2020, 275, 115336. [Google Scholar] [CrossRef]
- Gao, H.; Xu, S.; Liu, Y.; Wang, L.; Xiang, Y.; Liu, J. Decentralized optimal operation model for cooperative microgrids considering renewable energy uncertainties. Appl. Energy 2020, 262, 114579. [Google Scholar] [CrossRef]
- Ahmadi, S.E.; Rezaei, N. A new isolated renewable based multi microgrid optimal energy management system considering uncertainty and demand response. Int. J. Electr. Power Energy Syst. 2020, 118, 105760. [Google Scholar] [CrossRef]
- Luo, L.; Abdulkareem, S.S.; Rezvani, A.; Miveh, M.R.; Samad, S.; Aljojo, N.; Pazhoohesh, M. Optimal scheduling of a renewable based microgrid considering photovoltaic system and battery energy storage under uncertainty. J. Energy Storage 2020, 28, 101306. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, Y.; Wang, J.; Cao, X.; Khan, M.A. Multi-period planning of multi-energy microgrid with multi-type uncertainties using chance constrained information gap decision method. Appl. Energy 2020, 260, 114188. [Google Scholar] [CrossRef]
- Manohar, M.; Koley, E.; Ghosh, S. Microgrid protection under weather uncertainty using joint probabilistic modeling of solar irradiance and wind speed. Comput. Electr. Eng. 2020, 86, 106684. [Google Scholar] [CrossRef]
- Das, S.; Basu, M. Day-ahead optimal bidding strategy of microgrid with demand response program considering uncertainties and outages of renewable energy resources. Energy 2020, 190, 116441. [Google Scholar] [CrossRef]
- Gilani, M.A.; Kazemi, A.; Ghasemi, M. Distribution system resilience enhancement by microgrid formation considering distributed energy resources. Energy 2020, 191, 116442. [Google Scholar] [CrossRef]
- Hemmati, M.; Mohammadi-Ivatloo, B.; Abapour, M.; Anvari-Moghaddam, A. Day-ahead profit-based reconfigurable microgrid scheduling considering uncertain renewable generation and load demand in the presence of energy storage. J. Energy Storage 2020, 28, 101161. [Google Scholar] [CrossRef]
- Zakaria, A.; Ismail, F.B.; Lipu, M.H.; Hannan, M. Uncertainty models for stochastic optimization in renewable energy applications. Renew. Energy 2020, 145, 1543–1571. [Google Scholar] [CrossRef]
- Vergara, P.P.; López, J.C.; Rider, M.J.; Shaker, H.R.; da Silva, L.C.; Jørgensen, B.N. A stochastic programming model for the optimal operation of unbalanced three-phase islanded microgrids. Int. J. Electr. Power Energy Syst. 2020, 115, 105446. [Google Scholar] [CrossRef]
- Hong, B.; Zheng, Z. Stochastic multi-objective dynamic optimal dispatch for combined heat and power microgrid. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 2369–2373. [Google Scholar] [CrossRef]
- Jianhui, W.; Yang, S.; Ying, J.; Wenzhong, G.; Wenbo, S. Stochastic Energy Scheduling in Microgrids Considering Uncertainties of Renewable Energy and Stochastic Load. In Proceedings of the 2017 International Conference on Smart Grid and Electrical Automation (ICSGEA), Changsha, China, 27–28 May 2017; pp. 179–183. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Stochastic Investment Planning Model of Multi-energy Microgrids considering Network Operational Uncertainties. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 2583–2587. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Q.; Wang, L.; Feng, W. Robust optimization for energy transactions in multi-microgrids under uncertainty. Appl. Energy 2018, 217, 346–360. [Google Scholar] [CrossRef]
- Borges, N.; Soares, J.; Vale, Z. A Robust Optimization for Day-ahead Microgrid Dispatch Considering Uncertainties. IFAC-PapersOnLine 2017, 50, 3350–3355. [Google Scholar] [CrossRef]
- Kuznetsova, E.; Ruiz, C.; Li, Y.F.; Zio, E. Analysis of robust optimization for decentralized microgrid energy management under uncertainty. Int. J. Electr. Power Energy Syst. 2015, 64, 815–832. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q.; Ding, R.; Sun, M.; Wang, G. Integrated scheduling of energy supply and demand in microgrids under uncertainty: A robust multi-objective optimization approach. Energy 2017, 130, 1–14. [Google Scholar] [CrossRef]
- Ji, L.; Huang, G.; Xie, Y.; Zhou, Y.; Zhou, J. Robust cost-risk tradeoff for day-ahead schedule optimization in residential microgrid system under worst-case conditional value-at-risk consideration. Energy 2018, 153, 324–337. [Google Scholar] [CrossRef]
- Nadal, A.; Ruby, A.; Bourasseau, C.; Riu, D.; Berenguer, C. Accounting for techno-economic parameters uncertainties for robust design of remote microgrid. Int. J. Electr. Power Energy Syst. 2020, 116, 105531. [Google Scholar] [CrossRef] [Green Version]
- Khodaei, A.; Bahramirad, S.; Shahidehpour, M. Microgrid Planning Under Uncertainty. IEEE Trans. Power Syst. 2015, 30, 2417–2425. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y.; Dong, Z.; Wong, K.P. Robust Security Constrained-Optimal Power Flow Using Multiple Microgrids for Corrective Control of Power Systems Under Uncertainty. IEEE Trans. Ind. Inform. 2017, 13, 1704–1713. [Google Scholar] [CrossRef]
- Lara, J.D.; Olivares, D.E.; Cañizares, C.A. Robust Energy Management of Isolated Microgrids. IEEE Syst. J. 2019, 13, 680–691. [Google Scholar] [CrossRef]
- Zhao, B.; Qiu, H.; Qin, R.; Zhang, X.; Gu, W.; Wang, C. Robust Optimal Dispatch of AC/DC Hybrid Microgrids Considering Generation and Load Uncertainties and Energy Storage Loss. IEEE Trans. Power Syst. 2018, 33, 5945–5957. [Google Scholar] [CrossRef]
- Craparo, E.; Karatas, M.; Singham, D.I. A robust optimization approach to hybrid microgrid operation using ensemble weather forecasts. Appl. Energy 2017, 201, 135–147. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Gao, L. Stochastic Energy Scheduling in Microgrids Considering the Uncertainties in Both Supply and Demand. IEEE Syst. J. 2018, 12, 2589–2600. [Google Scholar] [CrossRef]
- Zepter, J.M.; Weibezahn, J. Unit commitment under imperfect foresight – The impact of stochastic photovoltaic generation. Appl. Energy 2019, 243, 336–349. [Google Scholar] [CrossRef]
- Nelson, J.R.; Johnson, N.G. Model predictive control of microgrids for real-time ancillary service market participation. Appl. Energy 2020, 269, 114963. [Google Scholar] [CrossRef]
- Castilla, M.; Bordons, C.; Visioli, A. Event-based state-space model predictive control of a renewable hydrogen-based microgrid for office power demand profiles. J. Power Source 2020, 450, 227670. [Google Scholar] [CrossRef] [Green Version]
- Batiyah, S.; Sharma, R.; Abdelwahed, S.; Zohrabi, N. An MPC-based power management of standalone DC microgrid with energy storage. Int. J. Electr. Power Energy Syst. 2020, 120, 105949. [Google Scholar] [CrossRef]
- Elkazaz, M.; Sumner, M.; Thomas, D. Energy management system for hybrid PV-wind-battery microgrid using convex programming, model predictive and rolling horizon predictive control with experimental validation. Int. J. Electr. Power Energy Syst. 2020, 115, 105483. [Google Scholar] [CrossRef]
- Sedhom, B.E.; El-Saadawi, M.M.; Hatata, A.Y.; Alsayyari, A.S. Hierarchical control technique-based harmony search optimization algorithm versus model predictive control for autonomous smart microgrids. Int. J. Electr. Power Energy Syst. 2020, 115, 105511. [Google Scholar] [CrossRef]
- Wen, S.; Xiong, W.; Cao, J.; Qiu, J. MPC-based frequency control strategy with a dynamic energy interaction scheme for the grid-connected microgrid system. J. Frankl. Inst. 2020, 357, 2736–2751. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y. Hierarchical model predictive control of wind farm with energy storage system for frequency regulation during black-start. Int. J. Electr. Power Energy Syst. 2020, 119, 105893. [Google Scholar] [CrossRef]
- Peng, H.; Li, F.; Kan, Z. A novel distributed model predictive control method based on a substructuring technique for smart tensegrity structure vibrations. J. Sound Vib. 2020, 471, 115171. [Google Scholar] [CrossRef]
- Li, B.; Roche, R. Optimal scheduling of multiple multi-energy supply microgrids considering future prediction impacts based on model predictive control. Energy 2020, 197, 117180. [Google Scholar] [CrossRef]
- Mishra, S.; Anderson, K.; Miller, B.; Boyer, K.; Warren, A. Microgrid resilience: A holistic approach for assessing threats, identifying vulnerabilities, and designing corresponding mitigation strategies. Appl. Energy 2020, 264, 114726. [Google Scholar] [CrossRef] [Green Version]
- Huadong Mo, G.S. Real-time coordination of distributed energy resources for frequency control in microgrids with unreliable communication. Int. J. Electr. Power Energy Syst. 2018, 96, 86–105. [Google Scholar] [CrossRef]
- Meng, X.; Zhou, N.; Wang, Q. Improved distributed event-triggered control for inverter-based AC microgrids under deceptive cyberattacks. Int. J. Electr. Power Energy Syst. 2020, 120, 106000. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Q.; He, B.; Wang, Y.; Yang, J.; Pan, X. Load frequency control in multiple microgrids based on model predictive control with communication delay. J. Eng. 2017, 2017, 1851–1856. [Google Scholar] [CrossRef]
- Lou, G.; Gu, W.; Sheng, W.; Song, X.; Gao, F. Distributed Model Predictive Secondary Voltage Control of Islanded Microgrids With Feedback Linearization. IEEE Access 2018, 6, 50169–50178. [Google Scholar] [CrossRef]
- Mariam, L.; Basu, M.; Conlon, M.F. A Review of Existing Microgrid Architectures. J. Eng. 2013, 2013, 937614. [Google Scholar] [CrossRef] [Green Version]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Sultana, W.R.; Sahoo, S.K.; Sukchai, S.; Yamuna, S.; Venkatesh, D. A review on state of art development of model predictive control for renewable energy applications. Renew. Sustain. Energy Rev. 2017, 76, 391–406. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J. Process Dynamics and Control; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Silvente, J.; Kopanos, G.M.; Dua, V.; Papageorgiou, L.G. A rolling horizon approach for optimal management of microgrids under stochastic uncertainty. Chem. Eng. Res. Des. 2018, 131, 293–317, Energy Systems Engineering. [Google Scholar] [CrossRef] [Green Version]
- Farrokhabadi, M.; Cañizares, C.A.; Bhattacharya, K. Unit Commitment for Isolated Microgrids Considering Frequency Control. IEEE Trans. Smart Grid 2018, 9, 3270–3280. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.; Zhu, W.; Bao, X.; Liu, C. Robust model predictive control for optimal energy management of island microgrids with uncertainties. Energy 2018, 164, 1229–1241. [Google Scholar] [CrossRef]
- Kachhap, S.; Mohanta, D.K.; Jha, R.C. Reliabilty evaluation of microgrid scheduling. In Proceedings of the 2017 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 17–18 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hu, W.; Wang, P.; Gooi, H.B. Toward Optimal Energy Management of Microgrids via Robust Two-Stage Optimization. IEEE Trans. Smart Grid 2018, 9, 1161–1174. [Google Scholar] [CrossRef]
- Barrios, L.A.; Valerino, J.B.; Nozal, R.; Escaño, J.M.; Martínez-Ramos, J.L.; Gonzalez-Longatt, F. Stochastic Unit Commitment in Microgrids based on Model Predictive Control. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Xie, L.; Ilic, M.D. Model predictive dispatch in electric energy systems with intermittent resources. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 42–47. [Google Scholar] [CrossRef]
- Kou, P.; Feng, Y.; Liang, D.; Gao, L. A model predictive control approach for matching uncertain wind generation with PEV charging demand in a microgrid. Int. J. Electr. Power Energy Syst. 2019, 105, 488–499. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Wang, R.; Liu, Y.; Guo, B.; Zhang, T. Dynamic dispatch of isolated neighboring multi-microgrids based on model predictive control. In Proceedings of the 2016 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Chengdu, China, 19–22 October 2016; pp. 50–55. [Google Scholar] [CrossRef]
- Gulin, M.; Matuško, J.; Vašak, M. Stochastic model predictive control for optimal economic operation of a residential DC microgrid. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 505–510. [Google Scholar] [CrossRef]
- Dao, L.A.; Dehghani-Pilehvarani, A.; Markou, A.; Ferrarini, L. A hierarchical distributed predictive control approach for microgrids energy management. Sustain. Cities Soc. 2019, 48, 101536. [Google Scholar] [CrossRef]
- Gambino, G.; Verrilli, F.; Meola, D.; Himanka, M.; Palmieri, G.; Vecchio, C.D.; Glielmo, L. Model predictive control for optimization of combined heat and electric power microgrid. IFAC Proc. Vol. 2014, 47, 2201–2206. [Google Scholar] [CrossRef] [Green Version]
- Bella, A.L.; Bonassi, F.; Farina, M.; Scattolini, R. Two-layer model predictive control of systems with independent dynamics and shared control resources. IFAC-PapersOnLine 2019, 52, 96–101. [Google Scholar] [CrossRef]
- Prodan, I.; Zio, E. A model predictive control framework for reliable microgrid energy management. Int. J. Electr. Power Energy Syst. 2014, 61, 399–409. [Google Scholar] [CrossRef]
- Nassourou, M.; Puig, V.; Blesa, J.; Ocampo-Martinez, C. Economic model predictive control for energy dispatch of a smart micro-grid system. In Proceedings of the 2017 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; pp. 0944–0949. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Li, S.; Tan, R. Distributed Model Predictive Control for On-Connected Microgrid Power Management. IEEE Trans. Control Syst. Technol. 2018, 26, 1028–1039. [Google Scholar] [CrossRef]
- Lee, J.; Zhang, P.; Gan, L.K.; Howey, D.A.; Osborne, M.A.; Tosi, A.; Duncan, S. Optimal Operation of an Energy Management System Using Model Predictive Control and Gaussian Process Time-Series Modeling. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1783–1795. [Google Scholar] [CrossRef]
- Xing, X.; Xie, L.; Meng, H. Cooperative energy management optimization based on distributed MPC in grid-connected microgrids community. Int. J. Electr. Power Energy Syst. 2019, 107, 186–199. [Google Scholar] [CrossRef]
- Mirakhorli, A.; Dong, B. Model predictive control for building loads connected with a residential distribution grid. Appl. Energy 2018, 230, 627–642. [Google Scholar] [CrossRef]
- Hu, J.; Xu, Y.; Cheng, K.W.; Guerrero, J.M. A model predictive control strategy of PV-Battery microgrid under variable power generations and load conditions. Appl. Energy 2018, 221, 195–203. [Google Scholar] [CrossRef]
- Bruni, G.; Cordiner, S.; Mulone, V.; Sinisi, V.; Spagnolo, F. Energy management in a domestic microgrid by means of model predictive controllers. Energy 2016, 108, 119–131. [Google Scholar] [CrossRef]
- Zhang, X.; Bao, J.; Wang, R.; Zheng, C.; Skyllas-Kazacos, M. Dissipativity based distributed economic model predictive control for residential microgrids with renewable energy generation and battery energy storage. Renew. Energy 2017, 100, 18–34. [Google Scholar] [CrossRef]
- Hooshmand, A.; Malki, H.; Mohammadpour, J. Power flow management of microgrid networks using model predictive control. Comput. Math. Appl. 2012, 64, 869–876. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, T.; Wang, R.; Liu, Y.; Guo, B. Optimal operation of a smart residential microgrid based on model predictive control by considering uncertainties and storage impacts. Sol. Energy 2015, 122, 1052–1065. [Google Scholar] [CrossRef]
- Prodan, I.; Zio, E.; Stoican, F. Fault tolerant predictive control design for reliable microgrid energy management under uncertainties. Energy 2015, 91, 20–34. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Niu, X.; Yang, X.; Jacquet, B.; Zheng, D. Microgrid energy management optimization using model predictive control: A case study in China. IFAC-PapersOnLine 2015, 48, 306–311. [Google Scholar] [CrossRef]
- Velasquez, M.A.; Barreiro-Gomez, J.; Quijano, N.; Cadena, A.I.; Shahidehpour, M. Distributed model predictive control for economic dispatch of power systems with high penetration of renewable energy resources. Int. J. Electr. Power Energy Syst. 2019, 113, 607–617. [Google Scholar] [CrossRef]
- Tedesco, F.; Mariam, L.; Basu, M.; Casavola, A.; Conlon, M.F. Economic Model Predictive Control-Based Strategies for Cost-Effective Supervision of Community Microgrids Considering Battery Lifetime. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1067–1077. [Google Scholar] [CrossRef]
- Raimondi Cominesi, S.; Farina, M.; Giulioni, L.; Picasso, B.; Scattolini, R. A Two-Layer Stochastic Model Predictive Control Scheme for Microgrids. IEEE Trans. Control Syst. Technol. 2018, 26, 1–13. [Google Scholar] [CrossRef]
- Utkarsh, K.; Srinivasan, D.; Trivedi, A.; Zhang, W.; Reindl, T. Distributed Model-Predictive Real-Time Optimal Operation of a Network of Smart Microgrids. IEEE Trans. Smart Grid 2019, 10, 2833–2845. [Google Scholar] [CrossRef]
- Parisio, A.; Wiezorek, C.; Kyntäjä, T.; Elo, J.; Johansson, K.H. An MPC-based Energy Management System for multiple residential microgrids. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 7–14. [Google Scholar] [CrossRef]
- Minchala-Avila, L.I.; Garza-Castañón, L.; Zhang, Y.; Ferrer, H.J.A. Optimal Energy Management for Stable Operation of an Islanded Microgrid. IEEE Trans. Ind. Inform. 2016, 12, 1361–1370. [Google Scholar] [CrossRef] [Green Version]
- Hans, C.A.; Nenchev, V.; Raisch, J.; Reincke-Collon, C. Approximate closed-loop minimax model predictive operation control of microgrids. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 241–246. [Google Scholar] [CrossRef]
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An Online Optimal Dispatch Schedule for CCHP Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 2017, 8, 2332–2342. [Google Scholar] [CrossRef]
- Sachs, J.; Gienger, A.; Sawodny, O. Combined probabilistic and set-based uncertainties for a stochastic model predictive control of island energy systems. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 6767–6772. [Google Scholar] [CrossRef]
- Jaboulay, P.; Zhu, W.; Niu, X.; Pan, X.; Gao, S. Real-Time Energy Management Optimization Using Model Predictive Control on a Microgrid Demonstrator. In Proceedings of the 2017 IEEE International Conference on Energy Internet (ICEI), Beijing, China, 17–21 April 2017; pp. 226–231. [Google Scholar] [CrossRef]
- Sachs, J.; Sonntag, M.; Sawodny, O. Two layer model predictive control for a cost efficient operation of island energy systems. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 4941–4946. [Google Scholar] [CrossRef]
- Incremona, G.P.; Cucuzzella, M.; Ferrara, A.; Magni, L. Model predictive control and sliding mode control for current sharing in microgrids. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 2661–2666. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, H.; Zheng, Y.; Li, S. Distributed model predictive control for efficient operation of islanded microgrid. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 6253–6258. [Google Scholar] [CrossRef]
- Tavakoli, A.; Negnevitsky, M.; Muttaqi, K.M. A Decentralized Model Predictive Control for Operation of Multiple Distributed Generators in an Islanded Mode. IEEE Trans. Ind. Appl. 2017, 53, 1466–1475. [Google Scholar] [CrossRef]
- La Bella, A.; Raimondi Cominesi, S.; Sandroni, C.; Scattolini, R. Hierarchical Predictive Control of Microgrids in Islanded Operation. IEEE Trans. Autom. Sci. Eng. 2017, 14, 536–546. [Google Scholar] [CrossRef]
- Minchala-Avila, L.I.; Vargas-Martínez, A.; Zhang, Y.; Garza-Castañón, L.E. A model predictive control approach for integrating a master generation unit in a microgrid. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013; pp. 674–679. [Google Scholar] [CrossRef]
- Hans, C.A.; Sopasakis, P.; Bemporad, A.; Raisch, J.; Reincke-Collon, C. Scenario-based model predictive operation control of islanded microgrids. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 3272–3277. [Google Scholar]
- Zhao, Y.; Lin, Z.; Ding, Y.; Liu, Y.; Sun, L.; Yan, Y. A Model Predictive Control Based Generator Start-Up Optimization Strategy for Restoration With Microgrids as Black-Start Resources. IEEE Trans. Power Syst. 2018, 33, 7189–7203. [Google Scholar] [CrossRef]
- Golsorkhi, M.S.; Lu, D.D. A Decentralized Control Method for Islanded Microgrids Under Unbalanced Conditions. IEEE Trans. Power Deliv. 2016, 31, 1112–1121. [Google Scholar] [CrossRef]
- Falahi, M.; Butler-Purry, K.; Ehsani, M. Dynamic Reactive Power Control of Islanded Microgrids. IEEE Trans. Power Syst. 2013, 28, 3649–3657. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; He, H.; Ren, S.; Weng, G. Real-Time Demand Side Management for a Microgrid Considering Uncertainties. IEEE Trans. Smart Grid 2019, 10, 3401–3414. [Google Scholar] [CrossRef]
- Yang, X.; He, H.; Zhang, Y.; Chen, Y.; Weng, G. Interactive Energy Management for Enhancing Power Balances in Multi-Microgrids. IEEE Trans. Smart Grid 2019, 10, 6055–6069. [Google Scholar] [CrossRef]
- Kong, X.; Liu, X.; Ma, L.; Lee, K.Y. Hierarchical Distributed Model Predictive Control of Standalone Wind/Solar/Battery Power System. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1570–1581. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Aguilera, R.P.; Agelidis, V.G. Model Predictive Control for Distributed Microgrid Battery Energy Storage Systems. IEEE Trans. Control Syst. Technol. 2018, 26, 1107–1114. [Google Scholar] [CrossRef] [Green Version]
- Velarde, P.; Maestre, J.M.; Ocampo-Martinez, C.; Bordons, C. Application of robust model predictive control to a renewable hydrogen-based microgrid. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 1209–1214. [Google Scholar] [CrossRef] [Green Version]
- Bracco, S.; Delfino, F.; Procopio, R.; Rossi, M.; Robba, M. A model predictive control approach for the optimization of polygeneration microgrids and demand response strategies. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Aldaouab, I.; Daniels, M.; Ordóñez, R. MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers. Appl. Sci. 2019, 9, 3709. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).