Abstract
When we compress a large amount of data, we face the problem of the time it takes to compress it. Moreover, we cannot predict how effective the compression performance will be. Therefore, we are not able to choose the best algorithm to compress the data to its minimum size. According to the Kolmogorov complexity, the compression performances of the algorithms implemented in the available compression programs in the system differ. Thus, it is impossible to deliberately select the best compression program before we try the compression operation. From this background, this paper proposes a method with a principal component analysis (PCA) and a deep neural network (DNN) to predict the entropy of data to be compressed. The method infers an appropriate compression program in the system for each data block of the input data and achieves a good compression ratio without trying to compress the entire amount of data at once. This paper especially focuses on lossless compression for image data, focusing on the image blocks. Through experimental evaluation, this paper shows the reasonable compression performance when the proposed method is applied rather than when a compression program randomly selected is applied to the entire dataset.
1. Introduction
Various algorithms of lossless data compression are widely applied to the fields such as medical storage [1], industrial manufacturing [2], IoT [3], database [4], cloud computing [5], and communication networks [6]. However, it is hard to find the best algorithm to compress the data dedicated to the target application because a conventional algorithm of lossless data compression has not been designed for a particular data pattern. Therefore, it is impossible to determine the best algorithm to shrink data of an application into the minimum size without performing several algorithms.
According to the Kolmogorov complexity [7], there does not exist a perfect lossless data compression able to fit any application. The complexity has proved that we are able to create an algorithm for lossless data compression that compresses a data pattern to maximize data entropy. However, the algorithm is not able to decompress the data because the compressed data does not include enough information to decode it to the original data patterns. In the other words, while the algorithm of a lossless data compression works to increase the randomness of the data (i.e., to increase the entropy), the decodable compression process adds margins to the compressed data so the decompressor can decode it to the original data. There are various methods to insert the decode margin and the margin tightly related to the compression ratio (the size of compressed data divided by the original data) derived from the algorithm.
Here, we assume that we can use multiple algorithms for the lossless data compression potentially installed in a computer system; however, we are not able to know which algorithm achieves the best compression ratio before any compression trials. If we need to compress a large amount of data, we must try all the algorithms to know which is the best one. This is an NP-hard problem. Therefore, even if we perform the compression trial with the newest algorithm proposed by advanced research, it might not achieve the best compression performance.
How can we apply data compression programs adaptively to achieve the best compression ratio without trials of all algorithms? We would select the best algorithm if we knew the complexity of the data. The hint is the decode margin inserted during the compression process discussed above. That is, if we can predict the data entropy before we apply a compression program to the data, it will be realized by predicting the best algorithm to minimize the decode margin. Then, we can decide the best compression program to use.
This paper proposes a novel method that selects the best algorithm of lossless data compression without trial and error. The method will use a deep neural network (DNN) by learning data blocks divided from the entire original data. The DNN will be used to infer the best data compression program from the available ones in the computer system for each data block. This paper will focus on compressing image data by using the inference from the method.
The contributions and the research outcomes of this research are as follows.
- Applying a DNN that infers a data compression algorithm from a data pattern of a data block divided from the original data, we have developed a novel method for lossless data compression that achieves a better compression ratio than the worst case of available data compression programs.
- We have applied the proposed method to an image data compression and achieved a better compression ratio than the case when we select the worst compression program available in a computer system to the entire image data.
The rest of this paper is as follows. The next section describes the background of this research. The third section will explain the proposed method that performs adaptive lossless data compression for image data applying entropy prediction by using DNN. Then, using image data, we will show the performance evaluations. Finally, we will conclude this paper.
2. Backgrounds and Definitions
2.1. Lossless Data Compression Algorithms
The modern lossless data compression programs are implemented by combinations of the universal compression techniques and the entropy encoding. Although each of those techniques can achieve the compression effect, the combination will result in a better effect for the compression ratio.
We can find major algorithms of the universal compression methods such as the dictionary-based, the sorting-based, and other encoding methods. For example, LZ77/78, LZW, and LZMA are dictionary-based. Sorting-based includes the burrows-wheeler transform known as the block sorting and Move-to-Front. Other encoding methods include run-length coding.
On the other hand, the entropy coding methods shrink a unit of original data (called a symbol ) to a minimal code as compressed data. Then, they maximize the entropy of the compressed data. Well-known methods are arithmetic coding and Huffman. Additionally, using a tree structure and a look-up table, we can find optimization techniques such as context-tree weighting [8] and PPM [9].
We can use the programs in our computer system for lossless data compression that combine universal coding and entropy coding. For example, we would often use zip (LZ77 + Huffman), gzip (LZMA + Huffman), 7-zip (LZMA + Arithmetic coding), and bzip2 (block sorting + Move-to-Front + Huffman). LZSS [10] is also available, which optimizes the matching operations in the look-up table to assign a smaller number of bits to the compressed data than LZ77.
As we have explained above, in the modern computer system, we can use compression programs. However, as we can find in the Kolmogorov complexity, it is impossible to generate complete compressed data that achieves the maximum entropy from the original data. Even if we can find an algorithm that achieves the maximum entropy, it is known that we are not able to decode the compressed data to the original. This means that the compressed data must include some redundancy for the decoding process. Therefore, the lossless data compression algorithms do not derive the compressed data with the entropy maximized perfectly. The algorithms can reduce the amount of data by adapting the strategy locally. According to the local entropy of a data pattern in the original data, the strategy eventually finds a possibility to shrink the number of bits of a symbol. Thus, we derive different compression ratios from different compression programs because a combination of an algorithm and a data pattern eventually derives a compression ratio. Therefore, the algorithms do not promise to achieve maximum entropy.
2.2. Lossless Data Compression with Neural Network
We can find the lossless data compression algorithms applying a neural network. The algorithms infer the data distribution of the original data and encode the data patterns frequently appearing to a smaller number of bits than the original symbols. Additionally, an entropy coding is applied after the encoding by the neural network.
The algorithms targeted to specific applications have been developed in advanced research. In particular, algorithms for image data have been proposed, such as PixelRNN [11], PixelCNN [12], and L3C [13]. These compress the pixel colors in the image data by inferring the distribution of the colors. These algorithms are called the visually lossless because the color data derived from the distribution is not precisely equal to the original one.
Lossless methods with neural networks have been proposed based on the Lempel-Ziv algorithms. The early study with neural networks suggests [14] that the neural network infers the distribution of the input data patterns and assigns the shortest bit patterns using a look-up table. The study [15] analyzes the English grammar of the input text using RNN (Recurrent Neural Network) and encodes the words into the smallest bit patterns. Recent studies in the same manner have proposed PAQ [16], DeepZip [17], and CMIX [18]. In application specific trials, the literature [19] used the same approach with arithmetic coding for medical image data. These kinds of approach for visual data compression is introduced in [20]. There are methods that directly generate compressed data in collaboration with additional compression methods. One study [21] proposed a deep generative model that directly generated the compressed data. Using a deep learning approach such as a codec of image data, another study [22] compressed image data. Using a recurrent neural network (RNN), a further study [23] proposed a method to generate the compressed data targeted to the hyperspectral image data.
As seen in the advanced studies above, lossless compression with a neural network infers the distribution of the symbols (or words) and encodes those to a smaller number of bits than the original. However, the inference by the neural network does not work directly to shrink the input data. The compression methods with the neural network apply entropy coding, such as arithmetic coding and Huffman to assign the smaller number of bits after the inference. Finally, those entropy coding methods compress the original data. Then, the compressed data maintains high entropy. However, as we consider that entropy coding can not achieve the maximum entropy due to the Kolmogorov complexity, the method of a neural network also retains redundancy for decoding the compressed data. Therefore, with respect to the data locality, some methods would work to maximize entropy, but the others would compress the data with high redundancy for the decoding process.
According to the background above, to achieve the best compression ratio, we can find the best algorithm that compresses the original data to the minimum size by trying all available programs in the system. However, when we treat original data of a terabyte size, the trial is not realistic for applications because it is an NP-complete problem, requiring execution of all programs to find the best algorithm. This needs times of compression trials on average, where n denotes the number of the programs. Additionally, we need to consider the complexities of the compression algorithms. Here, we focus on how to select the best algorithm by inferring the entropy of the original data before the compression process. Now, let us propose a lossless compression method that achieves the best compression ratio by selecting the best algorithm according to the inference of the entropy regarding data blocks from a machine learning approach, where the machine learning approach learns the combinations of a data pattern and the best algorithm from many data samples.
Our proposed methods would be available using a neural network approach. However, it is difficult to decide the size of a data block used for training and inference. When we apply the entire original data to train the network, we need to consider the large size of the original data. This is not a realistic approach. Here, when we consider the discussion regarding the difference of the locality in the data entropy, we can find the best algorithm if the original data is divided into small data blocks. Therefore, in this paper, we propose a method that learns the data patterns of blocks where the block size is fixed. Using a neural network, we will implement a compression method that autonomously selects the best algorithm in the system.
3. Lossless Image Data Compression with Predicting Entropy by Neural Network
3.1. System Overview
Figure 1 shows the system diagram of the proposed method. Figure 1a–c shows the learning phase, the compression phase, and the decompression phase, respectively. The learning phase uses data blocks; the original data are divided into blocks of n symbols. Each block is compressed once using the available compression programs in the system. Then, we prepare a set of the combinations of the data block and the best program, as the dataset uses for training in the learning process. Here, the learning process uses a DNN to infer the best program from a data block. Before the training of the DNN, we apply a principal component analysis (PCA) to reduce the number of data input into the DNN. The PCA reduces the number of dimensions in the data block. We reduce it to the half of the number of the original data block. Therefore, the learning process of the DNN receives half the amount of data in a block. Here, we let the entire data to be compressed be , where the i-th symbol is . The data block to be used for the training is . Here, k is an integer value more than or equal to zero. In addition, we let the compression program be , where P is defined as the number of available programs in the system. Additionally, the size of each block is defined as , and the compressed data after applying a compression program is defined as (bits). Here, the compression ratio is derived by . The dataset for the training consists of a combination l of (, ).
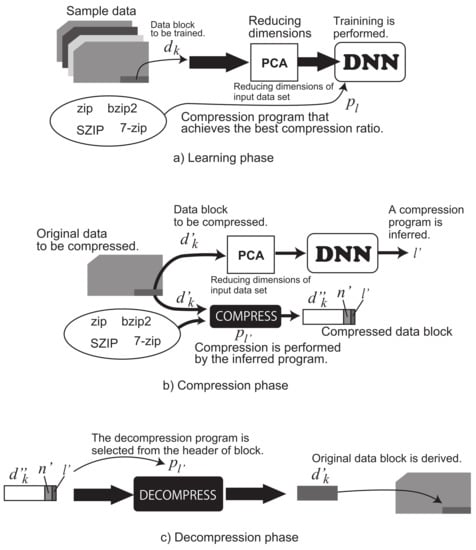
Figure 1.
The block diagram of the proposed system.
During the compression phase, using a data block with n symbols of the input original data of symbols to be compressed, an index of the compression program is inferred by the DNN trained in the learning phase. Here, the number of dimensions of the input data block to the DNN is reduced by half as well as the learning phase. The data block after compression of consists of a compressed data block by the program , the index , and the number of bits of . Here, is obtained in a header of bytes. is also obtained in a header of bits. Using the number of bits after the compression and the number of data blocks , the entire compressed data are derived as follows;
Here, each compressed block needs to obtain bits and bytes as the header. This causes an overhead for the entire compressed data size.
The decompression phase first reads and of the header at the beginning of each compressed data block. It decompresses the compressed data block of bits using the decompression program of . Iterating K times of this decompression operation, the original data D are decoded.
According to the system described above, the compressor will select a compression program by the inference of DNN using a data block of the input original data. Then, the data block is compressed by the selected compression program. Here, compressing an original data, we should focus on the situation when we are not able to know which compression program will achieve the best compression ratio. To overcome this situation, we inevitably need to try all programs. However, our proposed method with DNN just scans each original data block and infers the best algorithm that fits to the data pattern in the block. This mechanism will avoid the worst compression ratio (i.e., the ratio where the compressed data size divided by the original one becomes the largest) from intuitively selecting a compression program by the user of the computer system.
3.2. Deep Neural Network to Predict Data Entropy
We applied a fully connected network for the DNN used for the inference of the compression program, as shown in Figure 2. The network was organized with an input layer of 100 nodes and three intermediate layers of 1024, 512, and 256 nodes, respectively, from the input to the output. The output layer depends on the number of the available compression programs P. The number of nodes is . In the learning phase, the training of the DNN was performed by the input of a dataset (, l). After each dataset was entered into the DNN for the forward process, the backward process was performed. For each data set, the training was performed 10,000 times. This training process was repeated for all images. In the compression phase, the inference was performed by the input of and outputs .
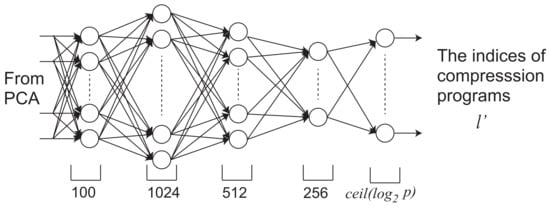
Figure 2.
The structure of the DNN used for the inference of the compression algorithms.
In this paper, we consider the case of the original data as images. We explain how to prepare the data block for the DNN in the case of image data. If we employ multiple lines of an image as the data block, entropy is not included among the lines. Therefore, we apply visual blocks of the image data to as shown in Figure 3. is a data block that is organized with the pixel data at i-th row and j-th column of image block. The pixel data can consist of the color data. In this paper, we treat RGB color data of = {, , }, where in a data block.
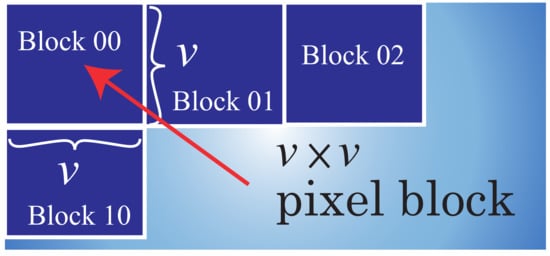
Figure 3.
The definition of image data blocks input into the DNN.
As explained above, our proposed method infers the appropriate compression program by using DNN with the input of data blocks. This helps us know the data entropy of each block before applying a compression program to the data block. The DNN approach is still an open discussion regarding the accuracy of the prediction ability for the best compression algorithm. However, we can avoid the worst compression ratio if the DNN will select the best algorithm at high accuracy.
4. Experimental Evaluations
To prove the validity of our proposed method, we performed experimental evaluations. The environment for the evaluations employed Keras and scikit-learn libraries on python 3.8.6 in a Windows 10 environment of an Intel Core i7 machine. On our system, we installed zip, bzip2, SZIP, and 7-zip. Therefore, P was 4, and the number of bits used in the header of the compressed data block for was 2.
We used an image from the 4K images, downloadable from [24]. We called this image ”Sky”. We also used the first frame images of 4K videos in the RAW format of ”Beauty”, ”Bosphorus”, and ”ReadySetGo” [25], which are downloadable from [26].
During the experiments, we evaluated v = 128, 256, 512, 1024, and 2048 for the size of each data block in the image data. These data blocks were used for the training and inference of the DNN. The training of the DNN was performed by applying all images used in the evaluations.
The graphs in Figure 4, Figure 5, Figure 6 and Figure 7 show the comparisons of the compression ratios (the compressed data size / the original data size × 100) among the block sizes of as the line graphs. The data sizes after compression are also shown as the bar graphs. In the figure, the ratios and the sizes of zip, bzip2, SZIP, and 7-zip are also shown. Those were entirely applied to the original data without the inference of DNN. The sizes of all images before the compression were 24Mbytes. In the cases when a program compressed uniquely the entire dataset, zip was the worst in any images, and 7-zip or SZIP was the best. For the cases of our proposed method with the DNN, the compression ratios improved as the block size became larger. However, the cases when showed worse compression ratios than . In all cases of our proposed method, we confirmed that the compression ratio was moderately better than the worst case when a compression program was uniquely applied to the entire data. In particular, the cases when showed the best compression ratios in all images. According to the results above, in our proposed method, the DNN inferred the best compression program appropriately and compressed the most blocks into the smallest sizes. Thus, we conclude that our proposed method is valid for effective lossless compression without trials of all available programs in the system.
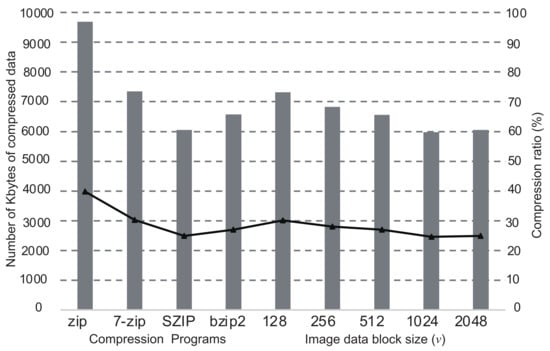
Figure 4.
Comparisons of compression ratios with/without the DNN inference in the case of Sky.
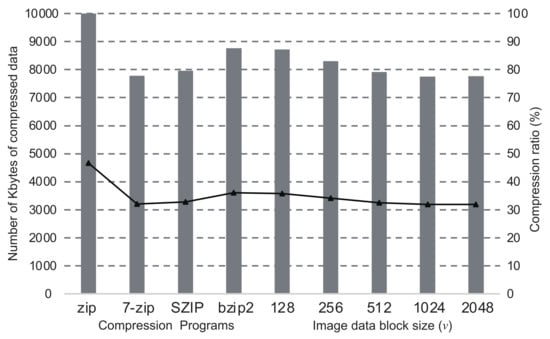
Figure 5.
Comparisons of compression ratios with/without the DNN inference in the case of Beauty.
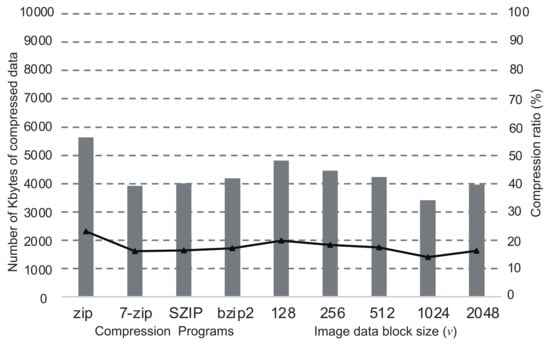
Figure 6.
Comparisons of compression ratios with/without the DNN inference in the case of Bosphorus.
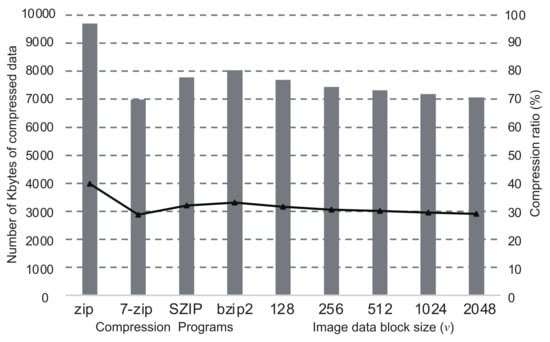
Figure 7.
Comparisons of compression ratios with/without the DNN inference in the case of ReadySetGo.
Figure 8, Figure 9, Figure 10 and Figure 11 show the mosaic images of distributions in which the compression program was selected for each block. In the case of training of DNN (the left side of each figure), the color of each block in the figures indicates the compression program that achieved the best compression ratio. As shown in the figures on the right side (i.e., the case of inferred), each block shows the compression program that the DNN inferred. The figure compares the cases of the training and the inferred when v = 128 and 256. The red colored block indicates 7-zip, green indicates bzip2, and blue indicates SZIP. Zip was not selected for the training data nor the inferred results in any case. If the DNN can infer the programs that match the training, the compression rate will become the best. In the image of Sky in Figure 8, almost all blocks selected 7-zip and SZIP. On the other hand, in Figure 9, Figure 10 and Figure 11, almost all blocks selected bzip2. This means that the data patterns (i.e., data entropy) of the images differed. Even though the data patterns had different characteristics, as we compare the distribution for the training and the inference, we confirm that both distributions were almost the same. Therefore, we confirm that the DNN predicted the entropy of each data block and selected the effective compression algorithm. Thus, our proposed method adaptively predicted the best compression program to minimize the original data size.
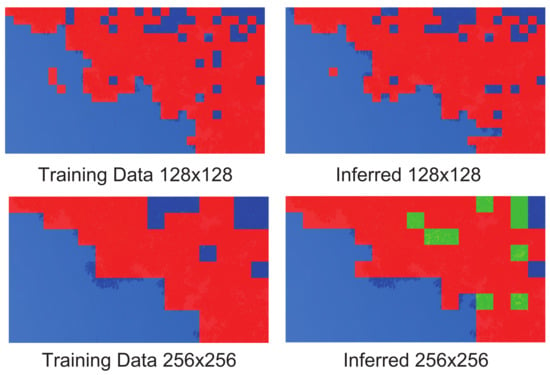
Figure 8.
Comparisons among distributions of compression programs used for training and inferred by DNN (Sky).
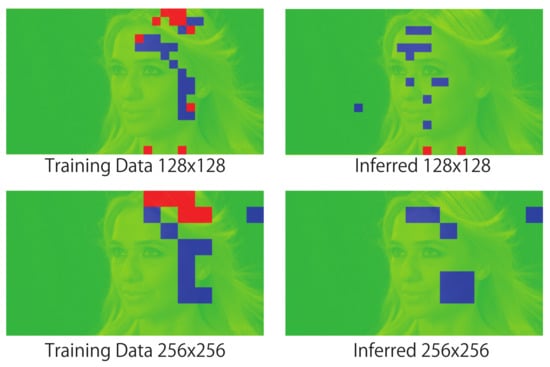
Figure 9.
Comparisons among distributions of compression programs used for training and inferred by DNN (Beauty).
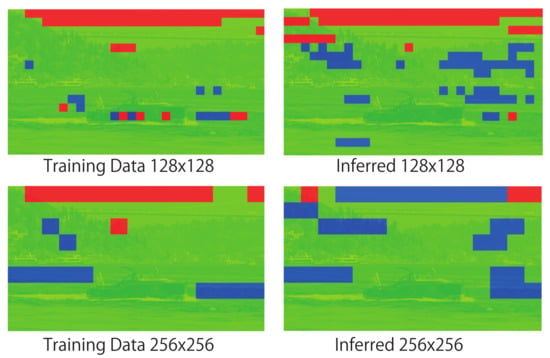
Figure 10.
Comparisons among distributions of compression programs used for training and inferred by DNN (Bosphorus).
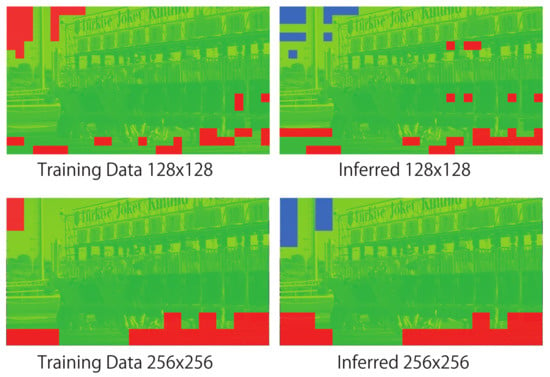
Figure 11.
Comparisons among distributions of compression programs used for training and inferred by DNN (ReadySetGo).
We have proposed a novel method where the compressor predicts the entropy of data blocks to be compressed by applying the inference of DNN and achieves an effective compression ratio without trying all the compression programs in the system. Through the experimental evaluations, we have shown the method is validated for the effective performance of lossless data compression.
5. Conclusions
To solve the problem of the trial and error of all compression programs in a system to achieve the best compression ratio, we proposed a lossless data compression method that predicted the data entropy of the input data blocks and selected an appropriate compression program in the system by using DNN. Mainly, we focused on compressing image data. The method avoided the worst compression ratio when we applied an inappropriate compression program in the system to compress the original data. According to the evaluations using the image data, we showed the validity of the proposed method. Depending on the block sizes for predicting the data entropy, the proposed method achieved better compression ratios than the case when a single compression program compressed the entire input data. In our evaluations, we confirmed the compression ratios were improved from 8% to 15% compared to the worst case when an algorithm was applied to the entire image data. Thus, we conclude that our proposed method is effective for compressing large amounts of data effectively. However, our method has two limitations. The first is that the inference depends on the images used to train the DNN. To avoid this limitation, we need to apply various image data for the training process. Another is that our approach in our paper used fixed data blocks for the training and inference by the DNN. In future work, we will investigate a method to accept variable sizes for the DNN.
In addition, we will extend the proposed method to the other types of multimedia data, such as acoustic data and sensor data.
Author Contributions
Conceptualization, S.Y. and K.W.; methodology, S.Y.; software, W.Y.; validation, S.Y. and K.W.; formal analysis, S.Y. and K.W.; investigation, S.Y. and K.W.; resources, S.Y. and W.Y.; data curation, S.Y. and W.Y.; writing—original draft preparation, S.Y.; writing—review and editing, S.Y. and K.W.; visualization, S.Y.; supervision, S.Y. and K.W.; project administration, S.Y.; funding acquisition, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by JSPS KAKENHI (Grant Number 20H04152) and JST PRESTO (Grant Number JPMJPR203A).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reddy, B.V.; Reddy, P.B.; Kumar, P.S.; Reddy, A.S. Lossless Compression of Medical Images for Better Diagnosis. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 404–408. [Google Scholar] [CrossRef]
- Gómez-Brandón, A.; Paramá, J.R.; Villalobos, K.; Illarramendi, A.; Brisaboa, N.R. Lossless compression of industrial time series with direct access. Comput. Ind. 2021, 132, 103503. [Google Scholar] [CrossRef]
- Gia, T.N.; Qingqing, L.; Queralta, J.P.; Tenhunen, H.; Zou, Z.; Westerlund, T. Lossless Compression Techniques in Edge Computing for Mission-Critical Applications in the IoT. In Proceedings of the 2019 Twelfth International Conference on Mobile Computing and Ubiquitous Network (ICMU), Kathmandu, Nepal, 4–6 November 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Huang, W.; Wang, W.; Xu, H. A Lossless Data Compression Algorithm for Real-time Database. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 2, pp. 6645–6648. [Google Scholar] [CrossRef]
- Nivedha, B.; Priyadharshini, M.; Thendral, E.; Deenadayalan, T. Lossless Image Compression in Cloud Computing. In Proceedings of the 2017 International Conference on Technical Advancements in Computers and Communications (ICTACC), Melmaurvathur, India, 10–11 April 2017; pp. 112–115. [Google Scholar] [CrossRef]
- Routray, S.K.; Javali, A.; Sharmila, K.P.; Semunigus, W.; Pappa, M.; Ghosh, A.D. Lossless Compression Techniques for Low Bandwidth Networks. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020; pp. 823–828. [Google Scholar] [CrossRef]
- Li, M.; Vitányi, P.M. An Introduction to Kolmogorov Complexity and Its Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Willems, F.; Shtarkov, Y.; Tjalkens, T. The context-tree weighting method: Basic properties. IEEE Trans. Inf. Theory 1995, 41, 653–664. [Google Scholar] [CrossRef] [Green Version]
- Cleary, J.; Witten, I. Data Compression Using Adaptive Coding and Partial String Matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef] [Green Version]
- Storer, J.A.; Szymanski, T.G. Data Compression via Textual Substitution. J. ACM 1982, 29, 928–951. [Google Scholar] [CrossRef]
- Oord, A.V.; Kalchbrenner, N.; Kavukcuoglu, K. Pixel Recurrent Neural Networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1747–1756. [Google Scholar]
- Oord, A.v.d.; Kalchbrenner, N.; Vinyals, O.; Espeholt, L.; Graves, A.; Kavukcuoglu, K. Conditional Image Generation with PixelCNN Decoders. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 4797–4805. [Google Scholar]
- Mentzer, F.; Agustsson, E.; Tschannen, M.; Timofte, R.; Gool, L.V. Practical Full Resolution Learned Lossless Image Compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Mahoney, M.V. Fast Text Compression with Neural Networks. In Proceedings of the Thirteenth International Florida Artificial Intelligence Research Society Conference, Orlando, FL, USA, 17–19 May 2000; AAAI Press: Menlo Park, CA, USA, 2000; pp. 230–234. [Google Scholar]
- Storer, J.A.; Szymanski, T.G. Syntactically Informed Text Compression with Recurrent Neural Networks. arXiv 2016, arXiv:1608.02893. [Google Scholar]
- Mahoney, M. Adaptive Weighing of Context Models for Lossless Data Compression; Technical Report of Florida Institute of Technology: Melbourne, FL, USA, 2016. [Google Scholar]
- Goyal, M.; Tatwawadi, K.; Chandak, S.; Ochoa, I. DeepZip: Lossless Data Compression Using Recurrent Neural Networks. In Proceedings of the 2019 Data Compression Conference (DCC), Snowbird, UT, USA, 26–29 March 2019; p. 575. [Google Scholar] [CrossRef] [Green Version]
- CMIX. Available online: https://github.com/byronknoll/cmix (accessed on 8 February 2022).
- Nagoor, O.H.; Whittle, J.; Deng, J.; Mora, B.; Jones, M.W. Lossless Compression For Volumetric Medical Images Using Deep Neural Network With Local Sampling. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, UAE, 25–28 September 2020; pp. 2815–2819. [Google Scholar] [CrossRef]
- Lu, G.; Yang, R.; Wang, S.; Liu, S.; Timofte, R. Deep Learning for Visual Data Compression. In Proceedings of the 29th ACM International Conference on Multimedia, New York, NY, USA, 8–12 March 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 5683–5685. [Google Scholar]
- Zhang, C.; Zhang, S.; Carlucci, F.M.; Li, Z. OSOA: One-Shot Online Adaptation of Deep Generative Models for Lossless Compression. arXiv 2021, arXiv:2111.01662. [Google Scholar]
- Schiopu, I.; Munteanu, A. Deep-Learning-Based Lossless Image Coding. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 1829–1842. [Google Scholar] [CrossRef]
- Luo, J.; Wu, J.; Zhao, S.; Wang, L.; Xu, T. Lossless compression for hyperspectral image using deep recurrent neural networks. Int. J. Mach. Learn. Cybern. 2019, 10, 2619–2629. [Google Scholar] [CrossRef]
- Yamagiwa, S.; Ichinomiya, Y. Stream-Based Visually Lossless Data Compression Applying Variable Bit-Length ADPCM Encoding. Sensors 2021, 21, 4602. [Google Scholar] [CrossRef] [PubMed]
- Mercat, A.; Viitanen, M.; Vanne, J. UVG Dataset: 50/120fps 4K Sequences for Video Codec Analysis and Development. In Proceedings of the 11th ACM Multimedia Systems Conference MMSys’20, Istanbul, Turkey, 8–11 June 2020; ACM: New York, NY, USA, 2020; pp. 297–302. [Google Scholar] [CrossRef]
- Ultra Video Group. Available online: http://ultravideo.fi/ (accessed on 8 February 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).