Uncertainty-Based Rejection in Machine Learning: Implications for Model Development and Interpretability
Abstract
:1. Introduction
- How can UQ contribute to choosing the most suitable model for a given classification task?
- Can UQ be used to combine different models in a principled manner?
- Can visualization techniques improve UQ’s interpretability?
2. Background and Related Work
2.1. Uncertainty Quantification
2.2. Classification with the Rejection Option
- Nonrejected accuracy measures the ability of the classifier to accurately classify nonrejected samples, and it is computed as,
- Classification quality measures the ability of the classifier with rejection to accurately classify nonrejected samples and to reject misclassified samples. It is computed as,
- Rejection quality measures the ability of the classifier with rejection to make errors on rejected samples only, and it is computed as,
3. Methods
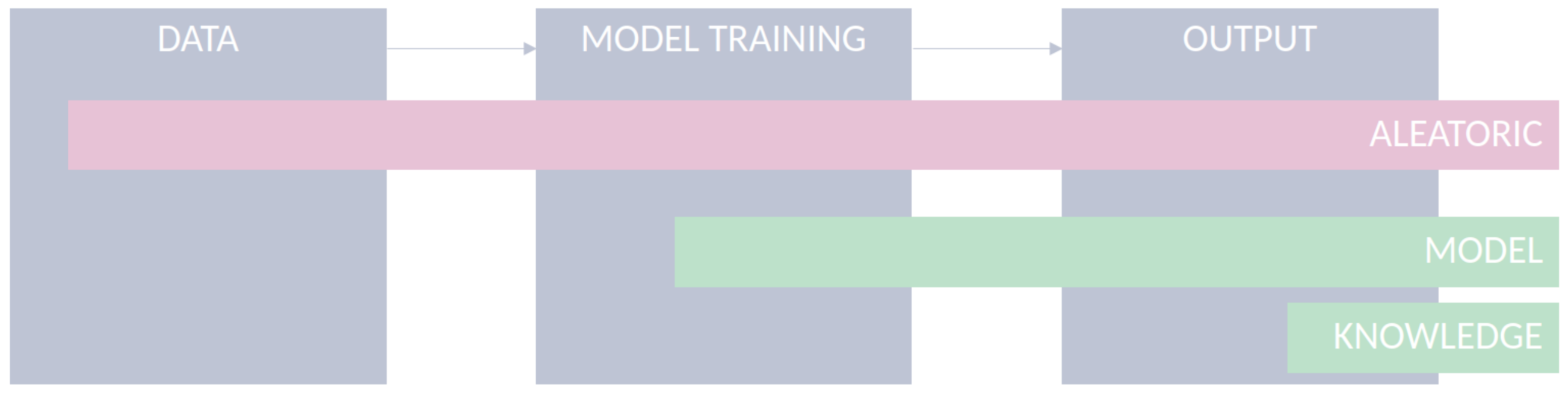
- Data: Data used to feed ML models are limited in their accuracy and potentially affected by various kinds of quality issues, which limits the models from being applied under optimal conditions [34,35]. For example, the uncertainty caused due to errors in the measurement might affect the performance of a given classification task. Although the aleatoric uncertainty is supposed to be irreducible for a specific dataset, incorporating additional features or improving the quality of the existing features can assist in its reduction [36];
- Model: For a given classification task, several ML models can be applied and developed. The choice of a model is arguably important and is often based on the degree of error in the model’s outcomes. However, besides models’ accuracy, the use of uncertainty quantification methods during model development can provide important elements to choose the right model for the problem at hand. Moreover, understanding the model’s uncertainty during training can give us insights about the specific limitations of each model and help in developing more robust models. The estimation of model uncertainty increases model interpretability, by allowing the user to interpret how confident the model is for a given prediction;
- Output: After the model’s training, estimating and quantifying uncertainty in a transductive way, in the sense of tailoring it to individual instances, are arguably relevant, all the more in safety-critical applications. For instance, in the context of computer-aided diagnosis systems, a prediction with high uncertainty shall justify either disregarding its output or conducting further medical examinations of the patient. In the latter, the goal is to retrieve additional evidence that supports or contradicts a given hypothesis. In the former, it is the case of classification with rejection, which is a viable option, where the presence and cost of errors can be detrimental to the performance of automated classification systems [33].
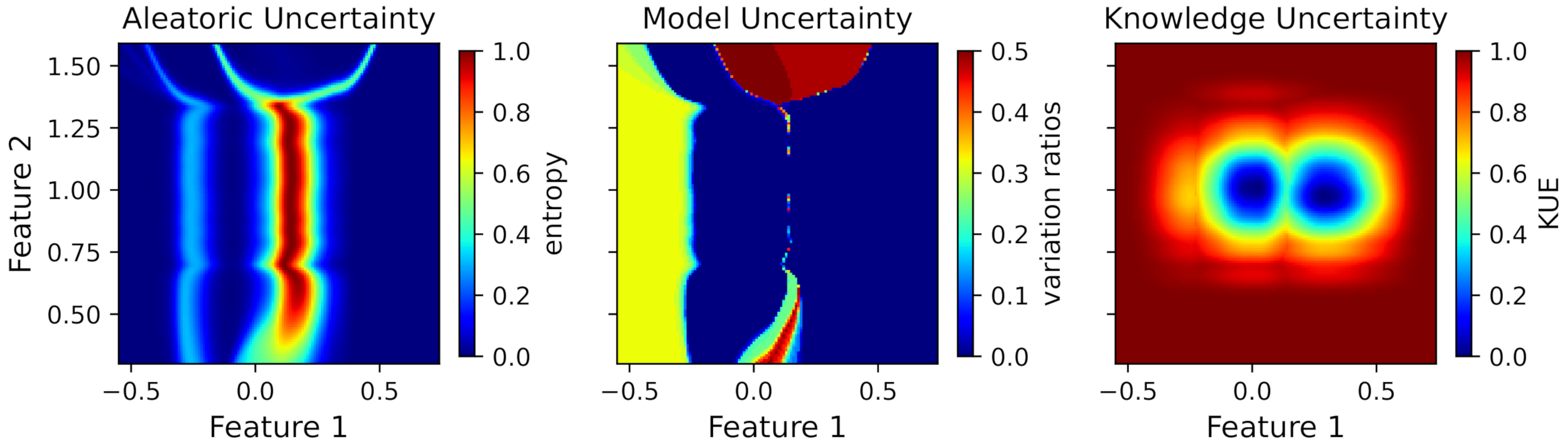
- Aleatoric uncertainty: The (Shannon) entropy is the most notable measure of uncertainty for probability distributions being more akin to aleatoric uncertainty. Equation (4), which measures the aleatoric uncertainty in terms of expectation over the entropies of distributions, was used for the rest of the analysis;
- Model uncertainty: Variation ratios (Equation (7)) were selected as a primary uncertainty quantification method, to estimate model uncertainty, as we were interested in evaluating the quality of the model fit. In this sense, changes in the predicted label have a significant impact on the variation ratio measure. Contrarily, measures based on entropies (Equation (6) is commonly used) can also be used, but the impact on the measure is lower, since in variation ratios, we are merely counting changes in the predictions, and in entropy measures, we are averaging the prediction probabilities [21];
- Knowledge uncertainty: Although the majority of works addressed the quantification of knowledge uncertainty with measures such as the mutual information using ensembles (Equation (6)), we argue that these kinds of measures are more akin to model uncertainty. The uncertainty related to the lack of data might be poorly modeled by these measures. In this perspective, we considered density estimation methods, commonly used for outlier or novelty detection, more prone to model knowledge uncertainty. Thus, the KUE measure (Equation (9)) was used to model knowledge uncertainty.
4. Experiments
- Q1. How can UQ contribute to choosing the most suitable model for a given classification task?
- Q2. Can UQ be use to combine different models?
- Q3. Can visualization techniques improve UQ’s interpretability?
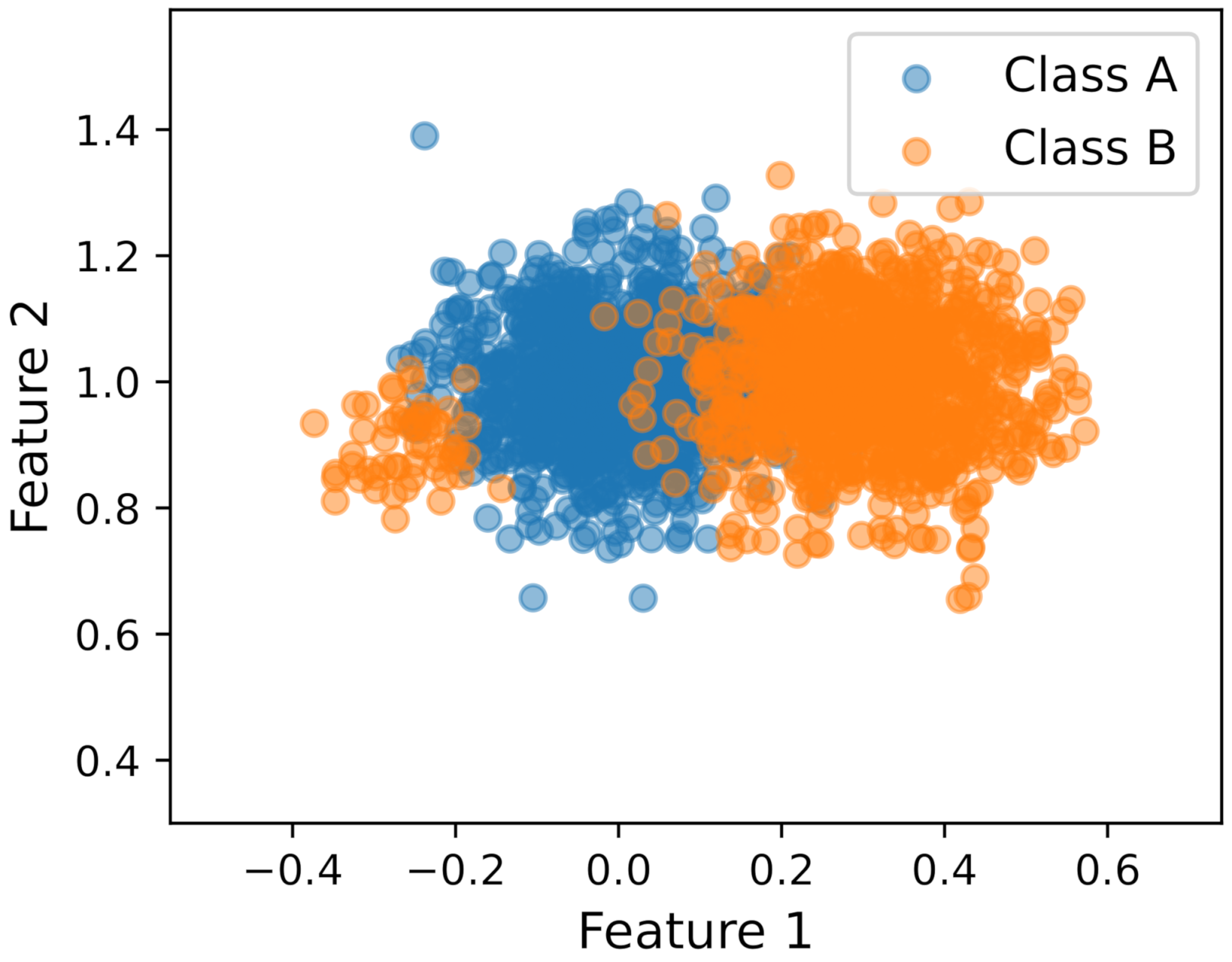
4.1. Analysis on Synthetic Data
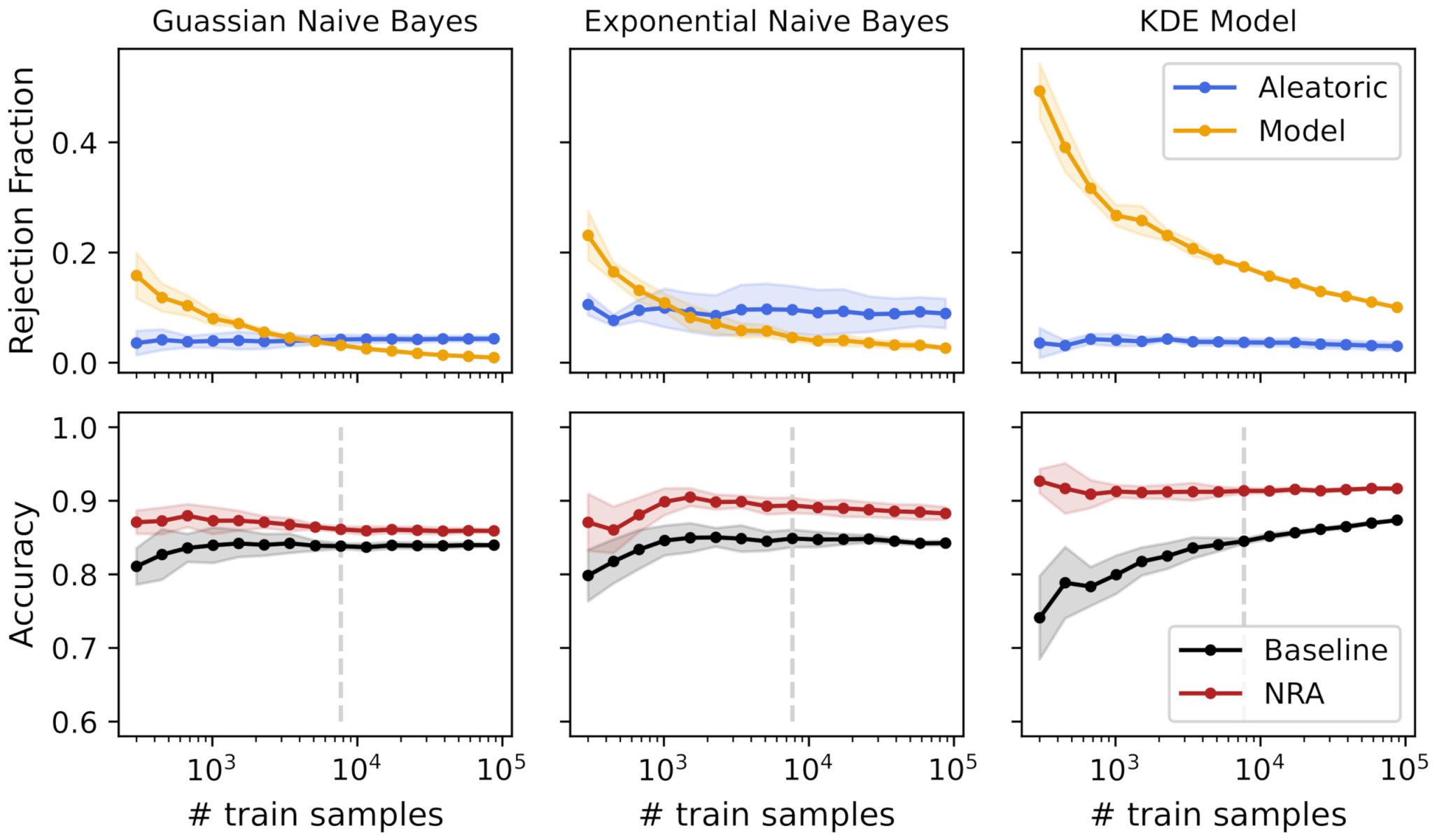
4.1.1. Uncertainty for Model Selection (Q1)
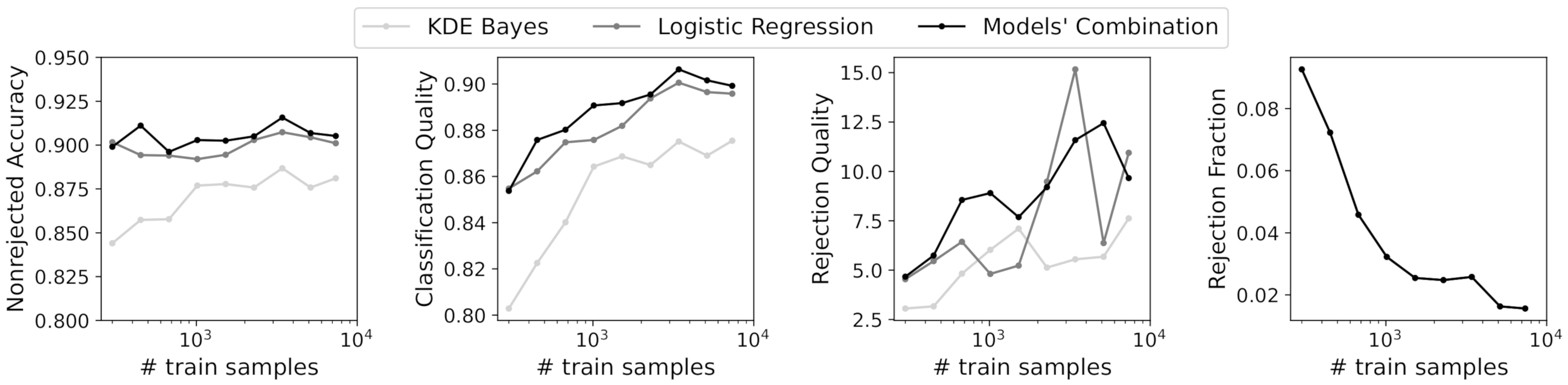
4.1.2. Uncertainty for Models’ Combination (Q2)
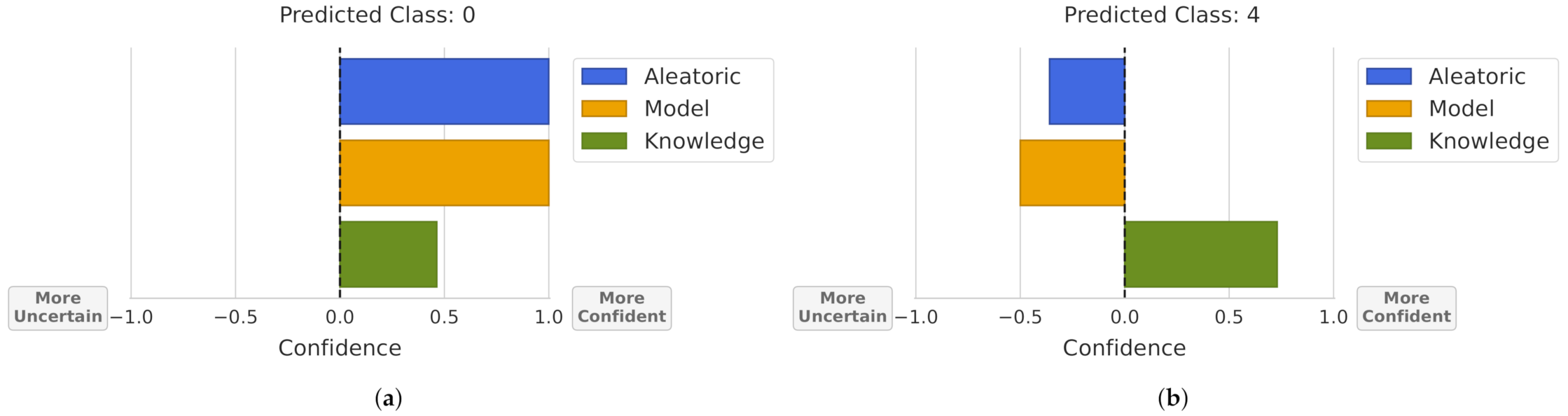
4.1.3. Uncertainty Visualization (Q3)
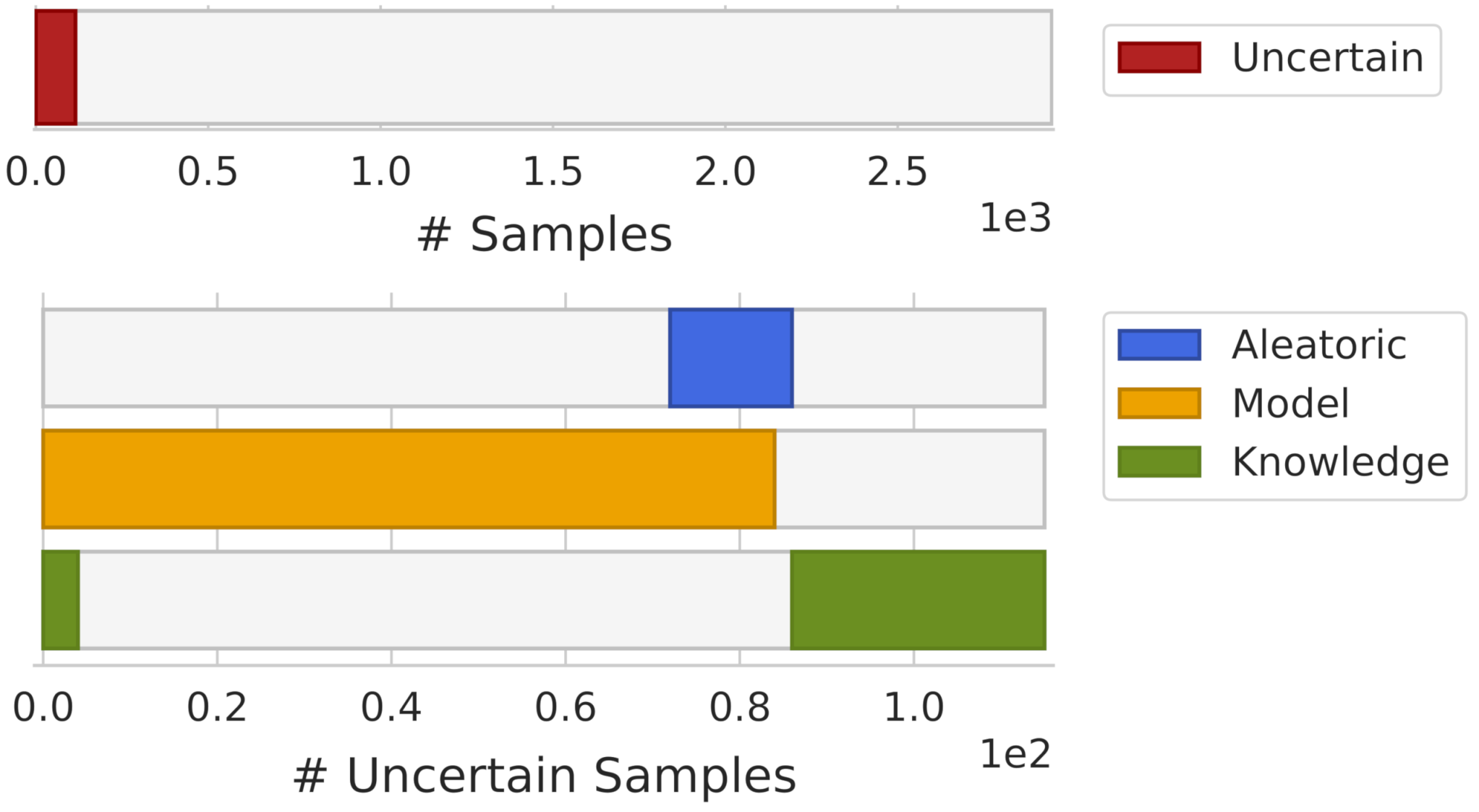
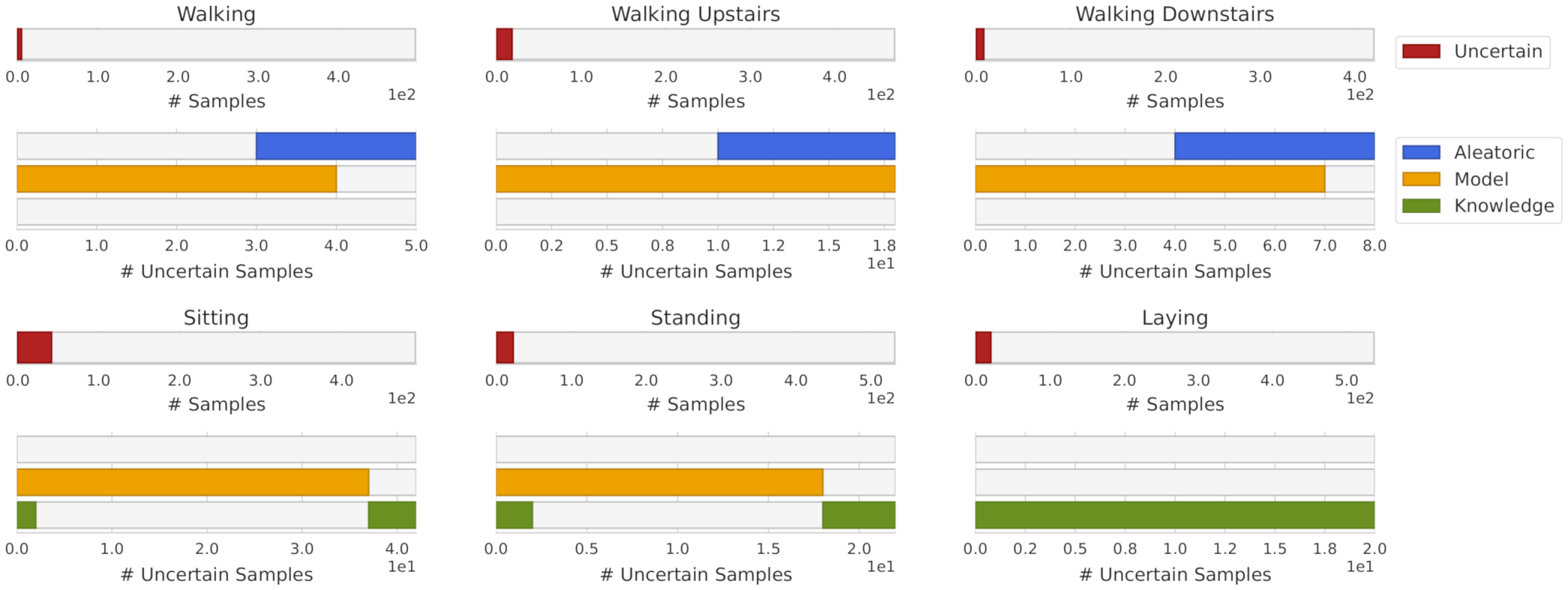
4.2. Experiments on a Human Activity Recognition Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cobb, A.D.; Jalaian, B.; Bastian, N.D.; Russell, S. Toward Safe Decision-Making via Uncertainty Quantification in Machine Learning. In Systems Engineering and Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2021; pp. 379–399. [Google Scholar]
- Senge, R.; Bösner, S.; Dembczyński, K.; Haasenritter, J.; Hirsch, O.; Donner-Banzhoff, N.; Hüllermeier, E. Reliable classification: Learning classifiers that distinguish aleatoric and epistemic uncertainty. Inf. Sci. 2014, 255, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Kompa, B.; Snoek, J.; Beam, A.L. Second opinion needed: Communicating uncertainty in medical machine learning. NPJ Digit. Med. 2021, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Huang, Z.; Lam, H.; Zhang, H. Quantifying Epistemic Uncertainty in Deep Learning. arXiv 2021, arXiv:2110.12122. [Google Scholar]
- Holzinger, A.; Langs, G.; Denk, H.; Zatloukal, K.; Müller, H. Causability and explainability of artificial intelligence in medicine. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, V.L.; Shaker, M.H.; Hüllermeier, E. How to measure uncertainty in uncertainty sampling for active learning. Mach. Learn. 2021, 1–34. [Google Scholar] [CrossRef]
- Bota, P.; Silva, J.; Folgado, D.; Gamboa, H. A semi-automatic annotation approach for human activity recognition. Sensors 2019, 19, 501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghosh, S.; Liao, Q.V.; Ramamurthy, K.N.; Navratil, J.; Sattigeri, P.; Varshney, K.R.; Zhang, Y. Uncertainty Quantification 360: A Holistic Toolkit for Quantifying and Communicating the Uncertainty of AI. arXiv 2021, arXiv:2106.01410. [Google Scholar]
- Chung, Y.; Char, I.; Guo, H.; Schneider, J.; Neiswanger, W. Uncertainty toolbox: An open-source library for assessing, visualizing, and improving uncertainty quantification. arXiv 2021, arXiv:2109.10254. [Google Scholar]
- Oala, L.; Murchison, A.G.; Balachandran, P.; Choudhary, S.; Fehr, J.; Leite, A.W.; Goldschmidt, P.G.; Johner, C.; Schörverth, E.D.; Nakasi, R.; et al. Machine Learning for Health: Algorithm Auditing & Quality Control. J. Med. Syst. 2021, 45, 1–8. [Google Scholar]
- Bosnić, Z.; Kononenko, I. An overview of advances in reliability estimation of individual predictions in machine learning. Intell. Data Anal. 2009, 13, 385–401. [Google Scholar] [CrossRef] [Green Version]
- Tornede, A.; Gehring, L.; Tornede, T.; Wever, M.; Hüllermeier, E. Algorithm selection on a meta level. arXiv 2021, arXiv:2107.09414. [Google Scholar]
- Neto, M.P.; Paulovich, F.V. Explainable Matrix-Visualization for Global and Local Interpretability of Random Forest Classification Ensembles. IEEE Trans. Vis. Comput. Graph. 2020, 27, 1427–1437. [Google Scholar] [CrossRef] [PubMed]
- Shaker, M.H.; Hüllermeier, E. Ensemble-based Uncertainty Quantification: Bayesian versus Credal Inference. arXiv 2021, arXiv:2107.10384. [Google Scholar]
- Malinin, A.; Prokhorenkova, L.; Ustimenko, A. Uncertainty in gradient boosting via ensembles. arXiv 2020, arXiv:2006.10562. [Google Scholar]
- Depeweg, S.; Hernandez-Lobato, J.M.; Doshi-Velez, F.; Udluft, S. Decomposition of uncertainty in Bayesian deep learning for efficient and risk-sensitive learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1184–1193. [Google Scholar]
- Shaker, M.H.; Hüllermeier, E. Aleatoric and epistemic uncertainty with random forests. arXiv 2020, arXiv:2001.00893. [Google Scholar]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
- Stracuzzi, D.J.; Darling, M.C.; Peterson, M.G.; Chen, M.G. Quantifying Uncertainty to Improve Decision Making in Machine Learning; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2018.
- Mena, J.; Pujol, O.; Vitrià, J. Uncertainty-based rejection wrappers for black-box classifiers. IEEE Access 2020, 8, 101721–101746. [Google Scholar] [CrossRef]
- Geng, C.; Huang, S.j.; Chen, S. Recent advances in open set recognition: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3614–3631. [Google Scholar] [CrossRef] [Green Version]
- Perello-Nieto, M.; Telmo De Menezes Filho, E.S.; Kull, M.; Flach, P. Background Check: A general technique to build more reliable and versatile classifiers. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 1143–1148. [Google Scholar]
- Pires, C.; Barandas, M.; Fernandes, L.; Folgado, D.; Gamboa, H. Towards Knowledge Uncertainty Estimation for Open Set Recognition. Mach. Learn. Knowl. Extr. 2020, 2, 505–532. [Google Scholar] [CrossRef]
- Chow, C. On optimum recognition error and reject tradeoff. IEEE Trans. Inf. Theory 1970, 16, 41–46. [Google Scholar] [CrossRef] [Green Version]
- Tax, D.M.; Duin, R.P. Growing a multi-class classifier with a reject option. Pattern Recognit. Lett. 2008, 29, 1565–1570. [Google Scholar] [CrossRef]
- Fumera, G.; Roli, F.; Giacinto, G. Reject option with multiple thresholds. Pattern Recognit. 2000, 33, 2099–2101. [Google Scholar] [CrossRef]
- Hanczar, B. Performance visualization spaces for classification with rejection option. Pattern Recognit. 2019, 96, 106984. [Google Scholar] [CrossRef]
- Franc, V.; Prusa, D.; Voracek, V. Optimal strategies for reject option classifiers. arXiv 2021, arXiv:2101.12523. [Google Scholar]
- Charoenphakdee, N.; Cui, Z.; Zhang, Y.; Sugiyama, M. Classification with rejection based on cost-sensitive classification. In Proceedings of the International Conference on Machine Learning, Virtual, 13–15 April 2021; pp. 1507–1517. [Google Scholar]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Dissertation, University of Cambridge, Cambridge, UK, 2016. [Google Scholar]
- Nadeem, M.S.A.; Zucker, J.D.; Hanczar, B. Accuracy-rejection curves (ARCs) for comparing classification methods with a reject option. In Proceedings of the third International Workshop on Machine Learning in Systems Biology, Ljubljana, Slovenia, 5–6 September 2009; pp. 65–81. [Google Scholar]
- Condessa, F.; Bioucas-Dias, J.; Kovačević, J. Performance measures for classification systems with rejection. Pattern Recognit. 2017, 63, 437–450. [Google Scholar] [CrossRef] [Green Version]
- Kläs, M. Towards identifying and managing sources of uncertainty in AI and machine learning models-an overview. arXiv 2018, arXiv:1811.11669. [Google Scholar]
- Campagner, A.; Cabitza, F.; Ciucci, D. Three-way decision for handling uncertainty in machine learning: A narrative review. In International Joint Conference on Rough Sets; Springer: Berlin/Heidelberg, Germany, 2020; pp. 137–152. [Google Scholar]
- Sambyal, A.S.; Krishnan, N.C.; Bathula, D.R. Towards Reducing Aleatoric Uncertainty for Medical Imaging Tasks. arXiv 2021, arXiv:2110.11012. [Google Scholar]
- Fischer, L.; Hammer, B.; Wersing, H. Optimal local rejection for classifiers. Neurocomputing 2016, 214, 445–457. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2019; Available online: http://archive.ics.uci.edu/ml (accessed on 20 December 2021).
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A public domain dataset for human activity recognition using smartphones. Esann 2013, 3, 3. [Google Scholar]
- Buckley, C.; Alcock, L.; McArdle, R.; Rehman, R.Z.U.; Del Din, S.; Mazzà, C.; Yarnall, A.J.; Rochester, L. The role of movement analysis in diagnosing and monitoring neurodegenerative conditions: Insights from gait and postural control. Brain Sci. 2019, 9, 34. [Google Scholar] [CrossRef] [PubMed] [Green Version]



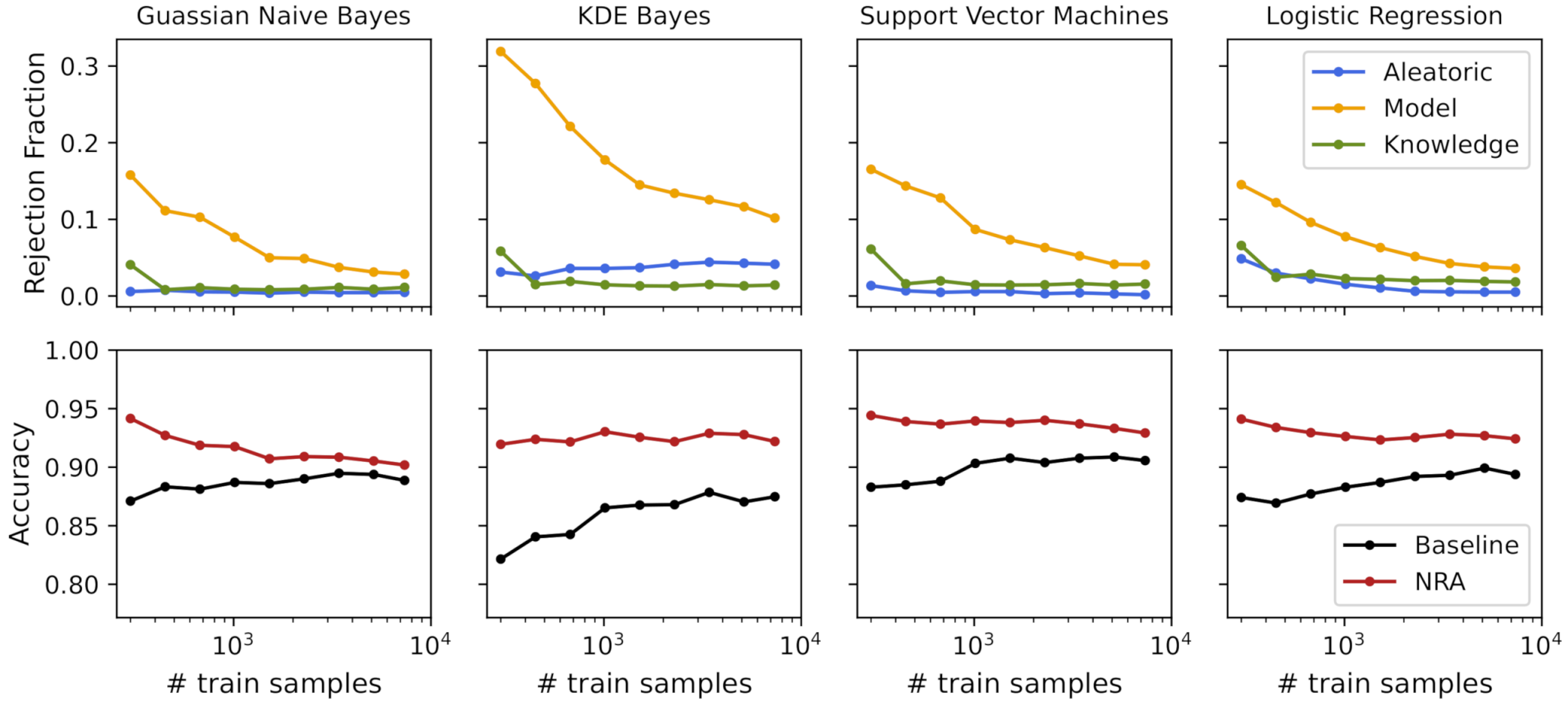
| Model | Baseline Accuracy | Nonrejected Accuracy | Rejection Fraction |
|---|---|---|---|
| Gaussian Naive Bayes | 0.838±0.004 | 0.861 ± 0.004 | 0.056 ± 0.006 |
| KDE Naive Bayes | 0.918 ± 0.004 | 0.929 ± 0.004 | 0.050 ± 0.007 |
| Exponential Naive Bayes | 0.848±0.012 | 0.894 ± 0.011 | 0.109 ± 0.041 |
| KDE Bayes | 0.845±0.003 | 0.914 ± 0.004 | 0.178 ± 0.004 |
| Logistic Regression | 0.717 ± 0.003 | 0.788 ± 0.005 | 0.198 ± 0.006 |
| Decision Tree | 0.764 ± 0.024 | 0.884 ± 0.004 | 0.328 ± 0.111 |
| Random Forest | 0.806 ± 0.004 | 0.871 ± 0.006 | 0.169 ± 0.004 |
| k-Nearest Neighbors | 0.820 ± 0.004 | 0.902 ± 0.007 | 0.202 ± 0.005 |
| Support Vector Machines | 0.744 ± 0.004 | 0.806 ± 0.005 | 0.173 ± 0.010 |
| Model | Nonrejected Accuracy | Classification Quality | Rejection Quality |
|---|---|---|---|
| Gaussian Naive Bayes | 0.72 | 0.72 | 2.60 |
| KDE Bayes | 0.85 | 0.82 | 5.84 |
| Model’s Combination | 0.86 | 0.83 | 6.89 |
| Model | Baseline Accuracy | Nonrejected Accuracy | Rejection Fraction |
|---|---|---|---|
| Gaussian Naive Bayes | 0.89 | 0.90 | 0.03 |
| KDE Bayes | 0.88 | 0.92 | 0.12 |
| Logistic Regression | 0.89 | 0.92 | 0.06 |
| Decision Tree | 0.82 | 0.92 | 0.23 |
| Random Forest | 0.84 | 0.91 | 0.16 |
| k-Nearest Neighbors | 0.87 | 0.94 | 0.13 |
| Support Vector Machines | 0.91 | 0.93 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barandas, M.; Folgado, D.; Santos, R.; Simão, R.; Gamboa, H. Uncertainty-Based Rejection in Machine Learning: Implications for Model Development and Interpretability. Electronics 2022, 11, 396. https://doi.org/10.3390/electronics11030396
Barandas M, Folgado D, Santos R, Simão R, Gamboa H. Uncertainty-Based Rejection in Machine Learning: Implications for Model Development and Interpretability. Electronics. 2022; 11(3):396. https://doi.org/10.3390/electronics11030396
Chicago/Turabian StyleBarandas, Marília, Duarte Folgado, Ricardo Santos, Raquel Simão, and Hugo Gamboa. 2022. "Uncertainty-Based Rejection in Machine Learning: Implications for Model Development and Interpretability" Electronics 11, no. 3: 396. https://doi.org/10.3390/electronics11030396
APA StyleBarandas, M., Folgado, D., Santos, R., Simão, R., & Gamboa, H. (2022). Uncertainty-Based Rejection in Machine Learning: Implications for Model Development and Interpretability. Electronics, 11(3), 396. https://doi.org/10.3390/electronics11030396









