Comparative Estimation of Electrical Characteristics of a Photovoltaic Module Using Regression and Artificial Neural Network Models
Abstract
1. Introduction
2. Theoretical Models
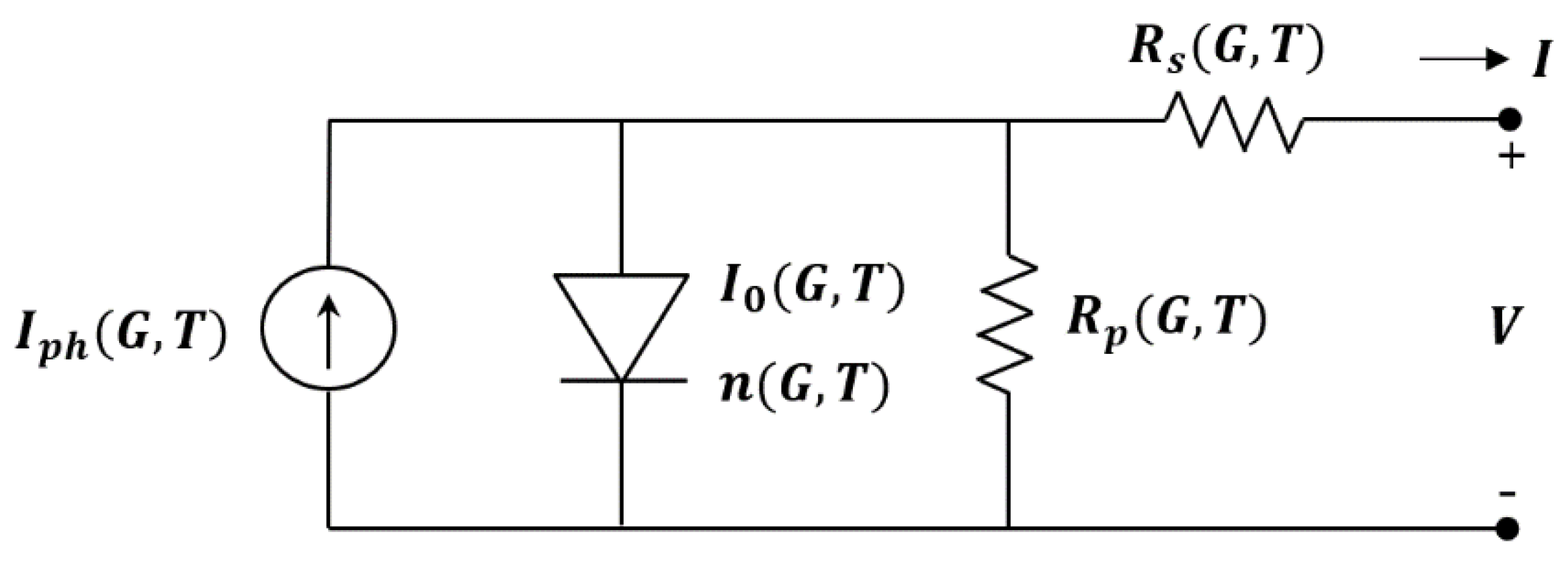
2.1. Explicit and Analytical I–V Model
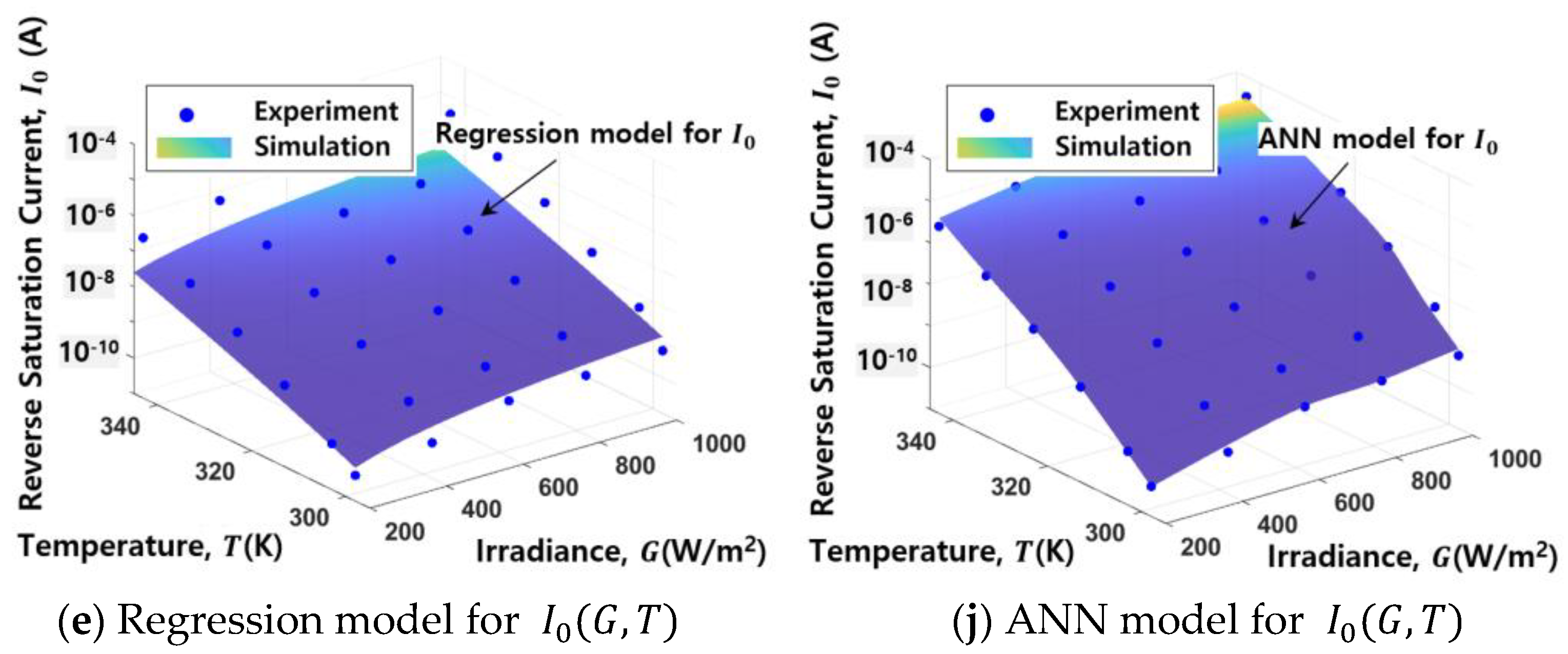
2.2. Five Parameters as a Function of Temperature and Solar Irradiance
3. Parameter Identification Approaches
3.1. Multiple Regression
3.2. Artificial Neural Network (ANN)
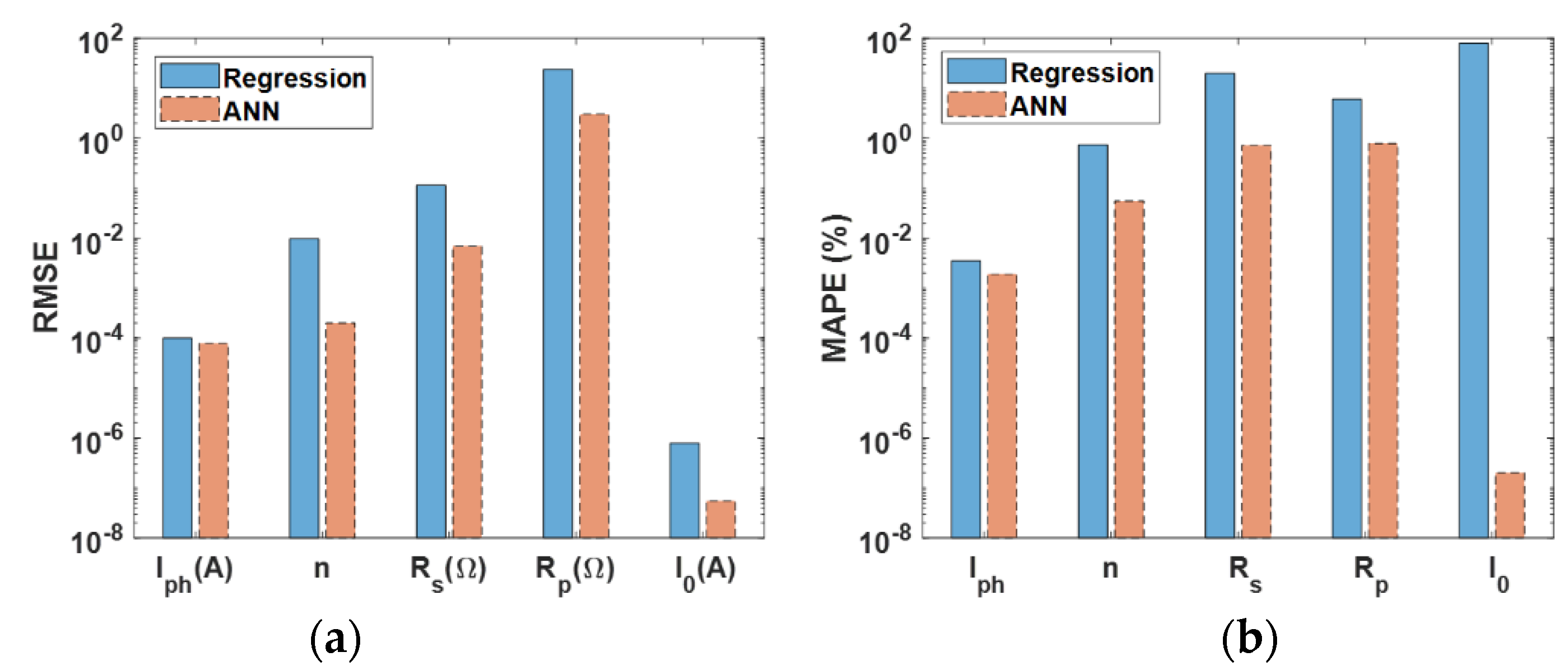
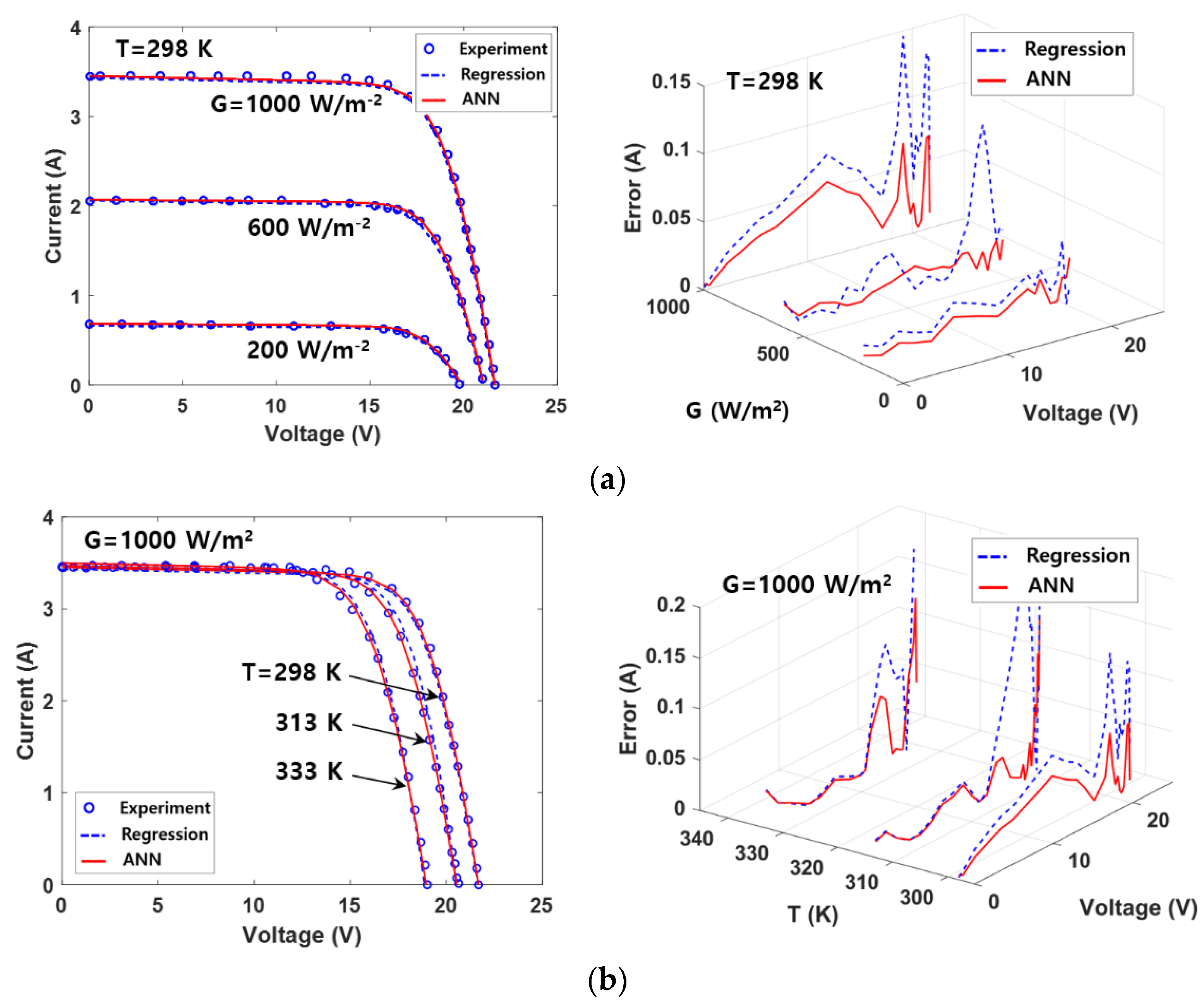
4. Model Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zaimi, M.; Achouby, E.; Ibral, A.; Assaid, E.M. Determining combined effects of solar radiation and panel junction temperature on all model-parameters to forecast peak power and photovoltaic yield of solar panel under non-standard conditions. Sol. Energy 2019, 191, 341–359. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variations of PV module parameters with irradiance and temperature. Energy Procedia 2017, 134, 276–285. [Google Scholar] [CrossRef]
- Teh, C.T.Q.; Drieberg, M.; Soeung, S.; Ahmad, R. Simple PV modeling under variable operating conditions. IEEE Access 2021, 9, 96546–96558. [Google Scholar] [CrossRef]
- Dongue, S.B.; Njomo, D.; Ebengai, L. An improved nonlinear five-point model for photovoltaic modules. Int. J. Photoenergy 2013, 2013, 680213-1-11. [Google Scholar]
- Shinong, W.; Qianlong, M.; Jie, X.; Yuan, G.; Shilin, L. An improved mathematical model of photovoltaic cells based on datasheet information. Sol. Energy 2020, 199, 437–446. [Google Scholar] [CrossRef]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Gangi, A.D. An improved five parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Anani, N.; Ibrahim, H. Adjusting the single-diode model parameters of a photovoltaic module with irradiance and temperature. Energies 2020, 13, 3326. [Google Scholar] [CrossRef]
- Hao, P.; Zhang, Y.; Lu, H.; Lang, Z. A novel method for parameter identification and performance estimation of PV module under varying operation conditions. Energy Convers. Manag. 2021, 247, 114689. [Google Scholar] [CrossRef]
- Deng, J.; Wang, Y. Research on MPPT of photovoltaic system based on PSO with time-varying compression factor. IEICE Electron. Express 2022, 19, 20220165. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, B.; Yang, Y.; Wen, H.; Zhang, Y.; Chen, X. A new optimized control system architecture for solar photovoltaic energy storage application. IEICE Electron. Express 2021, 18, 20200404. [Google Scholar] [CrossRef]
- Carrasco, J.A.; de Quiros, F.G.; Alaves, H.; Navalon, M. A PWM multiplier for maximum power point estimation of a solar panel. IEICE Electron. Express 2018, 15, 20180496. [Google Scholar] [CrossRef]
- Liu, H.D.; Lin, C.H.; Lu, S.D. A novel MPPT algorithm considering solar photovoltaic modules and load characteristics for a single stage standalone solar photovoltaic system. IEICE Electron. Express 2020, 17, 20200099. [Google Scholar] [CrossRef]
- Picault, D.; Raison, B.; Bacha, S.; de la Casa, J.; Aguilera, J. Forecasting photovoltaic array power production subject to mismatch losses. Sol. Energy 2010, 84, 1301–1309. [Google Scholar] [CrossRef]
- Jain, A.; Sharma, S.; Kapoor, A. Solar cell array parameters using Lambert W-function. Sol. Energy Mater. Sol. Cells 2006, 90, 25–31. [Google Scholar] [CrossRef]
- Fathabadi, H. Lambert W function-based technique for tracking the maximum power point of PV modules connected in various configurations. Renew. Energy 2015, 74, 214–226. [Google Scholar] [CrossRef]
- Hmamou, D.B.; Elyaqouti, M.; Arjdal, E.; Ibrahim, A.; Abdul-Ghaffar, H.I.; Aboelsaud, R.; Obukhov, S.; Diab, A.A.Z. Parameters identification and optimization of photovoltaic panels under real conditions using Lambert W-function. Energy Rep. 2021, 7, 9035–9045. [Google Scholar] [CrossRef]
- Achouby, E.; Zaimi, M.; Ibral, A.; Assaid, E.M. New analytical approach for modelling effects of temperature and irradiance on physical parameters of photovoltaic solar module. Energy Convers. Manag. 2018, 177, 258–271. [Google Scholar] [CrossRef]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J.; Michels, L., Jr.; Pietta, L.P. An eight-parameter adaptive model for the single diode equivalent circuit based on the photovoltaic module’s physics. IEEE J. Photovolt. 2017, 7, 1115–1123. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Su, J.; Gu, T.; Yang, M. Modeling and prediction of PV module performance under different operating conditions based on power-law I-V model. IEEE J. Photovolt. 2020, 10, 1816–1827. [Google Scholar] [CrossRef]
- Hejri, M.; Mokhtari, H. On the comprehensive parameterization of the photovoltaic cells and modules. IEEE J. Photovolt. 2017, 7, 250–258. [Google Scholar] [CrossRef]
- Silva, A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Parameter estimation method to improve the accuracy of photovoltaic electrical model. IEEE J. Photovolt. 2016, 6, 278–285. [Google Scholar] [CrossRef]
- Mittal, M.; Bora, B.; Saxena, S.; Gaur, A.M. Performance prediction of PV module using electrical model and artificial neural network. Sol. Energy 2018, 176, 104–117. [Google Scholar] [CrossRef]
- Karamirad, M.; Omid, M.; Alimardani, R.; Mousazadeh, H.; Heidari, S.N. ANN based simulation and experimental verification of analytical four- and five-parameters models of PV modules. Simul. Model. Pract. Theory 2013, 34, 86–98. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, L.; Yao, J.; Dai, S.; Hu, Y. Fault diagnosis approach for photovoltaic arrays based on unsupervised sample clustering and probabilistic neural network model. Sol. Energy 2018, 176, 395–405. [Google Scholar] [CrossRef]
- Chine, W.; Mellit, A.; Lughi, V.; Malek, A.; Sulligoi, G.; Massi Pavan, A. A novel fault diagnosis technique for photovoltaic systems based on artificial neural networks. Renew. Energy 2016, 90, 501–512. [Google Scholar] [CrossRef]
- Li, B.; Delpha, C.; Diallo, D.; Migan-Dubois, A. Application of artificial neural networks to photovoltaic fault detection and diagnosis: A review. Renew. Sustain. Energy Rev. 2021, 138, 110512. [Google Scholar] [CrossRef]
- Zecevic, Z.; Rolevski, M. Neural network approach to MPPT control and irradiance estimation. Appl. Sci 2020, 10, 5051. [Google Scholar] [CrossRef]
- Karatepe, E.; Boztepe, M.; Colak, M. Neural network based solar cell model. Energy Convers. Manage. 2006, 47, 1159–1178. [Google Scholar] [CrossRef]
- Xu, E.; Zhang, X.; Huang, Z.; Xie, S.; Gu, W.; Wang, X.; Zhang, L.; Zhang, Z. Current characteristics estimation of Si PV modules based on artificial neural network modeling. Materials 2019, 12, 3037. [Google Scholar] [CrossRef]
- Chikh, A.; Chandra, A. Adaptive neuro-fuzzy based solar cell model. IET Renew. Power Gener. 2014, 8, 679–686. [Google Scholar] [CrossRef]
- Rizzo, S.A.; Scelba, G. ANN based MPPT method for rapidly variable shading conditions. Appl. Energy 2015, 145, 124–132. [Google Scholar] [CrossRef]
- Cortes, B.; Sanchez, R.T.; Flores, J.J. Characterization of polycrystalline photovoltaic cell using artificial neural network. Sol. Energy 2020, 196, 157–167. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Elaziz, M.A.; Kabeel, A.E.; Guilan, W.; Haiou, Z. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Mathioulakis, E.; Belessiotis, V. Artificial neural network for the performance prediction of large solar systems. Renew. Energy 2014, 63, 90–97. [Google Scholar] [CrossRef]
- Castro, R. Data-driven PV modules modelling: Comparison between equivalent electric circuit and artificial intelligence based models. Sustain. Energy Technol. Assess. 2018, 30, 230–238. [Google Scholar] [CrossRef]
- Celik, A.N. Artificial neural network modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules. Sol. Energy 2011, 85, 2507–2517. [Google Scholar] [CrossRef]
- Almonacid, F.; Rus, C.; Hontoria, L.; Munoz, F.J. Characterization of PV CIS module by artificial neural networks. A comparative study with other methods. Renew. Energy 2010, 35, 973–980. [Google Scholar] [CrossRef]
- Huang, C.; Bensoussan, A.; Edesess, M.; Tsui, K.L. Improvement in artificial neural network-based estimation of grid connected photovoltaic power output. Renew. Energy 2016, 97, 838–848. [Google Scholar] [CrossRef]
- Bonanno, F.; Capizzi, G.; Graditi, G.; Napoli, C.; Tina, G.M. A radial basis function neural network based approach for the electrical characteristics estimation of a photovoltaic module. Appl. Energy 2012, 97, 956–961. [Google Scholar] [CrossRef]
- Zhang, L.; Bai, Y.F. Genetic algorithm-trained radial basis function neural networks for modelling photovoltaic panels. Eng. Appl. Artif. Intell. 2005, 18, 833–844. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, H.; Luo, L.; Wu, L.; Zheng, Q.; Wu, Z.; Cheng, S.; Lin, P. Rapid and accurate modeling of PV modules based on extreme learning machine and large datasets of I–V curves. Appl. Energy 2021, 292, 116929. [Google Scholar] [CrossRef]
- Liu, Y.H.; Liu, C.L.; Huang, J.W.; Chen, J.H. Neural-network-based maximum power point tracking methods for photovoltaic systems operating under fast changing environments. Sol. Energy 2013, 89, 42–53. [Google Scholar] [CrossRef]
- Barhmi, S.; Elfatni, O.; Belhaj, I. Forecasting of wind speed using multiple linear regression and artificial neural networks. Energy Syst. 2020, 11, 935–946. [Google Scholar] [CrossRef]
- Asilturl, I. Predicting surface roughness of hardened AISI 1040 based on cutting parameters using neural networks and multiple regression. Int. J. Adv. Manuf. Technol. 2012, 63, 249–257. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M.S. A comparison of neural network, evidential reasoning and multiple regression analysis in modelling bridge risks. Expert Syst. Appl. 2007, 32, 336–348. [Google Scholar] [CrossRef]
- Khalid, C.; Mohammed. F.; Mohcine, M. An accurate modelling of PV modules based on two-diode model. Renew. Energy 2021, 167, 294–305. [Google Scholar]


| Parameters | |
|---|---|
| , | |
| , | |
| , 92 | |
| , 38 | |
| , | |
| Temperature T (K) | Irradiance G (W/m2) | Maximum Absolute Errors (A) of I–V Curves for SM55 Panel | |||
|---|---|---|---|---|---|
| Proposed ANN Model | Model 1 [1] | Model 2 [4] | Model 3 [46] | ||
| 298 | 200 | 0.02 | 0.03 | 0.03 | 0.08 |
| 600 | 0.01 | 0.04 | 0.06 | 0.05 | |
| 1000 | 0.06 | 0.08 | 0.06 | 0.06 | |
| 298 | 1000 | 0.04 | 0.07 | 0.06 (293 K) | 0.10 (293 K) |
| 313 | 0.09 | 0.16 | 0.15 | 0.09 | |
| 333 | 0.09 | 0.12 | 0.10 | 0.20 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, Y. Comparative Estimation of Electrical Characteristics of a Photovoltaic Module Using Regression and Artificial Neural Network Models. Electronics 2022, 11, 4228. https://doi.org/10.3390/electronics11244228
Lee J, Kim Y. Comparative Estimation of Electrical Characteristics of a Photovoltaic Module Using Regression and Artificial Neural Network Models. Electronics. 2022; 11(24):4228. https://doi.org/10.3390/electronics11244228
Chicago/Turabian StyleLee, Jonghwan, and Yongwoo Kim. 2022. "Comparative Estimation of Electrical Characteristics of a Photovoltaic Module Using Regression and Artificial Neural Network Models" Electronics 11, no. 24: 4228. https://doi.org/10.3390/electronics11244228
APA StyleLee, J., & Kim, Y. (2022). Comparative Estimation of Electrical Characteristics of a Photovoltaic Module Using Regression and Artificial Neural Network Models. Electronics, 11(24), 4228. https://doi.org/10.3390/electronics11244228








