A Deep Learning Approach for Efficient Electromagnetic Analysis of On-Chip Inductor with Dummy Metal Fillings
Abstract
1. Introduction
2. Neural Network Equivalent Model
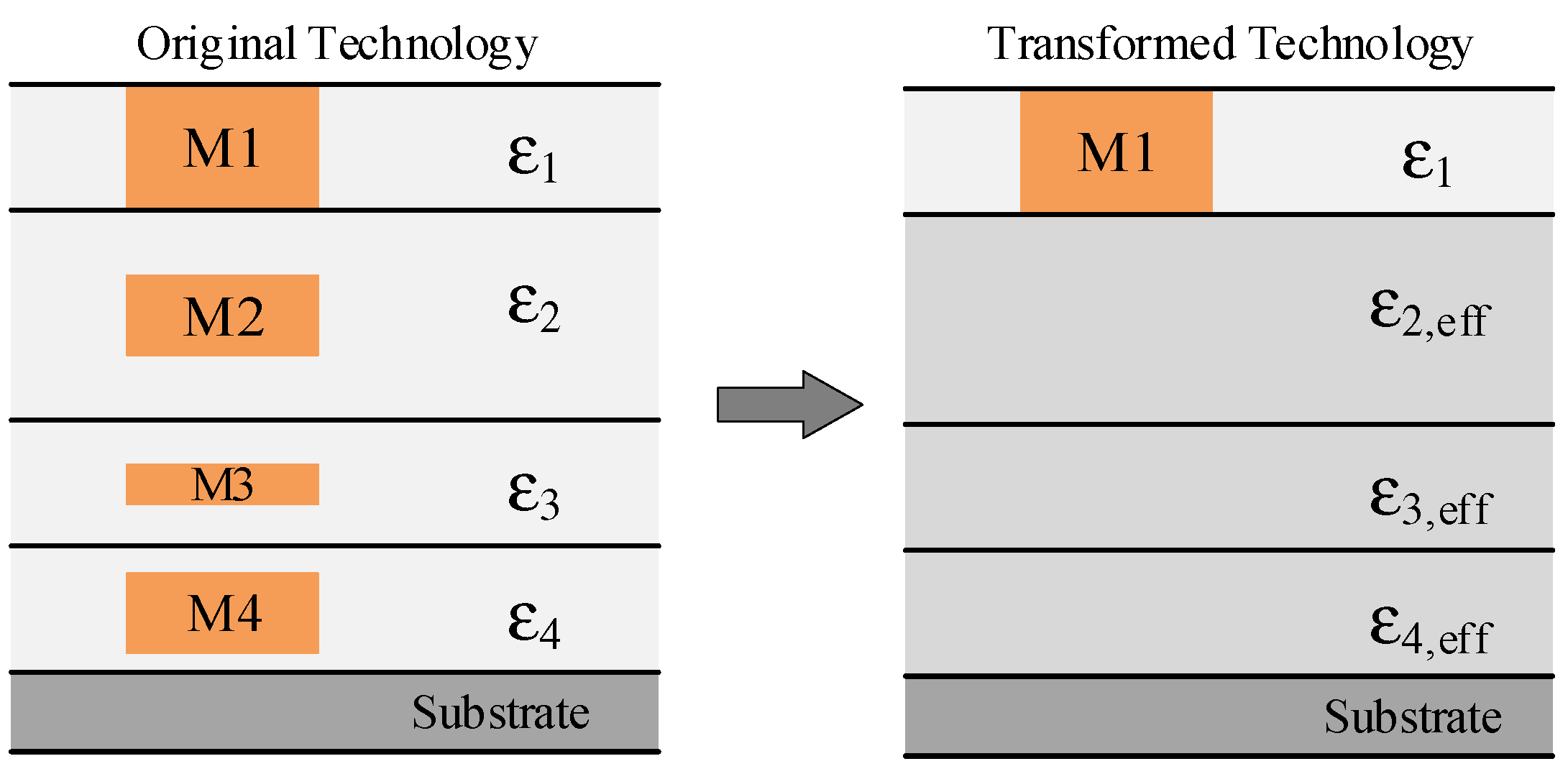
2.1. Equivalent Relative Permittivity
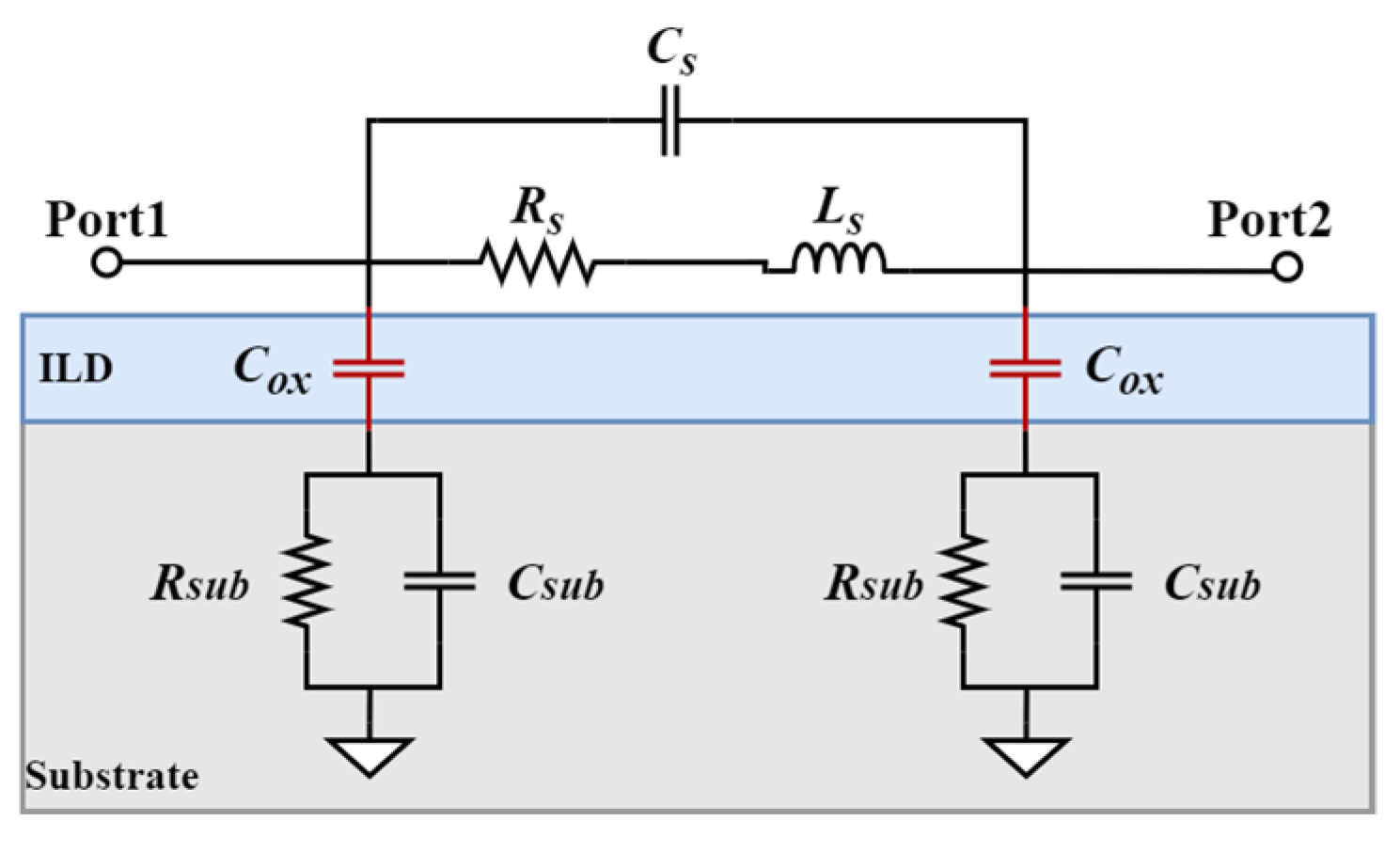
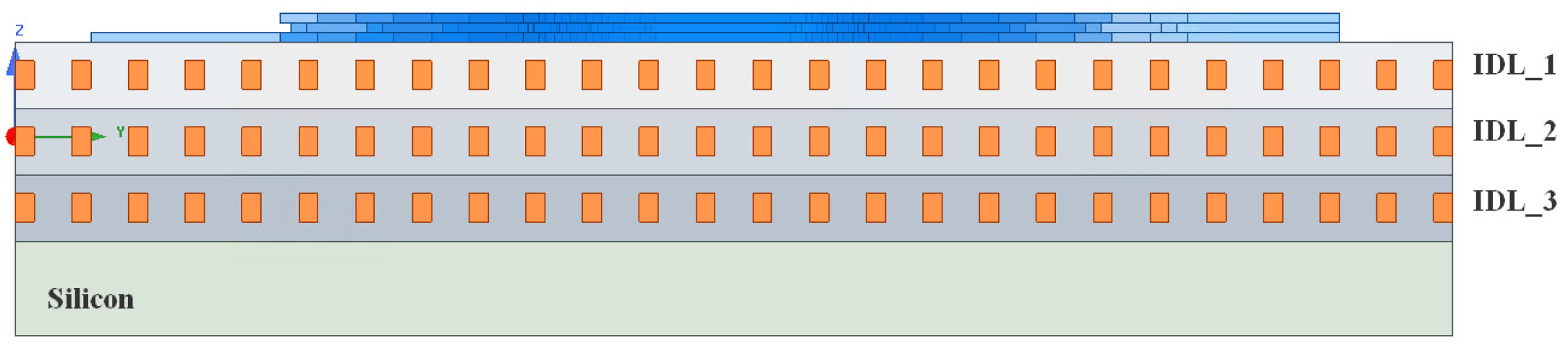
2.2. Equivalent Flat Capacitance Model with DMFs
2.3. Construction of DNN Capacitance Extraction Model Containing DMF (DNN-DMF Model)
2.3.1. Deep Neural Network Model
2.3.2. Loss Function and Optimization Algorithm
2.3.3. Training DNN-DMF Model
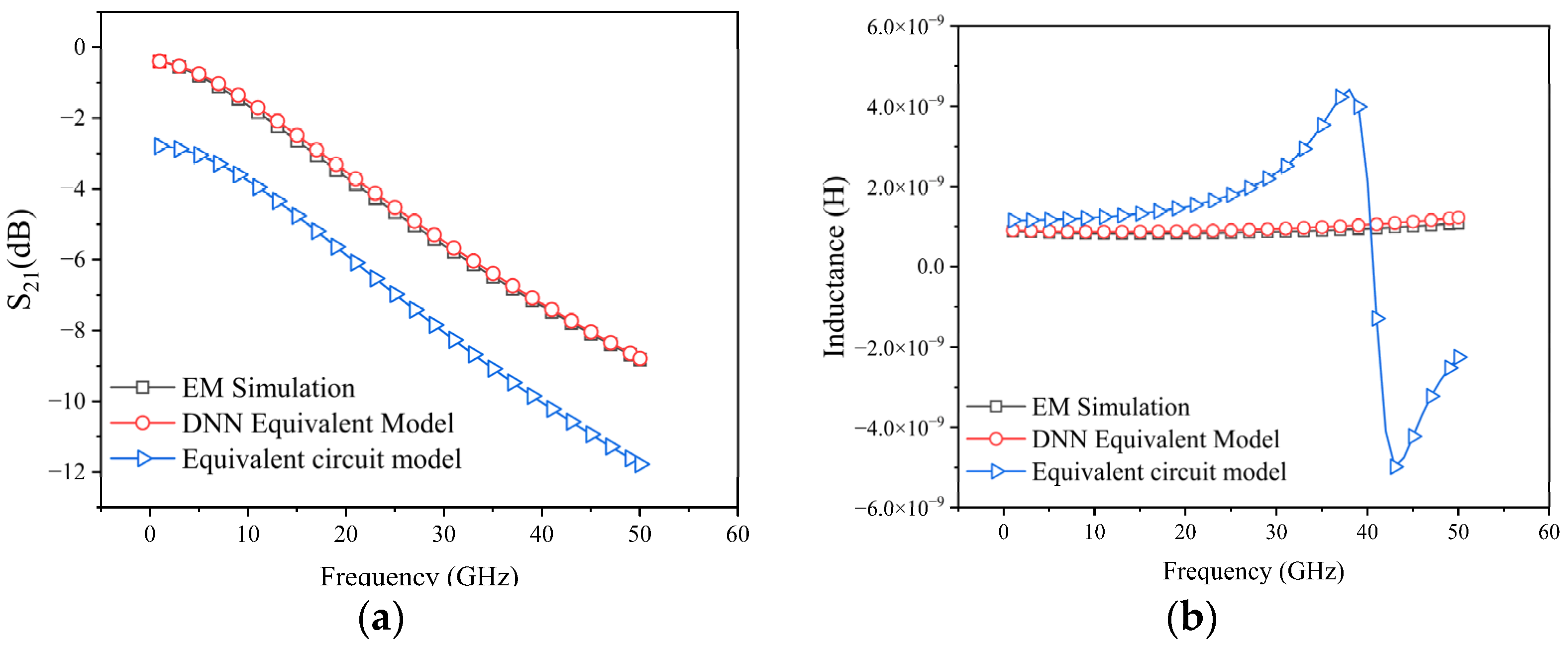
3. Validation of DNN Equivalent Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fury, M.A. Emerging Developments in CMP for Semiconductor Planarization. Solid State Technol. 1995, 38, 81–86. [Google Scholar]
- Stine, B.E.; Boning, D.S.; Chung, J.E.; Camilletti, L.; Kruppa, F.; Equi, E.R.; Loh, W.; Prasad, S.; Muthukrishnan, M.; Towery, D.; et al. The Physical and Electrical Effects of Metal-Fill Patterning Practices for Oxide Chemical-Mechanical Polishing Processes. IEEE Trans. Electron Devices 1998, 45, 665–679. [Google Scholar] [CrossRef]
- Lee, K.H.; Park, J.K.; Yoon, Y.N.; Jung, D.H.; Shin, J.P.; Park, Y.K.; Kong, J.T. Analyzing the Effects of Floating Dummy-Fills: From Feature Scale Analysis to Full-Chip RC Extraction. In Proceedings of the Technical Digest—International Electron Devices Meeting, Washington, DC, USA, 2–5 December 2001. [Google Scholar]
- Kim, Y.; Petranovic, D.; Sylvester, D. Simple and Accurate Models for Capacitance Considering Floating Metal Fill Insertion. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 1166–1170. [Google Scholar] [CrossRef]
- Hsu, H.M.; Hsieh, M.M. On-Chip Inductor above Dummy Metal Patterns. Solid-State Electron. 2008, 52, 998–1001. [Google Scholar] [CrossRef]
- Shilimkar, V.S.; Gaskill, S.G.; Weisshaar, A. Scalable Modeling of On-Chip Spiral Inductors Including Metal Fill Parasitics. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, San Francisco, CA, USA, 30 May 1984–1 June 1984. [Google Scholar]
- Ruehli, A.E. Equivalent Circuit Models for Three-Dimensional Multiconductor Systems. IEEE Trans. Microwave Theory Techn. 1974, 22, 216–221. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, B.; Liu, S.; Lou, L.; Tang, K.; Zhang, Y.; Zheng, Y. Analysis and Modelling on CMOS Spiral Inductor with Impact of Metal Dummy Fills. In Proceedings of the 14th International Symposium on Integrated Circuits, ISIC 2014, Singapore, 10–12 December 2014. [Google Scholar]
- Chen, D.; Wu, Y.; Liu, H.; Yin, W.-Y.; Kang, K. A Scalable Model of On-Chip Inductor Including Tunable Dummy Metal Density Factor. IEEE Trans. Compon. Packag. Manufact. Technol. 2019, 9, 296–305. [Google Scholar] [CrossRef]
- Kim, Y.; Petranovic, D.; Sylvester, D. Simple and Accurate Models for Capacitance Increment Due to Metal Fill Insertion. In Proceedings of the Asia and South Pacific Design Automation Conference, ASP-DAC, Yokohama, Japan, 23–26 January 2007. [Google Scholar]
- Kurokawa, A.; Kanamoto, T.; Kasebe, A.; Inoue, Y.; Masuda, H. Efficient Capacitance Extraction Method for Interconnects with Dummy Fills. In Proceedings of the Custom Integrated Circuits Conference, Orlando, FL, USA, 6 October 2004. [Google Scholar]
- Gaskill, S.G.; Shilimkar, V.S.; Weisshaar, A. Accurate Closed-Form Capacitance Extraction Formulas for Metal Fill in RFICs. In Proceedings of the Digest of Papers—IEEE Radio Frequency Integrated Circuits Symposium, Boston, MA, USA, 7–9 June 2009. [Google Scholar]
- Brownlee, J. A Gentle Introduction to the Rectified Linear Unit (ReLU) for Deep Learning Neural Networks. Available online: https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/ (accessed on 15 October 2022).
- Guan, Z.; Zhao, P.; Wang, X.; Wang, G. Modeling Radio-Frequency Devices Based on Deep Learning Technique. Electronics 2021, 10, 1710. [Google Scholar] [CrossRef]
- Lee, W.S.; Lee, K.H.; Park, J.K.; Kim, T.K.; Park, Y.K.; Kong, J.T. Investigation of the Capacitance Deviation Due to Metal-Fills and the Effective Interconnect Geometry Modeling. In Proceedings of the Proceedings—International Symposium on Quality Electronic Design, ISQED, San Jose, CA, USA, 24–26 March 2003. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Misra, D. Mish: A Self Regularized Non-Monotonic Activation Function. In Proceedings of the 31st British Machine Vision Conference, Manchester, UK, 7–10 September 2020. [Google Scholar] [CrossRef]
- Biswas, K.; Kumar, S.; Banerjee, S.; Pandey, A.K. Smooth Maximum Unit: Smooth Activation Function for Deep Networks Using Smoothing Maximum Technique. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Girod, B. Psychovisual Aspects of Image Processing: What’s Wrong With Mean Squared Error. In Proceedings of the Seventh Workshop on Multidimensional Signal Processing, Lake Placid, NY, USA, 23–25 September 1991. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Yue, C.P.; Wong, S.S. Physical Modeling of Spiral Inductors on Silicon. IEEE Trans. Electron Devices 2000, 47, 560–568. [Google Scholar] [CrossRef]








| Input Parameters | Starting Value | End Value | Step |
|---|---|---|---|
| WD (μm) | 1 | 5 | 1 |
| SD (μm) | 1 | 5 | 1 |
| TD (μm) | 1 | 5 | 1 |
| Tox (μm) | 1 | 5 | 1 |
| Test Loss | MSE | Log-Cosh |
|---|---|---|
| Relu | ||
| ELU | ||
| Mish | ||
| SMU |
| Metal Filling Densities | |
|---|---|
| 20% | 1.26 |
| 50% | 1.46 |
| 80% | 1.53 |
| Metal Filling Densities | Rs(Ω) | Ls(pH) | Rsub(Ω) | Csub(pF) | Cox(fF) |
|---|---|---|---|---|---|
| 20% | 37.62 | 1.17 | 36.57 | 2.5 | 12.9 |
| 50% | 32.29 | 1.08 | 30.51 | 2.66 | 19.35 |
| 80% | 38.24 | 1.18 | 37.32 | 2.48 | 26.57 |
| 20% (Triple DMF) | 37.62 | 1.17 | 36.57 | 2.5 | 4.3 |
| Method | Number of Layers of DMFs | Metal Filling Density | Time | Memory |
|---|---|---|---|---|
| EM Simulation | 1 | 20% | 54 min | 306 M |
| DNN-DMFs | 1 | 20% | 73 s | 77.5 M |
| EM Simulation | 1 | 50% | 78 min | 678 M |
| DNN-DMFs | 1 | 50% | 59 s | 77.1 M |
| EM Simulation | 1 | 80% | 28 min | 378 M |
| DNN-DMFs | 1 | 80% | 79 s | 76.9 M |
| EM Simulation | 3 | 20% | 118 min | 497 M |
| DNN-DMFs | 3 | 20% | 72 s | 77.6 M |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Tang, Y.; Zhao, P.; Chen, S.; Xu, K.; Wang, G. A Deep Learning Approach for Efficient Electromagnetic Analysis of On-Chip Inductor with Dummy Metal Fillings. Electronics 2022, 11, 4214. https://doi.org/10.3390/electronics11244214
Li X, Tang Y, Zhao P, Chen S, Xu K, Wang G. A Deep Learning Approach for Efficient Electromagnetic Analysis of On-Chip Inductor with Dummy Metal Fillings. Electronics. 2022; 11(24):4214. https://doi.org/10.3390/electronics11244214
Chicago/Turabian StyleLi, Xiangliang, Yijie Tang, Peng Zhao, Shichang Chen, Kuiwen Xu, and Gaofeng Wang. 2022. "A Deep Learning Approach for Efficient Electromagnetic Analysis of On-Chip Inductor with Dummy Metal Fillings" Electronics 11, no. 24: 4214. https://doi.org/10.3390/electronics11244214
APA StyleLi, X., Tang, Y., Zhao, P., Chen, S., Xu, K., & Wang, G. (2022). A Deep Learning Approach for Efficient Electromagnetic Analysis of On-Chip Inductor with Dummy Metal Fillings. Electronics, 11(24), 4214. https://doi.org/10.3390/electronics11244214






