Abstract
Crystal Structure Algorithm (CryStAl) is a new meta-heuristic algorithm, and it has been studied by many scholars because of its wide adaptability and the fact that there is no need to set parameters in advance. An improved crystal structure algorithm (GLCryStAl) based on golden sine operator and Levy flight is designed in this paper. The algorithm makes good use of the relationship between the golden sine operator and the unit circle to make the algorithm exploration space more comprehensive, and then gradually narrows the search space in the iterative process, which can effectively speed up the convergence rate of the algorithm. At the same time, a Levy operator is introduced to help the algorithm effectively get rid of the attraction of local optimal value. To evaluate the performance of GLCryStAl, 12 classic benchmark functions and eight CEC2017 test functions were selected to design a series of comparative experiments. In addition, the experimental data of these algorithms are analyzed using the Wilcoxon and Friedman tests. Through these two tests, it can be found that GLCryStAl has significant advantages over other algorithms. Finally, this paper further tests the optimization performance of GLCryStAl in engineering design. GLCryStAl was applied to optimize pressure vessel design problems and tension/compression spring design problems. The optimization results show that GLCryStAl is feasible and effective in optimizing engineering design.
1. Introduction
Nowadays, practical problems in the fields of traffic scheduling, engineering design, machinery manufacturing, etc., are becoming more and more complex and challenging. When dealing with these problems, people often use optimization algorithms to save some costs. Since most production practice problems are multivariate, nonlinear, and have many complex constraints, the traditional conjugate gradient method does not perform well in the optimization of these problems [1]. The meta-heuristic algorithm has the characteristics of not depending on gradient information and wide adaptability, which can effectively make up for the shortcomings of traditional optimization algorithms. At present, the meta-heuristic algorithm is applied in various industries, such as workshop scheduling [2], task planning [3], engineering management [4,5,6,7] and so on.
The meta-heuristic algorithm is a mathematical method inspired by the biological behavior and some physical phenomena in nature [8]. The meta-heuristic algorithms mainly include the swarm optimization algorithm [9], evolutionary algorithm [10], physical and chemical algorithms [11] and human based algorithms [12]. The simulated annealing algorithm [13,14] and differential evolution algorithm [15] are classical evolutionary algorithms. Some classic and newly proposed swarm intelligence optimization algorithms are as follows: the bee collecting pollen algorithm (BCPA) [16] is proposed by simulating the behavior of bees collecting pollen. The fruit fly optimization algorithm (FOA) [17] is proposed by simulating the process of drosophila predation using its keen sense of smell and vision. The bat-inspired algorithm (BA) [18] is proposed by simulating bats using a sonar to detect prey and avoid obstacles. The grey wolf optimizer (GWO) [19] and the tuna swarm optimization (TSO) [20] are proposed by simulating the hunting behavior of wolves and tuna swarms. At present, the metaheuristic algorithm is applied in more and more fields, which has caused more and more scholars to study it.
In nature, a large number of microscopic material units such as molecules, atoms and ions are regularly arranged to form material structures called crystals. “Lattice points” are the basic units of crystal; they form a periodic lattice in a predefined space. The “basis” associated with each lattice point determines the position of the molecule in the crystal structure. In 2021, SIAMAK TALATAHAR proposed a new meta-heuristic algorithm called crystal structure algorithm (CryStAl) [21], by studying the principle of adding basis to form crystal structures with lattice points. The crystal structure algorithm has the advantages of simple structure, no need to set parameters in advance and strong adaptability, so it has generated widespread interest since it was proposed. Although CryStAl has excellent performance in many aspects, there are still some deficiencies in the crystal structure algorithm. CryStAl is susceptible to local extremes during iteration, resulting in insufficient exploration. Furthermore, the convergence speed of CryStAl is relatively slow. Up to now, no scholars have made relevant improvements to the crystal structure algorithm. Because the crystal structure algorithm has the advantages of simple structure, being easy to understand and low time complexity, this paper improves the algorithm under the premise of retaining these advantages of the crystal structure algorithm so that it can obtain better comprehensive optimization performance.
In view of these shortcomings, this paper developed a crystal structure algorithm improved by using a Levy flight operator and golden sine operator.
To ensure CryStAl has a balanced exploration and development performance, random numbers subject to Levy distribution are added to the CryStAl, which can effectively avoid CryStAl being affected by the suboptimal solution iterative process, and the golden sine operator is applied to modify the update strategy of candidate solutions, so that the algorithm converges faster. GLCryStAl is designed according to the modification strategy above.
The main contents of the article are summarized as follows. Section 2 introduces the CryStAl algorithm. Section 3 introduces the improved algorithm GLCryStAl in detail. In Section 4, a series of comparative experiments are designed and experimental numerical analysis is carried out. Section 5 uses GLCryStAl to optimize two engineering problems. Section 6 provides a comprehensive discussion of GLCryStAl. The paper ends in Section 7.
2. An Overview of the Crystal Structure Algorithm
The crystal structure algorithm is inspired by the principle of adding basis to lattice points to form crystals. Based on this principle, SIAMAK TALATAHAR proposed a crystal structure algorithm in 2021.
The internal particles of the crystal are regularly arranged. The structural particles that make up a crystal are regularly arranged at certain points in three-dimensional space, and these points periodically form an infinite lattice with a certain geometric shape, called a “lattice”. The “basis” associated with each lattice point in the crystal determines the position of the particle in the crystal structure, adding basis to the lattice point to form the crystal structure. The mathematical model of the lattice position is as follows [22]:
where represents the number of crystal angles, is the shortest vector and is an integer.
CryStAl initializes crystals using the following formula:
where n is the total number of single crystals and d is the total number of variables. Single crystals are initialized using the following formula:
where and denote the two extreme values of the decision variable of the candidate solution, is a random value in the range of 0–1 and denotes the initial position of the single crystal.
In CryStAl, the crystal at the corner is called . The average value of randomly selected crystals is . Currently, the best crystal is . The crystal structure algorithm has four candidate solution updating strategies, as follows:
Simple cubicle strategy:
Cubicle with the optimal crystal:
Cubicle with the average crystal:
Cubicle with the optimal crystal and average crystal:
where – are four random values, is the position of the old crystal and is the position of the new crystal. The pseudocode of CryStAl is displayed in Algorithm 1:
| Algorithm 1. Pseudo-code of CryStAl |
| 1: Initialization: the positions of crystals, (I = 1, 2, …, n) |
2: Calculate the fitness value of all crystals 3: while t < tmax do 4: for (each crystal) do 5: Create 6: Create new crystals through formula (4) 7: Create 8: Create new crystals through formula (5) 9: Create 10: Create new crystals through formula (6) 11: Create new crystals through formula (7) 12: if (the new crystal goes beyond the preset boundary) then 13: Modify the position of the new crystal 14: end if 15: Calculate the fitness values of all new crystals 16: Update the crystal with the optimal fitness value 17: end for 18: t = t + 1 19: end while |
20: return the best crystal |
3. The Proposed Algorithm
In this chapter, we first introduce the golden sine operator and Levy flight operator. Based on these two operators, the original crystal structure algorithm is modified. Then, a crystal structure algorithm based on Levy flight and golden sine operators is proposed, which is called GLCryStAl.
3.1. Golden Sine Position Update Strategy
The golden sine algorithm [23] is called golden-SA for short. It is a new intelligent optimization algorithm proposed by Tanyildizi, inspired by the mathematical model of sine function. Golden-SA is widely studied because of its simple structure, fast convergence speed and strong stability. Golden-SA simulates the search space exploration process by using the sine function to scan the unit circle. It makes good use of the special relationship between the sine function and the unit circle and combines the golden section coefficients to search the algorithm space iteratively, and finally finds the optimal solution set.
The golden section coefficient is a concept proposed by the ancient Greek mathematician Eudoxus. It does not depend on gradient information and only needs to be iterated once per step, while its contraction steps are fixed per step. Scholars have found that the strategy of combining the traditional sine function with the golden section coefficient can help the algorithm quickly find the extreme value of the unimodal function. At the same time, the golden sine search strategy has good ergodicity, so it can effectively prevent the algorithm from being attracted by the local extreme value.
The mathematical description of the Golden-SA strategy is shown in Equation (8):
where t represents the current number of iterations and represents the position of the best individual in the population in the tth iteration. and are random numbers in [0,2π] and [0,π], respectively; they determine the moving distance of the current individual in the next iteration and the direction of the current individual position update. and represent the positions of the ith individual in iteration t and iteration t + 1, respectively. and are the golden section coefficients mentioned above, which can help the algorithm gradually narrow the search space and guide the ordinary individuals in the population toward the optimal individuals.
The mathematical expressions of and are as follows:
where and are the search interval, and the golden sine algorithm is segmented by the interval of the standard sine function. Since the period of the standard sine function is , according to the relationship between the standard sine and the unit circle, in order to enable the population to traverse the searched space in each dimension throughout the period, the values of and are usually and . is the golden ratio.
3.2. Levy Flight Position Update Strategy
Levy operator [24] is a search strategy consistent with Levy distribution, and its step size is random, which makes Levy operator more suitable for exploration in a wider space than Brownian motion [25]. In the search process, Levy flight uses long distance step in low frequency and short distance step in high frequency, which can effectively avoid the algorithm being attracted by local extrema in the optimization process. Due to the high complexity of Levy distribution, researchers often use the Mantegna [26] algorithm to simulate Levy flight step size, which is defined as follows:
where µ and ν are defined as follows:
where the value of β is usually 1.5.
In order to show the global exploration capability of Levy flight more intuitively, this paper compares Levy flight with random walk strategy. The comparison results are presented in Figure 1.
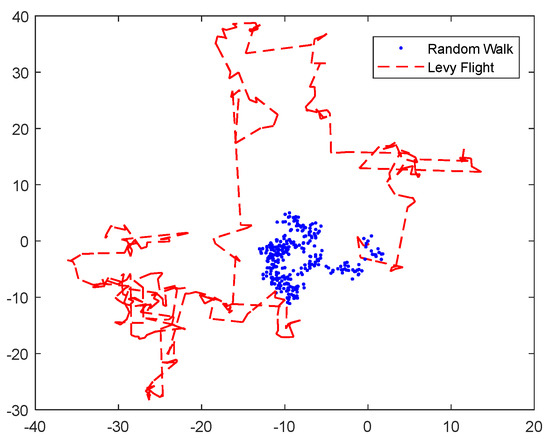
Figure 1.
Simulation comparison experiment diagram of Levy flight and random walk.
Figure 1 shows that the Levy flight has a larger search range. The jump points of random walk strategy are more concentrated, and the jump points of Levy flight strategy are widely distributed. This means that the crystal structure algorithm modified by Levy flight can effectively enhance its global search performance.
3.3. Improved Crystal Structure Algorithm
Aiming at the shortcomings of crystal structure algorithm, such as slow convergence speed and the requirement of practical engineering project for algorithm accuracy, this paper proposes a crystal structure algorithm (GLCryStAl) combining golden sine and Levy flight operator.
The GLCryStAl algorithm introduces the golden sine algorithm and the golden section coefficient into the three position update strategies mentioned in Equations (4)–(6), and determines its update position according to Equation (8). Because the golden sine operator has excellent ergodicity, it can make the optimization space of the algorithm more comprehensive and control the distance and direction of the candidate solution update through the parameters and , so the exploration space of the algorithm can be gradually reduced. Therefore, the introduction of the golden sine operator can reduce the solution time of the algorithm and help the algorithm to obtain a more ideal solution.
Levy operator can significantly enhance the algorithm’s global exploration performance. In this paper, the update strategy in Equation (7) is mutated by using the jump characteristics of the combination of long and short steps of the Levy operator, which can greatly improve the diversity of the algorithm population and make the optimization efficiency of the algorithm higher. The specific steps of GLCryStAl are as follows:
The modified simple cubicle strategy:
The modified cubicle with the optimal crystal:
The modified cubicle with the average crystal:
Cubicle with the optimal crystal and average crystal:
where is the optimal candidate in the current population. , and are the candidate solutions produced by Equations (16)–(18) in the last execution, is a distance control parameter, denotes point multiplication, and is the jump path whose jump distance obeys Levy distribution. Considering that the exploration step size of Levy flight is too aggressive, it may jump out of the main search range during the algorithm search process, so this paper sets α to 0.01.
The pseudocode of GLCryStAl is displayed in Algorithm 2:
| Algorithm 2. Pseudo-code of GLCryStAl |
| 1: Initialization: the positions of crystals, Cri (i = 1, 2, …, n) 2: Calculate the fitness value of all crystals 3: while t < tmax do 4: for (each crystal) do 5: Create Crmain, Crb 6: Create new crystals through formula (16) 7: Create new crystals through formula (17) 8: Create new crystals through formula (18) 9: Create Fc 10: Create new crystals through formula (19) 11: if (the new crystal goes beyond the preset boundary) then 12: Modify the position of the new crystal 13: end if 14: Calculate the fitness values of all new crystals 15: Update the crystal with the optimal fitness value 16: end for 17: t = t + 1 18: end while 19: return the best crystal |
4. Simulation Experiments and Results Analysis
In this section, 12 classic benchmark functions and eight CEC2017 test functions are applied to design comparative experiments of the other five algorithms of GLCryStAl in two different dimensions. To avoid the length of the article being too long, this paper selected part of the CEC2017 test function, which is also representative. Finally, the experimental results are numerically analyzed to verify the optimization performance of GLCryStAl.
4.1. Benchmark Functions and Experimental Design
The details of the test functions are displayed in Table 1. – are unimodal functions, which are applied to evaluate the solution speed of these algorithms. – are multimodal functions, which are applied to evaluate whether these algorithms have excellent global exploration capacity. – are combined functions, which are suitable for testing algorithm performance in fixed dimensions and are used to test the answer accuracy of these algorithms. – are the CEC2017 functions which are applied to test the comprehensive capability of these algorithms.

Table 1.
Benchmark functions.
Based on these 20 test functions, this paper designs a series of experiments comparing GLCryStAl with some of the latest algorithms and an improved algorithm. These competitor algorithms are CryStAl, Accelerated Particle Swarm Optimization Algorithm (APSO) [27], Whale Optimization Algorithm (WOA) [28], Golden Jackal Optimization (GJO) [29], Tunicate Swarm Algorithm (TSA) [30] and the newly proposed Dung beetle optimizer (DBO) [31]. Functions – are tested in 30 and 100 dimensions, respectively, and – are tested in their suitable dimension. Eight CEC2017 benchmark functions are tested in 50 dimensions. The maximum number of evaluations of – is 1000. Since CEC2017 benchmark functions are too complex, the number of evaluations of eight CEC2017 functions are simplified to 3000 without losing representativeness. The population size of each algorithm is 30. To avoid accidental interference, we run each algorithm 30 times independently in each experiment. The parameter values of these algorithms involved in these experiments are shown in Table 2.

Table 2.
Parameter values of the algorithms.
4.2. Results and Analysis
Table 3 displays the experimental results of GLCryStAl and other competitors in low dimensional benchmark functions (dimension = 30). Std is the standard deviation and mean is the average. The mean reflects the solution accuracy of these algorithms and Std reflects their robustness. – are tested in their suitable dimension.

Table 3.
Experimental results in 30 dimensions.
Table 4 displays the test data of GLCryStAl and competitors in high-dimensional benchmark functions (dimension = 100). The experimental results of eight test functions in CEC2017 are shown in Table 5.

Table 4.
Experimental results in 100 dimensions.

Table 5.
Test results of CEC2017 functions.
As can be seen from the above three tables, when the dimension is 30, GLCryStAl can obtain the theoretical optimal values in test functions – and –; GLCryStAl still shows excellent performance in other functions. The solution accuracy of GLCryStAl in is slightly worse than that of WOA, GJO and DBO, and the solution accuracy of GLCryStAl in is not good, but the gap between GLCryStAl and other competitive algorithms in these two test functions is not large. The results are analyzed according to the Std value. Among the functions other than and , the Std value of GLCryStAl is the smallest, which indicates that the optimization effect of GLCryStAl is very stable.
When the dimension is 100, GLCryStAl has the best solution accuracy in all benchmark functions, and GLCryStAl can find the theoretical optimal value in all functions except and . All the data were analyzed according to Std value. The Std value of CL in was only ever worse than CryStAl, and the Std value of GLCryStAl in was the second best, indicating that GLCryStAl still has excellent robustness when solving high-dimensional problems. From the data in Table 5, we can see that the optimization performance of GLCryStAl does not decrease as the test case dimensions increase.
The experimental results of CEC2017 function indicate that all algorithms do not obtain the theoretical optimal value. However, GLCryStAl can achieve better optimization accuracy than other competitors in all test functions. This indicates that the GLCryStAl algorithm modified by Levy operator and golden sine operator can get rid of the attraction of local extreme value more efficiently when solving difficult optimization problems. At the same time, the development and exploration ability of the algorithm are balanced to ensure that the algorithm has a fast convergence rate.
Based on the above three tables for overall analysis, GLCryStAl has the characteristics of high accuracy in 85% of the function optimization problems in the classical benchmark function. Combined with the experimental results of two different dimensions, the Std value of GLCryStAl shows obvious advantages in 76% of the functions. It is not difficult to see that the optimization effect of GLCryStAl is not easily affected by contingency probability, and GLCryStAl can always maintain a stable solution accuracy. In the CEC2017 experimental environment, GLCryStAl can calculate more accurate results within a limited number of executions. None of the comparison algorithms calculate the theoretical optimal value in eight CEC2017 experiments, but this can illustrate that the proposed Levy operator and golden sine operator can accelerate the convergence speed of GLCryStAl and enable it to obtain a better global exploration vision.
Because the golden sine operator has excellent ergodicity, the optimization space of the algorithm can be more comprehensive. The introduction of the golden section coefficient in the iterative process further reduces the search space of the algorithm, which greatly improves the convergence rate of GLCryStAl. Using the Levy flight strategy to modify the candidate solution update formula expands the exploration scope of GLCryStAl, and reduces the probability that GLCryStAl is attracted by local optimal solution. The above data strongly prove the superiority of GLCryStAl and the effectiveness of the proposed operator.
Figure 2 shows the convergence curves of GLCryStAl and other six comparison algorithms on 20 test functions, where Figure 2a–i are the curves of – in 100 dimensions, Figure 2j–l are the curves of – in their suitable dimension and Figure 2m–u are the curves of eight CEC2017 functions.
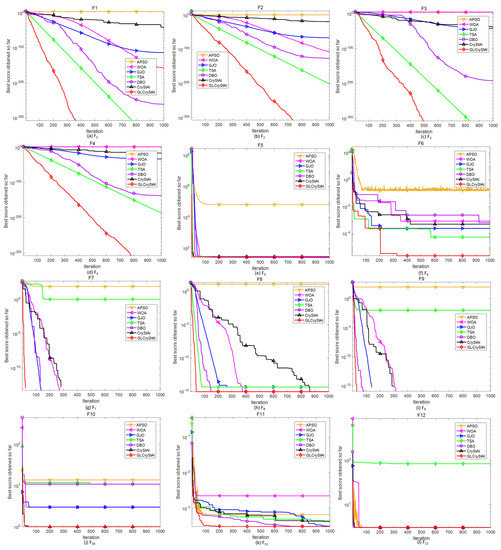
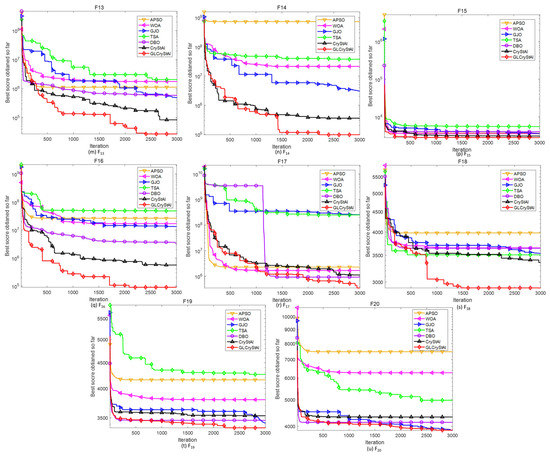
Figure 2.
Convergence curve of each algorithm.
The convergence curves of these algorithms indicate that GLCryStAl has more excellent convergence performance than its competitors. For simple optimization problems, GLCryStAl can obtain theoretical optimal values within 400–700 iterations. For complex and challenging problems, GLCryStAl can also maintain a faster convergence rate and get rid of the influence of local attraction points, and ultimately achieve higher optimization accuracy.
In order to further test whether GLCryStAl has an obvious enhancement advantage compared with other algorithms, this paper uses the Wilcoxon [32] statistical method and Friedman method to analyze the experimental data of these algorithms in 100-dimensional benchmark functions. The data of – are based on their respective dimensions. The experimental data of eight CEC2017 benchmark functions are measured in 50 dimensions. The results of Friedman and Wilcoxon tests are listed in Table 6 and Table 7.

Table 6.
Friedman analysis results.

Table 7.
p-value of Wilcoxon statistical test results.
The smaller the rank mean of the algorithm, the better its performance. As can be seen from Table 6, GLCryStAl has the smallest rank mean, CryStAl ranks second, followed by DBO, GJO, WOA, TSA, APSO. According to the statistical analysis results, the rank mean of the second-ranked competitive algorithm is almost twice that of GLCryStAl, and the rank mean of APSO is more than three times that of GL, which indicates that the improvement effect of the operator proposed in this paper is significant.
In the Wilcoxon statistical test results, if the p-value is less than 0.05 and close to 0, it proves that the experimental results of the two algorithms are significantly different. If the p-value exceeds 0.05, it proves that the experimental results of the two algorithms are not significantly different. If the p-value is equal to NaN, it proves that the experimental results of the two algorithms are not different.
As can be seen from Table 7, the p-values of GLCryStAl are basically less than 0.05 and close to 0, which means that GLCryStAl has significant advantages compared with other algorithms. A small number of the data in Table 7 are greater than 0.05, as are a small number for NaN. This is because the final solution accuracy of these competitive algorithms is not much different from that of GLCryStAl, but it can be seen from the convergence curves of all algorithms that although the solution accuracy of these competitive algorithms is not much different from that of GLCryStAl, their convergence speed is generally much slower than that of GLCryStAl.
5. Optimization Engineering Example Using GLCryStAl
5.1. Using GLCryStAl to Optimize Pressure Vessel Design Problem
The design of pressure vessel is a classical and important problem in practical engineering projects. The structure of the pressure vessel is shown in Figure 3, which consists of a cylindrical container and two hemispherical containers. In this optimization problem, there are four key variables, which are , , and . denotes the thickness of the shell of the cylindrical container, denotes the thickness of the hemispheric container lid, is the radius inside the hemispherical container and is the length of the cylinder container. These four variables can be expressed as the following equation when using algorithms to optimize the pressure vessel design problem.
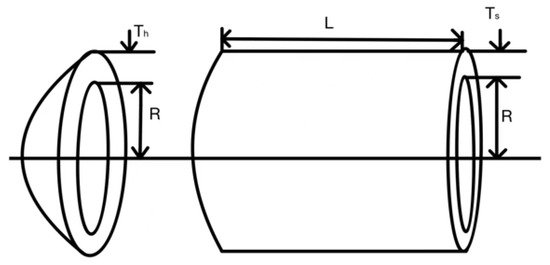
Figure 3.
Pressure vessel structure diagram.
In this optimization problem, we use heuristic algorithm to regulate these four variables, so as to minimize the sum of material cost, forming cost and welding cost of the pressure vessel, which is transformed into the problem of finding the minimum of objective function with constraints.
The objective function of the pressure vessel design optimization problem is as follows:
To verify the effectiveness of GLCryStAl in pressure vessel design, this paper selects PSO, WOA, GJO, TSA, DBO and CryStAl to compare with GLCryStAl, and runs each algorithm 10 times. The population size of all algorithms is 30, and the maximum number of iterations = 1000. The specific results are listed in Table 8 and Table 9.

Table 8.
Total cost of six algorithms for optimizing pressure vessel design problems.

Table 9.
The best results of six algorithms.
It is clear from the above two tables that the total cost calculated by GLCryStAl is the smallest in the pressure vessel optimization design problem. In addition, the Std of GLCryStAl is within an acceptable range, which proves from another aspect that GLCryStAl has excellent stability when solving constrained engineering design optimization problems.
5.2. Optimizing the Design of Tension/Compression Spring Using GLCryStAl
To fully prove the feasibility and effectiveness of the GLCryStAl algorithm in engineering optimization problems, this paper applies the GLCryStAl algorithm to the optimization design problem of a tension/compression spring. A schematic of the spring is shown in Figure 4. This optimization problem is to select the most appropriate wire diameter (D), the average coil diameter (L) and the number of effective coils (P) under a series of specific constraints, so as to minimize the weight of the spring. In this paper, the three variables D, L and P are represented as , and . The mathematical modeling of the optimization problem in this section is as follows:
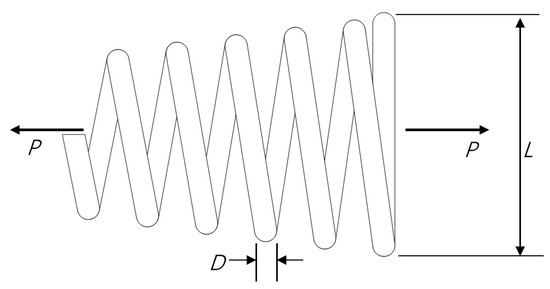
Figure 4.
Schematic diagram of tension/compression spring design.
To evaluate the effectiveness of GLCryStAl in the design of tension/compression spring, a comparative experiment is designed. PSO, WOA, GJO, TSA, DBO and CryStAl are selected to compare with GLCryStAl, and the results are listed in Table 10 and Table 11. In this comparison experiment, each algorithm runs 10 times independently. The population size of each algorithm is 30, and the maximum number of iterations = 1000.

Table 10.
Comparison results of six algorithms in spring design problem.

Table 11.
The best results of six algorithms.
From the experimental results, in the optimization results of all algorithms, the mean value obtained by GLCryStAl is second only to the mean value obtained by GJO. However, from another point of view, the best value of spring weight optimized by the GLCryStAl algorithm is smaller than that of all the competitors. This proves that the GLCryStAl algorithm proposed in this paper is feasible and effective in the optimization design problem of a tension/compression spring.
6. Discussion of GLCryStAl
CryStAl is a heuristic algorithm with a simple structure and no need to set hyperparameters. This paper uses Levy operator and golden sine operator to make targeted optimization based on some subsidies of the original CryStAl algorithm. Firstly, this paper uses the golden sine operator to optimize the candidate solution update equation in CryStAl. The golden sine operator has excellent ergodicity to speed up the convergence of the algorithm. Secondly, this paper uses the levy flight operator to perturb the candidate solution update method of the CryStAl algorithm. By using the method of combining the long and short steps of the operator for optimization, the algorithm is effectively prevented from being attracted by the local optimal value during execution. The excellent optimization capability of GLCryStAl is demonstrated by comparison with various competitive algorithms. A series of experiments have proved the effectiveness of GLCryStAl from multiple viewpoints, which strongly indicates that GLCryStAl has a wide range of engineering applications.
In a series of function test experiments, GLCryStAl has higher solution accuracy than other competitors in 85% of classical benchmark functions. GLCryStAl has a higher Std value than other competitors in 76% of classical functions, which proves that the accuracy of GLCryStAl is not easily affected by random factors. In the comparison of CEC2017 benchmark functions, although all algorithms cannot calculate the theoretical optimal value, GLCryStAl can calculate a more accurate solution in a limited number of executions. The comparison results of a series of functions are analyzed by statistical methods. GLCryStAl achieved the smallest rank mean in the Friedman analysis experiment, and the p-value in the Wilcoxon analysis experiment is basically less than 0.05 and close to 0. These statistical analyses prove that the two operators proposed in this paper have significant improvement effects on CryStAl. Applying GLCryStAl to the pressure vessel design problem and the tension/compression spring design problem, compared with other competitors, GLCryStAl can calculate the minimum cost pressure vessel design and the minimum weight stretch/compression spring design. It can be proven from a series of experiments in this paper that the optimization performance of GLCryStAl is significantly improved compared with the original CryStAl algorithm, but the performance of GLCryStAl in solving some multi-peak complex problems still needs to be improved, which is also a major research direction in our future.
7. Conclusions
Focusing on the problem of the crystal structure algorithm being easily attracted by local extremum and the solution accuracy not being high enough, GLCryStAl is proposed. In GLCryStAl, the golden sine operator and Levy operator are applied to modify the update strategy of the four candidate solutions in the crystal structure. This improvement can effectively prevent GLCryStAl from being attracted by local extreme values in the optimization process, and the optimization speed of GLCryStAl is significantly accelerated. In this paper, 10 classical benchmark functions and eight CEC2017 test functions are applied to design a series of comparison experiments with the latest algorithms and our improved algorithm. When solving low-dimensional functions, GLCryStAl can calculate the theoretical optimal value of the function in – and –, and GLCryStAl can maintain the minimum standard deviation in functions other than and . When solving high-dimensional functions, GLCryStAl obtains theoretical optimal values in seven functions. It can be concluded from the experimental results that the optimization capability of GLCryStAl is obviously stronger. In addition, the experimental data of the six algorithms were analyzed by Wilcoxon and Friedman method. The statistical results show that the rank mean of GL is only 1.7, which indicates that GLCryStAl algorithm is superior to other competitors.
Finally, this paper uses GLCryStAl to optimize two practical engineering problems. In the first engineering problem, GLCryStAl is applied to the optimal design of pressure vessels. GLCryStAl achieved the best performance in this experiment. In the second engineering problem, GLCryStAl is applied to optimize the stretch/compression spring design. In this experiment, the optimal spring weight designed by GLCryStAl is second only to that of GJO. These two design problems fully demonstrate the feasibility and effectiveness of GLCryStAl in optimizing practical engineering problems.
Author Contributions
Conceptualization, W.W. and J.T.; methodology, W.W.; software, D.W.; validation, W.W.; formal analysis, D.W.; investigation, W.W.; resources, W.W.; data curation, W.W.; writing—original draft preparation, W.W.; supervision, J.T.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, G.; Pedrycz, W.; Suganthan, P.N.; Mallipeddi, R. Avariabe reduction strategy for evolutionary algorithms handling equality constraints. Appl. Soft Comput. 2015, 37, 774–786. [Google Scholar] [CrossRef]
- Liu, W.; Dridi, M.; Fei, H.; El Hassani, A.H. Hybrid metaheuristics for solving a home health care routing and scheduling problem with time windows, synchronized visits and lunch breaks. Expert Syst. Appl. 2021, 183, 115307. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Han, T.; Zhou, H.; Li, C. A grey wolf optimizer using Gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem. Appl. Soft Comput. 2019, 78, 240–260. [Google Scholar] [CrossRef]
- Wang, Y.-G. A maximum-likelihood method for estimating natural mortality and catchability coefficient from catch-and-effort data. Mar. Freshw. Res. 1999, 50, 307–311. [Google Scholar] [CrossRef]
- Wu, J.; Ding, Z. Improved grey model by dragonfly algorithm for Chinese tourism demand forecasting. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Kitakyushu, Japan, 22–25 September 2020. [Google Scholar]
- Wu, J.; Cui, Z.; Chen, Y.; Kong, D.; Wang, Y.-G. A new hybrid model to predict the electrical load in five states of Australia. Energy 2019, 166, 598–609. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, G.; Xu, Y.; Wang, S.; Liu, M. An effective artificial bee colony algorithm for the flexible job-shop scheduling problem. Int. J. Adv. Manuf. Technol. 2012, 60, 303–315. [Google Scholar] [CrossRef]
- Webb, B. Swarm Intelligence: From Natural to Artificial Systems; IEEE Press: Piscataway, NJ, USA, 2002; Volume 14, pp. 163–164. [Google Scholar]
- Kennedy, J. Swarm Intelligence. In Nature-Inspired and Innovative Computing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 187–219. [Google Scholar]
- Ashlock, D. Evolutionary Computation for Modeling and Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2015, 27, 495–513. [Google Scholar] [CrossRef]
- Satapathy, S.; Naik, A. Social group optimization (SGO): A new population evolutionary optimization technique. Complex Intell. Syst. 2016, 2, 173–203. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Wang, L.; Lee, S.N.S.; Hing, W.Y. Solving channel assignment problems using local search methods and simulated annealing. In Independent Component Analyses, Wavelets, Neural Networks, Biosystems, and Nanoengineering IX; SPIE: Bellingham, WA, USA, 2011; Volume 8058, pp. 490–497. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, Y. A novel global convergence algorithm: Bee collecting pollen algorithm. In Proceedings of the International Conference on Intelligent Computing, Berlin, Germany, 15–18 September 2008. [Google Scholar]
- Pan, W.T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl. Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NISCO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna swarm optimization: A novel swarm-based metaheuristic algorithm for global optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef] [PubMed]
- Talatahari, S.; Azizi, M.; Tolouei, M.; Talatahari, B.; Sareh, P. Crystal Structure Algorithm (CryStAl): A Metaheuristic Optimization Method. IEEE Access 2021, 9, 71244–71261. [Google Scholar] [CrossRef]
- Averill, B.A.; Eldredge, P. Chemistry: Principles, Patterns, and Applications; Benjamin Cummings: San Francisco, CA, USA, 2021. [Google Scholar]
- Tanyildizi, E.; Demir, G. Golden Sine Algorithm: A Novel Math-Inspired Algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Havlin, S.; Da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. Levy fights search patterns of biological organisms. Phys. A Stat. Mech. Appl. 2001, 295, 85–88. [Google Scholar] [CrossRef]
- Biagini, F.; Hu, Y.; Øksendal, B.; Zhang, T. Stochastic optimal control and applications. In Stochastic Calculus for Fractional Brownian Motion and Applications; Springer Science & Business Media: Berlin, Germany, 2008; pp. 207–238. [Google Scholar]
- Mantegna, R.N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes. Phys. Rev. E 1994, 49, 4677–4689. [Google Scholar] [CrossRef]
- Reddy, B.R.; Uttara, K.M. Performance Analysis of Mimo Radar Waveform Using Accelerated Particle Swarm Optimization Algorithm. Signal Image Process. 2012, 3, 4. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 1–32. [Google Scholar] [CrossRef]
- Rosner, B.; Glynn, R.J.; Lee, M.T. Incorporation of Clustering Effects for the Wilcoxon Rank Sum Test: A Large-Sample Approach. Biometrics 2003, 59, 1089–1098. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).