Distributed Adaptive NN-Based Attitude Synchronous Tracking Control with Input Saturation
Abstract
1. Introduction
- The proposed distributed attitude coordination controller for SFF is robust against external disturbances and inertia uncertainties with input saturation. The stability of the controller is verified by Lyapunov’s method and the tracking errors are uniformly ultimately bounded (UUB).
- A ChNN-based approximator, which has the advantages of computational simplicity and easy application [31] is implemented in the proposed controller, and in simulation, it is discovered that chattering caused by the switch function can be avoided by applying a filter.
- A Nussbaum-type function is introduced to the ASTC to handle the nonlinearity arising from input saturation. This approach can be easily extended to other control problems.
2. Problem Statement
2.1. Attitude Dynamics of Rigid Spacecraft
2.2. Actuator with Input Saturation
2.3. Control Object
3. Preliminaries and Lemmas
3.1. Graph Theory
3.2. Nussbaum-Type Function
- 1.
- , where γ is a constant;
- 2.
- ;
- 3.
- ;
- 4.
- Suppose that and are invertible, then ;
- 5.
- Let be the eigenvalues of , and be those of . Then the eigenvalues of are .
3.3. The Chebyshev Neural Network
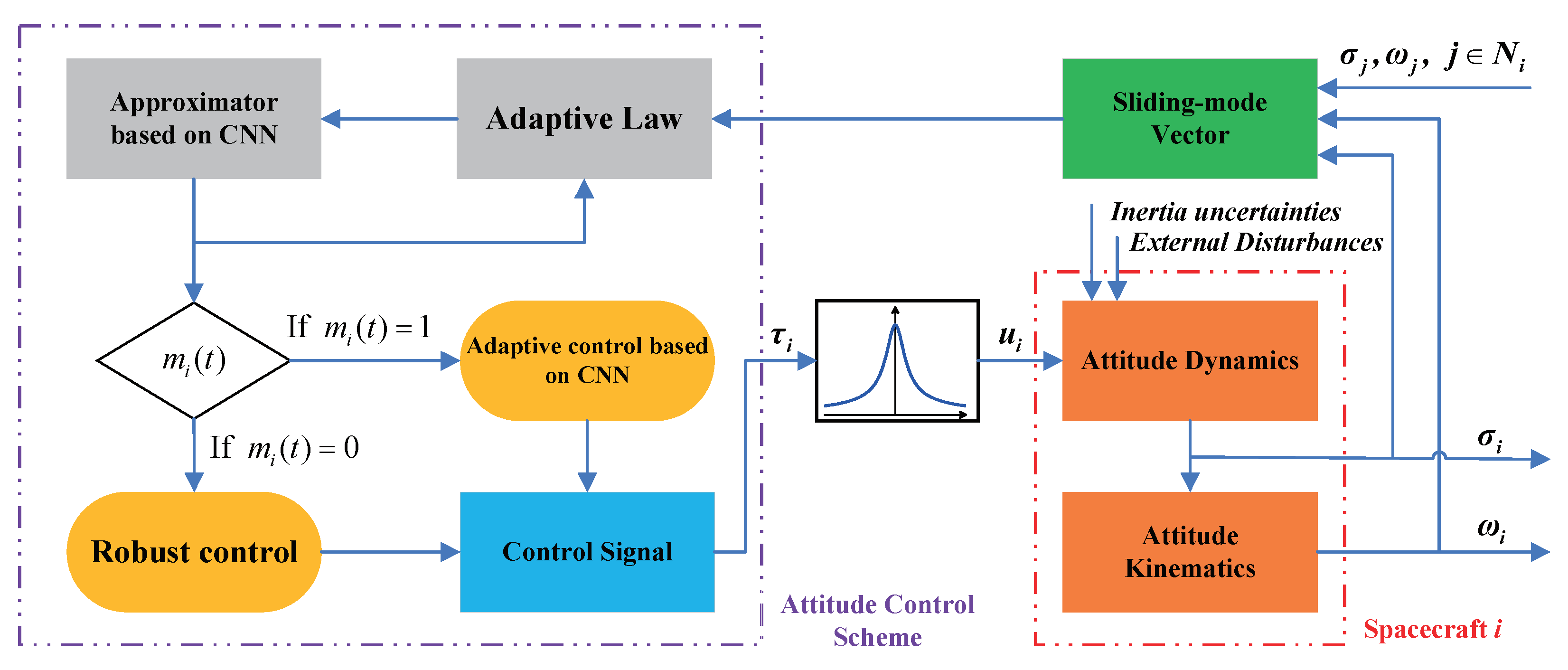
4. Main Results
4.1. Multi-Spacecraft Sliding Manifold Derivation
4.2. Controller Synthesis
4.2.1. Control Law Design
4.2.2. Stability Analysis
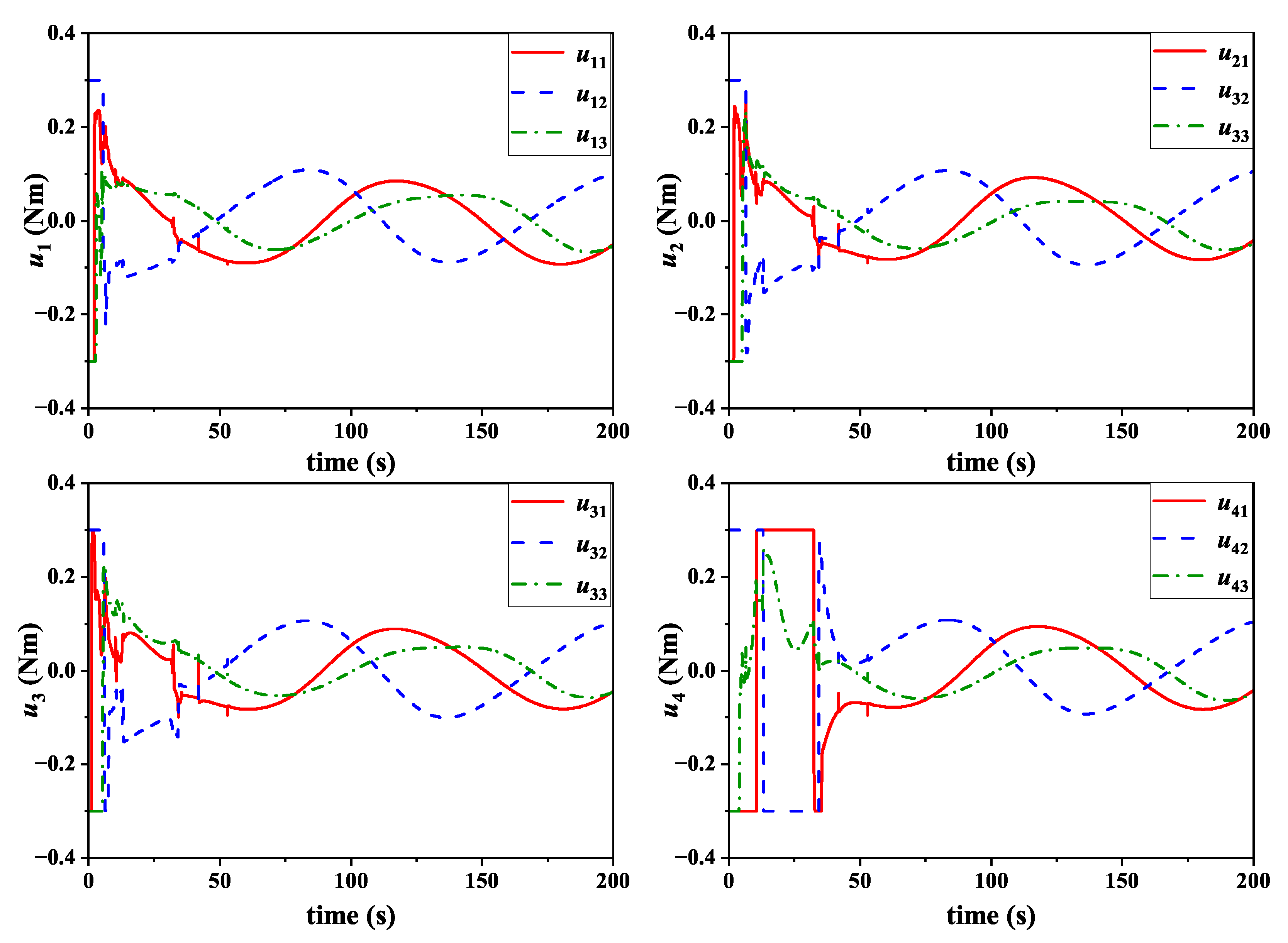
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| adjacency matrix | |
| connection matrix | |
| external disturbance vector, | |
| control torque vector, | |
| inertia tensor, | |
| nominal inertia tensor, | |
| Laplacian matrix | |
| S | multi-spacecraft sliding-mode vector |
| V | Lyapunov function |
| inertia uncertainty, | |
| in-degree matrix | |
| upper bound on the norm of external disturbance | |
| upper bound on the norm of inertia uncertainty | |
| minimum eigenvalue of matrix | |
| modified Rodriguez parameter vector | |
| attitude (MRPs) tracking error | |
| commanded control signal, | |
| angular velocity, | |
| angular velocity tracking error, | |
| Euclidean norm | |
| vector cross-product matrix | |
| ⊗ | Kronecker product |
| Acronyms | |
| NN | neural network |
| ChNN | Chebyshev neural network |
| SFF | spacecraft formation flying |
| ASTC | attitude synchronization and tracking control |
| SMC | sliding-mode control |
| MRPs | modified Rodriguez parameters |
| UUB | uniformly ultimately bounded |
References
- Dony, M.N.A.A.; Dong, W. Distributed Robust Formation Flying and Attitude Synchronization of Spacecraft. J. Aerosp. Eng. 2021, 34, 04021015. [Google Scholar] [CrossRef]
- Fan, L.; Huang, H. Coordinative coupled attitude and orbit control for satellite formation with multiple uncertainties and actuator saturation. Acta Astronaut. 2021, 181, 325–335. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, Y. Adaptive coordinated attitude control for spacecraft formation with saturating actuators and unknown inertia. J. Frankl. Inst. 2019, 356, 1021–1037. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, J.; Friswell, M.I. Finite-Time Coordinated Attitude Control for Spacecraft Formation Flying Under Input Saturation. J. Dyn. Syst. Meas. Control. 2015, 137, 061012. [Google Scholar] [CrossRef]
- Saeed Nasrolahi, S.; Abdollahi, F.; Rezaee, H. Decentralized active sensor fault tolerance in attitude control of satellite formation flying. Int. J. Robust Nonlinear Control. 2020, 30, 8340–8361. [Google Scholar] [CrossRef]
- Wu, B.; Wang, D.; Poh, E.K. Decentralized robust adaptive control for attitude synchronization under directed communication topology. J. Guid. Control. Dyn. 2011, 34, 1276–1282. [Google Scholar] [CrossRef]
- Yi, H.; Liu, M.; Li, M. Event-triggered fault tolerant control for spacecraft formation attitude synchronization with limited data communication. Eur. J. Control. 2019, 48, 97–103. [Google Scholar] [CrossRef]
- Cui, B.; Xia, Y.; Liu, K.; Zhang, J.; Wang, Y.; Shen, G. Truly Distributed Finite-Time Attitude Formation-Containment Control for Networked Uncertain Rigid Spacecraft. IEEE Trans. Cybern. 2020, 52, 5882–5896. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, Y.; Gao, Z. Adaptive finite-time actuator fault-tolerant coordinated attitude control of multispacecraft with input saturation. Int. J. Adapt. Control. Signal Process. 2019, 33, 644–663. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Sun, Y.; Ma, G. Distributed coordinated attitude tracking control for spacecraft formation with communication delays. ISA Trans. 2019, 85, 97–106. [Google Scholar] [CrossRef]
- Zou, A.; de Ruiter, A.H.; Kumar, K.D. Distributed finite-time velocity-free attitude coordination control for spacecraft formations. Automatica 2016, 67, 46–53. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J. Continuous constrained attitude regulation of multiple spacecraft on SO(3). Aerosp. Sci. Technol. 2020, 99, 105769. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Zhang, H. Distributed attitude control for multispacecraft via Takagi–Sugeno fuzzy approach. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 642–654. [Google Scholar] [CrossRef]
- Du, H.; Li, S. Attitude synchronization for flexible spacecraft with communication delays. IEEE Trans. Autom. Control. 2016, 61, 3625–3630. [Google Scholar] [CrossRef]
- Nazari, M.; Butcher, E.A.; Yucelen, T.; Sanyal, A. K Decentralized consensus control of a rigid-body spacecraft formation with communication delay. J. Guid. Control. Dyn. 2016, 39, 838–851. [Google Scholar] [CrossRef]
- Zou, Y.; Meng, Z. Velocity-free leader-follower cooperative attitude tracking of multiple rigid bodies on SO(3). IEEE Trans. Cybern. 2019, 39, 4078–4089. [Google Scholar] [CrossRef]
- Lu, K.; Li, T.; Zhang, L. Active attitude fault-tolerant tracking control of flexible spacecraft via the Chebyshev neural network. Trans. Inst. Meas. Control 2019, 41, 925–933. [Google Scholar] [CrossRef]
- Xia, R.; Chen, M.; Wu, Q. Neural network based optimal adaptive attitude control of near-space vehicle with system uncertainties and disturbances. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 641–656. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, D.; Chen, X.; Zhou, Z. Actor-critic-based predefined-time control for spacecraft attitude formation system with guaranteeing prescribed performance on SO(3). Aerosp. Sci. Technol. 2021, 117, 106898. [Google Scholar] [CrossRef]
- Cai, H.; Huang, J. Leader-following attitude consensus of multiple rigid body systems by attitude feedback control. Automatica 2016, 69, 87–92. [Google Scholar] [CrossRef]
- Hou, Z.; Zou, A.; Cheng, L.; Tan, M. Adaptive control of an electrically driven nonholonomic mobile robot via backstepping and fuzzy approach. IEEE Trans. Control. Syst. Technol. 2009, 17, 803–815. [Google Scholar]
- Li, A.; Liu, M.; Shi, Y. Adaptive sliding mode attitude tracking control for flexible spacecraft systems based on the Takagi-Sugeno fuzzy modelling method. Acta Astronaut. 2020, 175, 570–581. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Shi, P. Command filtered backstepping-based attitude containment control for spacecraft formation. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 1278–1287. [Google Scholar] [CrossRef]
- Amrr, S.M.; Alturki, A.; Kumar, A.; Nabi, M. Prescribed Performance-Based Event-Driven Fault-Tolerant Robust Attitude Control of Spacecraft under Restricted Communication. Electronics 2021, 10, 1709. [Google Scholar] [CrossRef]
- Liang, Y.; Ting, L.; Lin, L. Study of reliable control via an integral-type sliding mode control scheme. IEEE Trans. Ind. Electron. 2012, 59, 3062–3068. [Google Scholar] [CrossRef]
- Defoort, M.; Floquet, T. A novel higher order sliding mode control scheme. Syst. Control. Lett. 2009, 58, 102–108. [Google Scholar] [CrossRef]
- Wu, F.; Liu, M.; Feng, Z.; Cao, X. Fractional-order sliding mode attitude coordinated control for spacecraft formation flying with unreliable wireless communication. IET Control. Theory Appl. 2022. [Google Scholar] [CrossRef]
- Tang, G.; Dong, R.; Gao, H. Optimal sliding mode control for nonlinear systems with time-delay. Nonlinear Anal. Hybrid Syst. 2008, 2, 891–899. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Zou, A.; Kumar, K.D.; Hou, Z.G. Quaternion-based adaptive output feedback attitude control of spacecraft using Chebyshev neural networks. IEEE Trans. Neural Netw. 2010, 21, 1457–1471. [Google Scholar]
- Zou, A.; Kumar, K.D.; Hou, Z.; Liu, X. Finite-time attitude tracking control for spacecraft using terminal sliding mode and Chebyshev neural network. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 950–963. [Google Scholar]
- Yu, B.; Du, H.; Ding, L.; Wu, D.; Li, H. Neural network-based robust finite-time attitude stabilization for rigid spacecraft under angular velocity constraint. Neural Comput. Appl. 2022, 34, 5107–5117. [Google Scholar] [CrossRef]
- Ali, I.; Radice, G.; Kim, J. Backstepping control design with actuator torque bound for spacecraft attitude maneuver. J. Guid. Control. Dyn. 2010, 33, 254–259. [Google Scholar] [CrossRef]
- Gui, H.; Vukovich, G. Finite-time angular velocity observers for rigid-body attitude tracking with bounded inputs. Int. J. Robust Nonlinear Control 2017, 27, 15–38. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.; Ma, G.; Weilin, L. Review on Input Saturation in the Spacecraft Attitude Control. J. Astronaut. 2021, 42, 11–21. [Google Scholar]
- Hu, Q.; Tan, X.; Akella, M.R. Finite-Time Fault-Tolerant Spacecraft Attitude Control with Torque Saturation. J. Guid. Control. Dyn. 2017, 40, 2524–2537. [Google Scholar] [CrossRef]
- Gao, S.; Jing, Y.; Liu, X.; Zhang, S. Finite-time attitude-tracking control for rigid spacecraft with actuator failures and saturation constraints. Int. J. Robust Nonlinear Control 2020, 30, 1903–1937. [Google Scholar] [CrossRef]
- Ding, Z. Adaptive consensus output regulation of a class of nonlinear systems with unknown high-frequency gain. Automatica 2015, 51, 348–355. [Google Scholar] [CrossRef]
- Khettab, K.; Ladaci, S.; Bensafia, Y. Fuzzy adaptive control of fractional order chaotic systems with unknown control gain sign using a fractional order Nussbaum gain. IEEE/CAA J. Autom. Sin. 2016, 6, 816–823. [Google Scholar] [CrossRef]
- Wen, C.; Zhou, J.; Liu, Z.; Su, H. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Autom. Control. 2011, 56, 1672–1678. [Google Scholar] [CrossRef]
- Ji, N.; Liu, J. Vibration control for a flexible satellite with input constraint based on Nussbaum function via backstepping method. Aerosp. Sci. Technol. 2018, 77, 563–572. [Google Scholar] [CrossRef]
- Hu, Q.; Shao, X.; Guo, L. Adaptive fault-tolerant attitude tracking control of spacecraft with prescribed performance. IEEE/ASME Trans. Mechatronics 2017, 23, 331–341. [Google Scholar] [CrossRef]
- Schaub, H.; Junkins, J.L. Stereographic orientation parameters for attitude dynamics: A generalization of the Rodrigues parameters. J. Astronaut. Sci. 1996, 44, 1–19. [Google Scholar]
- Schaub, H.; Junkins, J.L. Analytical Mechanics of Space Systems; AIAA: Reston, VA, USA, 2003. [Google Scholar]
- Wallsgrove, R.J.; Akella, M.R. Globally stabilizing saturated attitude control in the presence of bounded unknown disturbances. J. Guid. Control. Dyn. 2005, 28, 957–963. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Nussbaum, R.D. Some remarks on a conjecture in parameter adaptive control. Syst. Control. Lett. 1983, 3, 243–246. [Google Scholar] [CrossRef]
- Ao, W.; Huang, J. Adaptive leaderless consensus control of a class of strict-feedback nonlinear multi-agent systems with unknown control directions: A non-Nussbaum function based approach. J. Frankl. Inst. 2020, 357, 12180–12196. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Zhihong, M.; Paplinski, A.P.; Wu, H.R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 1994, 39, 2464–2469. [Google Scholar] [CrossRef]






| n | Inertia Matrix | Inertia Uncertainty | External Disturbance |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
| Controller | MSTE | MSCT () |
|---|---|---|
| The proposed controller | 0.0061 | 0.0254 |
| The comparison controller | 0.1405 | 0.0427 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Wang, J.; Wan, N.; Li, H. Distributed Adaptive NN-Based Attitude Synchronous Tracking Control with Input Saturation. Electronics 2022, 11, 4093. https://doi.org/10.3390/electronics11244093
Feng Z, Wang J, Wan N, Li H. Distributed Adaptive NN-Based Attitude Synchronous Tracking Control with Input Saturation. Electronics. 2022; 11(24):4093. https://doi.org/10.3390/electronics11244093
Chicago/Turabian StyleFeng, Zhenyu, Jiawei Wang, Neng Wan, and Huayi Li. 2022. "Distributed Adaptive NN-Based Attitude Synchronous Tracking Control with Input Saturation" Electronics 11, no. 24: 4093. https://doi.org/10.3390/electronics11244093
APA StyleFeng, Z., Wang, J., Wan, N., & Li, H. (2022). Distributed Adaptive NN-Based Attitude Synchronous Tracking Control with Input Saturation. Electronics, 11(24), 4093. https://doi.org/10.3390/electronics11244093








