1. Introduction
Fuzz testing is a useful method for analyzing software vulnerabilities. The primary concept is to offer a large number of specific or random test cases to the program, monitor abnormal situations throughout the program’s execution, and manually evaluate abnormal test case data in order to find software vulnerabilities [
1]. Fuzzing has emerged as a popular topic in vulnerability analysis technology research, and grey-box fuzzing (GF) is regarded as the most recent fuzzing technique. Grey-box fuzzing makes use of a more lightweight instrument to identify unique identifiers for input execution routes with low performance cost. The created new input test cases are acquired by modifying the specified seeds; if these new inputs discover new interesting routes, they are added to the fuzzer’s seed queue.
As the most widely used fuzzer for grey-box fuzzing, AFL [
2] will instrument the program under test to monitor the path coverage information of each input and offer a foundation for the subsequent selection of input files for mutation. The AFL also includes a power schedule that distributes energy in a consistent manner regardless of the number of times seeds are picked for fuzzing. Each time a seed is chosen, about the same quantity of input is generated. In some cases, AFL may devote far more energy than is required to identify novel and intriguing pathways, while in others it may not devote enough energy.
Many scholars have developed various enhancements to directed fuzz testing in recent years. For instance, Hawkeye [
3] uses lightweight static analysis to enhance the number of callsite occurrences for a given caller as well as the number of basic blocks in the caller that contain at least one callsite. The accuracy of calculating the program’s distance from the target location is improved via a more robust distance-based approach that leads directional fuzzing by examining all target trajectories and preventing departures from specific trajectories. The author of BEACON [
4] claims that existing directed fuzzers suffer from infeasible path explosion since they run a large number of infeasible pathways and cannot reach the supplied target program point. As a result, they designed a quick and exact static analysis to compute the necessary conditions to achieve a particular test objective, allowing them to filter out infeasible program states while pruning a huge number of infeasible routes with minimum runtime overhead. The author of WindRanger [
5] intends to enhance AFLGO [
6] in static analysis by measuring the distance between each basic block and the target site on the call graph and control flow graph. The author of FuzzGuard [
7] presents a deep-learning-based solution for predicting the accessibility of inputs. It addresses the issue of a large number of generated inputs preventing the program from executing on the target, which has a significant impact on fuzzing efficiency. The aforementioned studies produced positive findings, indicating that the directional fuzzing test is improving. In comparison, the study effort of this research is directed at understanding and solving the difficulties that arise in the process of energy distribution of AFLGO utilizing simulated annealing power, and produced good results in subsequent experimental verification.
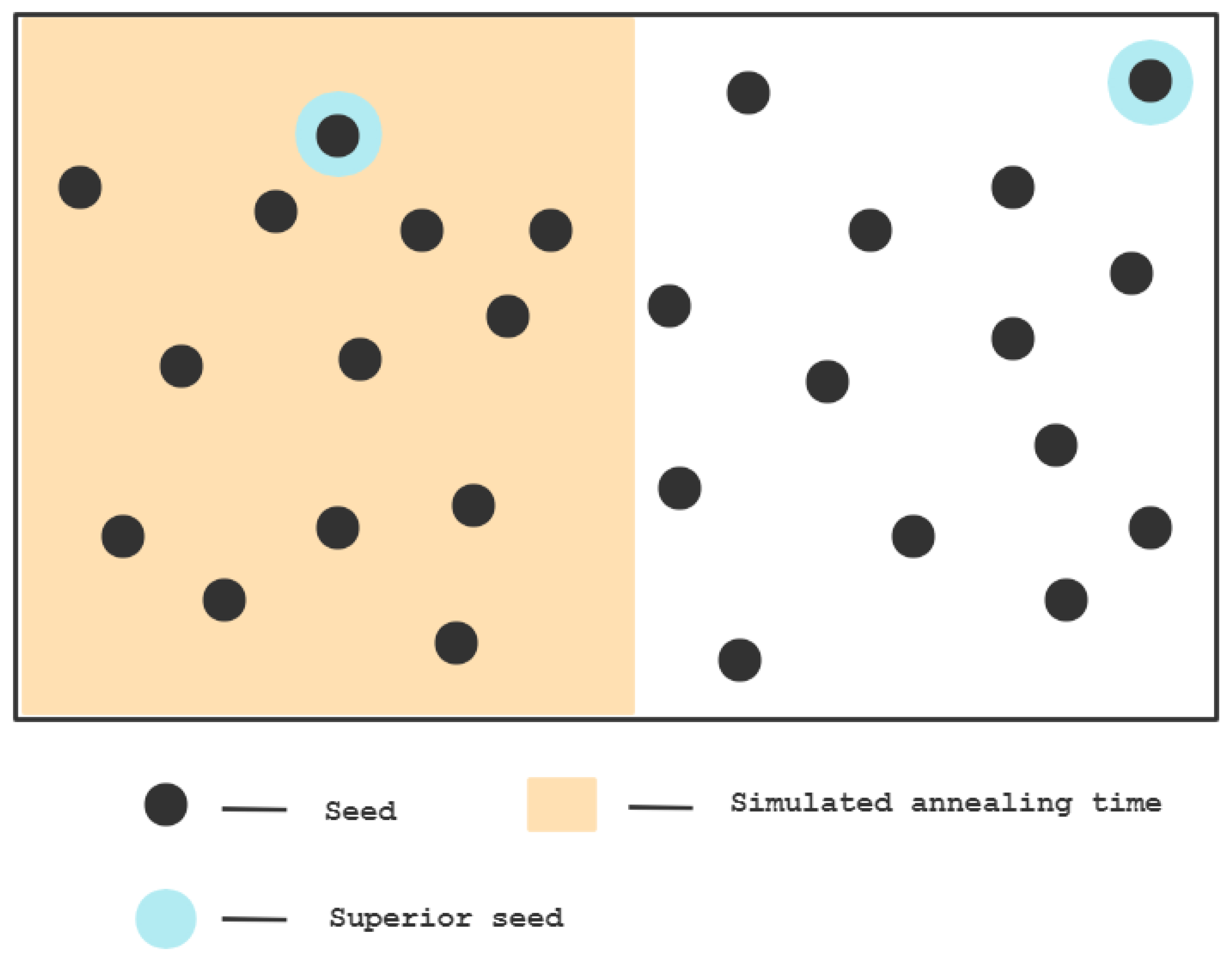
The energy management of the seeds is utilized to govern the mutation rate of chosen seeds. If the current seed is closer to the target region, more energy will be assigned to it, hence raising the number of mutations, which increases the likelihood of generating the desired test case (reaching the target area). In AFLGO, a power scheduling technique based on simulated annealing is devised, which distributes gradually more energy over time to seeds that are closer to the objective. The simulated annealing method may accept poor seeds with a predetermined probability and in a certain amount of time and can modify its acceptance of bad seeds over time. In the beginning, it accepts all seeds to the greatest extent possible. After a set annealing period, it will only accept the superior seeds in order to prevent over-focusing on the closer seeds in the beginning, which would cause the seeds to converge too quickly and reach a local maximum. This approach arranges the amount of test cases created by seeds over a period of time. It will be difficult to accomplish the desired impact if there are too many seeds in the set or if the software under test executes a test case for a much longer period of time than anticipated. After the set annealing time, the seed executes just a portion of it, and the intended impact of power scheduling is lost. It demonstrated insufficient impact on all seeds, and some seeds did not respond until the end of annealing or at the conclusion of annealing. The seed in fuzzing is the test case that has been identified to trigger a fault. In this case, we can think of the test path as a mountain, and a better seed is comparable to the highest peak point in the mountains. Discovering the highest peak within the limited time, according to the simulated annealing process, means finding the seed.
When the number of seeds is small, all of the seeds may be traversed during the simulated annealing time, and the highest peak point can be identified.
When the number of seeds is large, and at the end of the time set by simulated annealing there are still many seeds that have not been traversed, the result is only in a limited range, and the seeds that exist in the remaining paths that have not been explored will not be able to mutate, resulting in losses. As shown in the following
Figure 1:
Therefore, the power scheduling method based on annealing is neither reliable nor effective. To overcome this challenge, this research provides a dynamic energy regulation method: using the fruit fly function algorithm [
8], the paper dynamically regulates the energy of the seeds and controls the creation of test cases.
In summary, this paper makes the following contributions:
We construct the function call graph (CG) and control flow graph (CFGs) of the program using static analysis methods and provide an accurate approach for calculating the fundamental block-level target distance.
We propose a new method, which is to use the fruit fly algorithm to improve the problem of insufficient stability in power scheduling based on simulated annealing in AFLGo and to construct a dynamic energy control function to more effectively dynamically control the number of seeds in the fuzz test, in order to guide the generation of test cases that reach the target area, achieve the goal of testing the target area more quickly and effectively, and help discover more vulnerabilities.
The remainder of the article is structured as follows:
Section 2 introduces the technical context of fuzzing. The distance metric computation technique between the seed input and various target locations is shown in
Section 3.
Section 4 explains the Drosophila algorithm and its implementation. In
Section 5, we assess the performance of the approach based on the speed at which the given vulnerability is triggered and the number of times the vulnerability is successfully triggered in multiple vulnerability reproduction trials.
Section 6 is the conclusion, which includes a summary of the study’s research, an appraisal of the merits and drawbacks of the technique suggested in this paper, and an outlook for future research.
2. Technical Background
2.1. Grey-Box Fuzzing
Fuzz testing [
9,
10] is the current feedback-driven and coverage-based method for detecting vulnerabilities. Its concept is quite straightforward, and it has a high degree of automation, robust scalability, and broad application. It is one of the most efficient security testing approaches. Since Barton Miller presented the idea of fuzzing testing in 1988, after more than two decades of study and development, and with the introduction of new technological approaches such as feedback-based grey-box, taint analysis, and artificial intelligence [
11,
12], testing technology has been enhanced. Numerous automated testing tools, such as PROTOS, SPIKE, Sulley, Peach3, AFL, etc., have evolved as a result of constant development and promotion [
13]; they include PROTOS, SPIKE, Sulley, Peach3, AFL, etc. AFL (American Fuzzy Lop) is a tool created by Google engineer Michal Zalewski for fuzzing. Since its introduction in 2013, it has been considered to be one of the most promising feedback-based fuzzing tools due to its efficiency, speed, stability, and user-friendliness.
Symbolic execution-based white-box fuzzing [
14,
15] calls for intensive program analysis and constraint resolution. Grey-box fuzzing is positioned in the center and only employs modest instrumentation to gather the program structure. Grey-box fuzzing may be superior to white-box fuzzing in the absence of program analysis. When there is more information about the underlying structure, it might be more successful than black-box fuzzing. Coverage-based grey-box fuzzers (CGFs) use lightweight tools, such as AFL and LibFuzzer [
16], to collect coverage information. The AFL, for instance, records basic block conversions and crude branching to calculate hit counts. CGF utilizes coverage data to determine which produced inputs to retain for fuzzing, which it inputs into the fuzzer, and for how long. We have enhanced the tool such that it additionally considers the distance between a specified seed and a provided list of target sites. The computation of distance involves finding the shortest route to the target node in the call graph and intraprocedural control flow graph, and the shortest path analysis is implemented as Dijkstra’s algorithm [
17].
2.2. AFL
AFL is a coverage-guided fuzzing tool that tracks the code coverage of input samples and modifies input samples to enhance coverage and increase the likelihood of discovering vulnerabilities. It may collaborate with QEMU (quick emulator) to carry out fuzz testing on closed-source binary files [
18] and attack potential memory security flaws, such as stack overflow, double free, etc. The process [
19] roughly looks like this: (1) instrument the source code compilation program and record the code coverage; (2) select some input files as the original test set to join the input queue; (3) place the files in the queue according to a certain strategy “mutate”; (4) if the mutated file updates the coverage, keep it and add it to the queue; (5) the above process loops forever, during which the file that caused the program to crash is logged.
AFL uses lightweight instrumentation and a genetic algorithm to repeatedly update the input to enhance code coverage, and a fork server to enable efficient and rapid execution of test cases. The instrument has the following characteristics: a wide range of applications, support for multiple platforms, the ability to test a program with or without its source code, advanced instrumentation technology with a good effect, low performance consumption, and an effective fuzzing testing strategy, using genetic algorithm [
20]. With the aid of the program’s instrumentation information, the test cases of each round of mutation are the most valuable, so that that mutation of test cases is no longer blind; the use of the fork server operation mode eliminates the costs associated with program initialization each time the program under test is forked. AFL has been extensively used in the vulnerability mining of real-world applications, such as Firefox, Flash, and Openssl, where it has shown to be an effective and valuable fuzzing tool. The core of AFL fuzzing employs the genetic algorithm in the loop by picking a better seed as the parent sample, using a series of mutation techniques [
21], creating sub-samples for numbers and certain kinds, and running them by the program, which will find new vulnerabilities. Subsamples of covered routes are added to the queue in which the modification is carried out.
2.3. Directed Fuzzing (DGF)
In directional fuzzing, the target region consists of a function set including several target functions. The control flow graphs (CFGs) and function call graphs (CGs) of the program under test are collected via static analysis in order to compute the distance between the program’s basic block and the target region. By tracking the basic blocks executed by the seed in the program, defining the distance between the seed and the target position, and distributing the energy of the seed in the genetic variation, i.e., the number of test cases generated, the distance between the seed and the target position is utilized to achieve the orientation of fuzzy testing.
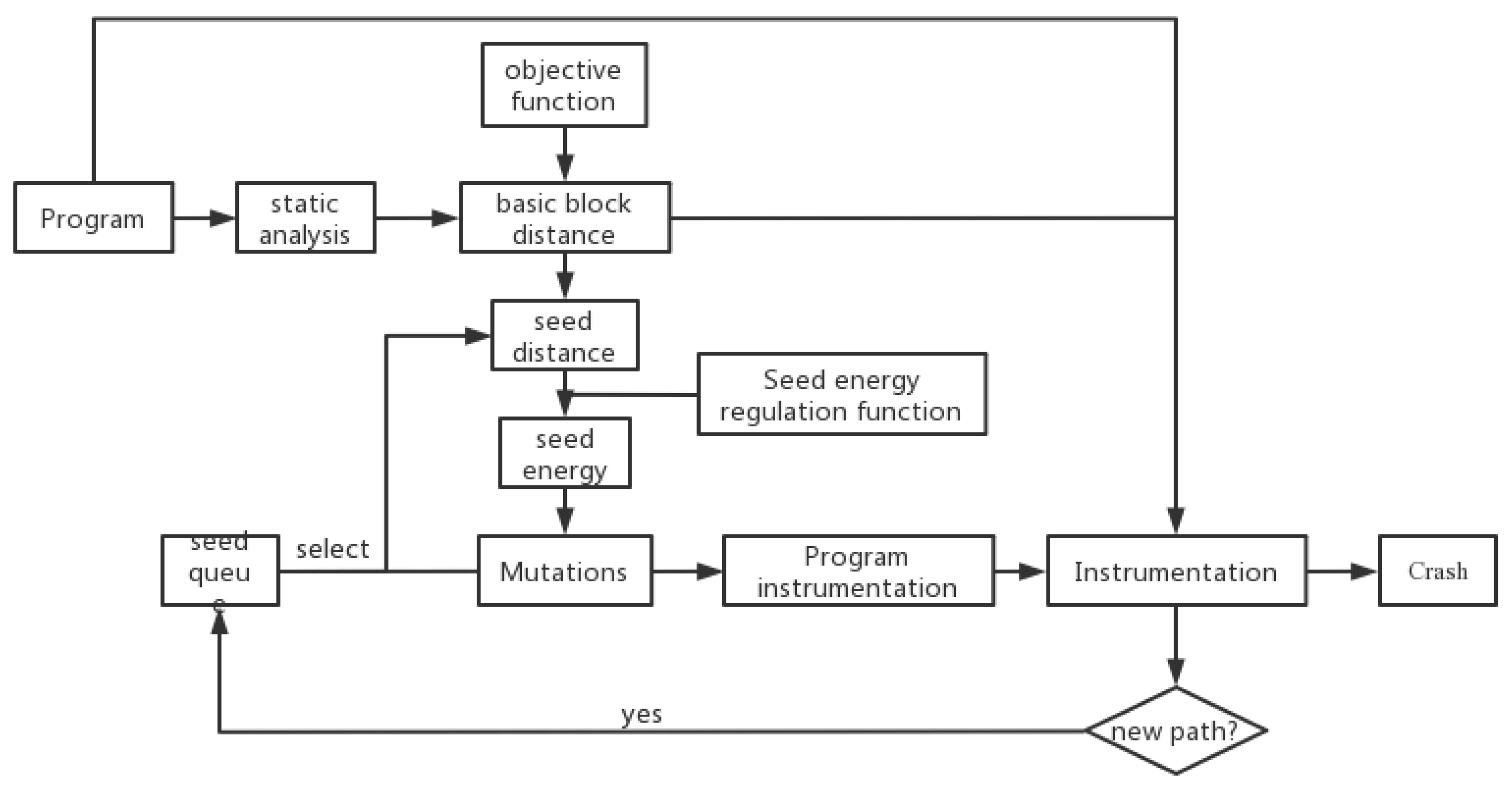
Figure 2 illustrates the general DGF design presented in this work.
Directional fuzzing is performed on a program, with the target region being a function set consisting of many functions. Following is the procedure for fuzzing: (1) Before the target program is executed, carry out a static analysis on the program and compute all basic program blocks using CFGs and CGs and the distance to the target region. Enter the computed distance into the target program. (2) Select a seed sequentially from the seed set, run the program, and compute the seed’s distance to the target region based on the distance information of the basic block and the basic block it executes. (3) Dynamically manage the energy of the seeds through the dynamic energy control function and regulate the number of test cases created by the mutation. (4) If the test case generated by the mutation runs a new route, it is added to the seed set. Crash, join the Crash set until the number of test cases created by the seed meets the preset number. (5) Repeat steps (2)~(4), and after all of the seeds in the seed set have been picked for one iteration, continue to choose seeds from the beginning for the subsequent iteration. Repetition to the end of time.
The DGF methodology is broken into two phases: the static analysis phase (step (1)) and the fuzz testing dynamic loop phase (steps (2)~(5)). The input of the static analysis stage is the target program and the specified program target area (function set made of several functions), and the output is a binary program with each basic block including distance information from the block to the target area. The instrumented binary program is the target of the dynamic loop portion of the fuzz test, while the input is the specified seed set, and the output is the test case that causes the target to crash or reach a preset duration.
2.4. AFLGo—Power Scheduling Based on Simulated Annealing
Directed Greybox Fuzzing (DGF) is a vulnerability discovery approach that focuses on reaching user-specified target regions. DGF preserves the efficacy of grey-box fuzzing, which performs no program analysis during runtime since all analysis is performed at compile-time. DGF is simple to parallelize, allowing for the allocation of additional processing resources as required. Multiple target locations may be specified with DGF.
AFLGo provides an inter-procedural distance metric (i.e., the seed to reach the destination location) that is completely set at the moment of detection and can be effectively calculated at runtime. While our metrics are interprocedural, our program analysis is based on call graphs (CGs) and process control flow graphs (CFGs). In comparison to interprocedural analysis, it demonstrates how this provides secondary savings. In the LLVM compiler architecture, CG and CFGs are freely accessible.
Using this new distance metric, AFLGo develops a new power schedule that combines the exponential cooling schedule, the most prevalent annealing function. The annealing-based power plan progressively allots more energy to seeds that are closer to the goal position and less energy to seeds that are farther from the target location, depending on distance measurements.
In 1953, N. Metropolis and others introduced the first concept of Simulated Annealing (SA) [
22]. S. Kirkpatrick et al. effectively brought annealing to the area of combinatorial optimization in 1983. It is a Monte-Carlo iterative solution-based stochastic optimization technique. It is based on the similarities between the annealing of solid matter in physics and generic combinatorial optimization issues. The global optimal solution of the objective function is found randomly in the solution space in conjunction with the probabilistic sudden jump characteristic, i.e., the local optimal solution can jump out probabilistically and eventually converge to the global optimal solution, beginning from a certain high initial temperature and with the temperature parameter decreasing continuously. AFLGo uses exponential cooling schedules to develop annealing-based power planning (APS). APS assists in energy allocation depending on the position of the seed and the target.
At the beginning of a route search, APS assigns the same amount of energy to seeds with big and small seed distances, whereas only the seeds utilized for goal execution obtain increasing amounts of energy with time.
3. Calculation of the Distance from the Seed to the Target Area
To accomplish the orientation of fuzz testing, more test cases must be created from seeds closer to the target region. Additionally, the distance between a seed and the target area must be determined, as well as the number of test cases that may be generated from this seed based on the distance. To precisely compute the distance between the seed and the target area, we offer a technique for calculating the distance between all the basic blocks in the target program and the target area. Basic block distance computation comprises two components: function-level distance calculation and basic block-level distance calculation. During the static analysis phase of the program, these two components are performed.
The function-level computation of distance is used to determine the distance between all functions in the target program and the target region. Here, static analysis is performed to determine the CFGs and CGs of the program in order to compute the distance at the function and basic block levels. Compiling the source code using the LLVM compiler will result in the CFGs and CGs of the program. In CFGs and CGs, the number of edges of the shortest route is utilized to express the distance between functions and basic blocks. Using Dijkstra’s method, the distance in the target region is calculated. The shortest path between each goal function and each fundamental block.
The purpose of the function-level distance computation is to determine the average distance between each CG function and all objective functions. For the distance calculation of a function f to multiple objective functions, based on its shortest distance to each objective function, use the harmonic mean to calculate the function’s average distance to the objective function as the distance to the target area, and derive the function-level distance formula:
where
is the smallest distance between objective function
and function
,
is the set of all objective functions, and
is the set of all objective functions that function
may attain.
Using the basic block-level distance computation, the distances between all basic blocks in the program and the target region are determined. Despite the fact that the distance between seeds is inter-program, the computation in this study examines CG and each inter-program CFG just once. The calculation resembles function-level computing. In the same interprocedural CFGs, the edge between adjacent basic blocks is utilized as their distance, and the distance between two basic blocks is used to determine the number of edges comprising the shortest route between them. The basic block target distance of a CFGs is defined by the functions that the basic block may call and is approximately equal to a constant multiple of the function-level distance of the calling function. When a basic block contains no callable functions, the function’s whole basic block may be called to decide. This yields the following method for calculating the distance between the basic block and the target area:
In the formula, is the basic block; is the target area; is the basic block set of the target function; is the function set that may be called by the basic block and meets the condition , ; is the number of connecting edges of the shortest route between basic blocks and ; is a constant.
The distance calculation for the first two levels is conducted during the static analysis phase, but the distance calculation for the seed level is implemented dynamically after the beginning of the fuzzing loop. The distance from the seed to the target region is computed by keeping track of which fundamental building blocks the seed executes. AFL and the LibFuzzer grey-box fuzzer gather coverage statistics for a program using lightweight instrumentation capable of acquiring basic block transition information and approximate branch hit counts. Here, add all the obtained basic block distance vectors to the instrumentation of the program, and obtain the binary program after instrumentation, so that the basic block executed by the seed and the distance information contained in the basic block can be tracked and recorded, and the seed can be determined. Average distance to target area:
where
is the fundamental block that the seed executes. This approach of determining the seed distance by averaging the lengths between the basic blocks performed by the seed and the target region has the issue of over-focusing on short pathways.
To shorten the distance between the long-path and short-path seeds, this study estimates the harmonic factor of the seed by computing
:
To address the issue of over-concentration on short pathways, the reconciled seed distance is:
Normalize the seed distance to produce the distance vector:
where
and
are the greatest and lowest distances, respectively, between all seeds and the target.
4. Dynamic Energy Regulation of Seeds
The objective of energy regulation for seeds is to severely restrict the mutation rate of chosen seeds. In layman’s words, it is to provide more energy to the seeds whose present seeds are closer to the goal region, so that the number of mutations increases and the probability of generating predicted test cases (the few reaching the target area) sharply increases.
AFLGO uses a power scheduling approach based on simulated annealing. Throughout the course of the game, this method may provide more energy to seeds that are closer to the target. The method of simulated annealing has the capability to change the acceptance of flawed seeds as more time passes and may accept crossing seeds with a certain probability in a predetermined amount of time. After the preset annealing process is complete, the software will only take seeds of a better grade than those first accepted when the procedure was started. This prevents initial focus from being directly aimed on seeds that are closer together, which would otherwise inevitably occur in the seeds converging too rapidly and reaching a local maximum.
Scheduling the quantity of test cases created by seeds over time is the objective of the annealing power scheduling approach. When there are too many seeds in the seed collection or when the software being tested performs a test case for longer than planned, fuzzing becomes challenging. After the prescribed annealing time has passed and the seeds are only half executed, the power scheduling no longer has the desired impact, i.e., it does not have sufficient influence on all the seeds. The power scheduling approach based on annealing is insufficiently reliable since it has reached the end of annealing and even the annealing duration when it operates on certain seeds.
This study provides a dynamic energy regulation approach to handle this problem: the dynamic energy regulation function based on the fruit fly algorithm dynamically manages the energy of the seeds, hence managing the creation of test cases.
4.1. Drosophila Algorithm
The Fruit Fly Optimization Technique (FOA) is a novel swarm intelligence optimization algorithm introduced in 2012 by Pan. It replicates the foraging activity of a colony of fruit flies and optimizes operations using a technique based on the fruit flies’ collaborative behavior. Based on Drosophila’s foraging behavior, the Drosophila optimization algorithm is a novel technique for pursuing global optimization. Drosophila’s sensory perception is superior to that of other species, particularly in terms of smell and eyesight. The olfactory apparatus of Drosophila can detect a variety of aromas in the air and may even detect food sources 40 km distant. After flying near to the area of the food, you may also utilize your sharp eyesight to determine the position where the food and your allies are gathered and fly in that direction.
This study combines the fruit fly algorithm with seed energy management to overcome the issue of DGF seeds prematurely converging on narrow execution routes, resulting in inadequate coverage of the program’s target region. The fruit fly algorithm is based on the following fundamental concept: N fruit flies search for food from a starting point, and a round of iterations is completed after all fruit flies have searched; when each fruit fly searches for food, it will release a taste pheromone, and the released taste concentration value is used to find the fruit fly with the highest concentration; then the next foraging search activity is performed, and it is determined whether the taste concentration is better than that of the previous iteration, in order to find the position of the fruit fly with the highest.
Throughout the iterative process, the number of fruit flies passing through will steadily rise, allowing for the identification of the location with the largest concentration. Nonetheless, if the location looked for in a particular iteration is the local optimum position and the visual length setting is inappropriate, the fruit flies will locate the site with the maximum concentration. After the fly population has gathered at this site, it is quite probable that it will fall into the local optimum and be unable to escape; as a result, it will be unable to seek in a larger area, limiting the algorithm’s optimization precision.
This paper improves the update method of the Drosophila individual’s position, namely, after determining the optimal position of a Drosophila individual, the remaining Drosophila individuals will not immediately gather to this position but will instead slowly approach the position of the optimal individual in the current iteration, with the entire process no longer being affected by the visual length. Since the optimal location found in each iteration is typically different, the step size and direction of each movement of the fruit fly are distinct. Additionally, the unpredictability and extensiveness of the fruit fly’s individual search are ensured, preventing the algorithm from getting into a rut. It is impossible to escape the local optimum.
4.2. Dynamic Energy Regulation Function Based on Enhanced Drosophila Algorithm
The seed in the fuzzing test is set as the route sought by the fruit fly, and the distance between the seed and the target represents the quality of the solution, i.e., the shorter the distance, the greater the quality. This constitutes the best location, based on a comparison of the concentration values of taste data produced at each cycle. Taking the probability of a fruit fly choosing a path as the energy regulation, as the number of iterations increases, the highest value of the flavor concentration content tends to be accurate, and the energy of the seeds increases gradually as well, thereby realizing the dynamic energy regulation function. The primary actions are as follows:
Set pertinent parameters, including primarily the Drosophila population size M, the maximum number of iterations of the population, the initial location and of the population, and the search visual length of the Drosophila individual ;
Update the location of each Drosophila as indicated by Equation (8):
Calculate the distance between the individual fruit fly and the coordinate origin
, and then utilize the reciprocal value of the distance
as the discovery “food”, that is, the target’s taste concentration judgment value:
- 1.
Calculate the food taste concentration
of the individual fruit fly, which is about to be
substituted into the fitness function (in the path planning of the smart car, the fitness function can be the shortest path, the least energy consumption, etc., which is typically set based on actual needs
).
- 2.
For the current iteration, the algorithm retains the location data and food flavor concentration data for the Drosophila individual with the highest
value by Formula (11)
- 3.
While recording the median value of the current iteration
into the array
, all Drosophila individuals move to
the Drosophila individual with the highest value:
Continue iterating, repeating steps (2) to (6) above, and determine whether the acquired in this iteration is superior to the one obtained in the prior iteration. If so, record it in ; otherwise, record the from the previous iteration. Once the number of iterations approaches , the iteration is terminated, and the optimum solution is produced.
In the enhanced Drosophila algorithm, because the aggregation technique of Drosophila is modified to progressively approach the position of the ideal individual in the present iteration, the update method of Drosophila’s individual position is upgraded, as seen in Equation (13):
where
is a random number between 0 and 1.
At the beginning of the program under test, the flavor concentration of all seeds in the seed set has the same value, their pathways have the same flavor concentration value and the same energy, and in each subsequent round of iteration, the flavor concentration value of the previous round will vary. After a number of iterations, the optimum value obtained by the comparison may be taken to determine the optimal route, and additional energy can be provided to it; the energy of various seeds will induce gaps in the iterations.
5. System Implementation and Experimental Analysis
5.1. Implementation of the Test System
Aiming at the aforementioned methodologies, this study proposes a prototype system AFL-DM for design experiments based on the AFL fuzzing testing framework. In this paper, a distance calculator is implemented in the form of python script; the input is CFGs, CG (CG) and the objective function; the networkx package is used to parse the graph; Djikstra’s algorithm is used to calculate the distance from the basic block to the target; the basic block distance information BB-distance is output. The fuzzer described in this work extends AFL’s instrumentation, inserts BB-distance into the basic block of the target program, and records the cumulative distance value of the executed basic block while simultaneously recording the conversion of the basic block. ASAN [
23] build is used for the program’s extensive instrumentation. In this paper, the fuzzer is based on AFL version 2.52b, calculates the current seed distance through the accumulated value of the recorded basic block distance, and uses the dynamic energy control method based on the fruit fly algorithm designed in this study to control the seed energy, and compares it with AFL Integrate in order to obtain the final energy regulation formula and regulate the number of test cases for seed generation.
5.2. Experiment and Evaluation
The system AFL-DM is created on the basis of the fuzz testing framework AFL to realize and assess the efficacy and practicability of the major technologies provided in the preceding part of DGF. For the purpose of determining the efficacy of our technique for guided fuzzing, a number of widely used target programs are chosen and their capabilities are tested using vulnerability recurrence [
24] and target site coverage tests.
Select several publicly documented vulnerabilities and compare the time required to replicate them to determine the guiding ability of the approach presented in this study. Two target programs, GNU Binutils and Libpng [
25], are picked in addition to the work previously accomplished by AFLGO. GNU Binutils is a collection of binary tools, including linkers, assemblers, and other tools for object files and archives, with nearly one million lines of code; Libpng is a cross-platform library for reading and writing PNG files, with nearly fifty ten thousand lines of code; and they are all widely used open-source projects. CVE numbers are assigned to vulnerabilities that have been reported to the US National Vulnerability Database (NCD) [
26]. The experiment employs three tools to test the target software, the maximum time restriction for each test is 8 h, and the experiment is repeated 15 times per vulnerability. The exposure time TTE is the time it takes for a given vulnerability to be triggered for the first time by the generated test case, using a specific version of the patch fix to determine the exposure and whether the error is a given vulnerability. When the input that causes the crash cannot be run again after the fixed version has been modified to generate an error, it is considered that the input triggers the given vulnerability. The improvement factor F is the quotient of the TTE of AFLGO and AFL-DM and the TTE of AFL, showing the extent to which the efficiency has been enhanced relative to AFL. The effect size Â12 [
27] reflects the likelihood that AFLGO and AFL-DM generate better results than AFL, i.e., the probability that the TTE in the experiment is less than that of AFL.
It can be seen from
Table 1 that in the vulnerability reproduction results of GNU Binutils, the rate of AFL-DM and AFLGO is one-third quicker than that of AFL, excluding CVE-2016-4490, and there are four recurrences of CVE. AFL-DM was quicker than AFLGO, but the other three CVEs duplicated AFLGO more quickly than AFL-DM. It is because AFL-DM will execute numerous iterative processes, which will consume more resources and cause the vulnerability to take longer. Reproducing CVE-2016-4491 and CVE-2016-6131 is complex and time consuming, with a low likelihood of success within the time allotted for the experiment. In 15 trials, AFL-DM successfully recreated these two CVEs 10 and 7 times, respectively; compared to 7 and 3 times in AFL and 5 and 5 times in AFLGO, the performance of AFL-DM is superior. In the reproduction experiment of CVE-2016-449 in GNU Binutils, the time taken by AFL is shorter because the vulnerability is in an easily exposed location and does not require guidance from the target area, and the fuzzer can find it faster, whereas the distance calculation and extended execution trace of AFLGO and AFL-DM seeds will consume more resources, resulting in a longer time required to reproduce this vulnerability. In CVE-2016-4491, AFL requires less time. Due to the fact that the distance calculation of guided fuzzing did not account for indirect calls and the position of the vulnerability required indirect calls, the experiment did not achieve the intended orientation. According to the overall condition shown in
Table 1, the technique in this research is successful and can play an effective role in vulnerability reproduction, which is much better than AFLGO.
As indicated in
Table 2, the speed of AFL-DM and AFLGO is 2~10 times quicker than that of AFL in the vulnerability reproduction findings for Libpng. Compared to the examined projects in GNU Binutils, Libpng is more sophisticated and has a larger amount of code, therefore it is obvious that DGF may demonstrate better results in big applications. In the experiment, four CVEs replicate AFL-DM more quickly than AFLGO, whereas one CVE reproduces AFLGO more quickly than AFL-DM. Each trial in the Libpng test successfully reproduced the vulnerability. Experiments demonstrate that the AFL-DM technique is successful, particularly in the testing of large-scale software, and may play an effective role in reproducing vulnerabilities, which is a substantial improvement to AFLGO. In terms of the total effect size of the trial, Â12, AFL-DM fared better than AFLGO in both tests, suggesting that it may provide a more stable and effective orientation.
The results of the target site coverage experiment are shown in
Table 3. In the trial, AFL-DM performed better than AFL, and the time to reach the destination was reduced by two to six times. In each set of testing, AFL-DM was faster at reaching the target location than AFLGO and AFL. In trials conducted at locations 1 and 3, the goal place was more accessible. In the 10 experiments, the three tools were able to successfully cover the target site within the allotted time. However, in the experiments at sites 2 and 4, where the target site was more in-depth and required more time to reach, AFL-DM covered the target site seven and nine times, AFLGO five and five times, and AFL three and four times, respectively.
The testing findings indicate that AFL-DM performs better than AFLGO in terms of target site coverage and can reach the target location in less time. In contrast, AFL-DM may reach the target spot more quickly. In terms of the number of successful coverage and effect size of sites 2 and 4, AFL-DM has a greater probability of reaching the target site in each set of 15 repeated trials and a greater probability of reaching the target site compared to AFLGO. Probability provides superior experimental outcomes and more consistent performance. The directional fuzzing test confirms that the static analysis approach and the dynamic energy control method based on the fruit fly algorithm are more practical and effective.
6. Conclusions and Prospects
This research provides a strategy for directed grey-box fuzzing based on the dynamic energy management of the Drosophila algorithm. Experiments were conducted on the GNU Binutils target dataset, and the trigger time and effect size were assessed. The conclusion demonstrates that the approach provided in this research may trigger the stated vulnerability in several trials of vulnerability recurrence, and the number of successful vulnerability triggers is comparable to the existing DGF technology. In the experiment on target site coverage, both the rate and frequency of successful target site coverages have grown. In other words, it demonstrates that the research technique described in this study is capable of achieving a more quick and efficient orientation, hence increasing the likelihood of discovering security flaws.
The approach suggested in this work bears the shortcomings of low seed variation quality and inadequate coverage of the program route. Future research might integrate taint analysis [
28] and dynamic symbolic execution [
29] methodologies to build more effective seed genetic variation strategies for enhancing the performance of DGF. In addition, in the directional fuzzing test, CGs and CFGs are utilized to compute the distance between seeds, but the indirect call connection is not taken into account, resulting in an erroneous estimate of the distance between functions of indirect calls. In the future, the static analysis technique can be enhanced and the indirect call connection in the program can be detected in order to improve the computation of seed distance.