Abstract
Developing numerical methods to solve dynamic electromagnetic problems has broad application prospects. In computational electromagnetics, traditional numerical methods are commonly used to deal with static electromagnetic problems. However, they can hardly be applied in the modeling of time-varying materials and moving objects. So far, the studies on numerical methods that can efficiently solve dynamic electromagnetic problems are still very limited. In this paper, a numerical method called the time-domain finite integration technique (TDFIT) is extended to tackle this problem via the introduction of time-varying iterative coefficients. In order to validate the effectiveness of the proposed algorithm, three numerical examples are demonstrated, including two microstrip structures with a time-varying medium and a rapidly rotating structure. The numerical results reveal that the time-varying medium can induce a nonlinear spectrum shift, and the radar cross section (RCS) of a rapidly rotating structure is highly dependent on the rotating speed. The proposed algorithm opens a new avenue for the exploration of many intriguing phenomena in fundamental physics, including frequency conversion and magnetless nonreciprocity. Meanwhile, it can also lead to a wide range of promising practical applications, such as active electron devices, space-time metamaterials, and hypersonic vehicles.
1. Introduction
In recent years, dynamic electromagnetic problems have gained a lot of attention because they can enrich the design process by adding one more degree (i.e., time) of freedom [1]. For instance, metamaterials are a kind of artificial materials that are composed of subwavelength-engineered patterns [2]. They have shown an extraordinary ability to manipulate electromagnetic waves. Researchers have found that time-varying metamaterials may have a better capability to manipulate waves than static metamaterials. For example, they can control the spatial and temporal spectra of light simultaneously [3]. Additionally, introducing time variance into metamaterials can contribute to the generation of new frequency. Because of the unidirectionality of the time variation, the generated new frequency may have a nonreciprocal property [4]. This property has allowed time-varying metamaterials to have more promising applications [5,6], which is why they have attracted a lot of interest. A comprehensive discussion about the recent progress of electromagnetic metamaterials has been presented in [7]. In addition to time-modulated metamaterials, there is another kind of dynamic electromagnetic problem, which is the simulation of fast-moving objects such as aircrafts, trains, propellers, and vehicles. The question of how much the electromagnetic response depends on the movement speed of dynamic objects has attracted much attention from the computational electromagnetic (CEM) community [8].
So far, researchers have made great achievements in developing a variety of numerical methods to solve static electromagnetic problems. For example, a conformal finite difference time domain (FDTD) technique was used to analyze curved dielectric surfaces [9] and three-dimensional, perfectly electrical conducting objects [10]. In addition, the time-domain finite integration technique (TDFIT) was developed to solve more complex static electromagnetic problems [11], and it has also been used to calculate electromagnetic fields with stochastic parameters [12]. However, the numerical modeling of dynamic electromagnetic problems is still a big challenge. By now, there have already been some earlier achievements in this field. For instance, a self-consistent analytical theory of electromagnetic scattering based on a sphere made with time-varying material has been presented [13]. More recently, researchers constructed a spherical particle whose permittivity could be manipulated in time and made a theoretical description of electromagnetic scattering using this model [14]. Furthermore, some other numerical methods have been discussed for the modeling of the time-varying medium, such as the finite difference time-domain method [15,16,17] and the time-domain method of moments. Moreover, a conversion matrix method of moment for time-varying electromagnetic analysis has been introduced [18]. In addition to time-domain numerical methods, frequency-domain solvers have also been utilized to model the electromagnetic properties of time-varying media [1]. In the case of the modeling of fast-moving objects, researchers have used the FDTD method to solve the electromagnetic wave scattering properties of a moving metallic mirror based on the FDTD method [19]. Furthermore, relativistic boundary conditions have been implemented into the FDTD algorithm to analyze the electromagnetic scattering properties of moving objects [20]. Recently, the Lorentz transform has also been used to solve the electromagnetic scattering problems of moving objects [21].
In this study, we extend the powerful TDFIT method to solve dynamic electromagnetic problems by modeling the time-varying medium with the use of time-varying iterative coefficients. Based on this method, two numerical examples (one is a microstrip line assembled with a time-varying medium, and the other is a microstrip line composed of two spiral resonators and a time-varying medium) are discussed. Additionally, in order to investigate the electromagnetic properties of fast-moving objects, we also simulate a rapidly rotating structure. The numerical results show the significant superiority of the proposed algorithm. This paper is organized as follows: A novel TDFIT method designed to solve dynamic electromagnetic problems is detailed in Section 2. In Section 3, three numerical examples are discussed to show the electromagnetic response of the time-varying medium and to validate the effectiveness and accuracy of our algorithm. Finally, we summarize our conclusions in Section 4.
2. Computational Methods
In 1966, KS Yee proposed an ingenious set of spatial discrete grid cells, that is, Yee’s grid [22]. As shown in Figure 1, KS Yee placed the electric field component on the edge of Yee’s grid and the magnetic field in the center of the cell. This placement ensured that each electric field component was surrounded by four magnetic field components, and that each magnetic field component was surrounded by four electric field components. This spatial configuration allowed for the discrete electromagnetic fields to naturally meet Faraday’s laws of magnetic induction and Ampere’s loop law. Therefore, it has been widely used in time-domain algorithms and has led to the development of the well-known time-domain finite difference method [23].
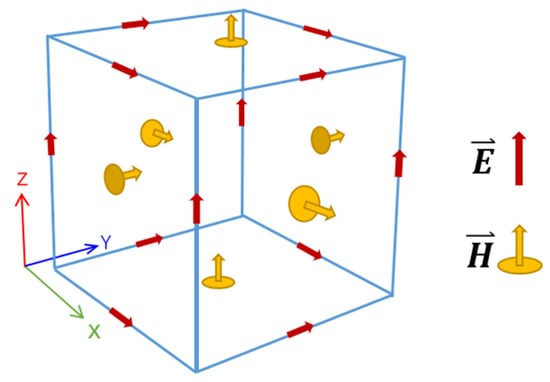
Figure 1.
Distribution of electromagnetic fields in Yee’s grid [24].
In Figure 1, one can see that Yee’s grid is a straight hexahedral mesh. Although this grid can well match Faraday’s law of electromagnetic induction and the rule of Ampere loop law, some curved boundaries must be approximated by straight hexahedral grids because of the straight hexahedral characteristics of Yee’s grids. This approximation strategy often causes staircase errors. In order to mitigate these errors, we propose a time-domain finite integration technique [25,26] based on Yee’s grids. Different from the FDTD method, the TDFIT method is derived from Maxwell’s equations in the integral form, which can be written as follows:
where E and B represent the electric field and magnetic flux density, respectively; S is an arbitrary 3D surface on the primary cell, and is the contour line of the surface S; H denotes the magnetic field, and D is related to the electric flux density; J and are the electric current density and surface on the dual cell, respectively; while V is the volume of each auxiliary cell, and the electric charge density is indicated by .
To simplify the derivation process, the closed-loop integration is divided into the piecewise line integrations that are represented by the following newly defined variables:
where and represent the electric and magnetic voltages on the edges of the primary and dual cells, respectively; , , and represent the electric flux, the magnetic flux, and the current-density flux passing through the primary and dual cells, respectively. Bringing these quantities into Maxwell’s Equations (1) and (2) yields the corresponding spatially discrete forms:
The symbols C and in the above equation represent the discrete curl operators on the primary and dual cells, respectively. For example, the definition of curl operator C can be expressed as follows:
where the subscript (i, j, k) represents the grid coordinates at Cartesian coordinates. In addition, in order to numerically solve Maxwell’s equations, constitutive relations in integration form should be introduced as well, which can be expressed as follows:
where Mε represents the average permittivity matrix; Mμ represents the average permeability matrix; Mσ represents the average conductivity matrix; and Mκ represents the average equivalent magnetic loss matrix. In static electromagnetic problems, these equivalent electromagnetic parameters are time-independent. However, in dynamic electromagnetic problems, they are time-dependent. Based on Yee’s cell, the diagonal form of these media matrices can be defined separately as follows:
where the subscript k represents the coordinate axis direction (i.e., k = x, y, z); S and represent the area on the primary and dual cells, respectively; l and represent the edges on the primary and dual cells, respectively. The symbols , , , and represent the equivalent permittivity, permeability, conductivity, and magnetic loss, respectively. In order to simplify the implementation of Equation (7), complex matrix operations in the classic FIT (Finite Integration Theorem) algorithm [27,28] need to be avoided. To achieve this, the leap-frog scheme in the FDTD algorithm should be chosen, that is, the central difference method should be used to discretize the time dimension in Equation (7). For example, assuming that the function f(t) is continuous at arbitrary time t, the derivative of the function f(t) for time t can be approximated as follows:
where is the discretized time step. Substituting Equations (9) and (14) into Equation (7), the recursion for the formula of Maxwell’s discrete equations in the time domain can be expressed as follows:
where n represents the discrete time step, the iteration coefficients αee, βeh, αhh, and βhe include the geometric information and media parameters on each Yee’s grid, defined as follows:
where the symbols and represent the length of the primary cell edge and the dual edge, respectively, while and represent the areas of primary and dual cells, respectively. Equation (15) above is the recursion formula of TDFIT. For ease of implementation, we present the recursive formulas of Maxwell’s discrete equations in the time domain:
where , the subscript d, , and satisfy the right-handed rule, and represents the coordinate axis direction. More specifically, the subscript is the prior spatial direction, and is the next spatial direction. For example, when d = x, then , . In such case, the simplified terms on the right-hand side of Equations (21) and (22) can be expanded as follows:
Based on the definitions of the iterative coefficients (αee, βeh, αhh, and βhe), their values can be comprehensively defined by electromagnetic parameters , the temporal interval , and the geometrical parameters at each Yee’s grid. Taking perfectly electrical conducting (PEC) materials as an example, the iterative coefficients have the following values: αee = 1, βeh = 0, αhh = 1, and βhe = 0. Then, Equations (21) and (22) can be rewritten as follows [29]:
Through the rigorous derivation process above, it can be found that the TDFIT method does not perform any approximation of the spatial dimension, so the TDFIT method can naturally suppress the staircase error in the traditional FDTD method. In fact, the idea of piecewise integration in Equation (22) is similar to the conformal technique in FDTD algorithms. In addition, in the mathematical derivation of TDFIT, we only perform a central difference approximation of the time dimension, the purpose of which is to avoid complex matrix operations in classical FIT and thus reduce the complexity of implementation. Moreover, it is obvious that the natural superiority of the FDTD method in dealing with the impulse behavior and the parallel computation is maintained, and it is for this reason that the leap-frog scheme is chosen.
Here, we should note that the introduction of time-varying iterative coefficients (i.e., αee, βeh, αhh, and βhe) enables the numerical modeling of dynamic electromagnetic problems, but it would burden the memory consumption and increase the computation time, as these time-varying iterative coefficients should be updated at each temporal iteration. In order to accelerate the numerical computation, it would be much better to classify the whole computation domain into two regions based on some prior knowledge, namely the time-dependent region with time-varying materials and the time-independent region without time-varying materials. In the time-dependent region, we use the proposed method. In the time-independent region, we use the traditional TDFIT method. Since the iterative coefficients (i.e., αee, βeh, αhh, and βhe) in the time-independent region are constant, these iterative coefficients can be calculated only once and stored in advance before carrying out the recursive Equations (15) and (16). As a result, we can avoid updating the iterative coefficients at each temporal iteration and significantly save computation time. Our proposed algorithm is a general method, which can also be applied in FDTD and other time-domain methods to enable their ability to solve dynamic electromagnetic problems.
3. Results
In this section, three numerical examples are given to investigate the electromagnetic response of dynamic objects. Meanwhile, the corresponding numerical results are also used to demonstrate the effectiveness of the proposed method. The CPU used in the following numerical simulation was the AMD Ryzen Threadripper 3960X 24-Core Processor @ 3.79 GHz, and the RAM was 256 GB.
3.1. Microstrip with Time-Varying Medium
3.1.1. Microstrip with PIN Diode
In this numerical example, we construct a microstrip. As depicted in Figure 2a, the size of the top PEC line is as follows: the length is 91.5 mm (i.e., L = 91.5 mm), the width is 4 mm (i.e., W =4 mm), and the thickness is 0.2 mm (i.e., H = 0.2 mm). In order to study the dynamic problem, we introduce a time-varying medium (i.e., positive-intrinsic-negative (PIN) diode) in the middle of the microstrip. More specifically, the PIN diode is placed 53.5 mm away from the waveguide port 1 and 35.5 mm away from the waveguide port 2. The microstrip and the PIN diode are assembled on an insulator substrate with a length of 91.5 mm, a width of 75.8 mm, and a thickness of 1.49 mm. The relative permittivity of this substrate is 2.62. In addition, at the bottom of the insulator substrate, there is a PEC background. As shown in Figure 2b, when the PIN diode is switched on, the electromagnetic wave can be propagated very well along the microstrip, from input port 1 to output port 2, as the corresponding transmission coefficient (i.e., S21) goes up to 1 within a wide frequency range. Furthermore, the electric field distribution of the microstrip at 5 GHz in the case of the PIN switching on is demonstrated in Figure 2c. In the case of the PIN switching off, the input electromagnetic wave cannot pass through the microstrip from input port 1 to output port 2. As a result, the corresponding transmission coefficient is close to zero, as shown in Figure 2d. This total reflection phenomenon can be further verified by its near-field distribution at 5 GHz, as shown in Figure 2e, where the propagating electromagnetic wave is obstructed by the switching-off PIN diode.
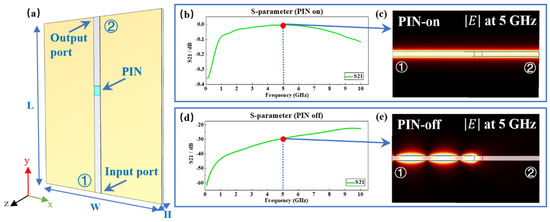
Figure 2.
Microstrip in the static case: (a) Schematic of a microstrip composed of a PIN diode; (b) Transmission coefficient (S21) when the PIN diode is switched on; (c) Near-field distribution at 5 GHz when the PIN diode is switched on; (d) Transmission coefficient (S21) when the PIN diode is switched off; (e) Near-field distribution at 5 GHz when the PIN diode is switched off.
In Figure 2, the PIN diode is switched on (or off) only once; thus, it is still a static electromagnetic problem. In order to study the dynamic electromagnetic problem, we use the switching on and off status of the PIN to mimic a time-varying material. To this end, the conductivity of the PIN is periodically changed, as shown in Figure 3b. More specifically, the PIN conductivity is set as 6 × 10−7 S/m to mimic the switched-on status, and the zero conductivity is used to mimic the switching-off status of the PIN diode. In this numerical example, the switching frequency of the time-varying material is 1 GHz. We pump a 5 GHz monochromatic signal at input port 1, and its spectrum is given in Figure 3a. In order to intuitively demonstrate the nonlinear effect of time-varying materials, a probe monitor is placed at output port 2 to record the electric field spectrum of the output signal. As shown in Figure 3c, there is a periodic spectrum shift in the output signal, and the value of such a spectrum shift is exactly equal to the switching frequency of the time-varying material. Moreover, the intensity of the first-order harmonic generation is the strongest, and this intensity would rapidly decay as the increment of the order of harmonic number. The electric field distributions at 4, 5, and 6 GHz are given in Figure 3d–f, respectively.
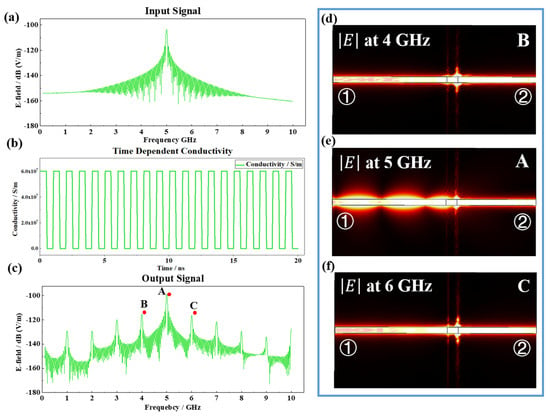
Figure 3.
Microstrip in the dynamic case: (a) Spectrum of a monochromatic input signal; (b) Switching frequency of a conductivity-time-varying material is 1 GHz; (c) Spectrum of the output signal; (d) Output electric field distribution at 4 GHz; (e) Output electric field distribution at 5 GHz; (f) Output electric field distribution at 6 GHz.
3.1.2. Microstrip with Spiral SPP Resonators
After analyzing the results of the example above, we found that there is a spectrum shift effect when a signal passes through the time-varying materials. The value of the spectrum shift is an integer multiple of the switching frequency of the time-varying material. This phenomenon can be clearly observed in the spectrum, as shown in Figure 3c. This interesting spectrum shift effect can be used to simultaneously excite two different surface plasmon polariton (SPP) resonators, as shown in Figure 4a. In the static electromagnetic problem, these two SPP resonators would isolate themselves from each other because they have different resonant frequencies. However, in the dynamic electromagnetic problem, these two different SPP resonators can interact with each other via the aforementioned spectrum shift effect.

Figure 4.
Microstrip with spiral SPP resonators in the static case: (a) Schematic of a microstrip composed of two different spiral SPP resonators; (b) Electric field distribution at 4 GHz when the PIN diode keeps the switched-on status; (c) Electric field distribution at 5.5 GHz when the PIN diode keeps the switched-on status.
More specifically, as shown in Figure 4a, a two-port microstrip line composed of two SPP spiral resonators is constructed. These two spiral resonators are 80 mm away from each other, and they are connected by a microstrip controlled by a PIN diode. The width of the microstrip is 4 mm. The thickness of the microstrip and SPP spiral resonators are 0.2 mm. The helical rotation angle of both spiral resonators is 360 degrees, and the diameter of the large resonator is 40 mm. The small resonator is thirty percent of the size of the large resonator. The size of the dielectric substrate is as follows: the length is L = 213.7 mm, the width is W = 100 mm, and the thickness is H = 1.5 mm. The relative permittivity of the substrate is 2.62. In the static case, we maintain the PIN diode in the switched-on status and pump a pulse signal at input port 1. In this case, the electric field distribution at 4 GHz is demonstrated in Figure 4b. Due to the filter functionality of the large resonator at 4 GHz, the input electromagnetic wave at 4 GHz cannot pass through the large SPP resonator. As a result, the electric field received near the small resonator is very weak.
In contrast, as shown in Figure 4c, we pump the input pulse signal at port 2. In this case, due to the filter functionality of the small resonator at 5.5 GHz, the input electromagnetic wave at 5.5 GHz cannot pass through the small SPP resonator. Thus, the electric field received at the large resonator is quite weak. To sum up, since the resonant frequencies of the two SPP spiral resonators are different (one has a strong light–matter interaction at 4 GHz, and the other has a strong light–matter interaction at 5.5 GHz), the coupling interaction between the large spiral resonator and the small spiral resonator is forbidden. In other words, due to the frequency isolation effect, it is impossible to simultaneously excite the resonant modes of the large spiral resonator and the small spiral resonator in the static case.
In order to break the limit of the frequency isolation effect, we studied the coupling interaction between the large spiral resonator and the small spiral resonator in the dynamic case. To demonstrate the role time-varying materials play in the spectrum shift phenomenon, we calculated the electric field spectrums and distributions in four different cases. In the first case, a monochromatic signal with a frequency of 4 GHz is input at port 1, and the PIN’s switching frequency is f = 0 GHz. The corresponding electric field spectrums and distributions are given in Figure 5a,b, where only the resonant mode of the large spiral resonator is successfully excited at 4 GHz. In the second case, as in the first case, we pump a monochromatic signal with a frequency of 4 GHz at input port 1. However, the switching frequency of the PIN diode is f = 1.5 GHz; the corresponding electric field spectrums and distributions are depicted in Figure 5c,d. Due to the aforementioned nonlinear effect of the spectrum shift, the resonant modes of both large and small spiral resonators can be excited simultaneously. As a result, a counterintuitive coupling interaction between two different SPP resonators can be achieved by breaking the limit of the frequency isolation effect.
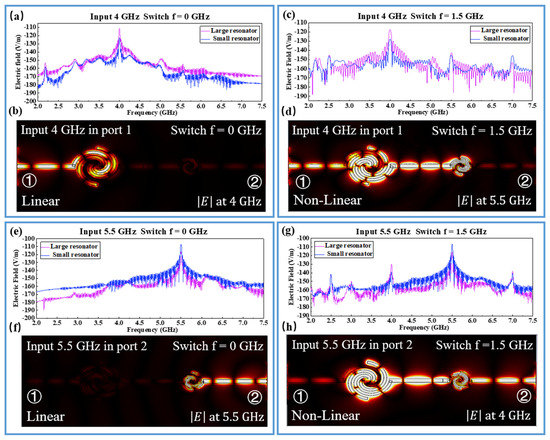
Figure 5.
Spiral SPP resonator in the dynamic case: (a) Spectrum in the first case: f_input = 4 GHz, f_ switch = 0 GHz; (b) Electric field distribution in the first case: f_input = 4 GHz, f_ switch = 0 GHz; (c) Spectrum in the second case: f_input = 4 GHz, f_ switch = 1.5 GHz; (d) Electric field distribution in the second case: f_input = 4 GHz, f_ switch = 1.5 GHz; (e) Spectrum in the third case: f_input = 5.5 GHz, f_ switch = 0 GHz; (f) Electric field distribution in the third case: f_input = 5.5 GHz, f_ switch = 0 GHz; (g) Spectrum in the fourth case: f_input = 5.5 GHz, f_ switch = 1.5 GHz; (h) Electric field distribution in the fourth case: f_input = 5.5 GHz, f_ switch = 0 GHz.
Similarly, we tested this conclusion in the third and fourth cases, as shown in Figure 5e–h, where we pumped a monochromatic signal with a frequency of 5.5 GHz at input port 2. More specifically, in the third case (Figure 5e,f), only the resonant mode of the small spiral resonator can be excited successfully at 5.5 GHz. However, in the fourth case (Figure 5g,h), the resonant modes of both large and small spiral resonators can be excited simultaneously due to the spectrum shift effect of the time-varying PIN diode.
3.2. Rapid Rotating Structures
Generally, the different motion postures and speeds of moving targets would lead to different electromagnetic responses due to some exotic effects, including the Doppler effect, among others. Because most experimental methods are expensive and time-consuming, numerical simulation methods show great potential in efficiently and rigorously studying the electromagnetic response of moving targets. The geometrical boundaries and physical positions of simulated objects are generally fixed in traditional computational electromagnetic methods. However, in the simulation of rapidly moving objects, all of them are time-dependent. As a result, most conventional computational electromagnetic methods are not applicable for solving this kind of dynamic problem. Since the iterative coefficients in our proposed method are updated at each time step, it can be used to overcome this challenge very well. Here, we will give a numerical example to demonstrate the effectiveness of our proposed method. Taking inspiration from the rapid rotation of helicopter propellers, we study the different electromagnetic responses of static propellers and fast rotating propellers.
3.2.1. Static Case
As shown in Figure 6a, one PEC arm was used here to mimic the propeller, and it was assembled in a PEC disc. The radius of the PEC disc is 8 mm, and its thickness is 1 mm. The length, width, and thickness of the PEC arm are 60 mm, 1 mm, and 1 mm, respectively. In addition to one PEC arm, we constructed 36 PEC arms in Figure 6d to mimic the rapidly rotating propeller with an infinite rotating frequency. In this case, the angle interval of each PEC arm is 10 degrees. Based on the TDFIT method, the total RCS curves and far-field patterns of these two static objects were calculated. The corresponding results are given in Figure 6e,h,i,l. In the numerical modelling, a plane wave with a pulse signal was used to illuminate the static objects.
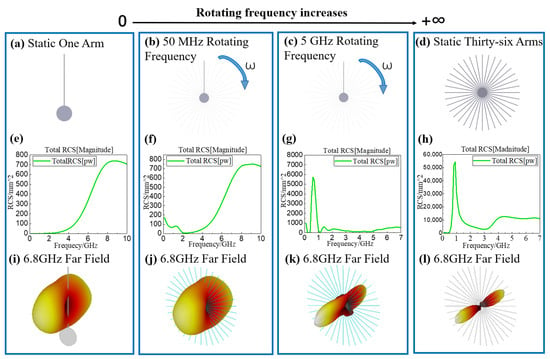
Figure 6.
Rapidly rotating propeller: (a) Schematic of one rotating arm in the static case, namely the rotating frequency is zero; (b) Schematic of one rotating arm with a 50 MHz rotating frequency; (c) Schematic of one rotating arm with a 5 GHz rotating frequency; (d) Schematic of a static thirty-six-arm structure to mimic the infinite rotating frequency; (e–h) the corresponding RCS spectrum; (i–l) the corresponding far-field pattern at 6.8 GHz.
3.2.2. Dynamic Case
In the dynamic case, we also constructed 36 arms, as can be seen in Figure 6b,c. In order to mimic the rapidly rotating propeller with a finite rotating frequency, each arm was made of time-varying material. The conductivity of the time-varying material was temporally changed using a particular switching frequency, which is equal to the rotating frequency in dynamic cases. More specifically, the maximum value of conductivity (i.e., 6 × 107 S/m) is used to model the PEC medium, and zero conductivity is used to model the vacuum. By properly designing the time-dependent conductivity of this time-varying material, we can ensure that there is only one PEC arm in each time step, and that the other arms are vacuum. Based on this well-designed scheme, if the material property of one arm is changed from PEC into a vacuum at a particular time step, its neighbored vacuum arm will be switched to the PEC material at the same time step. Meanwhile, other vacuum arms will remain unchanged. In this way, these 36 arms with time-varying materials can be used to mimic the rapidly rotating propeller with a finite rotating frequency, which is equal to the switching frequency of the time-varying material.
In order to study how the electromagnetic response of the rapidly rotating propeller depends on the rotating speed, the rotating frequencies in Figure 6b,c were set at 50 MHz and 5 GHz, respectively. Based on the proposed TDFIT method, we calculated the total RCS curves and far-field patterns of these two dynamic objects. The corresponding results are given in Figure 6f,g,j,k. In the simulations, a plane wave with a pulse signal was used to illuminate the dynamic objects. From these numerical results, we can see that the electromagnetic responses of the dynamic object with a relatively low rotating frequency (i.e., 50 MHz), as shown in Figure 6f,j, are highly similar to those of one static arm, as shown in Figure 6e,i. In contrast, the electromagnetic responses of the dynamic object with a relatively high rotating frequency (i.e., 5 GHz), as shown in Figure 6g,k, are more similar to those of the 36 static arms, as shown in Figure 6h,l. These intriguing phenomena prove that the electromagnetic response of the rapidly rotating propeller does depend on the rotating speed, and such speed dependence is more obvious at high rotating frequencies. From the general trend of the far-field pattern and RCS results shown in Figure 6e–l, one can conclude that the electromagnetic responses of one rapidly rotating arm gradually converge to its electromagnetic responses evaluated in the infinite frequency. This physically reasonable convergence verifies the effectiveness of our algorithm.
In addition to the far field, we also studied the near-field distribution of rapidly moving objects. As can be seen in Figure 7, the dynamic electric field distribution of one rotating arm is demonstrated at different time steps, and the field monitor plane is 1.5 mm away from the dynamic arm. From these numerical results, one can see clearly that one dynamic arm is rotating clockwise, which is consistent with the switching direction of our initial setting. Thus, we further confirm the effectiveness of the proposed method.

Figure 7.
Dynamic electric field distribution of one rotating arm at different time steps. In this example, the corresponding rotating frequency is 10 GHz.
4. Conclusions
In this study, a numerical modeling of dynamic electromagnetic problems was proposed based on the time-domain finite integration technique. Three numerical examples, including two different microstrip structures with time-varying materials and one rapidly rotating structure, were demonstrated to validate the accuracy and effectiveness of the proposed method and investigate the exotic electromagnetic response of dynamic objects. The numerical results showed that the time-varying medium can induce a spectrum shift. Meanwhile, we also found that the radar cross section of a rotating structure highly depends on the rotating speed. The proposed method provides a powerful tool for solving dynamic electromagnetic problems and paves a new way of exploring time-induced nonlinear phenomena. Moreover, this novel method can also be used in the design of time-modulated electronic devices and advanced high-speed aircraft.
Author Contributions
Conceptualization, J.Y. and T.C.; methodology, J.Y. and T.C.; software, Z.L., X.W. and J.Y.; validation, Z.L. and X.W.; investigation, Z.L., X.W. and J.Y.; writing—original draft preparation, Z.L., X.W. and J.Y.; writing—review and editing, J.H., J.Z., J.Y. and T.C.; supervision, J.Y. and T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Basic Scientific Center of Information Metamaterials of the National Natural Science Foundation of China (6228810001), the National Key Research and Development Program of China (2017YFA0700201, 2017YFA0700202, 2017YFA0700203), the National Natural Science Foundation of China (62101124), the 111 Project (111-2-05), the Major Project of Natural Science Foundation of Jiangsu Province (BK20212002), and the Natural Science Foundation of Jiangsu Province (BK20210209, BK20220808).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Du, Z.X.; Li, A.; Zhang, X.Y.; Sievenpiper, D.F. A Simulation Technique for Radiation Properties of Time-Varying Media Based on Frequency-Domain Solvers. IEEE Access 2019, 7, 112375–112383. [Google Scholar] [CrossRef]
- Salary, M.M.; Jafar-Zanjani, S.; Mosallaei, H. Time-varying metamaterials based on graphene-wrapped microwires: Modeling and potential applications. Phys. Rev. B 2018, 97, 115421. [Google Scholar] [CrossRef]
- Chamanara, N.; Vahabzadeh, Y.; Caloz, C. Simultaneous Control of the Spatial and Temporal Spectra of Light with Space-Time Varying Metasurfaces. IEEE Trans. Antennas Propag. 2019, 67, 2430–2441. [Google Scholar] [CrossRef]
- Taravati, S.; Kishk, A.A. Recent Advances in Theory, Concepts and Applications of Space-Time Modulated Media. In Proceedings of the 2018 12th International Congress on Artificial Materials for Novel Wave Phenomena (Metamaterials), Espoo, Finland, 27 August–1 September 2018; pp. 380–382. [Google Scholar]
- Ramaccia, D.; Sounas, D.L.; Alù, A.; Bilotti, F.; Toscano, A. Nonreciprocal Horn Antennas Using Angular Momentum-Biased Metamaterial Inclusions. IEEE Trans. Antennas Propag. 2015, 63, 5593–5600. [Google Scholar] [CrossRef]
- Reyes-Ayona, J.R.; Halevi, P. Electromagnetic Wave Propagation in an Externally Modulated Low-Pass Transmission Line. IEEE Trans. Microw. Theory Tech. 2016, 64, 3449–3459. [Google Scholar] [CrossRef]
- Emanuele, G.; Romain, T.; Shixiong, Y.; Huanan, L.; Stefano, V.; Paloma, A.H.; Mário, G.S.; Riccardo, S.; Andrea, A.; Pendry, J.B. Photonics of time-varying media. Adv. Photonics 2022, 4, 014002. [Google Scholar] [CrossRef]
- Sokolov, S.A.; Zubilevich, A.L.; Morozov, B.N. External electromagnetic fields influence upon moving objects. In Proceedings of the 2018 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 14–15 March 2018; pp. 1–6. [Google Scholar]
- Wenhua, Y.; Mittra, R. A conformal finite difference time domain technique for modeling curved dielectric surfaces. IEEE Microw. Wirel. Compon. Lett. 2001, 11, 25–27. [Google Scholar] [CrossRef]
- Dey, S.; Mittra, R. A locally conformal finite-difference time-domain (FDTD) algorithm for modeling three-dimensional perfectly conducting objects. IEEE Microw. Guid. Wave Lett. 1997, 7, 273–275. [Google Scholar] [CrossRef]
- Thoma, P. State of the Art Simulation of Electromagnetic Fields in Time Domain using the Finite Integration Technique. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019. [Google Scholar]
- Holzhey, M.; Römer, U.; Schuhmann, R. Uncertainty Analyses for 3D Electromagnetic Field Problems in Time-Domain Simulations with the Finite Integration Technique and Polynomial Chaos. In Proceedings of the 2019 Kleinheubach Conference, Miltenberg, Germany, 23–25 September 2019; pp. 1–4. [Google Scholar]
- Ptitcyn, G.; Lamprianidis, A.; Karamanos, T.; Asadchy, V.; Alaee, R.; Müller, M.; Albooyeh, M.; Mirmoosa, M.; Fan, S.; Tretyakov, S.; et al. Scattering from Spheres Made of Time-Varying and Dispersive Materials. arXiv 2021, arXiv:2110.07195. [Google Scholar]
- Asadchy, V.; Lamprianidis, A.; Ptitcyn, G.; Albooyeh, M.; Rituraj; Karamanos, T.; Alaee, R.; Tretyakov, S.; Rockstuhl, C.; Fan, S. Parametric Mie resonances and Kerker effects in time-modulated scatterers. arXiv 2022, arXiv:2202.11138. [Google Scholar]
- Taravati, S.; Kishk, A.A. Advanced Wave Manipulation through Oblique Illumination of Space-Time Modulated Media. In Proceedings of the 2018 12th International Congress on Artificial Materials for Novel Wave Phenomena (Metamaterials), Espoo, Finland, 27 August–1 September 2018; pp. 383–385. [Google Scholar]
- Liu, X.; McNamara, D.A. The Use of the FDTD Method for Electromagnetic Analysis in the Presence of Indepedently Time-Varying Media. Int. J. Infrared Millim. Waves 2007, 28, 759–778. [Google Scholar] [CrossRef]
- Stewart, S.A.; Smy, T.J.; Gupta, S. Finite-Difference Time-Domain Modeling of Space–Time-Modulated Metasurfaces. IEEE Trans. Antennas Propag. 2018, 66, 281–292. [Google Scholar] [CrossRef]
- Bass, S.F.; Palmer, A.M.; Schab, K.R.; Kerby-Patel, K.C.; Ruyle, J.E. Conversion Matrix Method of Moments for Time-Varying Electromagnetic Analysis. IEEE Trans. Antennas Propag. 2022, 70, 6763–6774. [Google Scholar] [CrossRef]
- Harfoush, F.; Taflove, A.; Kriegsmann, G.A. A numerical technique for analyzing electromagnetic wave scattering from moving surfaces in one and two dimensions. IEEE Trans. Antennas Propag. 1989, 37, 55–63. [Google Scholar] [CrossRef]
- Kuang, L.; Zhu, S.; Gao, J.; Zheng, Z.; Dong, D. A Numerical Method for Analyzing Electromagnetic Scattering Properties of a Moving Conducting Object. Int. J. Antennas Propag. 2014, 2014, 386315. [Google Scholar] [CrossRef]
- Fang, C.; Zhao, X.; Xia, N.; Fang, X. Scattering of Electromagnetic Plane Waves by Moving Objects in High Frequency. In Proceedings of the 2008 China-Japan Joint Microwave Conference, Shanghai, China, 10–12 September 2008; pp. 298–300. [Google Scholar]
- Kane, Y. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; 2005; Volume 2062. [Google Scholar]
- You, J.W.; Wang, H.G.; Zhang, J.F.; Cui, W.Z.; Cui, T.J. The Conformal TDFIT-PIC Method Using a New Extraction of Conformal Information (ECI) Technique. IEEE Trans. Plasma Sci. 2013, 41, 3099–3108. [Google Scholar] [CrossRef]
- You, J.; Tan, S.; Zhang, J.; Cui, W.; Cui, T. A uniform time-domain finite integration technique (TDFIT) using an efficient extraction of conformal information. IEEE Antennas Propag. Mag. 2014, 56, 63–75. [Google Scholar] [CrossRef]
- You, J.W.; Tan, S.R.; Zhou, X.Y.; Yu, W.M.; Cui, T.J. A New Method to Analyze Broadband Antenna-Radome Interactions in Time-Domain. IEEE Trans. Antennas Propag. 2014, 62, 334–344. [Google Scholar] [CrossRef]
- Clemens, M.; Weiland, T. Discrete Electromagnetism with the Finite Integration Technique—Abstract. J. Electromagn. Waves Appl. 2001, 15, 79–80. [Google Scholar] [CrossRef]
- Weiland, T. A Discretization Model for the Solution of Maxwell’s Equations for Six-Component Fields. Electron. Commun. 1977, 31, 116–120. [Google Scholar]
- You, J.W.; Wang, H.G.; Zhang, J.F.; Li, Y.; Cui, W.Z.; Cui, T.J. Highly Efficient and Adaptive Numerical Scheme to Analyze Multipactor in Waveguide Devices. IEEE Trans. Electron Devices 2015, 62, 1327–1333. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).