A Hierarchical Searchable Encryption Scheme Using Blockchain-Based Indexing

Abstract

Focusing on the fine-grained access control challenge of multi-user searchable encryption, we propose a hierarchical searchable encryption scheme using blockchain-based indexing (HSE-BI). First, we propose a hierarchical search index structure based on a DAG-type access policy and a stepwise hierarchical key derivation mechanism; which we outsourced to the blockchain network to achieve reliable hierarchical search. We design a dynamic append-only update protocol for the blockchain-based index to deal with adding and deleting files. Secondly, we propose a hierarchical authorization mechanism based on broadcast encryption to achieve fine-grained search permission granting and revoking, which can prevent a malicious server from colluding with corrupted users. The security and complexity analysis shows that HSE-BI achieves optimal search time while satisfying adaptive secure and revocation secure. Our experimental results are encouraging, e.g., compared with the traditional multi-user searchable encryption schemes, HSE-BI’s hierarchical search policy does not impact the search performance visually. The growth rate of the search latency decreases with the increasing number of hierarchical users, which can act as an efficient crypto tool to open up venues for other applications. We demonstrate that HSE-BI is more suitable for actual applications with fine-grained access requirements and can act as an efficient crypto tool to open up venues for other applications.

1. Introduction

1.1. Background and Motivation

As the demand for outsourced data storage and distributed computing grows, data privacy is becoming one of the primary considerations. Encryption can ensure the security of outsourced data, but how to effectively search and share outsourced encrypted data has become a new challenge. To that end, searchable encryption (SE) [1,2] is a family of cryptographic protocols that allow a data owner to outsource the encrypted data to a cloud server maintaining the server’s search capability. In recent years, multi-user searchable encryption (MUSE) [3,4,5] has been one crucial research line in searchable encryption. Compared with the majority of works in SE, the architecture in MUSE is more complicated, where not only the original data owner but a constant number of entities have the ability to send the server a search query for (part of) data. MUSE opens up avenues for other applications, such as collaborative data sharing. For example, all employees can be authenticated in an enterprise to access the company’s outsourced encrypted files for subsequent collaboration.

A typical design challenge of multi-user searchable encryption is achieving flexible access control for users [6,7]. Most MUSE schemes from the literature consider the case that authenticated users always have unrestricted access to the entire dataset. However, in the real-world data-sharing scenario, an organization often consists of a pyramid-shaped hierarchical access control strategy. Users in different hierarchies are assigned different access permissions. The sensitive data in the real world is likely to be hierarchical and different users should have different access rights. However, there are relatively few works in MUSE considering this situation.

In addition, another problem in MUSE is that the server is often treated as a semi-honest-but-curious party [5,8], which is assumed to store and search the secure index correctly and does not attend to learning user’s extra information. However, this assumption is too strong for many applications where the server is malicious. As most recent research shows [9,10], the existing verification approaches for MUSE do not provide efficient verification for search results over multiple users, and few works achieve a hierarchical verifiable search. Therefore, it is an urgent challenge to design a solution for the above problems.

In recent years, with the popularity of cryptocurrencies and decentralized applications, blockchain technology has received much attention from various industries. It has been a critical technology in constructing distributed storage platforms, such as Bigchain DB [11] and Bluzelle [12]. Therefore, a blockchain data structure offers a possible solution to the above problems in MUSE research. Some recent works have already considered building MUSE schemes on top of a blockchain network. However, most of them treat blockchain as a trusted third party to ensure reliable searches through consensus protocols [13,14,15], but few works achieve hierarchical search. In this work, we take advantage of a blockchain data structure to build a hierarchical searchable encryption scheme. Our design goal is to make HSE-BI achieve fine-grained access control and ensure the search results are reliable by the consistency and immutability of the blockchain-based index.

1.2. Our Contributions

We propose a hierarchical searchable encryption scheme using blockchain-based indexing (HSE-BI) to focus on the above challenges in MUSE. Our contributions are as follows:

• (Blockchain-based index) First, to achieve a multi-user hierarchical search, we explore the construction of a secure hierarchical index via a blockchain network. The index is built on a DAG-type access structure oriented real-world information flow policy. We deploy the blockchain network to collaboratively manage the index to achieve index immutability, aiming to make the search results reliable with no extra verification work on the user side. We further propose an append-only index update mechanism oriented in the blockchain index when adding/deleting is applied to outsourced files.
• (Hierarchical search control) Secondly, we propose a dynamic user authorization mechanism that realizes fine-grained search permission control through hierarchical key derivation. Based on this, authorized users have the right to search for the files under their hierarchies. By deploying broadcast encryption and a hierarchical key derivation strategy, HSE-BI can dynamically grant/revoke users’ search rights without updating other users’ keys. Each user only needs to store its secret key locally, which requires constant-size user storage.
• (Formal analysis evaluation) We give a formal security definition for HSE-BI, including adaptive secure and revocation secure, and show that HSE-BI satisfies them. We also implement HSE-BI and compare it with other related schemes. It shows that HSE-BI’s hierarchical search policy does not impact the search performance visually. The growth rate of the search latency decreases with the increasing number of hierarchical users, which can act as an efficient crypto tool to open up avenues for other applications.

The rest of the paper is summarized below: Section 2 is the literature review, which describes the related work, followed by a description of the proposed HSE-BI model in Section 3. Section 4 presents the concrete constructions of HSE-BI. Section 5 and Section 6 discuss HSE-BI’s security and theoretical complexity analysis, respectively. Section 6 shows the experimental investigations. Finally, the paper is concluded in Section 7.

2. Literature Review

Multi-User Searchable Encryption The concept of “multi-user searchable encryption (MUSE)” was proposed by Curtmola et al. by combining a single-user SE model with broadcast encryption [3]. In 2015, Li et al. proposed a self-authorized multi-user searchable encryption scheme, which allows group users to be authorized to perform keyword searches by generating shared keys to realize data sharing on mobile terminals [4]. In 2017, Deng et al. designed a multi-user searchable encryption scheme based on a non-collusive dual-server model, where the anti-revoking user and cloud server conspired [5] and constructed an access policy combining search keywords and user attributes.

In the last decade, many related works have combined hierarchical access with multi-user searchable encryption. In 2011, Hattori et al. [8] proposed a role-based multi-user searchable encryption scheme. In their scheme, the roles of users are mapped to policy vectors and associated with secure indexes; however, in this scheme, the authenticated user group is static, and the adversary must declare its corruption initially. In 2014, Kaci et al. [16] proposed a multi-user searchable encryption scheme based on attribute-based encryption to realize flexible access control but still retain the ability to update data dynamically. In 2017, Ye et al. [17] designed a dynamic, searchable cloud storage scheme with multiple access hierarchies using ciphertext policy-attribute-based encryption; it constructed an access tree for each file, which caused an exponential extra storage overhead. In 2018, Hamlin et al. [18] designed a multi-user searchable encryption scheme via ORAM-based proxy re-encryption, which allows data to be shared from multiple data owners to multi-level users for the searching of single keywords; its main limitation is that the search time is linear in the total number of files. Alderman et al. [19] proposed a multi-level searchable encryption that allows multiple users differential access control, but it is restricted to non-practical access policies where the set of access rights is totally ordered.

In 2019, Blomer et al. [9] proposed a verifiable multi-user searchable encryption scheme that realized the efficient verifiable search; however, at the same time, the search operation disclosed the attributes of users. Wang et al. [20] proposed a multi-user searchable encryption scheme that hides access policies that ensure the privacy of a user’s attributes, which takes the cost of too much computation and communication above the addition and deletion of users. When the user group changes, the scheme needs to re-perform the setup algorithm to generate a series of new parameters, and re-generate and distribute all users’ keys. In 2021, Chamani et al. [21] designed a multi-user searchable encryption scheme based on a multi-server model and an oblivious data structure to resist the collusion of revoked users and cloud servers. In 2022, Li et al. [22] considered the real-world application of MUSE and proposed a hierarchical multi-user searchable encryption scheme for a medical electronic sharing data scenario.

Blockchain-Assisted Searchable Encryption In recent years, several pioneering works have considered building searchable encryption schemes (especially multi-user searchable encryption) on top of the blockchain network. In 2018, Hu et al. designed the first searchable encryption scheme based on a blockchain, where the search interaction process is between the data owner and the blockchain. In 2018, Cai et al. [10] proposed the design of a blockchain-assisted encrypted database with expressive content search capabilities, assuring the trustworthiness of search results returned by various service providers. In 2019, Chen et al. [13] proposed a searchable encryption scheme for EHR (electronic health record), and Niu et al. [14] proposed an electronic health record-sharing scheme on the blockchain. In 2021, Guptaet al. [15] deployed blockchain-assisted searchable encryption into a cloud-based healthcare cyber-physical system. The above works [13,14,15] all treated blockchain as a trusted third party, which enforces the generalized solutions of theoretical crypto constructions in real-life scenarios. In 2022, Han et al. [6] formalized a flexible and privacy-preserving framework for MUSE by orienting blockchain and attribute-based encryption, which achieves fine-grained access control.

3. The Proposed Model

We present the model of the HSE-BI scheme in this section. We start by giving the architecture of the HSE-BI scheme in Section 3.1 and define its syntax in Section 3.2. We will use the notations from Table 1 throughout the rest of the paper.

Table 1. Notations.

Notation	Definition
F, P and G	pseudo-random functions
H	a collision-resistant hash function
$\mathcal{O}$, $\mathcal{S}$ and $\mathcal{B}$	data owner, server and blockchain network
$\mathcal{G}=(\mathcal{V},\mathcal{E})$	DAG access structure
$\mathbf{f}=(f_1,\dots ,f_m)$	the outsourced file set
$\mathbf{w}=(w_1,\dots ,w_{\theta })$	keyword dictionary
${\mathbf{w}}_f=(w_1,\dots ,w_d)$	keyword set in file f
$\mathcal{V}=\{v_1,\dots ,v_l\}$	hierarchy vertex set
$\mathcal{U}=\{u_1,\dots ,u_n\}$	user set
BC & T	blockchain-based index & look-up table
$e_i$ or $e\left[i\right]$	i-th element of a sequence of elements e
$e\left[i\right]\leftarrow j$	store j at location i in structure e
${\mathbf{f}}_w^i$	file set contains w in hiearchy $v_i$
${\mathsf{A}}_w$	hierarchy-sorted array for w in BC
$ad{d}_i$	the transaction address of ${\mathsf{n}}_i$ in ${\mathsf{A}}_w$
$A_w^i$	array for w and hierarchy $v_i$ in BC
${\mathsf{n}}_i$	the tail node of $A_w^i$
${\tilde{\mathsf{n}}}_i$	the masked ${\mathsf{n}}_i$ stored in BC’s transaction

3.1. Architecture

HSE-BI is designed to be executed among: a data owner $\mathcal{O}$, n users $\mathcal{U}=(u_1,\dots ,u_n)$, a server $\mathcal{S}$ and a blockchain network $\mathcal{B}$. The scheme model is illustrated in Figure 1:

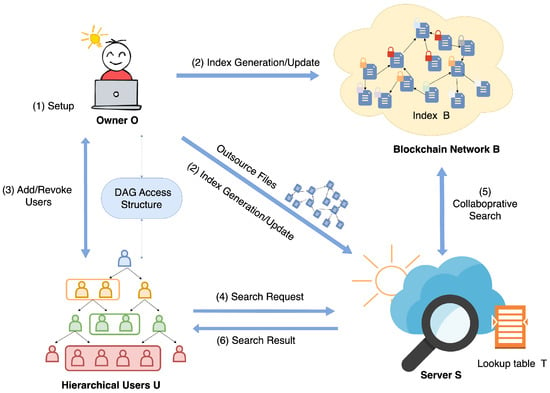
Figure 1. The architecture.

• Data owner$\mathcal{O}$ develops a hierarchical DAG search structure $\mathcal{G}$ and outsources encrypted files to $\mathcal{S}$.
• Each user$u\in \mathcal{U}$ can be mapped to a search hierarchy in $\mathcal{G}$ by $\mathcal{O}$ and has hierarchical search rights to the files in their hierarchy.
• Server$\mathcal{S}$ is an untrusted entity that stores encrypted files and answers search queries from $\mathcal{U}$ with the collaboration of $\mathcal{B}$.
• Blockchain network$\mathcal{B}$ is organized by a network of peer nodes, which manage the index and acts as a collaborator for searching.

The architecture is illustrated in Figure 1. To initialize the system, the data owner $\mathcal{O}$ constructs a hierarchical search index based on a DAG-type authentication structure $\mathcal{G}=(\mathcal{V},\mathcal{E})$, encrypts the index by hierarchical keys and outsources it to the blockchain network $\mathcal{B}$, stored as index BC. $\mathcal{O}$ also initializes a look-up table T outsourced to the server $\mathcal{S}$ for encrypted searches. A user u can interact with $\mathcal{O}$ to obtain the search authority under some hierarchy $v_i\in \mathcal{V}$. To search the files that include the keyword w, the authorized user $u\in \mathcal{U}$ can submit search tokens $\tau$ to $\mathcal{S}$ that contain the masked information of the searched keyword w and its hierarchy $v_i$. $\mathcal{S}$ interacts with the blockchain network $\mathcal{B}$ to conduct the encrypted search according to the search token $\tau$, and obtains search result R, which contains the matched file id under hierarchy $v_i$. $\mathcal{O}$ is able to change any user’s hierarchy or revoke a user’s search right at any time. $\mathcal{O}$ can also interact with $\mathcal{B}$ to dynamically update the index BC when adding/deleting files.

3.2. Syntax

The scheme HSE-BI (Setup, IndexGen, AddU, Search, RevokeU, Update) consists of six algorithms/protocols:

• $\mathsf{Setup}(1^k,\mathcal{G})\to (K_{\mathcal{O}},K_{\mathcal{S}},s{t}_{\mathcal{S}})$: On input, the security parameter k and the authentication structure $\mathcal{G}$, $\mathcal{O}$ computes $(K_{\mathcal{O}},K_{\mathcal{S}},s{t}_{\mathcal{S}})$, where $K_{\mathcal{O}}$ is $\mathcal{O}$’s key, $K_{\mathcal{S}}$ is $\mathcal{S}$’s key and $s{t}_{\mathcal{S}}$ is $\mathcal{S}$’s state.
• $\mathsf{IndexGen}(\mathbf{f},\mathcal{G},K_{\mathcal{O}})\to (\mathsf{BC},\mathsf{T})$: On input, $\mathcal{O}$’s key $K_{\mathcal{O}}$, the file set $\mathbf{f}$ and the authentication structure $\mathcal{G}$, $\mathcal{O}$ computes the hierarchical index $\mathsf{T}$ and $\mathsf{BC}$, sends $\mathsf{T}$ to $\mathcal{S}$ and sends $\mathsf{BC}$ to $\mathcal{B}$.
• $\mathsf{AddU}(u,\mathcal{G},K_{\mathcal{O}},\mathcal{U})\to (K_u,{\mathcal{U}}^{\prime },s{t}_{\mathcal{S}})$: On input, $\mathcal{O}$’s key, the authentication structure $\mathcal{G}$, the user’s identity u and $\mathcal{O}$ computes the user’s key $K_u$, the updated user group ${\mathcal{U}}^{\prime }$ and $\mathcal{S}$’s state $s{t}_{\mathcal{S}}$.
• $\mathsf{Search}(u:w;\mathcal{S}:\mathsf{T},s{t}_{\mathcal{S}};\mathcal{B}:\mathsf{BC})\to R$: To search for files contains w, a user u executes this protocol with $\mathcal{S}$ on input of w and $K_u$, $\mathcal{S}$ interacts with $\mathcal{B}$ to query $\mathsf{BC}$ on input $\mathsf{T}$. The final output for the user is R.
• $\mathsf{Update}(\mathcal{O}:K_{\mathcal{O}},\mathcal{G},f;\mathcal{S}:\mathsf{T},\mathcal{B}:\mathsf{BC})\to ({\mathsf{BC}}^{\prime },{\mathsf{T}}^{\prime })$: On input, $\mathcal{O}$’s key, file f, the authentication structure $\mathcal{G}$, $\mathcal{O}$ executes this protocol with $\mathcal{S}$ and $\mathcal{B}$ to compute the updated index ${\mathsf{T}}^{\prime }$ and ${\mathsf{BC}}^{\prime }$.
• $\mathsf{RevokeU}(u,K_{\mathcal{O}})\to ({\mathcal{U}}^{\prime },s{t}_{\mathcal{S}})$: On input, $\mathcal{O}$’s key and the revoked user’s identity u, $\mathcal{O}$ computes the updated user group ${\mathcal{U}}^{\prime }$ and $\mathcal{S}$’s current state $s{t}_{\mathcal{S}}$.

4. HSE-BI Constructions

4.1. Design Challenge

Before we present HSE-BI’s detailed concrete constructions, we need to describe our design challenge for the explicit algorithms. Since HSE-BI is designed for hierarchical searches, how do we build a hierarchical index structure to achieve this goal? Notice first that in a blockchain data structure, the transactions can be linked by storing the addresses of previous transactions in current transactions. Therefore, we organize the hierarchical DAG-type index as a constant number of sorted arrays; each array includes l nodes. To link the nodes in the same array that stores in different transactions together as a virtual link list, we insert each node with the transaction addresses of the previously connected nodes in such a way that can make the index achieve hierarchical and parallel searches. Secondly, recall that the blockchain is an append-only data store, i.e., once a block is created, it is final. It is not possible to subsequently delete or modify the index. How can the dynamic update can be applied to the secure index corresponding to the update of the actual outsourced files? To achieve dynamic update, we propose an append-only index update mechanism to support update operations on the encrypted blockchain-based index structure.

4.2. Concrete Constructions

Let k be a public parameter, $\mathcal{O}$ be the data owner, $\mathcal{U}$ be the authenticated users, $\mathcal{S}$ be a server and $\mathcal{B}$ be the blockchain network. Let $\mathbf{f}=(f_1,\dots ,f_m)$ be the file set, and $\mathbf{w}=(w_1,\dots ,w_{\theta })$ be the keyword dictionary. Let F and P be two pseudo-random functions of fixed length ${\{0,1\}}^k\times {\{0,1\}}^{*}\to {\{0,1\}}^k$ [15], G be a full-domain pseudo-random function ${\{0,1\}}^k\times {\{0,1\}}^{*}\to {\{0,1\}}^{*}$ and H be a collision-resistant hash function ${\{0,1\}}^k\times {\{0,1\}}^{*}\to {\{0,1\}}^{*}$. HSE-BI also makes black-box use of crypto primitives: a private key encryption scheme SKE = (Gen, Enc, Dec) [23], a CPA-secure broadcast encryption scheme BE = (KeyGen, Join, Enc, Dec) [24] and a blockchain data store ${\mathsf{\Omega }}_{\mathsf{BC}}=(\mathsf{Init},\mathsf{Put},\mathsf{Get})$ [25]. Consider that HSE-BI works as follows:

4.2.1. Setup

To initialize the system, the data owner $\mathcal{O}$ constructs the hierarchical authentication structure as a directed acyclic graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$. $\mathcal{V}$ contains l vertices $\{v_1,\dots ,v_l\}$, each of which represents an access hierarchy in $\mathcal{G}$. The directed edge set $\mathcal{E}$ represents the affiliations among hierarchies. If there exists $(v_i,v_j)\in \mathcal{E}$, then the hierarchy of $v_i$ is directly afflicted by the hierarchy of $v_j$. Any authenticated user $u\in \mathcal{U}$ or file $f\in \mathbf{f}$ can be mapped to a vertex in $\mathcal{V}$: $v_i^{\left(u\right)}\in \mathcal{V}$ and $v_j^{\left(f\right)}\in \mathcal{V}$. A user u can access file f if and only if $v_j^{\left(f\right)}$ is afflicted by $v_i^{\left(u\right)}$, which means that $v_j^{\left(f\right)}$ is reachable from $v_i^{\left(u\right)}$ in $\mathcal{G}$. After $\mathcal{G}$ is established, the data owner $\mathcal{O}$ generates the hierarchy keys as l triples of k-bit strings $\left\{{(k_{i,1},k_{i,2},k_{i,3})}_{i\in \left[l\right]}\right\}$. $\mathcal{O}$ also initializes the authenticated user group $\mathcal{U}$, and computes their master key $msk$ by $\mathsf{BE}.\mathsf{KeyGen}\left(1^k\right)$ for enrolling users. Then $\mathcal{O}$ inserts server $\mathcal{S}$ into $\mathcal{U}$. It also computes the server’s key $k_{\mathcal{S}}$ by $\mathsf{BE}.{\mathsf{Join}}_{msk}\left(S\right)$ and generates a k-bit string $k_r$ as the authentication key by $\mathsf{SKE}.\mathsf{Gen}\left(1^k\right)$, encrypts $k_r$ as the current server state $s{t}_{\mathcal{S}}$ by $\mathsf{BE}.{\mathsf{Enc}}_{k_r}\left(\mathcal{U}\right)$. Finally, $\mathcal{O}$ sends $(k_{\mathcal{S}},s{t}_{\mathcal{S}})$ to $\mathcal{S}$, and stores its key $K_{\mathcal{O}}$ as $(msk,k_r,\left\{{(k_{i,1},k_{i,2},k_{i,3})}_{i\in \left[l\right]}\right\})$ at local. This algorithm is shown in Algorithm 1.

Algorithm 1Setup$(1^k,\mathcal{G}).$

Require:  Security parameters $1^k$ Ensure:  $K_{\mathcal{O}},K_{\mathcal{S}},s{t}_{\mathcal{S}}$  1: initialize the DAG authentication structure $\mathcal{G}=(\mathcal{V},\mathcal{E})$  2: choose l triple of k bit strings ${\{k_{i,1},k_{i,2},k_{i,3}\}}_{i\in l}$  3: compute $k_r\leftarrow \mathsf{SKE}.\mathsf{Gen}\left(1^k\right)$  4: compute $msk\leftarrow \mathsf{BE}.\mathsf{KeyGen}\left(1^k\right)$  5: initialize the authenticated user group $\mathcal{U}$  6: set $\mathcal{U}\leftarrow \left\{\mathcal{S}\right\}$  7: compute $k_{\mathcal{S}}\leftarrow \mathsf{BE}.{\mathsf{Join}}_{msk}\left(\mathcal{S}\right)$  8: compute $s{t}_{\mathcal{S}}\leftarrow \mathsf{BE}.{\mathsf{Enc}}_{k_r}\left(\mathcal{U}\right)$  9: send $k_{\mathcal{S}},s{t}_{\mathcal{S}}$ to $\mathcal{S}$  10: store $K_{\mathcal{O}}$ as $(msk,{\{k_{i,1},k_{i,2},k_{i,3}\}}_{i\in l})$

4.2.2. IndexGen

Data owner $\mathcal{O}$ constructs a hierarchical secure index BC outsourced to blockchain network $\mathcal{B}$ and a look-up table T outsourced to server $\mathcal{S}$. This algorithm is shown in Algorithm 2.

• The index BC consists of $\theta$ keyword-guided hierarchy-sorted arrays ${\mathsf{A}}_{w_1},\dots ,{\mathsf{A}}_{w_{\theta }}$. Each array contains l nodes ${\mathsf{n}}_1,\dots ,{\mathsf{n}}_l$. At a high level, the information stored in ${\mathsf{n}}_i$ should at least include the identities of files in hierarchy $v_i$ that contain the keyword w. These nodes should be linked in the sorted arrays to generate a hierarchical DAG index. To outsource the index to the blockchain network, $\mathcal{O}$ interacts with $\mathcal{B}$ to initialize BC using ${\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Init}\left(1^k\right)$. To connect different nodes in ${\mathsf{A}}_w$, besides the above information stores in ${\mathsf{n}}_i$, $\mathcal{O}$ inserts ${\mathsf{n}}_i$ with additional address information $add{r}_j$—the transaction address of the connected nodes ${\left\{{\mathsf{n}}_j\right\}}_{\forall (v_i,v_j)\in \mathcal{E}}$ in ${\mathsf{A}}_w$, where $v_j$ is directly affiliated by $v_i$: $(v_i,v_j)\in \mathcal{E}$.
  To guarantee confidentiality and hierarchical search control, $\mathcal{O}$ should mask the information stored in each node. We define the structure of the masked node ${\tilde{\mathsf{n}}}_i$ as $({\mathbf{f}}_w^i,{\{add{r}_j,P_{k_{j,2}}\left(w\right)\}}_{(v_i,v_j)\in \mathcal{E}})\oplus H\left(P_{k_{i,2}}\left(w\right)\right)$, where ${\mathbf{f}}_w^i$ is the file set that contains the keyword w and corresponds to the hierarchy $v_i$, $ad{d}_j$ is the address of node ${\mathsf{n}}_j$ where $v_j$ is directly afflicted by $v_i$: $(v_i,v_j)\in \mathcal{E}$, $P_{k_{j,2}}\left(w\right)$ is the key to decrypt the masked node ${\tilde{\mathsf{n}}}_j$. $\mathcal{O}$ then encrypts each node ${\mathsf{n}}_i\in {\mathsf{A}}_w$ in an orderly way from $i=l$ to $i=1$, inserts ${\tilde{\mathsf{n}}}_i$ as a transaction into the blockchain index BC by ${\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_i)$, and receives the transaction address $add{r}_i$. Specifically, for ${\mathsf{n}}_l$, the tail node in ${\mathsf{A}}_w$, there is no node for the lower hierarchy in the ordered array ${\mathsf{A}}_w$, $\mathcal{O}$ computes the masked ${\tilde{\mathsf{n}}}_l$ as $(({\mathbf{f}}_w^l,\perp ,\perp )\oplus H\left(P_{k_{l,2}}\left(w\right)\right)$.
• To support the search, we design a look-up table T at the server side to store the masked tail address of each virtual hierarchy-sorted array in BC. The entries in T contain each masked $(w,v_i)$ pair, which does not point to the address of the initial node in each ${\mathsf{A}}_w$, but to the masked address of the tail node ${\mathsf{n}}_i$ of ${\mathsf{A}}_w^i$ in the blockchain BC. For example, to retrieve array ${\mathsf{A}}_w$ in hierarchy $v_i$, we should only retrieve its sub-array ${\mathsf{A}}_w^i$ from the blockchain BC. Since the search can not traverse back through the encrypted virtual link list, the available search results are the identifiers for the files that both contain the keyword w and are affiliated by hierarchy $v_i$, as required by DAG structure. Therefore, for each $i\in \left[l\right]$, $\mathcal{O}$ generates the entry $F_{k_{i,1}}\left(w\right)$ in T, which points to the masked address $add{r}_j\oplus G_{k_{i,3}}\left(w\right)$: $\mathsf{T}\left[F_{k_{i,1}}\left(w\right)\right]\leftarrow add{r}_i\oplus G_{k_{i,3}}\left(w\right)$. Finally, $\mathcal{O}$ sends T to server $\mathcal{S}$.

Algorithm 2$\mathsf{IndexGen}(\mathbf{f},\mathcal{G},K_{\mathcal{O}}).$

Require:  $\mathbf{f},\mathcal{G},K_{\mathcal{O}}$ Ensure:  $\mathsf{BC},\mathsf{T}$  1: initial the blockchain index $\mathsf{BC}\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Init}\left(1^k\right)$  2: initialize the lookup table T  3: extract the keyword dictionary $\mathbf{w}=(w_1,\dots ,w_{\theta })$  4: for each $f\in \mathbf{f}$  5:   set f as $(w_1,\dots ,w_d,i)$, where $i\in \left[l\right]$  6:   for every $w\in \mathbf{w}$:  7:    set ${\mathbf{f}}_w^l$ as ${\left\{f_d\right\}}_{l\in f_d}$  8:    initialize a list ${\mathsf{A}}_w$ as ${\mathsf{A}}_w=({\mathsf{n}}_1,\dots ,{\mathsf{n}}_l)$.  9:    compute $P_{k_{l,2}}\left(w\right)$  10:    compute $H\left(P_{k_{l,2}}\left(w\right)\right)$  11:    compute ${\tilde{\mathsf{n}}}_l=(({\mathbf{f}}_w^l,\perp ,\perp )\oplus H\left(P_{k_{l,2}}\left(w\right)\right)$  12:    send ${\tilde{\mathsf{n}}}_l$ to $\mathcal{B}$  13:    $\mathcal{B}$ runs $add{r}_l\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_l)$  14:    $\mathcal{B}$ sends $add{r}_l$ to $\mathcal{O}$  15:    for $i\in (l,1]$  16:     parse ${\mathbf{f}}_w^i$ as ${\left\{f_d\right\}}_{i\in f_d}$  17:     generate $P_{k_{i,2}}\left(w\right)$  18:     compute $H\left(P_{k_{i,2}}\left(w\right)\right)$  19:     $\forall (v_i,v_j)\in \mathcal{E}$, compute ${\tilde{\mathsf{n}}}_j=(f_w^j,\{add\left(j\right),$     $P_{k_{j,2}}\left(w\right)\left\}\right)\oplus H\left(P_{k_{j,2}}\left(w\right)\right)$  20:     send ${\tilde{\mathsf{n}}}_j$ to $\mathcal{B}$  21:     $\mathcal{B}$ runs $add{r}_j\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_j)$  22:     $\mathcal{B}$ sends $add{r}_j$ to $\mathcal{O}$  23:     compute $add{r}_j\oplus G_{k_{j,3}}\left(w\right)$  24:     set $\mathsf{T}\left[F_{k_{j,1}}\left(w\right)\right]\leftarrow add{r}_j\oplus G_{k_{j,3}}\left(w\right)$  25: send T to the server $\mathcal{S}$

4.2.3. AddU/RevokeU

A user u can interact with the data owner $\mathcal{O}$ to obtain the search authority under their hierarchy $v_i$. Data owner $\mathcal{O}$ adds the user id u to the authenticated user group $\mathcal{U}$ as $\mathcal{U}\cup \left\{u\right\}$, and generates the user’s key $k_u$ by $\mathsf{BE}.{\mathsf{Join}}_{msk}\left(u\right)$. Since group $\mathcal{U}$ is updated, $\mathcal{O}$ should also refresh $k_r$ as a new k-bit string by SKE.Gen($1^k$) and encrypts $k_r$ as a new server state $s{t}_{\mathcal{S}}$ by $\mathsf{BE}.{\mathsf{Enc}}_{k_r}\left(\mathcal{U}\right)$. Finally, $\mathcal{O}$ sends the user’s key $K_u=(k_u,k_{i,1},k_{i,2},k_{i,3})$ to u and sends $s{t}_{\mathcal{S}}$ to server $\mathcal{S}$.

If the data owner $\mathcal{O}$ would like to revoke u’s search right at any time, they need to delete the user id u from the authenticated user group $\mathcal{U}$ as $\mathcal{U}\backslash \left\{u\right\}$. $\mathcal{O}$ should also refresh $k_r$ as a new k-bit string by SKE.Gen($1^k$), and encrypt $k_r$ as the current server state $s{t}_{\mathcal{S}}$ by $\mathsf{BE}.{\mathsf{Enc}}_{k_r}\left(\mathcal{U}\right)$. Finally, $\mathcal{O}$ sends $s{t}_{\mathcal{S}}$ to $\mathcal{S}$. AddU and RevokeU algorithms are shown in Algorithms 3 and 4.

Algorithm 3$\mathsf{AddU}(u,\mathcal{G},K_{\mathcal{O}},\mathcal{U})).$

Require:  $\mathbf{f},\mathcal{G},K_{\mathcal{O}}$ Ensure:  $K_u,{\mathcal{U}}^{\prime },s{t}_{\mathcal{S}}$  1: set $\mathcal{U}\leftarrow \mathcal{U}\cup \left\{u\right\}$  2: compute $k_u\leftarrow \mathsf{BE}.{\mathsf{Join}}_{msk}\left(u\right)$  3: compute $k_r\leftarrow \mathsf{SKE}.\mathsf{Gen}\left(1^k\right)$  4: send $K_u=(k_u,k_{i,1},k_{i,2},k_{i,3})$ to u  5: compute $s{t}_{\mathcal{S}}\leftarrow \mathsf{BE}.{\mathsf{Enc}}_{k_r}\left(\mathcal{U}\right)$  6: send $s{t}_{\mathcal{S}}$ to $\mathcal{S}$

Algorithm 4$\mathsf{RevokeU}(u,K_{\mathcal{O}}).$

Require:  $u,K_{\mathcal{O}}$ Ensure:  ${\mathcal{U}}^{\prime },s{t}_{\mathcal{S}}$  1: set $\mathcal{U}\leftarrow \mathcal{U}\backslash \left\{u\right\}$  2: compute $k_r\leftarrow \mathsf{SKE}.\mathsf{Gen}\left(1^k\right)$  3: compute $s{t}_{\mathcal{S}}\leftarrow \mathsf{BE}.{\mathsf{Enc}}_{k_r}\left(\mathcal{U}\right)$  4: send $s{t}_{\mathcal{S}}$ to $\mathcal{S}$

4.2.4. Search

To search the files that contain the keyword w, the authorized user $u\in \mathcal{U}$ can submit search token $\tau$ to server $\mathcal{S}$, which contains the masked information of the search keyword w and its hierarchy $v_i$. $\mathcal{S}$ interacts with the blockchain network $\mathcal{B}$ to conduct an encrypted search according to the search token $\tau$. The specific process is as follows:

User u first retrieves the server’s current state $s{t}_{\mathcal{S}}$, uses their key $k_u$ to decrypt $s{t}_{\mathcal{S}}$ as r by running $\mathsf{BE}.{\mathsf{Dec}}_{k_u}$$\left(s{t}_{\mathcal{S}}\right)$ and generates the search token as $\tau \leftarrow \mathsf{SKE}.{\mathsf{Enc}}_r(F_{k_{j,1}}\left(w\right),G_{k_{j,1}}$$\left(w\right),P_{k_{j,1}}\left(w\right))$, then sends $\tau$ to server $\mathcal{S}$. $\mathcal{S}$ first runs $\mathsf{BE}.{\mathsf{Dec}}_{k_{\mathcal{S}}}\left(s{t}_{\mathcal{S}}\right)$ to decrypt $s{t}_{\mathcal{S}}$ as $r^{\prime }$ and uses $r^{\prime }$ to decrypt $\tau$ as $\mathsf{SKE}.{\mathsf{Dec}}_{r^{\prime }}\left(\tau \right)$. If $\tau$ is decrypted successfully, that means $r=r^{\prime }=k_r$; then the token sender u is an authorized user. $\mathcal{S}$ then initializes an empty search result set R, and parses $\mathsf{SKE}.{\mathsf{Dec}}_{r^{\prime }}\left(\tau \right)$ as $(r_1,r_2,r_3)$, uses $r_1$ as the entry to retrieve $\mathsf{T}\left[r_1\right]$, which points to the masked address of the tail node ${\mathsf{n}}_i$ of ${\mathsf{A}}_w^i$ in the blockchain B, uses $r_2$ to decrypt the address as $\mathsf{T}\left[r_1\right]\oplus r_2$ that stores masked ${\tilde{\mathsf{n}}}_i$—the tail node of the hierarchy-sorted $A_w^i$ in BC. $\mathcal{S}$ interacts with $\mathcal{B}$ to obtain the transaction ${\tilde{\mathsf{n}}}_i$ with address $\mathsf{T}\left[r_1\right]\oplus r_2$, uses $r_3$ to decrypt ${\tilde{\mathsf{n}}}_i$, and sets $(z_1,z_2,z_3)={\tilde{\mathsf{n}}}_j\oplus H\left(r_3\right)$. If $z_3\ne 0$, then $z_2$ is the transaction addresses set of ${\left\{{\tilde{\mathsf{n}}}_j\right\}}_{(v_i,v_j)\in \mathcal{E}}$, where each ${\mathsf{n}}_j$ is affiliated directly with ${\mathsf{n}}_i$. $\mathcal{S}$ adds $z_1$ to the result set R as $R\cup \left\{z_1\right\}$, and continues the above process parallel to retrieve the nodes by addresses in $z_2$ until $z_3=0$. After $\mathcal{S}$ has retrieved all the nodes in ${\mathsf{A}}_w^i=\{{\mathsf{n}}_1,\dots ,{\mathsf{n}}_i\}$, search result R then contains those identifiers for files containing w, and the hierarchy is affiliated with $v_i$, as required by the DAG structure. Finally, $\mathcal{S}$ sends the result R to u. This algorithm is shown in Algorithm 5.

Algorithm 5$\mathsf{Search}(u:w,K_u;S:\mathsf{T},s{t}_{\mathcal{S}};B:\mathsf{BC}).$

Require:  $u:w,K_u;S:\mathsf{T},s{t}_{\mathcal{S}};B:\mathsf{BC}$ Ensure:  R  1: u extracts $s{t}_{\mathcal{S}}$ from S  2: u computes $r\leftarrow \mathsf{BE}.{\mathsf{Dec}}_{k_u}\left(s{t}_{\mathcal{S}}\right)$  3: u computes $F_{k_{j,1}}\left(w\right),G_{k_{j,1}}\left(w\right),P_{k_{j,1}}\left(w\right)$;  4: u generates $\tau \leftarrow \mathsf{SKE}.{\mathsf{Enc}}_r(F_{k_{j,1}}\left(w\right),G_{k_{j,1}}\left(w\right),P_{k_{j,1}}\left(w\right))$  5: u sends $\tau$ to $\mathcal{S}$.  6: $\mathcal{S}$ computes $r^{\prime }\leftarrow \mathsf{BE}.{\mathsf{Dec}}_{k_{\mathcal{S}}}\left(s{t}_{\mathcal{S}}\right)$  7: $\mathcal{S}$ computes $(r_1,r_2,r_3)\leftarrow \mathsf{SKE}.{\mathsf{Dec}}_{r^{\prime }}\left(\tau \right)$  8: $\mathcal{S}$ initializes an empty search result R  9: $\mathcal{S}$ retrieves $\mathsf{T}\left[r_1\right]$  10: $\mathcal{S}$ computes $\mathsf{T}\left[r_1\right]\oplus r_2$  11: $\mathcal{S}$ sends $\mathsf{T}\left[r_1\right]\oplus r_2$ to $\mathcal{B}$.  12: $\mathcal{B}$ computes ${\tilde{\mathsf{n}}}_i\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Get}(\mathsf{T}\left[r_1\right]\oplus r_2)$.  13: $\mathcal{B}$ sends ${\tilde{\mathsf{n}}}_i$ to $\mathcal{S}$  14: $\mathcal{S}$ computes $(z_1,z_2,z_3)={\tilde{\mathsf{n}}}_j\oplus H\left(r_3\right)$  15: while $z_3\ne 0$,  16:   $\mathcal{S}$ sets $R\leftarrow R\cup z_1$  17:   $\mathcal{S}$ parses $z_2$ as ${\left(\left\{z_2^i\right\}\right)}_{i\in \left[t\right]}$  18:   $\mathcal{S}$ sends ${\left(\left\{z_2^i\right\}\right)}_{i\in \left[t\right]}$ to $\mathcal{B}$.  19:   for each $i\in \left[t\right]$  20:     $\mathcal{B}$ computes ${\tilde{\mathsf{n}}}_j\leftarrow \mathsf{BC}.\mathsf{Get}\left(z_2^i\right)$.  21:     $\mathcal{B}$ sends ${\left\{{\tilde{\mathsf{n}}}_j^i\right\}}_{i\in \left[t\right]}$ to $\mathcal{S}$  22: $\mathcal{S}$ and $\mathcal{B}$ repeats (15)–(21) until $z_3=0$.  23: $\mathcal{S}$ sends R to u.

4.2.5. Update

When adding or deleting file f in hierarchy $v_i$ with keywords ${\mathbf{w}}_f=(w_1,\dots ,w_d)$, data owner $\mathcal{O}$ should update the secure index BC and T accordingly. For $w_j\in {\mathbf{w}}_f$, $\mathcal{O}$ interacts with $\mathcal{B}$ and runs ${\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Get}(\mathsf{BC},add{r}_i)$ to get the transaction that stores masked ${\tilde{\mathsf{n}}}_i$. $\mathcal{O}$ decrypts it as ${\tilde{\mathsf{n}}}_i\oplus G_{k_{i,3}}\left(w_j\right)=(z_1,z_2,z_3)$. If file f is added, $\mathcal{O}$ computes the updated ${\tilde{\mathsf{n}}}_i$ as $(z_1\cup \left\{f\right\},z_2,z_3)\oplus G_{k_{i,2}}\left(w_j\right)$. If file f is deleted, $\mathcal{O}$ computes ${\tilde{\mathsf{n}}}_i$ as $(z_1\backslash \left\{f\right\},z_2,z_3)\oplus P_{k_{i,2}}\left(w_j\right)$. Then $\mathcal{O}$ inserts ${\tilde{\mathsf{n}}}_i$ as a new transaction into BC, and receives its new address $add{r}_i^{\prime }$ by ${\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_i)$.

For each q from $i-1$ to 1, $\mathcal{O}$ interacts with $\mathcal{B}$ and runs ${\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Get}(\mathsf{BC},add{r}_q)$ to get the transaction that stores the masked ${\tilde{\mathsf{n}}}_q$. $\mathcal{O}$ decrypts ${\mathsf{n}}_q$ as ${\tilde{\mathsf{n}}}_q\oplus G_{k_{q,3}}\left(w_j\right)$, computes ${\tilde{\mathsf{n}}}_q^{\prime }=(z_1,z_2\cup \left\{add{r}_{q+1}^{\prime }\right\}\backslash \left\{add{r}_{q+1}\right\},z_3)\oplus P_{k_{q,2}}\left(w_j\right)$, inserts a new transaction that stores masked ${\tilde{\mathsf{n}}}_q^{\prime }$ into $\mathsf{BC}$ and runs $add{r}_q^{\prime }$ as ${\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_q^{\prime })$ to get the transaction address $add{r}_q^{\prime }$, masks $add{r}_q^{\prime }$ with $G_{k_{q,3}}\left(w\right)$ and generates $add{r}_q^{\prime }\oplus G_{k_{q,3}}\left(w\right)$. $\mathcal{O}$ parses the update token $t_q=(t_1^q,t_2^q)$, where $t_1^q=F_{k_{q,1}}\left(w_1\right)$ and $t_2^q=add{r}_q^{\prime }\oplus G_{k_{q,3}}\left(w\right)$. Finally, $\mathcal{O}$ sends $t_q$ to $\mathcal{S}$. $\mathcal{S}$ updates the lookup table T by setting $\mathsf{T}\left[F_{k_{j,1}}\left(w_1\right)\right]$ as $add{r}_i\oplus G_{k_{i,3}}\left(w\right)$. This algorithm is shown in Algorithm 6.

Algorithm 6$\mathsf{Update}(\mathcal{O}:K_{\mathcal{O}},f;\mathcal{S}:\mathsf{T},\mathcal{B}:\mathsf{BC}).$

Require:  $\mathcal{O}:K_{\mathcal{O}},f;\mathcal{S}:\mathsf{T},\mathcal{B}:\mathsf{BC}$ Ensure:  ${\mathsf{BC}}^{\prime },{\mathsf{T}}^{\prime }$  1: $\mathcal{O}$ sets f as $(w_1,\dots ,w_d,i)$  2: for $j\in \left[d\right]$  3:   $\mathcal{O}$ computes $t_i=(t_i^1,t_i^2,t_i^3)=(F_{k_{i,1}}\left(w_j\right),P_{k_{i,2}}\left(w_j\right),G_{k_{i,3}}\left(w_j\right))$  4:   $\mathcal{O}$ sends $t_i$ to $\mathcal{S}$.  5:   $\mathcal{S}$ sets ${\theta }_i\leftarrow \mathsf{T}\left[t_i^1\right]$,  6:   $\mathcal{S}$ computes $add{r}_i={\theta }_i\oplus t_i^2$,  7:   $\mathcal{S}$ computes ${\tilde{\mathsf{n}}}_i\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Get}(\mathsf{BC},\mathsf{T}\left[t_i^1\right]\oplus t_i^2)$  8:   $\mathcal{S}$ computes ${\mathsf{n}}_i\leftarrow {\tilde{\mathsf{n}}}_j\oplus t_i^3$  9:   $\mathcal{S}$ parses ${\mathsf{n}}_i$ as $(z_1,z_2,z_3)$  10:   If add f, $\mathcal{S}$ computes ${\tilde{\mathsf{n}}}_i=(f\cup z_1,z_2,z_3)\oplus t_i^2$   If delete f, $\mathcal{S}$ computes ${\tilde{\mathsf{n}}}_i=(f\backslash z_1,z_2,z_3)\oplus t_i^2$  11:   $\mathcal{S}$ computes $add{r}_i^{\prime }\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_i)$.  12:   $\mathcal{S}$ sends $(add{r}_i^{\prime },add{r}_i)$ to $\mathcal{O}$  13:   for j from $i-1$ to 1:  14:     $\mathcal{O}$ computes ${\tilde{\mathsf{n}}}_j\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Get}(\mathsf{BC},add{r}_j)$.  15:     $\mathcal{O}$ computes ${\mathsf{n}}_j={\tilde{\mathsf{n}}}_j\oplus t_i^3$  16:     $\mathcal{O}$ parses ${\mathsf{n}}_j$ as $(z_1,z_2,z_3)$  17:     $\mathcal{O}$ computes ${\tilde{\mathsf{n}}}_j^{\prime }=(z_1,z_2\cup \left\{add{r}_{j+1}^{\prime }\right\}\backslash \left\{add{r}_{j+1}\right\},z_3)\oplus t_i^2$  18:     $\mathcal{O}$ computes $add{r}_j^{\prime }\leftarrow {\mathsf{\Omega }}_{\mathsf{BC}}.\mathsf{Put}(\mathsf{BC},{\tilde{\mathsf{n}}}_i^{\prime })$  19:     $\mathcal{O}$ computes $add{r}_j^{\prime }\oplus G_{k_{j,3}}\left(w\right)$  20:     $\mathcal{O}$ sets $t_1^j=F_{k_{j,1}}\left(w_1\right)$  21:     $\mathcal{O}$ sets $t_2^j=add{r}_j^{\prime }\oplus G_{k_{j,3}}\left(w\right)$  22:     $\mathcal{O}$ parses $t_j=(t_1^j,t_2^j)$  23:     $\mathcal{O}$ sends $t_j$ to S  24:     $\mathcal{S}$ sets $T\left(t_1^j\right)=t_2^j$  25:     $i--$

5. Security Analysis

We present the security analysis for HSE-BI in this section. The notions of security focus on two aspects: (1) User’s view: for each user $u\in \mathcal{U}$ with hierarchy $v_i$, it cannot learn any information for the files whose hierarchy is higher than $v_i$. (2) Server’s view: although it can conclude with some revoked or relegated users, it cannot provide a valid search token.

We formalize the security required in HSE-BI. Suppose $\mathcal{A}$ is an adversary with pseudo-random polynomial time (PPT) computation ability, who is given the security parameter k. In that case, the search policy is $\mathcal{G}$, and the server key is $K_{\mathcal{S}}$, also provided is access to the following oracles, where · denotes the parameters that are provided by $\mathcal{A}$ themselves.

-

${\mathcal{O}}_{\mathsf{IndexGen}}(·,\mathcal{G},K_{})$: $\mathcal{A}$ can send index generation to this oracle, which runs $\mathsf{IndexGen}$ by the input provided by $\mathcal{A}$. The oracle ${\mathcal{O}}_{\mathsf{IndexGen}}$ outputs $BC,T$.

-

${\mathcal{O}}_{\mathsf{AddU}}(·,\mathcal{U},u_i,v_j)$: $\mathcal{A}$ can send an add user request to this oracle, which runs $\mathsf{AddU}$ by the input provided by $\mathcal{A}$. If $u_i\in \mathcal{U}$, then the oracle ${\mathcal{O}}_{\mathsf{Revoke}}$ outputs ⊥.

-

${\mathcal{O}}_{\mathsf{RevokeU}}(·,\mathcal{U},u_i,v_j)$: $\mathcal{A}$ can send a revoke request to this oracle, who runs Revoke by the input provided by $\mathcal{A}$. If $u_i\notin \mathcal{U}$, then the oracle ${\mathcal{O}}_{\mathsf{Revoke}}$ outputs ⊥.

-

${\mathcal{O}}_{\mathsf{Search}}(·,\mathsf{T},\mathsf{BC},k_u,s{t}_{\mathcal{S}},w)$: $\mathcal{A}$ can send a search request for keyword w to this oracle. $\mathcal{A}$ generates a search token ${\tau }_w$ and sends it to ${\mathcal{O}}_{\mathsf{Search}}$ which runs Search and outputs the search result $R_w$ to $\mathcal{A}$.

Definition 1 (Adaptive Secure).

The security definition of adaptive secure requires that the execution of the scheme in the real-world, Real $\left(1^k\right)$, is indistinguishable from an ideal-world, Ideal $\left(1^k\right)$. In Real $\left(1^k\right)$, the protocols between $\mathcal{A}$ and $\mathcal{U}$ execute just as in the real scheme. In Ideal $\left(1^k\right)$, there exist a simulator $Sim$ that can obtain the leakage information from the oracles above and try to simulate the execution of $\mathcal{A}$ in Real $\left(1^k\right)$. HSE-BI achieves adaptive secure if, for all polynomial times of $\mathcal{A}$, there exists a polynomial time simulator $Sim$ such that the following two distribution ensembles are computationally indistinguishable: ${Output}_{\mathcal{A}}^{Real\left(1^k\right)}\approx {Output}_{Sim}^{Ideal\left(1^k\right)}$.

Theorem 1.

If SKE is CPA secure, and functions $F,G,P$ and H are pseudo-random, let HSE-BI be the hierarchical searchable symmetric encryption scheme with a blockchain-based index, then HSE-BI satisfies adaptive secure, which is defined in Definition 1.

Proof Sketch.

To show adaptive secure we reduce the security to that of the indistinguishability of the output of SKE.Enc and functions $F,G,P$ and H are indistinguishable from the output of a truly random function. We assume the possibility of an adversary $\mathcal{A}$ that is able to break the adaptive secure property of HSE-BI, then we build a distinguisher $\mathcal{D}$ that is able to use $\mathcal{A}$ as a sub-routine to distinguish between the output of SKE.Enc and functions $F,G,P,H$ and a truly random function with non-negligible probability. □

Definition 2 (Revocation Secure).

Consider ${\mathsf{Exp}}_{\mathcal{A}}^{\mathsf{Revoke}}\left(1^k\right)$, which is interactively executed by a challenger $\mathcal{C}$ and an adversary $\mathcal{A}$ who have the ability to add and revoke users in the real scheme. After a polynomial number of queries, $\mathcal{C}$ revokes all users that are queried to the ${\mathcal{O}}_{\mathsf{AddU}}$ oracle but are not subsequently queried to ${\mathcal{O}}_{\mathsf{RevokeU}}$ (i.e., all users for which $\mathcal{A}$ holds their valid user keys). $\mathcal{A}$ generates a search token τ in the Search protocol. If the output of the Search is not ⊥, then it returns 1, otherwise, it returns 0. After several rounds of queries, if $\mathcal{A}$’s probability of winning the revocation secure experiment with PPT computation ability is negligible, then we can say that HSE-BI satisfies revocation secure.

Theorem 2.

If BE is CPA secure, let HSE-BI be the hierarchical searchable symmetric encryption scheme with a blockchain-based index, then HSE-BI satisfies revocation secure, which is defined in Definition 2.

Proof Sketch.

Assuming the advantage of $\mathcal{A}$ winning ${\mathsf{Exp}}_{\mathcal{A}}^{\mathsf{Revoke}}\left(1^k\right)$ is negligible, we can construct an adversary ${\mathcal{A}}_{be}$, who can break the CPA secure of BE with assistance from $\mathcal{A}$. If $\mathcal{A}$ has a non-negligible advantage in ${\mathsf{Exp}}_{\mathcal{A}}^{\mathsf{Revoke}}\left(1^k\right)$, then we can construct an adversary ${\mathcal{A}}_{be}$ that uses $\mathcal{A}$ as a subroutine to break the CPA secure of BE. Since BE is proven to be CPA secure [6]; there exists no $\mathcal{A}$ to produce a valid search token, even though it does not hold a non-revoked key that can win ${\mathsf{Exp}}_{\mathcal{A}}^{\mathsf{Revoke}}\left(1^k\right)$ with non-negligible probability, and HSE-BI satisfies revocation secure as defined in Definition 2. □

6. Theoretical Analysis

We give the theoretical analysis of HSE-BI in this section. Table 2 presents a detailed complexities analysis of HSE-BI. In the Setup phase, the computation and storage complexity of data owner $\mathcal{O}$ is linear with the number of hierarchies l, since $\mathcal{O}$ needs to generate the keys for all hierarchies. The IndexGen phase, as shown in Section 4.2.2, needs the data owner $\mathcal{O}$ to construct the search index into: (1) $\theta$ keyword-guided arrays ${\mathsf{A}}_{w_1},\dots ,{\mathsf{A}}_{w_{\theta }}$ with l nodes ${\mathsf{n}}_1,\dots ,{\mathsf{n}}_l$, which need O($(l+m)\theta$) operations; (2) a look-up table T contains all masked $(w,v_i)$ pairs as entries with O($l\theta$) operations. The arrays are outsourced to $\mathcal{B}$, and T is outsourced to $\mathcal{S}$, so their storage overheads are O($(l+m)\theta$) and O($l\theta$), respectively. To search for $w_q$, a user sends a constant size token to $\mathcal{S}$, $\mathcal{S}$ interacts with $\mathcal{B}$ to perform $2^{\log l-\log i}$ works to operate XOR functions from the array $A_{w_q}$ in the subtree-rooted $v_i$, as presented in Section 4.2.4. Therefore, we require that the computational complexities included user-side and $\mathcal{S}$-side are O(1) and $\left(2^{\log l-\log i}\right)$, respectively, which are both independent in the number of files that contain $w_q$.

Table 2. Complexity.

	${\mathit{Stor}}_{\mathcal{O}}$	${\mathit{Stor}}_{\mathit{u}}$	${\mathit{Stor}}_{\mathcal{S}}$	${\mathit{Stor}}_{\mathcal{B}}$	${\mathit{Comp}}_{\mathcal{O}}$	${\mathit{Comp}}_{\mathit{u}}$	${\mathit{Comp}}_{\mathcal{S}}$	${\mathit{Comp}}_{\mathcal{B}}$
Setup	O(l)	–	O(1)	–	O(l)	–	–	–
IndexGen	O(1)	–	O($l\theta$)	O($(l+m)\theta$)	O($(l+m)\theta$)	–	–	–
Add/RevokeU	–	O(1)	O(1)	–	O(1)	–	–	–
Search	–	O$\left(1\right)$	O(1)	O(1)	–	O(1)	O$\left(2^{\log l-\log i}\right)$	O$\left(2^{\log l-\log i}\right)$
Update	O(d)	–	O(1)	O(1)	O(d)	–	O($\left(\log i\right)d$)	O($\left(\log i\right)d$)

l: number of hierarchies; θ: keywords number; m: files number; i: the hierarchy of search user; d: the number of keywords in updated file.

Moreover, HSE-BI also achieves a constant-time computation and storage cost to add/delete user. The owner can dynamically add or revoke users by updating the state parameter. Each user only needs to store their secret key locally, which requires constant user storage O(1). The search and update complexities is related to the concrete instance of the DAG-type index, which can be formalized as a full and complete binary tree. To update the index for a file f of hierarchy $v_i$ with keywords ${\mathbf{w}}_f=(w_1,\dots ,w_d)$, $\mathcal{O}$ adds $\left(\log i\right)d$ new transactions as newer versions of ${\mathsf{A}}_{w_1},\dots ,{\mathsf{A}}_{w_d}$ in all subtrees rooted from $v_i$ to $v_1$, which is described in Section 4.2.5, which needs to update $\left(\log i\right)d$-related entries in T with O($\left(\log i\right)d$) operations.

Table 3 shows the complexities and property comparisons of HSE-BI with the existing related multi-user searchable encryption schemes [16,18,19,20]. From the figure, we can see that the search and update complexities in HSE-BI are less than other schemes, which does not depend on the number of files. The DAG authentication structure makes the search complexity depend on the user’s search hierarchy, while in [18], the number of data items searched for is linear with the user’s rights and the files contain keywords; further, searching in [16,18,20] requires traversing all files. The index storage complexity in HSE-BI is linear with the size of the keyword dictionary and the hierarchy number. It is comparable with [19], the index of which is designed specifically for partial order access. Compared with [19], the size of the server’ storage overload of HSE-BI is about $m/l$ times larger, where l is the number of access hierarchies and m is the total file number. The hierarchical search property of HSE-BI will not significantly affect the index generation and search complexity. In terms of other properties, compared with the existing schemes, HSE-BI is secure from attacks from adaptive adversaries and supports the efficient updating for index and users while satisfying the revocation secure.

Table 3. Comparison.

	[16]	[18]	[19]	[20]	HSE-BI
Index Size	O$\left(\theta m\right)$	O$\left(\theta ln\right)$	O$\left(l\theta \right)$	O$\left(\theta \right)$	O$\left(\right(m+l\left)\theta \right)$
Search Cost	O$\left(m\right)$	O$\left(m\right)$	O$\left(\right(1-n\backslash l\left)m\right)$	O$\left(m\right)$	O$\left(2^{\log l-\log i}\right)$
Update Cost	O$\left(dm\right)$	$\left(dm\right)$	–	O$\left(dm\right)$	O($\left(\log i\right)d$)
Hierarchical search	∘	∘	•∘	∘	•
Adaptive Secure	•	•	•	∘	•
Revocation Secure	•	∘	∘	∘	•
Collusion Resistant	•	∘	∘	∘	•

l: number of hierarchies; θ: keywords number; m: files number; i: the hierarchy of search user; d: the number of keywords in updated file.

7. Experimental Evaluation

We implement HSE-BI in C++ and Python. In the simulation experiments, security parameter k is 256 bits, and the key length of broadcast encryption is 1024 bits. The experiment uses OpenSSL library [26] to implement basic cryptography algorithms, such as AES-CBC-256 for private-key encryption and SHA256 for hash and pseudo-random functions. Since running experiments on the blockchain main net is expensive, we simulate the blockchain network on Ropsten’s testnet [27], which provides custom transaction input of up to 1 KB, which we use to store the index BC. We fund our wallet using Ropsten’s faucet. In addition, we use BGW2 [24] to realize broadcast encryption. We use the U.S. National Science Foundation (NSF) Research Awards Abstracts 1990–2003 [28] as the hierarchical file collection. The experiment simulates a hierarchical DAG authentication structure $\mathcal{G}$ on top of the collection containing 10 hierarchies. The hierarchy affiliation, number of files and users in each hierarchy is illustrated in Figure 2.

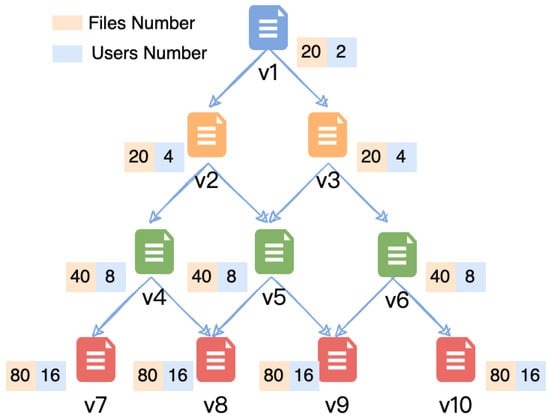
Figure 2. The Simulated Authentication Structure.

7.1. Search Performance

We analyzed the search performance for answering requests from users of different hierarchies. The search is performed by the server, and the process includes querying and communicating with the blockchain network to obtain transaction data. The search latency and communication overhead for the different hierarchy is presented in Figure 3 and Figure 4.

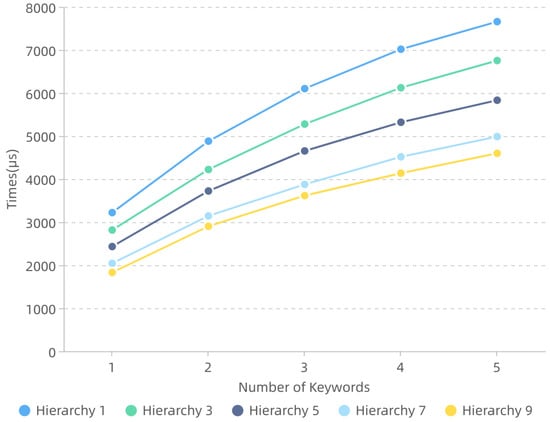
Figure 3. The Relationship of Search Times and Hierarchies.

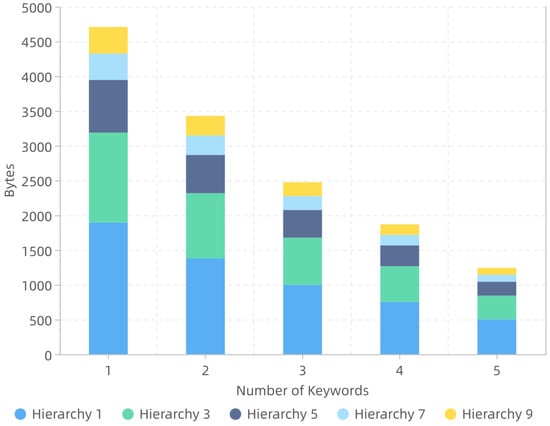
Figure 4. The Relationship of Communication Sizes and Hierarchies.

To analyze the search latency, we performed a keyword search with different hierarchies. Figure 3 plots the average search latency per 50 searches for 1, 2, 3, 4 and 5 independent keywords with 1, 3, 5, 7 and 9 hierarchies. From the figure, we can learn that, with the hierarchy of search users increasing, the search latency decreases with a smooth and orderly curve, i.e., the search times for three keywords are about 0.61, 0.53, 0.47, 0.39 and 0.36 ms with 1, 3, 5, 7 and 9 hierarchies, respectively. We identified the main efficiency bottleneck to be the on-chain processing. In fact, as long as enough transaction data size is deployed in transactions, the broadcast transactions will be mined and processed efficiently. The XOR operation and the PRF evaluation for the transaction data are related to the hierarchy directly, which decreases as the hierarchy increases. Therefore, from the performance shown in Figure 3, we observe that Search in HSE-BI is efficient, and the search latency (around a few milliseconds) is acceptable.

In terms of communication, we mainly analyze the amount of data transformed between the search user and the server. Figure 4 plots the average communication overhead between them per 50 searches when we have performed 1, 2, 3, 4 and 5 independent keywords, with 1, 3, 5, 7 and 9 hierarchies. We do not record the blockchain network communication overhead since it depends on the real-time network connection condition. From the figure, we can see the communication size decreases with the increasing hierarchy of search users, i.e., to search for three keywords, the communication sizes are 0.99, 0.68, 0.40, 0.21 and 0.20 kb for 1, 3, 5, 7 and 9 hierarchies, respectively, and each search only needs one round of interaction, which is tolerable with bandwidth latency. It is worth mentioning that as the hierarchy gets lower, the communication size slows down due to the specific DAG-type access structure shown in Figure 2. In general, from the performance shown in Figure 4, we can observe that the communication overhead is acceptable and is consistent with the theoretical analysis.

7.2. Comparison

We also implement schemes [18,19] and compare their experimental results with HSE-BI. We analyzed the influence of search users’ hierarchies and the number of users on the search latency of the three schemes. We assume that the number of searched keywords in the above schemes are all set to three. Figure 5 plots the relationship between search times and hierarchies. Figure 6 plots the relationship between the number of users and the search times. It should be mentioned that we implemented multiple user searches by deploying several hosts acting as users to submit search requests to the server host simultaneously. Each user host stores one user’s private information locally and interacts with the server independently.

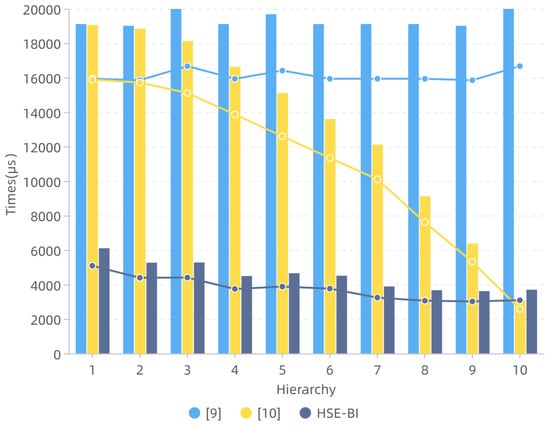
Figure 5. The Relationship between Hierarchy and Search Time.

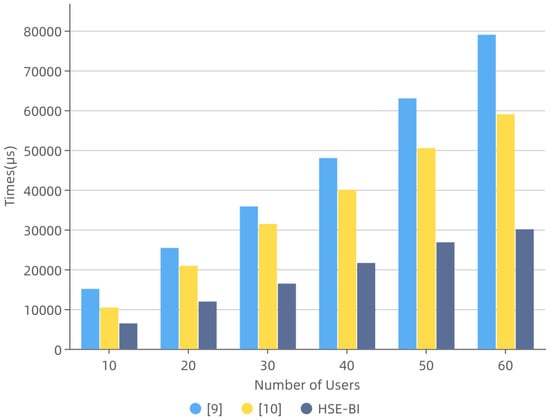
Figure 6. The Relationship between Number of Users and Search Time.

Search Latency The experimental results in Figure 5 demonstrate that HSE-BI spends much less time searching than that of [18,19], where 10 users with the same hierarchy submit search requests simultaneously in the three schemes. In detail, compared to [18], the search time of which does not change visibly and remains approximately 19 ms, the search time of HSE-BI is maintained in [3 ms, 6 ms], which is significantly better. One reason is the search operation in [18] needs to traverse the whole index and is independent of the hierarchies of users. Another reason is that searching operations in HSE-BI is not as complicated as [18], where the latter needs to traverse more of the index for the same hierarchy and consists of ORAM operations, which are not very efficient since ORAM incurs heavy computational and communication costs.

Compared with [19], the search performance of HSE-BI is less affected by hierarchy, while that in [19] has a stable, approximately linear relationship with the number of hierarchies. In detail, we observe that the HSE-BI’s search time for hierarchy 10 is 0.37 ms, which is slightly more than that in [19] (0.31 ms). Still, from hierarchy 9 to hierarchy 1, HSE-BI’s search performance is better than [19]. The increasing rate of efficiency is improved by 73% (for hierarchy 9) to 110% (for hierarchy 1), and as the hierarchy gets lower, the search latency in [19] considerably increases, more steeply than HSE-BI. One important reason is that HSE-BI supports parallel searches with a hierarchical index (especially the specific DAG-type access structure in Figure 2).

Scalability We also compared the scalability of the three schemes, which is the impact of the increasing number of users on search performance. We recorded the search times for 10, 20, 30, 40, 50 and 60 users who submitted search requests simultaneously to the server in the three schemes and plotted the relationship between the number of users and the search time, as illustrated in Figure 6. We observe that, for the same number of search users, the search performance of HSE-BI is better than others. In detail, the search time in HSE-BI is 38–49% less than [19] and 35–62% less than [18], where the curves in [18,19] are stably linear with the number of users. It is essential to notice that, in HSE-BI, the increase in search time slows down with the growing number of search users. Therefore, in the case of a large number of users, the growing number of search users has a weaker impact on the time consumption of the search protocol than [18,19]; that is, the number of users that the scheme can carry has an extensible space to meet the actual scalability requirements of hierarchical multi-user search.

8. Conclusions

In this paper, we propose a hierarchical searchable encryption scheme using blockchain-based indexing (HSE-BI). We focus on fine-grained access control policy, which is a crucial aspect for multi-user searchable encryption, but there are relatively few works considering this research area. We designed a hierarchical search index structure based on stepwise hierarchical key derivation and outsourced it to the blockchain network to achieve search reliability. We also propose a hierarchical user authorization mechanism based on broadcast encryption to achieve efficient user permission granting and revoking while preventing the malicious server from colluding with corrupted users. The security and performance analysis show that HSE-BI is adaptive secure and revocation secure. Our experimental results are encouraging in that HSE-BI’s hierarchical search policy does not impact the search performance visually, which is more suitable for actual complex application scenarios with fine-grained access requirements.