All Directional Search Motion Estimation Algorithm

Abstract

The search performance of block-matching motion estimation algorithms, i.e., search speed and motion estimation quality, mainly depends on the shape and size of the search pattern. Most motion estimation algorithms employ search patterns of square, diamond, hexagonal, cross diamond or cross hexagonal shapes. These search patterns achieve good results for video sequences with simple motion activity, but unfavourable results for video sequences with complex motion activity. After a thorough investigation of the effect of search pattern on search performance, this paper proposes an all-direction search (ADS) pattern, which searches for the best block in all possible directions. For further improvement in search speed, a half way stop technique is applied in search process. The results show that the proposed ADS algorithm outperforms other state-of-the-art and eminent motion estimation algorithms. The higher the direction complexity in the neighbouring motion vectors, the better the prediction quality of ADS, which is further proved by the simulation results.

1. Introduction

In this digital universe, the amount of video data that is to be stored or transmitted through the internet is growing rapidly and it leads to many challenges in video coding techniques. Motion Estimation (ME) plays an important role in having an effective video compression performance in video coding. The block-matching motion estimation algorithms in video encoders are mainly employed for estimating the motion of objects between successive pictures of a video sequence. However, these algorithms demand huge computation when compared to the remaining processes of the video encoder. Hence, researchers have concentrated on developing fast block-matching motion estimation algorithms to enhance the search speed.

The full-search (FS) algorithm gives the utmost quality i.e., high peak signal to noise ratio (PSNR), but it takes an enormous amount of computation. In order to alleviate this problem, many block-matching motion estimation algorithms have been developed [1]. These algorithms are classified as fast-full-search block-matching motion-estimation algorithms (FFSB-ME) [2,3,4,5,6,7,8,9,10] and fast-search block-matching motion-estimation algorithms (FSB-ME) [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. In the first category, the algorithms estimate motion with a PSNR which is equal to that of the FS algorithm. The computational cost of these algorithms is definitely less than that of FS but greater than that of second category algorithms. The second category algorithms estimate motion with fewer computations when compared to FFSB-ME algorithms, but the PSNR yielded is less than that of FS.

The motion information between reference and current frames of a video sequence is characterized with motion vectors. The motion vectors are found by selecting the best candidate blocks or search points in the reference frame. The current frame is portioned into non-overlapping equal sized blocks (macro blocks). It is required to find the motion of each block of a current frame with respect to a best matched block in a predefined search area of reference frame. The spatial difference between the coordinators of a macro block and a best matched candidate block is given by the motion vector. The complete description of the motion estimation process is depicted in Figure 1. The error measurement for finding the best matched candidate block is given by the sum of absolute difference (SAD). The SAD between a macro block A and a candidate block B is given by Equation (1).

$$SAD={\displaystyle \sum }_{i=0}^{M-1}{\displaystyle \sum }_{j=0}^{N-1}\left|A\left(i, j\right)-B \left(i, j\right)\right|$$

(1)

where M and N represent the number of rows and columns of the blocks A and B.

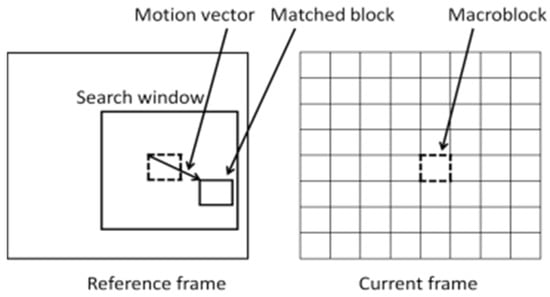
Figure 1. The basic idea of motion estimation.

The most popular block-matching motion estimation algorithm in the first category is the successive elimination algorithm (SEA) [1]. This algorithm calculates a boundary, i.e., a sum norm difference (SND), before calculating the full distortion measure, i.e., SAD. This SND boundary is a partial distortion measure which takes fewer computations when compared to SAD computations. Each candidate block (search point) is tested with SND to check the possibility of the search point being the best one. If any search point is decided as being an impossible search point, then it is skipped from the calculation of SAD. In this way, many computations are saved without loss in PSNR. Many enhancements to the SEA are proposed in the literature and these algorithms improve the speed of the search process.

The algorithms in the second category [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] check only the most promising search points instead of all the search points, as in fast full search algorithms. The most promising motion vectors are selected by various search patterns. Since only a few search points are checked, the resulting motion vectors may not be optimum. Thus, the second category algorithms are sub-optimal motion estimation algorithms. These sub-optimal motion estimation algorithms generally employ a coarse search pattern and a fine search pattern. At first, a coarse search pattern is applied continuously until a search centre becomes the best search point. The fine search pattern is applied once at the search centre to obtain the final motion vector.

The algorithms in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] were developed to improve both the search speed and prediction quality (PSNR). The search patterns in these algorithms are directional search algorithms. If at any search step, there is a wrong direction, it leads to a local minimum. This is mainly because of directional search patterns. This paper proposes an all directional search (ADS) pattern. The proposed ADS searches for minimum search points in all eight possible directions. The rest of the paper is organized as follows: Section 2 briefs on fast search block-matching motion estimation algorithms. The proposed algorithm is presented in Section 3. Results and conclusions are given in Section 4 and Section 5, respectively.

2. Remarks on Fast Search Block-Matching Motion Estimation Algorithms

The algorithm that is highly suitable for finding the motion vectors with large motion is the three-step search (TSS) algorithm [10]. The coarse search pattern is in the shape of a rectangle. There are nine search points in this coarse search. Firstly, if the search range is ±7 then the eight search points at distance of 4 (ceil (7/2)) from the centre are checked in the first step, as shown in Figure 2a. Next, in the second step, the eight new search points are checked at a distance of (4/2) = 2 from the minimum search point in the first step, as shown in Figure 2b. Finally, the third step checks the eight new search points which are located at a distance of (2/2) = 1 from the minimum search point in the second step, as shown in Figure 2c. If the search range is ±s then, in total, the TSS takes log₂(s + 1) search steps and has 1 + 8[log₂(s + 1)] checking points.

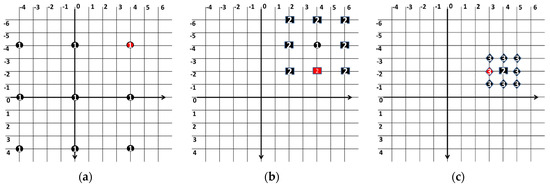
Figure 2. The rectangular search patterns of TSS at (a) first search step (assume s = ±7), (b) second search step, a rectangular search pattern is placed around the minimum search point of the first search step and the step size is half of the first step, (c) third search step, a rectangular search pattern is placed around the minimum search point of the second step and the step size is half of the second step. The minimum search point at any search step is highlighted with red colour.

The most popular sub-optimal motion estimation algorithm is the diamond search (DS) algorithm [12,13]. The coarse search pattern of the DS is a large diamond search pattern (LDSP) and the fine search pattern is a small diamond search pattern (SDSP). The DS algorithm applies the LDSP at the centre of the search window as shown in Figure 3a. If the minimum distortion search point is not the centre of the search window, then this LDSP is applied at a minimum distortion search point to find the new minimum distortion search point, as shown in Figure 3b. This process is continued until the minimum distortion search point is the centre of the LDSP. At any search step, if the minimum distortion search point is the centre of the LDSP then it applies the SDSP at the centre of the LDSP as shown in Figure 3c. The minimum distortion search point of this SDSP is the final motion vector.

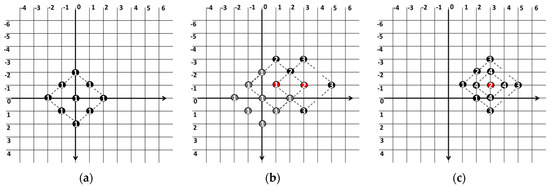
Figure 3. (a) A large diamond search pattern (LDSP) at search window centre, (b) new LDSPs are applied at minimum distortion search points if the minimum distortion search point is not at the centre of the LDSP, (c) a small diamond search pattern (SDSP) at the centre of the LDSP. The minimum search point at any search step is highlighted with red colour.

The new three step search (NTSS) algorithm [14] is an improved version of the TSS. At the first search step, the eight search points around the search window centre and eight search points at distance of ceil (s/2) from the search window centre are checked, as shown in Figure 4a. If the minimum distortion point is at the search window centre then the search stops and the final motion vector is the search window centre. If the minimum distortion point is any one of the eight search points around the search window centre, then eight search points around the minimum distortion point are checked to find the final motion vector. If the minimum distortion point is any one of the eight search points at distance of ceil (s/2) from the search window centre, then the next two search steps of the TSS continue. The hexagon search (HS) algorithm [15] is an improved version of the DS. The coarse search pattern and fine search pattern in the HS are a large hexagon search pattern and small hexagon search pattern, respectively. The large HS pattern shape is closer to the circle.

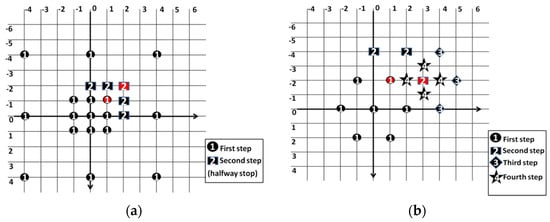
Figure 4. Motion vector searching procedure with an example, (a) using NTSS at (2, −2), (b) using HS (3, −2). Each search point is identified by a step number and a point with red colour indicates the minimum search point.

The LDSP shape is not closer to the circle and so, the results obtained by the HS are more accurate than those of the DS. Figure 4b shows an example of searching for the motion vector by the HS algorithm. The cross-diamond search (CDS) algorithm [16] shows better performance when compared to DS. At first, it employs a cross shaped pattern (CSP) before applying the search patterns of the DS. A small amount of a motion vector related block within 5 × 5 search window is found by the CSP. This algorithm also uses a halfway-stop technique in order to locate the blocks that have a small amount of motion. The cross-diamond-hexagonal search (CDHS) [17] shows better performance when compared to the HS. At first, it employs a cross shaped pattern before applying the search patterns of the HS. A small amount of motion vector related blocks within 5 × 5 search window are found by the cross shaped pattern. This algorithm also uses a halfway-stop technique in order to locate the blocks that have a small amount of motion. A star-diamond (SD) search pattern is proposed in [23]. This algorithm applies a star shaped search pattern with nine search points for coarse search and applies a small diamond pattern for fine search. It provides better performance than the diamond search algorithm. In [24], the authors have proposed a diamond–hexagon search algorithm which provides the benefits of both diamond and hexagonal search patterns for better results. The authors of [25] have proposed a prediction-biased motion estimation algorithm by employing the diamond search pattern. This algorithm provides reduced computational cost with good image quality. In [26], an enhanced adaptive threshold motion estimation algorithm is described, which assigns a weight adaptively to the search for better performance in terms of computational cost.

3. All Directional Search (ADS) Pattern

This paper proposes a search pattern which searches for the best point in all possible eight directions as shown Figure 5. These eight possible search directions are given by 0, π/4, π/2, 3π/4, π, 5π/4, 3π/2, and 7π/4. There are two search points in each search direction. In total, 16 search points enclose the search window centre evenly. The main aim of the ADS is to search for the minimum search point in all directions. Thus, the possibility of being trapping into a local optimum is reduced. The way to find a motion vector by using the ADS is effective and simple. First, the ADS is applied at the search window centre. The new ADS is placed at the minimum search point, which is obtained in the previous search step. This procedure is repeated until the search centre becomes the minimum search point. This minimum search point is the final motion vector. The procedure for finding a motion vector by using the ADS is summarized as follows.

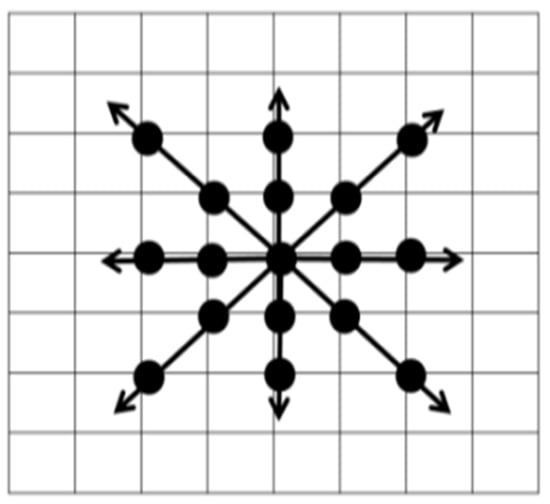
Figure 5. The All-Directional Search (ADS) pattern.

• The ADS is applied at the search window centre.
• Calculate the SAD values at the all the search points and find the minimum SAD among them.
• If the minimum SAD point is in the centre go to step 5.
• Apply the ADS at the minimum SAD point and go to step 2.
• The minimum SAD point at the centre is the final motion vector.

When the ADS is continuously applied, some search points are common in two consecutive search steps. The common search points are not checked and non-common search points are checked in the new search step. The procedure for searching the motion vector with the ADS is shown in Figure 6. The ADS searches slightly more search points: but it attains nearly as much PSNR as the FS does. In order to reduce the number of search points, a half way stop technique is employed in this paper. First, check the eight search points around the search window centre. If the minimum SAD point is at the centre, then stop the search i.e., the remaining search points of the ADS are eliminated from checking. In this way, the computational cost is saved with an insignificant PSNR drop.

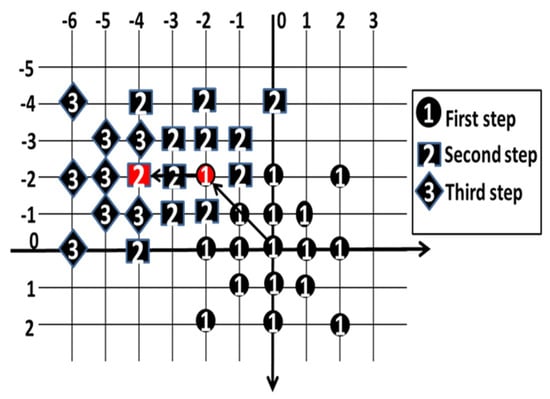
Figure 6. An illustration of an ADS search algorithm and procedure for searching for the motion vector (−4, −2). Each search point is identified by a step number and a point with red colour indicates the minimum search point.

4. Results

The simulation results from the proposed algorithm and other famous motion estimation algorithms are obtained with the experimental arrangement as follows: The PSNR measurement is used to check the error between the current frame and predicted frame. The computational cost is represented by the average number of operations including additions, subtractions and absolute operations per block. The first 100 frames of various video sequences are considered and these sample frames of test video sequences are shown in Figure 7. The block size and search range are set to 16 × 16 and ±15, respectively.

Figure 7. Sample frames of test video sequences used for simulation of the proposed ADS algorithm and other state-of-the-art and well-known motion estimation algorithms: (a) Foreman, (b) Mobile, (c) Rhinos, (d) Robot boat, (e) Suzie, (f) Akiyo, (g) Cricket, (h) Flower, (i) Kari-Jobe, (j) News Flash.

The average number of operations per block (ANOB) and average PSNR values for the proposed ADS algorithm and other state-of-the-art and well-known motion estimation algorithms for various videos are summarized in Table 1 and Table 2, respectively. It can be observed from Table 1 and Table 2 that the proposed ADS algorithm shows better PSNR performance with a lesser computational cost performance when compared with other famous motion estimation algorithms. As the ADS searches in all the directions, the average PSNR achieved with the ADS is larger than that achieved by the NTSS, DS, HS, CD, CDHS SDS, DHS and PDS. It can be observed from Table 1 that, on average, the proposed ADS algorithm achieves 47.85%, 38.27%, 33.53%, 28.31% and 23.96% of computation reduction when compared to well-known motion estimation algorithms such as NTSS, DS, HS, CD and CDHS, respectively. Similarly, 19.66%, 14.91% and 10.98% of computation reduction is achieved when compared to state-of-the-art motion estimation algorithms such as SDS, DHS and PDS.

Table 1. The average number of operations per block in each algorithm.

Video Sequence	All Directional Search (ADS) Proposed	New Three-Step Search (NTSS) [13]	Diamond Search (DS) [12]	Hexagon-Based Search (HS) [14]	Cross-Diamond Search (CDS) [15]	Cross-Diamond Hexagonal Search (CDHS) [16]	Star-Diamond Search (SDS) [22]	Diamond-Hexagon Search (DHS) [23]	Prediction-Biased Diamond Search (PDS) [24]
Foreman	7862	17,449	14,179	12,015	11,308	10,864	10,032	9206	8741
Mobile	10,248	17,006	16,153	15,634	13,781	13,017	12,411	11,791	11,064
Rhinos	12,850	20,537	18,444	17,790	17,073	16,572	16,034	15,530	14,987
Boat	13,697	21,201	20,458	19,025	18,375	17,426	16,705	16,093	15,673
Suzie	8723	15,732	13,912	12,694	11,571	10,632	9906	9100	9020
Akiyo	6520	14,162	9813	9436	8914	8367	7918	7309	6983
Cricket	7572	16,913	13,885	12,545	10,580	9633	9219	8807	8008
Flower	7150	17,095	15,053	13,832	12,353	11,692	10,380	9559	9005
Kari Jobe	11,167	19,991	16,428	15,282	14,828	14,029	13,633	13,031	12,796
Rocket	7203	18,244	12,340	11,661	10,941	10,064	9510	8865	8187

Table 2. The degree of motion prediction quality of every algorithm with respect to the full search algorithm.

Video Sequence	All Directional Search (ADS) Proposed	New Three-Step Search (NTSS) [13]	Diamond Search (DS) [12]	Hexagon-Based Search (HS) [14]	Cross-Diamond Search (CDS) [15]	Cross-Diamond Hexagonal Search (CDHS) [16]	Star-Diamond Search (SDS) [22]	Diamond-Hexagon Search (DHS) [23]	Prediction-Biased Diamond Search (PDS) [24]
Foreman	28.86	25.30	28.15	27.64	28.03	28.19	28.26	28.28	28.29
Mobile	24.25	21.71	23.52	23.35	23.85	23.89	23.91	23.95	23.99
Rhinos	30.21	26.03	27.62	27.31	27.81	28.49	28.66	28.73	28.75
Boat	30.58	27.30	29.21	28.13	29.10	29.51	29.63	29.79	29.86
Suzie	35.86	34.49	35.02	34.78	35.10	35.19	35.33	35.53	35.64
Akiyo	44.16	43.85	44.16	44.16	44.16	44.16	44.16	44.16	44.16
Cricket	35.88	30.26	33.66	32.59	33.95	34.13	34.55	34.96	34.98
Flower	33.65	29.26	33.02	31.19	33.19	33.31	33.47	33.51	33.55
Kari Jobe	44.68	39.05	43.15	42.21	43.21	43.30	43.45	43.68	43.73
Rocket launch	38.92	36.20	37.53	36.69	37.69	37.83	37.92	37.95	37.96

For the Mobile video sequence which contains complex motions, i.e., motion in all directions, the proposed ADS algorithm achieves a maximum of 2.54 dB and a minimum of 0.26 dB better PSNR when compared with other algorithms. For the Rhinos and Boat video sequences which contain large motion, the proposed ADS algorithm achieves a better PSNR of maximum 4.18 dB and 3.28 dB and minimum 1.46 dB and 0.72 dB, respectively, compared to other algorithms.

For video sequences which contain medium motion such as the Foreman, Suzie, Cricket, Flower and News Flash video sequences, the proposed ADS algorithm achieves a better PSNR of maximum 3.56 dB, 1.37 dB, 5.62 dB, 4.39 dB and 2.72 dB and minimum 0.57 dB, 0.22 dB, 0.9 dB, 0.1 dB and 0.96 dB, respectively, compared to other algorithms. For other video sequences with small motion, the PSNR values of all the algorithms are almost the same, but the ADS has a slightly better PSNR.

To more clearly understand the comparative results shown in Table 1 and Table 2, a frame by-frame comparison of ANOB and PSNR of all the algorithms for various videos is shown in Figure 8 and Figure 9, respectively. In these figures, the X-axis represents the sequence number of each frame in the video sequence. Figure 8a–j clearly shows that the proposed ADS algorithm demands less computational cost compared to other algorithms. For the Mobile, Rhinos and Boat video sequences with complex motions and large motion, the proposed ADS algorithm substantially reduces the computations compared to other algorithms at each frame as shown in Figure 8b, Figure 8c, Figure 8d, respectively. As the ADS searches in all the directions, it can obtain a good motion prediction quality for video sequences with complex motions and large motion such as in the Mobile, Rhinos and Boat video sequences. This can be clearly observed from Figure 9b–d, where the average PSNR achieved with the ADS is larger than that obtained by other algorithms for the Mobile, Rhinos and Boat video sequences, respectively. For other video sequences with small and medium motion, the PSNR values of all the algorithms are almost same at each frame, but the ADS shows a slightly better PSNR as shown in Figure 9, and a computational reduction, as shown in Figure 8.

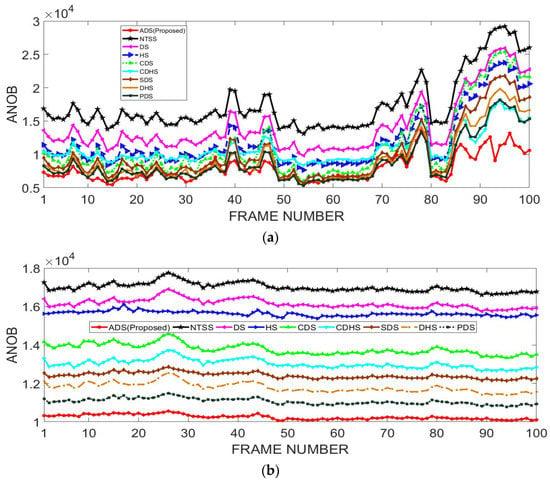
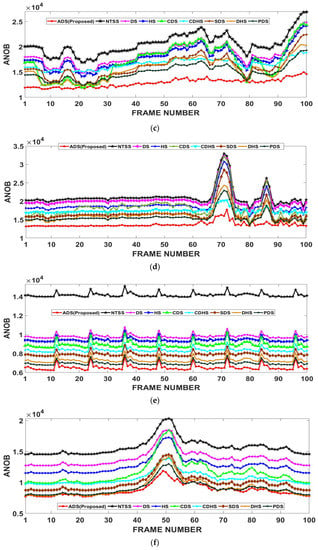
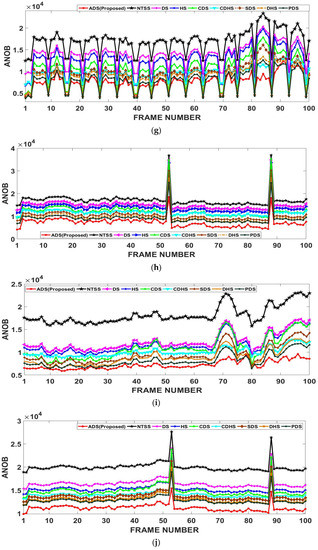
Figure 8. Computational cost comparison of the proposed ADS algorithm and other state-of-the-art and well-known motion estimation algorithms in terms of average number of operations per block (ANOB) for various video sequences: (a) Foreman, (b) Mobile, (c) Rhinos, (d) Robot boat, (e) Suzie (f) Akiyo, (g) Cricket, (h) Flower, (i) Kari-Jobe, and (j) News Flash.

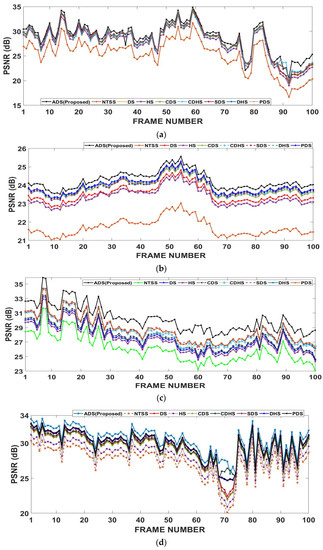
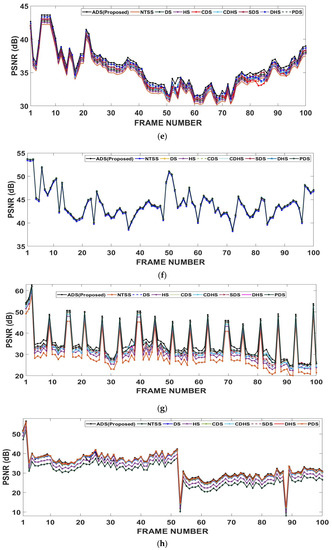
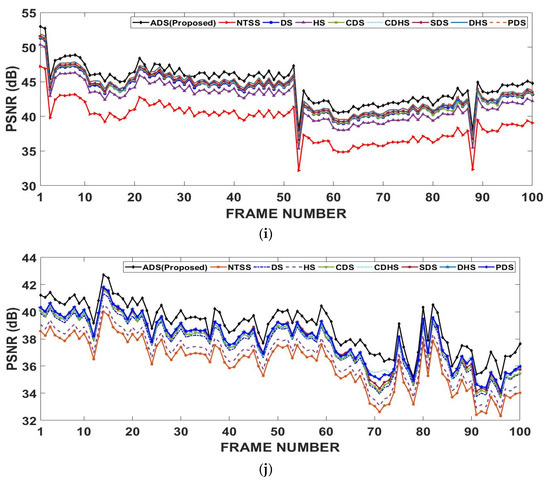
Figure 9. Motion prediction quality comparison of the proposed ADS algorithm and other state-of-the-art and well-known motion estimation algorithms in terms of the peak signal-to-noise ratio (PSNR) for various video sequences: (a) Foreman, (b) Mobile, (c) Rhinos, (d) Robot boat, (e) Suzie, (f) Akiyo, (g) Cricket, (h) Flower, (i) Kari-Jobe, and (j) News Flash.

5. Conclusions

An efficient block-matching motion estimation algorithm using an all directional search (ADS) pattern is developed in this paper. The ADS algorithm demonstrates a substantial improvement in motion prediction quality, i.e., PSNR over the CDS, CDHS, SDS, DHS and PDS algorithms, while reducing computational cost. It is clear that the proposed ADS algorithm has a more reliably good quality performance than the CDHS and PDS, irrespective of large amounts of motion or small amounts of motion or medium amounts of motion or completely no motion. Furthermore, for video sequences with large amounts of motion, the ADS will possibly achieve much higher PSNR than that of the CDHS and PDS algorithms, while reducing computational cost.