Federated Deep Reinforcement Learning for Joint AeBSs Deployment and Computation Offloading in Aerial Edge Computing Network
Abstract
1. Introduction
- 1.
- A federated DRL algorithm was designed to jointly optimize the AeBSs’ deployment and computation offloading to achieve lower energy consumption and task processing delay.
- 2.
- A new training mechanism is presented in the aerial edge computing network where low-altitude AeBSs are controlled by their own agents and cooperate in a distributed manner, and an HAP acts as a global node for model aggregation to improve the training efficiency.
- 3.
- Two neural networks trained together were set up for each agent to deploy the AeBSs and generate the computation offloading policies, respectively.
2. Related Work
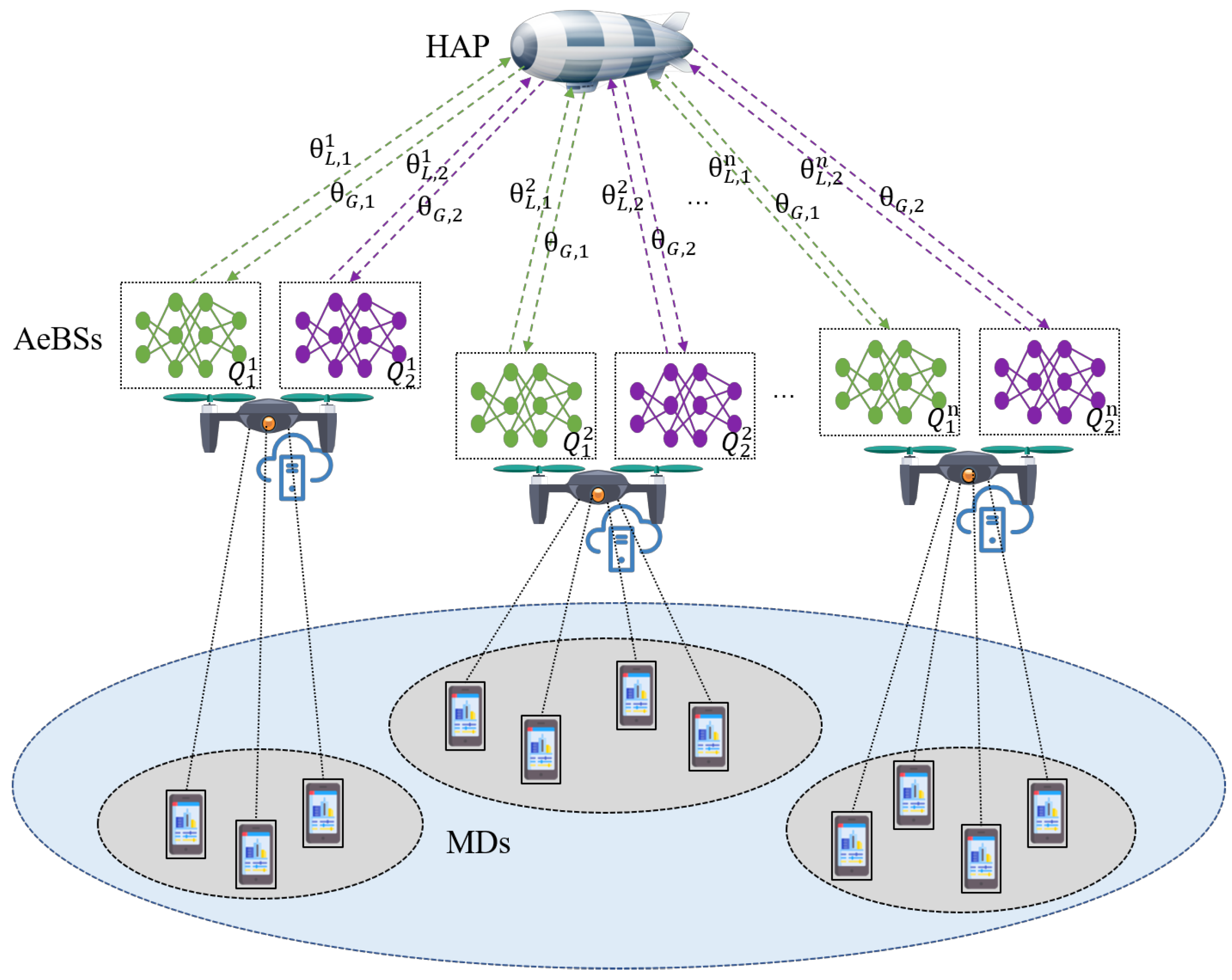
3. System Model
3.1. Communication Model
3.2. Computation Model
3.2.1. Local Execution
3.2.2. Offloading Execution
3.3. Energy Model
3.4. Problem Formulation
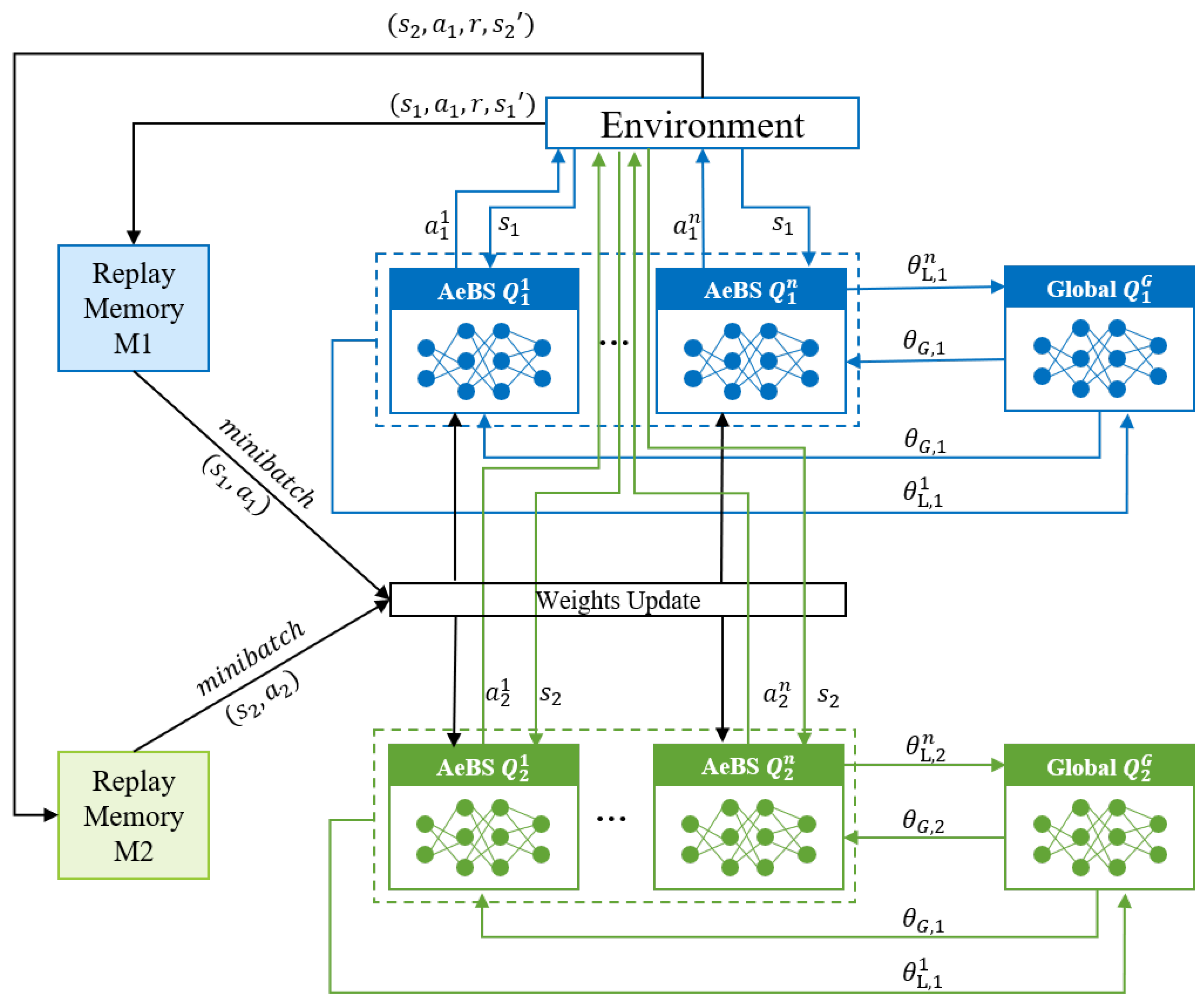
4. Federated Deep-Reinforcement-Learning-Based AeBS Deployment and Computation Offloading

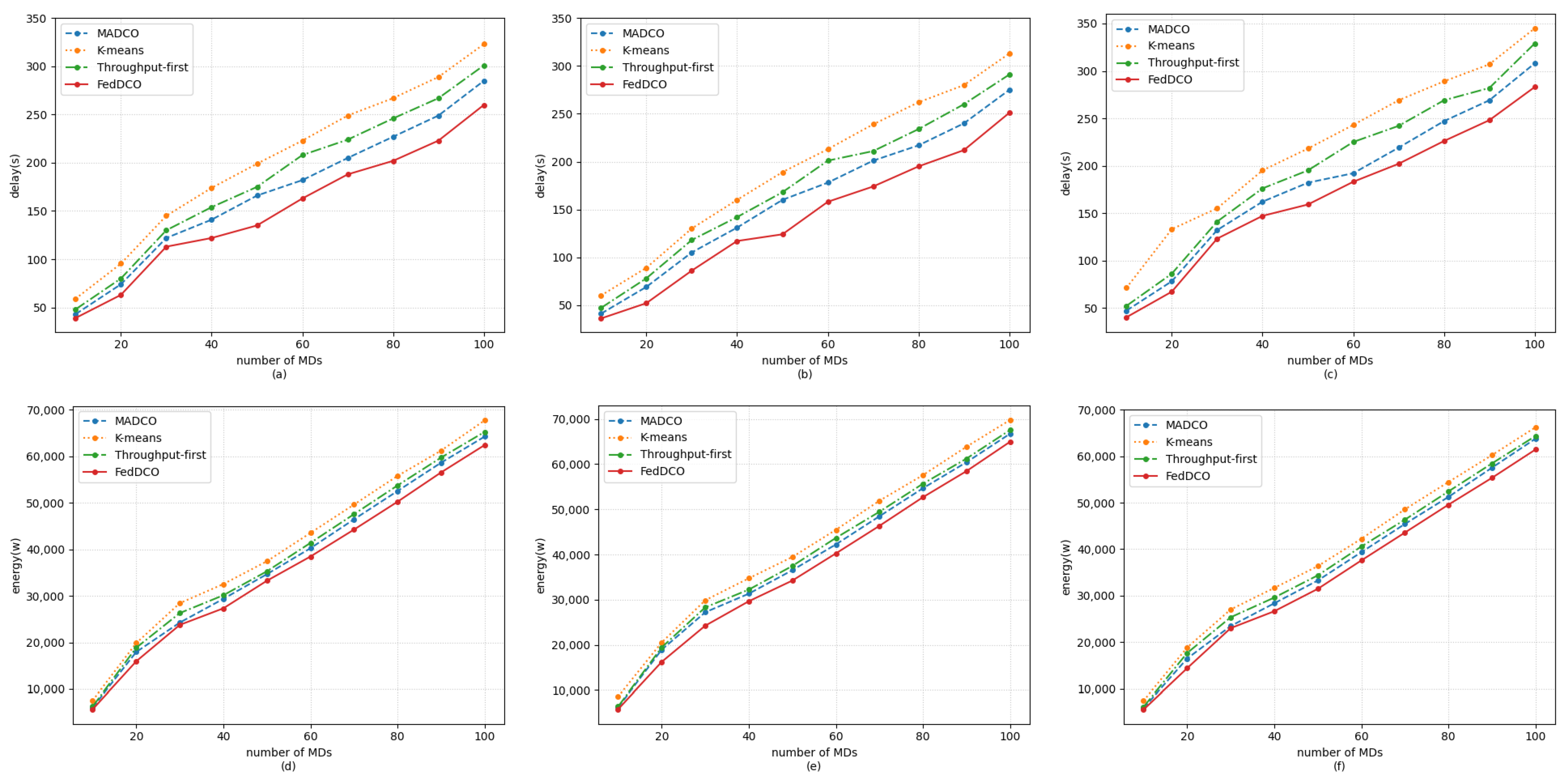
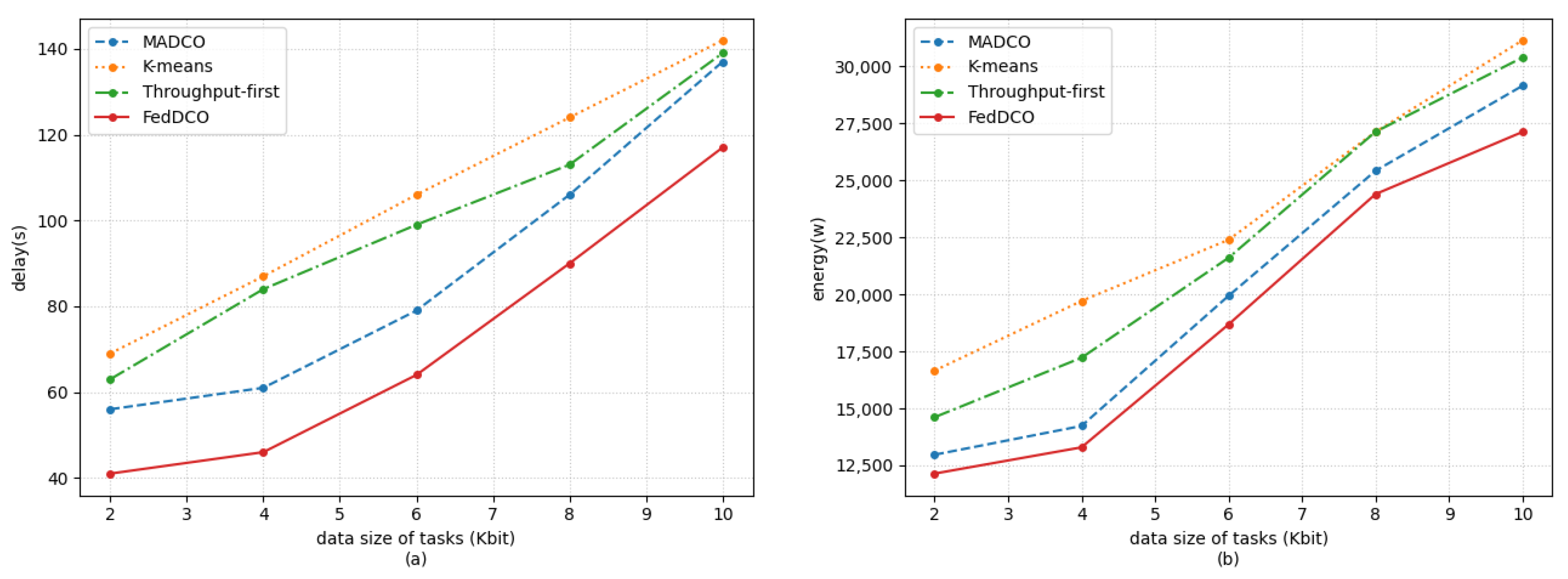
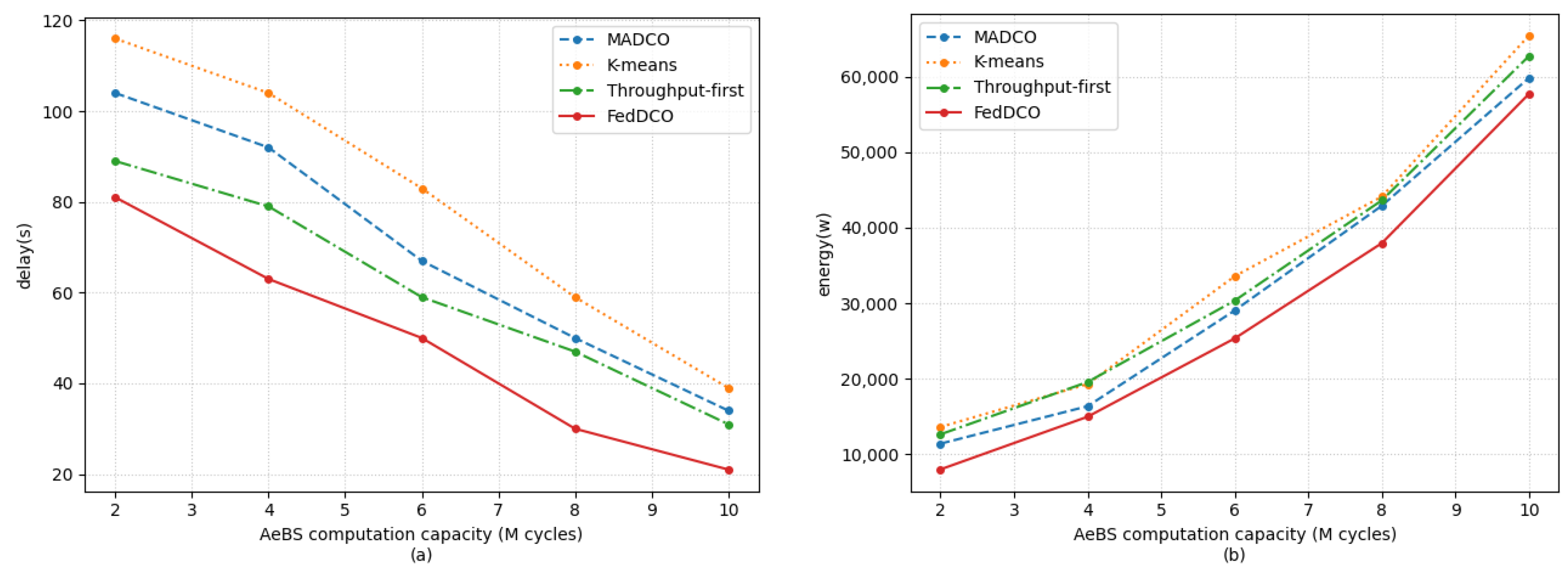
5. Simulation Results and Discussions
- 1.
- FedDCO: Each AeBS has two deep Q-networks, and , and they are trained simultaneously to generate deployment and offloading policies. During the training process, AeBSs upload the and weights instead of the raw state and action data to the global node for model aggregation, and the global node sends the aggregated global model weight of and back to the AeBSs, then each AeBS updates its own model.
- 2.
- MADCO: MADCO optimizes the AeBS deployment schemes and offloading strategies by training two neural networks together to minimize the latency and energy consumption of computational task processing. Each AeBS exchanges action and state information with each other when making decisions. Its settings for the input/output, parameters, and DNN structure are consistent with FedDCO.
- 3.
- K-means: AeBSs are deployed based on the MD distribution through the K-means algorithm. The number of clusters of K-means was set as the number of AeBSs, and then, each AeBS is deployed directly above each cluster center of MDs. Specifically, the maximum number of iterations of K-means was 300, and if the sum of squares within all clusters between two iterations is less than 1 × 10, the iteration is terminated. After the location of AeBSs is fixed, the offloading policy is generated through the -network, whose input/output settings, parameter settings, and network structure are the same as in FedDCO.
- 4.
- Throughput-first: AeBSs are first deployed based on the -network with the goal of maximizing throughput, and the offloading policy is later generated through the -network. The settings of the input/output, parameters. and DNN structure in throughput-first are also consistent with FedDCO.
- 1.
- General communication scenario: In this scenario, we regarded delay and energy consumption as equally important indicators. Thus, we set in the simulation.
- 2.
- Delay-sensitive scenario: There may be some real-time services in the network, which makes the MDs sensitive to delay. For this scenario, we set in the simulation.
- 3.
- Energy-sensitive scenario: For some aerial platforms with limited payload capacity, such as small multi-rotor unmanned aerial vehicles, the battery capacity is limited, so it is necessary to reduce the energy consumption as much as possible to ensure the completion of the mission. For this scenario, we set in the simulation.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MEC | Mobile edge computing |
| HAP | High altitude platform |
| AeBS | Aerial base station |
| MD | Mobile device |
| FL | Federated learning |
| RL | Reinforcement learning |
| DRL | Deep reinforcement learning |
| DQN | Deep Q-network |
| DDPG | Deep deterministic policy gradient |
| MADRL | Multi-agent deep reinforcement learning |
| LOS | Line-of-sight |
References
- Ji, B.; Wang, Y.; Song, K.; Li, C.; Wen, H.; Menon, V.G.; Mumtaz, S. A Survey of Computational Intelligence for 6G: Key Technologies, Applications and Trends. IEEE Trans. Ind. Informatics 2021, 17, 7145–7154. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, J.; Geng, Y.; Xiao, Z.; Sun, T.; Zhang, N.; Liu, J.; Wu, Q.; Cao, X. Space-air-ground integrated network (SAGIN) for 6G: Requirements, architecture and challenges. China Commun. 2022, 19, 90–108. [Google Scholar] [CrossRef]
- Pham, Q.V.; Ruby, R.; Fang, F.; Nguyen, D.C.; Yang, Z.; Le, M.; Ding, Z.; Hwang, W.J. Aerial Computing: A New Computing Paradigm, Applications, and Challenges. IEEE Internet Things J. 2022, 9, 8339–8363. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, T.; Liu, Y.; Yang, D.; Xiao, L.; Tao, M. UAV-Assisted MEC Networks With Aerial and Ground Cooperation. IEEE Trans. Wirel. Commun. 2021, 20, 7712–7727. [Google Scholar] [CrossRef]
- Shakeri, R.; Al-Garadi, M.A.; Badawy, A.; Mohamed, A.; Khattab, T.; Al-Ali, A.K.; Harras, K.A.; Guizani, M. Design Challenges of Multi-UAV Systems in Cyber-Physical Applications: A Comprehensive Survey and Future Directions. IEEE Commun. Surv. Tutorials 2019, 21, 3340–3385. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, X.; Li, E.; Zeng, L.; Luo, K.; Zhang, J. Edge Intelligence: Paving the Last Mile of Artificial Intelligence With Edge Computing. Proc. IEEE 2019, 107, 1738–1762. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, M.; Yang, J.; Zhang, Q.; Zhang, X. Improvement of Generalization Ability of Deep CNN via Implicit Regularization in Two-Stage Training Process. IEEE Access 2018, 6, 15844–15869. [Google Scholar] [CrossRef]
- You, L.; Jiang, H.; Hu, J.; Chang, C.H.; Chen, L.; Cui, X.; Zhao, M. GPU-accelerated Faster Mean Shift with euclidean distance metrics. In Proceedings of the 2022 IEEE 46th Annual Computers, Software, and Applications Conference (COMPSAC), Alamitos, CA, USA, 27 June–1 July 2022; pp. 211–216. [Google Scholar] [CrossRef]
- Zhao, M.; Chang, C.H.; Xie, W.; Xie, Z.; Hu, J. Cloud Shape Classification System Based on Multi-Channel CNN and Improved FDM. IEEE Access 2020, 8, 44111–44124. [Google Scholar] [CrossRef]
- Jin, B.; Cruz, L.; Gonçalves, N. Pseudo RGB-D Face Recognition. IEEE Sensors J. 2022. [Google Scholar] [CrossRef]
- Arshad, M.A.; Khan, S.H.; Qamar, S.; Khan, M.W.; Murtza, I.; Gwak, J.; Khan, A. Drone Navigation Using Region and Edge Exploitation-Based Deep CNN. IEEE Access 2022, 10, 95441–95450. [Google Scholar] [CrossRef]
- Liang, F.; Yu, W.; Liu, X.; Griffith, D.; Golmie, N. Toward Edge-Based Deep Learning in Industrial Internet of Things. IEEE Internet Things J. 2020, 7, 4329–4341. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, F.; Li, W.; Gao, Y.; Feng, L.; Yu, P. 3D Deployment and User Association of CoMP-assisted Multiple Aerial Base Stations for Wireless Network Capacity Enhancement. In Proceedings of the 2021 17th International Conference on Network and Service Management (CNSM), Izmir, Turkey, 25–29 October 2021; pp. 56–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Mou, Z.; Gao, F.; Jiang, J.; Ding, R.; Han, Z. UAV-Enabled Secure Communications by Multi-Agent Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2020, 69, 11599–11611. [Google Scholar] [CrossRef]
- Xu, Y.; Bhuiyan, M.Z.A.; Wang, T.; Zhou, X.; Singh, A. C-fDRL: Context-Aware Privacy-Preserving Offloading through Federated Deep Reinforcement Learning in Cloud-Enabled IoT. IEEE Trans. Ind. Inform. 2022. [Google Scholar] [CrossRef]
- Yang, W.; Xiang, W.; Yang, Y.; Cheng, P. Optimizing Federated Learning With Deep Reinforcement Learning for Digital Twin Empowered Industrial IoT. IEEE Trans. Ind. Inform. 2022. [Google Scholar] [CrossRef]
- Tehrani, P.; Restuccia, F.; Levorato, M. Federated Deep Reinforcement Learning for the Distributed Control of NextG Wireless Networks. In Proceedings of the 2021 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Los Angeles, CA, USA, 13–15 December 2021; pp. 248–253. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, M.; Yan, S.; Sun, Y. Deep-Reinforcement-Learning-Based Mode Selection and Resource Allocation for Cellular V2X Communications. IEEE Internet Things J. 2020, 7, 6380–6391. [Google Scholar] [CrossRef]
- Jia, Z.; Wu, Q.; Dong, C.; Yuen, C.; Han, Z. Hierarchical Aerial Computing for Internet of Things via Cooperation of HAPs and UAVs. IEEE Internet Things J. 2022. [Google Scholar] [CrossRef]
- Jeong, S.; Simeone, O.; Kang, J. Mobile Edge Computing via a UAV-Mounted Cloudlet: Optimization of Bit Allocation and Path Planning. IEEE Trans. Veh. Technol. 2018, 67, 2049–2063. [Google Scholar] [CrossRef]
- Truong, T.P.; Tran, A.T.; Nguyen, T.M.T.; Nguyen, T.V.; Masood, A.; Cho, S. MEC-Enhanced Aerial Serving Networks via HAP: A Deep Reinforcement Learning Approach. In Proceedings of the 2022 International Conference on Information Networking (ICOIN), Jeju-si, Korea, 12–15 January 2022; pp. 319–323. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Sun, H.; Chu, Z. UAV-Enabled Mobile Edge Computing: Offloading Optimization and Trajectory Design. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, L.; Feng, X.; Feng, A.; Huang, Y.; Qian, L.P. Distributed Deep Learning-based Offloading for Mobile Edge Computing Networks. Mob. Netw. Appl. 2022, 27, 1123–1130. [Google Scholar] [CrossRef]
- Yang, B.; Cao, X.; Yuen, C.; Qian, L. Offloading Optimization in Edge Computing for Deep-Learning-Enabled Target Tracking by Internet of UAVs. IEEE Internet Things J. 2021, 8, 9878–9893. [Google Scholar] [CrossRef]
- Min, M.; Xiao, L.; Chen, Y.; Cheng, P.; Wu, D.; Zhuang, W. Learning-Based Computation Offloading for IoT Devices With Energy Harvesting. IEEE Trans. Veh. Technol. 2019, 68, 1930–1941. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wu, C.; Mao, S.; Ji, Y.; Bennis, M. Optimized Computation Offloading Performance in Virtual Edge Computing Systems Via Deep Reinforcement Learning. IEEE Internet Things J. 2019, 6, 4005–4018. [Google Scholar] [CrossRef]
- Yang, L.; Yao, H.; Wang, J.; Jiang, C.; Benslimane, A.; Liu, Y. Multi-UAV-Enabled Load-Balance Mobile-Edge Computing for IoT Networks. IEEE Internet Things J. 2020, 7, 6898–6908. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q.; Wu, P.; Shu, F.; Jin, S. Task Offloading for UAV-based Mobile Edge Computing via Deep Reinforcement Learning. In Proceedings of the 2018 IEEE/CIC International Conference on Communications in China (ICCC), Beijing, China, 16–18 August 2018; pp. 798–802. [Google Scholar] [CrossRef]
- Wang, L.; Huang, P.; Wang, K.; Zhang, G.; Zhang, L.; Aslam, N.; Yang, K. RL-Based User Association and Resource Allocation for Multi-UAV enabled MEC. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 741–746. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Z.; Guo, S. Multi-Agent Imitation Learning for Pervasive Edge Computing: A Decentralized Computation Offloading Algorithm. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 411–425. [Google Scholar] [CrossRef]
- Wang, Z.; Rong, H.; Jiang, H.; Xiao, Z.; Zeng, F. A Load-Balanced and Energy-Efficient Navigation Scheme for UAV-Mounted Mobile Edge Computing. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3659–3674. [Google Scholar] [CrossRef]
- Wang, L.; Wang, K.; Pan, C.; Xu, W.; Aslam, N.; Hanzo, L. Multi-Agent Deep Reinforcement Learning-Based Trajectory Planning for Multi-UAV Assisted Mobile Edge Computing. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 73–84. [Google Scholar] [CrossRef]
- Waqar, N.; Hassan, S.A.; Mahmood, A.; Dev, K.; Do, D.T.; Gidlund, M. Computation Offloading and Resource Allocation in MEC-Enabled Integrated Aerial-Terrestrial Vehicular Networks: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2022. [Google Scholar] [CrossRef]
- Nie, Y.; Zhao, J.; Gao, F.; Yu, F.R. Semi-Distributed Resource Management in UAV-Aided MEC Systems: A Multi-Agent Federated Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2021, 70, 13162–13173. [Google Scholar] [CrossRef]
- Zhu, Z.; Wan, S.; Fan, P.; Letaief, K.B. An Edge Federated MARL Approach for Timeliness Maintenance in MEC Collaboration. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, Z.; Wan, S.; Fan, P.; Letaief, K.B. Federated Multiagent Actor–Critic Learning for Age Sensitive Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 1053–1067. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Li, X.; Leung, V.; Taleb, T. Federated Deep Reinforcement Learning for Internet of Things with Decentralized Cooperative Edge Caching. IEEE Internet Things J. 2020, 7, 9441–9455. [Google Scholar] [CrossRef]
- Majidi, F.; Khayyambashi, M.R.; Barekatain, B. HFDRL: An Intelligent Dynamic Cooperate Cashing Method Based on Hierarchical Federated Deep Reinforcement Learning in Edge-Enabled IoT. IEEE Internet Things J. 2022, 9, 1402–1413. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutorials 2017, 19, 2322–2358. [Google Scholar] [CrossRef]
- Huang, L.; Bi, S.; Zhang, Y.J.A. Deep Reinforcement Learning for Online Computation Offloading in Wireless Powered Mobile-Edge Computing Networks. IEEE Trans. Mob. Comput. 2020, 19, 2581–2593. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, F.; Feng, L.; Wu, Z. MARL-Based Joint Computation Offloading and Aerial Base Stations Deployment in MEC Systems. In Proceedings of the 2022 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Bilbao, Spain, 15–17 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Dai, B.; Niu, J.; Ren, T.; Hu, Z.; Atiquzzaman, M. Towards Energy-Efficient Scheduling of UAV and Base Station Hybrid Enabled Mobile Edge Computing. IEEE Trans. Veh. Technol. 2022, 71, 915–930. [Google Scholar] [CrossRef]


| Reference | Optimization Goal | Offloading | Deployment | Method |
|---|---|---|---|---|
| [4] | Maximize the weighted computational efficiency of the system | Proportional | ✔ | Alternative computational efficiency maximization |
| [19] | Maximize the total IoT data computed by the aerial MEC platforms | Binary | / | Matching game-theory-based algorithm and a heuristic algorithm |
| [20] | Minimize the total energy consumption | / | ✔ | Successive convex approximation (SCA) |
| [21] | Minimize the total cost function of the system | Proportional | / | Deep deterministic policy gradient (DDPG) |
| [22] | Minimize the energy consumed at the AeBS | Binary | ✔ | Alternative optimization |
| [23] | Minimize overall system utility including both the total energy consumption and the delay in finishing the task | Binary | ✔ | DNN |
| [24] | Minimize the delay and energy consumption, while considering the data quality input into the DNN and inference error | Binary and proportional | / | CNN |
| [25] | Optimal offloading policy | Proportional | / | Fast deep-Q-network (DQN) |
| [26] | Maximize the long-term utility performance | Binary | / | Double DQN |
| [27] | Average slowdown for offloaded tasks | One-to-one correspondence | ✔ | DQN |
| [28] | Maximize the migration throughput of user tasks | Binary | / | DQN |
| [29] | Maximize the average throughput of user tasks | Binary | ✔ | Q-learning |
| [30] | Minimize average task completion time | Binary | / | Multi-agent imitation learning |
| [31] | Minimize the total energy consumption of AeBSs | Binary | ✔ | Multi-agent deep deterministic policy gradient (MADDPG) |
| [32] | Maximize the fairness among all the user equipment (UE) and the fairness of the UE load of each AeBS | Binary | ✔ | MADDPG |
| [33] | Minimize the total computation and communication overhead of the joint computation offloading and resource allocation strategies | Binary | / | Multi-agent double-deep Q-learning |
| [34] | Minimize the overall consumed power | Binary | / | Federated DQN |
| [35] | Minimize the average source age (elapsed time) | Binary | ✔ | Federated multi-agent actor–critic |
| [36] | Minimize the average age of all data sources | Binary | ✔ | Federated multi-agent actor–critic |
| [37] | Maximize the expected long-term reward | Three-way | ✔ | Federated DQN |
| [38] | Improve the hit rate | Binary | / | Federated DQN |
| Our work | Jointly minimize overall task latency and energy consumption | Binary | ✔ | Federated DQN |
| Simulation Parameters | Values |
|---|---|
| AeBS altitude H | 100 m |
| Transmit power | 0.5 W |
| Channel bandwidth B | 1 MHz |
| Reference channel gain | 10,096 |
| Energy efficiency parameter | 2 |
| Noise | W |
| in -greedy | 0.1 |
| Memory size | 10,000 |
| Batch size | 512 |
| Discount factor | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhao, Y.; Qi, F.; Zhou, F.; Xie, W.; He, H.; Zheng, H. Federated Deep Reinforcement Learning for Joint AeBSs Deployment and Computation Offloading in Aerial Edge Computing Network. Electronics 2022, 11, 3641. https://doi.org/10.3390/electronics11213641
Liu L, Zhao Y, Qi F, Zhou F, Xie W, He H, Zheng H. Federated Deep Reinforcement Learning for Joint AeBSs Deployment and Computation Offloading in Aerial Edge Computing Network. Electronics. 2022; 11(21):3641. https://doi.org/10.3390/electronics11213641
Chicago/Turabian StyleLiu, Lei, Yikun Zhao, Fei Qi, Fanqin Zhou, Weiliang Xie, Haoran He, and Hao Zheng. 2022. "Federated Deep Reinforcement Learning for Joint AeBSs Deployment and Computation Offloading in Aerial Edge Computing Network" Electronics 11, no. 21: 3641. https://doi.org/10.3390/electronics11213641
APA StyleLiu, L., Zhao, Y., Qi, F., Zhou, F., Xie, W., He, H., & Zheng, H. (2022). Federated Deep Reinforcement Learning for Joint AeBSs Deployment and Computation Offloading in Aerial Edge Computing Network. Electronics, 11(21), 3641. https://doi.org/10.3390/electronics11213641








