ELAA Channel Characterization with Parameter Estimation Based on a Generalized Array Manifold Model
Abstract
1. Introduction
- The channel parameters for ELAAs are estimated by the GAM-SAGE. The performance of the GAM-SAGE is evaluated by the measurement data, showing that it outperforms the SP-SAGE, especially in reproducing the spatial consistency.
- Measurement-based stochastic channel models, namely SBCMs for LoS and NLoS corridors, were proposed. The proposed models are capable of reproducing the spatial non-stationarity and consistency effectively in the ELAA channel; hence, this property leads to the better scalability of these models. Moreover, two established models reveal important characteristics of the millimeter-wave ELAA channels.
2. GAM-Based Signal Model
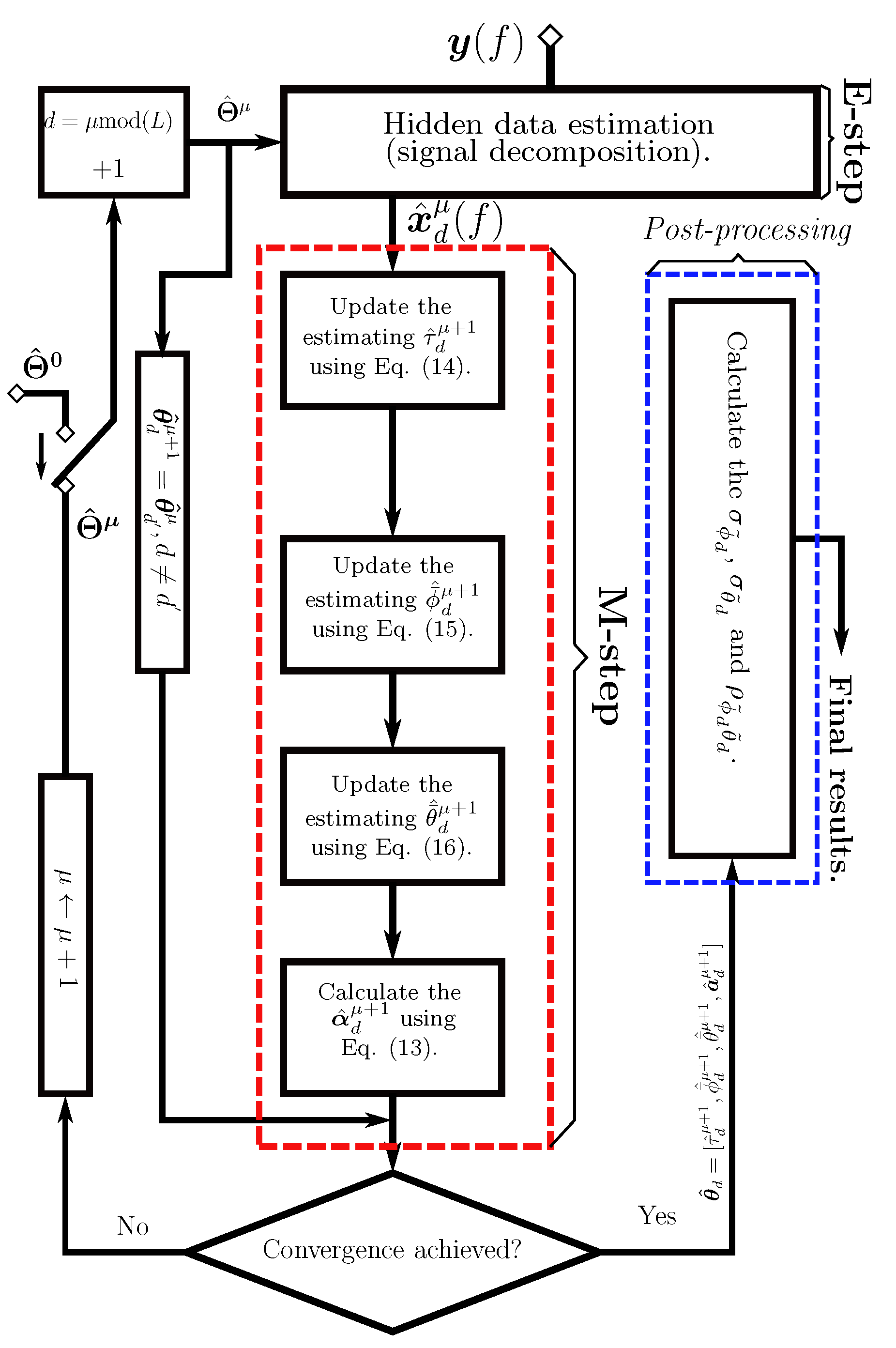
3. Generalized Array-Manifold Space-Alternating Generalized Expectation-Maximization
Maximum Likelihood Estimator
- The slight deviations of the azimuth and elevation , , , are independent and identical Gaussian distributions with a zero mean. The azimuths and elevations of sub-paths are concentrated, with a high probability around the nominal AoA and EoA , respectively.
- The weight processes are independent and identically complex, circularly symmetric, wide-sense, stationary processes, and these weights have zero mean and equal variance.
- The total number of sub-paths L is large.
- Any two random elements in the set consisting of the azimuth and elevation deviations as well as the sub-path weights are independent.
| Algorithm 1:Proposed GAM-SAGE after initialization () |
 |
4. Channel Measurement Campaigns
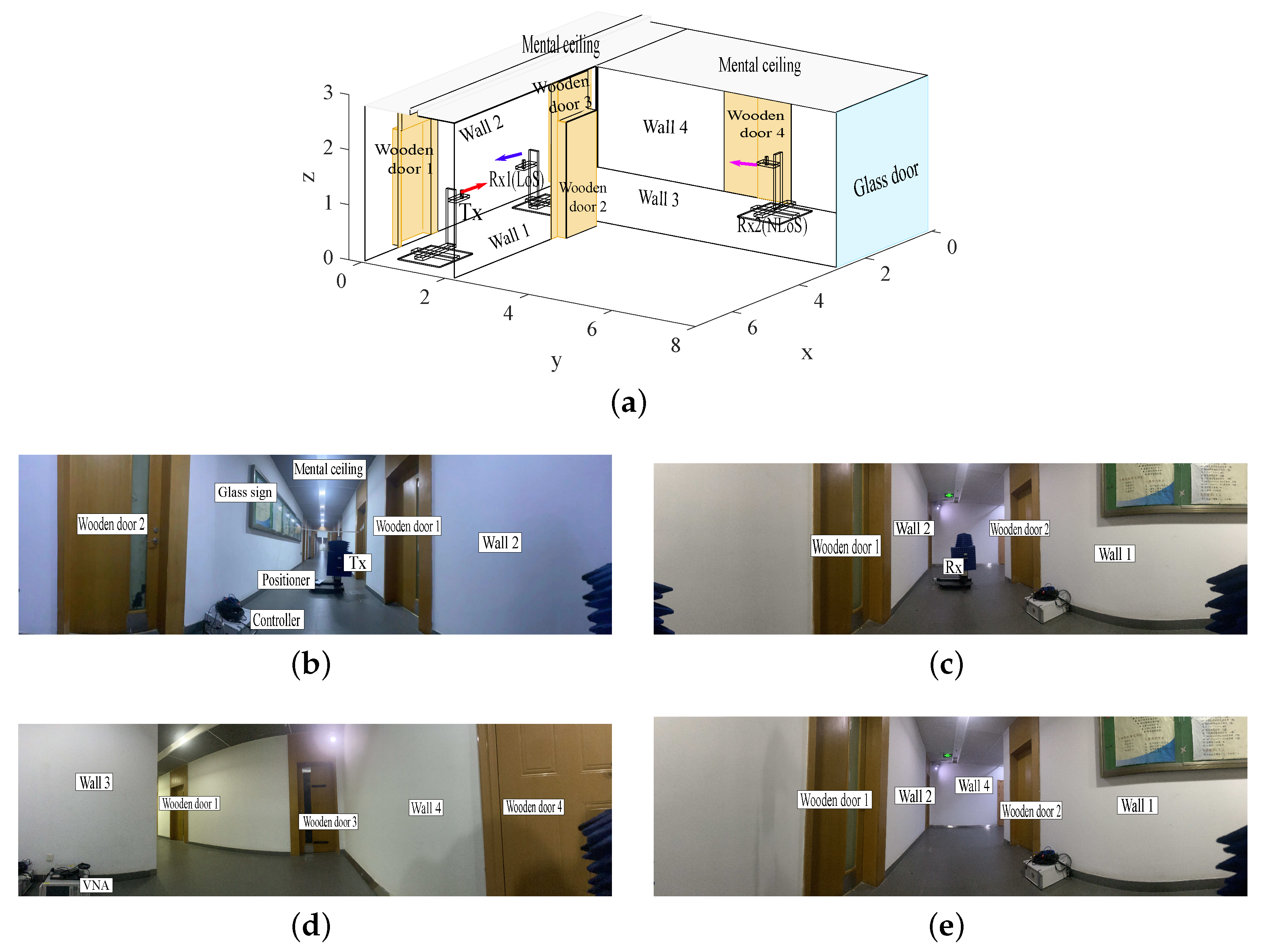
4.1. Measurement Environments
4.2. Measurement Setup
5. Performance Evaluation of the GAM-SAGE Using the Measurements
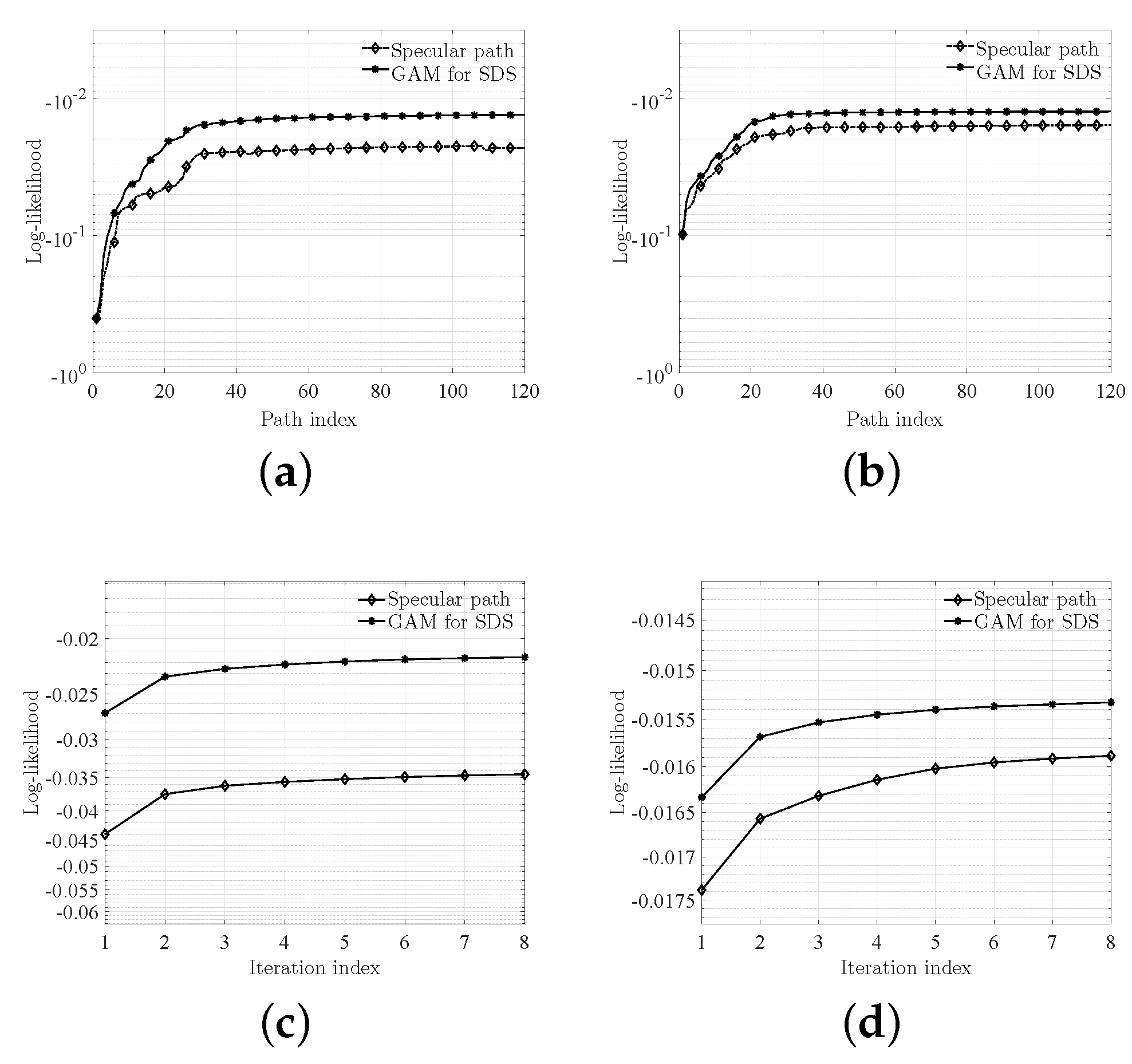
5.1. Performance of the GAM-SAGE and SP-SAGE
5.2. The Results Estimated by GAM-SAGE
6. Stochastic SBCM Establishment
6.1. Modeling Procedure for the SBCM
- GAM adopted in channel parameter estimation: One major difference between SBCM modeling and SCM/SCME modeling is that the HRPE algorithm integrated in the GAM model is applied in the former, whereas the SP model is considered for the latter. Consequently, the parameter set for an MPC in the SP model is extended to the . Thus, GAM can be used to describe the scattering generated by the SDSs, and the results illustrate that the GAM-SAGE outperforms the SP-SAGE in fitting the ELAA channel response and reproducing the spatial consistency.
- The shape of SDS included in the SBCM: As the shape and spreading of SDS can be naturally obtained with the parameter set , the shapes, spreading in angular domain, and the number of the SDSs become new elements in addition to the traditional geometrical parameters considered by the SCM. The benefits of including these characteristics into the model are: (1) they allow the dispersion in the angular domain, and (2) spatially consistent properties of the channel are reasonably generated, especially in the case of the ELAAs. Moreover, due to the application of the new definition of the SDS, the clustering step of the SCM/SCME can be omitted.
- Generating the dominant SDS: The dominant SDS can be generated using the dominant SDS parameters modeled in the SBCM. As the dominant SDS is a reference for generating the NLoS SDSs (by using inter-SDS parameter offsets, as indicated in Section 6.4), some parameters of the dominant SDS, such as the nominal AoA, nominal EoA, and delay, should be included in the model.
- Generating the NLoS SDSs: The inter-SDS offsets are used to generate the delay, nominal AoA, and nominal EoA. Then, the intra-SDS spreads and the correlation coefficients are applied in order to reproduce the shape of the SDS. The power of the SDSs can be allocated by the inter-SDS power offsets. It is worth noting that the power allocation must satisfy the K-factor.
- Generating the overall channel response: The overall channel response can be obtained by the summation of the responses reconstructed using the NLoS and LoS SDSs.
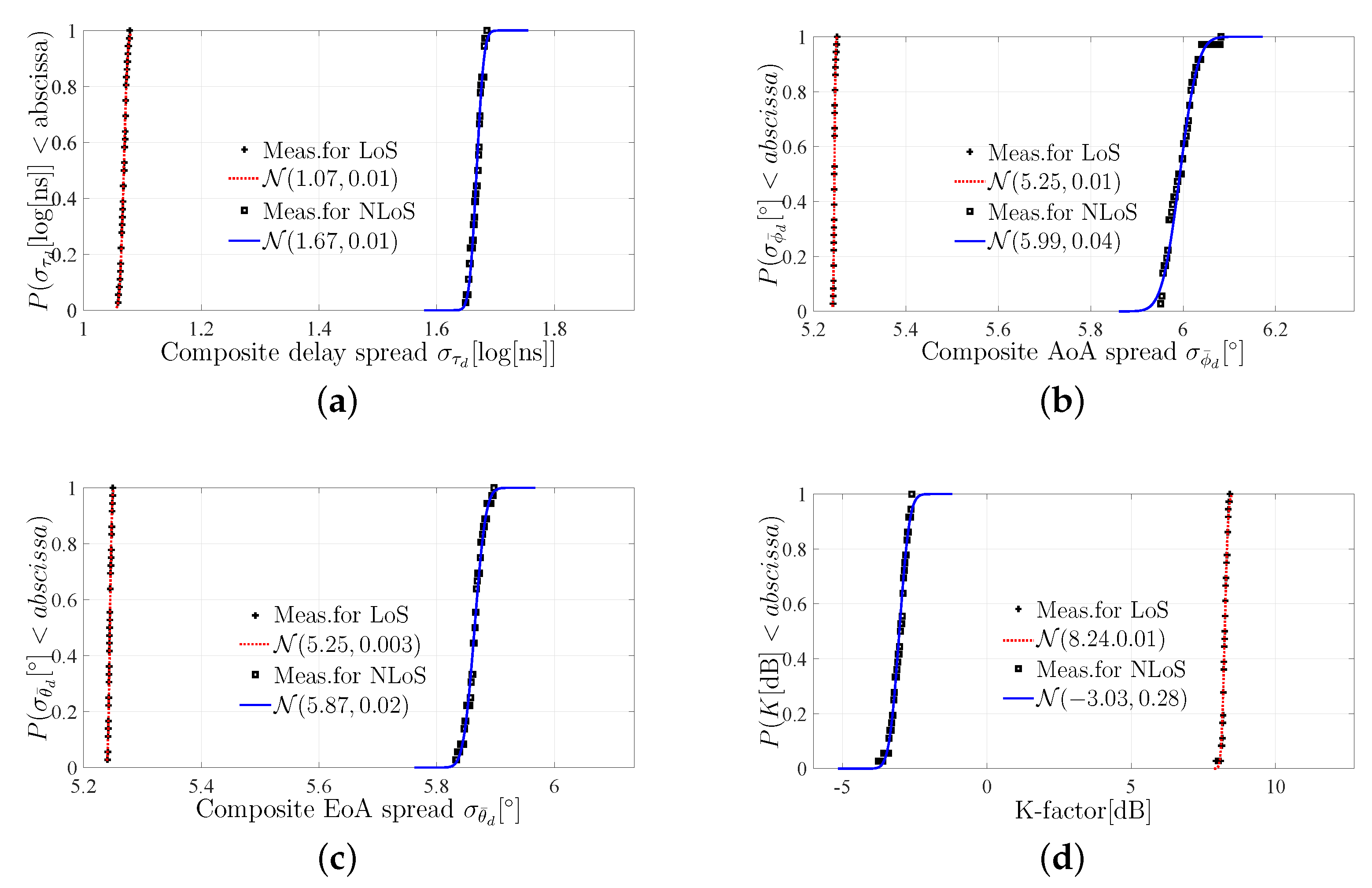
6.2. Composite Delay, AoA, EoA Spreads, and the K-factor
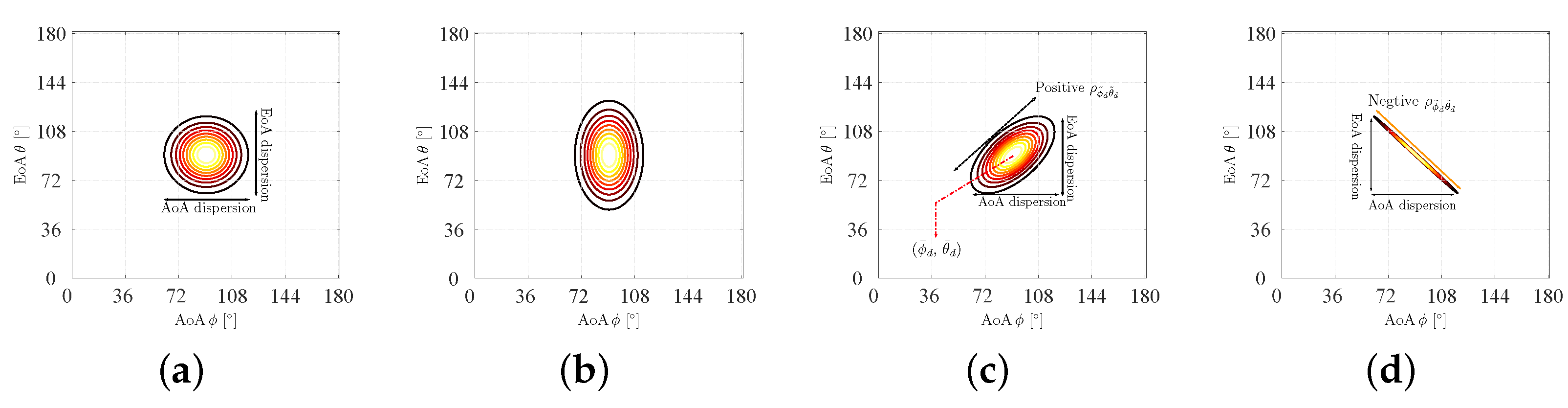
6.3. Intra-Cluster AoA, EoA Spread, and the Correlation Coefficient between Slight Deviations of AoA and EoA
6.4. Inter-SDS AoA, EoA, and Power Offsets
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.X.; Huang, J.; Wang, H.; Gao, X. A General 3D Space-Time-Frequency Non-Stationary THz Channel Model for 6G Ultra-Massive MIMO Wireless Communication Systems. IEEE J. Sel. Areas Commun. 2021, 39, 1576–1589. [Google Scholar] [CrossRef]
- Xiao, M.; Mumtaz, S.; Huang, Y.; Dai, L.; Li, Y.; Matthaiou, M.; Karagiannidis, G.K.; Björnson, E.; Yang, K.; Chih-Lin, I.; et al. Millimeter Wave Communications for Future Mobile Networks. IEEE J. Sel. Areas Commun. 2017, 35, 1909–1935. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Zhong, Z.; Yang, M. A Non-Stationary Geometry-Based MIMO Channel Model for Millimeter-Wave UAV Networks. IEEE J. Sel. Areas Commun. 2021, 39, 2960–2974. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Wang, W.Q.; Zheng, Z. Hybrid MIMO and Phased-Array Directional Modulation for Physical Layer Security in mmWave Wireless Communications. IEEE J. Sel. Areas Commun. 2018, 36, 1383–1396. [Google Scholar] [CrossRef]
- Haneda, K.; Khatun, A.; Dashti, M.; Laitinen, T.A.; Kolmonen, V.; Takada, J.; Vainikainen, P. Measurement-Based Analysis of Spatial Degrees of Freedom in Multipath Propagation Channels. IEEE Trans. Antennas Propag. 2013, 61, 890–900. [Google Scholar] [CrossRef]
- Haneda, K.; Omaki, N.; Imai, T.; Raschkowski, L.; Peter, M.; Roivainen, A. Frequency-Agile Pathloss Models for Urban Street Canyons. IEEE Trans. Antennas Propag. 2016, 64, 1941–1951. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO Communications With MIMO Radar: From Co-Existence to Joint Transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- Ni, W.; Dong, X. Hybrid Block Diagonalization for Massive Multiuser MIMO Systems. IEEE Trans. Commun. 2016, 64, 201–211. [Google Scholar] [CrossRef]
- Yin, X.; Ouyang, L.; Wang, H. Performance Comparison of SAGE and MUSIC for Channel Estimation in Direction-Scan Measurements. IEEE Access 2016, 4, 1163–1174. [Google Scholar] [CrossRef]
- Li, J.; Ai, B.; He, R.; Yang, M.; Wang, Q.; Zhang, B.; Zhong, Z. Cluster-Based 3-D Channel Modeling for Massive MIMO in Subway Station Environment. IEEE Access 2018, 6, 6257–6272. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Wang, G.; Niu, Y.; Yang, M.; Wang, J.; Li, Y.; Zhong, Z. Impact of UAV Rotation on MIMO Channel Characterization for Air-to-Ground Communication Systems. IEEE Trans. Veh. Technol. 2020, 69, 12418–12431. [Google Scholar] [CrossRef]
- Fleury, B. First- and second-order characterization of direction dispersion and space selectivity in the radio channel. IEEE Trans. Inf. Theory 2000, 46, 2027–2044. [Google Scholar] [CrossRef]
- Besson, O.; Stoica, P. Decoupled estimation of DOA and angular spread for a spatially distributed source. IEEE Trans. Signal Process. 2000, 48, 1872–1882. [Google Scholar] [CrossRef]
- Alshammari, A.; Albdran, S.; Ahad, M.A.R.; Matin, M. Impact of angular spread on massive MIMO channel estimation. In Proceedings of the 2016 19th International Conference on Computer and Information Technology (ICCIT), Shenzhen, China, 18–19 April 2016; pp. 84–87. [Google Scholar] [CrossRef]
- Han, Y.; Wang, J.; Song, X.; Zhang, Y. Joint Estimation of the Central Direction of Arrival and Angular Spread for Distributed Source Based on Beamspace Propagator. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 1, pp. 1693–1696. [Google Scholar] [CrossRef]
- Iwase, S.; Kikuma, N.; Sakakibara, K. Angular Spread Estimation of MIMO Radar Using Transmission Beam Diversity. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Nagoya, Japan, 29–31 August 2018; p. 1. [Google Scholar] [CrossRef]
- Asztely, D.; Ottersten, B. The effects of local scattering on direction of arrival estimation with MUSIC and ESPRIT. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP ’98 (Cat. No.98CH36181), Seattle, DC, USA, 12–15 May 1998; Volume 6, pp. 3333–3336. [Google Scholar] [CrossRef]
- Fleury, B.H.; Tschudin, M.; Heddergott, R.; Dahlhaus, D.; Ingeman Pedersen, K. Channel parameter estimation in mobile radio environments using the SAGE algorithm. IEEE J. Sel. Areas Commun. 1999, 17, 434–450. [Google Scholar] [CrossRef]
- Richter, A. On the Estimation of Radio Channel Parameters: Models and Algorithms (RIMAX); Dissertation: ISLE Blacksburg, VA, USA, 2005. [Google Scholar]
- Shutin, D.; Fleury, B.H. Sparse Variational Bayesian SAGE Algorithm With Application to the Estimation of Multipath Wireless Channels. IEEE Trans. Signal Process. 2011, 59, 3609–3623. [Google Scholar] [CrossRef]
- Chong, C.; Laurenson, D.; Tan, C.; McLaughlin, S.; Beach, M.; Nix, A. Joint detection-estimation of directional channel parameters using the 2-D frequency domain SAGE algorithm with serial interference cancellation. In Proceedings of the 2002 IEEE International Conference on Communications. Conference Proceedings, ICC 2002 (Cat. No.02CH37333), New York, NY, USA, 28 April–2 May 2002; Volume 2, pp. 906–910. [Google Scholar] [CrossRef]
- Noschese, M.; Babich, F.; Comisso, M.; Marshall, C. Multi-Band Time of Arrival Estimation for Long Term Evolution (LTE) Signals. IEEE Trans. Mob. Comput. 2021, 20, 3383–3394. [Google Scholar] [CrossRef]
- Ji, Y.; Hejselbæk, J.; Fan, W.; Pedersen, G.F. A Map-Free Indoor Localization Method Using Ultrawideband Large-Scale Array Systems. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1682–1686. [Google Scholar] [CrossRef]
- Ji, Y.; Fan, W.; Pedersen, G.F. Channel Characterization for Wideband Large-Scale Antenna Systems Based on a Low-Complexity Maximum Likelihood Estimator. IEEE Trans. Wirel. Commun. 2018, 17, 6018–6028. [Google Scholar] [CrossRef]
- Zhang, N.; Yin, X.; Tian, L.; Duan, W.; Boqué, S.R. Performance evaluation of interference cancellation using a generalized-array-manifold model. In Proceedings of the 2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014; pp. 670–675. [Google Scholar] [CrossRef]
- Universal Mobile Telecommunications System (UMTS); Spatial Channel Model for Multiple Input Multiple Output (MIMO) Simulations (V16.0.0; 3GPP TR 25.996 Version 16.0.0 Release 16); European Telecommunications Standards Institute: Headquarters, French, 2010.
- Meinilä, J.; Kyösti, P.; Jämsä, T.; Hentilä, L. WINNER II Channel Models. In Radio Technologies and Concepts for IMT-Advanced; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Liu, L.; Oestges, C.; Poutanen, J.; Haneda, K.; Vainikainen, P.; Quitin, F.; Tufvesson, F.; Doncker, P.D. The COST 2100 MIMO channel model. IEEE Wirel. Commun. 2012, 19, 92–99. [Google Scholar] [CrossRef]
- Zhu, M.; Eriksson, G.; Tufvesson, F. The COST 2100 Channel Model: Parameterization and Validation Based on Outdoor MIMO Measurements at 300 MHz. IEEE Trans. Wirel. Commun. 2013, 12, 888–897. [Google Scholar] [CrossRef]
- Carton, I.; Fan, W.; Kyösti, P.; Pedersen, G.F. Validation of 5G METIS map-based channel model at mmwave bands in indoor scenarios. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Kim, J.G.; Lim, J.T. MAP-Based Channel Estimation for MIMO–OFDM Over Fast Rayleigh Fading Channels. IEEE Trans. Veh. Technol. 2008, 57, 1963–1968. [Google Scholar] [CrossRef]
- Yin, X.; Wang, S.; Zhang, N.; Ai, B. Scatterer Localization Using Large-Scale Antenna Arrays Based on a Spherical Wave-Front Parametric Model. IEEE Trans. Wirel. Commun. 2017, 16, 6543–6556. [Google Scholar] [CrossRef]
- Yin, X.; Cheng, X. Measurement-based Statistical Channel Modeling. In Propagation Channel Characterization, Parameter Estimation, and Modeling for Wireless Communications; Wiley: Hoboken, NJ, USA, 2016; pp. 236–259. [Google Scholar] [CrossRef]
- Yin, X.; Ling, C.; Kim, M.D. Experimental Multipath-Cluster Characteristics of 28-GHz Propagation Channel. IEEE Access 2015, 3, 3138–3150. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, G.; Zhang, C.; Fan, W.; Li, J.; Pedersen, G.F. Dynamic Channel Modeling for Indoor Millimeter-Wave Propagation Channels Based on Measurements. IEEE Trans. Commun. 2020, 68, 5878–5891. [Google Scholar] [CrossRef]
- Study on Channel Model for Frequencies From 0.5 to 100 GHz; document 3GPP TR 38.901 V17.0.0; ETSI: Sophia Antipolis Cedex, France, 2022.


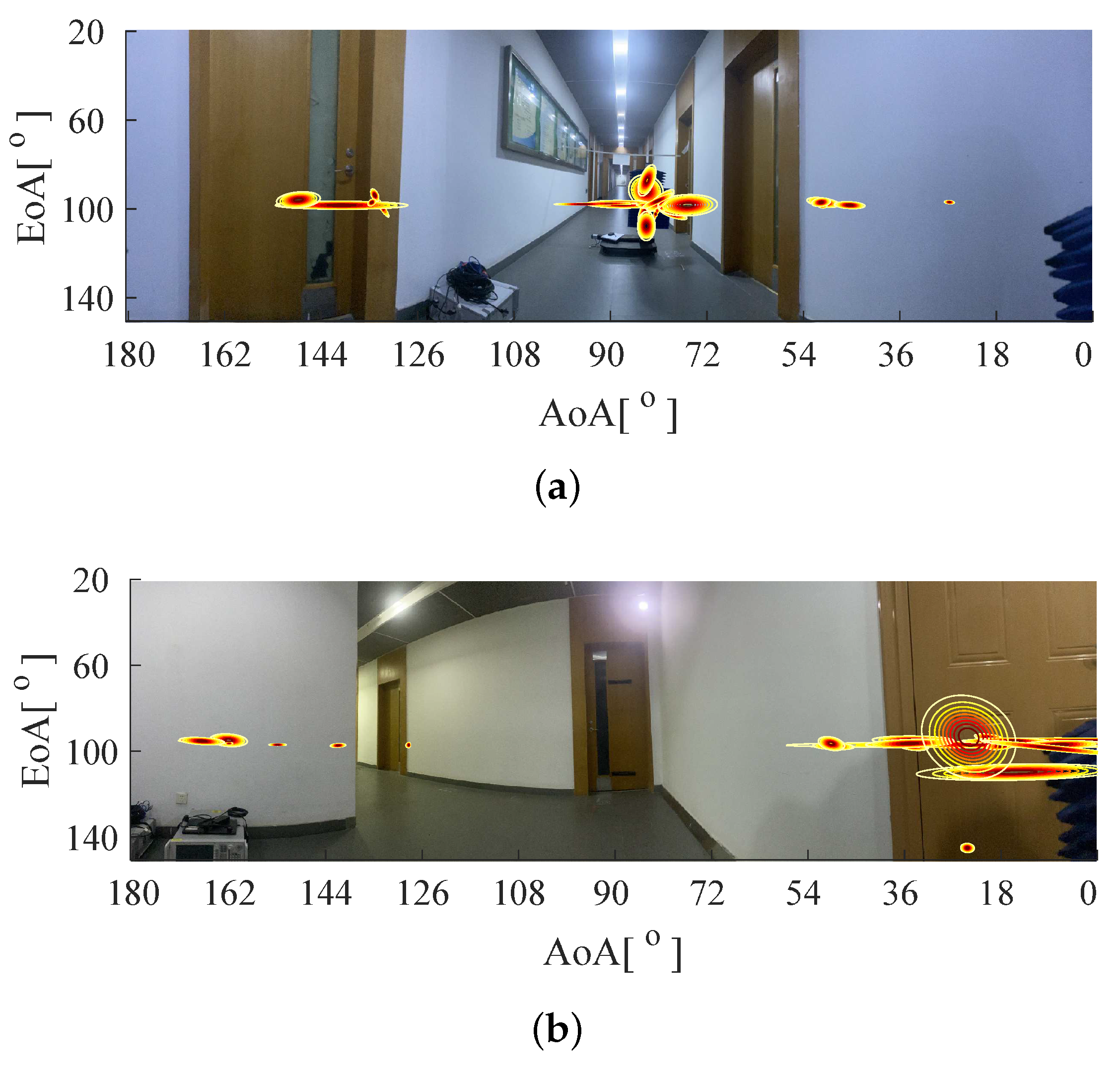


| Antenna Configuration | Measurement VNA Configuration | Virtual Array Configuration | |||
|---|---|---|---|---|---|
| Antenna type | Bi-conical | Frequency range (GHz) | 36–40 | Type of array | 2D planar array |
| Gain (dBi) | 4 | Frequency points | 1001 | Space Interval (mm) | 3.75 |
| Polarization | Vertical | Transmitted power (dBm) | 0 | Number of elements | |
| Model | SBCM | SCM/SCME | |||
|---|---|---|---|---|---|
| Category | |||||
| Composite-level characteristics | Delay spread, AoA spread, EoA spread, K-factor | ||||
|
Cluster-level characteristics | SDS number, correlation coefficient | Cluster number | |||
| Intra-SDS | spread, spread | Intra-cluster | spread, spread | ||
| Inter-SDS | offsets, offsets | Inter-cluster | offsets, offsets | ||
| Dominant component parameters | Delay, (nominal) , (nominal) , power | ||||
| Composite Channel Parameters | ||||||
|---|---|---|---|---|---|---|
| Scenarios | Distribution | LoS | NLoS | |||
| Parameters | ||||||
| Composite delay spread [] | Normal | 1.07 | 1.67 | |||
| 0.01 | 0.01 | |||||
| Composite AoA spread () | Normal | 5.25 | 5.59 | |||
| 0.01 | 0.04 | |||||
| Composite EoA spread () | Normal | 5.25 | 5.87 | |||
| 0.003 | 0.02 | |||||
| Number of SDSs | - | 20 | 35 | |||
| K-factor(dB) | Normal | 8.24 | −3.03 | |||
| 0.01 | 0.28 | |||||
| Cluster-level channel parameters | ||||||
| Intra-SDS AoA spread [] | Normal | −0.08 | 0.21 | |||
| 0.42 | 0.53 | |||||
| Intra-SDS EoA spread [] | Normal | 0 | −0.34 | |||
| 0.43 | 0.51 | |||||
| Correlation coefficient | Normal | 0.02 | 0.02 | |||
| 0.41 | 0.38 | |||||
| Inter-SDS delay offsets (ns) | - | 17.48 | 46.33 | |||
| 22.37 | 60.58 | |||||
| Inter-SDS AoA offsets () | - | 22.16 | 39.37 | |||
| 22.40 | 52.51 | |||||
| Inter-SDS EoA offsets () | - | 2.13 | 4.19 | |||
| 2.29 | 10.86 | |||||
| Inter-SDS power offsets (dB) | Normal | 32.78 | 9.04 | |||
| 16.84 | 7.59 | |||||
| Dominant-SDS parameters | - | (ns) | (ns) | |||
| (dB) | (dB) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, G.; Hong, J.; Yin, X.; Rodríguez-Piñeiro, J.; Yu, Z. ELAA Channel Characterization with Parameter Estimation Based on a Generalized Array Manifold Model. Electronics 2022, 11, 3442. https://doi.org/10.3390/electronics11213442
Jing G, Hong J, Yin X, Rodríguez-Piñeiro J, Yu Z. ELAA Channel Characterization with Parameter Estimation Based on a Generalized Array Manifold Model. Electronics. 2022; 11(21):3442. https://doi.org/10.3390/electronics11213442
Chicago/Turabian StyleJing, Guangzheng, Jingxiang Hong, Xuefeng Yin, José Rodríguez-Piñeiro, and Ziming Yu. 2022. "ELAA Channel Characterization with Parameter Estimation Based on a Generalized Array Manifold Model" Electronics 11, no. 21: 3442. https://doi.org/10.3390/electronics11213442
APA StyleJing, G., Hong, J., Yin, X., Rodríguez-Piñeiro, J., & Yu, Z. (2022). ELAA Channel Characterization with Parameter Estimation Based on a Generalized Array Manifold Model. Electronics, 11(21), 3442. https://doi.org/10.3390/electronics11213442






