Scalable Hardware Efficient Architecture for Parallel FIR Filters with Symmetric Coefficients
Abstract
:1. Introduction
2. Proposed STB-FIR
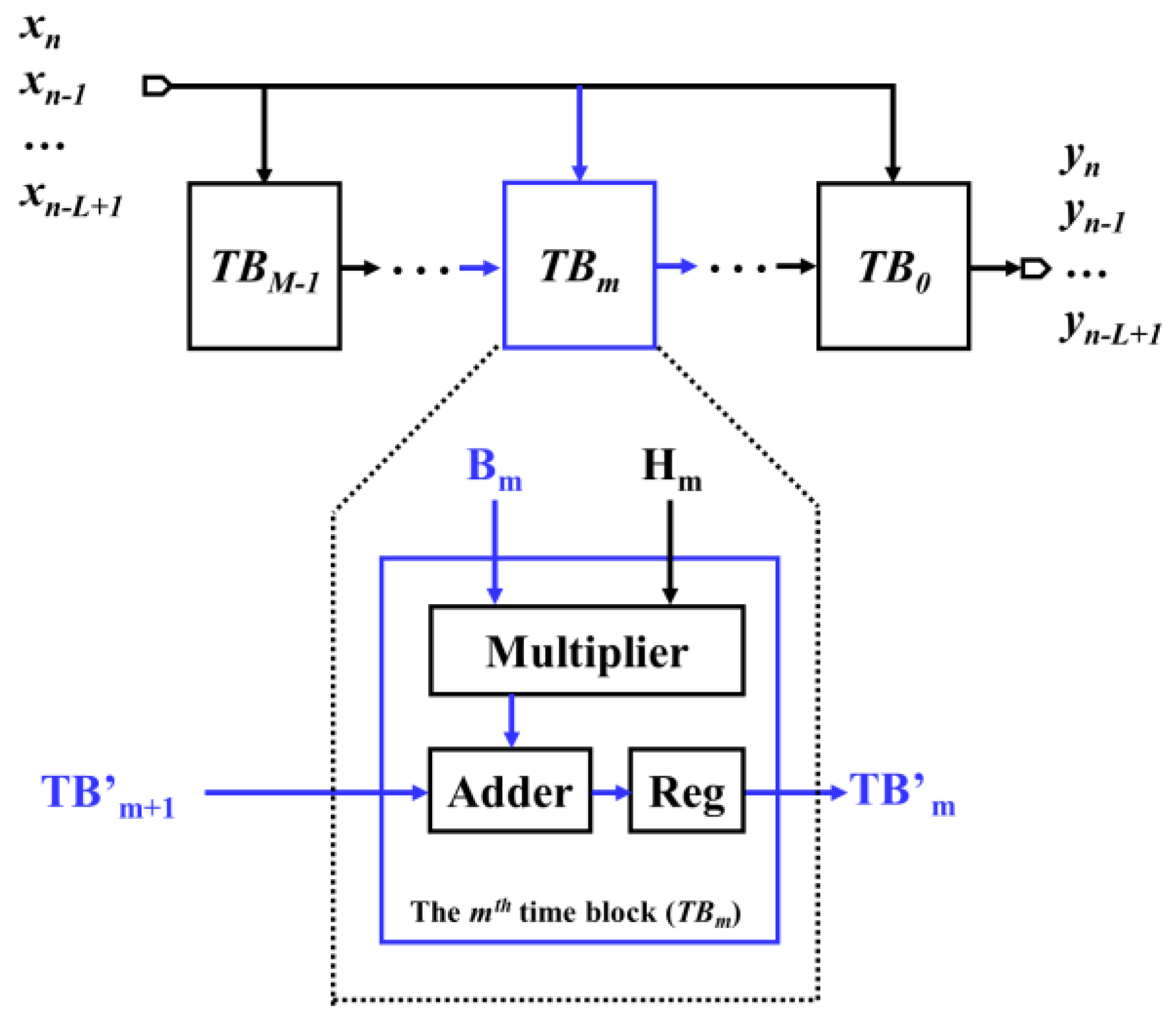
2.1. Generalized Mathematical Formulation for TB-Based FIRs
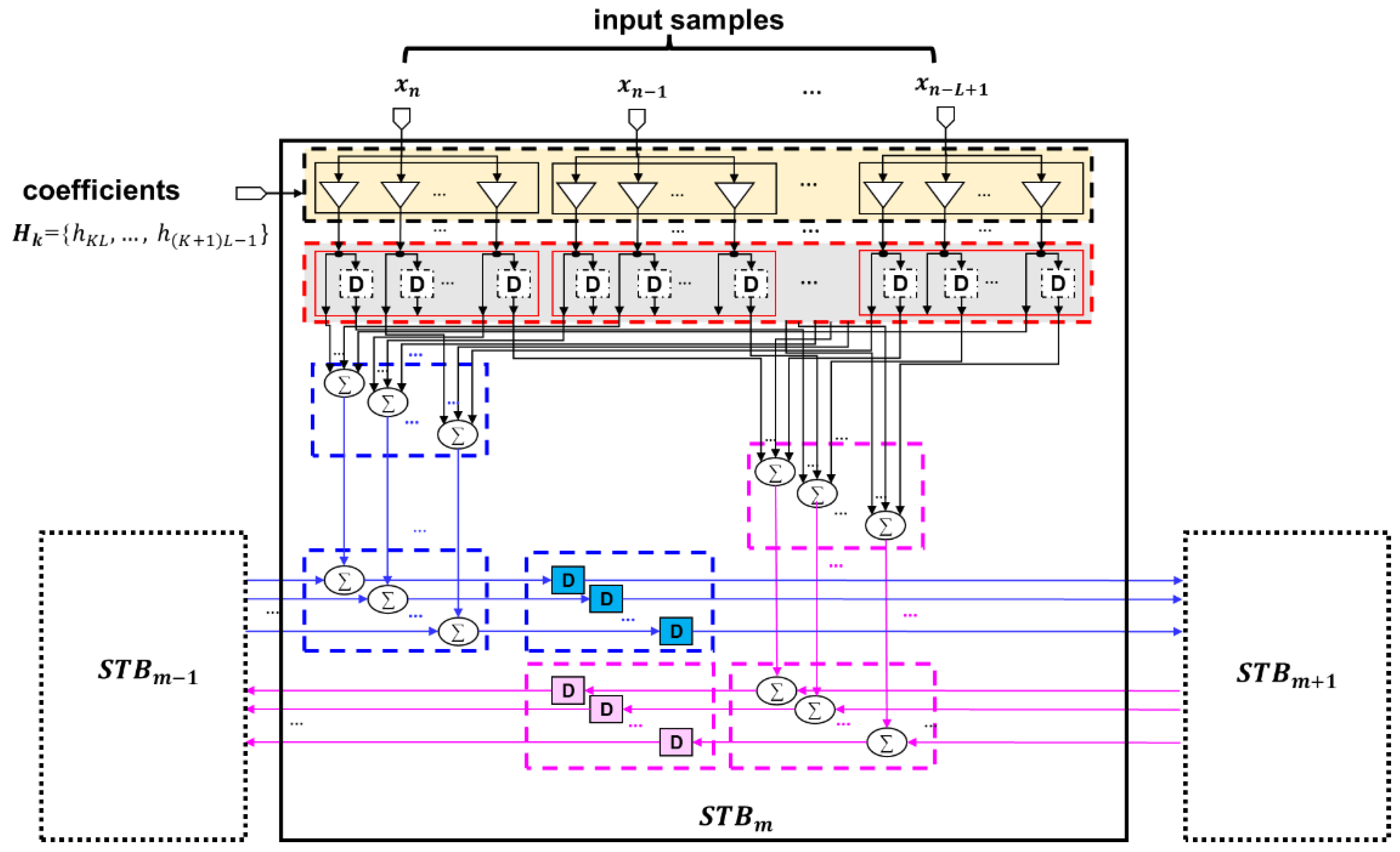
2.2. Proposed STB-FIR Design
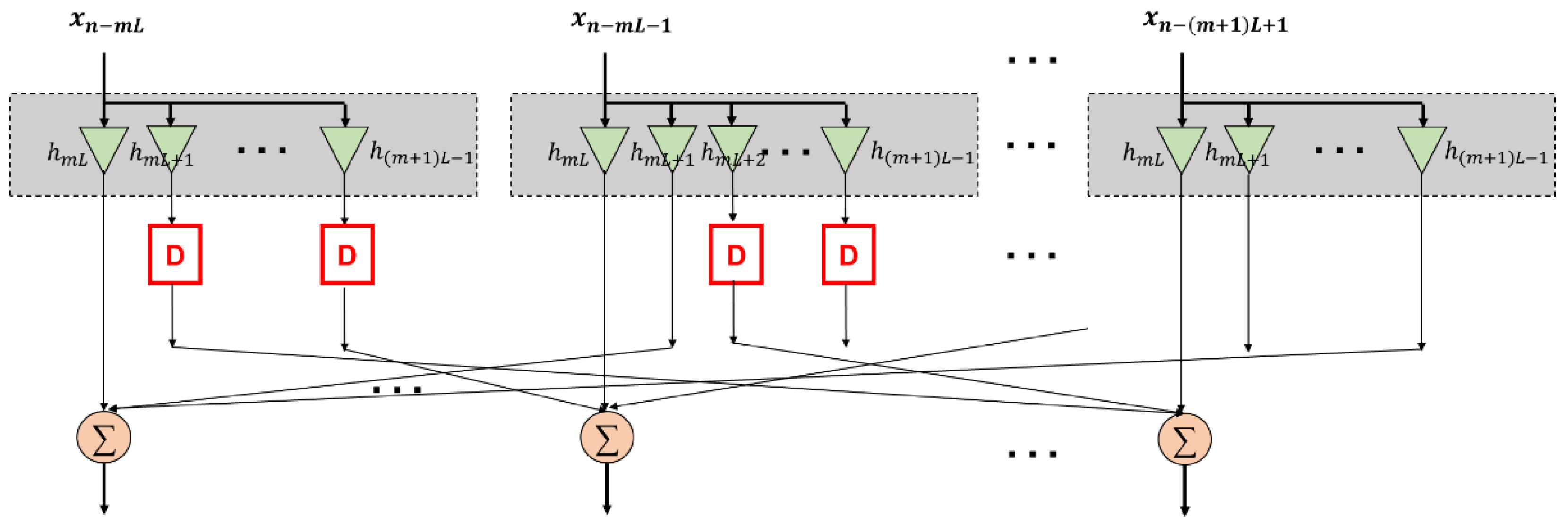
2.2.1. Case 1: M Is Even
2.2.2. Case 2: M Is Odd
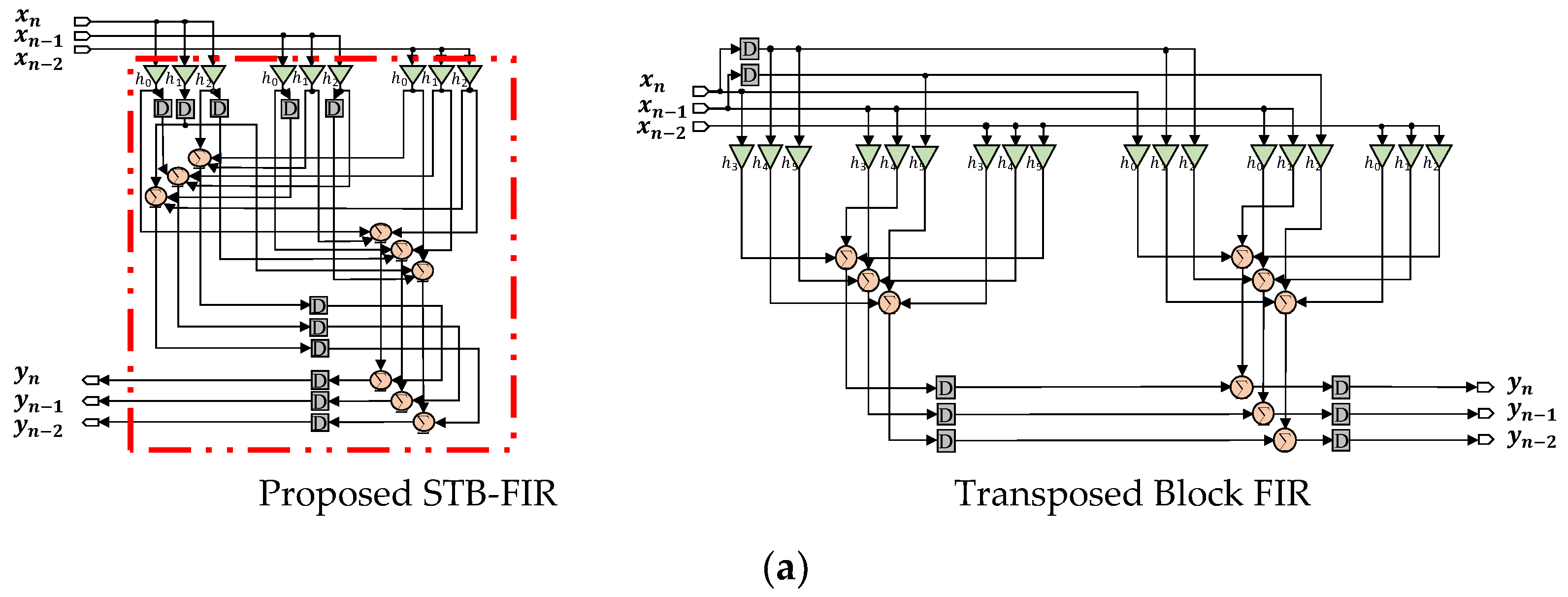
3. Evaluation Results and Comparisons
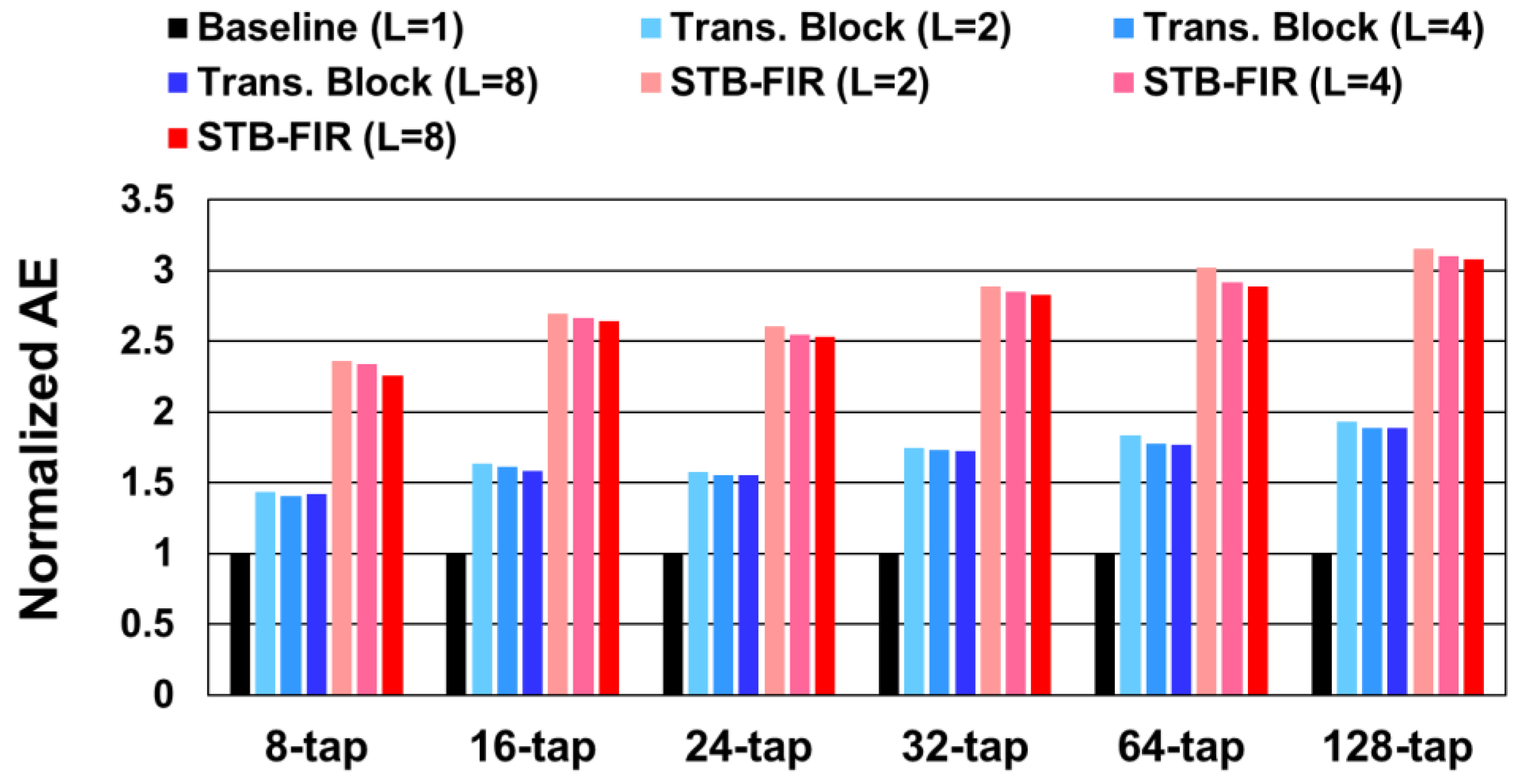
3.1. Comparison of Hardware Complexity
3.2. Comparison of Reconfigurable FIR Implementations
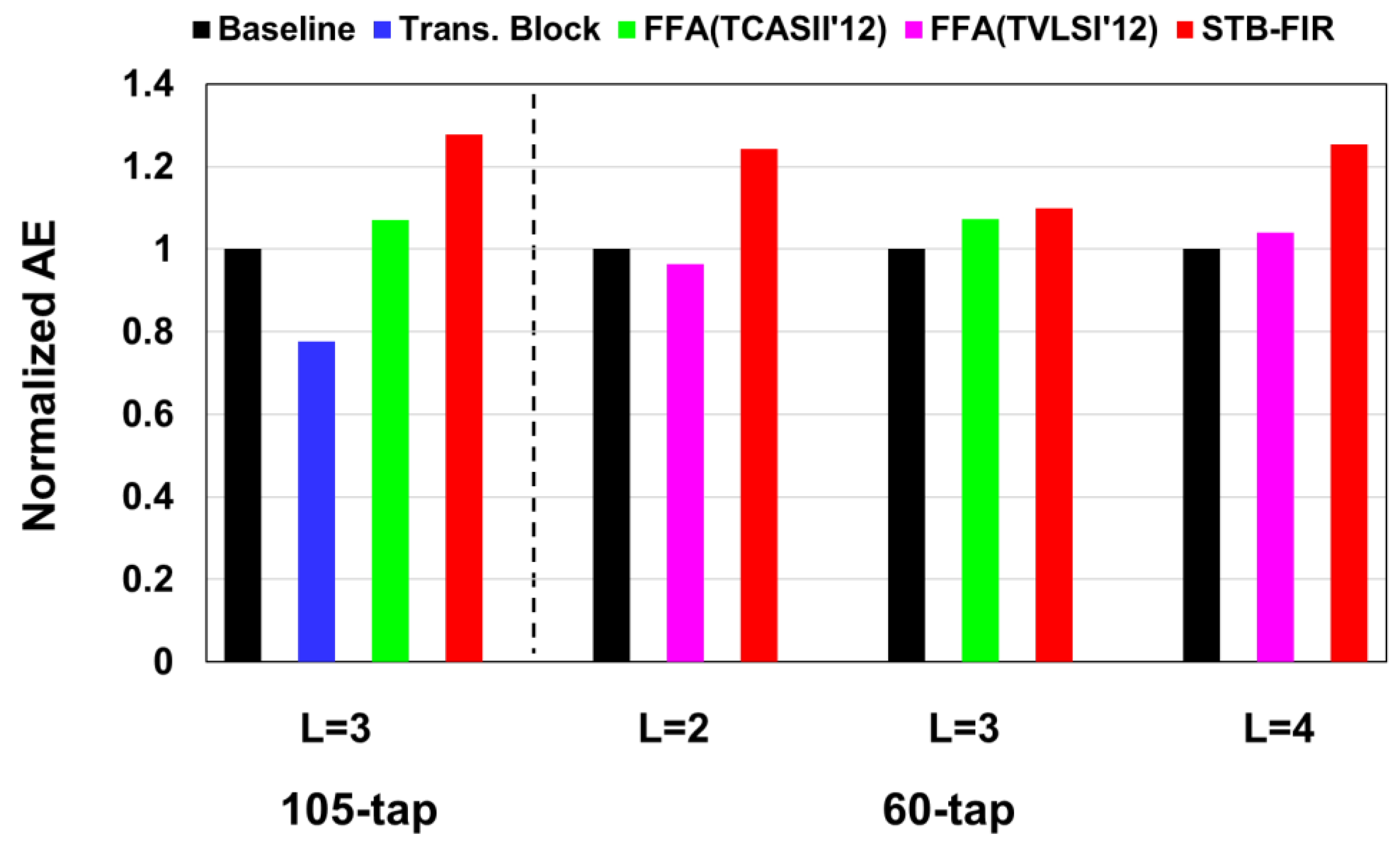
3.3. Comparison of Fixed FIR Implementations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Parhi, K.K. VLSI Digital Signal Processing Systems: Design and Implementation; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Mirchandani, G.; Zinser, R.L.; Evans, J.B. A new adaptive noise cancellation scheme in the presence of crosstalk [speech signals]. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1995, 39, 681–694. [Google Scholar] [CrossRef]
- Dempster, A.G.; Macleod, M.D. Use of minimum-adder multiplier blocks in FIR digital filters. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1995, 42, 569–577. [Google Scholar] [CrossRef]
- Mahesh, R.; Vinod, A.P. A new common subexpression elimination algorithm for realizing low-complexity higher order digital filters. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2008, 27, 217–229. [Google Scholar] [CrossRef]
- Lou, X.; Yu, Y.J.; Meher, P.K. Fine-grained critical path analysis and optimization for area-time efficient realization of multiple constant multiplications. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 863–872. [Google Scholar] [CrossRef]
- Meidani, M.; Mashoufi, B. Introducing new algorithms for realizing an FIR filter with less hardware in order to eliminate power line interference from the ECG signal. IET J. Signal Process. 2016, 10, 709–716. [Google Scholar] [CrossRef]
- Ye, J.; Togawa, N.; Yanagisawa, M.; Shi, Y. A low cost and high speed CSD-based symmetric transpose block FIR implementation. In Proceedings of the IEEE International Conference on ASIC (ASICON), Guiyang, China, 25–28 October 2017. [Google Scholar]
- Ye, J.; Togawa, N.; Yanagisawa, M.; Shi, Y. Static error analysis and optimization of faithfully truncated adders for area-power efficient FIR designs. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019. [Google Scholar]
- Park, J.; Jeong, W.; Meimand, H.M.; Wang, Y.; Choo, H.; Roy, K. Computation sharing programmable FIR filter for low-power and high-performance applications. IEEE J. Solid-State Circuits 2004, 39, 348–357. [Google Scholar] [CrossRef]
- Parker, D.A.; Parhi, K.K. Low-area/power parallel FIR digital filter implementations. J. VLSI Signal Process. Syst. 1997, 17, 75–92. [Google Scholar] [CrossRef]
- Tsao, Y.; Choi, K. Area-efficient parallel FIR digital filter structures for symmetric convolutions based on fast FIR algorithm. IEEE Trans. Very Large Scale Integr. Syst. 2012, 20, 366–371. [Google Scholar] [CrossRef]
- Tsao, Y.; Choi, K. Area-efficient VLSI implementation for parallel linear-phase FIR digital filters of odd length based on fast FIR algorithm. IEEE Trans. Circuits Syst. II Express Briefs. 2012, 59, 371–375. [Google Scholar] [CrossRef]
- Mohanty, B.K.; Meher, P.K. A high-performance energy-efficient architecture for FIR adaptive filter based on new distributed arithmetic formulation of block LMS algorithm. IEEE Trans. Signal Process. 2013, 61, 921–932. [Google Scholar] [CrossRef]
- Mohanty, B.K.; Meher, P.K.; Al-Maadeed, S.; Amira, A. Memory footprint reduction for power-efficient realization of 2-D finite impulse response filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 120–133. [Google Scholar] [CrossRef]
- Mohanty, B.K.; Meher, P.K. A high performance FIR filter architecture for fixed and reconfigurable applications. IEEE Trans. Very Large Scale Integr. Syst. 2016, 24, 444–452. [Google Scholar] [CrossRef]
- Shahein, A.; Zhang, Q.; Lotze, N.; Manoli, Y. A novel hybrid monotonic local search algorithm for FIR filter coefficients optimization. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 59, 616–627. [Google Scholar] [CrossRef]




| Architecture. | No. of Multipliers | No. of Adders | No. of Registers |
|---|---|---|---|
| Transposed block | |||
| DA | |||
| L-Parallel FFA | |||
| Proposed STB-FIR |
| Tap | FIR Structure | No. of Multipliers | No. of Adders | No. of Registers | Sampling Freq. (MHz) | Area Saving (%) | Power (mw) | Power Saving (%) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | Parallel L = 2 | Transposed block | 16 | 14 | 9 | 207.04 | 203,380 | 39.35 | 12.47 | 34.40 |
| Proposed STB-FIR | 8 | 14 | 10 | 206.83 | 123,353 | 8.18 | ||||
| Parallel L = 4 | Transposed block | 32 | 28 | 11 | 382.78 | 383,343 | 39.97 | 21.72 | 34.16 | |
| Proposed STB-FIR | 16 | 28 | 18 | 382.41 | 230,127 | 14.30 | ||||
| Parallel L = 8 | Transposed block | 64 | 56 | 15 | 735.97 | 731,514 | 37.39 | 42.17 | 35.83 | |
| Proposed STB-FIR | 32 | 56 | 30 | 733.27 | 457,993 | 27.06 | ||||
| 16 | Parallel L = 2 | Transposed block | 32 | 30 | 17 | 207.04 | 410,745 | 39.28 | 26.29 | 37.31 |
| Proposed STB-FIR | 16 | 30 | 24 | 206.83 | 249,384 | 16.48 | ||||
| Parallel L = 4 | Transposed block | 64 | 60 | 19 | 382.78 | 769,615 | 39.49 | 44.72 | 36.67 | |
| Proposed STB-FIR | 32 | 60 | 36 | 382.41 | 465,661 | 28.32 | ||||
| Parallel L = 8 | Transposed block | 128 | 120 | 23 | 717.49 | 1,474,409 | 39.03 | 88.39 | 41.23 | |
| Proposed STB-FIR | 64 | 120 | 60 | 732.60 | 898,994 | 51.95 | ||||
| 24 | Parallel L = 2 | Transposed block | 48 | 46 | 25 | 207.04 | 618,293 | 39.66 | 34.96 | 36.13 |
| Proposed STB-FIR | 24 | 46 | 36 | 206.83 | 373,099 | 22.33 | ||||
| Parallel L = 4 | Transposed block | 96 | 92 | 27 | 382.78 | 1,155,887 | 39.07 | 64.99 | 36.42 | |
| Proposed STB-FIR | 48 | 92 | 54 | 382.41 | 704,290 | 41.32 | ||||
| Parallel L = 8 | Transposed block | 192 | 184 | 31 | 733.27 | 2,217,483 | 38.81 | 120.65 | 32.95 | |
| Proposed STB-FIR | 96 | 184 | 90 | 732.60 | 1,356,819 | 80.90 | ||||
| 32 | Parallel L = 2 | Transposed block | 64 | 62 | 33 | 207.04 | 827,379 | 39.62 | 50.40 | 32.34 |
| Proposed STB-FIR | 32 | 62 | 48 | 206.83 | 499,542 | 34.10 | ||||
| Parallel L = 4 | Transposed block | 128 | 124 | 35 | 382.78 | 1,542,082 | 39.26 | 88.22 | 33.51 | |
| Proposed STB-FIR | 64 | 124 | 72 | 382.41 | 936,727 | 58.66 | ||||
| Parallel L = 8 | Transposed block | 256 | 248 | 39 | 733.27 | 2,963,939 | 39.00 | 159.96 | 33.09 | |
| Proposed STB-FIR | 128 | 248 | 120 | 732.60 | 1,808,023 | 107.03 | ||||
| 64 | Parallel L = 2 | Transposed block | 128 | 126 | 65 | 207.04 | 1,613,977 | 39.29 | 99.83 | 36.44 |
| Proposed STB-FIR | 64 | 126 | 96 | 206.83 | 979,802 | 63.45 | ||||
| Parallel L = 4 | Transposed block | 256 | 252 | 67 | 382.78 | 3,087,828 | 39.30 | 177.32 | 34.97 | |
| Proposed STB-FIR | 128 | 252 | 144 | 382.41 | 1,874,254 | 115.32 | ||||
| Parallel L = 8 | Transposed block | 512 | 504 | 71 | 733.27 | 5,932,523 | 38.87 | 322.64 | 33.07 | |
| Proposed STB-FIR | 256 | 504 | 240 | 732.60 | 3,626,413 | 215.93 | ||||
| 128 | Parallel L = 2 | Transposed block | 256 | 254 | 129 | 207.04 | 3,272,258 | 38.90 | 208.11 | 36.97 |
| Proposed STB-FIR | 128 | 254 | 192 | 206.83 | 1,999,407 | 131.18 | ||||
| Parallel L = 4 | Transposed block | 512 | 508 | 131 | 382.78 | 6,178,507 | 39.12 | 356.05 | 34.70 | |
| Proposed STB-FIR | 256 | 508 | 288 | 382.41 | 3,761,321 | 232.5 | ||||
| Parallel L = 8 | Transposed block | 1024 | 1016 | 135 | 733.27 | 11,872,904 | 38.82 | 648.16 | 32.76 | |
| Proposed STB-FIR | 512 | 1016 | 480 | 732.60 | 7,263,638 | 435.81 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Yanagisawa, M.; Shi, Y. Scalable Hardware Efficient Architecture for Parallel FIR Filters with Symmetric Coefficients. Electronics 2022, 11, 3272. https://doi.org/10.3390/electronics11203272
Ye J, Yanagisawa M, Shi Y. Scalable Hardware Efficient Architecture for Parallel FIR Filters with Symmetric Coefficients. Electronics. 2022; 11(20):3272. https://doi.org/10.3390/electronics11203272
Chicago/Turabian StyleYe, Jinghao, Masao Yanagisawa, and Youhua Shi. 2022. "Scalable Hardware Efficient Architecture for Parallel FIR Filters with Symmetric Coefficients" Electronics 11, no. 20: 3272. https://doi.org/10.3390/electronics11203272
APA StyleYe, J., Yanagisawa, M., & Shi, Y. (2022). Scalable Hardware Efficient Architecture for Parallel FIR Filters with Symmetric Coefficients. Electronics, 11(20), 3272. https://doi.org/10.3390/electronics11203272









