Localization of Small Objectives from Scattering Parameter via Bistatic Measurement Configuration
Abstract
1. Introduction
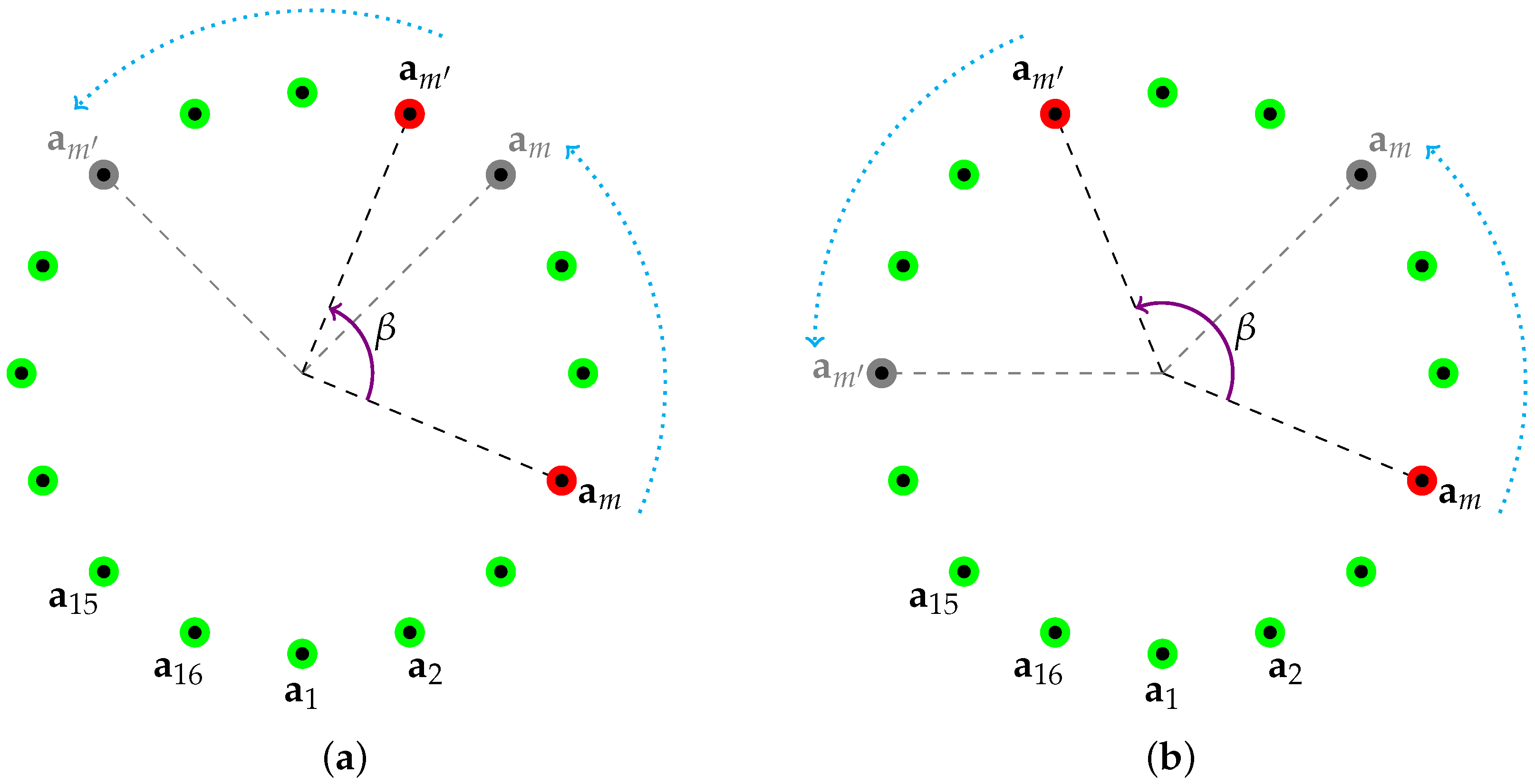
2. Overview of Scattering Parameter and Design of Imaging Function
3. Analysis of Imaging Function and Some Properties
- If then since , , and ,
- If , then since and , these terms do not contribute to determining , i.e., it is impossible to recognize the objective location through the map of .
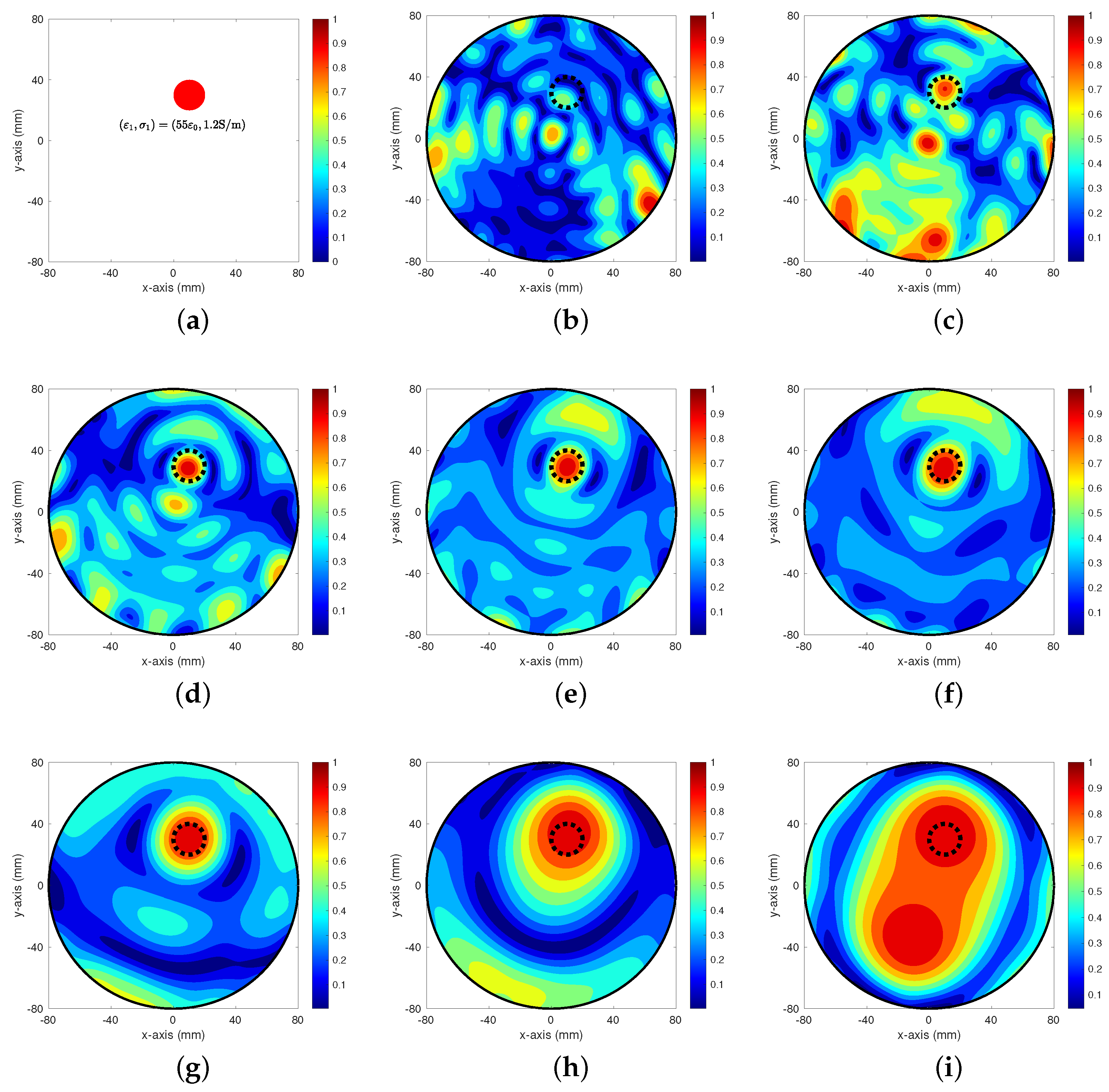
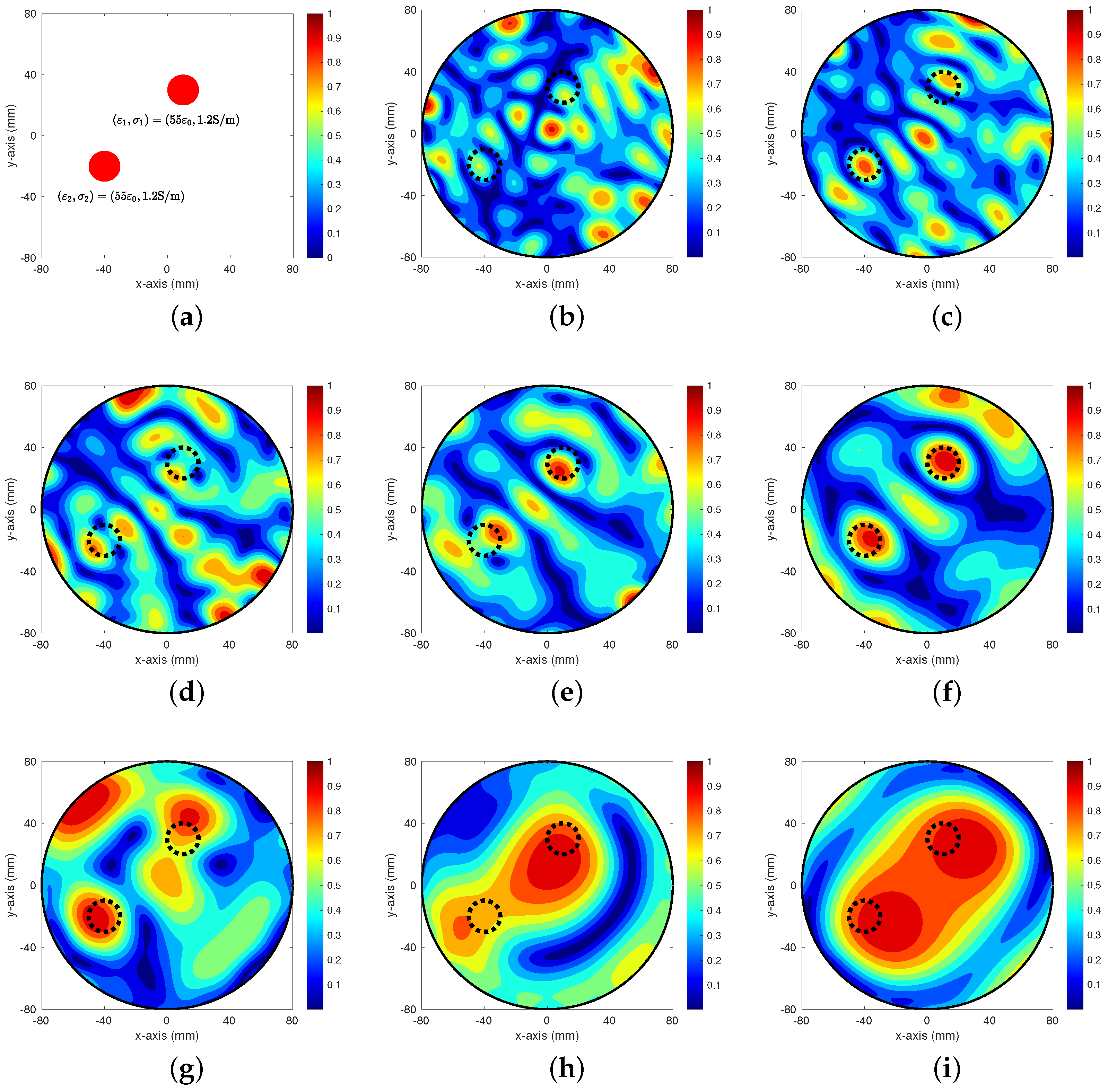
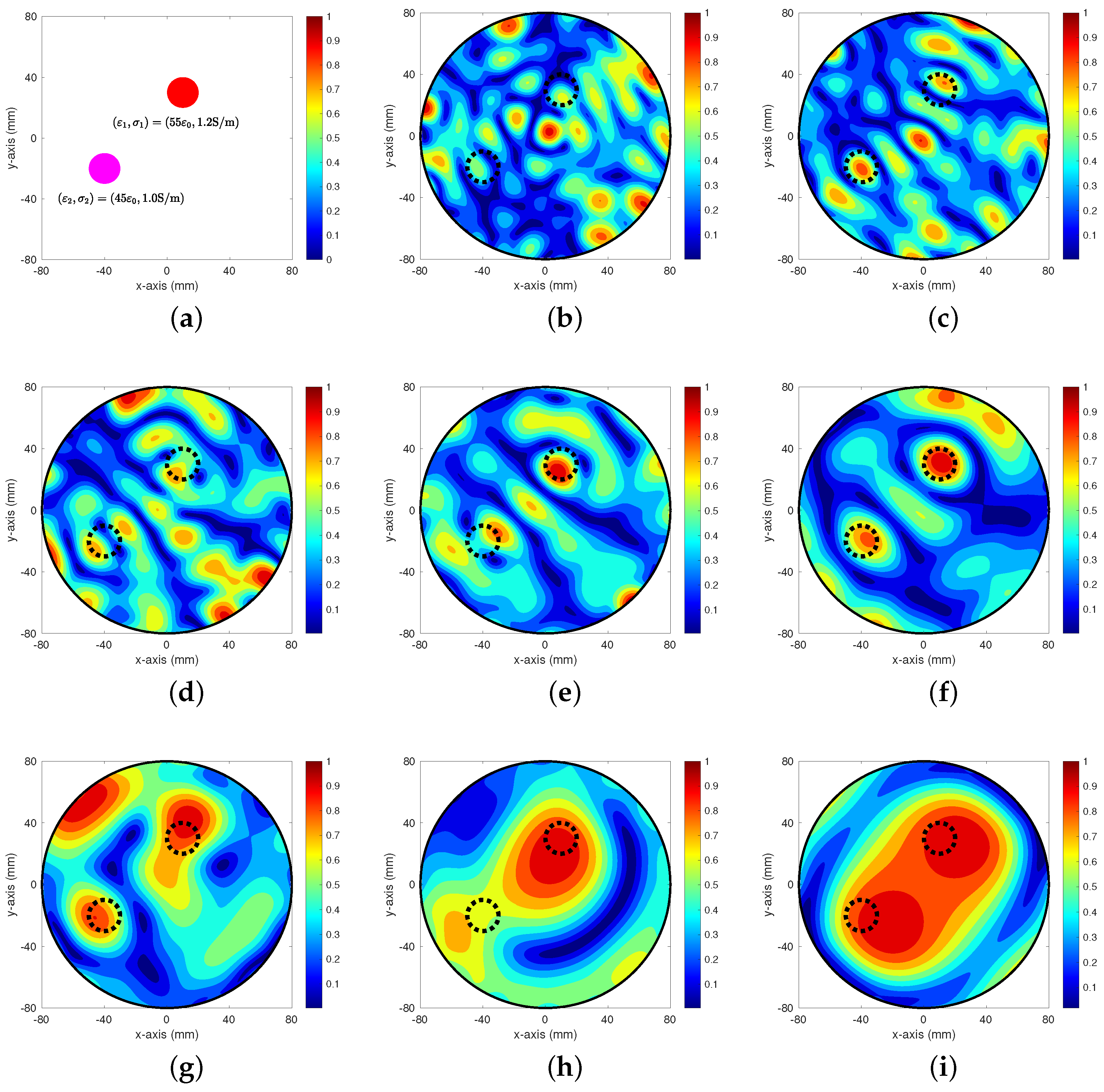
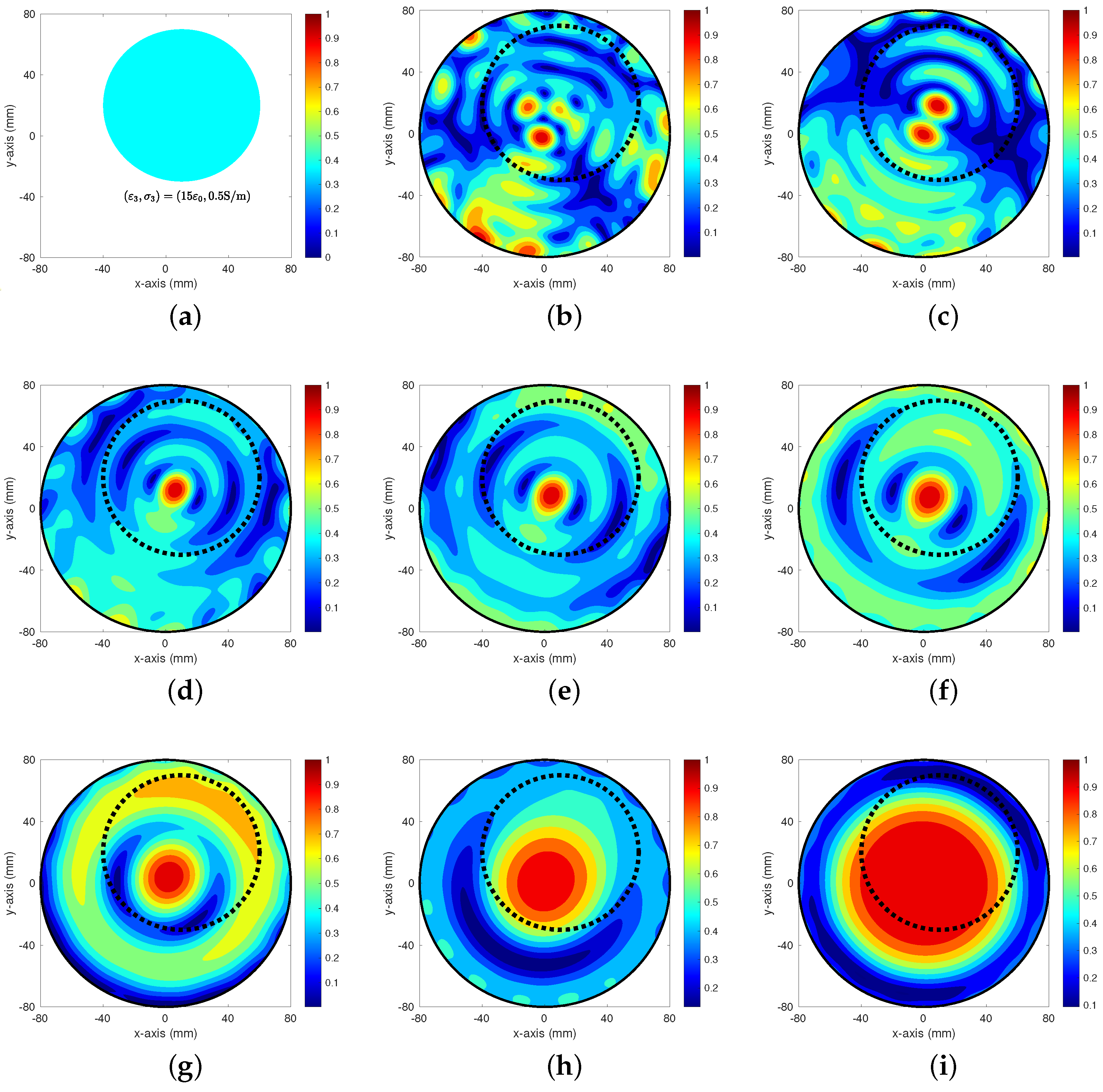
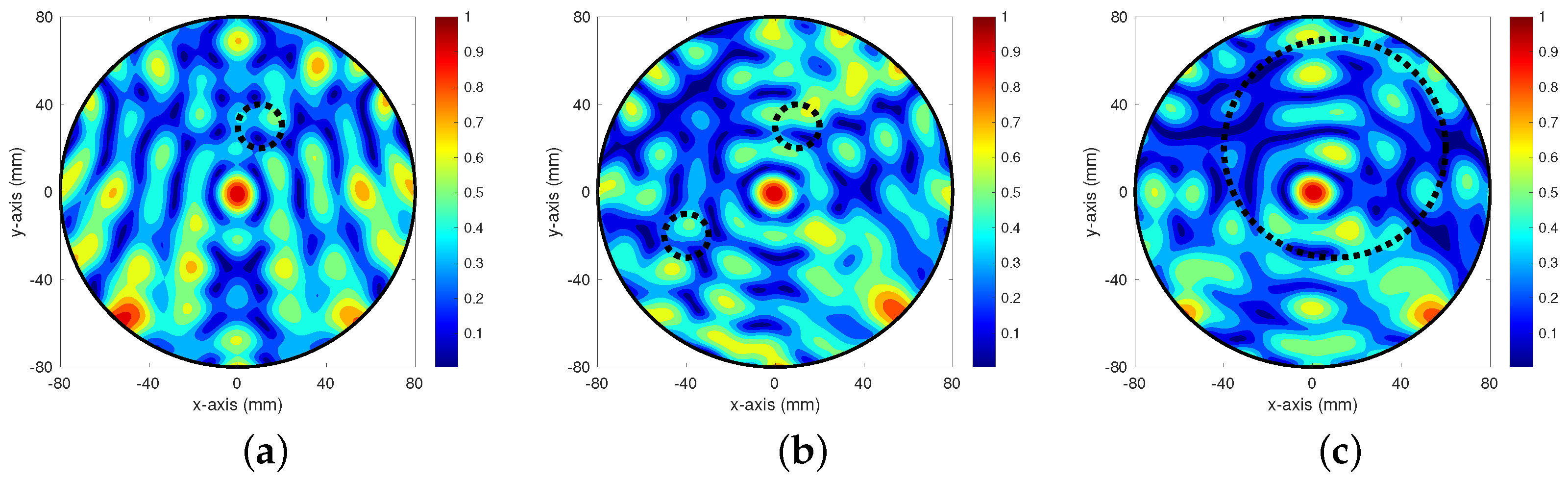
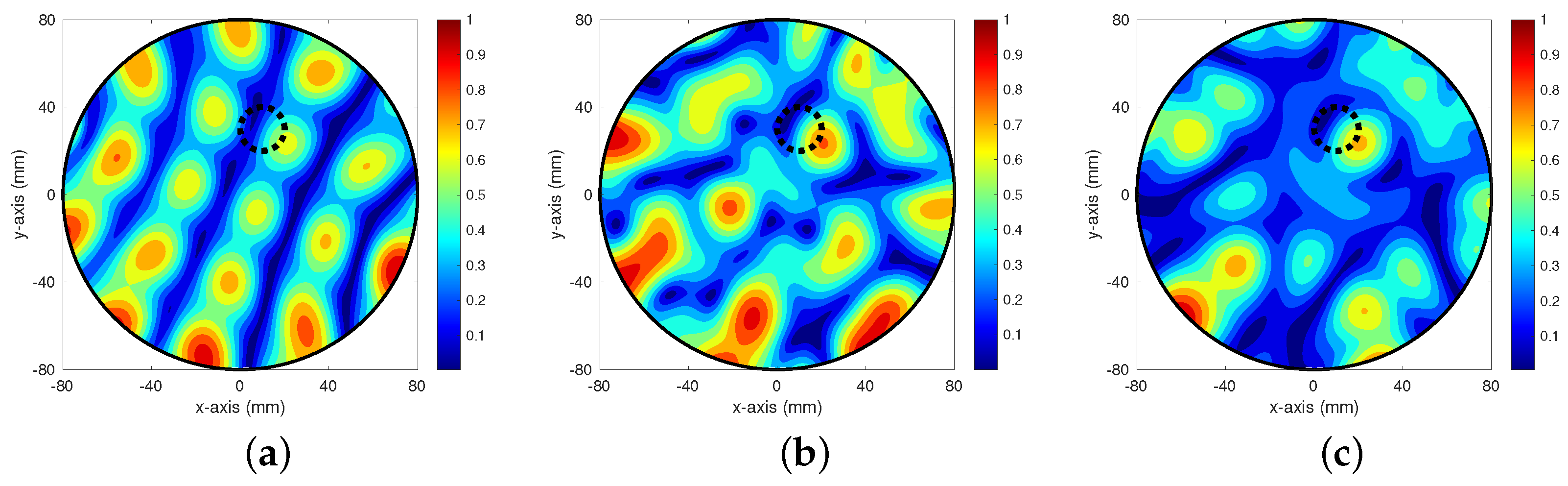
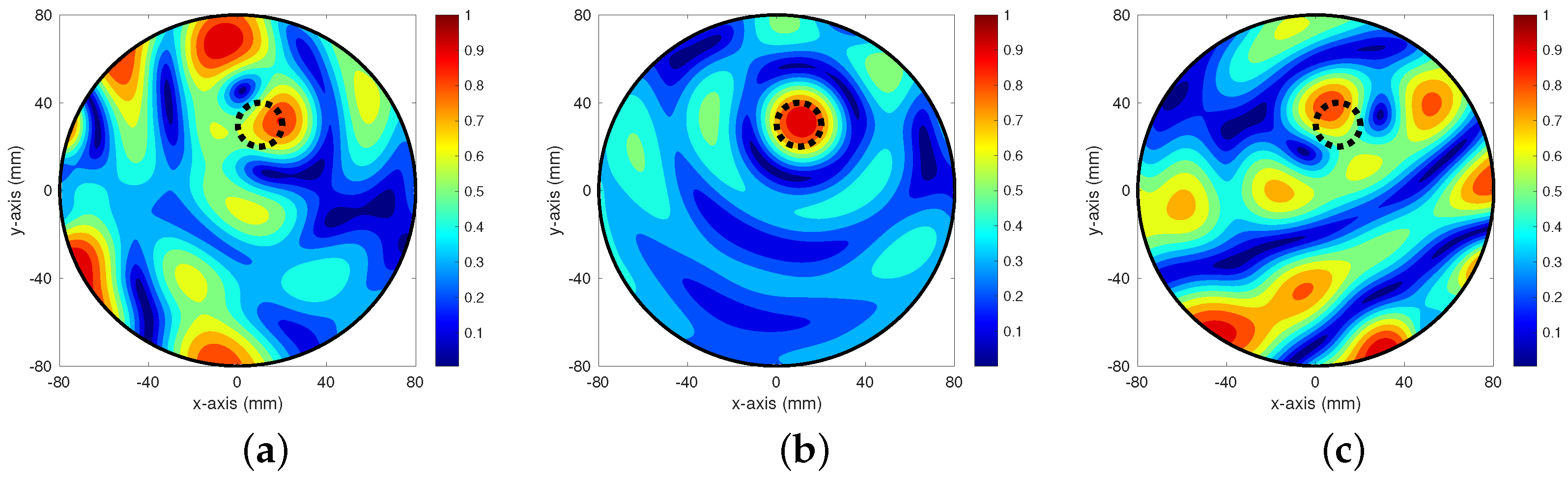
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arridge, S. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41–R93. [Google Scholar] [CrossRef]
- Simonov, N.; Kim, B.R.; Lee, K.J.; Jeon, S.I.; Son, S.H. Advanced fast 3-D electromagnetic solver for microwave tomography imaging. IEEE Trans. Med. Imaging 2017, 36, 2160–2170. [Google Scholar] [CrossRef] [PubMed]
- Coşğun, S.; Bilgin, E.; Çayören, M. Microwave imaging of breast cancer with factorization method: SPIONs as contrast agent. Med. Phys. 2020, 47, 3113–3122. [Google Scholar] [CrossRef]
- Shea, J.D.; Kosmas, P.; Hagness, S.C.; Veen, B.D.V. Three-dimensional microwave imaging of realistic numerical breast phantoms via a multiple-frequency inverse scattering technique. Med. Phys. 2010, 37, 4210–4226. [Google Scholar] [CrossRef] [PubMed]
- Caorsi, S.; Massa, A.; Pastorino, M. A crack identification microwave procedure based on a genetic algorithm for nondestructive testing. IEEE Trans. Antennas Propag. 2001, 49, 1812–1820. [Google Scholar] [CrossRef]
- Foudazix, A.; Mirala, A.; Ghasr, M.T.; Donnell, K.M. Active microwave thermography for nondestructive evaluation of surface cracks in metal structures. IEEE Trans. Instrum. Meas. 2019, 68, 576–585. [Google Scholar] [CrossRef]
- Haynes, M.; Stang, J.; Moghaddam, M. Real-time microwave imaging of differential temperature for thermal therapy monitoring. IEEE Trans. Biomed. Eng. 2014, 61, 1787–1797. [Google Scholar] [CrossRef]
- Persson, M.; Fhager, A.; Trefnà, H.D.; Yu, Y.; McKelvey, T.; Pegenius, G.; Karlsson, J.E.; Elam, M. Microwave-based stroke diagnosis making global prehospital thrombolytic treatment possible. IEEE Trans. Biomed. Eng. 2014, 61, 2806–2817. [Google Scholar] [CrossRef]
- Salucci, M.; Vrba, J.; Merunka, I.; Massa, A. Real-time brain stroke detection through a learning-by-examples technique—An experimental assessment. Microw. Opt. Technol. Lett. 2017, 59, 2796–2799. [Google Scholar] [CrossRef]
- Mojabi, P.; LoVetri, J. Microwave biomedical imaging using the multiplicative regularized Gauss-Newton inversion. IEEE Antennas Propag. Lett. 2009, 8, 645–648. [Google Scholar] [CrossRef]
- Rubæk, T.; Meaney, P.M.; Meincke, P.; Paulsen, K.D. Nonlinear microwave imaging for breast-cancer screening using Gauss–Newton’s method and the CGLS inversion algorithm. IEEE Trans. Antennas Propag. 2007, 55, 2320–2331. [Google Scholar] [CrossRef]
- Chew, W.C.; Wang, Y.M. Reconstruction of two-dimensional permittivity distribution using the distorted Born iterative method. IEEE Trans. Med. Imaging 1990, 9, 218–225. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. A new scheme based on Born iterative method for solving inverse scattering problems with noise disturbance. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1021–1025. [Google Scholar] [CrossRef]
- Bergou, E.; Diouane, Y.; Kungurtsev, V. Convergence and complexity analysis of a Levenberg–Marquardt algorithm for inverse problems. J. Optim. Theory Appl. 2020, 185, 927–944. [Google Scholar] [CrossRef]
- Franchois, A.; Pichot, C. Microwave imaging-complex permittivity reconstruction with a Levenberg-Marquardt method. IEEE Trans. Antennas Propag. 1997, 45, 203–215. [Google Scholar] [CrossRef]
- Abubakar, A.; van den Berg, P.M.; Mallorqui, J.J. Imaging of biomedical data using a multiplicative regularized contrast source inversion method. IEEE Trans. Microw. Theory Tech. 2002, 50, 1761–1771. [Google Scholar] [CrossRef]
- Van den Berg, P.M.; Kleinman, R.E. A contrast source inversion method. Inverse Probl. 1997, 13, 1607–1620. [Google Scholar] [CrossRef]
- Dorn, O.; Lesselier, D. Level set methods for inverse scattering. Inverse Probl. 2006, 22, R67–R131. [Google Scholar] [CrossRef]
- Irishina, N.; Dorn, O.; Moscoso, M. A level set evolution strategy in microwave imaging for early breast cancer detection. Comput. Math. Appl. 2008, 56, 607–618. [Google Scholar] [CrossRef][Green Version]
- Park, W.K. Application of MUSIC algorithm in real-world microwave imaging of unknown anomalies from scattering matrix. Mech. Syst. Signal Proc. 2021, 153, 107501. [Google Scholar] [CrossRef]
- Ruvio, G.; Solimene, R.; D’Alterio, A.; Ammann, M.J.; Pierri, R. RF breast cancer detection employing a noncharacterized vivaldi antenna and a MUSIC-inspired algorithm. Int. J. RF Microw. Comput. Aided Eng. 2013, 23, 598–609. [Google Scholar] [CrossRef]
- Park, W.K. Real-time microwave imaging of unknown anomalies via scattering matrix. Mech. Syst. Signal Proc. 2019, 118, 658–674. [Google Scholar] [CrossRef]
- Park, W.K. Real-time detection of small anomaly from limited-aperture measurements in real-world microwave imaging. Mech. Syst. Signal Proc. 2022, 171, 108937. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Isernia, T.; Palmeri, R.; Akinci, M.N.; Crocco, L. Physical insight unveils new imaging capabilities of orthogonality sampling method. IEEE Trans. Antennas Propag. 2020, 68, 4014–4021. [Google Scholar] [CrossRef]
- Son, S.H.; Lee, K.J.; Park, W.K. Application and analysis of direct sampling method in real-world microwave imaging. Appl. Math. Lett. 2019, 96, 47–53. [Google Scholar] [CrossRef]
- Kirsch, A. The factorization method for Maxwell’s equations. Inverse Probl. 2004, 20, 117–134. [Google Scholar] [CrossRef]
- Chouiti, S.M.; Merad, L.; Meriah, S.M.; Derraz, F.; Raimundo, X. Monostatic imaging of an embedded object using a confocal algorithm. Int. J. Numer. Model. 2018, 31, 1–14. [Google Scholar] [CrossRef]
- Kang, S.; Lambert, M.; Park, W.K. Analysis and improvement of direct sampling method in the mono-static configuration. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1721–1725. [Google Scholar] [CrossRef]
- Zetik, R.; Thoma, R.S. Monostatic imaging of small objects in UWB sensor networks. In Proceedings of the 2008 IEEE International Conference on Ultra-Wideband, Hannover, Germany, 10–12 September 2008; Volume 2, pp. 191–194. [Google Scholar]
- Son, S.H.; Simonov, N.; Kim, H.J.; Lee, J.M.; Jeon, S.I. Preclinical prototype development of a microwave tomography system for breast cancer detection. ETRI J. 2010, 32, 901–910. [Google Scholar] [CrossRef]
- Park, W.K. Theoretical identification of coupling effect and performance analysis of single-source direct sampling method. Mathematics 2021, 9, 1065. [Google Scholar] [CrossRef]
- Chernyak, V.S. Fundamentals of Multisite Radar Systems: Multistatic Radars and Multiradar Systems; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Sasada, S.; Masumoto, N.; Song, H.; Emi, A.; Kadoya, T.; Arihiro, K.; Kikkawa, T.; Okada, M. Microwave breast imaging using rotational bistatic impulse radar for the detection of breast cancer: Protocol for a prospective diagnostic study. JMIR Res. Protoc. 2020, 9, e17524. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.B.; Chu, T.H. Bistatic frequency-swept microwave imaging: Principle, methodology and experimental results. IEEE Trans. Microw. Theory Tech. 1993, 41, 855–861. [Google Scholar] [CrossRef]
- Comblet, F.; Khenchaf, A.; Baussard, A.; Pellen, F. Bistatic synthetic aperture radar imaging: Theory, simulations, and validations. IEEE Trans. Antennas Propag. 2006, 54, 3529–3540. [Google Scholar] [CrossRef]
- Welsh, B.M.; Gardner, C.S. Bistatic imaging lidar technique for upper atmospheric studies. Appl. Opt. 1989, 28, 82–88. [Google Scholar] [CrossRef]
- Liang, B.; Shang, X.; Zhuge, X.; Miao, J. Bistatic cylindrical millimeter-wave imaging for accurate reconstruction of high-contrast concave objects. Opt. Express 2019, 27, 14881–14892. [Google Scholar] [CrossRef]
- Cherniakov, M. Bistatic Radar: Principles and Practice; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Griffiths, H.D. Bistatic and multistatic radar. In Proceedings of the Institution of Electrical Engineers Military Radar Seminar, Shrivenham, UK, 28–30 October 2004. [Google Scholar]
- Kang, S.; Lim, M.; Park, W.K. Fast identification of short, linear perfectly conducting cracks in the bistatic measurement configuration. J. Comput. Phys. 2022, 468, 111479. [Google Scholar] [CrossRef]
- Willis, N.J.; Griffiths, H.D. Advances in Bistatic Radar; The Institution of Engineering and Technology: London, UK, 2007. [Google Scholar]
- Slaney, M.; Kak, A.C.; Larsen, L.E. Limitations of imaging with first-order diffraction tomography. IEEE Trans. Microw. Theory Tech. 1984, 32, 860–874. [Google Scholar] [CrossRef]
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Problems; Mathematics and Applications Series; Springer: New York, NY, USA, 1998. [Google Scholar]
- Kang, S.; Chae, S.; Park, W.K. A study on the orthogonality sampling method corresponding to the observation directions configuration. Res. Phys. 2022, 33, 105108. [Google Scholar] [CrossRef]
- Wang, C.; Qin, C.; Yao, Y.; Li, Y.; Wang, W. Low complexity interference alignment for mmWave MIMO channels in three-cell mobile network. IEEE J. Sel. Areas Commun. 2017, 35, 1513–1523. [Google Scholar] [CrossRef]
- Xu, W.; Gao, F.; Zhang, J.; Tao, X.; Alkhateeb, A. Deep learning based channel covariance matrix estimation with user location and scene images. IEEE Trans. Commun. 2021, 69, 8145–8158. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, S.-H.; Park, W.-K. Localization of Small Objectives from Scattering Parameter via Bistatic Measurement Configuration. Electronics 2022, 11, 3054. https://doi.org/10.3390/electronics11193054
Son S-H, Park W-K. Localization of Small Objectives from Scattering Parameter via Bistatic Measurement Configuration. Electronics. 2022; 11(19):3054. https://doi.org/10.3390/electronics11193054
Chicago/Turabian StyleSon, Seong-Ho, and Won-Kwang Park. 2022. "Localization of Small Objectives from Scattering Parameter via Bistatic Measurement Configuration" Electronics 11, no. 19: 3054. https://doi.org/10.3390/electronics11193054
APA StyleSon, S.-H., & Park, W.-K. (2022). Localization of Small Objectives from Scattering Parameter via Bistatic Measurement Configuration. Electronics, 11(19), 3054. https://doi.org/10.3390/electronics11193054






