Constructing a Gene Regulatory Network Based on a Nonhomogeneous Dynamic Bayesian Network
Abstract
1. Introduction
2. Bayesian Regression Model
| Algorithm 1: Pseudocode for updating the signal-to-noise ratio hyperparameter |
| For each node Input: , , Output: |
| MCMC iteration: ① Sampling a concrete variance hyperparameter from Equation (8) ② Sampling regression parameter vectors ,from Equation (7) set: ③ Sampling a new SNR hyperparameter from Equation (6), and output: |
3. PCCs-ED-DBN Model
3.1. Network Structure M Inference Based on PCCs of Data Points
| Algorithm 2: Pseudocode for updating the parent node sets |
| For each node Input: , , Output: |
| MCMC iteration: ① Get the system of parent sets : Randomly select node , ,, a = rand(1), if (i) adding the node to else (ii) deleting the node from (iii) exchanging a node for a node . Randomly select a new candidate parent set from ② According to the probability Equation (13). If accepted, set: from . Otherwise, set . Output: |
3.2. Component Vector Vg Infer Based on Euclidean Distance of Data Points
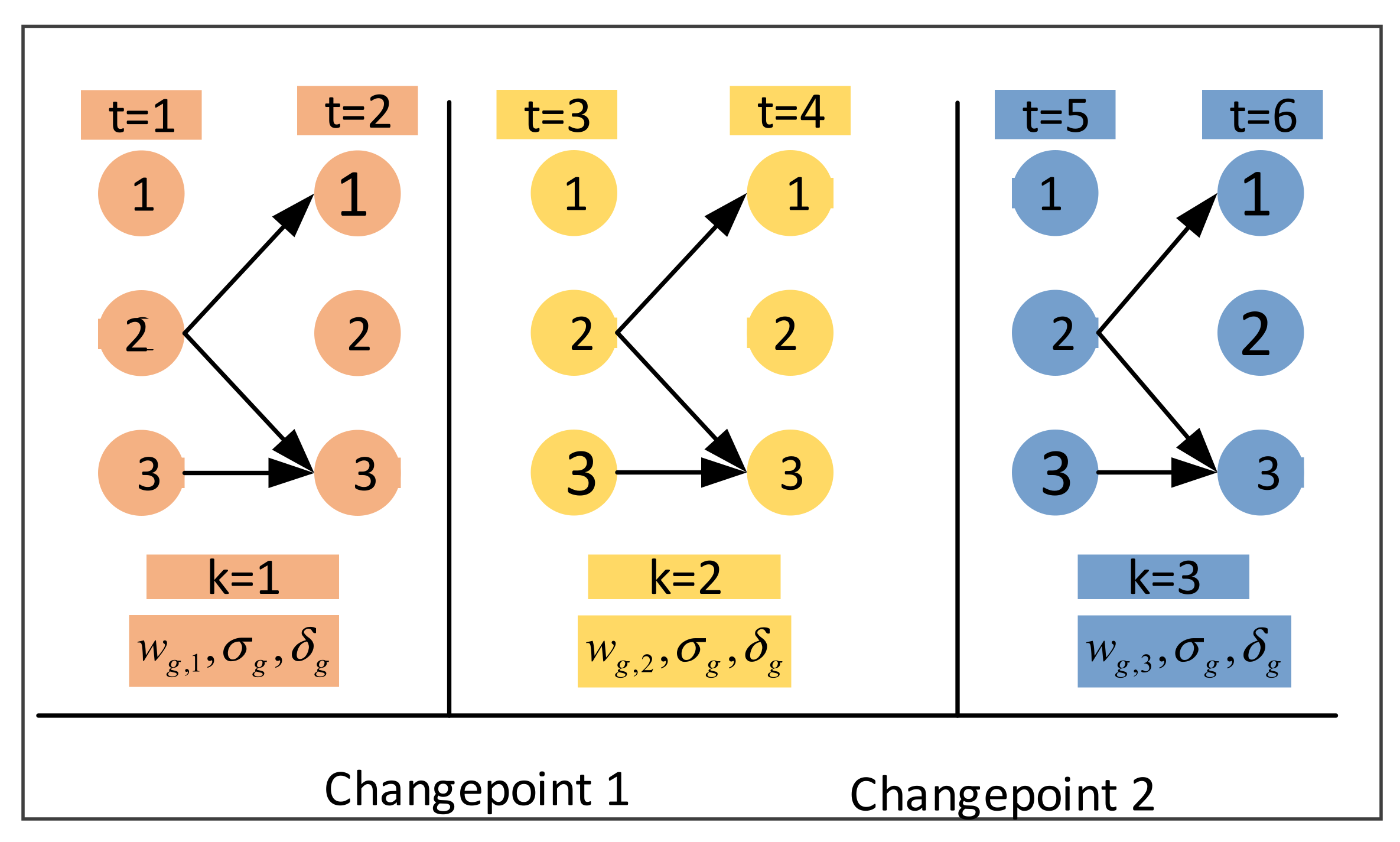
3.2.1. Component Transition
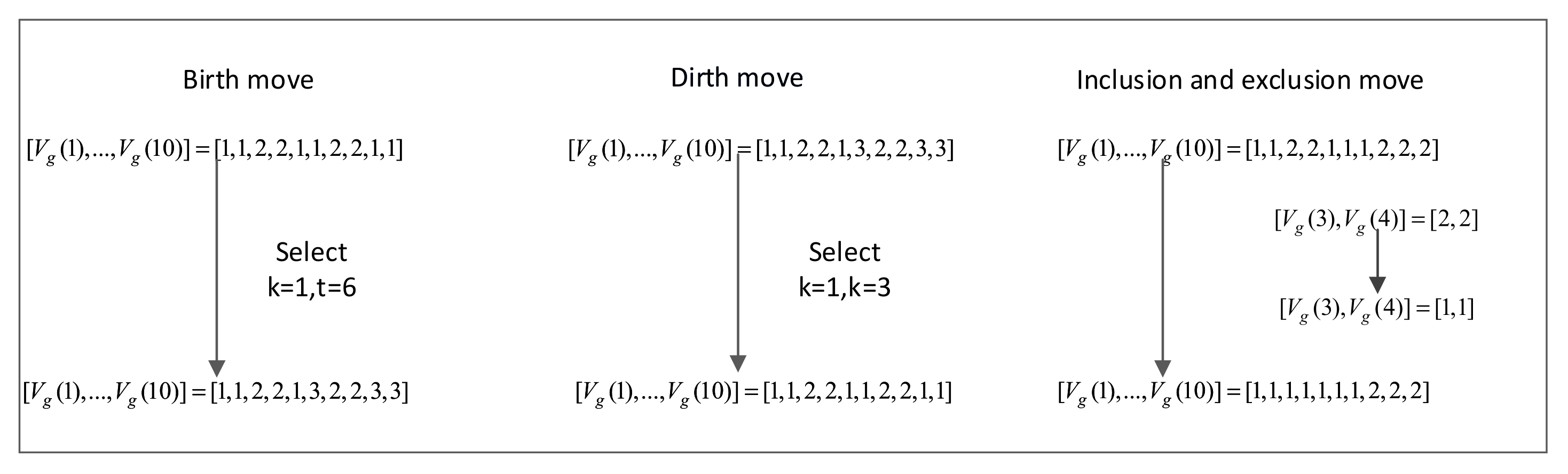
3.2.2. Birth Move Based on the Euclidean Distance
| Algorithm 3: Pseudocode for changepoint birth move detection based on the Euclidean distance of data points |
| Input: The component vector of the current node g and the maximum number of changepoint Output: , |
| ① for for u = rand (0,1), if break; end end ② Change the component of all data points with state after to a new component , and update and to calculate the acceptance rate . |
| Algorithm 4: Pseudocode of RJ-MCMC sampling changepoint based on Euclidean distance of data points |
| Input: The component vector of the current node and the maximum number of changepoint , network M Output: , |
| ① For each sampling process, calculate based on the current number of conversion points ② Gibbs Sampler move A = rand (0,1) If A < birth move according to Algorithm 3 If A < death move If A < Inclusion and Exclusion move ③ Output: , |
| Algorithm 5: MCMC sampling pseudocode for the PCCs-ED-DBN model |
| Input: MCMC samples the current state: Output: New MCMC status: |
| ① Keep the current , fixed, and update to according to Algorithm 1. ② Keep the current and fixed, and update to according to Algorithm 2. ③ Keep the current , , fixed, and update to according to Algorithm 4. |
4. Empirical Results
4.1. Evaluation Standard
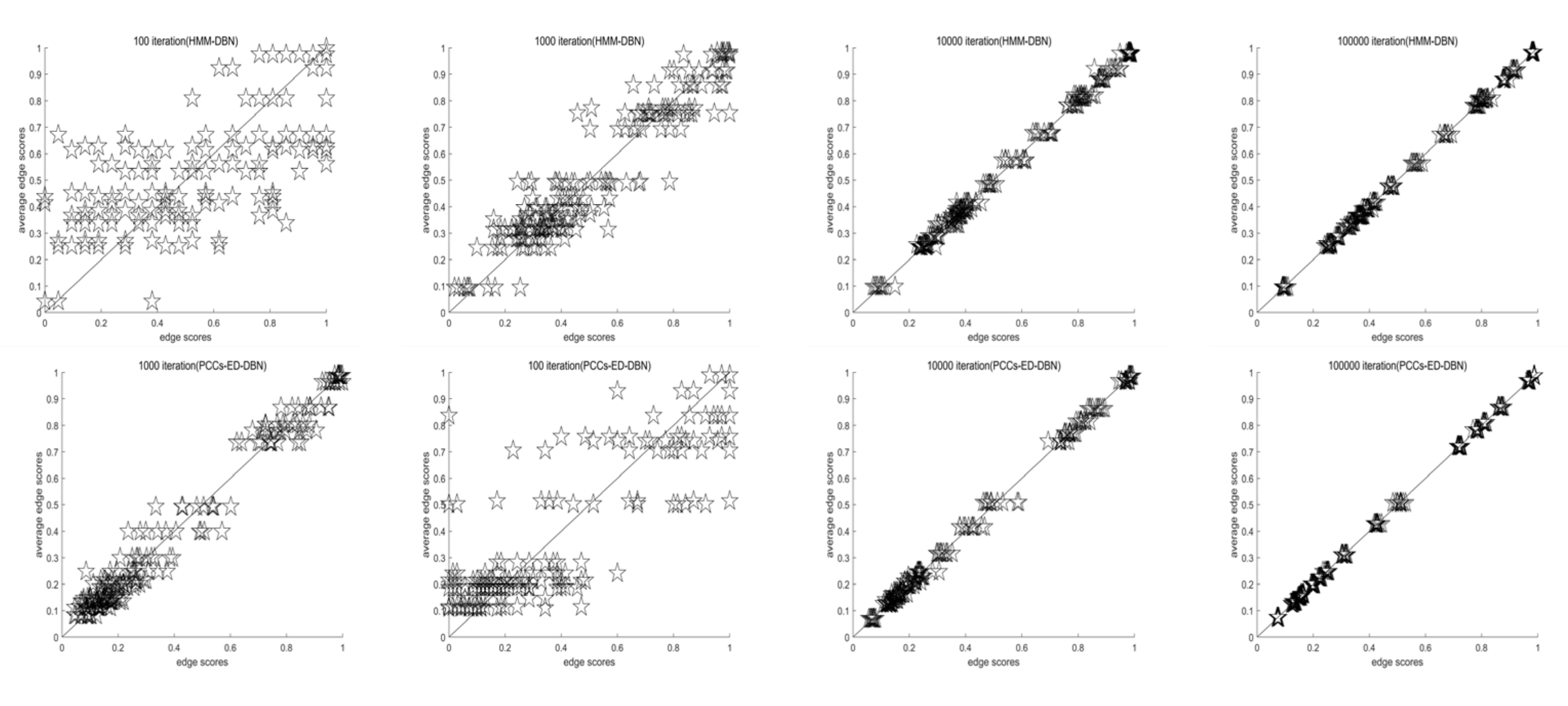
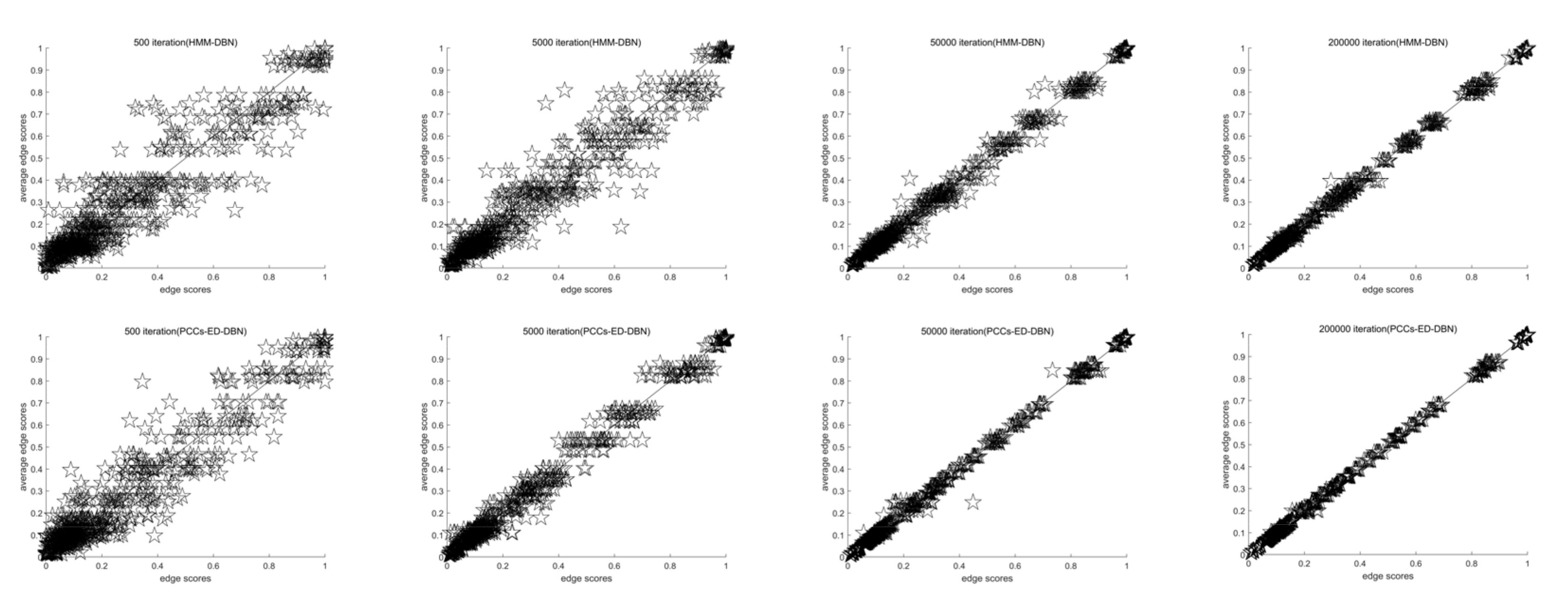
4.1.1. Convergence Evaluation Criteria
4.1.2. Network Structure Accuracy Evaluation Criteria
4.1.3. Criteria for Model Stability
4.2. Experimental Results
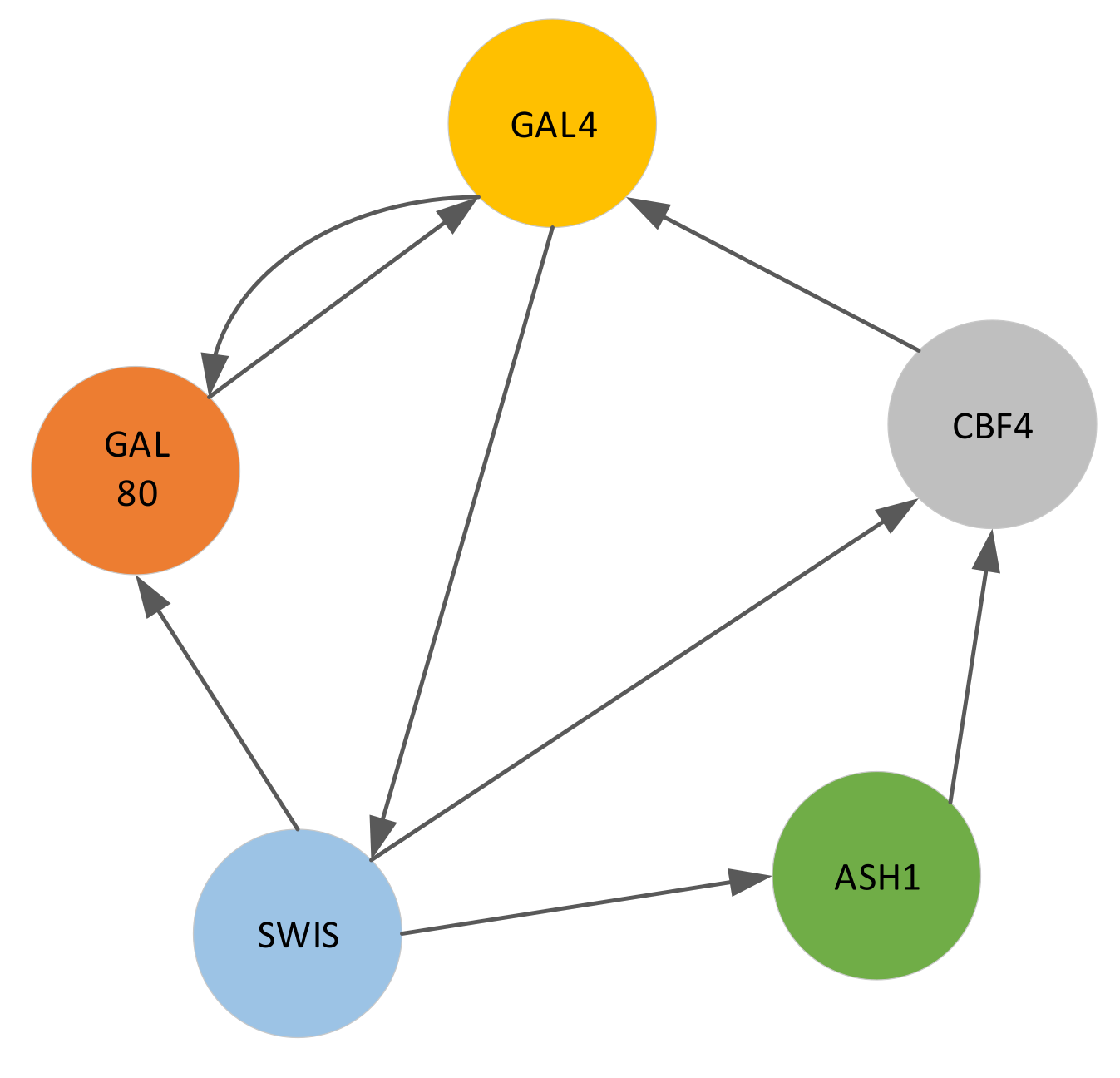
4.2.1. Saccharomyces Cerevisiae
4.2.2. Synthetic Yeast Data
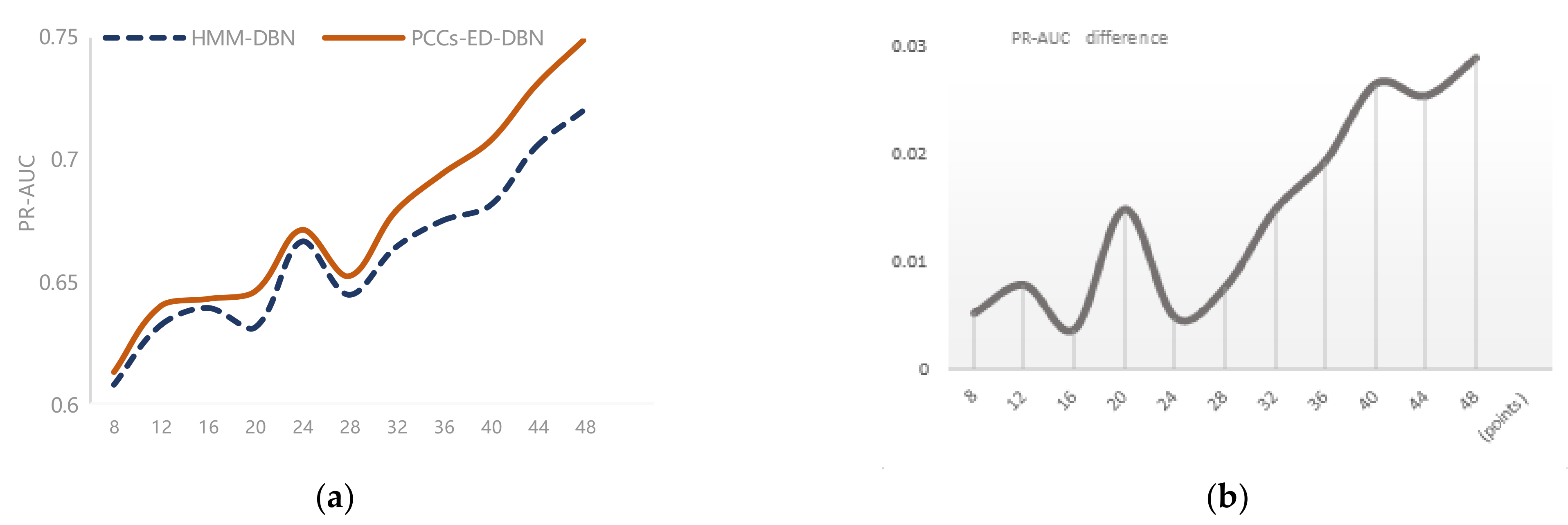
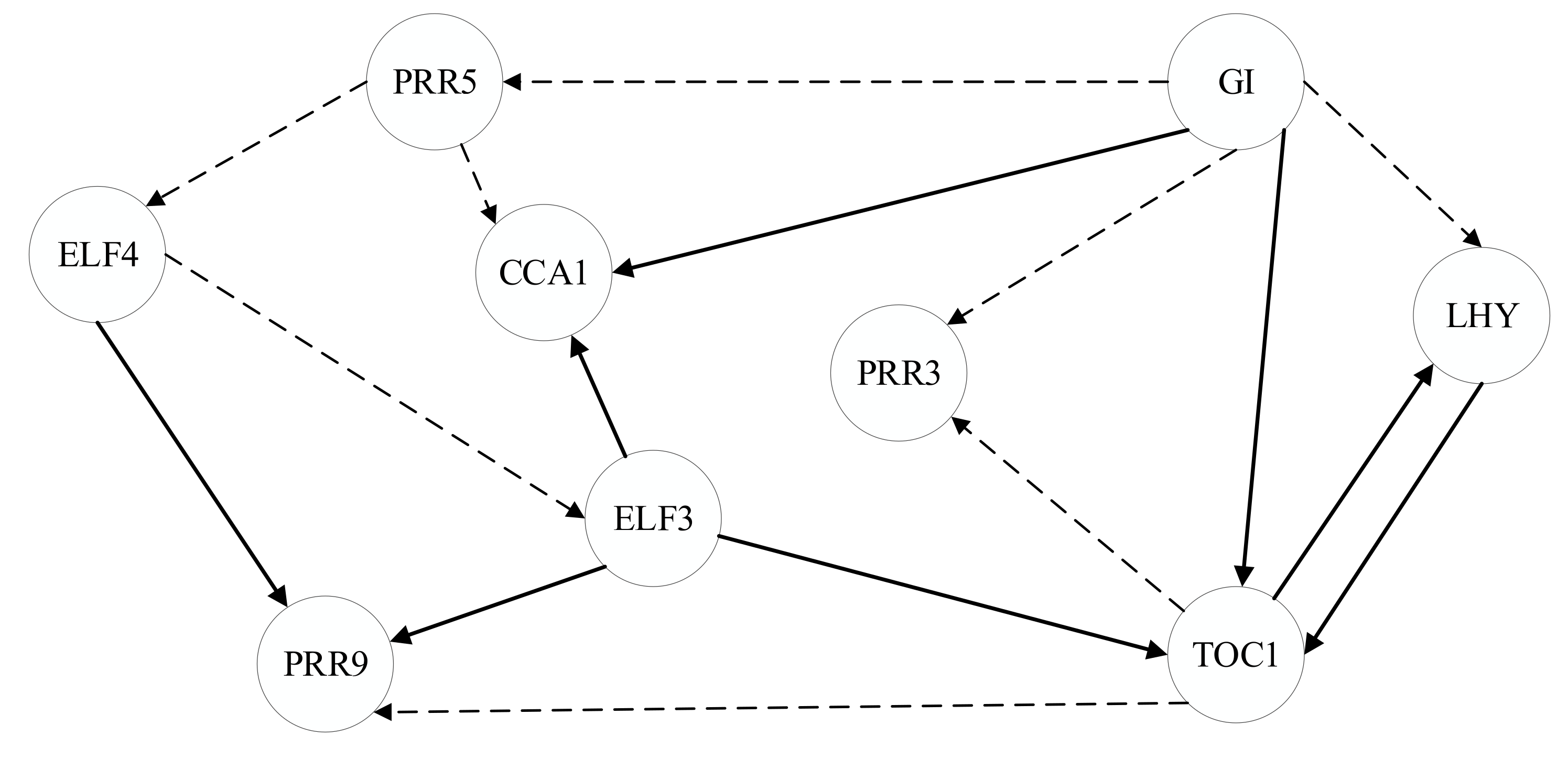
4.2.3. Gene Regulatory Network in Arabidopsis
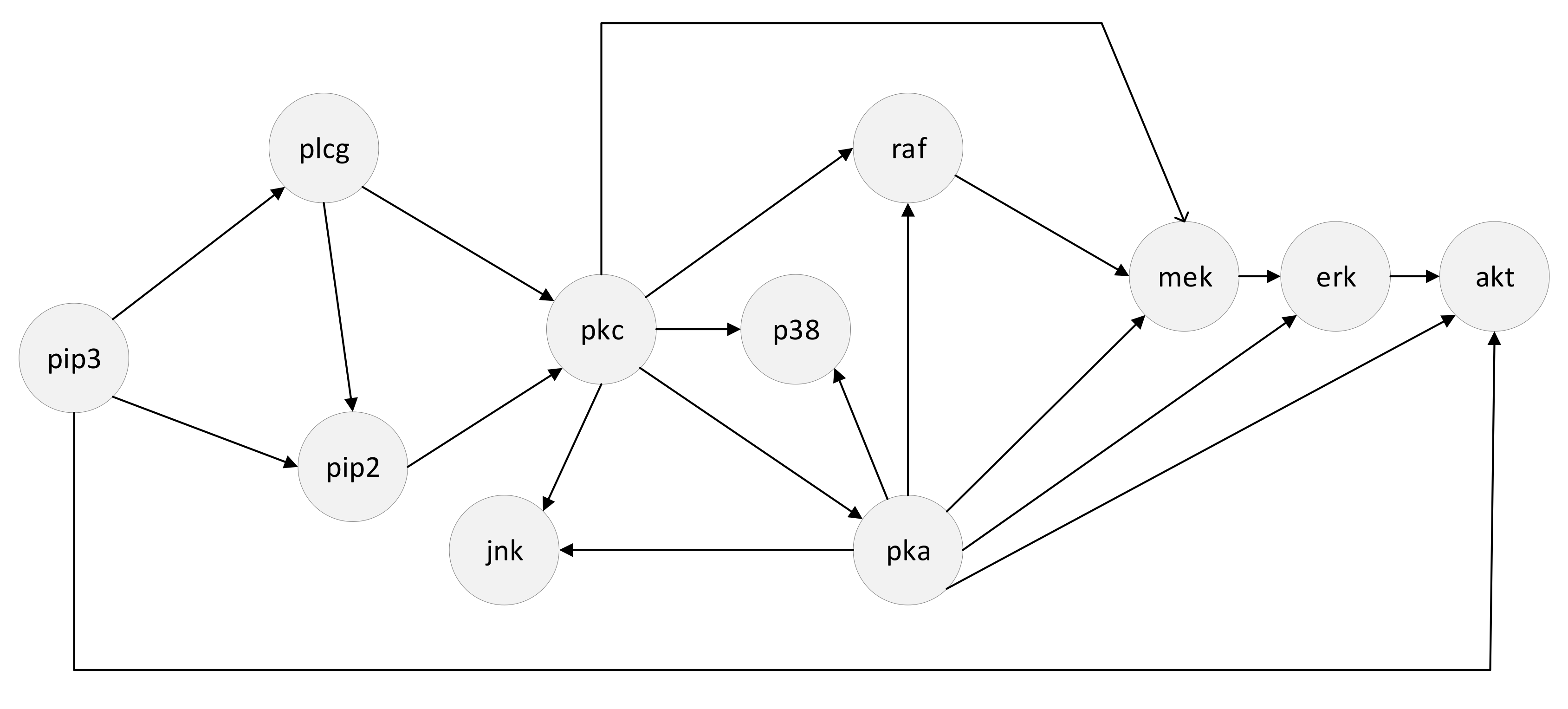
4.2.4. Simulated Data from the RAF Pathway
4.2.5. Time Overhead
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ajmal, H.B.E.; Madden, M.G. Dynamic Bayesian Network Learning to Infer Sparse Models from Time Series Gene Expression Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021. [Google Scholar] [CrossRef] [PubMed]
- Che, D.; Guo, S.; Jiang, Q.; Chen, L. PFBNet: A Priori-Fused Boosting Method for Gene Regulatory Network Inference. BMC Bioinform. 2020, 21, 308. [Google Scholar] [CrossRef] [PubMed]
- Shafiee Kamalabad, M.; Grzegorczyk, M. A New Bayesian Piecewise Linear Regression Model for Dynamic Network Reconstruction. BMC Bioinform. 2021, 22, 196. [Google Scholar] [CrossRef]
- Timmermann, T.; González, B.; Ruz, G.A. Reconstruction of a Gene Regulatory Network of the Induced Systemic Resistance Defense Response in Arabidopsis Using Boolean Networks. BMC Bioinform. 2020, 21, 142. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; He, W.; Tang, J.; Zou, Q.; Guo, F. A Comprehensive Overview and Critical Evaluation of Gene Regulatory Network Inference Technologies. Brief. Bioinform. 2021, 22, bbab009. [Google Scholar] [CrossRef] [PubMed]
- Friedman, N.; Linial, M.; Nachman, I.; Pe’Er, D. Using Bayesian Networks to Analyze Expression Data. J. Comput. Biol. 2000, 7, 601–620. [Google Scholar] [CrossRef]
- Talih, M.; Hengartner, N. Structural Learning with Time-Varying Components: Tracking the Cross-Section of Financial Time Series. J. R. Stat. Soc. Ser. B 2005, 67, 321–341. [Google Scholar] [CrossRef]
- Xuan, X.; Murphy, K. Modeling Changing Dependency Structure in Multivariate Time Series. In Proceedings of the 24th International Conference on Machine Learning, New York, NY, USA, 20–24 June 2007. [Google Scholar]
- Lebre, S. Stochastic Process Analysis for Genomics and Dynamic Bayesian Networks Inference. Master’s Thesis, Université d’Evry-Val d’Essonne, Évry-Courcouronnes, France, 2007. [Google Scholar]
- Robinson, J.; Hartemink, A. Non-stationary Dynamic Bayesian Networks. In Advances in Neural Information Processing Systems 21 (NIPS 2008); Curran Associates Inc.: Red Hook, NY, USA, 2008. [Google Scholar]
- Robinson, J.W.; Hartemink, A.J.; Ghahramani, Z. Learning Non-Stationary Dynamic Bayesian Networks. J. Mach. Learn. Res. 2010, 11, 3647–3680. [Google Scholar]
- Kolar, M.; Song, L.; Xing, E. Sparsistent Learning of Varying-Coefficient Models with Structural Changes. Adv. Neural Inf. Processing Syst. 2009, 22, 1006–1014. [Google Scholar]
- Aderhold, A.; Husmeier, D.; Grzegorczyk, M. Statistical Inference of Regulatory Networks for Circadian Regulation. Stat. Appl. Genet. Mol. Biol. 2014, 13, 227–273. [Google Scholar] [CrossRef]
- Shafiee Kamalabad, M.; Heberle, A.M.; Thedieck, K.; Grzegorczyk, M. Partially Non-Homogeneous Dynamic Bayesian Networks Based on Bayesian Regression Models with Partitioned Design Matrices. Bioinformatics 2019, 35, 2108–2117. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Xing, E.P. Recovering Time-Varying Networks of Dependencies in Social and Biological Studies. Proc. Natl. Acad. Sci. USA 2009, 106, 11878–11883. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.; He, D. A Segmental Hidden Semi-Markov Model (HSMM)-Based Diagnostics and Prognostics Framework and Methodology. Mech. Syst. Signal Processing 2007, 21, 2248–2266. [Google Scholar] [CrossRef]
- Dondelinger, F.; Lebre, S.; Husmeier, D. Heterogeneous Continuous Dynamic Bayesian Networks with Flexible Structure and Inter-Time Segment Information Sharing. In International Conference on Machine Learning (ICML); Furnkranz, J., Joachims, T., Eds.; Omnipress: Haifa, Israel, 2010; pp. 303–310. [Google Scholar]
- Dondelinger, F.; Lèbre, S.; Husmeier, D. Non-Homogeneous Dynamic Bayesian Networks with Bayesian Regularization for Inferring Gene Regulatory Networks with Gradually Time-Varying Structure. Mach. Learn. 2013, 90, 191–230. [Google Scholar] [CrossRef]
- Lèbre, S.; Becq, J.; Devaux, F.; Stumpf, M.P.; Lelandais, G. Statistical Inference of the Time-Varying Structure of Gene-Regulation Networks. BMC Syst. Biol. 2010, 4, 130. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Husmeier, D. Non-Homogeneous Dynamic Bayesian Networks for Continuous Data. Mach. Learn. 2011, 83, 355–419. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Husmeier, D. Regularization of Non-Homogeneous Dynamic Bayesian Networks with Global Information-Coupling Based on Hierarchical Bayesian Models. Mach. Learn. 2013, 91, 105–154. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Husmeier, D. A Non-Homogeneous Dynamic Bayesian Network with Sequentially Coupled Interaction Parameters for Applications in Systems and Synthetic Biology. Stat. Appl. Genet. Mol. Biol. 2012, 11, 1–62. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Husmeier, D.; Edwards, K.D.; Ghazal, P.; Millar, A.J. Modelling Non-stationary Gene Regulatory Processes with a Non-homogeneous Bayesian Network and the Allocation Sampler. Bioinformatics 2008, 24, 2071–2078. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Husmeier, D. Modelling Non-stationary Gene Regulatory Processes with a Non-homogeneous Dynamic Bayesian Network and the Change Point Process. In Proceedings of the 6th International Workshop on Computational Systems Biology, Aarhus, Denmark, 10–12 June 2009. [Google Scholar]
- Grzegorczyk, M. A Non-homogeneous Dynamic Bayesian Network with a Hidden Markov Model Dependency Structure among the Temporal Data Points. Mach. Learn. 2016, 102, 155–207. [Google Scholar] [CrossRef]
- Grzegorczyk, M.; Husmeier, D. Non-stationary Continuous Dynamic Bayesian Networks. In Advances in Neural Information Processing Systems 22 (NIPS 2009); Curran Associates Inc.: Red Hook, NY, USA, 2009. [Google Scholar]
- Cohen, I.; Juang, Y.; Chen, J.; Benesty, J. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Davis, J.; Goadrich, M. The Relationship between Precision-Recall and Roc Curves. In Proceedings of the 23rd International Conference on Machine Learning, New York, NY, USA, 25–29 June 2006. [Google Scholar]
- Cantone, I.; Marucci, L.; Iorio, F.; Ricci, M.A.; Belcastro, V.; Bansal, M.; Santini, S.; di Bernardo, M.; di Bernardo, D.; Cosma, M.P. A Yeast Synthetic Network for In Vivo Assessment of Reverse-Engineering and Modeling Approaches. Cell 2009, 137, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Shafiee Kamalabad, M.; Grzegorczyk, M. Non-Homogeneous Dynamic Bayesian Networks with Edge-Wise Sequentially Coupled Parameters. Bioinformatics 2020, 36, 1198–1207. [Google Scholar] [CrossRef] [PubMed]
- Aluru, M.; Shrivastava, H.; Chockalingam, S.P.; Shivakumar, S.; Aluru, S. EnGRaiN: A Supervised Ensemble Learning Method for Recovery of Large-Scale Gene Regulatory Networks. Bioinformatics 2021, 38, 1312–1319. [Google Scholar] [CrossRef] [PubMed]
- Dávila-Velderrain, J.; Caldú-Primo, J.L.; Martínez-García, J.C.; Álvarez-Buylla Roces, M.A. Gene Regulatory Network Dynamical Logical Models for Plant Development. In Plant Systems Biology; Springer: Berlin/Heidelberg, Germany, 2022; Volume 2395, pp. 59–77. [Google Scholar]
- Monga, I.; Randhawa, V.; Dhanda, S.K. Connecting the Dots: Using Machine Learning to Forge Gene Regulatory Networks from Large Biological Datasets. At the Intersection of GRNs: Where System Biology Meets Machine Learning. In Machine Learning and Systems Biology in Genomics and Health; Springer: Berlin/Heidelberg, Germany, 2022; pp. 103–121. [Google Scholar] [CrossRef]
- Miwa, K.; Serikawa, M.; Suzuki, S.; Kondo, T.; Oyama, T. Conserved Expression Profiles of Circadian Clock-related Genes in Two Lemna Species Showing Long-day and Short-day Photoperiodic Flowering Responses. Plant Cell Physiol. 2006, 47, 601–612. [Google Scholar] [CrossRef]
- Dixon, L.E.; Knox, K.; Kozma-Bognar, L.; Southern, M.M.; Pokhilko, A.; Millar, A.J. Temporal Repression of Core Circadian Genes Is Mediated through EARLY FLOWERING 3 in Arabidopsis. Curr. Biol. 2011, 21, 120–125. [Google Scholar] [CrossRef]
- Chow, B.Y.; Helfer, A.; Nusinow, D.A.; Kay, S.A. ELF3 Recruitment to the PRR9 Promoter Requires Other Evening Complex Members in the Arabidopsis Circadian Clock. Plant Signal. Behav. 2012, 7, 170–173. [Google Scholar] [CrossRef]
- Locke, J.C.W.; Kozma-Bognár, L.; Gould, P.D.; Fehér, B.; Kevei, É.; Nagy, F.; Turner, M.S.; Hall, A.; Millar, A.J. Experimental Validation of a Predicted Feedback Loop in the Multi-Oscillator Clock of Arabidopsis Thaliana. Mol. Syst. Biol. 2006, 2, 59. [Google Scholar] [CrossRef]
- Herrero, E.; Kolmos, E.; Bujdoso, N.; Yuan, Y.; Wang, M.; Berns, M.C.; Uhlworm, H.; Coupland, G.; Saini, R.; Jaskolski, M.; et al. EARLY FLOWERING4 Recruitment of EARLY FLOWERING3 in the Nucleus Sustains the Arabidopsis Circadian Clock. Plant Cell 2012, 24, 428–443. [Google Scholar] [CrossRef]
- Sachs, K.; Perez, O.; Pe’Er, D.; Lauffenburger, D.A.; Nolan, G.P. Causal Protein-Signaling Networks Derived from Multiparameter Single-Cell Data. Science 2005, 308, 523–529. [Google Scholar] [CrossRef]




| Symbol | Explanation |
|---|---|
| The number of components for node g | |
| k | ) |
| The noise parameter for the k-th component of node g | |
| M | |
| The signal-to-noise hyperparameter for node g see (4) | |
| The noise variance hyperparameter for node g see (5) | |
| The parent node set of node g | |
| The interaction parameter vector for the k-th component of node g | |
| The target values of node g in component k | |
| The design matrix for component k of node g | |
| The set of candidate parent nodes |
| Iteration | 200 | 400 | 600 | 800 | 1000 | 1200 | 1500 | 2000 | 2500 | 3000 | 5000 | 10,000 |
| HMM-DBN | 0.0070 | 0.0062 | 0.0050 | 0.0038 | 0.0030 | 0.0024 | 0.0026 | 0.0018 | 0.0016 | 0.0010 | 0.0008 | 0.0004 |
| PCCs-ED-DBN | 0.0051 | 0.0028 | 0.0026 | 0.0013 | 0.0010 | 0.0009 | 0.0008 | 0.0007 | 0.0006 | 0.0006 | 0.0005 | 0.0001 |
| Iteration | 100 | 200 | 300 | 500 | 1000 | 1500 | 2000 | 3000 | 4000 | 8000 | 10,000 |
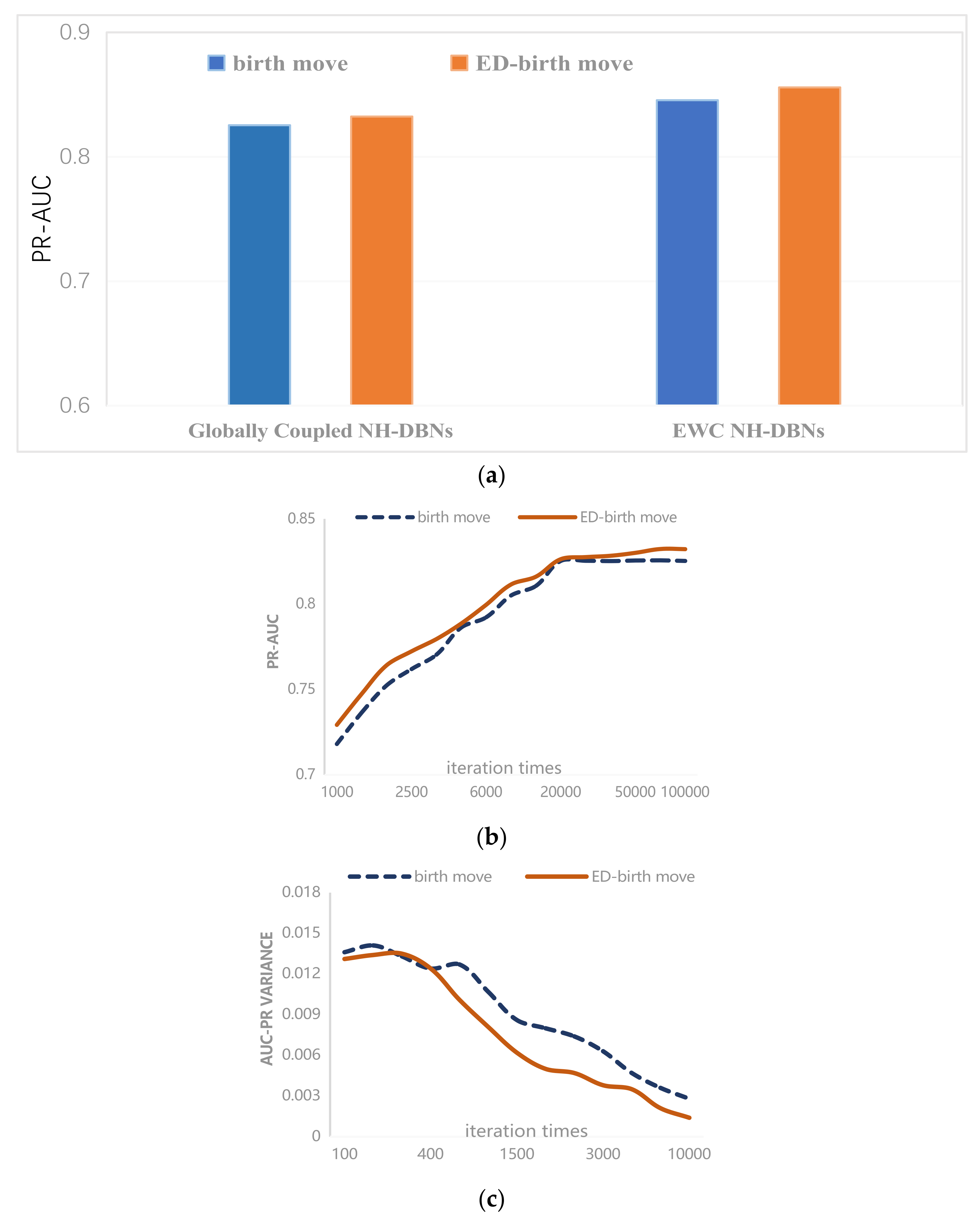
| Birth | 0.0136 | 0.0141 | 0.0133 | 0.0124 | 0.0107 | 0.0086 | 0.0080 | 0.0063 | 0.0047 | 0.0036 | 0.0028 |
| ED-birth | 0.0131 | 0.0134 | 0.0135 | 0.0124 | 0.0101 | 0.0081 | 0.0062 | 0.0055 | 0.0038 | 0.0035 | 0.0021 |
| DATA | Iteration | HMM-DBN | PCCs-ED-DBN | |
|---|---|---|---|---|
| Saccharomyces cerevisiae | 10,000 | 315 s | 325 s | |
| Arabidopsis | 50,000 | 2706 s | 2757 s | |
| RAF pathway | data_1 | 50,000 | 5371 s | 5497 s |
| data_2 | 50,000 | 5364 s | 5488 s | |
| data_3 | 50,000 | 5370 s | 5480 s | |
| data_4 | 50,000 | 5399 s | 5501 s | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Hu, C.; Zhang, Q. Constructing a Gene Regulatory Network Based on a Nonhomogeneous Dynamic Bayesian Network. Electronics 2022, 11, 2936. https://doi.org/10.3390/electronics11182936
Zhang J, Hu C, Zhang Q. Constructing a Gene Regulatory Network Based on a Nonhomogeneous Dynamic Bayesian Network. Electronics. 2022; 11(18):2936. https://doi.org/10.3390/electronics11182936
Chicago/Turabian StyleZhang, Jiayao, Chunling Hu, and Qianqian Zhang. 2022. "Constructing a Gene Regulatory Network Based on a Nonhomogeneous Dynamic Bayesian Network" Electronics 11, no. 18: 2936. https://doi.org/10.3390/electronics11182936
APA StyleZhang, J., Hu, C., & Zhang, Q. (2022). Constructing a Gene Regulatory Network Based on a Nonhomogeneous Dynamic Bayesian Network. Electronics, 11(18), 2936. https://doi.org/10.3390/electronics11182936






