ASARIMA: An Adaptive Harvested Power Prediction Model for Solar Energy Harvesting Sensor Networks
Abstract
:1. Introduction
- We present the ASARIMA (adaptive seasonal auto-regressive integrated moving average), a new energy prediction model that varies seasonal changes in solar energy harvested based on ARIMA.
- In the ASARIMA model, the similarity of weather between days makes the model dynamically adaptive and adjusts the training set at the same time.
- We use the dataset with much less data than the neural network algorithm in order to make the complexity of the model moderate.
- We evaluate the performance of our algorithm by comparing it with the classical prediction algorithm, indicating that the proposed ASARIMA model can effectively improve the accuracy of solar energy prediction.
2. Related Work
3. SARIMA Time Series Model
3.1. Stationarity of Time Series
3.2. ARMA Model
3.2.1. AR Model
3.2.2. MA Model
3.2.3. SARIMA Model
4. ASARIMA Model
4.1. Method Design
- In accordance with the time-series diagram of the training set , determine the seasonal period S.
- Perform seasonal difference on the time series to obtain the seasonal periodic time series as Equation (16):where .
- Perform the ADF stationarity test on the sequence. If , then the sequence is stationary; otherwise, the difference is made until the sequence after the difference is stationary. If the d-th difference sequence is smooth, then we can obtain a seasonal difference sequence through Equation (17):where , and denotes the d-th difference. After ensuring that the sequence is stable, our goal is to determine the optimal order of the model according to the AIC.
- Judge the properties of the time series using the ACF and PACF graphs, and determine the ranges of p and q preliminarily through truncation and trailing.
- Using a traversal method to enumerate each set of possible , select the optimal SARIMA () model using the AIC. The representation of the AIC is shown in Equation (18):where L is the likelihood function, and Q is the number of parameters. A small denotes a favorable model.
- Combine the training set and predicted M time slots with the optimal SARIMA model to yield Equation (19):
- Perform the d-order differential reduction of the abovementioned results. The recursive formula is expressed as Equation (20):where ; and .
- Perform periodic restoration to acquire the predicted value as shown in Equation (21):
4.2. Flow of the ASARIMA
- Use N historical data before the time slot as the training set, and then calculate the similarity between the current and reference days in accordance with the Euclidean distance.
- Adaptively adjust the position of the historical data in the training set in accordance with the similarity, that is, the data of the reference day with the similarity are close to the current predicted time, thereby obtaining a new training set.
- Perform the seasonal decomposition of new training sets to eliminate trends.
- Conduct the ADF test on the sequence after seasonal decomposition for its stationarity. If the sequence is unstable, then make the difference until it is stable. The time series of solar power harvesting is a stationary sequence, which will not fall into an endless cycle.
- Form the value range of p and q in the ACF/PACF estimation model of the time series in accordance with the new training set. Then, fit the historical data with each possible ARIMA model through the traversal method. Finally, select the optimal model based on the AIC.
- Use the optimal model above for prediction. Perform the d-order differential and seasonal reductions for this value, and obtain the predicted power of the harvested solar energy.
5. Analysis of Results and Performance
5.1. Rationality Analysis of the ASARIMA Model
5.1.1. Determining the Parameters of ARIMA
5.1.2. SARIMA Model
5.1.3. ASARIMA Model
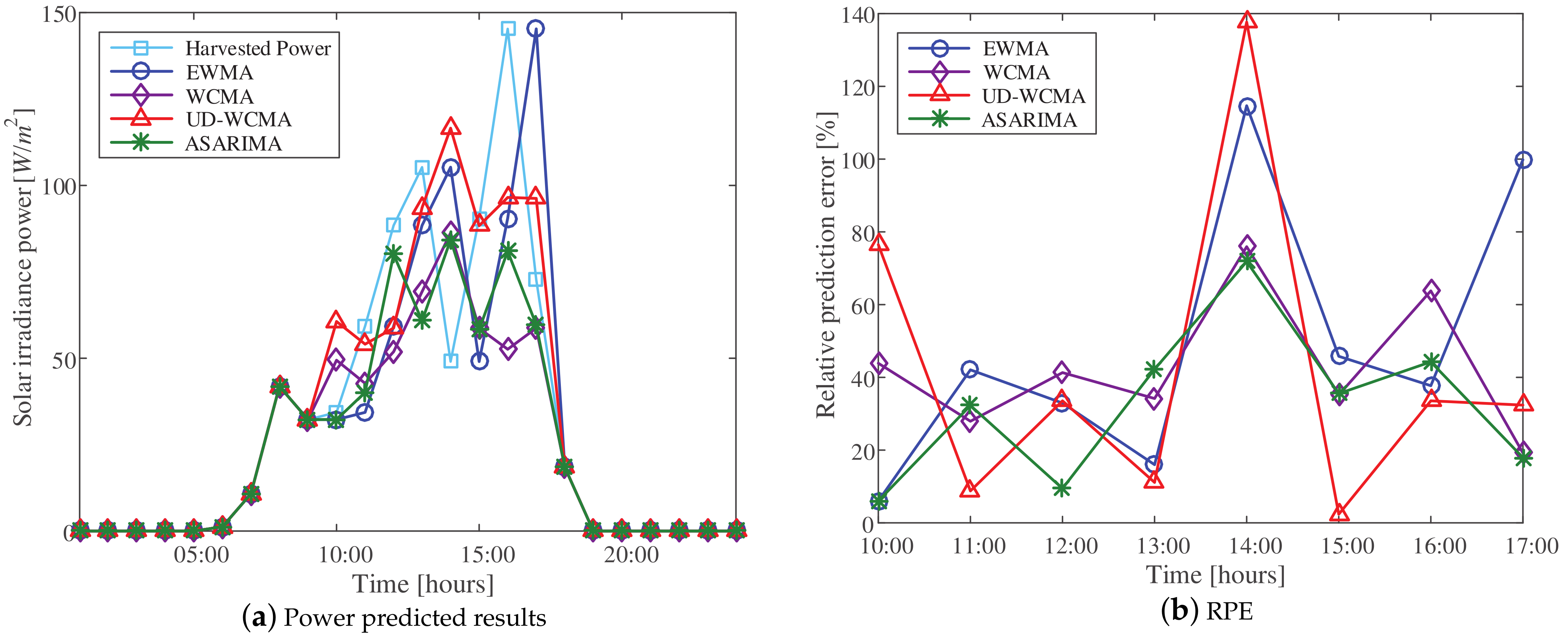
5.2. Comparing the Relative Errors of Different Schemes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akyildiz, I.F.; Vuran, M.C. Wireless Sensor Networks; John Wiley & Sons, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Zhou, J.; Han, T.; Xiao, F.; Gui, G.; Adebisi, B.; Gacanin, H.; Sari, H. Multi-scale network traffic prediction method based on deep echo state network for internet of things. IEEE Internet Things J. 2022. [Google Scholar] [CrossRef]
- Adu-Manu, K.S.; Adam, N.; Tapparello, C.; Ayatollahi, H.; Heinzelman, W. Energy-Harvesting Wireless Sensor Networks (EH-WSNs): A Review. ACM Trans. Sens. Netw. 2018, 14, 2. [Google Scholar] [CrossRef]
- Du, X.; Li, Y.; Zhou, S.; Zhou, Y. ATS-LIA: A lightweight mutual authentication based on adaptive trust strategy in flying ad-hoc networks. Peer-to-Peer Netw. Appl. 2022, 15, 1979–1993. [Google Scholar] [CrossRef] [PubMed]
- Engmann, F.; Katsriku, F.A.; Abdulai, J.D.; Adu-Manu, K.S.; Banaseka, F.K. Prolonging the lifetime of wireless sensor networks: A review of current techniques. Wirel. Commun. Mob. Comput. 2018. [Google Scholar] [CrossRef]
- Ashraf, N.; Faizan, M.; Asif, W.; Qureshi, H.K.; Iqbal, A.; Lestas, M. Energy management in harvesting enabled sensing nodes: Prediction and control. J. Netw. Comput. Appl. 2019, 132, 104–117. [Google Scholar] [CrossRef]
- Kansal, A.; Hsu, J.; Zahedi, S.; Srivastava, M.B. Power management in energy harvesting sensor networks. ACM Trans. Embed. Comput. Syst. 2007, 6, 32es. [Google Scholar] [CrossRef]
- Introduction of ARIMA. Available online: http://people.duke.edu/~rnau/411arim.htm (accessed on 20 May 2022).
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Wiley Interdiscip. Rev. Comput. Stat. 2019, 11, E1460. [Google Scholar] [CrossRef]
- Ding, M.; Wang, L.; Bi, R. An ANN-based Approach for Forecasting the Power Output of Photovoltaic System. Procedia Environ. Sci. 2011, 11, 1308–1315. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Q. Accuracy improvement of energy prediction for solar-energy-powered embedded systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 2062–2074. [Google Scholar] [CrossRef]
- Asrari, A.; Wu, T.X.; Ramos, B. A Hybrid Algorithm for Short-Term Solar Power Prediction-Sunshine State Case Study. IEEE Trans. Sustain. Energy 2017, 8, 582–591. [Google Scholar] [CrossRef]
- Recas Piorno, J.; Bergonzini, C.; Atienza, D.; Rosing, T.S. Prediction and management in energy harvested wireless sensor nodes. In Proceedings of the 2009 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace & Electronic Systems Technology, Aalborg, Denmark, 17–20 May 2009; pp. 6–10. [Google Scholar]
- Cammarano, A.; Petrioli, C.; Spenza, D. Pro-energy: A novel energy prediction model for solar and wind energy-harvesting wireless sensor networks. In Proceedings of the 2012 IEEE 9th International Conference on Mobile Ad-Hoc and Sensor Systems (MASS 2012), Las Vegas, NV, USA, 8–11 October 2012; pp. 75–83. [Google Scholar]
- Cammarano, A.; Petrioli, C.; Spenza, D. Online energy harvesting prediction in environmentally powered wireless sensor networks. IEEE Sens. J. 2016, 16, 6793–6804. [Google Scholar] [CrossRef]
- Dehwah, A.H.; Elmetennani, S.; Claudel, C. Ud-WCMA: An energy estimation and forecast scheme for solar powered wireless sensor networks. J. Netw. Comput. Appl. 2017, 90, 17–25. [Google Scholar] [CrossRef]
- Long, H.; Zhang, C.; Geng, R.; Wu, Z.; Gu, W. A Combination Interval Prediction Model based on Biased Convex Cost Function and Auto Encoder. IEEE Trans. Sustain. Energy 2021, 12, 1561–1570. [Google Scholar] [CrossRef]
- Ye, X. The application of ARIMA model in chinese mobile user prediction. In Proceedings of the 2010 IEEE International Conference on Granular Computing, San Jose, CA, USA, 14–16 August 2010; pp. 586–591. [Google Scholar]
- Ma, W.; Pang, Y.; Zou, J. The application of ARIMA in short-timely forecasting for motion of planning boat. In Proceedings of the 2011 International Conference on Computer Science and Service System (CSSS), Nanjing, China, 27–29 June 2011; pp. 3651–3654. [Google Scholar]
- Li, Q.; Guo, N.-N.; Han, Z.Y.; Zhang, Y.B.; Qi, S.X.; Xu, Y.G.; Wei, Y.-M.; Han, X.; Liu, Y.Y. Application of an autoregressive integrated moving average model for predicting the incidence of hemorrhagic fever with renal syndrome. AM J. Trop. Med. Hyg. 2012, 87, 364–370. [Google Scholar] [CrossRef] [PubMed]
- Juang, W.C.; Huang, S.J.; Huang, F.D.; Cheng, P.W.; Wann, S.R. Application of time series analysis in modelling and forecasting emergency department visits in a medical centre in southern taiwan. BMJ Open 2017, 7, e018628. [Google Scholar] [CrossRef] [PubMed]
- Etuk, E.H.; Ojekudo, N. Another look at the SARIMA modelling of the number of dengue cases in campinas, State of Sao Paulo, Brazil. Int. J. Nat. Sci. Res. 2014, 2, 156–164. [Google Scholar]
- Elganainy, M.; Eldwer, A.E. Stochastic forecasting models of the monthly streamflow for the blue nile at eldiem station. Water Resour. 2018, 45, 326–337. [Google Scholar] [CrossRef]
- Maxey, C.; Andreas, A. Oak Ridge National Laboratory (ORNL); Rotating Shadowband Radiometer (RSR); Oak Ridge, Tennessee (Data); NREL Report No. DA-5500-56512; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007. [Google Scholar] [CrossRef]
- Liu, S.; Kong, X.; Xie, A.; Shen, Y.; Zhu, J.; Li, C.; Zhang, Q. A study of the fractal structure of the precipitate and the mechanism of its formation from the gallbladder bile of a patient. Russ. J. Phys. Chem. A 2007, 81, 2084–2089. [Google Scholar] [CrossRef]
- Benjamin, M.A.; Rigby, R.A.; Stasinopoulos, D.M. Generalized autoregressive moving average models. J. Am. Stat. Assoc. 2003, 98, 214–223. [Google Scholar] [CrossRef]








| AR(p) | MA(q) | ARMA() | |
|---|---|---|---|
| ACF | trailing | truncation after q dot | trailing after p dot |
| PACF | truncation after p dot | trailing | trailing after q dot |
| p | q | AIC |
|---|---|---|
| ⋯ | ⋯ | ⋯ |
| 7 | 2 | 8.083049 |
| 7 | 3 | 8.086511 |
| 7 | 4 | 8.099256 |
| 7 | 5 | 8.003247 |
| 7 | 6 | 7.759073 |
| 7 | 7 | 8.068407 |
| 7 | 8 | 8.043562 |
| 8 | 1 | 8.095791 |
| 8 | 2 | 7.838927 |
| 8 | 3 | 7.851368 |
| 8 | 4 | 7.771635 |
| ⋯ | ⋯ | ⋯ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Han, C. ASARIMA: An Adaptive Harvested Power Prediction Model for Solar Energy Harvesting Sensor Networks. Electronics 2022, 11, 2934. https://doi.org/10.3390/electronics11182934
Li L, Han C. ASARIMA: An Adaptive Harvested Power Prediction Model for Solar Energy Harvesting Sensor Networks. Electronics. 2022; 11(18):2934. https://doi.org/10.3390/electronics11182934
Chicago/Turabian StyleLi, Lingsheng, and Chong Han. 2022. "ASARIMA: An Adaptive Harvested Power Prediction Model for Solar Energy Harvesting Sensor Networks" Electronics 11, no. 18: 2934. https://doi.org/10.3390/electronics11182934
APA StyleLi, L., & Han, C. (2022). ASARIMA: An Adaptive Harvested Power Prediction Model for Solar Energy Harvesting Sensor Networks. Electronics, 11(18), 2934. https://doi.org/10.3390/electronics11182934






