Cascade Direct Yaw Moment Control for an Independent Eight In-Wheel Motor-Driven Autonomous Vehicle
Abstract
:1. Introduction
2. Control-Oriented Vehicle Dynamics Modeling
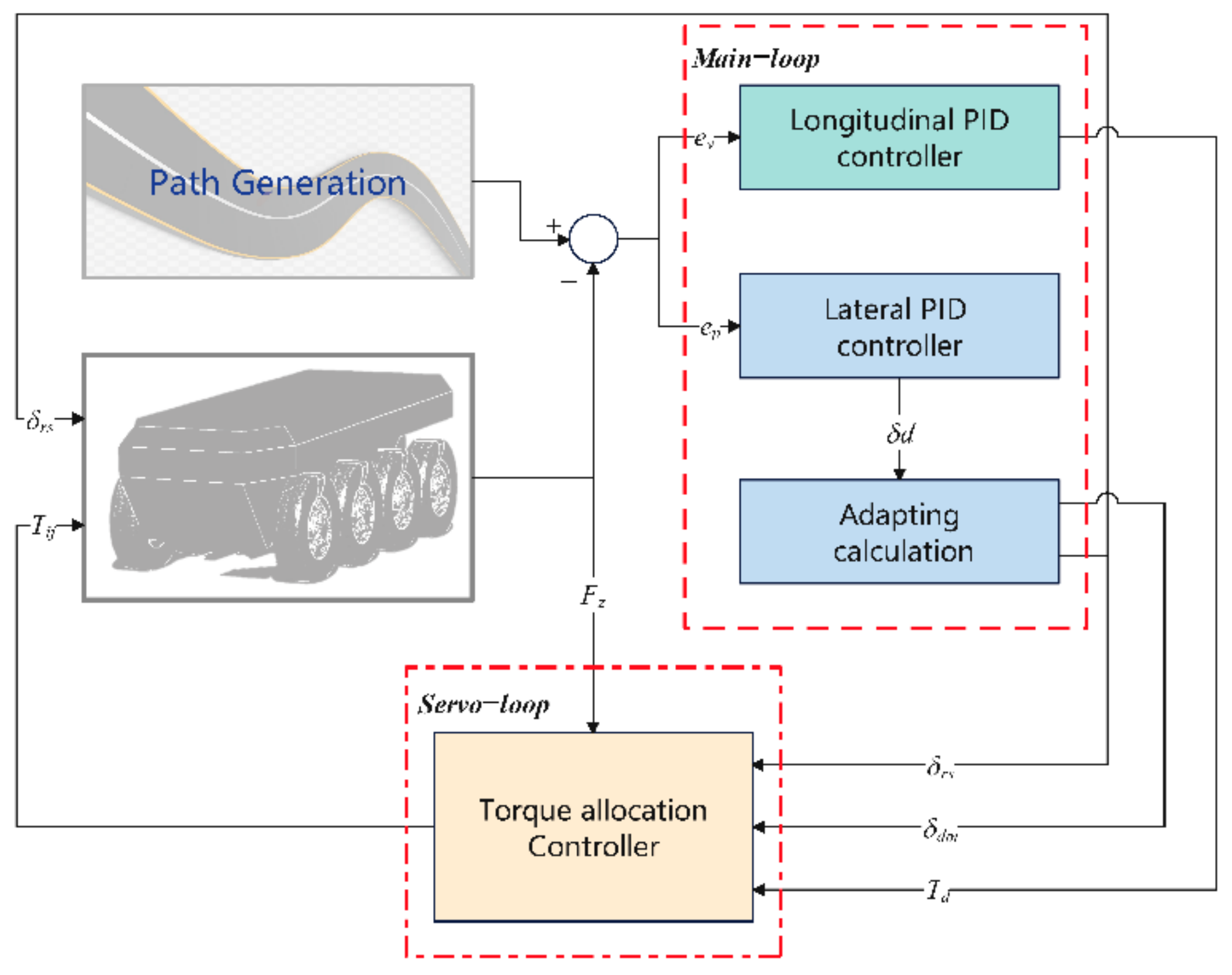
3. The Cascade Controller Design
3.1. The Main Loop Controller
3.2. The Servo Loop Controller
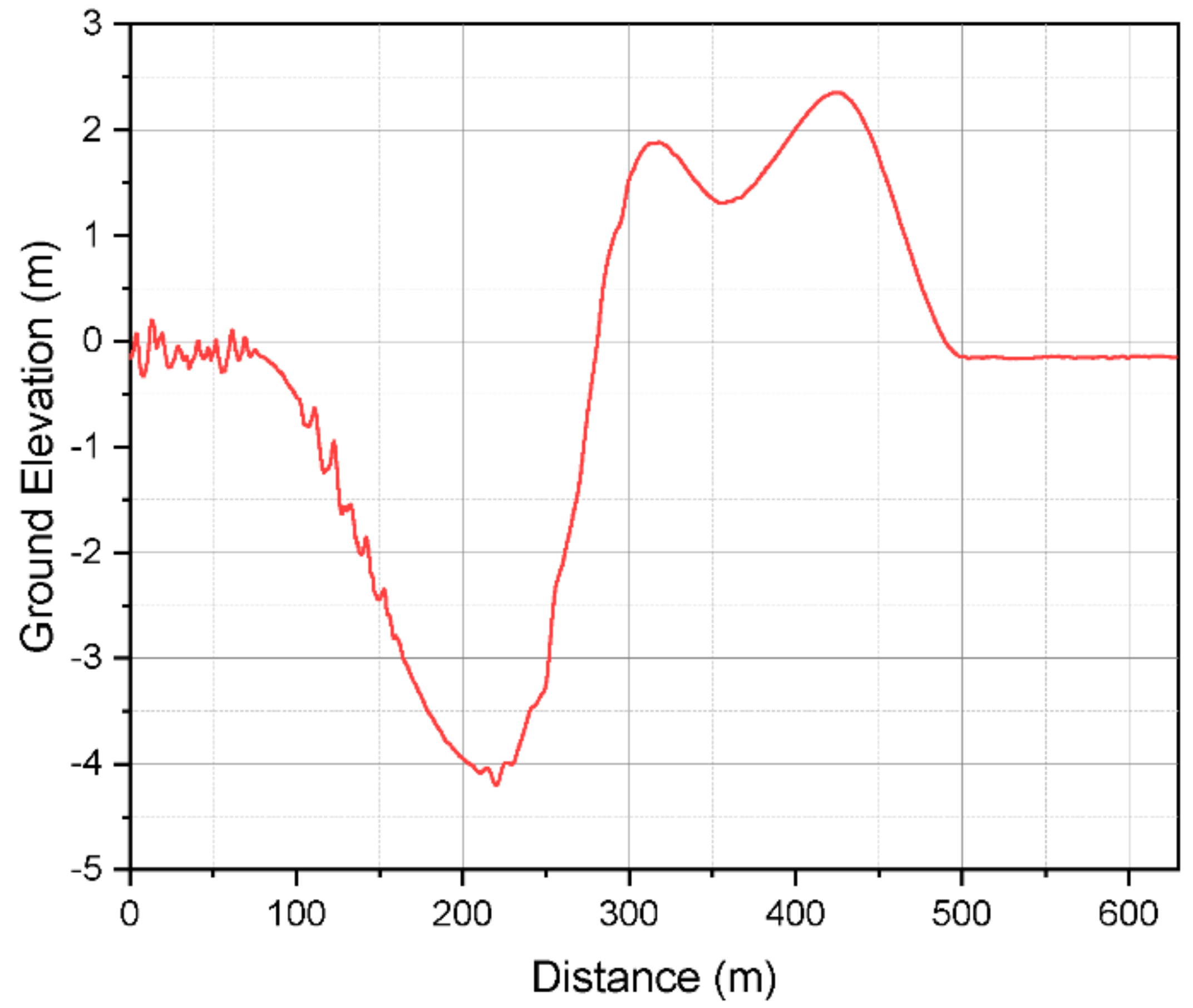
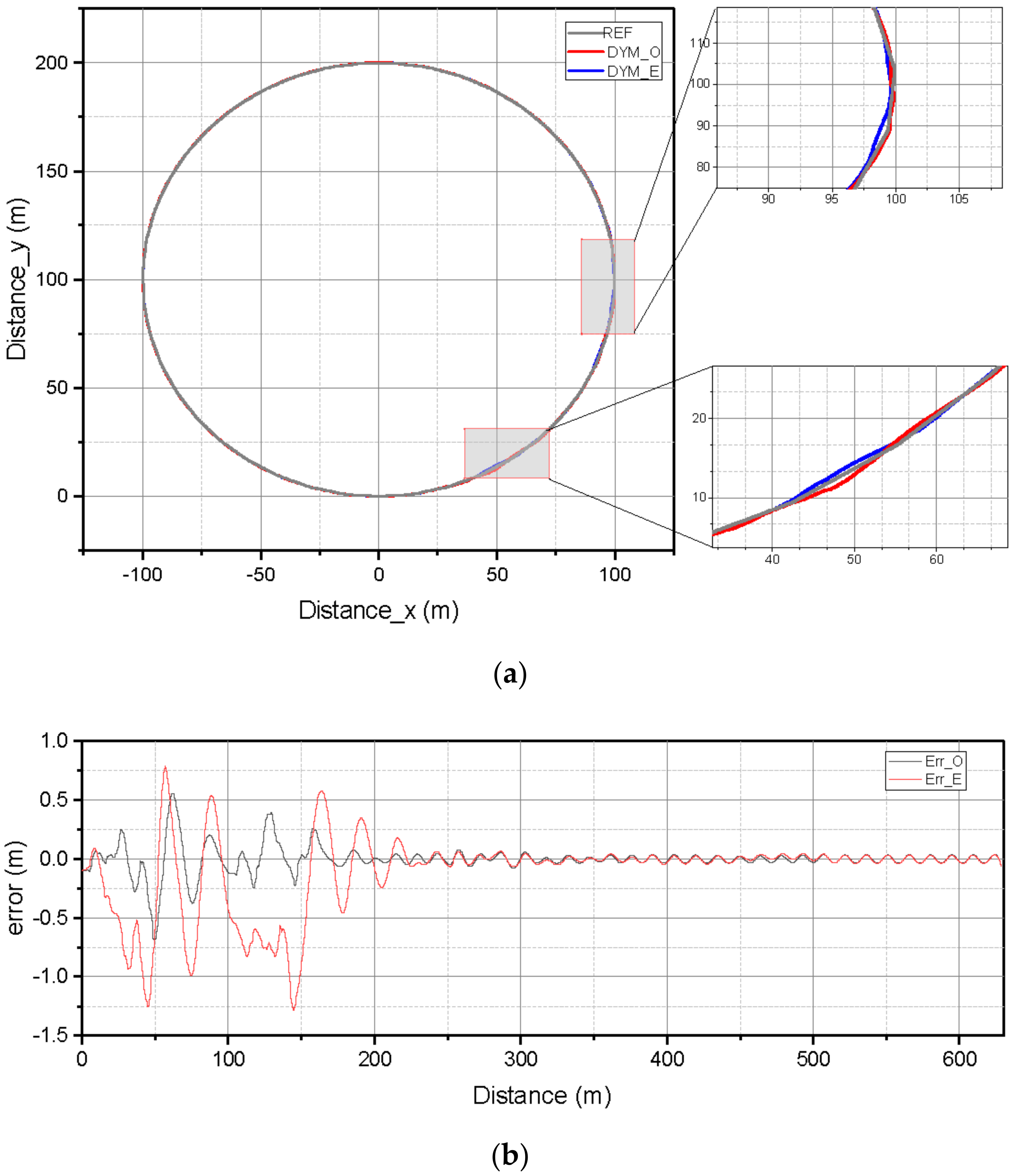
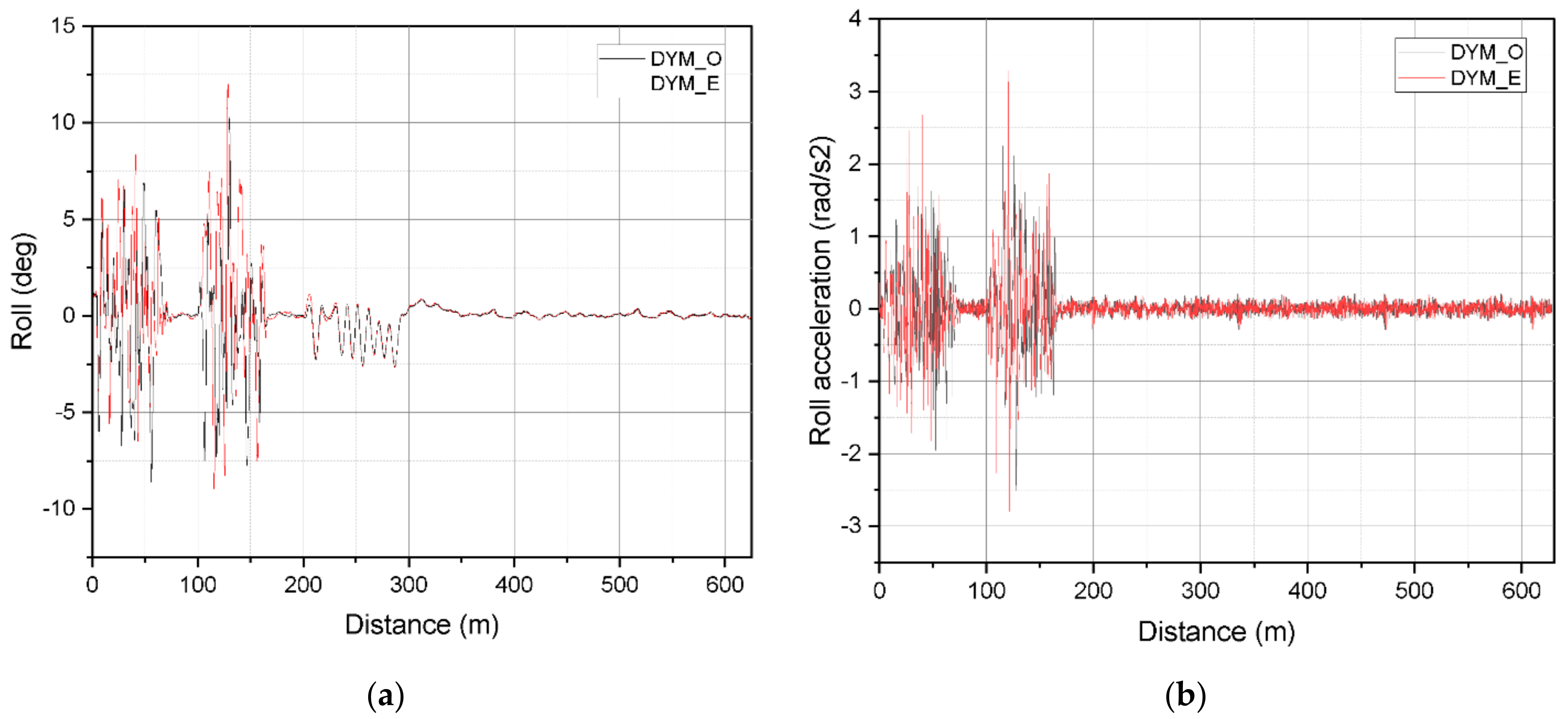
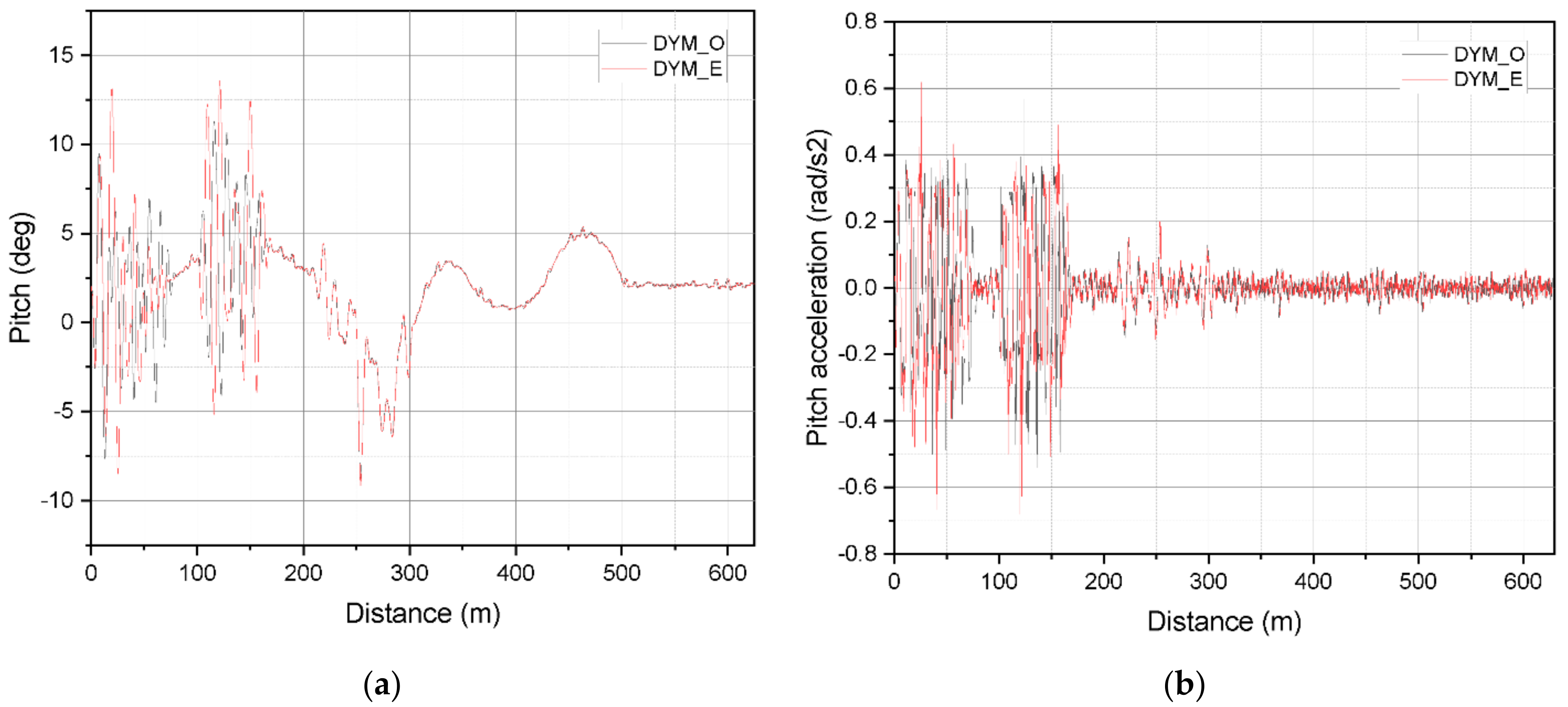
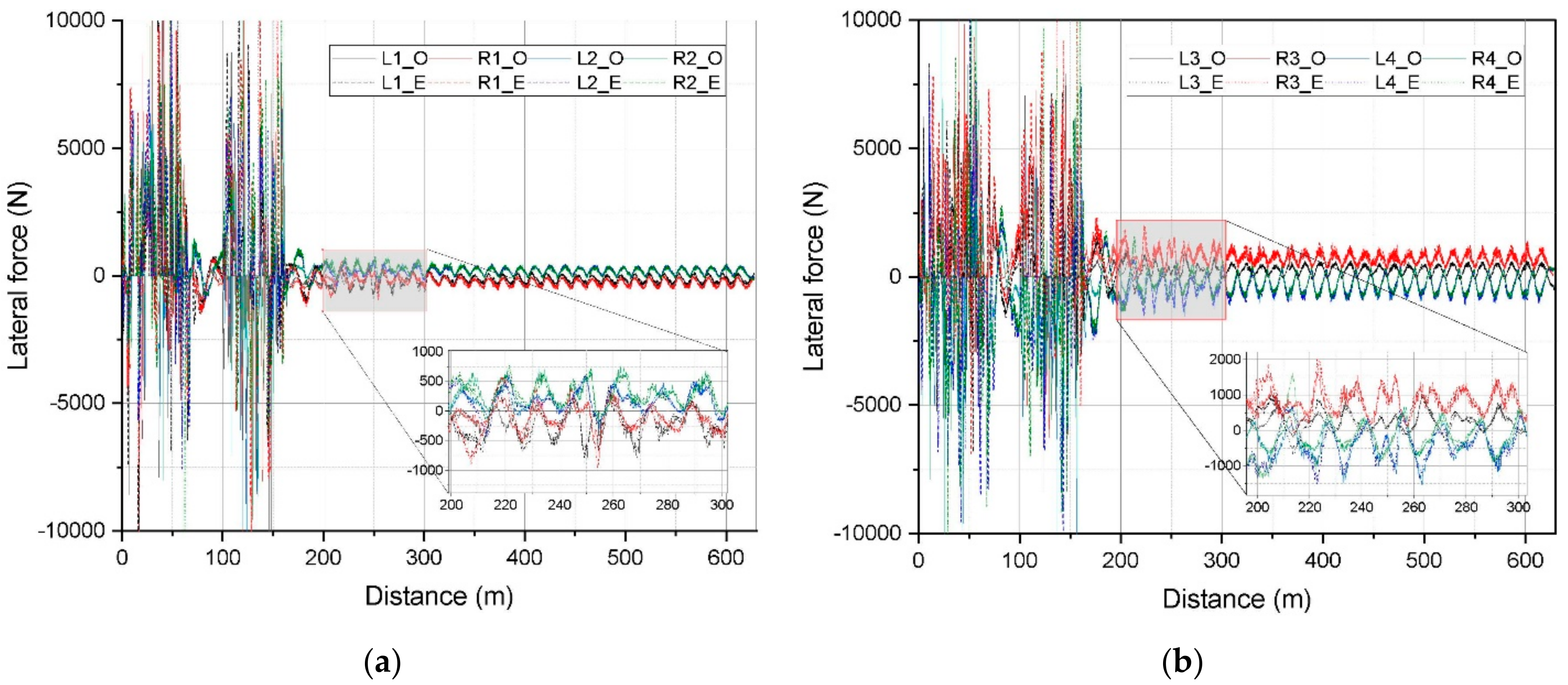
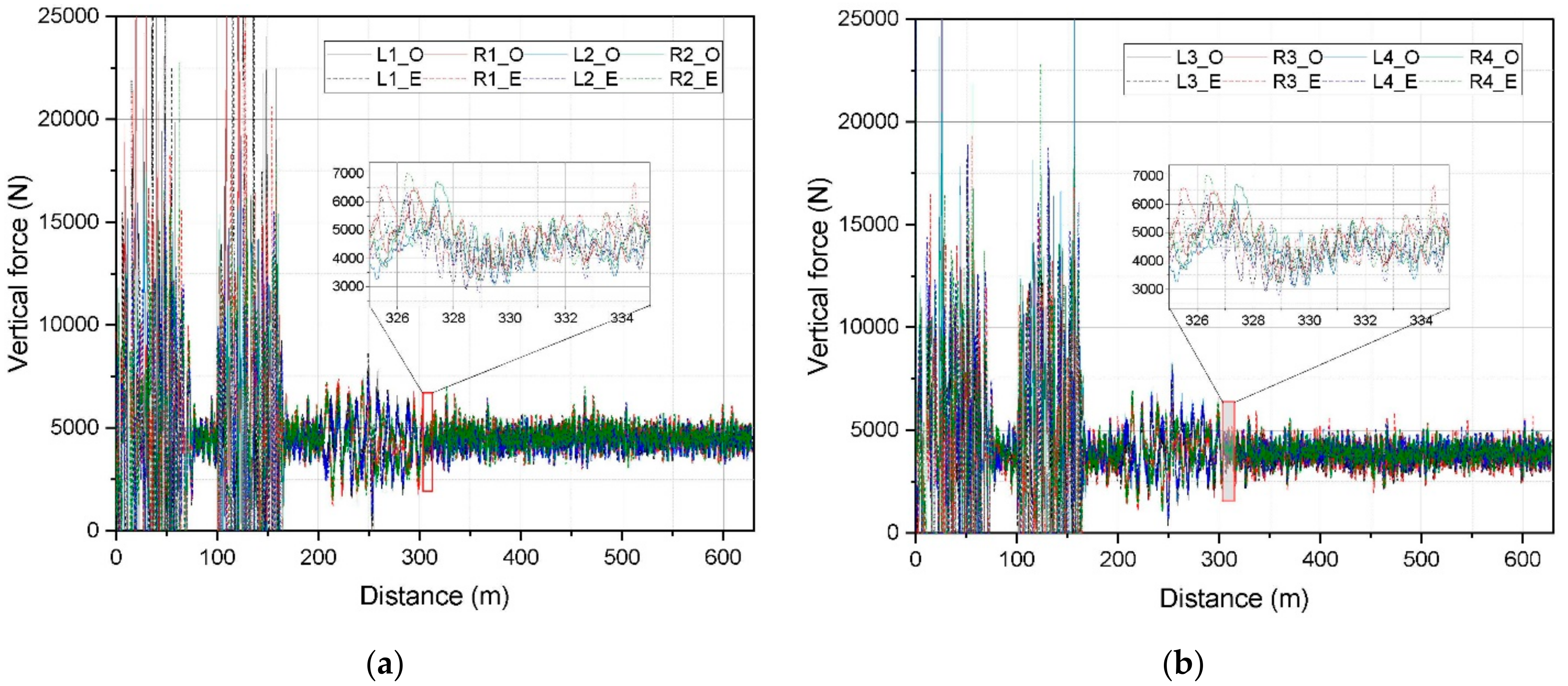
4. Numerical Simulation and Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, G.D.; Jin, X.J.; Zhang, Y. Overview for chassis vehicle dynamics control of distributed drive electric vehicle. J. Chongqing Univ. Technol. 2016, 30, 13–19. [Google Scholar]
- Kumar, M.S.; Revankar, S.T. Development scheme and key technology of an electric vehicle: An overview. Renew. Sustain. Energy Rev. 2017, 70, 1266–1285. [Google Scholar] [CrossRef]
- Luo, T.; Su, B.; Zhang, N.; Tan, S. A control allocation strategy of multi-axle unmanned distributed drive vehicle. In Proceedings of the 2021 2nd International Conference on Artificial Intelligence and Computer Engineering (ICAICE), Hangzhou, China, 5–7 November 2021. [Google Scholar]
- Jackson, A.; Crolla, D.; Woodhouse, A.; Parsons, M. Improving Performance of a 6 × 6 Off-Road Vehicle through Individual Wheel Control; SAE Technical Paper No. 2002-01-0968; SAE International: Warrendale, PA, USA, 2002; pp. 2–3. [Google Scholar]
- Goodarzi, A.; Esmailzadeh, E. Design of a VDC System for All-Wheel Independent Drive Vehicles. IEEE/ASME Trans. Mechatron. 2007, 12, 632–639. [Google Scholar] [CrossRef]
- Geng, C.; Mostefai, L.; Denai, M.; Hori, Y. Direct Yaw-Moment Control of an In-Wheel-Motored Electric Vehicle Based on Body Slip Angle Fuzzy Observer. IEEE Trans. Ind. Electron. 2009, 56, 1411–1419. [Google Scholar] [CrossRef]
- Kim, W.; Yi, K.; Lee, J. Drive control algorithm for an independent 8 in-wheel motor drive vehicle. J. Mech. Sci. Technol. 2011, 25, 1573–1581. [Google Scholar] [CrossRef]
- Yim, S. Coordinated control with electronic stability control and active steering devices. J. Mech. Sci. Technol. 2015, 29, 5409–5416. [Google Scholar] [CrossRef]
- Jin, X.J.; Yin, G.; Chen, N. Gain-scheduled robust control for lateral stability of four-wheel-independent-drive electric vehicles via linear parameter-varying technique. Mechatronics 2015, 30, 286–296. [Google Scholar] [CrossRef]
- Kim, C.J.; Mian, A.A.; Kim, S.H.; Back, S.H.; Jang, H.B.; Jang, J.H.; Han, C.S. Performance evaluation of integrated control of direct yaw moment and slip ratio control for electric vehicle with rear in-wheel motors on split-mu road. Int. J. Automot. Technol. 2015, 16, 939–946. [Google Scholar] [CrossRef]
- Ren, B.; Chen, H.; Zhao, H.; Yuan, L. MPC-based yaw stability control in in-wheel-motored EV via active front steering and motor torque distribution. Mechatronics 2016, 38, 103–114. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. An Adaptive Hierarchical Trajectory Following Control Approach of Autonomous Four-Wheel Independent Drive Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2482–2492. [Google Scholar] [CrossRef]
- Yue, S.; Fan, Y. Hierarchical Direct Yaw-Moment Control System Design for In-Wheel Motor Driven Electric Vehicle. Int. J. Automot. Technol. 2018, 19, 695–703. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, X.; Li, S.; Su, B.; Gao, J. Path tracking of eight in-wheel driving autonomous vehicle: Controller design and experimental results. In Proceedings of the 2019 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019. [Google Scholar]
- Nah, J.; Yim, S. Vehicle Stability Control with Four-Wheel Independent Braking, Drive and Steering on In-Wheel Motor-Driven Electric Vehicles. Electronics 2020, 9, 1934. [Google Scholar] [CrossRef]
- Liu, D.; Huang, S.; Wu, S.; Fu, X. Direct Yaw-Moment Control of Electric Vehicle with in-Wheel Motor Drive System. Int. J. Automot. Technol. 2020, 21, 1013–1028. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Liu, C.-Z.; Wu, X.; Fang, S.-N.; Yong, J.-W. Robust LMI-Based H-Infinite Controller Integrating AFS and DYC of Autonomous Vehicles with Parametric Uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6901–6910. [Google Scholar] [CrossRef]
- He, Y.; King, I.; Britam, E.; Cai, Y.; Yuan, C. Design and analysis of robust state constraint control for direct yaw moment control system. Int. J. Model. Simul. 2021, 42, 551–560. [Google Scholar] [CrossRef]
- Seo, Y.; Cho, K.; Nam, K. Integrated Yaw Stability Control of Electric Vehicle Equipped with Front/Rear Steer-by-Wire Systems and Four In-Wheel Motors. Electronics 2022, 11, 1277. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Han, L.; Xiang, C. Handling and Stability Integrated Control of AFS and DYC for Distributed Drive Electric Vehicles Based on Risk Assessment and Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 1–16, Early Access. [Google Scholar] [CrossRef]
- Tan, S.; Zhao, X.; Yang, J.; Zhang, W. A path tracking algorithm for articulated vehicle: Development and simulations. In Proceedings of the 2017 IEEE transportation electrification conference and expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017. [Google Scholar]



| Parameters | Value | Unit |
|---|---|---|
| Vehicle mass | 2500 | kg |
| Length | 3600 | mm |
| Width | 1900 | mm |
| Wheelbase | 900 | mm |
| Wheel track | 1660 | mm |
| Tire radius | 375 | mm |
| Frontal area | 3.5 | m2 |
| Air drag coefficient | 0.6 | / |
| Motor rate power | 16 | kW |
| Motor peak power | 30 | kW |
| Motor rate torque | 1100 | Nm |
| Motor peak torque | 1200 | Nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, S.; Wang, Y.; Cheng, W.; Luo, T.; Zhang, N.; Li, S.; Pan, B.; Cui, X. Cascade Direct Yaw Moment Control for an Independent Eight In-Wheel Motor-Driven Autonomous Vehicle. Electronics 2022, 11, 2930. https://doi.org/10.3390/electronics11182930
Tan S, Wang Y, Cheng W, Luo T, Zhang N, Li S, Pan B, Cui X. Cascade Direct Yaw Moment Control for an Independent Eight In-Wheel Motor-Driven Autonomous Vehicle. Electronics. 2022; 11(18):2930. https://doi.org/10.3390/electronics11182930
Chicago/Turabian StyleTan, Senqi, Yang Wang, Wen Cheng, Tian Luo, Naisi Zhang, Shengfei Li, Bo Pan, and Xing Cui. 2022. "Cascade Direct Yaw Moment Control for an Independent Eight In-Wheel Motor-Driven Autonomous Vehicle" Electronics 11, no. 18: 2930. https://doi.org/10.3390/electronics11182930
APA StyleTan, S., Wang, Y., Cheng, W., Luo, T., Zhang, N., Li, S., Pan, B., & Cui, X. (2022). Cascade Direct Yaw Moment Control for an Independent Eight In-Wheel Motor-Driven Autonomous Vehicle. Electronics, 11(18), 2930. https://doi.org/10.3390/electronics11182930







