Abstract
Extraordinary transmission structures show promising capabilities for highly selective filters in both frequency and angle of incidence. However, their realistic response once manufacturing limitations are taken into account remains unexplored. In this manuscript, we explore a novel degree of freedom: disorder. We expand on previously developed highly efficient method of moment (MoM) implementations to study the effects on the transmission properties of large but finite chains of slots due to different families of disorder: lateral and vertical displacements as well as scatterer manipulation (modifying sizes and rotation angles), showing their effects on the transmission spectrum.
1. Introduction
Periodic structures are a fundamental tool for the design of wave emitting and control devices such as antennas and filters for a wide range of frequency regimes from microwaves to optics. In the microwave research community, frequency-selective surfaces [1] appeared in the last century as a distributed version of passband or bandstop electronic devices and are still an active field of research in the form of much more advanced metasurfaces [2,3]. These structures rely on the interaction between resonating elements (such as patches and/or apertures) to tailor the propagation and radiation of waves leading to integrated lensing/radiating devices and metasurface antennas [4].
With the discovery of extraordinary optical transmission (EOT) in the 1990s [5], which allows for a very narrow transmission band when a periodic arrangement of small apertures was properly tailored, a new wave of optical applications for periodic surfaces was unveiled [6]. It was shown that, additionally to the wide-used natural resonance of apertures when their electrical length corresponds to half of the operating wavelength, a special type of resonance, so-called extraordinary, could be achieved at frequencies well-below such natural resonance when the periodicity of the array was larger than twice the electrical length of the aperture. In other words, for a constant periodicity of the array, as the electrical length of the aperture decreases, the resonance frequency increases (as predicted for resonances) until it reaches the onset of the first set of grating lobes. As the electrical length of the aperture is decreased below half of the periodicity, the transmission peak is squeezed against the transmission zero known as the Wood’s anomaly, giving place to the narrow peak called extraordinary transmission.
Such experimental evidence (corroborated by full-wave simulations) was surprising at first and had no direct equivalence in the literature of the microwave FSS community. Due to the experiments being performed at optical frequencies, the first measurements and knowledge of the ability of periodic structures to couple bound plasma waves known as surface plasmons [7,8], the first explanations were based on the interactions between plasmons propagating on both sides of the aperture array, which were coupled through the fields inside the apertures [9,10,11,12]. Such explanations led to good predictions, but the subsequent finding of EOT in microwave structures in which such plasmons cannot exist (as the metal can be treated as a perfect conductor) [13], also demonstrated inside a waveguide with no equivalent grating coupling to any possible type of surface wave), meant the theory was not complete [14]. It was later shown that a generalized explanation based on an equivalent circuit model explained the narrowband phenomenon for any type of waveguide, whether Bloch/Floquet-type or reallistic metallic waveguides [15]. Another more general theory extended the concept of surface plasmons to effective plasmonic materials, which can support surface waves known as spoof surface plasmons. In this framework, hole- and dielectric-backed slit arrays can themselves support bound waves which take the role of true plasmons at microwave and terahertz frequencies [16,17,18,19].
Despite the great interest attracted by periodic extraordinary transmitting structures, only limited attention has been paid to aperiodic arrays, i.e., those with arbitrary or even random separations between scatterers (either apertures or metallizations) [20,21] given the difficulty of their modeling [22,23]. For practical applications, local periodicity is assumed, and only smooth variations of geometrical parameters are used to limit aperiodicity effects [24,25]. Among the aperiodic structures studied in the literature, we find metamaterial absorbers [26], resonant slot arrays [27,28], photonic crystals [29,30,31] and antennas [32,33,34]. It is worth mentioning that aperiodic structures have recently received a lot of interest from the topological photonics and acoustics communities thanks to their potential for novel edge and bandgap modes [35,36,37].
In this paper, we focus on the presence of extraordinary transmission in disordered slot arrays in perfectly conducting screens. To do so, we will study the original one-dimensionally periodic slot array studied in [38] composed of a single row of slots, to which we apply different types of disorder: some related to the arrangement of the slots and others related to the slot scatterers. Although all of them break the strict periodicity of the structure, we will show that they have large differences in their effect. With these results, we expect that these results will help develop custom finite structures with known edge effects [39,40] not considered by traditional unit cell-based analysis.
2. Numerical Methods
Let us briefly present the Galerkin’s version of the Method of Moments (MoM) exploited in previous works [41] and then emphasize the advancements introduced for the efficient analysis of the scattering by a disordered array of slots in a perfectly conducting screen as shown in Figure 1. The electric field on the plane of a perfectly conducting screen of negligible thickness with a number M of apertures can be shown to obey the following integral equation:
where is the surface current in the absence of the slots and is the dyadic Green’s function that relates the tangential electric field vector at the origin with the electric current density vector at a given point and where is the surface of the i-th slot.
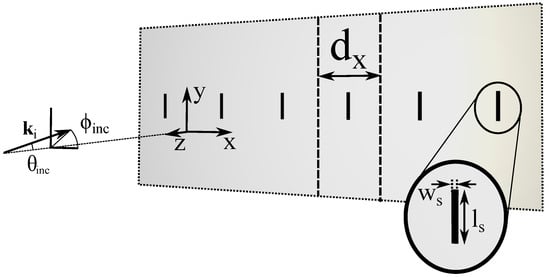
Figure 1.
Perspective view of a chain of slot apertures cut into an infinite perfectly conducting screen of negligible thickness.
The Method of Moments can be then applied by proposing a set of basis functions for each of the apertures.
which in the Galerkin’s version of the MoM are also used as testing functions to convert (1) into a system of linear equations for the set of unknown weights
where
and where
For the sake of efficiency of the method, it is convenient to reformulate (4) so that the interactions between the different basis functions can be precomputed numerically, which can be shown to be equivalent to
where corresponds to a scalar free space Green’s function given by
Thanks to a physically-insightful choice of basis functions, these expressions can be calculated efficiently using tailored quadrature formulas. In particular, we use a set of basis functions with the proper choice of zero or singular behavior at the edge of the aperture based on Chebyshev polynomials which are shown to be a basis for the kernel of the integral equation which present logarithmic singularities near the edges of the slots. Mathematically, they are expressed in the frame of each slot as
where , and where () and () are Chebyshev polynomials of the first and second kind, respectively.
When these basis functions are introduced into (7) and (8) it can be shown that they can be rewritten in the form of
where for the case of , the integrand has the form
These singularities arise from the derivatives of the zeros imposed by the edges parallel to the electric field, where is a nonsingular function in the integration domain. These four integrals can be iteratively calculated using the Gauss–Chebyshev quadrature rule of first order [42]) whose weights and sampling points are given by
which can be applied in a nested loop.
In the case of , (12) consists of two summands, . The first summand will contain a factor of the form of
while the second will be of the form of
for which and are nonsingular functions. In this case, it is convenient to combine the first- and second-order Gauss–Chebyshev quadrature rules aforementioned. The weights and sampling points of the second order quadrature are given by [42]
Once these integrals are computed, the system of equations can be solved to retrieve the electric field on the surface of the array, from which the far-field distribution can be calculated via its Fourier transform, provided analytically by the analytical Fourier transforms of the chosen basis functions. Then, the scattering cross section of the array is calculated as [43,44]
from which the effective receiving area of the screen (i.e., the effective surface that is transparent to the incoming wave) is calculated as
3. Numerical Validation
Let us validate the numerical method employed for the construction of the entries of the matrix of the Method of Moments using commercially available software. In our case, we employ the well-known Ansys HFSS software for the simulation of two slots of different sizes and orientation which constitute a square unit cell as depicted in Figure 2. To analyze such problem, the Green’s function has to be modified to account for the periodicity as shown elsewhere [41], but this has no impact in the validation of the numerical integration scheme presented here. In Figure 2, we analyze the transmission spectrum of two distinct slot apertures using the numerical approach presented in this manuscript. We have found that five basis functions ( and are sufficient to accurately reproduce the results from the commercial software.
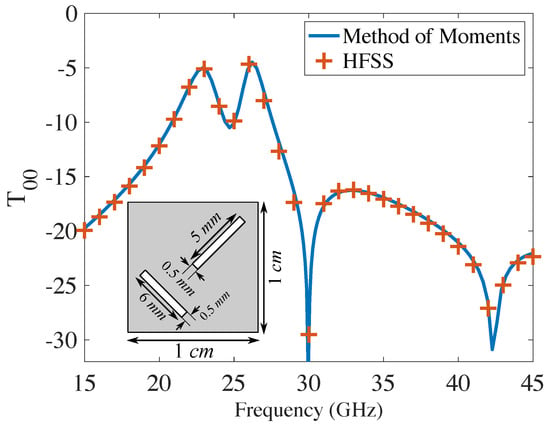
Figure 2.
Copolar transmission coefficient comparison between the method presented here and that obtained from the commercial software HFSS. The unit cell is depicted in the inset, containing two slots with , , , , , , .
We have found a rapid convergence in the calculation of the inter-slot coupling elements of the MoM matrix (i.e., the off-diagonal terms) with errors below five percent with just 7 quadrature points per integral, leading to a total of 2401 evaluations. In terms of CPU time, due to the nested nature of these evaluations, the CPU time will increase as the number of evaluations to the fourth power, so it is important to optimise the number of evaluations required. It has been found that the MoM implementation shown here outperforms the commercial software in CPU time consumption by a factor of 200, supporting the efforts devoted to the development of this method.
4. Results and Discussion
Once the numerical method has been presented, we can embark on the study of the effects introduced by disorder in extraordinary transmission through finite slots chains. However, extraordinary transmission is a consequence of periodicity, which is broken merely by considering a finite chain. Therefore, we first need to establish whether EOT can be associated with the transmission spectra through these chains. In all cases, we study the transmission when the array is illuminated by an infinite plane wave at normal incidence whose electric field is polarized along the x direction, i.e., perpendicular to the axis of the slots in the absence of rotations. For practical applications, it may be desirable to consider Gaussian-type beam illumination, which can be introduced in the numerical method in a straight-forward way [45,46].
In Figure 3, we study the appearance of the EOT peak with the number of slots M when these are all equal , , and distanced by a constant value . When comparing all curves with those for a single aperture (blue line, ), the extraordinary transmission peak is found at a normalized frequency compared to the resonance of the isolated slot, with a maximum effective area around . From these results, one can approximate, for practical reasons, the transmission from an array with more than 25 elements so as to behave similarly to an infinite array. In the following, we will keep .
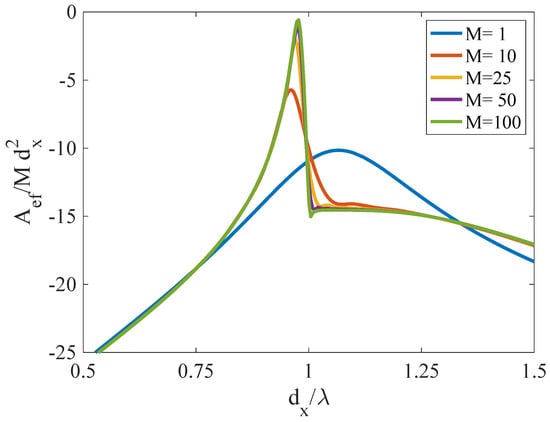
Figure 3.
Normalized effective transmitting area of a finite chain of M slots with dimensions , for different values of M under plane wave illumination at normal incidence.
Let us now consider the first type of disorder, in which the resonant elements (i.e., the slots) are kept the same as well as their relative distances (), but a random set of rotations is applied to the set of slots. In this manner, each slot is rotated by an angle , given by a normal distribution with a given standard deviation and a null mean (i.e., slots should be rotated with respect to their original vertical position). This type of disorder does not affect the natural resonance of the scatterer itself. We then study the effective frequency-dependent receiving area for different values of standard deviation, which are shown in Figure 4.
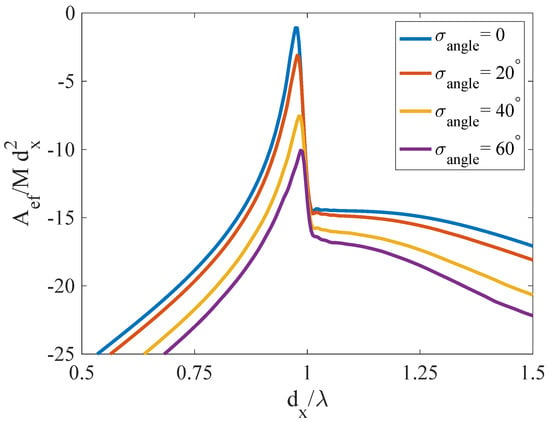
Figure 4.
Normalized effective transmitting area of a finite chain of M slots with dimensions , with different rotation angles given by a random normal distribution of different standard deviations under normal incidence.
We see that, given (5), one expects the electric field amplitude excited in the slots to be reduced by a factor , which should be lower and lower on average with increasing standard deviation as even if the mean value of is zero, the cosine is an even function, therefore having a mean lower than one. This reasoning is consistent with the findings in Figure 4. Of course, such reasoning neglects the change in coupling between neighboring elements, but as has been found in many works [47,48], small rotations do not introduce big changes in the overall coupling among elements in large arrays, a condition used as a local periodicity which has yielded good results in the literature.
Let us now consider a different type of disorder, in which we modify the scatterer itself, and with that we modify the natural resonance of each slot. In the literature, it has been shown that the natural resonance of the slot itself plays a secondary role in the existence of extraordinary transmission, as long as it is located above the first transmission zero (i.e., the Wood’s anomaly). However, the precise location of the EOT peak is dictated by such resonance. As we did for the angle of rotation, let us consider now that each slot has a length given by with given by a constant plus a random value given by a normal distribution centered at zero with a standard deviation given by , which is given as a percentage of the value of . The frequency-dependent effective receiving area normalized to the surface of the strip is shown in Figure 5.
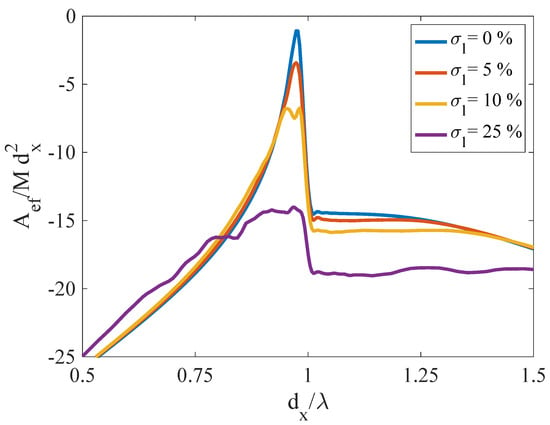
Figure 5.
Normalized effective transmitting area of a finite chain of M slots with and with given by a set of random numbers following a normal distribution with mean for different values of the standard deviation.
As can be seen in Figure 5, as the standard deviation of the distribution increases, the peak maintains its center frequency, but the height of the transmission is reduced. This can be understood from the fact that each slot will present a slightly displaced EOT resonance, leading to a wider peak, but with a lower transmission coefficient. It is interesting to note that only a 5% standard deviation already reduces the height of the peak by almost 40% in power, and a 10% deviation leads to a reduction of 75% of power compared to the non-disordered structure. Finally, for a standard deviation of 25%, the peak becomes much wider, but the strong reduction of transmitted power at the onset of the first diffraction mode is still clearly visible in the transmission spectrum.
Next, we study a different type of disorder independent of the scatterer: the spacing along the x or y directions. Let us focus first on the former: instead of maintaining an arithmetic sequence for , that is, keeping a constant separation of between each pair of neighboring elements, let us add a random value given again by a normal distribution with different values of the standard deviation. In Figure 6, we see that as the standard deviation increases, the peak becomes less and less defined until the transmission spectrum is very similar to that found for a single slot () in Figure 3. This means that a collection of slots with random distances along a chain actually follows the original hypothesis broken by the discovery of extraordinary transmission, i.e., the coupling between the apertures plays no role. It is worth noting that recently it has been shown that special modes can be created by using deterministic randomness as created by an iterative sequence such as Fibonacci’s [49].
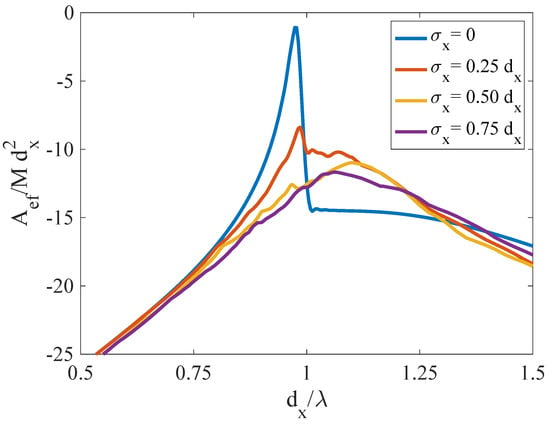
Figure 6.
Normalized effective transmitting area of a finite chain of M slots with , and with given by a set of random numbers following a normal distribution with mean for different values of standard deviation.
In Figure 7 instead of modifying the position x of each slot, let us now add a random value to their position y, so that their centers are not placed on the x axis. Interestingly, as shown in Figure 7, this type of disorder has the least effect on the definition and height of the EOT peak from all of those studied previously. Additionally, we find that a secondary peak starts to follow near the expected natural resonance of the slots when very extreme values are chosen for the standard deviation for . This means that a chain of slots positioned randomly will present a well-defined EOT resonance as long as their horizontal separation is kept constant.
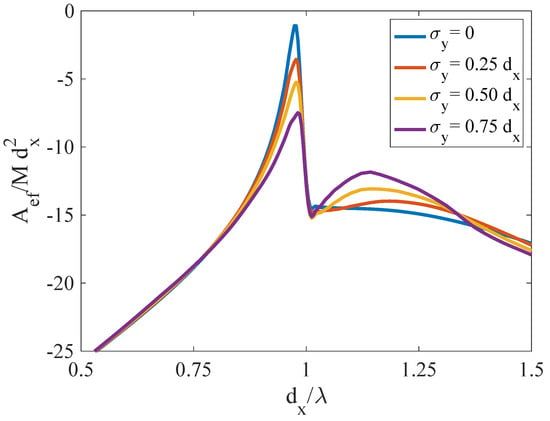
Figure 7.
Normalized effective transmitting area of a finite chain of M slots with , and with given by a set of random numbers following a normal distribution with mean 0 for different values of standard deviation.
5. Conclusions
In this paper, we study the consequences of introducing disorder to extraordinary transmission through a finite chain of slots cut into a perfectly conducting screen. We have found that a finite chain converges to a maximum transmission for as few as 50 slots, but 25 already allow for an almost full transmission. When introducing disorder, random individual rotation of the slots allows for a controllable reduction of the peak transmission level while also reducing the transmission level of the Wood’s anomaly and the low-frequency tail. By modifying the length of the slots in a random fashion, one can maintain the low frequency and Wood’s anomaly levels while reducing the transmission value at the peak, therefore increasing the relative bandwidth. If one is to replicate the transmission properties of a single isolated slot, introducing random displacements along the x direction is the most effective manner. Additionally, introducing random displacements along the direction perpendicular to the array allows for the introduction of a secondary higher-frequency peak whose level increases with the standard deviation of the displacement distribution, while the level of the EOT peak is reduced and the low frequency and Wood’s anomaly levels are maintained. We believe this results could pave the way for EOT filtering devices for optical communications.
Author Contributions
M.C. and F.M. conceived the idea. M.C. and R.R.B. developed the numerical method. M.C. and A.F.-P. obtained the results. M.C. wrote the first draft and all authors revised and finalized the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the grant PID2020-116739GB-I00 funded by MCIN/AEI/10.13039/501100011033.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are available from the authors upon reasonable request.
Acknowledgments
M.C. wishes to acknowledge fruitful discussions with J. Roy Sambles while at the University of Exeter.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Munk, B.A. Frequency Selective Surfaces: Theory and Design; John Wiley: Hoboken, NJ, USA, 2000; p. 410. [Google Scholar]
- Maci, S.; Minatti, G.; Casaletti, M.; Bosiljevac, M. Metasurfing: Addressing waves on impenetrable metasurfaces. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1499–1502. [Google Scholar] [CrossRef]
- Meinzer, N.; Barnes, W.L.; Hooper, I.R. Plasmonic meta-atoms and metasurfaces. Nat. Photonics 2014, 8, 889–898. [Google Scholar] [CrossRef]
- Holloway, C.L.; Kuester, E.F.; Gordon, J.A.; O’Hara, J.; Booth, J.; Smith, D.R. An overview of the theory and applications of metasurfaces: The two-dimensional equivalents of metamaterials. IEEE Antennas Propag. Mag. 2012, 54, 10–35. [Google Scholar] [CrossRef]
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Garcia-Vidal, F.J.; Martin-Moreno, L.; Ebbesen, T.W.; Kuipers, L. Light passing through subwavelength apertures. Rev. Mod. Phys. 2010, 82, 729–787. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer US: Boston, MA, USA, 2007; pp. 1–223. [Google Scholar] [CrossRef]
- Sambles, R. More than transparent. Nature 1998, 391, 641. [Google Scholar] [CrossRef]
- Ghaemi, H.F.; Thio, T.; Grupp, D.E.; Ebbesen, T.W.; Lezec, H.J. Surface plasmons enhance optical transmission through subwavelength holes. Phys. Rev. B 1998, 58, 6779–6782. [Google Scholar] [CrossRef]
- Martín-Moreno, L.; García-Vidal, F.J.; Lezec, H.J.; Pellerin, K.M.; Thio, T.; Pendry, J.B.; Ebbesen, T.W. Theory of extraordinary optical transmission through subwavelength hole arrays. Phys. Rev. Lett. 2001, 86, 1114–1117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- García De Abajo, F.J.; Gómez-Medina, R.; Sáenz, J.J. Full transmission through perfect-conductor subwavelength hole arrays. Phys. Rev. -Stat. Nonlinear Soft Matter Phys. 2005, 72, 016608. [Google Scholar] [CrossRef]
- Beruete, M.; Sorolla, M.; Campillo, I.; Dolado, J.S.; Martín-Moreno, L.; Bravo-Abad, J.; García-Vidal, F.J. Enhanced millimeter-wave transmission through subwavelength hole arrays. Opt. Lett. 2004, 29, 2500. [Google Scholar] [CrossRef]
- Medina, F.; Ruiz-Cruz, J.A.; Mesa, F.; Rebollar, J.M.; Montejo-Garai, J.R.; Marqués, R. Experimental verification of extraordinary transmission without surface plasmons. Appl. Phys. Lett. 2009, 95, 071102. [Google Scholar] [CrossRef]
- Medina, F.; Mesa, F.; Marqués, R. Extraordinary transmission through arrays of electrically small holes from a circuit theory perspective. IEEE Trans. Microw. Theory Tech. 2008, 56, 3108–3120. [Google Scholar] [CrossRef]
- Pendry, J.B.; Martín-Moreno, L.; Garcia-Vidal, F.J. Mimicking surface plasmons with structured surfaces. Science 2004, 305, 847–848. [Google Scholar] [CrossRef]
- Hibbins, A.; Evans, B.; Sambles, J. Experimental verification of designer surface plasmons. Science 2005, 308, 670–672. [Google Scholar] [CrossRef] [PubMed]
- García De Abajo, F.J.; Sáenz, J.J. Electromagnetic surface modes in structured perfect-conductor surfaces. Phys. Rev. Lett. 2005, 95, 233901. [Google Scholar] [CrossRef]
- Freer, S.; Camacho, M.; Kuznetsov, S.A.; Boix, R.R.; Beruete, M.; Navarro-Cía, M. Revealing the underlying mechanisms behind TE extraordinary THz transmission. Photonics Res. 2020, 8, 430–439. [Google Scholar] [CrossRef]
- Matsui, T.; Agrawal, A.; Nahata, A.; Vardeny, Z.V. Transmission resonances through aperiodic arrays of subwavelength apertures. Nature 2007, 446, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, J.K.; Hooper, I.R.; Lawrence, C.R. Exploring microwave absorption by non-periodic metasurfaces. Adv. Electromagn. 2021, 10, 1–6. [Google Scholar] [CrossRef]
- Bravo-Abad, J.; Fernández-Domínguez, A.I.; García-Vidal, F.J.; Martín-Moreno, L. Theory of extraordinary transmission of light through quasiperiodic arrays of subwavelength holes. Phys. Rev. Lett. 2007, 99, 203905. [Google Scholar] [CrossRef]
- Agrawal, A.; Matsui, T.; Vardeny, Z.V.; Nahata, A. Extraordinary optical transmission through metallic films perforated with aperture arrays having short-range order. Opt. Express 2008, 16, 6267. [Google Scholar] [CrossRef] [PubMed]
- Minatti, G.; Caminita, F.; Martini, E.; Sabbadini, M.; Maci, S. Synthesis of modulated-metasurface antennas with amplitude, phase, and polarization control. IEEE Trans. Antennas Propag. 2016, 64, 3907–3919. [Google Scholar] [CrossRef]
- Huang, J.; Encinar, J.A. Reflectarray Antennas; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Yang, Q.; Chen, X.; Li, Y.; Zhang, X.; Xu, Y.; Tian, Z.; Ouyang, C.; Gu, J.; Han, J.; Zhang, W. Aperiodic-metamaterial-based absorber. APL Mater. 2017, 5, 096107. [Google Scholar] [CrossRef]
- Fernández-Domínguez, A.; Hernández-Carrasco, I.; Martín-Moreno, L.; García-Vidal, F. Transmission resonances through a Fibonacci array of subwavelength slits. Electromagnetics 2008, 28, 186–197. [Google Scholar] [CrossRef]
- Li, J.; Liu, S.; Huang, C.; Li, T.; Wang, Q.; Zhu, Y. Light transmission through Fibonacci and periodic sub-wavelength slit arrays. J. Opt. Pure Appl. Opt. 2008, 10, 075202. [Google Scholar] [CrossRef]
- Capaz, R.B.; Koiller, B.; de Queiroz, S.L.A. Gap states and localization properties of one-dimensional Fibonacci quasicrystals. Phys. Rev. B 1990, 42, 6402–6407. [Google Scholar] [CrossRef]
- Dal Negro, L.; Oton, C.J.; Gaburro, Z.; Pavesi, L.; Johnson, P.; Lagendijk, A.; Righini, R.; Colocci, M.; Wiersma, D.S. Light Transport through the Band-Edge States of Fibonacci Quasicrystals. Phys. Rev. Lett. 2003, 90, 055501. [Google Scholar] [CrossRef] [PubMed]
- Tavakoli, M.; Jalili, Y.S. One-dimensional Fibonacci fractal photonic crystals and their optical characteristics. J. Theor. Appl. Phys. 2014, 8, 113. [Google Scholar] [CrossRef]
- Ozbakis, B.; Kustepeli, A. The resonant behavior of the Fibonacci fractal tree antennas. Microw. Opt. Technol. Lett. 2008, 50, 1046–1050. [Google Scholar] [CrossRef] [Green Version]
- Sharma, C.; Vishwakarma, D.K. Miniaturization of Spiral Antenna Based on Fibonacci Sequence Using Modified Koch Curve. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 932–935. [Google Scholar] [CrossRef]
- Chauhan, M.; Pandey, A.K.; Mukherjee, B. A novel cylindrical dielectric resonator antenna based on Fibonacci series approach. Microw. Opt. Technol. Lett. 2019, 61, 2268–2274. [Google Scholar] [CrossRef]
- Della Villa, A.; Enoch, S.; Tayeb, G.; Pierro, V.; Galdi, V.; Capolino, F. Band gap formation and multiple scattering in photonic quasicrystals with a Penrose-type lattice. Phys. Rev. Lett. 2005, 94, 183903. [Google Scholar] [CrossRef]
- Apigo, D.J.; Cheng, W.; Dobiszewski, K.F.; Prodan, E.; Prodan, C. Observation of topological edge modes in a quasiperiodic acoustic waveguide. Phys. Rev. Lett. 2019, 122, 095501. [Google Scholar] [CrossRef]
- Rosa, M.I.; Guo, Y.; Ruzzene, M. Exploring topology of 1D quasiperiodic metastructures through modulated LEGO resonators. Appl. Phys. Lett. 2021, 118, 131901. [Google Scholar] [CrossRef]
- Camacho, M.; Boix, R.R.; Medina, F.; Hibbins, A.P.; Sambles, J.R. Extraordinary Transmission and Radiation from Finite by Infinite Arrays of Slots. IEEE Trans. Antennas Propag. 2019, 68, 581–586. [Google Scholar] [CrossRef]
- Camacho, M.; Hibbins, A.P.; Capolino, F.; Albani, M. Diffraction by a truncated planar array of dipoles: A Wiener–Hopf approach. Wave Motion 2019, 89, 28–42. [Google Scholar] [CrossRef]
- Camacho, M.; Capolino, F.; Albani, M. Asymmetric surface wave excitation through metasurface-edge diffraction. Opt. Lett. 2020, 45, 5420. [Google Scholar] [CrossRef] [PubMed]
- Camacho, M.; Boix, R.R.; Medina, F. Computationally efficient analysis of extraordinary optical transmission through infinite and truncated subwavelength hole arrays. Phys. Rev. E - Stat. Nonlinear Soft Matter Phys. 2016, 93, 063312. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1970. [Google Scholar]
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Collin, R.E. Antennas and Radiowave Propagation; Mc-Graw Hill: New York, NY, USA, 1985. [Google Scholar]
- Navarro-Cía, M.; Pacheco-Pe na, V.; Kuznetsov, S.A.; Beruete, M. Extraordinary THz Transmission with a Small Beam Spot: The Leaky Wave Mechanism. Adv. Opt. Mater. 2018, 6, 1701312. [Google Scholar] [CrossRef]
- Camacho, M.; Boix, R.R.; Kuznetsov, S.A.; Beruete, M.; Navarro-Cia, M. Far-Field and Near-Field Physics of Extraordinary THz Transmitting Hole-Array Antennas. IEEE Trans. Antennas Propag. 2019, 67, 6029–6038. [Google Scholar] [CrossRef]
- Martini, E.; Mencagli Jr, M.; Maci, S. Metasurface transformation for surface wave control. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2015, 373, 20140355. [Google Scholar] [CrossRef] [PubMed]
- Florencio, R.; Boix, R.R.; Encinar, J.A.; Toso, G. Optimized periodic MoM for the analysis and design of dual polarization multilayered reflectarray antennas made of dipoles. IEEE Trans. Antennas Propag. 2017, 65, 3623–3637. [Google Scholar] [CrossRef]
- Hamilton, J.K.; Camacho, M.; Boix, R.; Hooper, I.R.; Lawrence, C.R. Effective-periodicity effects in Fibonacci slot arrays. Phys. Rev. B 2021, 104, L241412. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).