Modeling Push–Pull Converter for Efficiency Improvement
Abstract
:1. Introduction
2. Materials and Methods
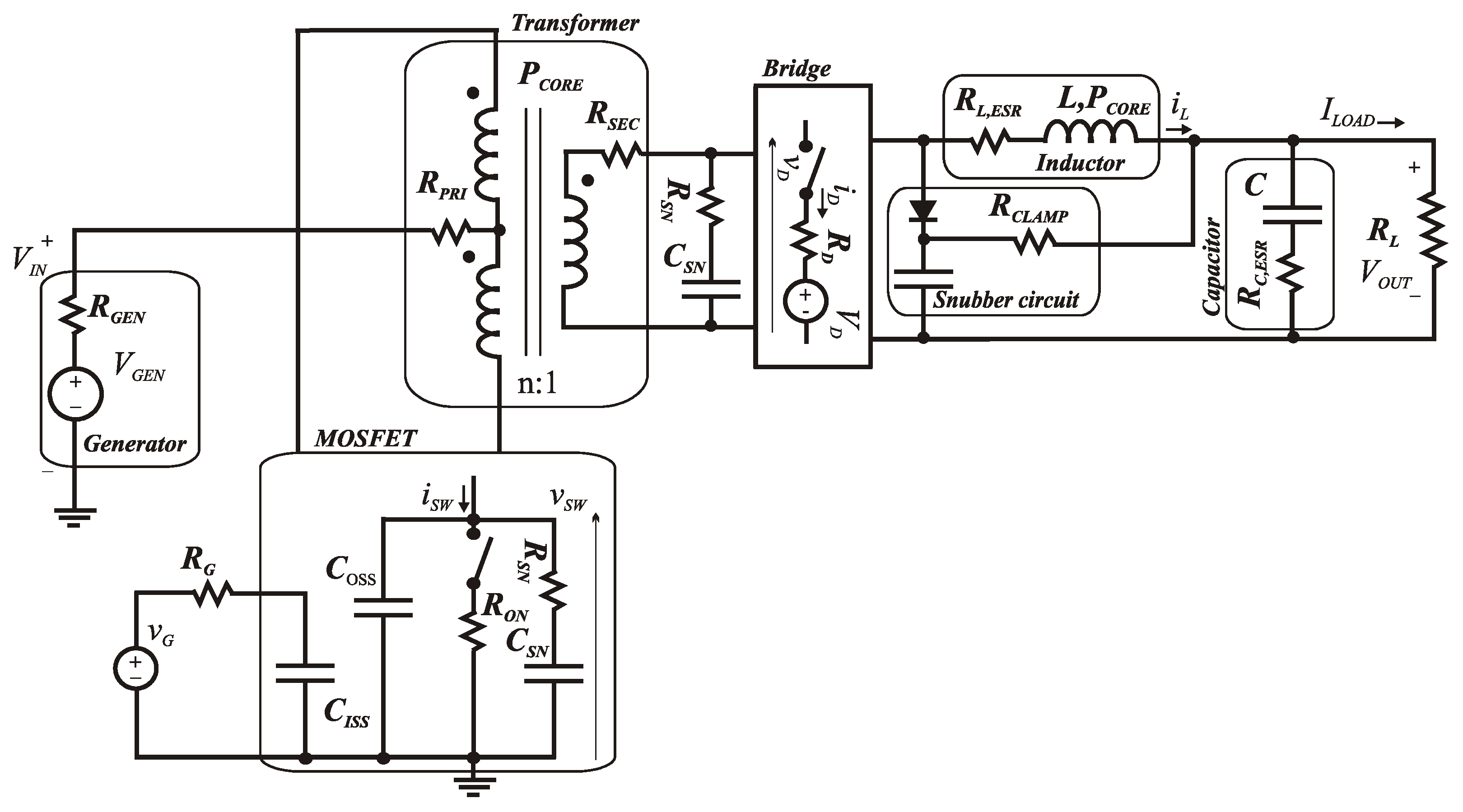
2.1. Power Losses of Push–Pull Converter
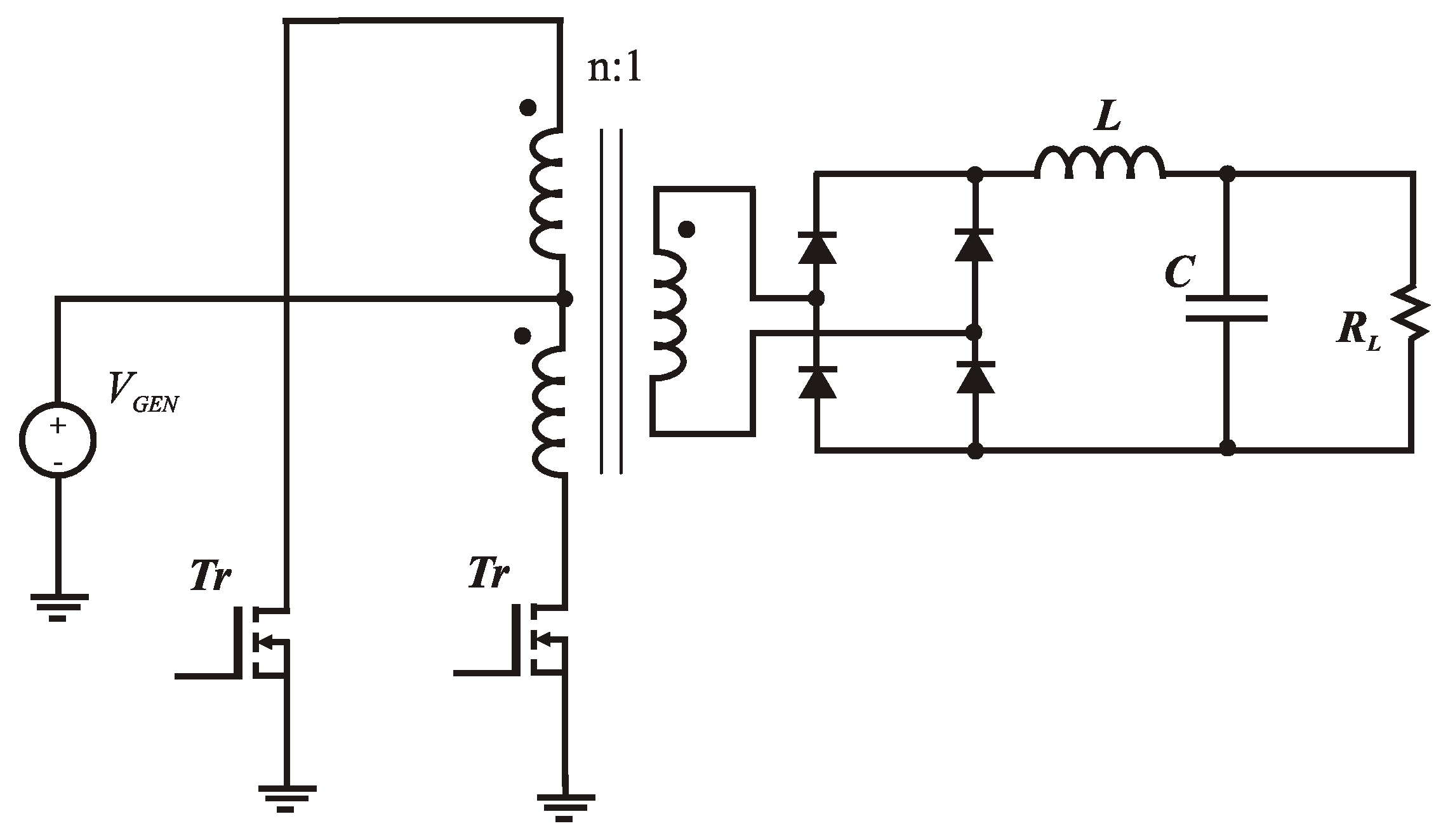
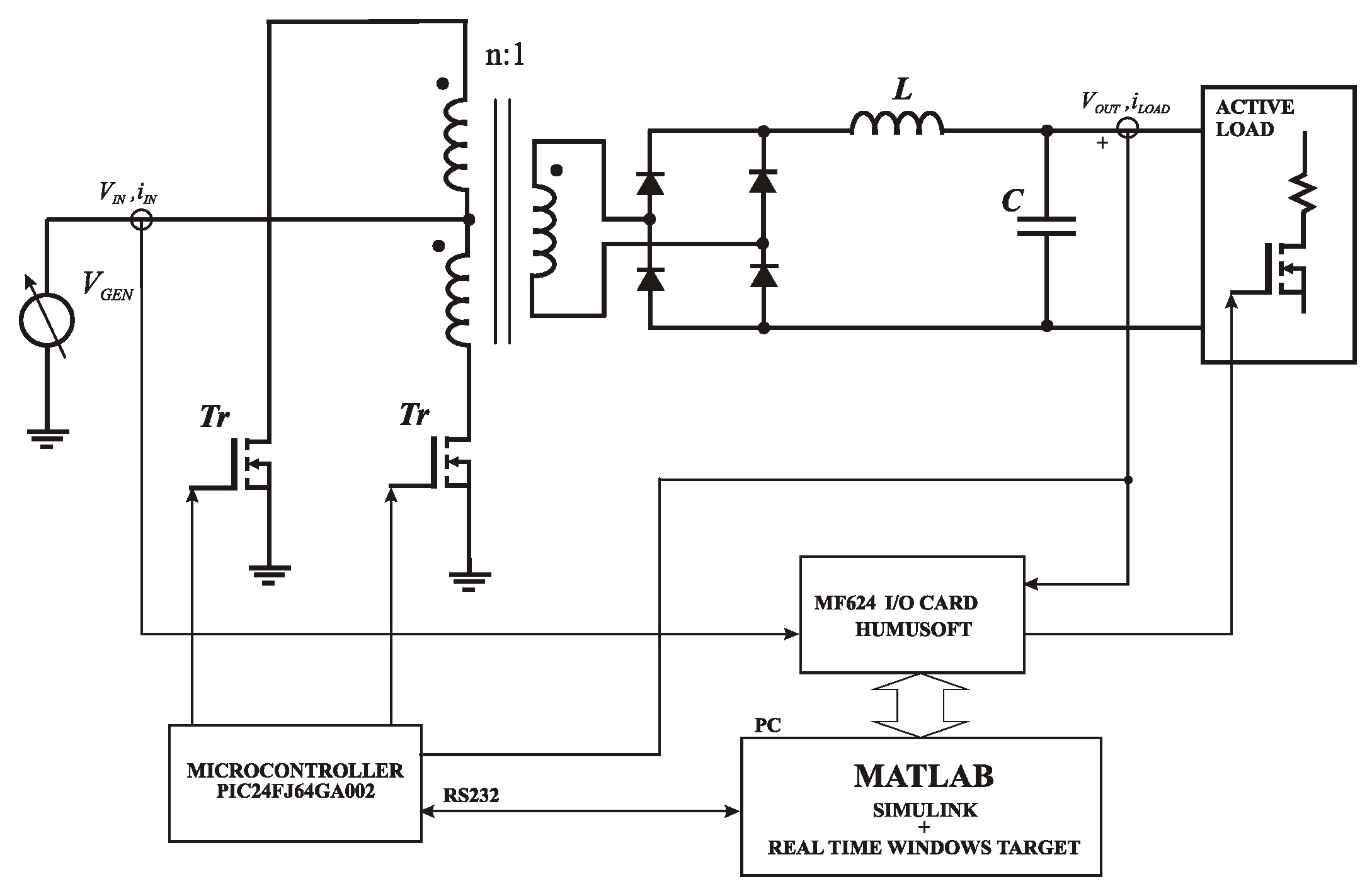
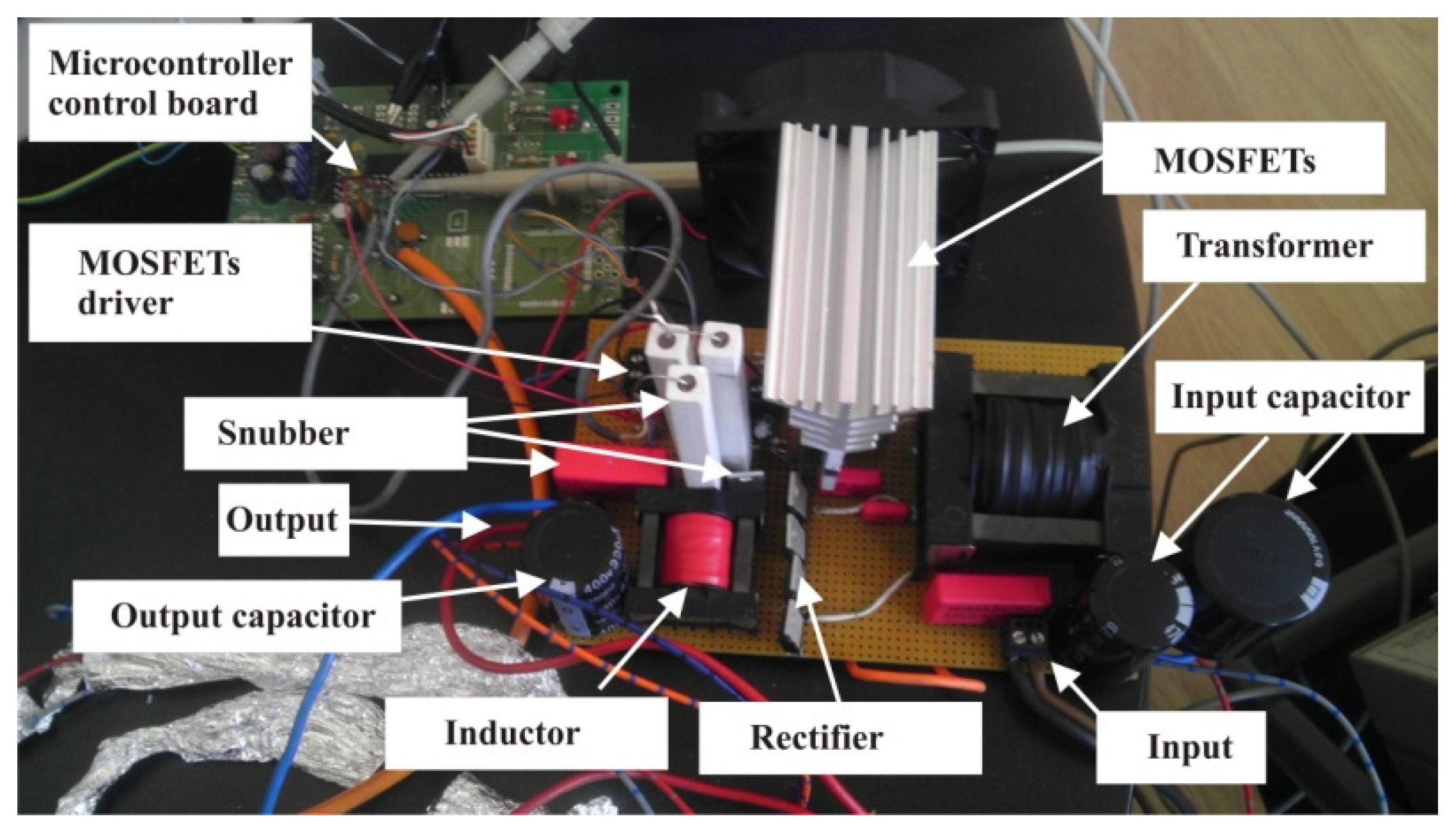
2.2. Experimental Setup of Push–Pull Converter
- DC input voltage VIN = 30–58 V;
- DC output voltage VOUT = 300 V (0–100% load);
- maximum output power POUT = 500 W;
- switching frequency fsw = 10–100 kHz.
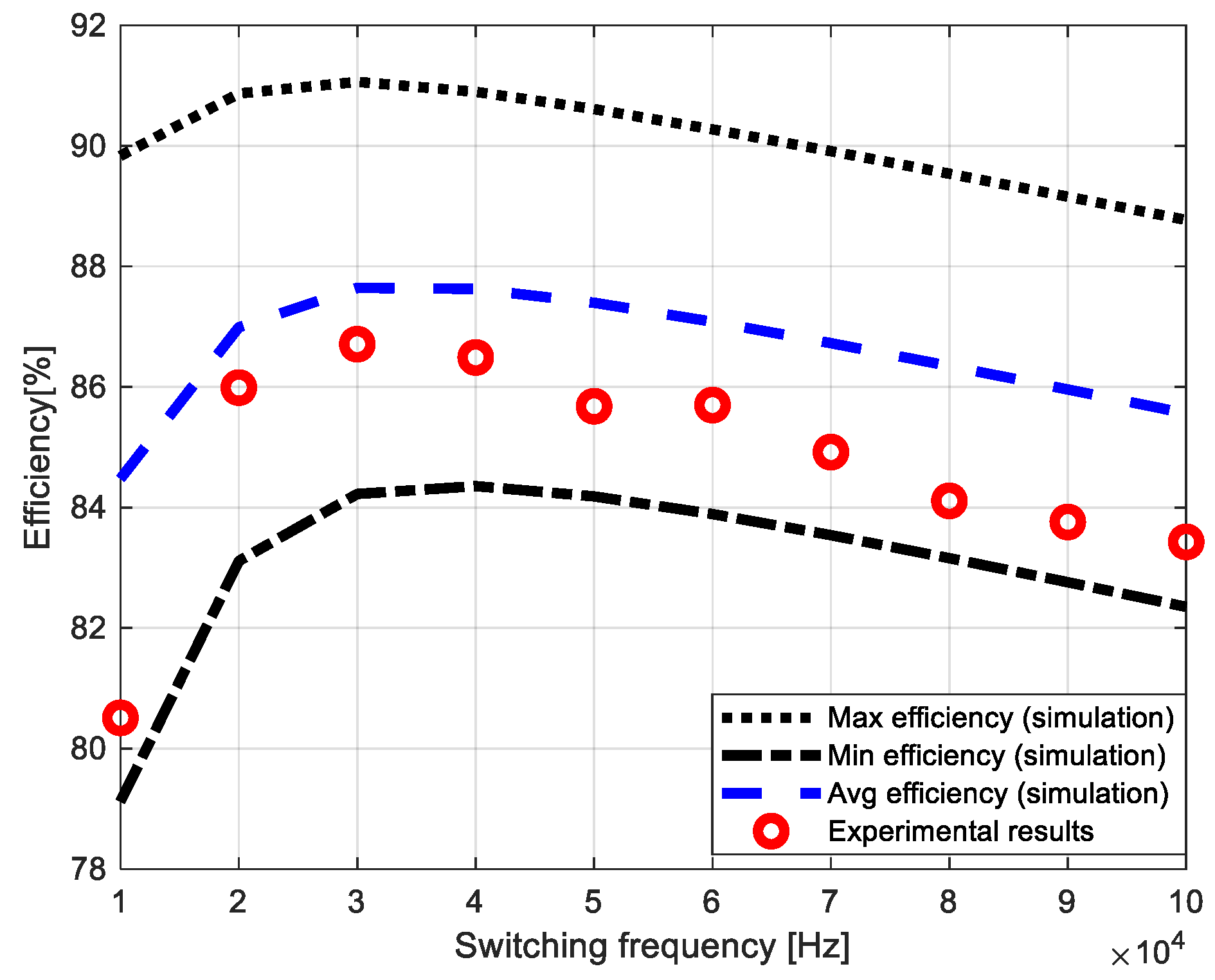
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| List of abbreviations | |
| AC | Alternating current |
| AWG | American wire gauge |
| CCM | Continuous current mode |
| DC | Direct current |
| DCM | Discontinuous current mode |
| ESR | Equivalent series resistance |
| MOSFET | Metal oxide semiconductor field effect transistor |
| PM | Permanent magnet |
| SPICE | Simulation Program with Integrated Circuit Emphasis |
| List of symbols | |
| AW | Wire cross-sectional area |
| CISS | MOSFET input capacitance |
| COSS | Output capacitance |
| CSN | Capacitance of the snubber circuit |
| d | Wire diameter |
| fsw | Switching frequency |
| gm | MOSFET transconductance |
| IC,eff | Effective value of the current through output capacitor |
| ID,avg | Average diode current |
| ID,eff | Effective value of the diode current |
| IIN,eff | Effective value of the converter input current |
| IL,avg | Average inductor current |
| IL,eff | Effective inductor current |
| ILOAD | Load current |
| IPRI,max | Primary winding maximum current |
| IPRI,min | Primary winding minimum current |
| ISW,eff | Effective value of the current through switch |
| I1L,EFF | Effective value of the inductor’s current first harmonic |
| lm,turn | One turn wire length |
| m | Number of layers of the inductor winding |
| Nm | Number of turns in the mth layer |
| NP | Number of turns in primary winding |
| n | Transformer’s turns ratio |
| PBRIDGE | Power loss in rectifier |
| PCOND | Conduction losses |
| PCLAMP | Power dissipation of the limiting circuit of the rectifier output |
| PFIXED | Fixed losses |
| PIN | Input power |
| PISS | Power loss in transistor gate, |
| PL,COND | Conduction losses in inductor |
| PL,CORE | Dynamic power loss in inductor core |
| PLOSS | Total power losses |
| POUT | Output power |
| PSW | Power loss during switching |
| PTR,COND | Conduction losses in transformer windings |
| PTR,CORE | Dynamic power loss in transformer core |
| PSEC,SNUB | Power loss in snubber circuit of the transformer’s secondary winding |
| PSW,SNUB | Power loss in snubber circuit of the switch |
| QG | Total charge in the gate |
| QG (SW) | Gate charge at the switching point |
| Qr | Pn junction accumulated charge |
| RC,ESR | Equivalent series resistance of the output filter capacitance |
| RD | Diode resistance in on state |
| RDC,m | Resistance of the mth layer for DC current |
| RDS,MAX | Maximum value of drain–source resistance |
| RDS,TYP | Typical value of drain–source resistance |
| RGEN | Resistance of the generator |
| RL,ESR | Inductor equivalent series resistance |
| RL,ESR,AC | Inductor resistance for the AC current |
| RL,ESRL,DC | Inductor’s equivalent serial resistance for DC current |
| RON | MOSFET resistance in on state |
| trr | Diode recovery time |
| tvf | Falling time of the output voltage |
| tvr | Rising time of the output voltage |
| VCG | Supply voltage of gate control circuit |
| VCORE | Volume of the inductor core |
| VD | Diode voltage in on state |
| VG | Gate threshold voltage |
| VIN | DC input voltage |
| VOUT | DC output voltage |
| VSEC | Voltage amplitude on transformer’s secondary winding |
| VSP,ON | Voltages at the switching on point |
| VSP,OFF | Voltages at the switching off point |
| WTOT | Total energy consumed |
| ΔB | Maximum induction in the core |
| ΔiL | Inductor current change |
| δ | Skin depth |
| η | Energy efficiency |
| ρ | Resistivity of the wire |
References
- Wu, Q.; Wang, Q.; Xu, J.; Xu, Z. Active-clamped ZVS current-fed push–pull isolated dc/dc converter for renewable energy conversion applications. IET Power Electron. 2018, 11, 373–381. [Google Scholar] [CrossRef]
- Bose, B. Modelling of Microinverter and PushPull Flyback Converter for SPV Application. In Proceedings of the 2020 8th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 4–5 June 2020; pp. 458–462. [Google Scholar] [CrossRef]
- Das, M.; Agarwal, V. Design and Analysis of a High-Efficiency DC–DC Converter With Soft Switching Capability for Renewable Energy Applications Requiring High Voltage Gain. IEEE Trans. Ind. Electron. 2016, 63, 2936–2944. [Google Scholar] [CrossRef]
- Gu, A.; Sun, W.; Zhang, G.; Chen, S.; Wang, Y.; Yang, L.; Zhang, Y. Boost-type push–pull converter with reduced switches. J. Power Electron. 2020, 20, 645–656. [Google Scholar] [CrossRef]
- Junior, M.E.T.S.; Freitas, L.C.G. Power Electronics for Modern Sustainable Power Systems: Distributed Generation, Microgrids and Smart Grids—A Review. Sustainability 2022, 14, 3597. [Google Scholar] [CrossRef]
- Mangkalajan, S.; Ekkaravarodome, C.; Sukanna, S.; Jirasereeamongkul, K.; Higuchi, K. Design of Digital Robust Control of A2DOF with Push-Pull Convert for Renewable Energy Application. In Proceedings of the 2019 16th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Pattaya, Thailand, 10–13 July 2019; pp. 537–540. [Google Scholar] [CrossRef]
- Joseph, P.K.; Devaraj, E. Design of hybrid forward boost converter for renewable energy powered electric vehicle charging applications. IET Power Electron. 2019, 12, 2015–2021. [Google Scholar] [CrossRef]
- Sunarno, E.; Sudiharto, I.; Nugraha, S.D.; Qudsi, O.A.; Eviningsih, R.P.; Raharja, L.P.S.; Arifin, I.F. A Simple And Implementation of Interleaved Boost Converter For Renewable Energy. In Proceedings of the 2018 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 1–2 November 2018; pp. 75–80. [Google Scholar] [CrossRef]
- Abhishek, M.; Reddy, K.S.; Shanthini, C.; Devi, V.S.K. Comparative Analysis of Boost and Quadratic Boost Converter for Wind Energy Conversion System. In Proceedings of the 2022 International Conference on Electronics and Renewable Systems (ICEARS), Tuticorin, India, 16–18 March 2022; pp. 283–287. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Nugraha, S.D.; Qudsi, O.A.; Yanaratri, D.S.; Sunarno, E.; Sudiharto, I. MPPT-current fed push pull converter for DC bus source on solar home application. In Proceedings of the 2017 2nd International conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 1–2 November 2017; pp. 378–383. [Google Scholar] [CrossRef]
- Tarzamni, H.; Babaei, E.; Esmaeelnia, F.P.; Dehghanian, P.; Tohidi, S.; Sharifian, M.B.B. Analysis and Reliability Evaluation of a High Step-Up Soft Switching Push–Pull DC–DC Converter. IEEE Trans. Reliab. 2019, 69, 1376–1386. [Google Scholar] [CrossRef]
- Hassan, T.-U.; Abbassi, R.; Jerbi, H.; Mehmood, K.; Tahir, M.; Cheema, K.; Elavarasan, R.; Ali, F.; Khan, I. A Novel Algorithm for MPPT of an Isolated PV System Using Push Pull Converter with Fuzzy Logic Controller. Energies 2020, 13, 4007. [Google Scholar] [CrossRef]
- Maksimovic, D.; Stankovic, A.M.; Thottuvelil, V.J.; Verghese, G.C. Modeling and simulation of power electronic converters. Proc. IEEE 2001, 89, 898–912. [Google Scholar] [CrossRef]
- Aloisi, W.; Palumbo, G. Efficiency model of boost dc-dc PWM converters. Int. J. Circuit Theory Appl. 2005, 33, 419–432. [Google Scholar] [CrossRef]
- Sven, F.; Nagy, B. Buck/Boost Converter Modeling and Simulation for Performance Optimization. In Proceedings of the 22nd IASTED Internation-al Conference on Modelling and Simulation (MS 2011), Canada, Calgary, 4–6 July 2011; pp. 1–8. [Google Scholar]
- Xiong, Y.; Sun, S.; Jia, H.; Shea, P.; Shen, Z.J. New Physical Insights on Power MOSFET Switching Losses. IEEE Trans. Power Electron. 2009, 24, 525–531. [Google Scholar] [CrossRef]
- Salima, K.; Achour, B. Efficiency Model of DC/DC PWM Converter Photovoltaic Applications. In Proceedings of the Global Conference on Re-newables and Energy Efficiency for Desert Regions and Exhibition, GCREEDER 2009, Amman, Jordan, 31 March–2 April 2009; pp. 1–5. [Google Scholar]
- Ayachit, A.; Kazimierczuk, M.K. Averaged Small-Signal Model of PWM DC-DC Converters in CCM Including Switching Power Loss. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 262–266. [Google Scholar] [CrossRef]
- Yao, L.; Li, D.; Liu, L. An improved power loss model of full-bridge converter under light load condition. PLoS ONE 2018, 13, e0208239. [Google Scholar] [CrossRef]
- Lai, Y.-S.; Su, Z.-J. New Integrated Control Technique for Two-Stage Server Power to Improve Efficiency Under the Light-Load Condition. IEEE Trans. Ind. Electron. 2015, 62, 6944–6954. [Google Scholar] [CrossRef]
- Zhao, L.; Li, H.; Liu, Y.; Li, Z. High Efficiency Variable-Frequency Full-Bridge Converter with a Load Adaptive Control Method Based on the Loss Model. Energies 2015, 8, 2647–2673. [Google Scholar] [CrossRef] [Green Version]
- Ivanovic, Z.; Blanusa, B.; Knezic, M. Analytical power losses model of boost rectifier. IET Power Electron. 2014, 7, 2093–2102. [Google Scholar] [CrossRef]
- Kondrath, N.; Kazimierczuk, M. Inductor winding loss owing to skin and proximity effects including harmonics in non-isolated pulse-width modulated dc–dc converters operating in continuous conduction mode. IET Power Electron. 2010, 3, 989–1000. [Google Scholar] [CrossRef]
- Nan, X.; Sullivan, C. An improved calculation of proximity-effect loss in high-frequency windings of round conductors. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, 2003. PESC ‘03, Acapulco, Mexico, 15–19 June 2003. [Google Scholar] [CrossRef]
- Jon, K. Synchronous Buck MOSFET Loss Calculation with Excel Model; Fairchild Semiconductor Publication: 2006. Available online: https://www.overclock.net/attachments/an-6005-pdf.270912/ (accessed on 3 April 2022).
- Wilson, E. Mosfet Current Source Gate Drivers, Switching Loss Modeling and Frequency Dithering Control for MHz Switching Frequency DC-DC Converters. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, February 2008. [Google Scholar]
- Van den Bossche, A.; Valchev, V.C. Modeling Ferrite Core Losses in Power Electronics. International Review of Electrical Engineering. 2006, pp. 14–22. Available online: https://biblio.ugent.be/publication/373054/file/459940 (accessed on 3 April 2022).
- Li, J.; Abdallah, T.; Sullivan, C. Improved calculation of core loss with nonsinusoidal waveforms. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 7 August 2002; Volume 4, pp. 2203–2210. [Google Scholar] [CrossRef]
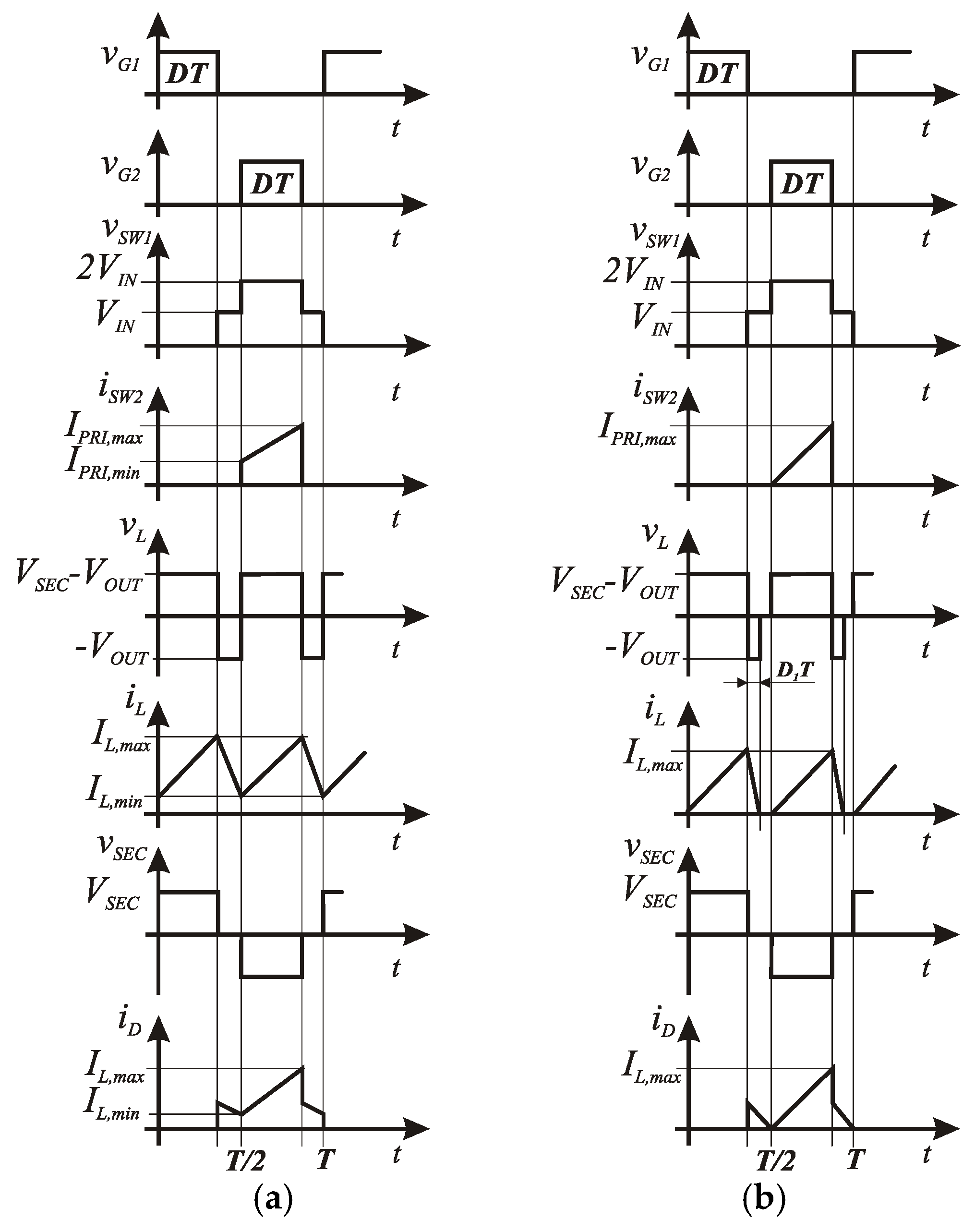





| Characteristic | Proposed Model | SPICE | Ref. [15] | Ref. [18] | Ref. [19] | Ref. [20] | Ref. [21] | Ref. [22] |
|---|---|---|---|---|---|---|---|---|
| Converter type | Push–pull | Any | Boost | Boost | Boost | Full bridge | Full bridge | Full bridge |
| Operating mode | CCM, DCM | CCM, DCM | CCM, DCM | CCM, DCM | CCM | CCM | CCM | CCM, DCM |
| Diode dynamic losses | Yes | Yes | No | No | No | Yes | No | Yes |
| MOSFET dynamic losses | Yes | Yes | Yes | No | Yes | Yes | Yes | Yes |
| Skin effect | Yes | No | No | No | No | Yes | No | No |
| Proximity effect | Yes | No | No | No | No | No | No | No |
| Transformer/Inductor core | Yes | Yes | No | No | No | Yes | Yes | Yes |
| Snubber circuit | Yes | Yes | No | No | No | No | No | No |
| Gate driver | Yes | Yes | No | No | No | No | No | No |
| Capacitor ESR | Yes | Yes | Yes | No | Yes | Yes | No | No |
| Time-consuming | No | Yes | No | No | No | No | No | No |
| Convergence issues | No | Yes | No | No | No | No | No | No |
| PIN (W) | 150 | 300 | 500 | |||
|---|---|---|---|---|---|---|
| fsw (kHz) | 10 | 100 | 10 | 100 | 10 | 100 |
| PCOND (W) | 11.22 | 15.23 | 43.37 | 30.41 | 93.74 | 71.04 |
| PCOND/PLOSS (%) | (91%) | (72.4%) | (92.4%) | (70%) | (93.2%) | (73.7%) |
| PDYN (W) | 1.11 | 5.82 | 3.59 | 13.06 | 6.82 | 25.35 |
| PDYN/PLOSS (%) | (9%) | (27.6%) | (7.6%) | (30%) | (6.8%) | (26.3%) |
| PLOSS (W) | 12.33 | 21.05 | 46.96 | 43.47 | 100.55 | 96.39 |
| ηmodel (%) | (91.9%) | (91.1%) | (84.4%) | (85.6%) | (79.9%) | (80.7%) |
| ηexper (%) | (85.3%) | (86.3%) | (80.5%) | (83.4%) | (73.1%) | (78.2%) |
| |ηmodel–ηexper| (%) | (6.47%) | (4.75%) | (3.9%) | (2.2%) | (6.8%) | (2.5%) |
| PCOND/fsw (kHz) | 10 | 100 |
|---|---|---|
| PMOSFET (W) | 24.8 | 13.54 |
| PBRIDGE (W) | 1.92 | 1.79 |
| PINDUCTOR (W) | 0.18 | 0.12 |
| PC ESR (W) | 2.59 | 1.33 |
| PTRANS (W) | 0.55 | 0.3 |
| PCLAMP (W) | 13.33 | 13.33 |
| PCOND_TOT (W) | 43.37 | 30.41 |
| PDYN/fsw (kHz) | 10 | 100 |
|---|---|---|
| PMOSFET (W) | 0.40 | 3.00 |
| PBRIDGE (W) | 0.00 | 3.60 |
| PINDUCTOR (W) | 0.83 | 4.23 |
| PTRANS (W) | 2.00 | 0.07 |
| PSNUBBER (W) | 0.36 | 2.16 |
| PDYN_TOT (W) | 3.59 | 13.06 |
| Efficiency, PLOSS | PIN = 150 W | PIN = 300 W | PIN = 500 W |
|---|---|---|---|
| η100k (%) | (86.26%) | (83.43%) | (78.22%) |
| PLOSS|100k (W) | 20.61 | 49.71 | 108.9 |
| ηopt (%) | (88.90%) | (86.71%) | (82.59%) |
| PLOSS|opt (W) | 16.65 | 39.87 | 87.05 |
| PLOSS|100k–PLOSS|opt | 3.96 | 9.84 | 21.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanovic, Z.; Knezic, M. Modeling Push–Pull Converter for Efficiency Improvement. Electronics 2022, 11, 2713. https://doi.org/10.3390/electronics11172713
Ivanovic Z, Knezic M. Modeling Push–Pull Converter for Efficiency Improvement. Electronics. 2022; 11(17):2713. https://doi.org/10.3390/electronics11172713
Chicago/Turabian StyleIvanovic, Zeljko, and Mladen Knezic. 2022. "Modeling Push–Pull Converter for Efficiency Improvement" Electronics 11, no. 17: 2713. https://doi.org/10.3390/electronics11172713
APA StyleIvanovic, Z., & Knezic, M. (2022). Modeling Push–Pull Converter for Efficiency Improvement. Electronics, 11(17), 2713. https://doi.org/10.3390/electronics11172713







