Mean Phase Voltages and Duty Cycles Estimation of a Three-Phase Inverter in a Drive System Using Machine Learning Algorithms
Abstract
:1. Introduction
- Black-box inverter model;
- Black-box inverter compensation scheme.
- Is it possible to achieve high estimation accuracies of black-box inverter models and a black-box inverter compensation scheme targeted variables (to clarify, the targeted variables in the black-box inverter model are mean phase voltages , while the targeted variables in the case of the black-box inverter compensation scheme are duty cycles at sample ), using different ML algorithms with default parameters;
- Is it possible to improve the estimation accuracies of black-box inverter models and a black-box inverter compensation scheme targeted variables, with a randomized hyper-parameter search with 5-fold cross-validation applied on ML algorithms used in the previous step;
- Is it possible to develop the stacking ensemble (using ML algorithms that achieved the highest estimation accuracies in the previous step) and, on that stacking ensemble, apply the randomized hyper-parameter search with 5-fold cross-validation to achieve high estimation accuracy with improved generalization and robustness of targeted variables in the black-box inverter model and black-box inverter compensation scheme.
2. Materials and Methods
2.1. Dataset Description
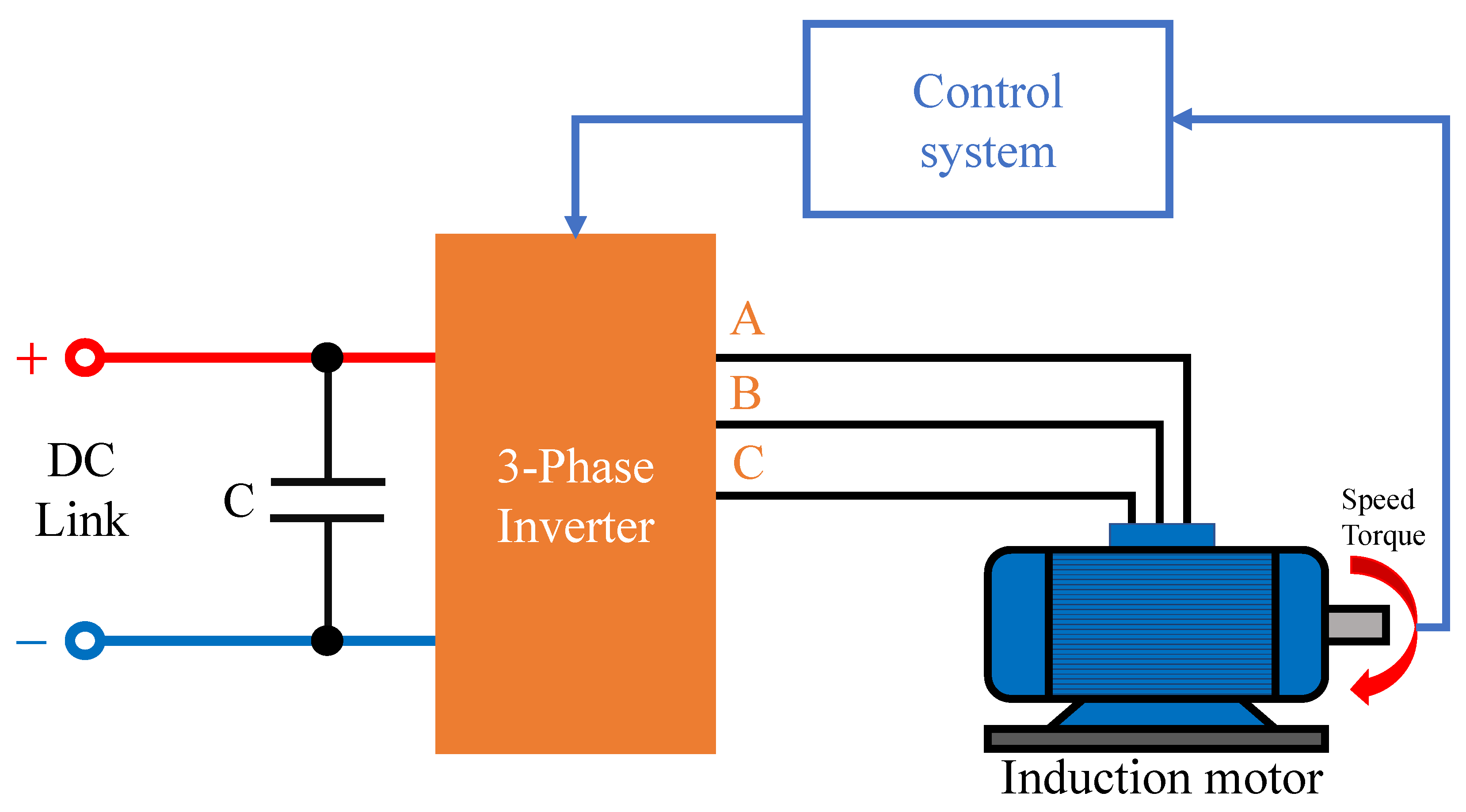
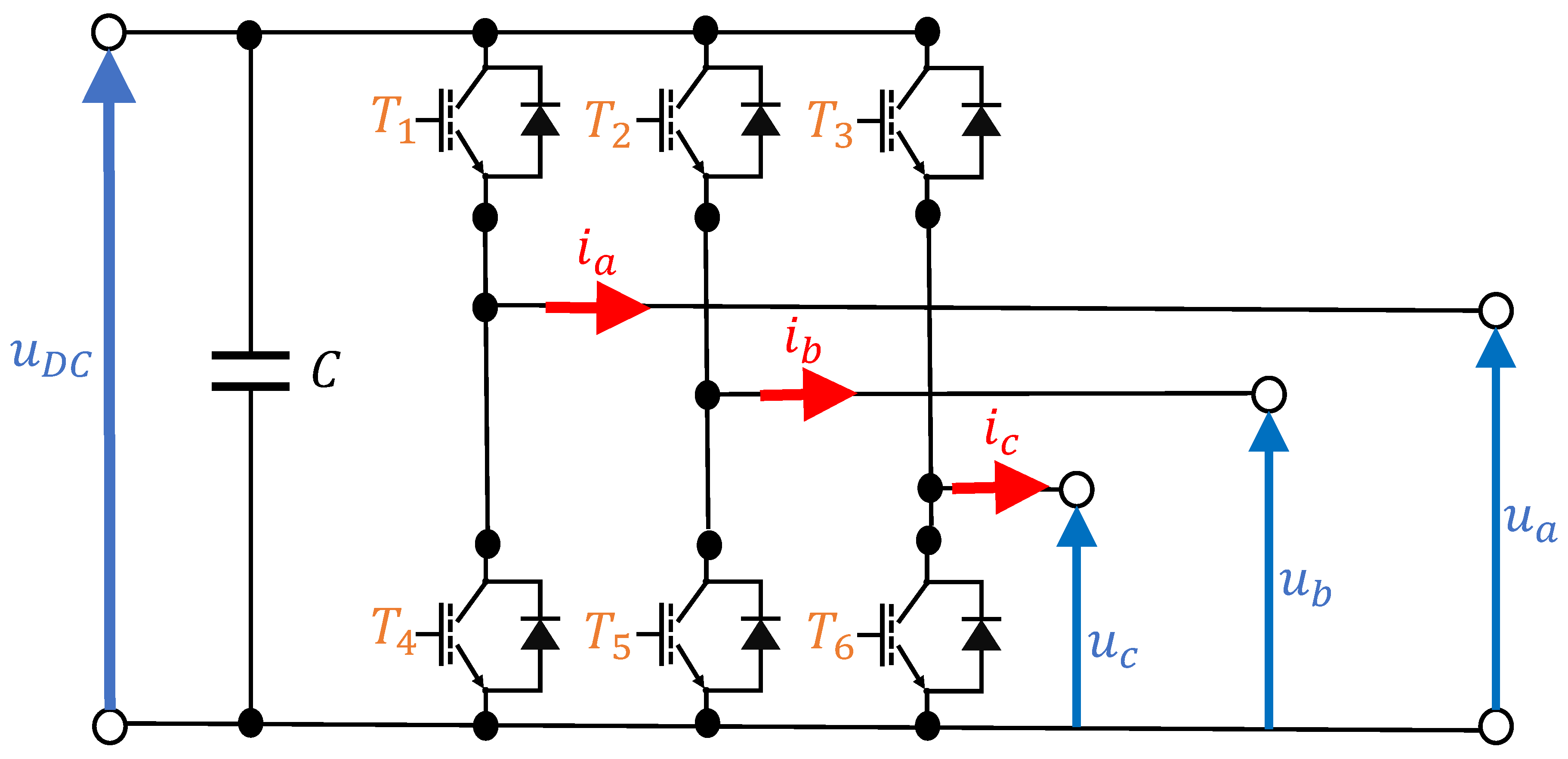
2.1.1. System Description
2.1.2. Dataset Statistical Analysis
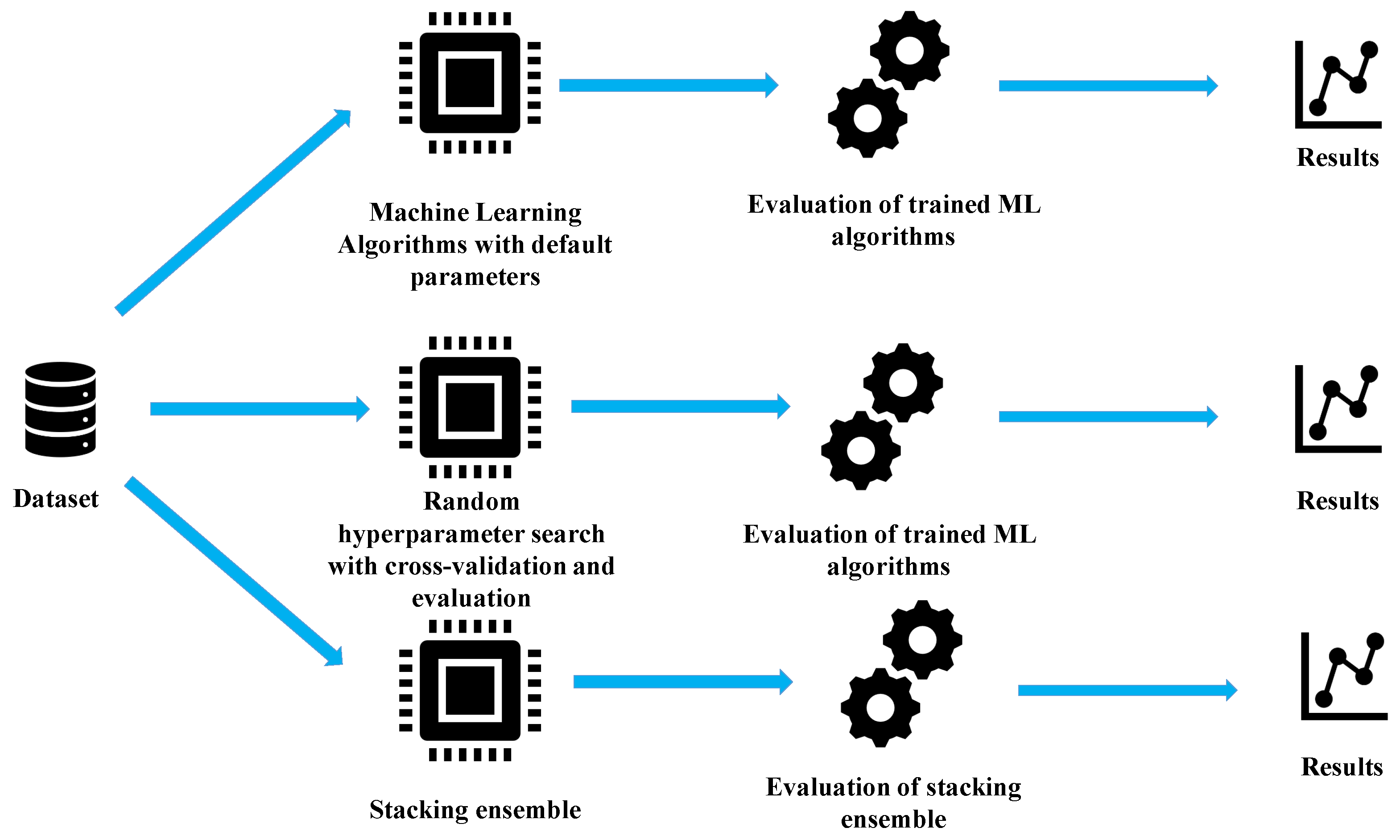
2.2. Research Methodology
- Perform the initial investigation using the original dataset with various ML algorithms with default parameters to select only those that achieve reasonable high accuracy in mean phase voltages and duty cycle estimation.
- On selected ML regression algorithms, perform a randomized hyper-parameter search with 5-fold cross-validation to find which combination of hyper-parameters for each ML algorithm achieves the highest estimation accuracies.
- Select ML algorithms that achieved the highest estimation accuracies in previous steps to build a stacking ensemble and to investigate if even higher estimation accuracies could be achieved.
2.3. Various Machine Learning Algorithms
2.3.1. ARD Regression Algorithm
2.3.2. Bayesian Ridge Regression Algorithm
2.3.3. ElasticNet Regression Algorithm
2.3.4. Huber Regression Algorithm
2.3.5. K-Neighbors Regression Algorithm
2.3.6. Lasso Regression Algorithm
2.3.7. Linear Regression Algorithm
2.3.8. Multi-Layer Perceptron
2.3.9. Ridge Regression
2.4. Randomized Hyper-Parameter Search with Cross-Validation
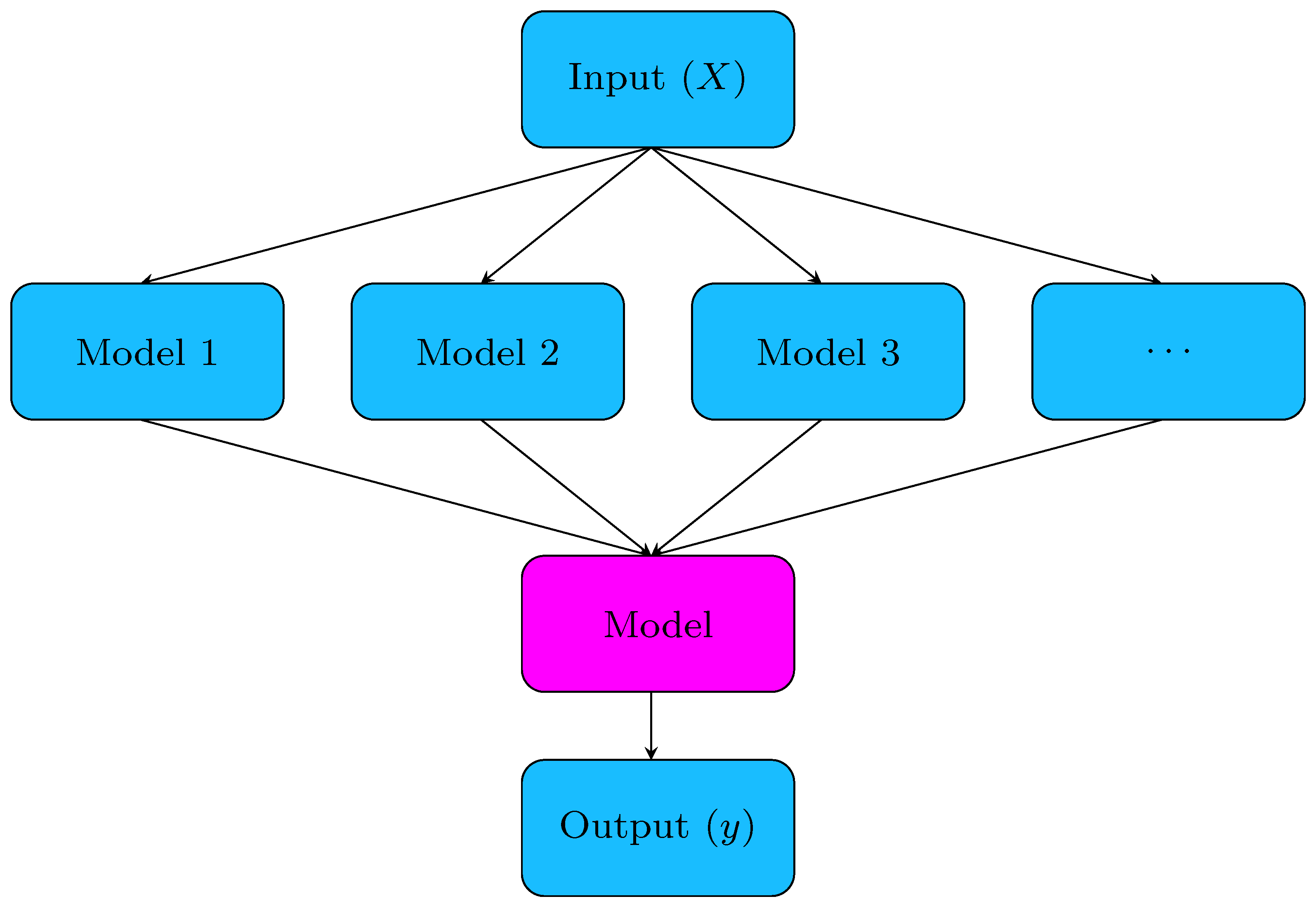
2.5. Stacking Ensemble Method
2.6. Evaluation Methodology
- Train an ML algorithm on the training part of the dataset;
- Evaluate the ML algorithm on the training dataset using the previously mentioned evaluation metric methods;
- Evaluate the ML model on the testing dataset using previously mentioned evaluation metric methods;
- Calculate the mean value of train and test evaluation metrics scores using the formula
- Calculate the standard deviation of train and test evaluation metric scores using formulas
3. Results
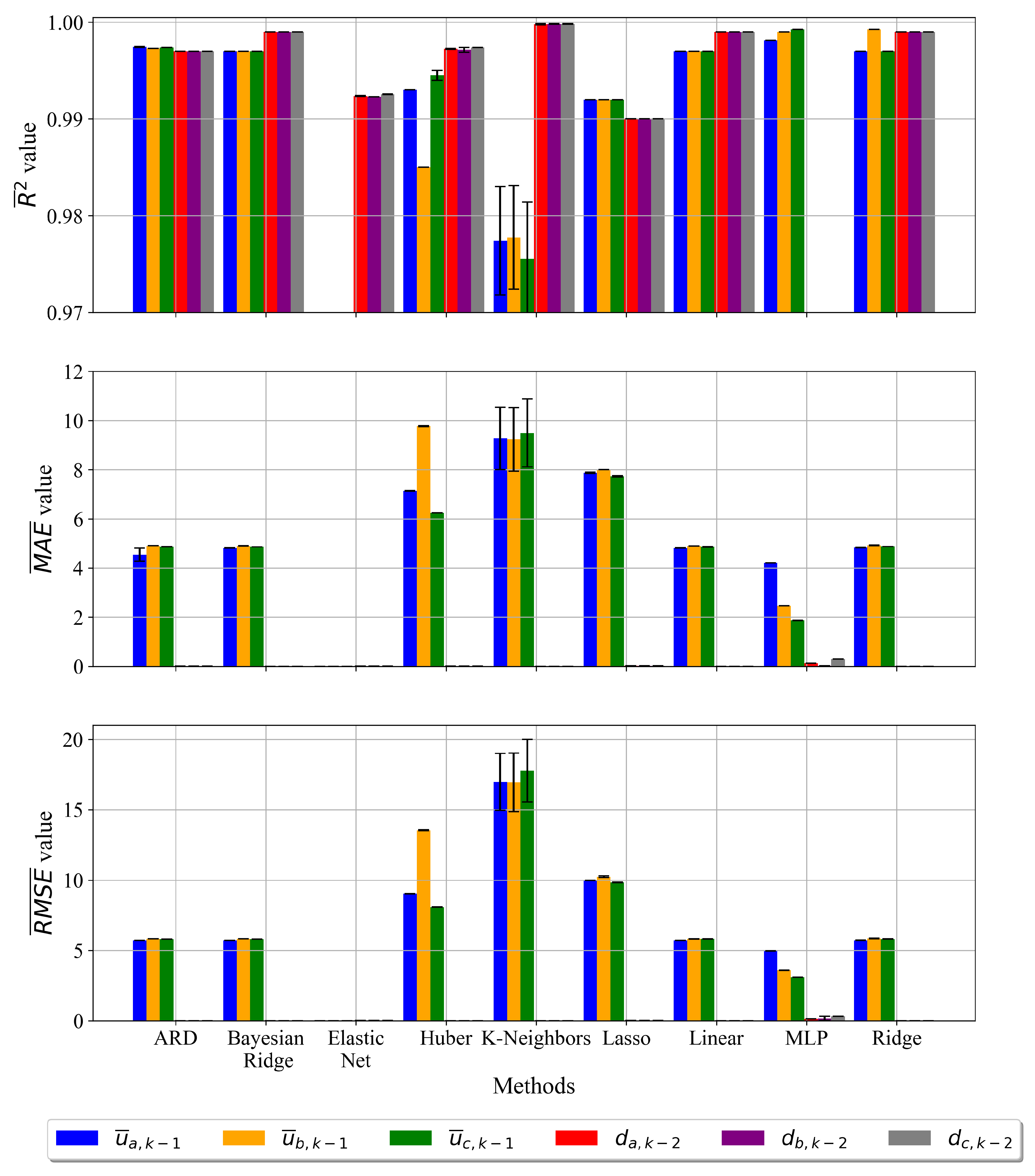
3.1. Results of Initial Investigation
3.2. Randomized Hyper-Parameter Search with Cross-Validation
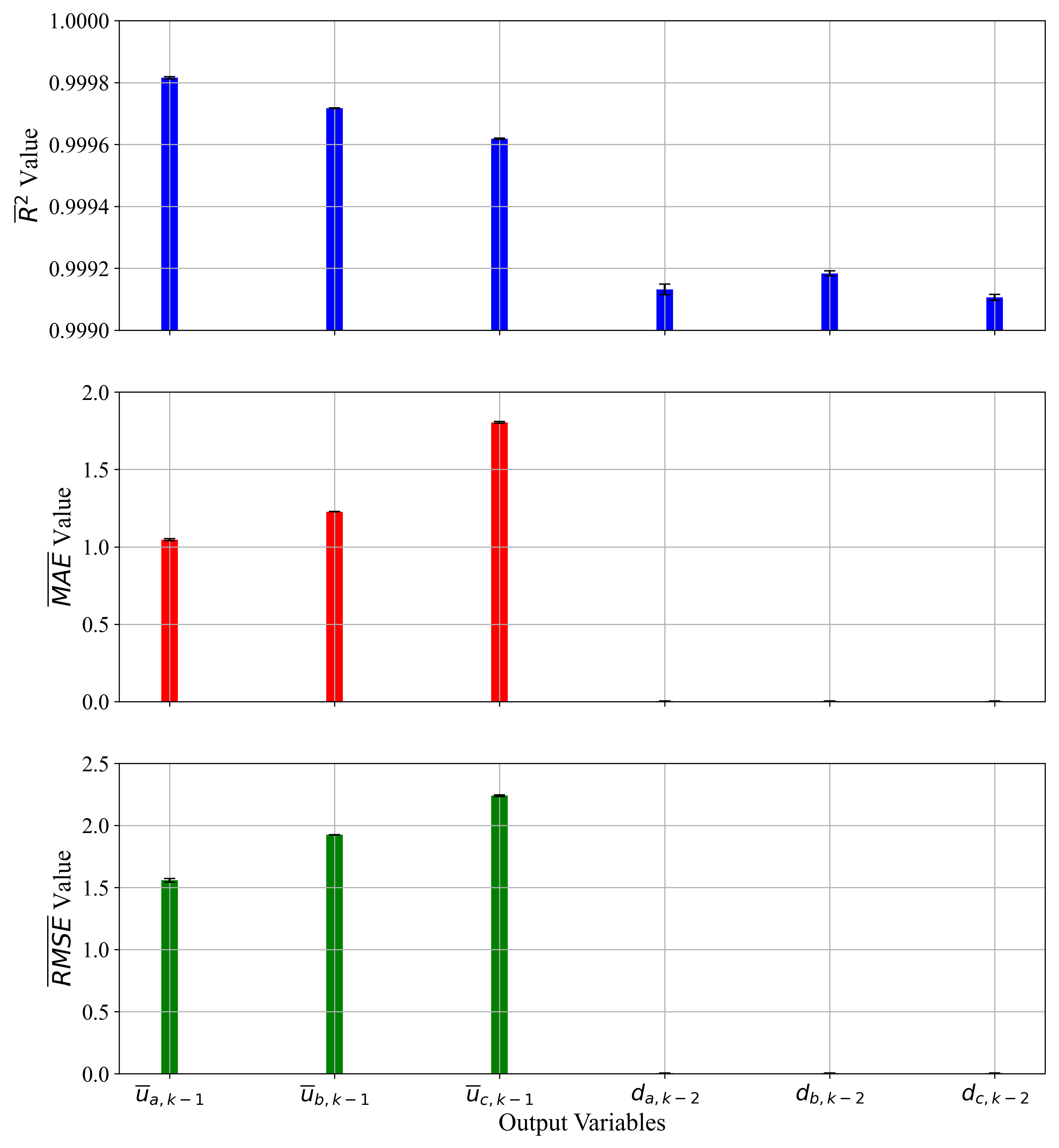
3.3. Ensemble Methods
4. Discussion
5. Conclusions
- The initial investigation showed that with the original dataset and ML algorithms with default parameters good estimation accuracies could be achieved, so it was not necessary to perform classic scaling and normalization techniques on the dataset.
- The randomized hyper-parameter search with 5-fold cross-validation on the training dataset showed that estimation accuracy values were improved for the majority of ML algorithms with the exception of K-Neighbors, which showed the same behavior as in the previous investigation.
- The final investigation with stacking ensemble with randomized hyper-parameter search used for each ML algorithm and with 5-fold cross-validation showed improved estimation performance when compared with the previous case.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IEEE Std 100-2000; The Authoritative Dictionary of IEEE Standards Terms. IEEE: Manhattan, NY, USA, 2000.
- Muljadi, E. PV water pumping with a peak-power tracker using a simple six-step square-wave inverter. IEEE Trans. Ind. Appl. 1997, 33, 714–721. [Google Scholar] [CrossRef]
- Doucet, J.; Eggleston, D.; Shaw, J. DC/AC Pure Sine Wave Inverter; PFC Worcester Polytecnic Institute: Worcester, MA, USA, 2007. [Google Scholar]
- Patel, D.C.; Sawant, R.R.; Chandorkar, M.C. Three-dimensional flux vector modulation of four-leg sine-wave output inverters. IEEE Trans. Ind. Electron. 2009, 57, 1261–1269. [Google Scholar] [CrossRef] [Green Version]
- Malesani, L.; Tenti, P.; Tomasin, P.; Toigo, V. High efficiency quasi-resonant DC link three-phase power inverter for full-range PWM. IEEE Trans. Ind. Appl. 1995, 31, 141–148. [Google Scholar] [CrossRef]
- Nagao, M.; Harada, K. Power flow of photovoltaic system using buck-boost PWM power inverter. In Proceedings of the Second International Conference on Power Electronics and Drive Systems, Singapore, 26–29 May 1997; Volume 1, pp. 144–149. [Google Scholar]
- Chen, W.; Lee, F.C.; Zhou, X.; Xu, P. Integrated planar inductor scheme for multi-module interleaved quasi-square-wave (QSW) DC/DC converter. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Record, (Cat. No. 99CH36321), Charleston, SC, USA, 1 July 1999; Volume 2, pp. 759–762. [Google Scholar]
- Chen, Z.; Spooner, E. Voltage source inverters for high-power, variable-voltage DC power sources. IEE Proc.-Gener. Transm. Distrib. 2001, 148, 439–447. [Google Scholar] [CrossRef]
- Ryan, M.J.; Brumsickle, W.E.; Lorenz, R.D. Control topology options for single-phase UPS inverters. IEEE Trans. Ind. Appl. 1997, 33, 493–501. [Google Scholar] [CrossRef] [Green Version]
- Pei, Y.; Jiang, G.; Yang, X.; Wang, Z. Auto-master-slave control technique of parallel inverters in distributed AC power systems and UPS. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; Volume 3, pp. 2050–2053. [Google Scholar]
- Guerrero, J.M.; De Vicuna, L.G.; Matas, J.; Castilla, M.; Miret, J. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control. IEEE Trans. Ind. Electron. 2005, 52, 1126–1135. [Google Scholar] [CrossRef]
- Lavi, A.; Polge, R. Induction motor speed control with static inverter in the rotor. IEEE Trans. Power Appar. Syst. 1966, PAS-85, 76–84. [Google Scholar] [CrossRef]
- Lu, B.; Sharma, S.K. A literature review of IGBT fault diagnostic and protection methods for power inverters. IEEE Trans. Ind. Appl. 2009, 45, 1770–1777. [Google Scholar]
- Ye, H.; Yang, Y.; Emadi, A. Traction inverters in hybrid electric vehicles. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–6. [Google Scholar]
- Tassou, S.; Qureshi, T. Performance of a variable-speed inverter/motor drive for refrigeration applications. Comput. Control Eng. J. 1994, 5, 193–199. [Google Scholar] [CrossRef]
- Qureshi, T.; Tassou, S. Variable-speed capacity control in refrigeration systems. Appl. Therm. Eng. 1996, 16, 103–113. [Google Scholar] [CrossRef]
- Cho, H.; Chung, J.T.; Kim, Y. Influence of liquid refrigerant injection on the performance of an inverter-driven scroll compressor. Int. J. Refrig. 2003, 26, 87–94. [Google Scholar] [CrossRef]
- Wu, W.; Sun, Y.; Huang, M.; Wang, X.; Wang, H.; Blaabjerg, F.; Liserre, M.; Chung, H.S.h. A robust passive damping method for LLCL-filter-based grid-tied inverters to minimize the effect of grid harmonic voltages. IEEE Trans. Power Electron. 2013, 29, 3279–3289. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of DQ small-signal impedance of grid-tied inverters. IEEE Trans. Power Electron. 2015, 31, 675–687. [Google Scholar] [CrossRef]
- Athari, H.; Niroomand, M.; Ataei, M. Review and classification of control systems in grid-tied inverters. Renew. Sustain. Energy Rev. 2017, 72, 1167–1176. [Google Scholar] [CrossRef]
- Kavya Santhoshi, B.; Mohana Sundaram, K.; Padmanaban, S.; Holm-Nielsen, J.B.; K.K., P. Critical review of PV grid-tied inverters. Energies 2019, 12, 1921. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2010, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Nguyen, P.L.; Ma, Z.; Sheng, W. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2013, 29, 617–630. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Konstantopoulos, G.C.; Ren, B.; Krstic, M. Improved synchronverters with bounded frequency and voltage for smart grid integration. IEEE Trans. Smart Grid 2016, 9, 786–796. [Google Scholar] [CrossRef] [Green Version]
- Rosso, R.; Engelken, S.; Liserre, M. Robust stability analysis of synchronverters operating in parallel. IEEE Trans. Power Electron. 2019, 34, 11309–11319. [Google Scholar] [CrossRef]
- Dawson, F.P.; Jain, P. A comparison of load commutated inverter systems for induction heating and melting applications. IEEE Trans. Power Electron. 1991, 6, 430–441. [Google Scholar] [CrossRef]
- Dieckerhoff, S.; Ruan, M.; De Doncker, R.W. Design of an IGBT-based LCL-resonant inverter for high-frequency induction heating. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference, Thirty-Forth IAS Annual Meeting (Cat. No. 99CH36370), Phoenix, AZ, USA, 3–7 October 1999; Volume 3, pp. 2039–2045. [Google Scholar]
- Esteve, V.; Jordán, J.; Sanchis-Kilders, E.; Dede, E.J.; Maset, E.; Ejea, J.B.; Ferreres, A. Improving the reliability of series resonant inverters for induction heating applications. IEEE Trans. Ind. Electron. 2013, 61, 2564–2572. [Google Scholar] [CrossRef]
- Esteve, V.; Jordan, J.; Sanchis-Kilders, E.; Dede, E.J.; Maset, E.; Ejea, J.B.; Ferreres, A. Enhanced pulse-density-modulated power control for high-frequency induction heating inverters. IEEE Trans. Ind. Electron. 2015, 62, 6905–6914. [Google Scholar] [CrossRef]
- Cheng, F.F.; Yeh, S.N. Application of fuzzy logic in the speed control of AC servo system and an intelligent inverter. IEEE Trans. Energy Convers. 1993, 8, 312–318. [Google Scholar] [CrossRef]
- Sivakotiah, S.; Rekha, J. Speed control of brushless DC motor on resonant pole inverter using fuzzy logic controller. Int. J. Eng. Sci. Technol. 2011, 3, 7357–7360. [Google Scholar]
- Masrur, M.A.; Chen, Z.; Murphey, Y. Intelligent diagnosis of open and short circuit faults in electric drive inverters for real-time applications. IET Power Electron. 2010, 3, 279–291. [Google Scholar] [CrossRef]
- Salehi, R.; Farokhnia, N.; Abedi, M.; Fathi, S.H. Elimination of low order harmonics in multilevel inverters using genetic algorithm. J. Power Electron. 2011, 11, 132–139. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Okou, F. Strategies to accelerate harmonic minimization in multilevel inverters using a parallel genetic algorithm on graphical processing unit. IEEE Trans. Power Electron. 2014, 29, 5087–5090. [Google Scholar] [CrossRef]
- Rajeswaran, N.; Swarupa, M.L.; Rao, T.S.; Chetaswi, K. Hybrid artificial intelligence based fault diagnosis of svpwm voltage source inverters for induction motor. Mater. Today Proc. 2018, 5, 565–571. [Google Scholar] [CrossRef]
- Babakmehr, M.; Harirchi, F.; Dehghanian, P.; Enslin, J. Artificial intelligence-based cyber-physical events classification for islanding detection in power inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 5282–5293. [Google Scholar] [CrossRef]
- Stender, M.; Wallscheid, O.; Bocker, J. Data Set—Three-Phase Igbt Two-Level Inverter for Electrical Drives (Data). Available online: https://www.kaggle.com/datasets/stender/inverter-dataset (accessed on 3 January 2022).
- Stender, M.; Wallscheid, O.; Böcker, J. Data Set Description: Three-Phase IGBT Two-Level Inverter for Electrical Drives; Department of Power Electronics and Electrical Drives, University at Paderborn: Paderborn, Germany, 2020. [Google Scholar]
- Mørup, M.; Hansen, L.K. Automatic relevance determination for multi-way models. J. Chemom. A J. Chemom. Soc. 2009, 23, 352–363. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shi, Q.; Abdel-Aty, M.; Lee, J. A Bayesian ridge regression analysis of congestion’s impact on urban expressway safety. Accid. Anal. Prev. 2016, 88, 124–137. [Google Scholar] [CrossRef] [PubMed]
- Yi, C.; Huang, J. Semismooth Newton coordinate descent algorithm for elastic-net penalized Huber loss regression and quantile regression. J. Comput. Graph. Stat. 2017, 26, 547–557. [Google Scholar] [CrossRef] [Green Version]
- Nevendra, M.; Singh, P. Empirical investigation of hyperparameter optimization for software defect count prediction. Expert Syst. Appl. 2022, 191, 116217. [Google Scholar] [CrossRef]
- Devroye, L.; Gyorfi, L.; Krzyzak, A.; Lugosi, G. On the strong universal consistency of nearest neighbor regression function estimates. Ann. Stat. 1994, 22, 1371–1385. [Google Scholar] [CrossRef]
- Yang, Y.; Zou, H. A fast unified algorithm for solving group-lasso penalize learning problems. Stat. Comput. 2015, 25, 1129–1141. [Google Scholar] [CrossRef]
- Naseem, I.; Togneri, R.; Bennamoun, M. Linear regression for face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2106–2112. [Google Scholar] [CrossRef]
- Riedmiller, M.; Lernen, A. Multi Layer Perceptron; Machine Learning Lab Special Lecture; University of Freiburg: Freiburg, Germany, 2014; pp. 7–24. [Google Scholar]
- Jamil, W.; Bouchachia, A. Iterative ridge regression using the aggregating algorithm. Pattern Recognit. Lett. 2022, 158, 34–41. [Google Scholar] [CrossRef]
- Lorencin, I.; Anđelić, N.; Mrzljak, V.; Car, Z. Genetic algorithm approach to design of multi-layer perceptron for combined cycle power plant electrical power output estimation. Energies 2019, 12, 4352. [Google Scholar] [CrossRef] [Green Version]
- Divina, F.; Gilson, A.; Goméz-Vela, F.; García Torres, M.; Torres, J.F. Stacking ensemble learning for short-term electricity consumption forecasting. Energies 2018, 11, 949. [Google Scholar] [CrossRef] [Green Version]
- Di Bucchianico, A. Coefficient of determination (R 2). Encycl. Stat. Qual. Reliab. 2008, 1. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Brassington, G. Mean absolute error and root mean square error: Which is the better metric for assessing model performance? In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2017; p. 3574. [Google Scholar]





| Model | Variable Name | Symbol | Mean | STD | Min | Max |
|---|---|---|---|---|---|---|
| Input Variables | Phase Currents | 0.0005 | 2.19 | −7.3 | 7.47 | |
| −0.0076 | 2.1553 | −6.3202 | 6.6681 | |||
| −0.0089 | 2.2162 | −7.1129 | 7.4371 | |||
| Phase Currents at | 0.0005 | 2.1992 | −7.3001 | 7.4702 | ||
| −0.0077 | 2.1553 | −6.3202 | 6.6681 | |||
| −0.0089 | 2.2161 | −7.1129 | 7.4371 | |||
| Duty cycles at | 0.5002 | 0.2119 | 0 | 1 | ||
| 0.5002 | 0.2117 | 0 | 1 | |||
| 0.5001 | 0.2117 | 0 | 1 | |||
| Duty cycles at | 0.5002 | 0.2119 | 0 | 1 | ||
| 0.5002 | 0.2117 | 0 | 1 | |||
| 0.5001 | 0.2117 | 0 | 1 | |||
| DC-link voltage at k | 567.13 | 4.9936 | 548.01 | 575.55 | ||
| DC-link voltage at | 567.13 | 4.9934 | 548.01 | 575.55 | ||
| Output Variables | Mean phase voltages at | 283.41 | 114.64 | −2.2884 | 573.34 | |
| 283.46 | 114.29 | −2.0879 | 573.2 | |||
| 283.74 | 114.6 | −2.3124 | 573.17 |
| Model | Variable Name | Symbol | Mean | STD | Min | Max |
|---|---|---|---|---|---|---|
| Input Variables | Mean phase voltages at | 283.41 | 114.65 | −2.2884 | 573.33 | |
| 283.46 | 114.29 | −2.0879 | 573.2 | |||
| 283.74 | 114.6 | −2.31 | 573.17 | |||
| Duty cycles at k-3 | 0.5002 | 0.212 | 0 | 1 | ||
| 0.5002 | 0.2117 | 0 | 1 | |||
| 0.5001 | 0.2117 | 0 | 1 | |||
| Phase currents at | 0.0005 | 2.1989 | −7.3 | 7.47 | ||
| −0.0078 | 2.1551 | −6.32 | 6.6681 | |||
| −0.0088 | 2.216 | −7.1129 | 7.4371 | |||
| Phase currents at | 0.0005 | 2.199 | −7.3 | 7.47 | ||
| −0.0077 | 2.1552 | −6.32 | 6.6681 | |||
| −0.0089 | 2.2161 | −7.1129 | 7.4371 | |||
| DC-link voltage at | 567.13 | 4.9931 | 548.01 | 575.5533 | ||
| DC-link voltage at | 567.13 | 4.9933 | 548.01 | 575.55 | ||
| Output Variables | Duty cycles at | 0.5 | 0.2119 | 0 | 1 | |
| 0.5002 | 0.2117 | 0 | 1 | |||
| 0.5001 | 0.2117 | 0 | 1 |
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| 100 | 1000 | |
| _1 | ||
| _2 | ||
| _1 | ||
| _2 | ||
| True, False | ||
| 1000 | 100,000 | |
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| 500 | 1000 | |
| _1 | ||
| _2 | ||
| _1 | ||
| _2 | ||
| _init | None | |
| _init | None | |
| True, False | ||
| True, False | ||
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| −10 | 10 | |
| 0 | 1 | |
| 10,000 | 100,000 | |
| 0 | 50 | |
| cyclic, random | ||
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| 1.1 | 10 | |
| 10,000 | 100,000 | |
| True, False | ||
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| 2 | 10 | |
| uniform, distance | ||
| auto, ball_tree, kd_tree, brute | ||
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| 0.1 | 10 | |
| True, False | ||
| 1000 | 10,000 | |
| 0 | 50 | |
| cyclic, random | ||
| Hyper-Parameter | Bounds |
|---|---|
| True, False |
| Parameter Name | Lower Bound | Upper Bound |
|---|---|---|
| Number of Hidden Layers | 2 | 5 |
| No. Neurons per Hidden Layer | 10 | 200 |
| identity, logistic, tanh, relu | ||
| lbfgs, sgd, adam | ||
| 200 | 300 | |
| constant, invscaling, adaptive | ||
| 200 | 2000 | |
| 10 | 10,000 | |
| Hyper-Parameter | Lower Bound | Upper Bound |
|---|---|---|
| 1.0 | 1000 | |
| True | False | |
| 100 | 100,000 | |
| , , , , , , | ||
| ML algorithm | Hyper-parameters (, , , , , ) |
| ARD | number of iterations = 300, tolerance = , alpha1 = , alpha2 = , lambda1 = , lambda2 = , threshold lambda = 10,000 |
| Bayesian ridge | number of iterations = 300, tolerance = , alpha1 = , alpha2 = , lambda1 = , lambda2 = , alpha initial = None, lambda initial = None, |
| Huber | epsilon = 1.35, max_iter = 100, alpha = 0.0001, tolerance = |
| Elastic Net | alpha = 1.0, l1_ratio = 0.5, max_iter = 1000, tolerance = positive = False, selection = cyclic |
| K-Neighbors | n_neighbors = 5, weights = uniform, algorithm = auto, leaf_size = 30 p = 2, metric = minkowski, metric_params = None |
| Lasso | alpha = 1.0, fit_intercept = True, max_iter = 1000, tolerance = positive = False, random_state = None, selection = cyclic |
| Linear | fit_intercept = True, False |
| MLP | hidden_layer_sizes = (100), activation = relu, solver = adam, alpha = 0.0001, batch_size = auto, learning_rate = constant, learning_rate_init = 0.001, power_t = 0.5, max_iter = 200, shuffle = True, random_state = None, tolerance = |
| Ridge | alpha = 1.0, max_iter = None, tolerance = , solver = auto, positive = False, random_state = None |
| ML Algorithm | Hyper-parameters (, , , , , ) |
| ARD | n_iter = 854, 286, 934, 555, 284, 354 tolerance = , , , , , alpha1 = 0.023148, 0.0648, 0.05917, 0.05919, 0.0947, 0.0237 alpha2 = 0.02833, 0.00509, 0.01208, 0.09771, 0.05974, 0.058 lambda1 =0.0864, 0.04028, 0.03316, 0.03642, 0.0789, 0.076 lambda2 = 0.06796, 0.00708, 0.08056, 0.03634, 0.02163, 0.0746 threshold_lambda = 37,335, 21,754, 41,212, 59,922, 53,871 |
| Bayesian ridge | n_iter = 566, 784, 880, 830, 974, 733 tolerance = 0.00028, 0.00049, 0.00033, 0.00055, 0.00099, 0.00059 alpha1 = 0.0577, 0.036, 0.0045, 0.017, 0.062, 0.057 alpha2 = 0.081, 0.0205, 0.0233, 0.025, 0.08, 0.098 lambda1 = 0.052, 0.0558, 0.065, 0.037, 0.052, 0.09 lambda2 = 0.0301, 0.006, 0.023, 0.065, 0.085, 0.066 lambda_init = None, 6.329, 0.34, None, 3.368, None |
| Huber | epsilon = 1.703, 67.87, 72.22, 1.15, 1.631, 9.89 max_iter = 80,657, 26,744, 14,533, 41,745, 24,066, 93,820 alpha = 0.00027, 0.04, 0.0071, 0.00036, , 0.00014 tolerance = , 0.0184, 0.07, , , |
| Elastic Net | alpha = 0.62, 0.048, 0.029, 0.94, 1.29, 0.51 l1_ratio = 0.99, 0.93, 0.845, 0.36, 0.27, 0.98 max_iter = 83,712, 11,323, 69,707, 17,535, 27,655, 41,066 tolerance = , , , , , random_state = 33, 10, 9, 19, 20, 14 selection = cyclic, random, cyclic, random, cyclic, random |
| Lasso | alpha = 0.74, 0.67, 0.32, 0.58, 0.76, 0.28 max_iter = 2814, 9494, 1431, 3395, 2852, 2568 tolerance = , , , , , random_state = None, None, None, 48, None, 7 selection = cyclic, random, cyclic, cyclic, random, cyclic |
| Linear | fit_intercept = False, True, True, True, True, True |
| MLP | hidden_layer_size = (107, 139), (140, 76, 99, 64, 113), (139, 144, 128, 157), (111, 45, 121) (129, 71, 75), (152, 178, 110) activation_function = logistic, relu, relu, relu, logistic, logistic solver = adam, adam, adam, adam, adam, adam alpha = 0.00019, 0.007, 0.005, 0.0078, 0.0028, 0.0059 batch_size = 214, 246, 238, 277, 263, 220 learning_rate = constant, invscaling, constant, adaptive, constant, constant max_iter = 1153, 299, 1346, 338, 1169, 1967 tolerance = , , , , nIter_no_change = 956, 23, 1310, 193, 1140, 710 |
| Ridge | alpha = 682.580, 368.425, 254.265, 805.43, 453.45, 580.24 fit_intercept = False, True, False, True, False, False max_iter = 66,120, 78,658, 34,453, 25,145, 82,456, 75,458 tolerance = , , , , , solve = sag, saga, cholesky, sag, saga, sag |
| ML algorithm | Hyper-parameters (, , , , , ) |
| ARD | num_iter = 804, 957, 808, 375, 828, 813 tol = , , , alpha_1 = 0.064, 0.0689, 0.0772, 0.0707, 0.0674, 0.03, alpha_2 = 0.0868, 0.0819, 0.0603, 0.0432, 0.0936, 0.063 lambda_1 = 0.0351, 0.0655, 0.0839, 0, 073, 0.068, 0.007 lambda_2 = 0.0914, 0.0323, 0.0983, 0, 083, 0.0904, 0.08, compute_score = True, True, False, True, True, True threshold_lambda = 21,256, 89,378, 43,190, 60,432, 69,129, 26,796 |
| Bayesian ridge | num_iter = 997, 837, 948, 504, 777, 656 tol = 0.0003, 0.00063, 0.000707, 0.000546, 0.00078, 0.0005 alpha_1 = 0.0155, 0.036, 0.062, 0.0051, 0.0094, 0.058 alpha_2 = 0.0437, 0.055, 0.055, 0.065, 0.027, 0.022 lambda_1 = 0.0334, 0.019, 0.0103, 0.0576, 0.0996 lambda_2 = 0.0991, 0.019, 0.031, 0.0135, 0.0482, 0.076 lambda_init = 1.7039, 1.815, 5.966, None, 4.96, None compute_score = False, False, False, True, False, False fit_intercept = True, False, False, False, True, False |
| Huber | epsilon = 9.68, 5.699, 7.41, 6.08, 1.36, 4.79 max_iter = 67884, 90043, 42378, 19418, 32229, 68369, alpha = 0.000261, , 0.000617, 0.00067, 0.00037, fit_intercept = True, True, True, True, True, True tol = , , , , |
| Elastic Net | alpha = −9.79, 2.09, −9.98, −9.264, −2.35, −1.13 l1_ratio = 0.245, 0.143, 0.37, 0.924, 0.27, 0.9 fit_intercept = False, False, False, False, False, False max_iter = 32841, 41891, 35791, 54745, 54209, 84589 tol = , , , , random_state = 28, 25, 31, 42, 3, 13 selection = random, random, random, random, random, cyclic |
| Lasso | alpha = 5.38, 7.606, 0.334, 2.01, 1.026, 5.52 fit_intercept = True, True, False, True, False, True max_iter = 8423, 9285, 4220, 2606, 6958, 8770 tol = , , , , random_state = None, None, 27, 45, 16, None, selection = cyclic, cyclic, cyclic, cyclic, random, random |
| Linear | fit_intercept = True, True, False, True, False, False |
| MLP | hid_layer_size = (70, 125, 157, 187), (18, 118, 199), (162, 191, 172), (130, 176, 53, 40, 111), (107, 26, 116), (174, 170, 88, 122, 111) activation = tanh, relu, relu, identity, logistic, identity solver = lbfgs, adam, adam, adam, lbfgs, adam alpha = 0.0066, 0.00201, 0.0039, 0.00158, 0.0063, 0.0072 batch_size = 264, 247, 285, 222, 290, 287 learning_rate = constant, constant, constant, adaptive, invscaling, invscaling max_iter = 1108, 447, 1942, 1942, 1436, 1755 tol = , , , , n_iter_no_change = 195, 218, 282, 959, 768, 494 |
| Ridge | alpha = 813.31, 149.53, 829.864, 897.206, 590.799, 846.2 fit_intercept = False, True, False, True, False, True max_iter = 25,174, 60,066, 58,733, 45,444, 84,797, 60,136 tol = , 0.000618, 0.00095, 0.00039 0.000669, 0.00078 solver = auto, lsqr, auto, lsqr, svd, lsqr |
| Stage | Description |
|---|---|
| Initial investigation | Advantages: -good estimation accuracies (), -accuracies of duty cycles better than in the case of mean phase voltages Disadvantages: -large STD between estimation accuracies achieved on the train and test dataset in case of KNN |
| Random grid search with 5-Fold Cross- Validation | Advantages: -improved average estimation accuracy, -mean phase voltages and duty cycle accuracies improved, -STD between accuracies on the train and test dataset lowered Disadvantages: -KNN omitted from further investigation due to the same STD as in previous case -ElasticNet and MLP showed slight increase in , , and values |
| Ensemble Method | Advantages: -estimation accuracies are optimal since algorithm combines estimations of 8 basic estimators Disadvantages: -training time longer than training individual ML algorithm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anđelić, N.; Lorencin, I.; Glučina, M.; Car, Z. Mean Phase Voltages and Duty Cycles Estimation of a Three-Phase Inverter in a Drive System Using Machine Learning Algorithms. Electronics 2022, 11, 2623. https://doi.org/10.3390/electronics11162623
Anđelić N, Lorencin I, Glučina M, Car Z. Mean Phase Voltages and Duty Cycles Estimation of a Three-Phase Inverter in a Drive System Using Machine Learning Algorithms. Electronics. 2022; 11(16):2623. https://doi.org/10.3390/electronics11162623
Chicago/Turabian StyleAnđelić, Nikola, Ivan Lorencin, Matko Glučina, and Zlatan Car. 2022. "Mean Phase Voltages and Duty Cycles Estimation of a Three-Phase Inverter in a Drive System Using Machine Learning Algorithms" Electronics 11, no. 16: 2623. https://doi.org/10.3390/electronics11162623
APA StyleAnđelić, N., Lorencin, I., Glučina, M., & Car, Z. (2022). Mean Phase Voltages and Duty Cycles Estimation of a Three-Phase Inverter in a Drive System Using Machine Learning Algorithms. Electronics, 11(16), 2623. https://doi.org/10.3390/electronics11162623









