An Overview of Systolic Arrays for Forward and Inverse Discrete Sine Transforms and Their Exploitation in View of an Improved Approach
Abstract
:1. Introduction
- We have appropriately reformulated the DST algorithm such that an efficient VLSI implementation using systolic arrays with an optimal SD representation integration has been obtained. Due to the efficient use of the SD representation, a significant improvement of the speed performances and the hardware complexity has been achieved.
- We have split the computation of the DST algorithm into eight regular and modular computational structures that can be efficiently mapped on linear systolic arrays and can be computed in parallel, considerably improving the throughput of the VLSI architecture.
- Moreover, due to the appropriate reformulation of the DST algorithm, we have efficiently incorporated the hardware security techniques with low overheads. This is very important for common goods devices.
2. Different Solutions to Implement the Forward and Inverse DST Using Systolic Arrays
- The processing elements have a simple function that does not change over time;
- There are a few types of processing elements;
- The data flow in the algorithm are simple and regular;
- The data communications in the algorithm have a locality feature.
2.1. A Systolic VLSI Algorithm Based on a Direct Decomposition of Even and Odd Output Sequences
2.2. A Systolic VLSI Algorithm for the Forward DST Based on Two Cycle Convolutions
2.3. A VLSI Algorithm for the Inverse DST Based on Two Cyclic Convolutions
2.4. A Systolic Algorithm for Forward DST Using Short Cyclic Convolutions
| and | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 6 | 3 | 5 | 4 | 2 | |
| 1 | 2 | 4 | 5 | 3 | 6 |
2.5. A New VLSI Algorithm for Inverse DST Using a Pseudo-Band Correlation
- -
- The first bit of the element in the matrix designates the sign before the brackets (minus if “1” and plus if “0”);
- -
- The second bit of the element in the matrix denotes the operation inside the brackets (subtraction if “1” and addition if “0”).
2.6. A Systolic Algorithm for Inverse DST Based on Quasi-Band Correlation Structures for a Length N Power of Two
3. An Improved Systolic Array for Forward DST
3.1. A New VLSI Algorithm for Forward DST
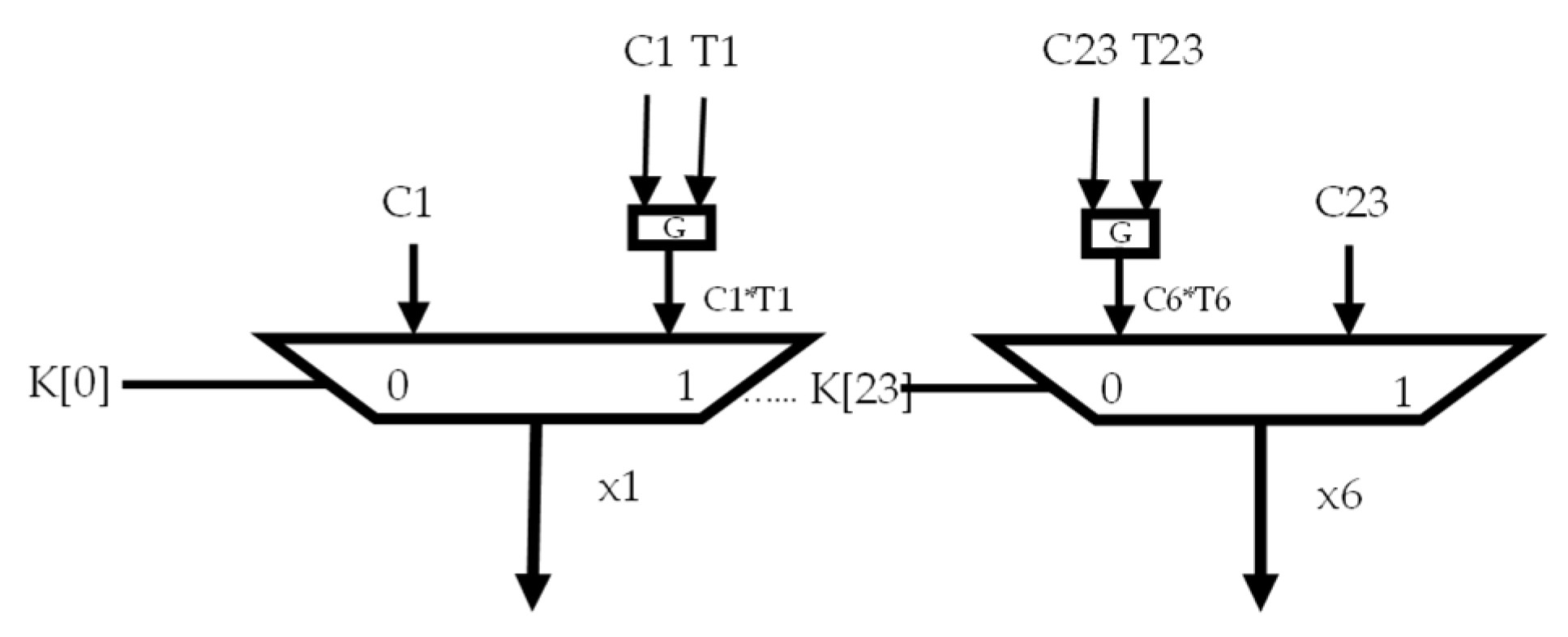
3.2. A VLSI Architecture for the Proposed Systolic Algorithm for DST
- A short overview of the signed digit (SD) representations
- B.
- Our SD based VLSI Implementation
4. Discussion
5. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilbert, P.; Lopez, M. The World’s Technological Capacity to Store, Communicate, and Compute Information. Science 2011, 332, 60–65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kane, G.C.; Pear, A. The Rise of Visual Content Online. MIT Sloan Management Review. Available online: https://sloanreview.mit.edu/article/the-rise-of-visual-content-online/ (accessed on 4 April 2021).
- Jain, A.K. A fast Karhunen-Loeve transform for a class of random processes. IEEE Trans. Commun. 1976, 24, 1023–1029. [Google Scholar] [CrossRef]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete cosine transform. IEEE Trans. Comput. 1974, 23, 90–94. [Google Scholar] [CrossRef]
- Jain, A.K. Fundamentals of Digital Image Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Kalali, E.; Mert, A.C.; Hamzaoglu, I. A computation and energy reduction technique for HEVC Discrete Cosine Transform. IEEE Trans. Consum. Electron. 2016, 62, 166–174. [Google Scholar] [CrossRef]
- Ali, M.; Islam, M.; Memon, M.; Asif, D.M.; Lin, F. Optimum DCT type-I based transceiver model and effective channel estimation for uplink NB-IoT system. Phys. Commun. 2021, 48, 101431. [Google Scholar] [CrossRef]
- Domínguez-Jiménez, M.E.; Luengo, D.; Sansigre-Vidal, G.; Cruz-Roldán, F. A novel channel estimation scheme for multicarrier communications with the Type-I even discrete cosine transform. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 2239–2243. [Google Scholar]
- Domínguez-Jiménez, M.E.; Luengo, D.; Sansigre-Vidal, G.; Cruz-Roldán, F. A Novel Scheme of Multicarrier Modulation with the Discrete Cosine Transform. IEEE Trans. Wirel. Commun. 2021, 20, 7992–8005. [Google Scholar] [CrossRef]
- Lee, C.F.; Shen, J.J.; Chen, Z.R.; Agrawal, S. Self-Embedding Authentication Watermarking with Effective Tampered Location Detection and High-Quality Image Recovery. Sensors 2019, 19, 2267. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.; Chen, Z.; Li, L.; Cao, X.; Wei, J.; Xiong, N.; Li, J.; Dang, J. Watermarking Based on Compressive Sensing for Digital Speech Detection and Recovery. Sensors 2018, 18, 2390. [Google Scholar] [CrossRef] [Green Version]
- Boukhechba, K.; Wu, H.; Bazine, R. DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis. Sensors 2018, 18, 1138. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Chen, B.; Xue, L.; Zhang, J.; Zhu, L. A Prediction-Based Spatial-Spectral Adaptive Hyperspectral Compressive Sensing Algorithm. Sensors 2018, 18, 3289. [Google Scholar] [CrossRef] [Green Version]
- Kamisli, F. Lossless Image and Intra-Frame Compression with Integer-to-Integer DST. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 502–516. [Google Scholar] [CrossRef] [Green Version]
- Panda, J.; Meher, S. A Novel Approach of Image Interpolation using DST. In Proceedings of the 2019 Fifth International Conference on Image Information Processing (ICIIP), Shimla, India, 15–17 November 2019. [Google Scholar]
- Ajmera, A.; Divecha, M.; Ghosh, S.S.; Raval, I.; Chaturvedi, R. Video Steganography: Using Scrambling-AES Encryption and DCT, DST Steganography. In Proceedings of the 2019 IEEE Pune Section International Conference (PuneCon), Pune, India, 18–20 December 2019. [Google Scholar]
- Lu, K.-S.; Ortega, A.; Mukherjee, D.; Chen, Y. DCT and DST Filtering with Sparse Graph Operators. IEEE Trans. Signal Process. 2022, 70, 1641–1656. [Google Scholar] [CrossRef]
- Rose, K.; Heiman, A.; Dinstein, I. DCT/DST alternate-transform of image coding. IEEE Trans. Commun. 1990, 38, 94–101. [Google Scholar] [CrossRef]
- Koc, U.T.; Ray Liu, K.J. Discrete Cosine/sine transform based motion estimation. In Proceedings of the 1994 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; pp. 771–775. [Google Scholar]
- Cinemre, I.; Hacioglu, G. A DCT/DST Based Fast OFDM Method in IM/DD Systems. IEEE Commun. Lett. 2021, 25, 3013–3016. [Google Scholar] [CrossRef]
- Guo, J.I.; Liu, C.M.; Jen, C.W. A New Array Architecture for Prime-Length Discrete Cosine Transform. IEEE Trans. Signal Process. 1993, 41, 436. [Google Scholar]
- Chiper, D.F. A new systolic array algorithm for memory-based VLSI array implementation of DCT. In Proceedings of the 1997 Proceedings Second IEEE Symposium on Computers and Communications, Alexandria, Egypt, 1–3 July 1997; pp. 297–301. [Google Scholar]
- Meher, P.K. Systolic designs for DCT using low-complexity concurrent convolutional formulation. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 1041–1050. [Google Scholar] [CrossRef]
- Chiper, D.F.; Ungureanu, P. Novel VLSI Algorithm and Architecture with Good Quantization Properties for a High-Throughput Area Efficient Systolic Array Implementation of DCT. EURASIP J. Adv. Signal Process. 2010, 2011, 639043. [Google Scholar] [CrossRef]
- Chan, Y.H.; Siu, W.C. Generalized approach for the realization of discrete cosine transform using cyclic convolutions. In Proceedings of the 1993 IEEE Conference on Acoustic, Speech, and Signal Processing, Minneapolis, MN, USA, 27–30 April 1993; pp. 277–280. [Google Scholar]
- Chan, Y.H.; Siu, W.C. On the realization of discrete cosine transform using the distributed arithmetic. IEEE Trans. Circuits Syst. I: Regul. Pap. 1992, 39, 705–712. [Google Scholar] [CrossRef]
- Nikara, J.; Takola, J.; Akopian, D.; Saarinen, J. Pipeline architecture for DCT/IDCT. In Proceedings of the ISCAS 2001, the 2001 IEEE International Symposium on Circuits and Systems, Sydney, Australia, 6–9 May 2001; pp. 902–905. [Google Scholar]
- Chiper, D.F.; Swamy, M.N.S.; Ahmad, M.O. An efficient unified framework for the VLSI implementation of a prime-length DCT/IDCT with high throughput. IEEE Trans. Signal Process. 2007, 55, 2925–2936. [Google Scholar] [CrossRef]
- Cheng, C.; Parhi, K.K. A novel systolic array structure for DCT. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 366–369. [Google Scholar] [CrossRef]
- Chiper, D.F. A New VLSI algorithm and Architecture for the hardware implementation of type IV discrete cosine transform using a pseudo-band correlation structure. Cent. Eur. J. Comput. Sci. 2011, 1, 90–97. [Google Scholar] [CrossRef]
- Chiper, D.F. New VLSI Algorithm for a High-Throughput Implementation of Type IV DCT. In Proceedings of the 2016 International Conference on Communications (COMM), Bucharest, Romania, 9–10 June 2016. [Google Scholar]
- Cheng, C.; Parhi, K.K. Hardware efficient fast DCT based on novel cyclic convolution structures. IEEE Trans. Signal Process. 2006, 54, 4419–4434. [Google Scholar] [CrossRef]
- Xie, J.; Meher, P.K.; He, J. Hardware-Efficient Realization of Prime-Length DCT Based on Distributed Arithmetic. IEEE Trans. Comput. 2013, 62, 1170–1178. [Google Scholar] [CrossRef]
- Chiper, D.F. A parallel VLSI algorithm for a high throughput systolic array VLSI implementation of type IV DCT. In Proceedings of the 2009 International Symposium on Signals, Circuits and Systems (ISSCS2009), Iasi, Romania, 9–10 July 2009; pp. 257–260. [Google Scholar]
- Pan, S.B.; Park, R.-H. Unified systolic array for computation of DCT/DST/DHT. IEEE Trans. Circuits Syst. Video Technol. 1997, 7, 413–419. [Google Scholar]
- Chiper, D.F.; Swamy, M.N.S.; Ahmad, M.O.; Stouraitis, T. Systolic Algorithm Algorithms and Algorithm a Memory-Based Design Approach for a Unified Architecture for the Computation of DCT/DST/IDCT/IDST. IEEE Trans. Circuits Syst.-I Regul. Pap. 2005, 52, 1125–1137. [Google Scholar] [CrossRef]
- Meher, P.K.; Swamy, M.N.S. New Systolic Algorithm and Array Architecture for Prime-Length Discrete Sine Transform. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 262–266. [Google Scholar] [CrossRef]
- Chiper, D.F.; Cracan, A.; Burdia, D. A new systolic array algorithm and architecture for the VLSI implementation of IDST based on a pseudo-band correlation structure. Adv. Electr. Comput. Eng. 2017, 17, 75–80. [Google Scholar] [CrossRef]
- Chiper, D.F.; Cracan, A. An Efficient Algorithm for the VLSI Implementation of the Inverse DST Based on Quasi-Band Correlation Structures. In Proceedings of the 2021 International IEEE Symposium on Circuits and Systems (ISSCS2021), Iasi, Romania, 15–16 July 2021. [Google Scholar]
- Chiper, D.F.; Cracan, A. A novel algorithm and architecture for a high-throughput VLSI implementation of DST using short pseudo-cycle convolutions. In Proceedings of the 2017 International Symposium on Signals, Circuits and Systems (ISSCS), Iasi, Romania, 13–14 July 2017. [Google Scholar]
- Chiper, D.F.; Swamy, M.N.S.; Ahmad, M.O.; Stouraits, T. A systolic array architecture for the discrete sine transform. IEEE Trans. Signal Process. 2002, 50, 2347–2354. [Google Scholar] [CrossRef]
- Chakraborty, R.S.; Bhunia, S. Security against hardware Trojan through a novel application of design obfuscation. In Proceedings of the 2009 IEEE/ACM International Conference on Computer-Aided Design-Digest of Technical Papers, San Jose, CA, USA, 2–5 November 2009; pp. 113–116. [Google Scholar]
- Pilato, C.; Garg, S.; Wu, K.; Karri, R.; Regazzoni, F. Securing hardware accelerators: A new challenge for high-level synthesis. IEEE Embed. Syst. Lett. 2018, 10, 77–80. [Google Scholar] [CrossRef]
- Shamsi, K.; Li, M.; Meade, T.; Zhao, Z.; Pan, D.Z.; Jin, Y. AppSAT: Approximately deobfuscating integrated circuits. In Proceedings of the 2017 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), Mclean, VA, USA, 1–5 May 2017; pp. 95–100. [Google Scholar]
- Sengupta, A.; Roy, D.; Mohanty, S.P.; Corcoran, P. Low-cost obfuscated JPEG CODEC IP core for secure CE hardware. IEEE Trans. Consum. Electron. 2018, 64, 365–374. [Google Scholar] [CrossRef]
- Zhang, J. A practical logic obfuscation technique for hardware security. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 1193–1197. [Google Scholar] [CrossRef]
- Koteshwara, S.; Kim, C.H.; Parhi, K.K. Key-Based Dynamic Functional Obfuscation of Integrated Circuits Using Sequentially Triggered Mode-Based Design. IEEE Trans. Inf. Forensics Secur. 2018, 13, 79–93. [Google Scholar] [CrossRef]
- Parhi, K.K.; Koteshwara, S. Dynamic Functional Obfuscation. U.S. Patent 15/667 776, 3 August 2017. [Google Scholar]
- Koteshwara, S.; Kim, C.H.; Parhi, K.K. Hierarchical functional obfuscation of integrated circuits using a mode-based approach. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017. [Google Scholar]
- Kung, S.Y. VLSI Array Processors; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Jen, C.W.; Hsu, H.Y. The design of systolic arrays with tag input. In Proceeding of the International Symposium on Circuits and Systems, Espoo, Finland, 7–9 June 1988; pp. 2263–2266. [Google Scholar]
- Parvin, A.; Ahmadi, M.; Muscedere, R. Application of neural networks with CSD coefficients for human face recognition. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; pp. 1628–1631. [Google Scholar]
- Pinjare, S.L.; Kumar, E.H. Implementation of Artificial Neural Network Architecture for Image Compression Using CSD Multiplier. In Proceedings of the 2013 International Conference on Emerging Research in Computing, Information, Communication and Applications (ERCICA), Baku, Azerbaijan, 23–25 October 2013; pp. 581–587. [Google Scholar]
- Ahn, B.; Kim, T. Deeper Weight Pruning Without Accuracy Loss in Deep Neural Networks: Signed-Digit Representation-Based Approach. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 656–668. [Google Scholar] [CrossRef]
- Riaz, M.; Hafiz, R.; Khaliq, S.A.; Faisal, M.; Iqbal, H.T.; Ali, M.; Shafique, M. CAxCNN: Towards the Use of Canonic Sign Digit Based Approximation for Hardware-Friendly Convolutional Neural Networks. IEEE Access 2020, 8, 127014–127021. [Google Scholar] [CrossRef]
- Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Nannarelli, A.; Re, M. Approximated Canonical Signed Digit for Error Resilient Intelligent Computation. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019. [Google Scholar]
- Mahdavi, H.; Timarchi, S. Area–Time–Power Efficient FFT Architectures Based on Binary-Signed-Digit CORDIC. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3874–3881. [Google Scholar] [CrossRef]
- Peled, A. On the Hardware Implementation of Digital Signal Processors. IEEE Trans. Acoust. Signal Proc. 1976, 24, 76–86. [Google Scholar] [CrossRef]
- Hashmian, R. A new method for conversion of a 2’s complement to canonic signed digit number system and its representation. In Proceedings of the Conference Record of The Thirtieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 1996. [Google Scholar]
- Rezai, A.; Keshavarzi, P. Compact SD: A new encoding algorithm and its application in multiplication. Int. J. Comput. Math. 2017, 94, 554–569. [Google Scholar] [CrossRef]
- Rezai, A.; Keshavarzi, P. CCS Representation: A New Non-Adjacent Form and its Application in ECC. J. Basic. Appl. Sci. Res. 2012, 2, 4577–4586. [Google Scholar]
- Joye, M.; Yen, S.M. Optimal left-to-right binary signed-digit recoding. IEEE Trans. Comput. 2000, 49, 740–748. [Google Scholar] [CrossRef] [Green Version]
- Zaman, K.S.; Reaz, M.B.I.; Bakar, A.A.A.; Bhuiyan, M.A.S.; Mohd, N.A.; Mokhtar, H.H.B.; Ali, S.H. Minimum signed digit approximation for faster and more efficient convolutional neural network computation on embedded devices. Eng. Sci. Technol. Int. J. 2022, 36, 101153. [Google Scholar] [CrossRef]
- Chiper, D.F.; Cotorobai, L. A New VLSI Algorithm for type IV DCT for an Efficient Implementation of Obfuscation Technique. In Proceedings of the 2020 43rd International Conference on Telecommunications and Signal Processing (TSP), Milan, Italy, 7–9 July 2020. [Google Scholar]


| Representation | No. of Adders | |||
|---|---|---|---|---|
| 0.5263671875 | −13.9 | 3 | ||
| 0.9619140625 | −13.5 | 3 | ||
| 0.7978515625 | −12.6 | 4 | ||
| 0.89501953125 | −12.8 | 4 | ||
| 0.99609375000 | −11.4 | 1 | ||
| 0.67382812500 | −12.9 | 4 | ||
| 0.36132812500 | −13.5 | 3 | ||
| 0.18359375000 | −12.6 | 2 |
| Binary Representation | Minimum Signed Digit Representation | ||
|---|---|---|---|
| 0.5263671875 | |||
| 0.9619140625 | |||
| 0.7978515625 | |||
| 0.89501953125 | |||
| 0.99609375000 | |||
| 0.67382812500 | |||
| 0.36132812500 | |||
| 0.18359375000 |
| Structures | Multipliers | Adders | ROM Words | Through-Put | I/O Channels |
|---|---|---|---|---|---|
| [36] | |||||
| [37] | |||||
| [41] | |||||
| Proposed |
| Constrained Clock Period/Fre-Quency | Critical Path Delay + Setup Time [ps] | Static Power [uW] | Dynamic Power at Constrained Clock Frequency [mW] |
|---|---|---|---|
| 50 ns/20 MHz | 225 | 110.2 | 0.2 for 20 MHz |
| 10 ns/100 MHz | 225 | 110.2 | 0.46 for 100 MHz |
| 1 ns/1 GHz | 229 | 110.0 | 4.6 for 1 GHz |
| 300 ps/3.33 GHz | 228 | 110.3 | 15.4 for 3.33 GHz |
| 250 ps/4 GHz | 235 | 109.7 | 18.6 for 4 GHz |
| 200 ps/5 GHz | 200 | 128.2 | 27.8 for 5 GHz |
| 175 ps/5.71 GHz | 175 | 151.4 | 36.4 for 5.71 GHz |
| 150 ps/6.67 GHz | 161 | 178.5 | 45.9 For 6.67 GHz |
| Constrained Clock Period/Frequency | Interconnect Area [um2] | Combinational Area [um2] | Flop Area [um2] | Total Area [um2] | Equivalent Gate Count |
|---|---|---|---|---|---|
| 50 ns/20 MHz | 865.36 | 1763.57 | 1391.59 | 4020.53 | 20,449.3 |
| 10 ns/100 MHz | 865.36 | 1763.57 | 1391.59 | 4020.53 | 20,449.3 |
| 1 ns/1 GHz | 864.67 | 1772.08 | 1391.59 | 4028.34 | 20,489.0 |
| 300 ps/3.33 GHz | 870.20 | 1775.67 | 1391.59 | 4037.45 | 20,535.8 |
| 250 ps/4 GHz | 883.97 | 1802.16 | 1391.59 | 4077.72 | 20,740.3 |
| 200 ps/5 GHz | 1220.68 | 2041.78 | 1391.59 | 4654.04 | 23,671.5 |
| 175 ps/5.71 GHz | 1434.74 | 2343.37 | 1391.59 | 5169.70 | 26,294.5 |
| 150 ps/6.67 GHz | 1562.45 | 2679.82 | 1391.59 | 5633.86 | 28,655.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiper, D.F.; Cracan, A.; Andries, V.-D. An Overview of Systolic Arrays for Forward and Inverse Discrete Sine Transforms and Their Exploitation in View of an Improved Approach. Electronics 2022, 11, 2416. https://doi.org/10.3390/electronics11152416
Chiper DF, Cracan A, Andries V-D. An Overview of Systolic Arrays for Forward and Inverse Discrete Sine Transforms and Their Exploitation in View of an Improved Approach. Electronics. 2022; 11(15):2416. https://doi.org/10.3390/electronics11152416
Chicago/Turabian StyleChiper, Doru Florin, Arcadie Cracan, and Vasilica-Daniela Andries. 2022. "An Overview of Systolic Arrays for Forward and Inverse Discrete Sine Transforms and Their Exploitation in View of an Improved Approach" Electronics 11, no. 15: 2416. https://doi.org/10.3390/electronics11152416
APA StyleChiper, D. F., Cracan, A., & Andries, V.-D. (2022). An Overview of Systolic Arrays for Forward and Inverse Discrete Sine Transforms and Their Exploitation in View of an Improved Approach. Electronics, 11(15), 2416. https://doi.org/10.3390/electronics11152416






