A New Modified MARS Cryptosystem Based on Niho Exponent with an Enhanced S-Box Generation
Abstract
1. Introduction
- The novel system uses the SHA-512 algorithm to generate a secret key used in S-box generation to ensure that the S-box was totally dependent on every bit in the secret key.
- The subkeys generation is modified by using the Niho exponent, which is subset of Boolean bent functions. This base property of bent functions is used for protecting ciphers against linear cryptanalysis.
- After each cipher block, different rotations for S-boxes are selected based on the hashed key’s array to overcome the letter repetition problem.
- The ciphertext is mainly diffused after encrypting every plaintext block with the bitwise exclusive-OR operation so we guarantee that the ciphertext mix together.
- We perform an “image diffusion” step that makes randomization in the image so that if one pixel changes, it will have a large effect on the output of the diffusion step.
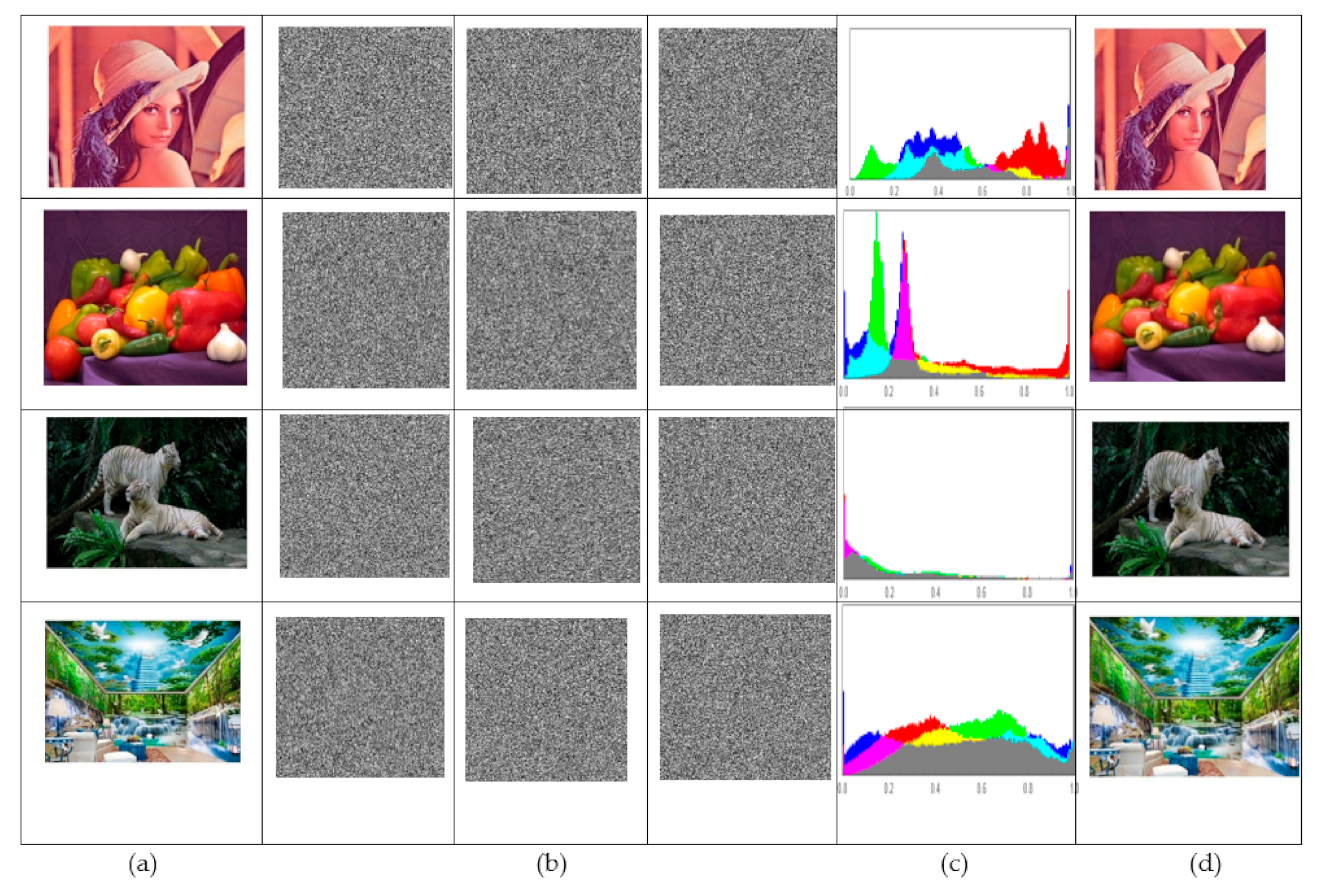
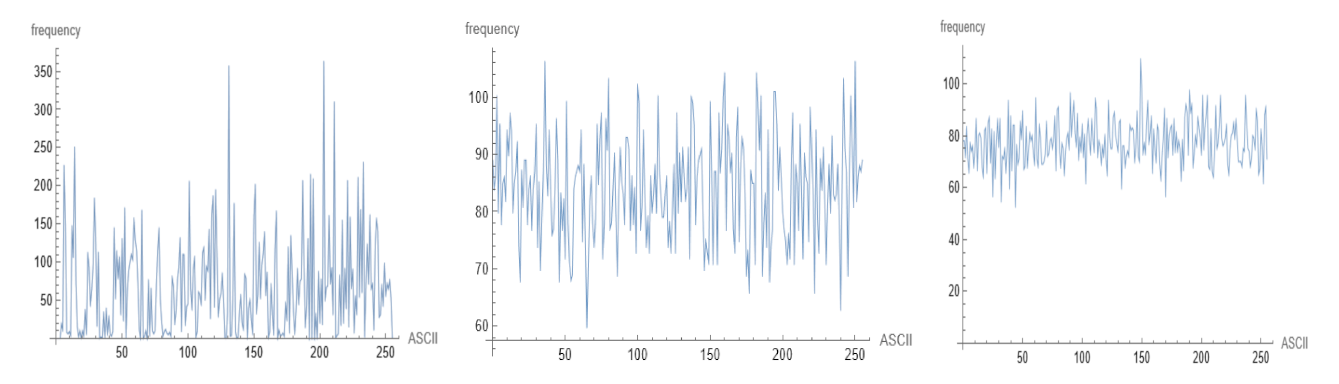
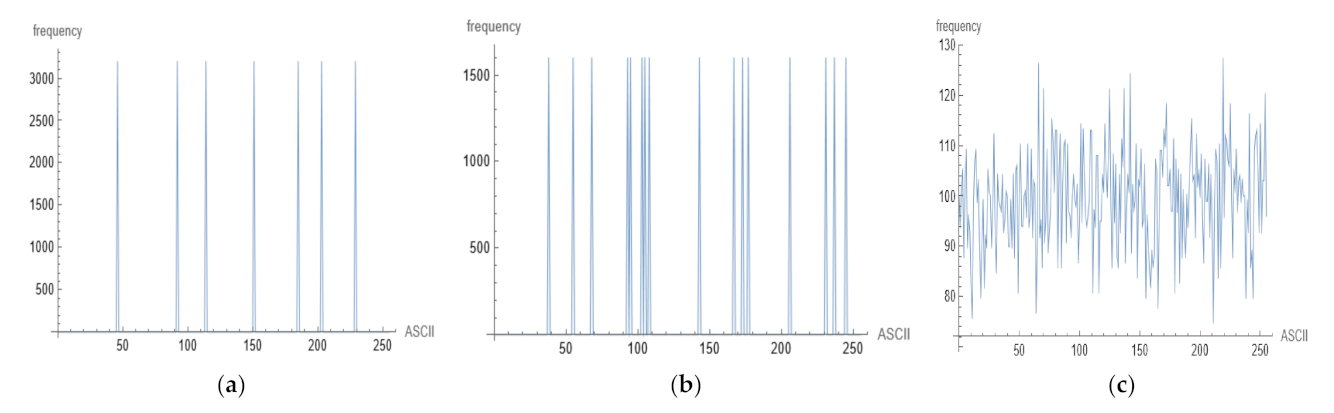
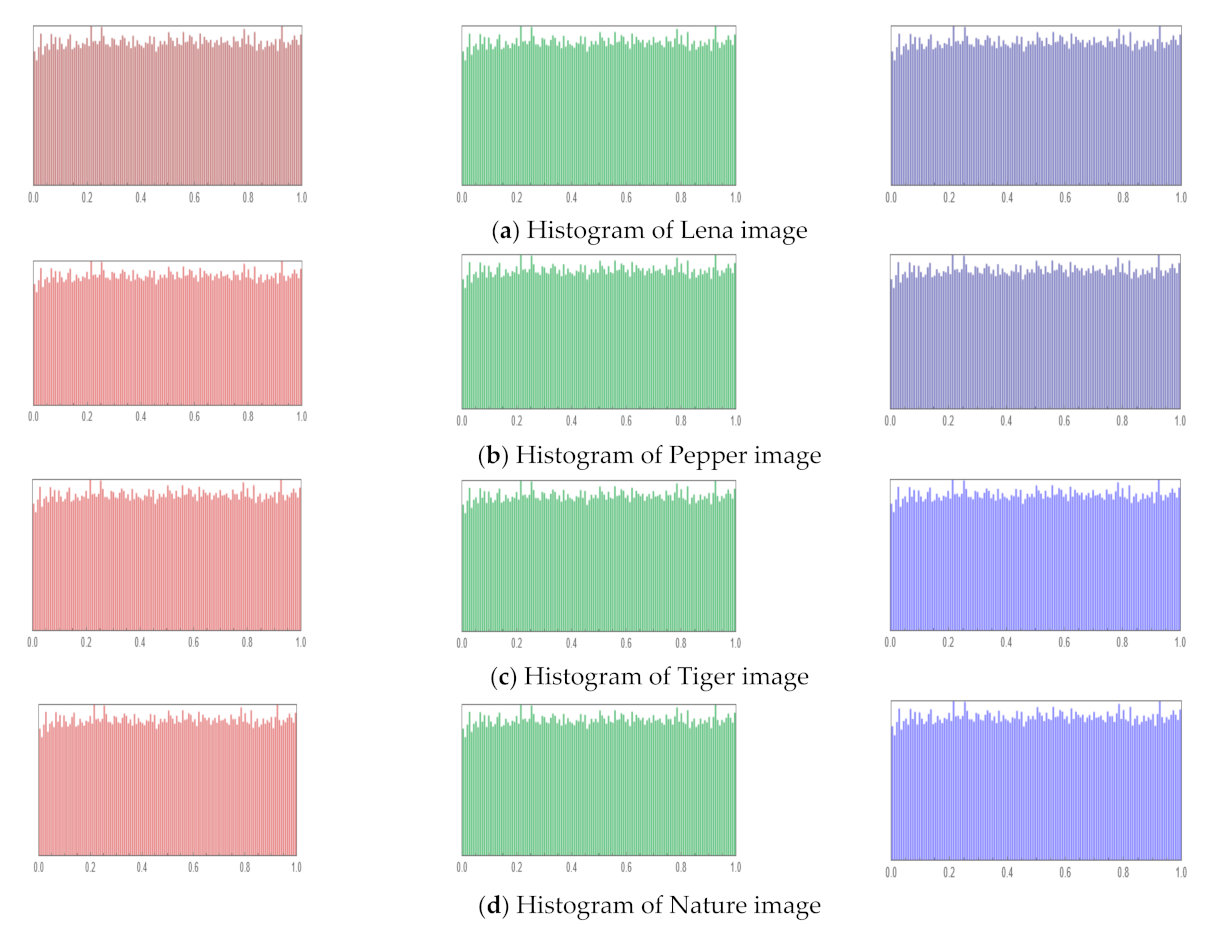
- Overcoming the letter repetition problem (this problem will cause the histogram to not be flat).
- Making high randomization in the image so that if one pixel will change so it will affect the whole image, and if we encrypt the same image with one pixel change it will cause a different ciphertext to be obtained.
- Making a generation of subkeys robust against linear and differential attacks by using the Niho exponent function.
2. Related Work
3. Background Review
3.1. The Niho Exponent
- (1)
- (2)
- or
Binomial Bent Functions
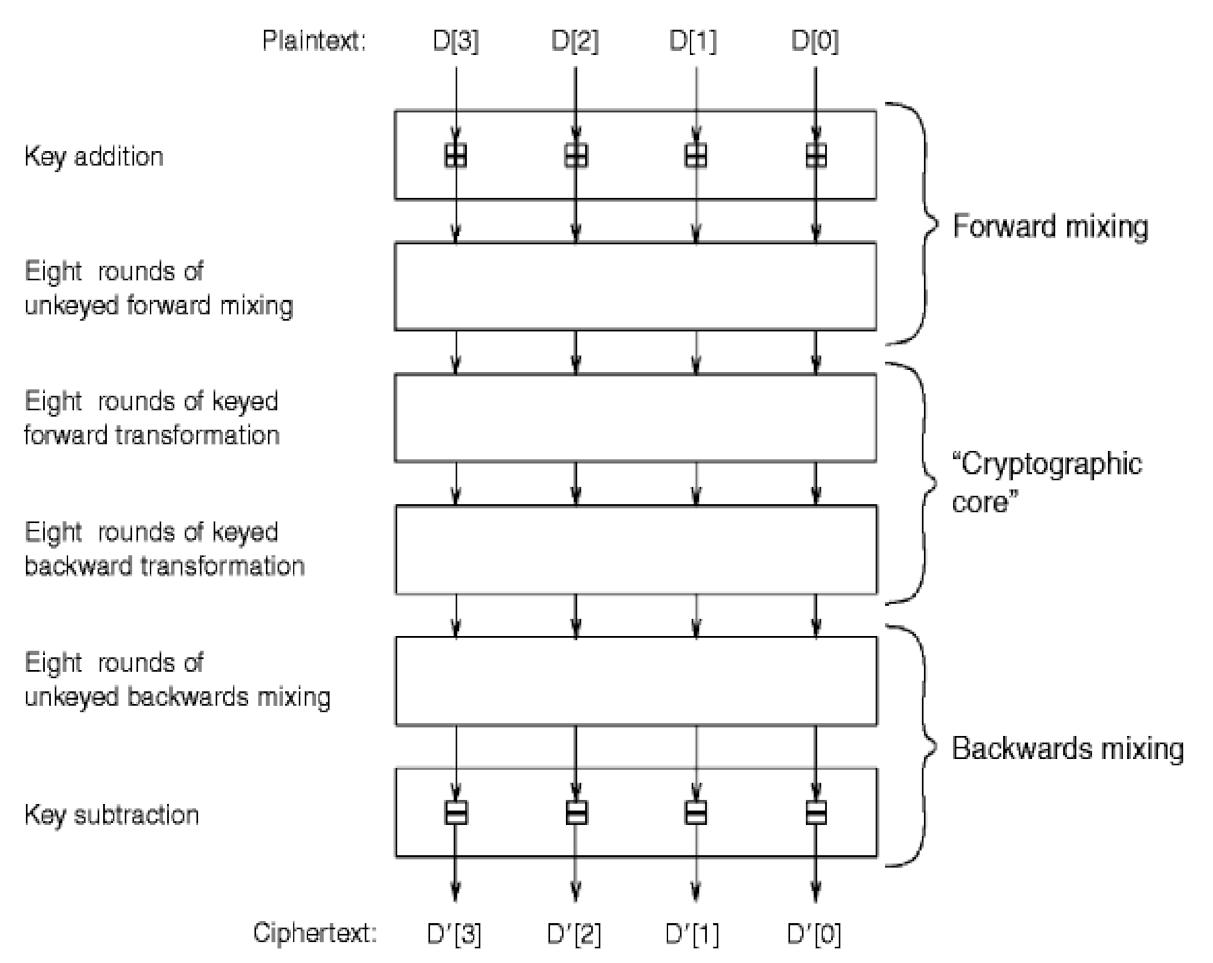
3.2. Description of the MARS Cryptosystem
The MARS Framework
- a.
- Pre-Whitening Level: The plaintext’s words have 128 bits of key material modulo 232 added to them.
- b.
- Forward Mixing Level: An unkeyed mixing procedure consisting of eight rounds utilizing the MARS S-box extensively.
- c.
- Forward Core Level: A keyed unbalanced Feistel encryption of eight rounds, which resists cryptanalytic assault by combining S-box lookups, data-dependent rotations, multiplications, xors, and additions.
- d.
- Backward Core Level: A keyed unbalanced Feistel encryption of eight rounds, which resists cryptanalytic assault by combining S-box lookups, data-dependent rotations, multiplications, xors, and additions.
- e.
- Backward Mixing Level: An unkeyed mixing operation of eight rounds utilizing the MARS S-box extensively.
- f.
- Post-Whitening Level: A key material of 128bits have been withdrew from the block’s words modulo 232.
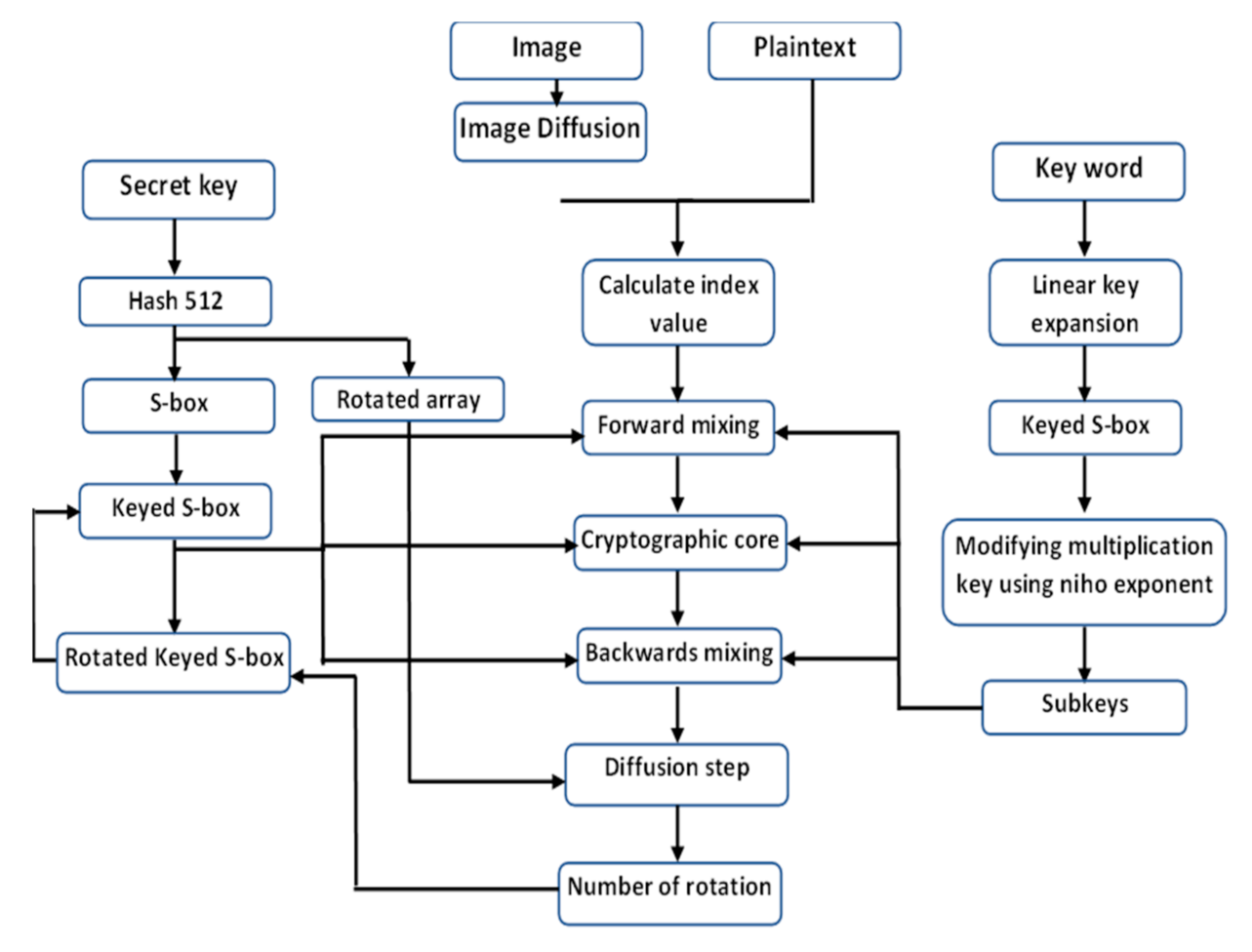
4. Proposed Cryptosystem:
4.1. Proposed Keyed S Box
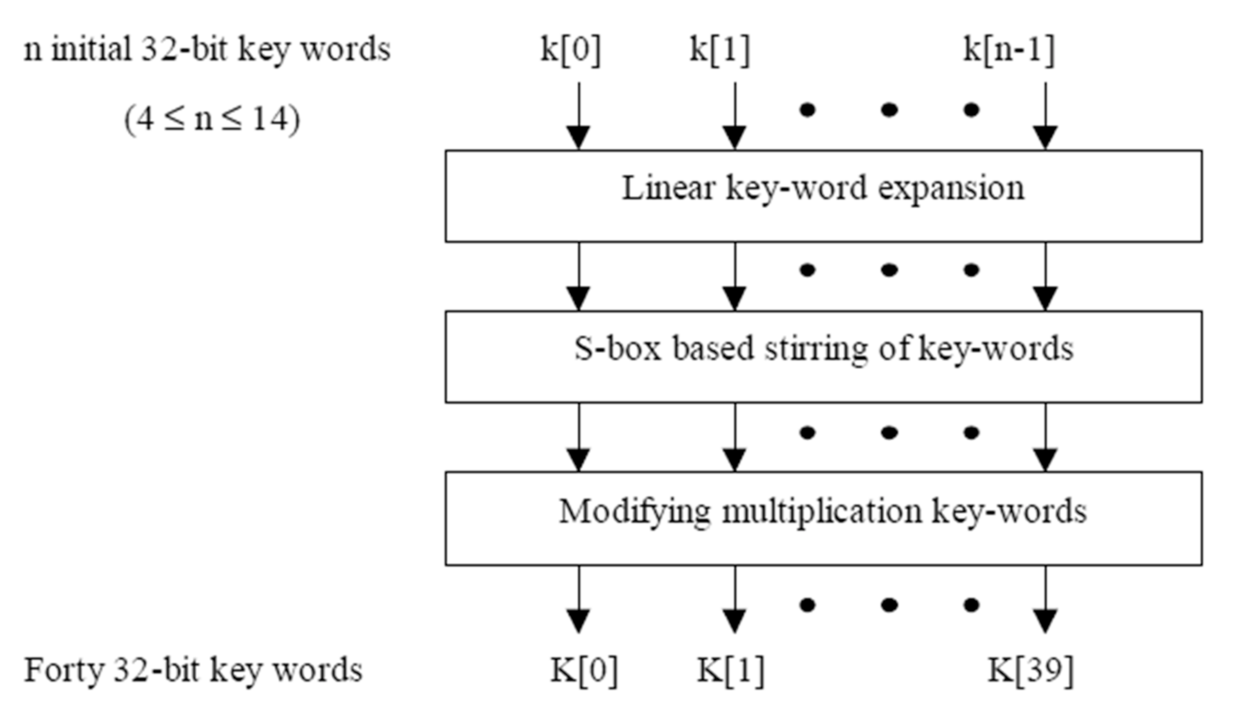
4.2. Key Expansion Process
- The subsequent linear function is utilized to transform the array T[]:
- The array T[] is then stirred via four rounds of Feistel networks of type 1. We replicate the process four times in total.
- Later, ten words are taken from T[], then rearranged into the extended key array’s following ten words, K[]. This is accomplished by establishingand using the relation:where satisfying and , and where m is even equal.
- We choose secret value and calculate the secret value Then we convert the expanded key array into the polynomial array and applied it into the relationwhere:After we execute the trace function, we convert the function back into the binary array.
- Finally, we partition the function into subkeys.
4.3. Encryption Process
4.4. Image Diffusion
4.5. Decryption Process
5. Simulation Results
6. Performance and Security Analysis
6.1. For Plaintext
6.1.1. Avalanche Effect
6.1.2. Language Statistics
6.1.3. NIST Statistical Suite
6.2. For Image
6.2.1. Key Space
6.2.2. Key Sensitivity
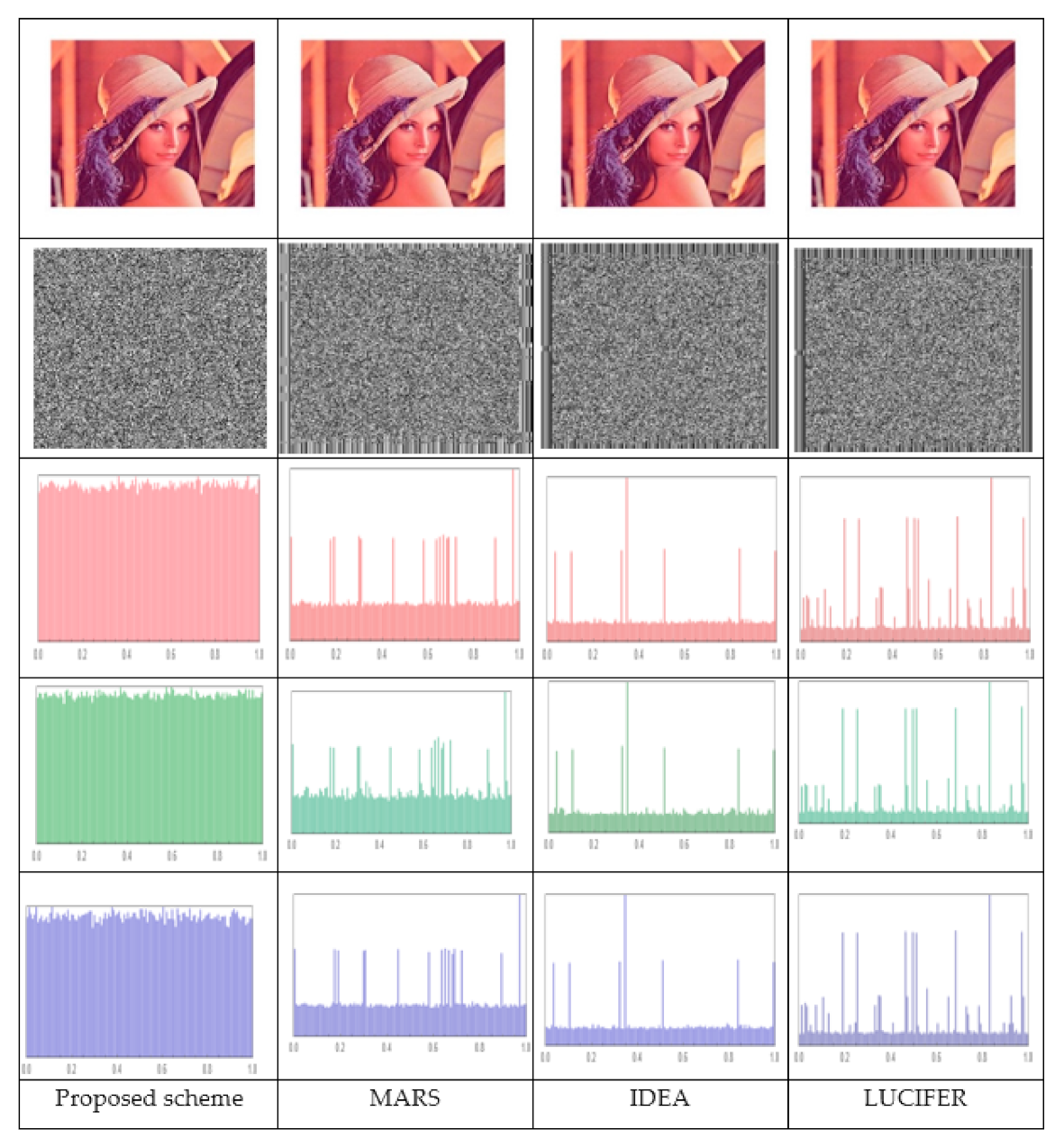
6.2.3. Histogram Analysis
6.2.4. Pixel Correlation Analysis
6.2.5. Plaintext Sensitivity
6.2.6. Chi-Square Test
6.2.7. PSNR Evaluation
6.2.8. Complexity Analysis
6.2.9. Comparison with Existing Methods
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyer, C.H. Cryptography-a state of the art review. In Proceedings of the VLSI and Computer Peripherals. COMPEURO 89, Hamburg, Germany, 8–12 May 1989; pp. 4/150–4/154. [Google Scholar] [CrossRef]
- Ahmed, H.E.-D.H.; Kalash, H.M.; Allah, O.S.F. Encryption quality analysis of the RC5 block Cipher algorithm for digital images. Opt. Eng. 2006, 45, 107003. [Google Scholar] [CrossRef]
- Li, S.; Zheng, X. Cryptanalysis of a chaotic image encryption method. In Proceedings of the 2002 IEEE International Symposium on Circuits and Systems (ISCAS), Scottsdale, AZ, USA, 26–29 May 2002; p. II. [Google Scholar] [CrossRef]
- Reddy, A.R. A Candidate Cipher for Advanced Encryption Algorithm and its Diffusion Strength. In Proceedings of the National Conference on Recent trends in Information Technology, Bangalore, India, 12 May 2007. [Google Scholar] [CrossRef]
- Helmy, A.; Saeb, M.; Mohamed, A.B. A Metamorphic-Enhanced MARS Block Cipher. Int. J. Comput. Sci. Commun. Secur. (IJCSCS) 2013, 3, 61–66. [Google Scholar]
- Ebrahim, M.; Khan, S.; Khalid, U.B. Symmetric Algorithm Survey: A Comparative Analysis. arXiv 2013, arXiv:1405.0398. [Google Scholar]
- Naguib, M.M.; Khater, H.; Mohamed, A.B. Improved Mars ciphering using a metamorphic-enhanced function. Int. J. Comput. Inf. Eng. 2014, 8, 7–10. [Google Scholar] [CrossRef]
- Aung, Y.Y.; Kyi, T.M.; Win, M.T. Security of Digital Images Using Cryptographic Algorithms. Int. J. Res. Innov. Appl. Sci. IJRIAS 2019, IV, 103–106. [Google Scholar]
- Li, N.; Zeng, X. A survey on the applications of Niho exponents. Cryptogr. Commun. 2019, 11, 509–548. [Google Scholar] [CrossRef]
- Nurgaliyev, A.; Wang, H. Comparative study of symmetric cryptographic algorithms. In Proceedings of the 2021 International Conference on Networking and Network Applications (NaNA), Lijiang, China, 29 October–1 November 2021; pp. 107–112. [Google Scholar] [CrossRef]
- Liu, Q. Two classes of permutation polynomials with Niho exponents over finite fields with even characteristic. Turk. J. Math. 2022, 46, 17. [Google Scholar] [CrossRef]
- Preneel, B.; Bosselaers, A.; Rijmen, V.; Rompay, B.V.; Granboulan, L.; Stern, J.; Murphy, S.; Dichtl, M.; Serf, P.; Biham, E.; et al. Comments by the NESSIE Project on the AES Finalists. 2000. Available online: https://www.researchgate.net/publication/2646004_Comments_by_the_NESSIE_Project_on_the_AES_Finalists (accessed on 28 April 2022).
- Kelsey, J.; Schneier, B. MARS Attacks! Preliminary Cryptanalysis of reduced-Round MARS Variants. In Proceedings of the Third AES Candidate Conference, New York, NY, USA, 13–14 April 2000; pp. 169–185. [Google Scholar]
- Dillon, J.F. Elementary Hadamard Difference Sets. Ph.D. Dissertation, University of Maryland, College Park, MD, USA, 1974. [Google Scholar] [CrossRef]
- Leander, N. Monomial bent functions. IEEE Trans. Inf. Theory 2006, 52, 738–743. [Google Scholar] [CrossRef]
- Canteaut, A.; Charpin, P.; Kyureghyan, G.M. A new class of monomial bent functions. Finite Fields Their Appl. 2008, 14, 221–241. [Google Scholar] [CrossRef]
- Charpin, P.; Gong, G. Hyperbent Functions, Kloosterman Sums, and Dickson Polynomials. IEEE Trans. Inf. Theory 2008, 54, 4230–4238. [Google Scholar] [CrossRef][Green Version]
- Mesnager, S. A new class of bent boolean functions in polynomial forms. In Proceedings of the International Workshop on Coding and Cryptograph WCC, Ullensvang, Norway, 10–15 May 2009; pp. 5–18. Available online: http://eprint.iacr.org/2008/512 (accessed on 16 April 2022).
- Mesnager, S. A new family of hyper-bent boolean functions in polynomial form. In Proceedings of the IMA 12th International Conference on Cryptography and Coding, IMACC, Cirencester, UK, 15–17 December 2009; Parker, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5921, pp. 402–417. [Google Scholar] [CrossRef]
- Mesnager, S. A new class of bent and hyper-bent Boolean functions in polynomial forms. Des. Codes Cryptogr. 2011, 59, 265–279. [Google Scholar] [CrossRef]
- Wang, B.; Tang, C.; Qi, Y.; Yang, Y.; Xu, M. A New Class of Hyper-bent Boolean Functions with Multiple Trace Terms. Report 2011/600. Cryptol. Eprint Arch. 2011. Available online: https://eprint.iacr.org/2011/600 (accessed on 22 April 2022).
- Wang, B.; Tang, C.; Qi, Y.; Yang, Y. A generalization of the class of hyper-bent Boolean functions in binomial forms. Report 2011/698. Cryptol. Eprint Arch. 2011. Available online: http://eprint.iacr.org/2011/698 (accessed on 10 May 2022).
- Mesnager, S.; Flori, J.-P. A note on hyper-bent functions via Dillon-like exponents. Report 2012/033. Cryptol. Eprint Arch. 2012. Available online: http://eprint.iacr.org/2012/033 (accessed on 10 May 2022).
- Dobbertin, H.; Canteaut, G.L.A.; Carlet, C.; Felke, P.; Gaborit, P. Construction of bent functions via Niho power functions. J. Combin. Theory Ser. A Vol. 2006, 113, 779–798. [Google Scholar] [CrossRef]
- Burwick, C.; Coppersmith, D.; D’Avignon, E.; Gennaro, R.; Halevi, S.; Jutla, C.; Matyas, S.M.; O’Connor, L.; Peyravian, M.; Safford, D.; et al. The MARS Encryption AlgorithmI. BM, 27 August 1999. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.35.5887 (accessed on 2 June 2022).
- Dewangan, C.P.; Agrawal, S.; Mandal, A.K.; Tiwari, A. Study of avalanche effect in AES using binary codes. In Proceedings of the 2012 IEEE International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 23–25 August 2012; pp. 183–187. [Google Scholar] [CrossRef]
- Stoyanov, B.P. Pseudo-random bit generator based on chebyshev map. In Application of Mathematics in Technical and Natural Sciences; Todorov, M.D., Ed.; American Institute of Physics: College Park, MD, USA, 2013; Volume 1561, pp. 369–372. [Google Scholar] [CrossRef]
- Ghadirli, H.M.; Nodehi, A.; Enayatifar, R. An overview of encryption algorithms in color images. Signal Process. 2019, 164, 163–185. [Google Scholar] [CrossRef]
- Xu, X.; Feng, J. Research and Implementation of Image Encryption Algorithm Based on Zigzag Transformation and Inner Product Polarization Vector. In Proceedings of the 2010 IEEE International Conference on Granular Computing, San Jose, CA, USA, 14–16 August 2010; pp. 556–561. [Google Scholar] [CrossRef]
- Ahmad, J.; Larijani, H.; Emmanuel, R.; Mannion, M.; Qureshi, A. Secure Occupancy Monitoring System for IoT Using Lightweight Intertwining Logistic Map. In Proceedings of the 2018 10th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 19–21 September 2018; pp. 208–213. [Google Scholar] [CrossRef]
- Ahmad, J.; Hwang, S.O. A secure image encryption scheme based on chaotic maps and affine transformation. Multimed Tools Appl. 2016, 75, 13951–13976. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Khanzadi, H.; Eshghi, M.; Borujeni, S.E. Image encryption using random bit sequence based on chaotic maps. Arab. J. Sci. Eng. 2014, 39, 1039–1047. [Google Scholar] [CrossRef]
- Chen, J.; Xue, D.; Lai, X. An analysis of international data encryption algorithm(IDEA) security against differential cryptanalysis. Wuhan Univ. J. Nat. Sci. 2008, 13, 697–701. [Google Scholar] [CrossRef]
- Sorkin, A. Lucifer, a cryptographic algorithm. Cryptologia 1984, 8, 22–42. [Google Scholar] [CrossRef]



| +: | Addition. |
| ⊕: | Xor. |
| Length: | Gives the number of elements in expr. |
| Partition: | Partitions list into sub-lists of length n. |
| FromDigits: | Takes the digits to be given in base b. |
| Rotateleft: | Cycles the elements in expr n positions to the left. |
| Transpose: | Transposes the first two levels in list. |
| Quotient: | Gives the integer quotient of m and n. |
| Imagedata: | Gives the array of pixel values in an image. |
| :. | The key hashed by using SHA3- 512. |
| : | The expanded hash_key to 512 bit. |
| The array that will cause the S-boxes to rotate with different values. | |
| Index: | The address of element that is located in the rotated array. |
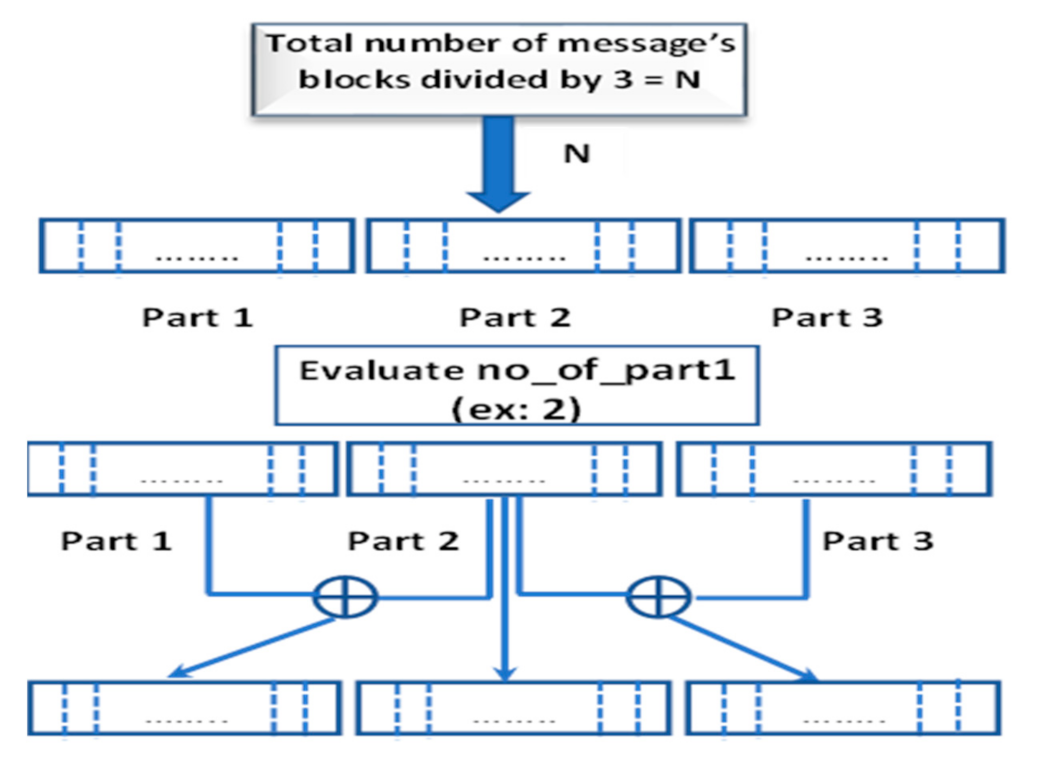
| num_of_subblocks: | The subblocks of ciphertext. |
| no_of_part1: | The number of the parts that XORed with the other two parts in ciphertext. |
| Plaintext | Length of Plaintext in Bits | Changing Plaintest’s 1st Bit | Changing Plaintext’s Last Bit | Changing Plaintest’s Middle Bit | |||
|---|---|---|---|---|---|---|---|
| MARS | Proposed | MARS | Proposed | MARS | Proposed | ||
| 1st Case | 128 | 47.5% | 52.34% | 50% | 52.78% | 49% | 50.17% |
| 2nd Case | 128 | 46% | 51.2% | 50% | 50.31% | 48% | 50.8% |
| 3rd Case | 1024 | 0.04% | 53.5% | 0.04% | 54.3% | 0.03% | 54.5% |
| 4th Case | 1024 | 0.11% | 52.6% | 5.9% | 52.8% | 0.03% | 52.5% |
| Plaintext | Length of plaintext in bits | Changing key’s 1st bit | Changing key’s last bit | Changing key’s middle bit | |||
| MARS | Proposed | MARS | Proposed | MARS | Proposed | ||
| 1st Case | 128 | 49.9% | 50.1% | 49.9% | 50.2% | 50% | 50.3% |
| 2nd Case | 128 | 47.4% | 53.125% | 49.8% | 51.56% | 46% | 53.2% |
| 3rd Case | 1024 | 34.4% | 50.2% | 45.3% | 50.1% | 45.3% | 50.2% |
| 4th Case | 1024 | 49% | 50% | 50% | 50.3% | 51.2% | 51.5% |
| Algorithm | Proposed Cryptosystem | MARS | |||
|---|---|---|---|---|---|
| Test | |||||
| Monobit Frequency | 100% | Pass | 99% | Pass | |
| Frequency within a Block | 99% | Pass | 100% | Pass | |
| Runs | 100% | Pass | 100% | Pass | |
| Longest Run of Ones | 100% | Pass | 100% | Pass | |
| Binary Matrix Rank | 100% | Pass | 96% | Failed | |
| D Fourier Transform | 100% | Pass | 100% | Pass | |
| Non-overlap Template Match | 100% | Pass | 100% | Pass | |
| Overlap Template Match Test | 100% | Pass | 100% | Pass | |
| Universal Statistical of Maurer | 100% | Pass | 99% | Pass | |
| Lempel–Ziv Compression | 99% | Pass | 98% | Failed | |
| Linearity Complexity | 100% | Pass | 99% | Pass | |
| Serial | 99% | Pass | 97% | Failed | |
| Approximate Entropy Test | 100% | Pass | 100% | Pass | |
| Cumulative Sums | 100% | Pass | 100% | Pass | |
| Random Excursions | 100% | Pass | 97% | Failed | |
| Random Excursions Variant for Test(α = 0.05) | 96% | Pass | 93% | Failed | |
| Lena | Pepper | Tiger | Nature | ||
|---|---|---|---|---|---|
| R | Diff1 | 99.62% | 99.63% | 99.61% | 99.61% |
| Diff2 | 33.58% | 33.36% | 33.52% | 33.5% | |
| Diff3 | 99.62% | 99.64% | 99.61% | 99.62% | |
| Diff4 | 33.45% | 33.89% | 33.9% | 33.52% | |
| G | Diff1 | 99.62% | 99.61% | 99.64% | 99.61% |
| Diff2 | 33.46% | 33.84% | 33.4% | 33.52% | |
| Diff3 | 99.61% | 99.61% | 99.61% | 99.62% | |
| Diff4 | 33.34% | 34% | 33.49% | 35.8% | |
| B | Diff1 | 99.61% | 99.61% | 99.61% | 99.61% |
| Diff2 | 33.34% | 33.5% | 33.5% | 33.47% | |
| Diff3 | 99.62% | 99.61% | 99.62% | 99.65% | |
| Diff4 | 33.58% | 34% | 34% | 33.59% |
| Lena | Pepper | Tiger | Nature | ||
|---|---|---|---|---|---|
| R | Vertical correlation | −0.002 | −0.003 | 0.001 | −0.001 |
| Horizontal correlation | 0.006 | −0.001 | 0.001 | 0.0001 | |
| Diagonal correlation | 0.004 | 0.0009 | −0.002 | 0.001 | |
| G | Vertical correlation | −0.004 | 0.0001 | −0.001 | 0.0008 |
| Horizontal correlation | 0.004 | 0.002 | 0.0002 | −0.002 | |
| Diagonal correlation | −0.004 | 0.005 | 0.003 | 0.004 | |
| B | Vertical correlation | −0.001 | 0.0004 | −0.0001 | −0.001 |
| Horizontal correlation | −0.005 | 0.0001 | 0.00008 | −0.001 | |
| Diagonal correlation | 0.004 | 0.005 | 0.001 | −0.001 |
| Lena | Pepper | Tiger | Nature | ||
|---|---|---|---|---|---|
| R | NPCR | 99.61% | 99.61% | 99.64% | 99.61% |
| UACI | 33.5% | 33.4% | 33.2% | 33.4% | |
| G | NPCR | 99.61% | 99.61% | 99.66% | 99.61% |
| UACI | 33,7% | 33.5% | 33.3% | 33.2% | |
| B | NPCR | 99.62% | 99.63% | 99.64% | 99.65% |
| UACI | 33.6% | 33.5% | 33.5% | 33.7% |
| Lena | Pepper | Tiger | Nature | ||
|---|---|---|---|---|---|
| R | Chi-square | 253.035 | 247.9 | 221.6 | 234.97 |
| pvalue | 0.476 | 0.3 | 0.064 | 0.189 | |
| H | pass | pass | pass | pass | |
| G | Chi-square | 261 | 243.67 | 293.2 | 262.4 |
| pvalue | 0.384 | 0.315 | 0.032 | 0.361 | |
| H | pass | pass | pass | pass | |
| B | Chi-square | 223.33 | 267.7 | 280.32 | 239.55 |
| pvalue | 0.075 | 0.279 | 0.015 | 0.251 | |
| H | pass | pass | pass | pass |
| Lena | Pepper | Tiger | Nature | ||
|---|---|---|---|---|---|
| R | MSE | 13,462.3 | 9826.3 | 16,777.9 | 13,003.4 |
| PSNR | 6.84 | 8.206 | 5.88 | 6.9 | |
| G | MSE | 12,324.6 | 11,816.7 | 16,014.1 | 12,531.9 |
| PSNR | 7.22 | 7.405 | 6.08 | 7.1 | |
| B | MSE | 10,954.9 | 12,043.1 | 16,852.4 | 14,099.8 |
| PSNR | 7.734 | 7.32 | 5.86 | 6.6 |
| Proposed | MARS | IDEA | LUCIFER | ||
|---|---|---|---|---|---|
| R | V correlation | −0.002 | 0.168 | 0.21907 | 0.144 |
| H correlation | 0.006 | −0.04 | 0.0691 | −0.028 | |
| D correlation | 0.004 | −0.03 | 0.071 | −0.025 | |
| Entropy | 7.998 | 7.76 | 7.608 | 7.78 | |
| NPCR | 99.61% | 0.015 | 0.0076 | 0.0156 | |
| UACI | 33.5% | 0.0034 | 0.0021 | 0.00266 | |
| G | V correlation | −0.004 | 0.1705 | 0.221 | 0.1518 |
| H correlation | 0.004 | −0.039 | 0.063 | −0.027 | |
| D correlation | −0.004 | −0.033 | 0.064 | −0.019 | |
| Entropy | 7.999 | 7.84 | 7.67 | 7.84 | |
| NPCR | 99.61% | 0.0156 | 0.0058 | 0.01562 | |
| UACI | 33.7% | 0.0057 | 0.0022 | 0.0064 | |
| B | V correlation | −0.001 | 0.179 | 0.223 | 0.1491 |
| H correlation | −0.005 | −0.04 | 0.071 | −0.0286 | |
| D correlation | 0.004 | −0.034 | 0.062 | −0.024 | |
| Entropy | 7.995 | 7.77 | 7.626 | 7.788 | |
| NPCR | 99.62% | 0.01561 | 0.0078 | 0.01562 | |
| UACI | 33.6% | 0.0052 | 0.0019 | 0.0045 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, F.; Elkamchouchi, D.H. A New Modified MARS Cryptosystem Based on Niho Exponent with an Enhanced S-Box Generation. Electronics 2022, 11, 2318. https://doi.org/10.3390/electronics11152318
Ahmed F, Elkamchouchi DH. A New Modified MARS Cryptosystem Based on Niho Exponent with an Enhanced S-Box Generation. Electronics. 2022; 11(15):2318. https://doi.org/10.3390/electronics11152318
Chicago/Turabian StyleAhmed, Fatma, and Dalia H. Elkamchouchi. 2022. "A New Modified MARS Cryptosystem Based on Niho Exponent with an Enhanced S-Box Generation" Electronics 11, no. 15: 2318. https://doi.org/10.3390/electronics11152318
APA StyleAhmed, F., & Elkamchouchi, D. H. (2022). A New Modified MARS Cryptosystem Based on Niho Exponent with an Enhanced S-Box Generation. Electronics, 11(15), 2318. https://doi.org/10.3390/electronics11152318






