Research on Optimization of Horizontal Omnidirectional Misalignment Tolerance of WPT Based on Double D Coupler
Abstract
:1. Introduction
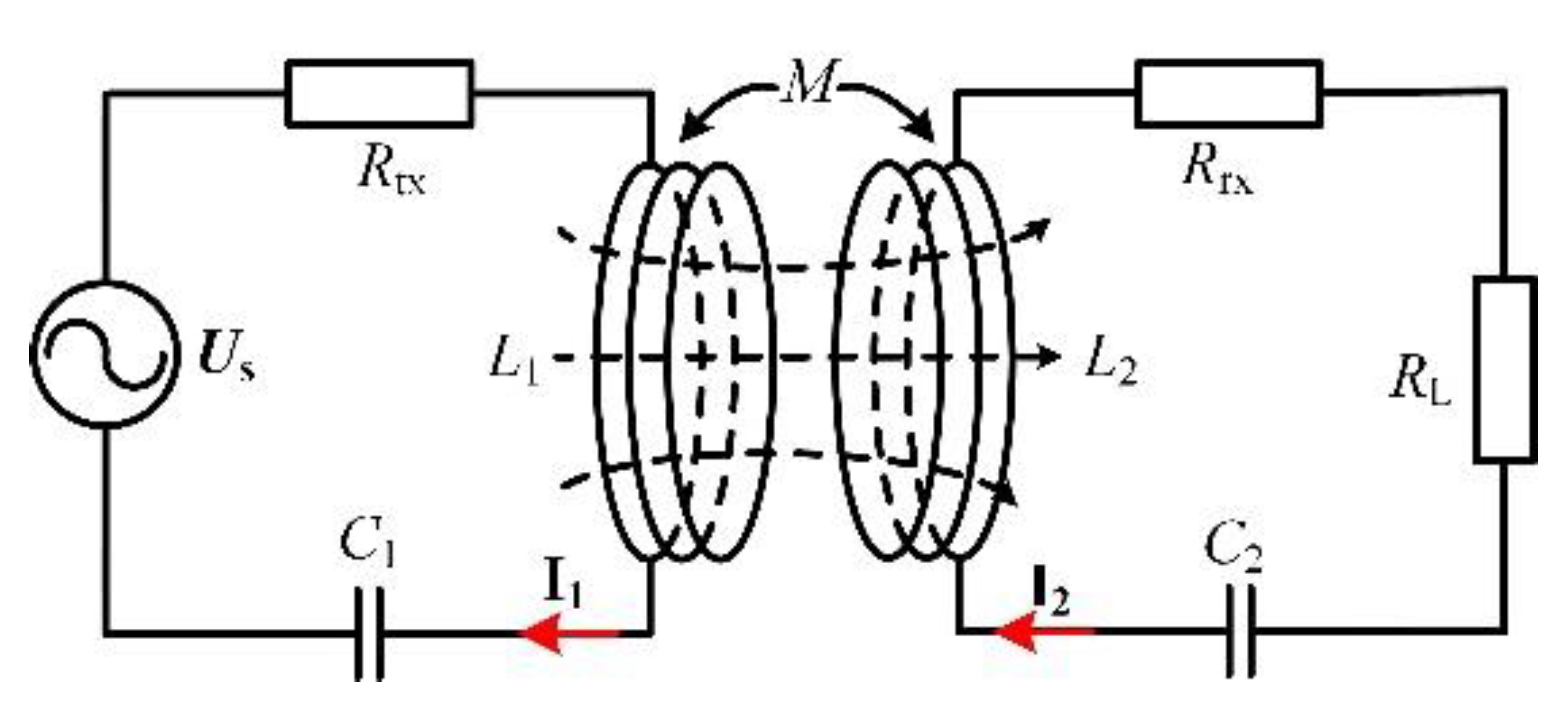
2. Theoretical Analysis of WPT
3. Optimization of Circular DD Coupler WPT System
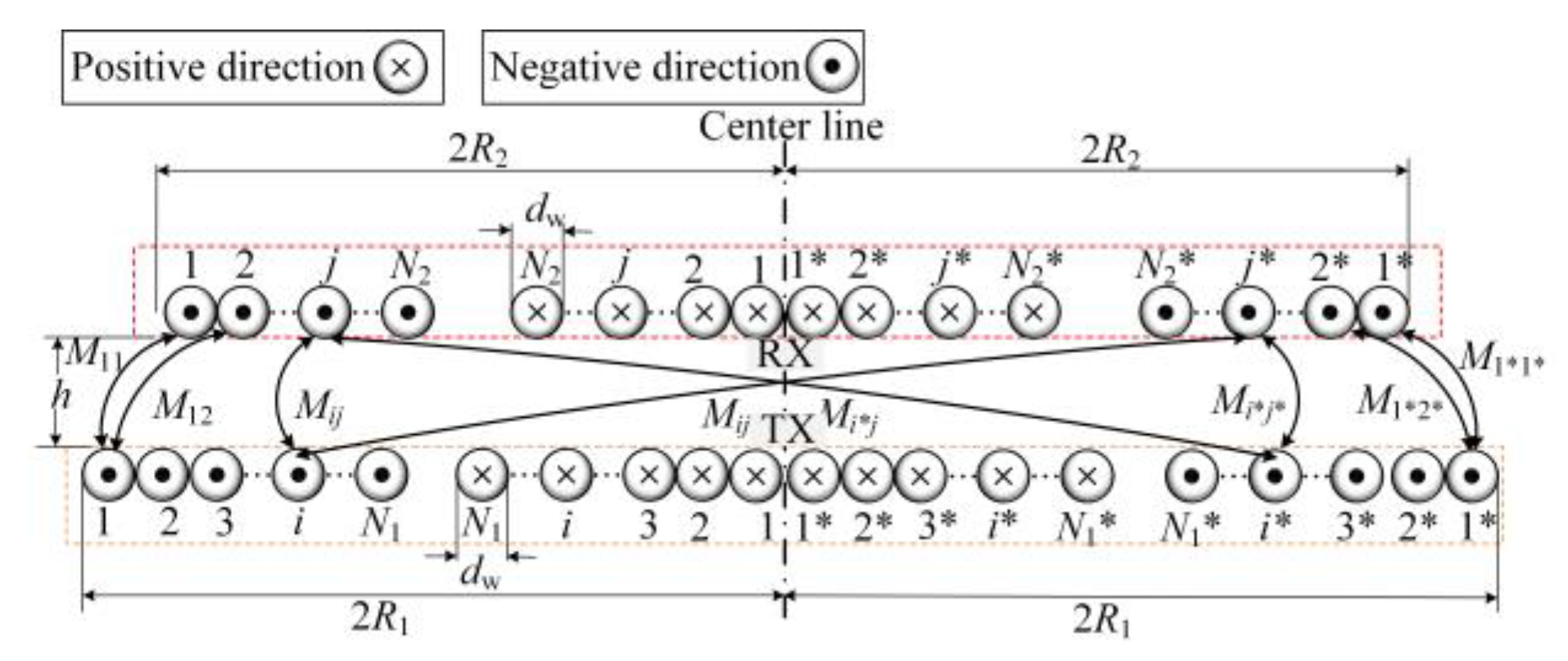
3.1. Mutual Inductance Calculation of Non-Coaxial Circular Coils
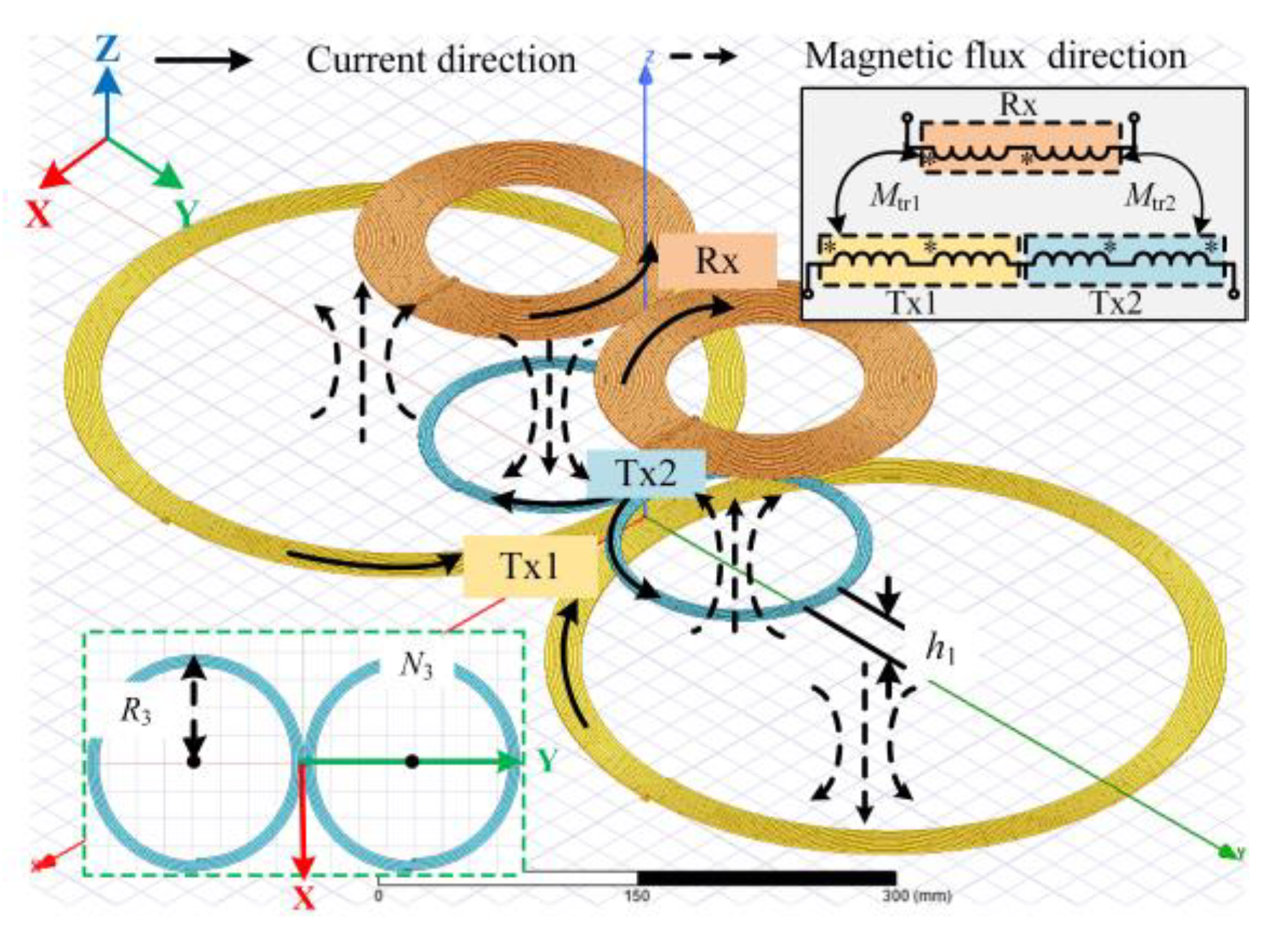
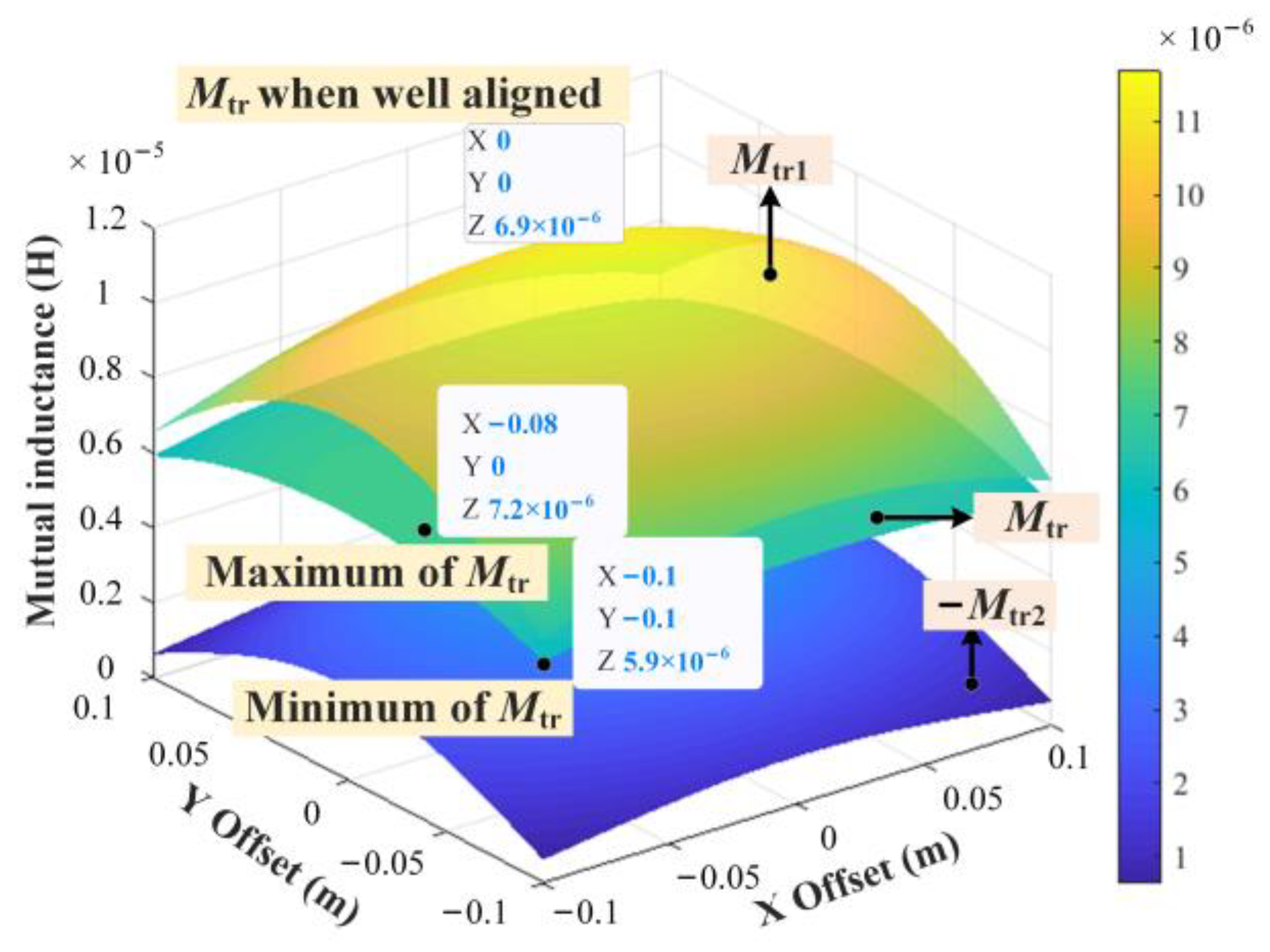
3.2. Analysis of Antimisalignment Characteristics of DD Coupler
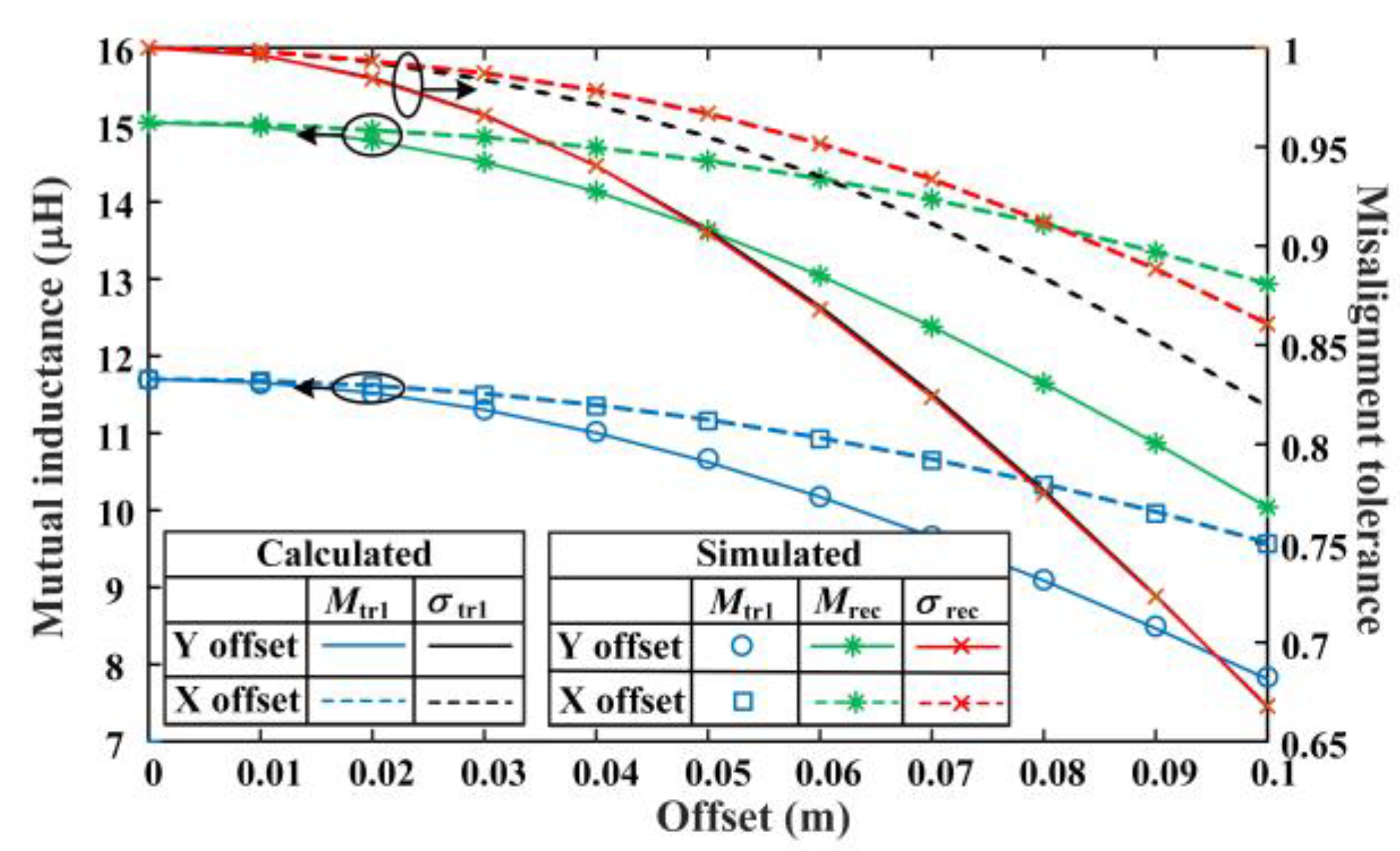
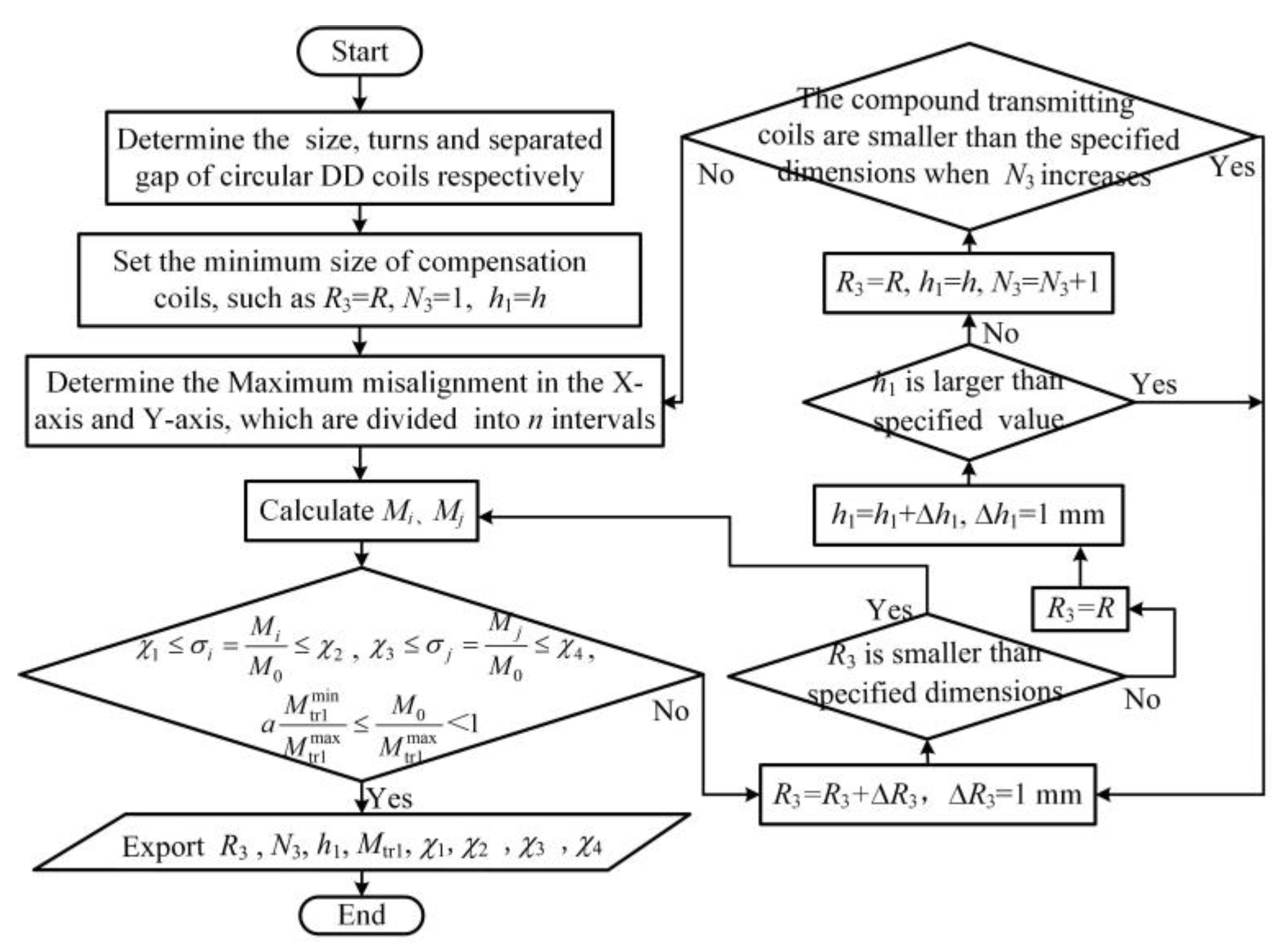
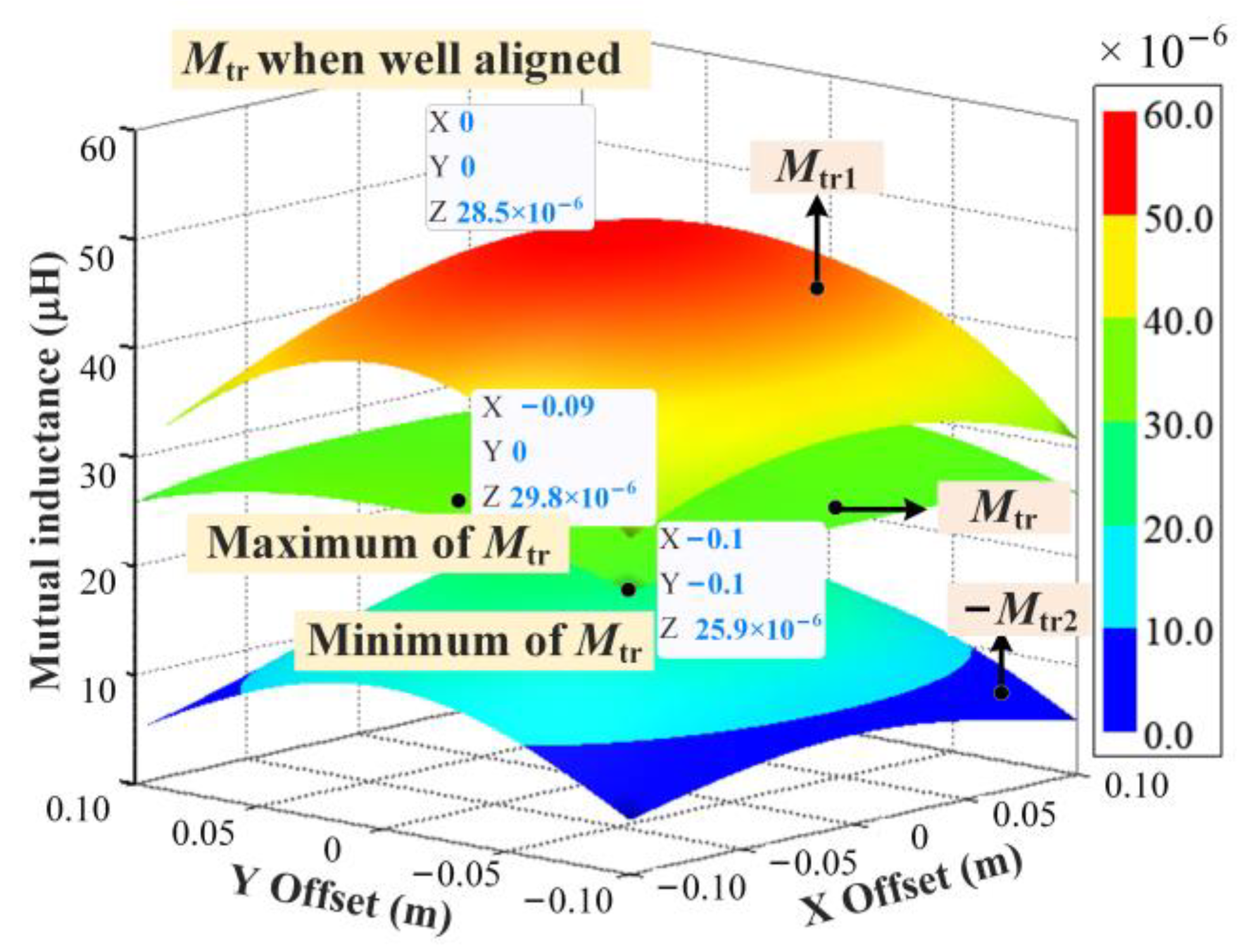
3.3. Analysis on Optimization Strategy for Misalignment Tolerance of Circular DD Coils
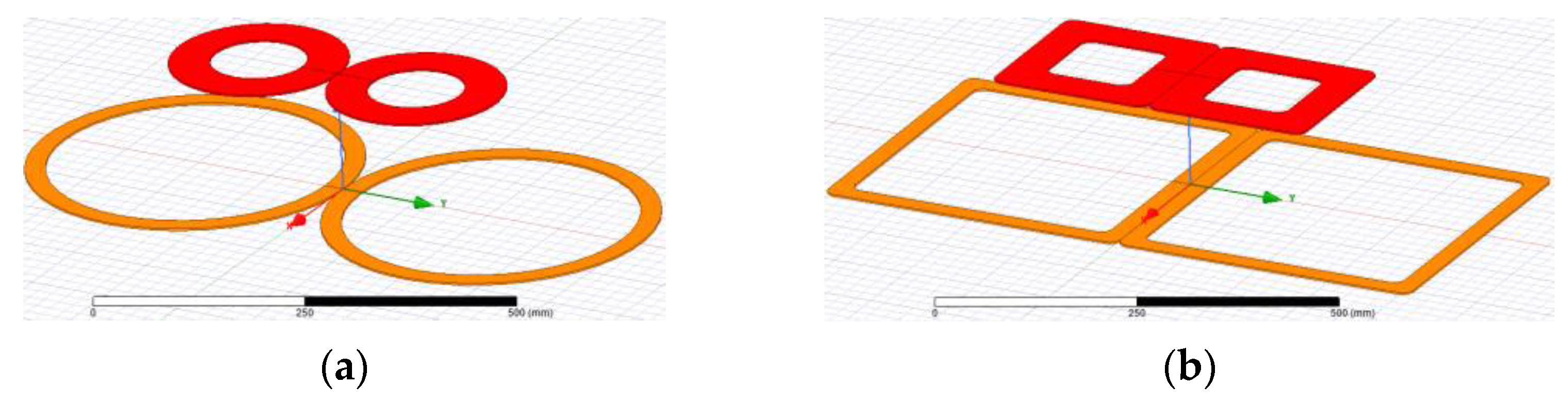
4. Verification Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Zhang, C.; Wang, J.; Tang, X. Multi-purpose flexible positioning device based on electromagnetic balance for EVS wireless charging. IEEE Trans. Ind. Electron. 2021, 68, 10229–10239. [Google Scholar] [CrossRef]
- Wang, W.; Xu, C.; Zhang, C.; Yang, J. Optimization of transmitting coils based on uniform magnetic field for unmanned aerial vehicle wireless charging system. IEEE Trans. Magn. 2021, 57, 8600105. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, H.; Georgiadis, A.; Cecati, C. Wireless power transfer—An Overview. IEEE Trans. Ind. Electron. 2019, 66, 1044–1058. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Xu, C.; Yang, J. Research on uniform magnetic field compensation structure of array circular coils for wireless power transfer. IEEE Trans. Magn. 2021, 57, 8600105. [Google Scholar] [CrossRef]
- Wang, W.; Yang, J.; Wang, Q.; Cao, W. Comparative design methods of wireless power system for sensors with extended range using Class E inverter at a certain frequency. IET Microw. Antennas Propag. 2020, 14, 908–918. [Google Scholar] [CrossRef]
- Shao, Y.; Liu, M.; Ma, C. A multi-receiver MHz WPT system with hybrid coupler. In Proceedings of the 2021 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), San Diego, CA, USA, 1–4 June 2021; pp. 1–6. [Google Scholar]
- Tan, P.; Cao, S.; Gao, X. Adjustable coupler for inductive contactless power transfer system to improve lateral misalignment tolerance. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMCECCE Asia), Hefei, China, 22–26 May 2016; pp. 2423–2426. [Google Scholar]
- Zhang, Z.; Zhang, B.; Wang, J. Optimal design of quadrature-shaped pickup for omnidirectional wireless power transfer. IEEE Trans. Magn. 2018, 54, 8600305. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, B.; Qiu, D.; Zhang, Y. Frequency splitting phenomena of magnetic resonant coupling wireless power transfer. IEEE Trans. Magn. 2014, 50, 8600204. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, X.; Wang, W. Wireless power transfer with two-dimensional resonators. IEEE Trans. Magn. 2014, 50, 4002804. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, Z.; Kan, T.; Liu, Y.; Mi, C.C. Modelling and analysis of the distortion of strongly-coupled wireless power transfer systems with SS and LCC–LCC compensations. IET Power Electron. 2019, 12, 1321–1328. [Google Scholar] [CrossRef] [Green Version]
- Budhia, M.; Boys, J.T.; Covic, G.A.; Huang, C. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Prosen, N.; Domajnko, J.; Milanovič, M. Wireless Power Transfer Using Double DD Coils. Electronics 2021, 10, 2528. [Google Scholar] [CrossRef]
- Prasanth, V.; Bauer, P. Distributed IPT Systems for Dynamic Powering: Misalignment Analysis. IEEE Trans. Ind. Electron. 2014, 61, 6013–6021. [Google Scholar] [CrossRef]
- Yang, G.; Dong, S.; Zhu, C.; Lu, R.; Wei, G.; Song, K. Design of a high lateral misalignment tolerance magnetic coupler for wireless power transfer systems. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqin, China, 20–22 May 2017; pp. 34–39. [Google Scholar]
- Yao, Y.; Gao, S.; Mai, J.; Liu, X.; Zhang, X.; Xu, D. A novel misalignment tolerant magnetic coupler for electric vehicle wireless charging. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 219–229. [Google Scholar] [CrossRef]
- Bima, M.E.; Bhattacharya, I.; Neste, C.W.V. Experimental evaluation of layered DD coil structure in a wireless power transfer system. IEEE Trans. Electromagn. Compat. 2020, 62, 1477–1484. [Google Scholar] [CrossRef]
- Bima, M.E.; Bhattacharya, I.; Hasan, S.R. Comparative analysis of magnetic materials, coil structures and shielding materials for efficient wireless power transfer. In Proceedings of the 2019 IEEE International Symposium on Electromagnetic Compatibility, Signal & Power Integrity (EMC + SIPI), Orleans, LA, USA, 22–26 July 2019; pp. 95–100. [Google Scholar]
- Yang, Z.; Chen, Y.; Yang, D.; Du, W.; He, G.; Zhang, X.; Xu, C.; Wang, W. Research on parameter optimization of Double-D coils for electric vehicle wireless charging based on magnetic circuit analysis. IEICE Electron. Expre. 2020, 17, 20200067. [Google Scholar] [CrossRef] [Green Version]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Solacic, M. Wireless power transfer via strongly coupled magnetic resonances. Sci. Express 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, J.; Kim, D.; Hwang, K.; Park, H.H.; Kwak, S.I.; Kwon, J.H.; Ahn, S. A resonant reactive shielding for planar wireless power transfer system in smartphone application. IEEE Trans. Electromagn. Compat. 2017, 59, 695–703. [Google Scholar] [CrossRef]
- Qian, L.; Chen, M.; Cui, K.; Shi, G.; Wang, J.; Xia, Y. Modeling of mutual inductance between two misalignment planar coils in wireless power transfer. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 814–817. [Google Scholar] [CrossRef]

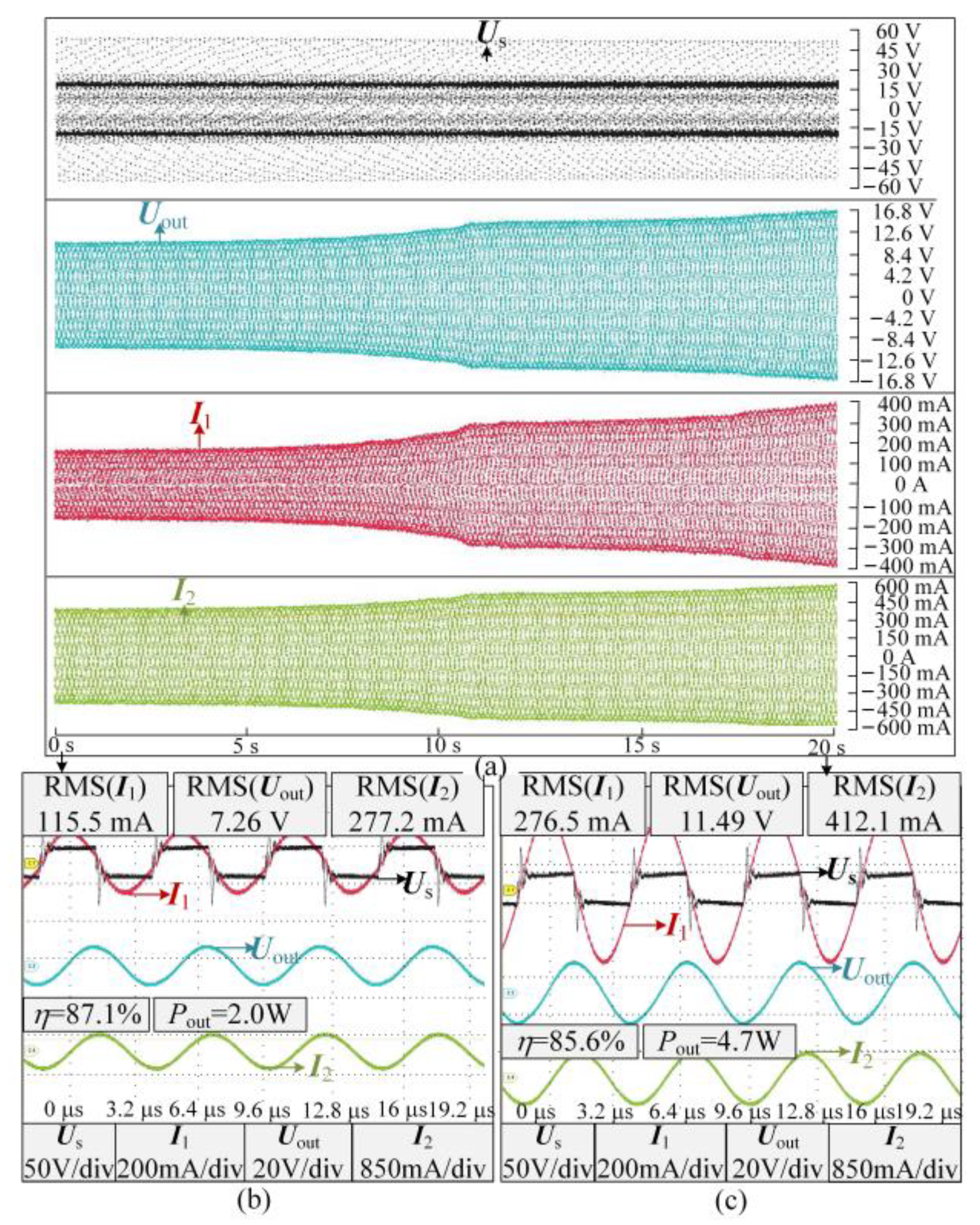
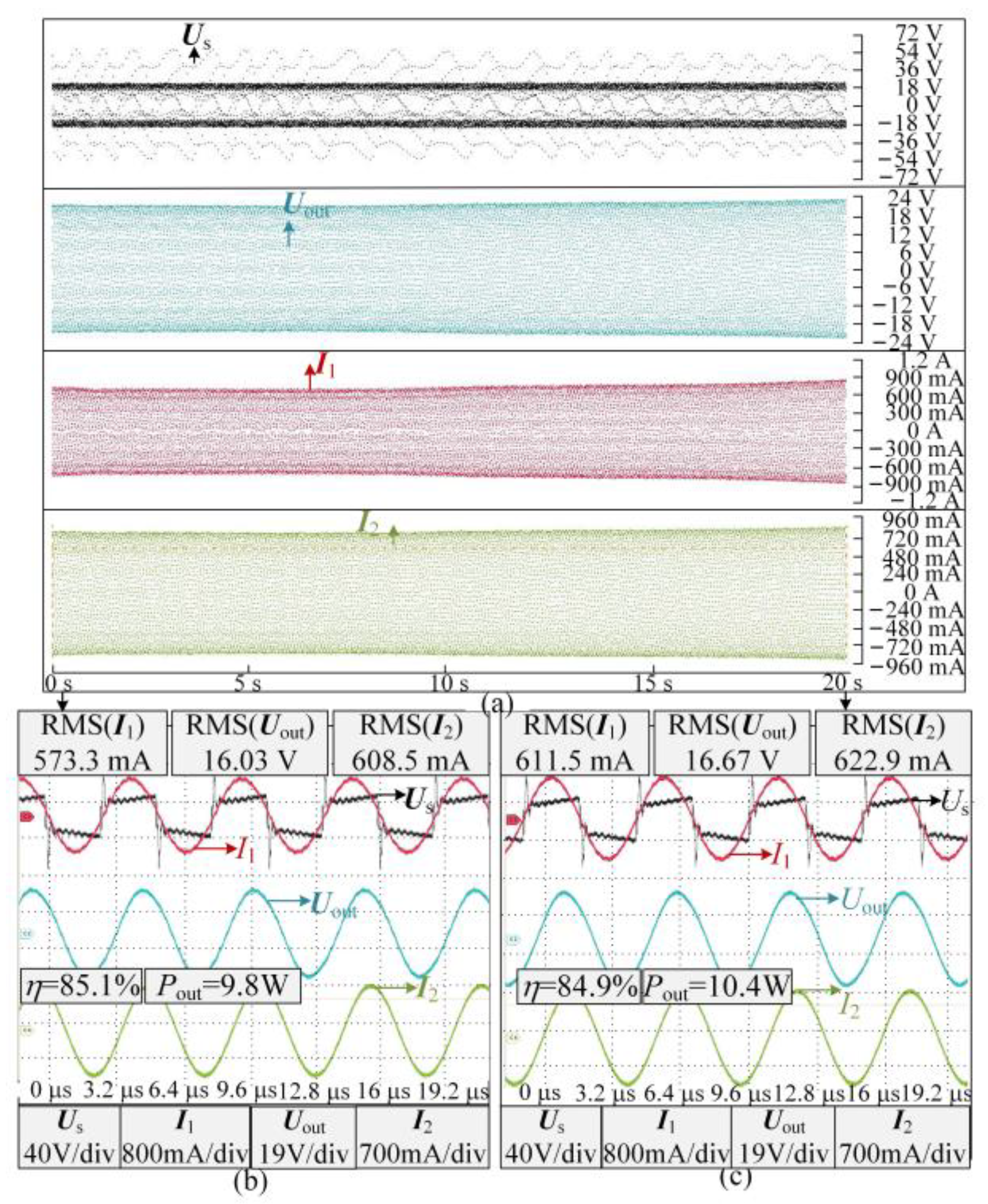
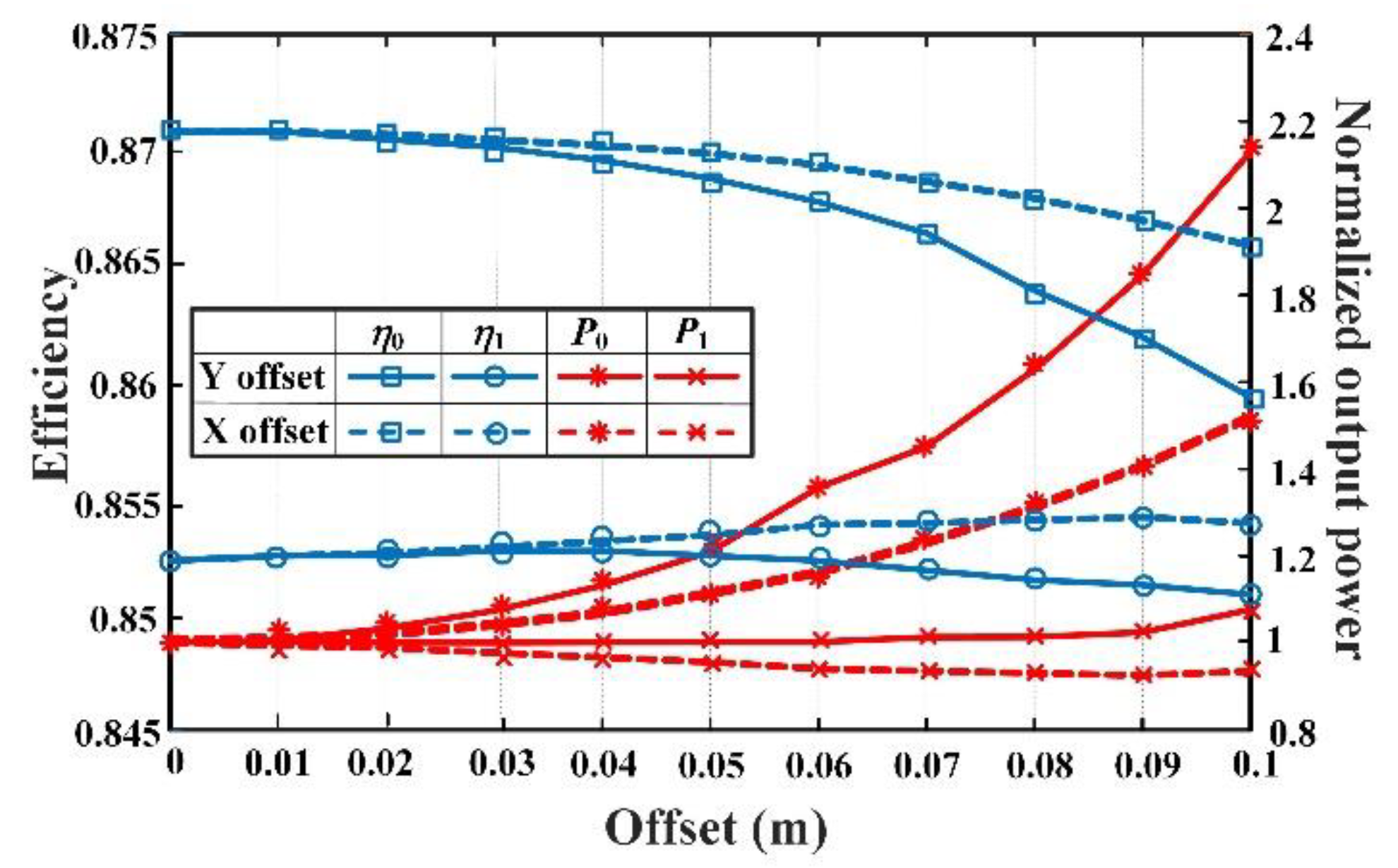
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| L1 | Before compensation 315 μH After compensation 297 μH | L2 | 329 μH |
| R1 | Before compensation 1.6 Ω After compensation 1.7 Ω | R2 | 1.7 Ω |
| US | 20 V | RL | 24 Ω |
| f | 190 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, F.; Wang, P.; Sun, C.; Wu, Y.; Dou, Z.; Xu, C.; Wang, S.; Wang, W. Research on Optimization of Horizontal Omnidirectional Misalignment Tolerance of WPT Based on Double D Coupler. Electronics 2022, 11, 2163. https://doi.org/10.3390/electronics11142163
Chi F, Wang P, Sun C, Wu Y, Dou Z, Xu C, Wang S, Wang W. Research on Optimization of Horizontal Omnidirectional Misalignment Tolerance of WPT Based on Double D Coupler. Electronics. 2022; 11(14):2163. https://doi.org/10.3390/electronics11142163
Chicago/Turabian StyleChi, Fuhai, Pan Wang, Chenglong Sun, Yuming Wu, Zhenlan Dou, Chenjin Xu, Shuo Wang, and Wei Wang. 2022. "Research on Optimization of Horizontal Omnidirectional Misalignment Tolerance of WPT Based on Double D Coupler" Electronics 11, no. 14: 2163. https://doi.org/10.3390/electronics11142163
APA StyleChi, F., Wang, P., Sun, C., Wu, Y., Dou, Z., Xu, C., Wang, S., & Wang, W. (2022). Research on Optimization of Horizontal Omnidirectional Misalignment Tolerance of WPT Based on Double D Coupler. Electronics, 11(14), 2163. https://doi.org/10.3390/electronics11142163





