Abstract
When performing low-frequency noise measurements on low-impedance electron devices, transformer coupling can be quite effective in reducing the contribution of the equivalent input noise voltage of the preamplifier to the background noise of the system. However, noise measurements on electron devices are usually performed with a biased device under test. A bridge configuration must be used to null the DC component at the input of the transformer. Unfortunately, using a bridge results in a complication of the set-up and degradation of the system’s sensitivity because of the noise introduced by the nulling arm. We propose an alternative approach for blocking the DC component that exploits the fact that supercapacitors with capacitances in excess of a few Farads are nowadays easily available. Actual measurement results in conventional and advanced measurement configurations are discussed that demonstrate the advantages of the approach we propose.
1. Introduction
Low-frequency noise measurements (LFNMs) are non-destructive, very-high-sensitive diagnostic tools in electron devices, materials, and sensor characterization [1,2,3,4,5,6,7,8,9].
Different measurement set-up configurations need to be used depending on the nature of the device under test (DUT) to obtain sufficient sensitivity and reliable results [10]. In most cases, LFNMs have employed general-purpose commercial instrumentation to target relatively high-impedance DUTs. However, the fast progress in semiconductors and new materials process technologies often results in the need to develop dedicated instrumentation and new methodologies for noise measurement and analysis [11,12,13]. Obtaining reliable noise characterization is especially challenging in the case of low-resistance DUTs (impedances below 10 Ω), and in these cases it is necessary to resort to a dedicated amplifier design and/or to the application of cross-correlation methods [14,15]. Besides resorting to these solutions, especially in the case of low-resistance DUTs, signal transformers can be used in the measurement chain between the DUT and the preamplifier’s input to reduce the system’s background noise (BN). This approach is effective when the BN is dominated by the equivalent input voltage noise of the preamplifiers, and the equivalent input current noise plays a minor role. This is the typical situation when noise measurements are employed to characterize the quality and reliability of electron devices with a low equivalent impedance [16,17,18]. In [19], the possibility of combining the cross-correlation approach and the use of signal transformers has been explored for the accurate investigation of advanced infrared detector (IR) devices, characterized by a very low equivalent resistance (in the order of a few ohms). Because of transformers connected to the DUT, a bridge arrangement had to be used to bias the DUT with a constant current while avoiding that a DC current flowed through the transformers’ primary winding. The bridge approach is still the one used almost exclusively in low-frequency noise measurements with transformer coupling, although using a blocking capacitor would be, at least in principle, simpler and capable of resulting in lower background noise. The most obvious reason why capacitors have not been used in this type of application is that even with magnetization inductances as large as tens of Hs, as it is not uncommon in signal transformers used in this type of measurement, obtaining a resonance frequency well below 1 Hz would require blocking capacitors with capacitances in excess of 0.1 F. Up to not many years ago, obtaining capacitors in the order of 1 F in a reasonable size and compatible with low-noise instrumentation was simply not possible [10]. Nowadays, supercapacitors that combine capacitances in the orders of a few Fs are available in small sizes and, more importantly, have been proven to be compatible with low-noise instrumentation [20,21,22,23]. In this paper, we investigate the possibility of using supercapacitors instead of a Wheatstone bridge to solve the problem of the connection of biased devices to transformer-coupled low-noise amplifiers. The design procedure is described, and the results show that the proposed approach can offer better performances in terms of background noise and results in a significant simplification in the measurement procedure. Thanks to these advantages, low-frequency noise measurements on low-impedance electron devices can be performed faster and with higher accuracy. This work is organized as follows: in Section 2, we introduce the approach and propose and discuss its advantages with respect to the conventional approach; in Section 3, we discuss the actual implementation of the measurement set-up, and we report on actual noise measurements that demonstrate the soundness of the approach we propose; in Section 4, we draw some conclusions.
2. Proposed Approach
The way in which a transformer can reduce the BN can be understood with reference to the simplified diagram in Figure 1.
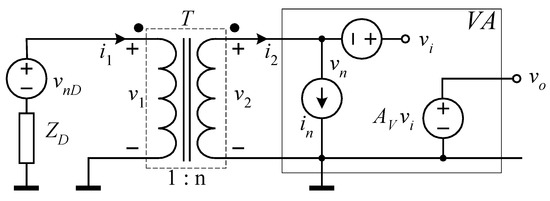
Figure 1.
Simplified schematic of a transformer-coupled amplifier. VA is a voltage amplifier based on FET input operational amplifier with a constant gain AV and very large input impedance.
To simplify the discussion at this stage, we assume that an ideal transformer T is available with a turn ratio of 1:n, for which we have:
The source vnD represents the noise generated by the DUT while vn and in represent the equivalent input voltage noise (EIVN) and the equivalent input current noise (EICN) sources at the input of the voltage amplifier, respectively. Assuming, for the sake of simplicity, that all noise sources are uncorrelated, the power spectral density (PSD) of the voltage noise at the output of the system (SVOID) can be expressed as follows:
where SnD, Svn, and Sin are the PSDs of the noise sources vnD, vn, and in, respectively, and we have indicated with Sein the PSD of the equivalent input noise source of the entire system. The BN of the system is obtained assuming SnD = 0. When using field-effect transistor (FET) input voltage amplifiers and when dealing with low-impedance DUTs, the contribution from Sin to the BN can be usually neglected while, at the same time, the contribution from the EIVN of the amplifier that would represent the largest contribution to the BN in the absence of the transformer is greatly reduced. While Equation (2) explains in a simple way how a transformer can help in reducing the background noise of the system, Equation (1) can be regarded as a reasonable approximation of the behavior of an actual transformer only in a limited range of frequencies. Moreover, other nonidealities, such as parasitic capacitances and the intrinsic resistances associated with the wires used for obtaining the primary and secondary windings, can significantly modify Equation (2). When dealing with noise measurements in electron devices to characterize their quality and reliability, we are mostly interested in flicker noise, which is more easily detected at low frequencies [24]. When restricting to the low-frequency range, we can safely neglect the presence of the parasitic capacitances and obtain a quite good representation of the behavior of an actual transformer by using the equivalent circuit in the box labelled T in Figure 2 [25]. To simplify the discussion, in Figure 2 we have assumed that the DUT can be represented by the resistance RD. The voltage noise source representing the noise generated by the DUT is not shown in Figure 2. All other resistances in the circuit are assumed to produce purely thermal noise (the corresponding noise sources in series with the resistances also are not shown in Figure 2).
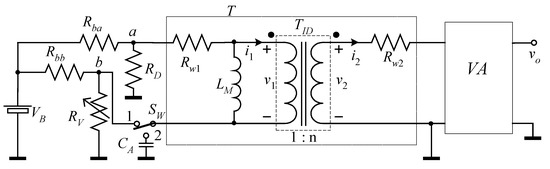
Figure 2.
Simplified schematic of a transformer-coupled amplifier. VA is a FET input operational amplifier with a constant gain AV and very large input impedance.
With the switch SW in position one, Figure 2 represents the most common low-frequency noise measurement configuration on biased electron devices [25]. In this configuration, the bridge arrangement made of Rba, Rbb, RV, and RD is required to bias the DUT with a constant current while avoiding that a DC current flows through the primary winding of the transformer. Typically, Rba = Rbb and RV needs to be adjusted until RV = RD. The resistances Rba and Rbb are typically chosen much higher than RD, so their noise contribution and loading effect can be neglected. With the further assumption of a negligible contribution from the EICN of the voltage amplifier VA, the PSD of the voltage noise SVO at the output of the system can be written as [19]:
where SnRV, Snw1, and Snw2 are the PSD of the voltage fluctuations due to the thermal noise of the resistance RV in the bridge and the winding resistances Rw1 and Rw2, respectively. LM is magnetization inductance.
When comparing Equation (3) with Equation (2), with the assumption of negligible contribution from the EICN of the amplifier, the following observations can be made:
- (a)
- There is a cut-in frequency (fP1) below which the transformer is ineffective in transferring the noise generated by the DUT toward the voltage preamplifier. This limitation is particularly important in the field of low-frequency noise measurements since the flicker noise generated by the DUT is, typically, inversely proportional to the frequency;
- (b)
- There are three contributions to the background noise in Equation (3) that are not present in the simplified expression in Equation (2), namely the noise coming from the resistances of the two transformer windings and the noise introduced by the resistance RV in the bridge.
The minimum value of fP1 that can be obtained (with negligible small RD and RV) depends on the transformer, and it is proportional to the ratio between the primary winding resistance and the magnetization inductance. For the same wire and core cross section, the magnetization inductance is proportional to the number n1 of primary turns squared, while the resistance is proportional to n1. This means that increasing the number of turns results in a decrease in the cut-in frequency. However, the fact that increasing the number of turns results in an increase in the resistance and hence in the background noise means that we should increase the magnetization inductance without increasing the resistance. This, however, may result in a significant increase in the size of the transformer (larger section for the wires) that, besides being problematic in itself, also results in an increase in the parasitic capacitances that reduce the higher frequencies at which the system can be usefully employed. Since the noise generated by the secondary winding is divided by n2 in Equation (2), the main contribution to the background noise of a transformer-coupled amplifier can be reduced to the noise introduced by the primary winding and by the resistance RV. In a recent paper [19], it has been demonstrated that by applying the cross-correlation approach to a pair of nominally identical transformer-coupled amplifiers, the contribution to the BN by the transformer winding resistances can be greatly reduced so that the main contribution to the background noise remains the one introduced by the resistance RV. Note that RV also contributes to an increase of the cut-in frequency fP1. In conclusion, we can observe that the presence of RV, while necessary for obtaining a null DC voltage at the input of the transformer (the voltage between nodes a and b in Figure 2), has serious drawbacks as it sets the minimum level of the background noise of the system. Moreover, it also limits the bandwidth of the system at low frequencies, not to mention the amount of time and effort that is wasted any time the bias on the DUT is changed and the value of RV has to be recalibrated accordingly.
Let us now assume that the switch SW in Figure 2 is in position two. In this situation, because of the presence of the capacitor in series with the primary winding of the transformer, no DC current can flow through the transformer, and this means that the resistances Rbb and RV are no longer required. In other words, with the switch in position two, the bridge configuration is no longer necessary. With the same approximations made for obtaining Equation (2), we can obtain the PSD of the noise at the output of the circuit in Figure 2 when the switch SW is in position two as follows:
For frequencies above the series resonance frequency fP2, Equation (4) assumes a form very close to the ideal expression in Equation (2), save that we have the additional noise coming from the windings of the transformer. As we have noted before, however, the contribution from the secondary winding can be often neglected and, provided we resort to a cross-correlation arrangement as in [19], extremely low levels of BN can be obtained that are not bounded, as in the case of the bridge approach, by the noise generated by the resistance RV.
As we have noted in the introduction, the main problem in using this approach is that even with magnetization inductances as large as tens of H, as it is not uncommon in signal transformers used in this type of measurement, obtaining a resonance frequency well below 1 Hz requires capacitances in the order of 1.1 F or more; therefore, we need to resort to supercapacitors. The fact that the rated voltage for supercapacitors is relatively low compared to other technologies is not a limitation for low-frequency noise measurement applications. Indeed, transformer-coupled low-noise amplifiers are especially effective in the case of very low-impedance DUTs, which means that the DC voltage to be blocked by the capacitor CA in Figure 2, even when relatively large bias currents are tested, are well within the voltage rating of typical supercapacitors available on the market.
3. Circuit Design and Experimental Results
In order to select the most proper value for the capacitance CA in Figure 2, we need to set a value for the resonance frequency, and we need information on the primary inductance of the coupling transformer. As far as the resonance frequency is concerned, to extend measurements down to at least 1 Hz, we clearly need fP2 << 1 Hz. As far as the estimation of the magnetization inductance is concerned, this can be obtained by performing noise measurements with a known and relatively high-value resistance connected directly to the primary input of the transformer. In principle, this configuration can be thought of as obtained in Figure 2 with the switch in position one, VB = 0, RV = 0, and Rbx >> RD, so LM can be obtained from fp1 in Equation (3) since RD is known and Rw1 can be easily measured in DC. However, to avoid any possible source of error, actual measurements were performed by removing VB, Rba, Rbb, RV, and the switch SW from the circuit and connecting the other end of the primary winding (the one not connected to RD in Figure 2) to ground. Our experiments used UNIPAN 233-7-1 transformers to provide a bandwidth that extends below 1 Hz when dealing with low-DUT impedances [19]. The primary winding resistance for these transformers is RW1 = 10 Ω. The results of noise measurements on two nominally identical UNIPAN transformers to extract the value of the magnetization inductance are reported in Figure 3.
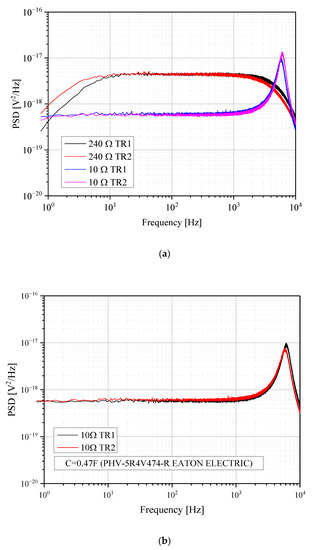
Figure 3.
Noise measurements of different DUT resistances in configuration of bridge (a), position 1, and supercapacitor (b), position 2.
Measures have been performed using a 240 Ω resistor as a DUT. Fitting at low frequencies against Equation (3) (with RV = 0 and Rbx >> RD) provides fp11 = 2 Hz and fp12 = 4 Hz pole frequencies, corresponding to magnetization inductances of LM1= 20 H and LM2 = 10 H. The large difference in the magnetization inductances in the case of two nominally identical transformers is not a limiting issue in our application: once we know the order of magnitude of these inductances, we just need to select capacitances that are large enough so that we can ensure a flat response from the transformer-coupled amplifier down to the minimum frequency of interest. The measurements obtained when a low-value resistance is used as a DUT are also shown in Figure 3. It can be noticed that regardless of the actual value of the magnetization inductance, we obtain a flat response down to 1 Hz.
An obvious criterion for dimensioning CA in Figure 2 is to ensure that the resonance frequency fp2 in Equation (4) is much smaller than the minimum frequency of interest fMIN. This means:
For fMIN = 1 Hz and the worst case of LM2 = 10 H, the CA value must be much larger than 2.5 mF. It can be conveniently obtained by resorting to supercapacitors with hundreds of mF or more capacitances. We selected a good quality 0.47 F supercapacitor (PHV-5R4V474-R EATON ELECTRIC) characterized by a low equivalent series resistance (ESR) of 0.3 Ω at 1 kHz and 0.4 Ω at 100 Hz. We repeated the measurement with a 10 Ω resistor as a DUT using a circuit in Figure 2 without bias (without VB and Rba). As shown in Figure 3b, we obtained the same results as in Figure 3a, which demonstrates that the presence of the supercapacitors does not modify the system’s performances in terms of background noise and frequency response down to 1 Hz.
To verify our analyses of the noise measurement performances on biased devices, we used an advanced InAsSb IR photodetector as the DUT [26]. We applied our two-channel noise measurement set-up with the cross-correlation method presented in Figure 4a [19].
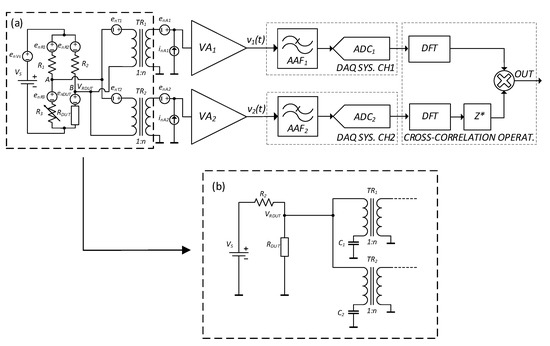
Figure 4.
Cross-correlation set-up with transformed coupled amplifiers developed in [19] (a) *. The set-up can be greatly simplified, with the added advantage of a lower background noise, modifying the leftmost section as shown in (b), according to the approach we propose. * Reprinted with permission from Ref. [19]. Copyright 2022, Elsevier.
In this set-up, we removed the bridge and biased the device using a supercapacitor (Figure 4b). The photodetector has a DC resistance of about 4.5 Ω at 293 K. The system’s proper operation was tested with a 10 Ω resistor.
The results of these preliminary measurements are reported in Figure 5a. For 40 min of averaging (the record length of 217 points), the measured noise corresponds to a 10 Ω -resistance theoretical thermal one. Note that when using two supercapacitors, one for each transformer, the possible contribution to the background noise from the supercapacitors ESRs is also reduced by cross-correlation. We employed a 100 Ω wirewound resistor (R2 in Figure 4b) to bias the photodetector. Both signal acquisition and spectral estimation parameters were not changed. The measured spectra for some bias voltages (VS) are reported in Figure 5b. The dashed blue line in Figure 5b represents the level of thermal noise that would have been obtained in the case of the bridge configuration because of the contribution from R3 in Figure 4b (R1 = R2 >> R3, RDUT) that plays the role of RV in Figure 2. Since with the proposed approach we have eliminated the bridge, RV is no longer present, and we can obtain a much more detailed picture of the flicker noise coming from the DUT even at very low biases. Moreover, there is no need to balance the bridge configuration, and the experimental procedure is relatively more straightforward and less time-consuming.
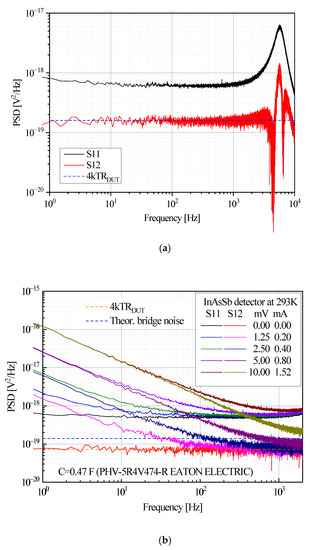
Figure 5.
Noise measurements obtained using supercapacitor’s configuration of 10 Ω resistor (a) and InAsSb IR photodetector for few bias voltages (b). S11 is power spectra density obtained without cross-correlation, and S12 is the modulus of the cross-correlation.
4. Conclusions
In this paper, we have investigated the possibility of using supercapacitors instead of a Wheatstone bridge to solve the problem of the connection of biased devices to transformer-coupled low-noise amplifiers. The proposed approach, that to the best of our knowledge has never been reported before, provides better background noise performances and a more straightforward measurement procedure with respect to more conventional approaches based on a balanced bridge configuration. In our approach, the bridge is eliminated; therefore, the contribution to the noise coming from the balancing arm of the bridge is also eliminated. Moreover, without the bridge, the time-consuming balancing process is also eliminated. The approach we propose is expected to be especially useful in the case of low-frequency noise measurements on low-impedance devices since it results in faster measurement set-up and higher sensitivity. Future work will be devoted to the exploration of the potential advantages resulting from the design of customized low-noise transformers in combination with the approach we propose. What we hope to achieve in this way is an extension of the useful bandwidth down to the hundreds of mHz range, where the flicker component of the noise generated by the device under test can be more easily detected even at very low bias levels.
Author Contributions
Conceptualization, G.S.; methodology, G.S.; validation, C.C.; formal analysis, C.C.; investigation, K.A.; resources, K.A., J.M. and Z.B.; data curation, C.C.; writing—original draft preparation, G.S. and C.C.; writing—review and editing, K.A., J.M. and Z.B.; supervision, G.S. and K.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The experimental part was carried out in the Institute of Optoelectronics MUT laboratory and supported in the frame of grant no. UGB-22/732.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rehman, A.; Krajewska, A.; Stonio, B.; Pavlov, K.; Cywinski, G.; Lioubtchenko, D.; Knap, W.; Rumyantsev, S.; Smulko, J.M. Generation-recombination and 1/f noise in carbon nanotube networks. Appl. Phys. Lett. 2021, 118, 242102-1–242102-5. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, M.; Deng, S.; Yang, Y.; Wong, M.; Kwok, H.S. Evaluation of Positive-Bias-Stress-Induced Degradation in InSnZnO Thin-Film Transistors by Low Frequency Noise Measurement. IEEE Electron. Device Lett. 2022, 43, 886–889. [Google Scholar] [CrossRef]
- Szewczyk, A.; Gaweł, Ł.; Darowicki, K.; Smulko, J. Assessment of Fuel Cells’ State of Health by Low-Frequency Noise Measurements. Energies 2021, 14, 8340. [Google Scholar] [CrossRef]
- Cardillo, E.; Scandurra, G.; Giusi, G.; Ciofi, C. A Two-Channel DFT Spectrum Analyzer for Fluctuation Enhanced Sensing Based on a PC Audio Board. Sensors 2021, 21, 4307. [Google Scholar] [CrossRef] [PubMed]
- Dub, M.; Sai, P.; Sakowicz, M.; Janicki, L.; But, D.B.; Prystawko, P.; Cywiński, G.; Knap, W.; Rumyantsev, S. Double-Quantum-Well AlGaN/GaN Field Effect Transistors with Top and Back Gates: Electrical and Noise Characteristics. Micromachines 2021, 12, 721. [Google Scholar] [CrossRef]
- Vail, O.; Hankinson, J.; Berger, C.; de Heer, W.A.; Jiang, Z. 1/f Noise in epitaxial sidewall graphene nanoribbons. Appl. Phys. Lett. 2020, 117, 083105-1–083105-5. [Google Scholar] [CrossRef]
- Wei, W.; Zeng, Z.; Liao, W.; Chim, W.K.; Zhu, C. Extended Gate Ion-Sensitive Field-Effect Transistors Using Al2O3/Hexagonal Boron Nitride Nanolayers for pH Sensing. ACS Appl. Nano Mater. 2020, 3, 403–408. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Kang, C.; Chai, G. Low-Frequency Noise Evaluation on a Commercial Magnetoimpedance Sensor at Submillihertz Frequencies for Space Magnetic Field Detection. Sensors 2019, 19, 4888. [Google Scholar] [CrossRef] [Green Version]
- Wojtas, J.; Bielecki, Z.; Stacewicz, T.; Mikolajczyk, J.; Medrzycki, R.; Rutecka, B. Application of quantum cascade lasers in nitric oxide and nitrous oxide detection. Acta Phys. Pol. A 2011, 120, 794–797. [Google Scholar] [CrossRef]
- Ciofi, C.; Giusi, G.; Scandurra, G.; Neri, B. Dedicated instrumentation for high sensitivity, low frequency noise measurement systems. Fluct. Noise Lett. 2004, 4, 385–402. [Google Scholar] [CrossRef]
- Ciura, L.; Kolek, A.; Michalczewski, K.; Hackiewicz, K.; Martyniuk, P. 1/f noise in InAs/InAsSb superlattice photoconductors. IEEE Trans. Electron. Devices 2020, 67, 3205–3210. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kolek, A.; Gawron, W.; Kowalewski, A.; Stanaszek, D. Measurements of low frequency noise of infrared photodetectors with transimpedance detection system. Metrol. Meas. Syst. 2014, 21, 461–472. [Google Scholar] [CrossRef] [Green Version]
- Scandurra, G.; Beyne, S.; Giusi, G.; Ciofi, C. On the design of an automated system for the characterization of the electromigration performance of advanced interconnects by means of low-frequency noise measurements. Metrol. Meas. Syst. 2019, 26, 13–21. [Google Scholar]
- Scandurra, G.; Giusi, G.; Ciofi, C. Single JFET Front-End Amplifier for Low Frequency Noise Measurements with Cross Correlation-Based Gain Calibration. Electronics 2019, 8, 1197. [Google Scholar] [CrossRef] [Green Version]
- Levinzon, F.A. Ultra-low-noise high-input impedance amplifier for low-frequency measurement applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1815–1822. [Google Scholar] [CrossRef]
- Motchenbacher, C.D.; Connelly, J.A. Low-Noise Electronic System Design; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Netzer, Y. The Design of Low-Noise Amplifiers. Proc. IEEE 1981, 69, 728–741. [Google Scholar] [CrossRef]
- Leach, W.M. Fundamentals of Low-Noise Analog Circuit Design. Proc. IEEE 1994, 82, 1515–1538. [Google Scholar] [CrossRef] [Green Version]
- Achtenberg, K.; Mikołajczyk, J.; Ciofi, C.; Scandurra, G.; Bielecki, Z. Transformer-based low frequency noise measurement system for the investigation of infrared detectors’ noise. Measurement 2022, 190, 110657-1–110657-9. [Google Scholar] [CrossRef]
- Davis, A.K.; Gunasekaran, M.K. Microprocessor-conducted noise reduction with switched supercapacitors. Electron. Lett. 2015, 51, 92–94. [Google Scholar] [CrossRef]
- Scandurra, G.; Ciofi, C. Supercapacitors in bias systems for low frequency noise measurements. In Proceedings of the 2011 21st International Conference on Noise and Fluctuations, Toronto, ON, Canada, 12–16 June 2011; IEEE: Piscataway Township, NJ, USA, 2011; pp. 389–392. [Google Scholar]
- Scandurra, G.; Cannatà, G.; Giusi, G.; Ciofi, C. A new approach to DC removal in high gain, low noise voltage amplifiers. In Proceedings of the 2017 International Conference on Noise and Fluctuation (ICNF), Vilnius, Lithuania, 20–23 June 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Ivanov, V.E.; Chye, E.U. Simple programmable voltage reference for low frequency noise measurements. J. Phys. Conf. Ser. 2018, 1015, 052011. [Google Scholar] [CrossRef]
- Wong, H. Low-frequency noise study in electron devices: Review and update. Microelectron. Reliab. 2003, 43, 585–599. [Google Scholar] [CrossRef]
- Stadler, A.W.; Kolek, A.; Mleczko, K.; Zawiślak, Z.; Dziedzic, A. Noise properties of thick-film conducting lines for integrated inductors. Metrol. Meas. Syst. 2015, 17, 229–240. [Google Scholar] [CrossRef]
- Rogalski, A.; Martyniuk, P.; Kopytko, M.; Madejczyk, P.; Krishna, S. InAsSb-Based Infrared Photodetectors: Thirty Years Later On. Sensors 2020, 20, 7047. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).