Feature Activation through First Power Linear Unit with Sign
Abstract
:1. Introduction
2. Related Works
3. Proposed Method
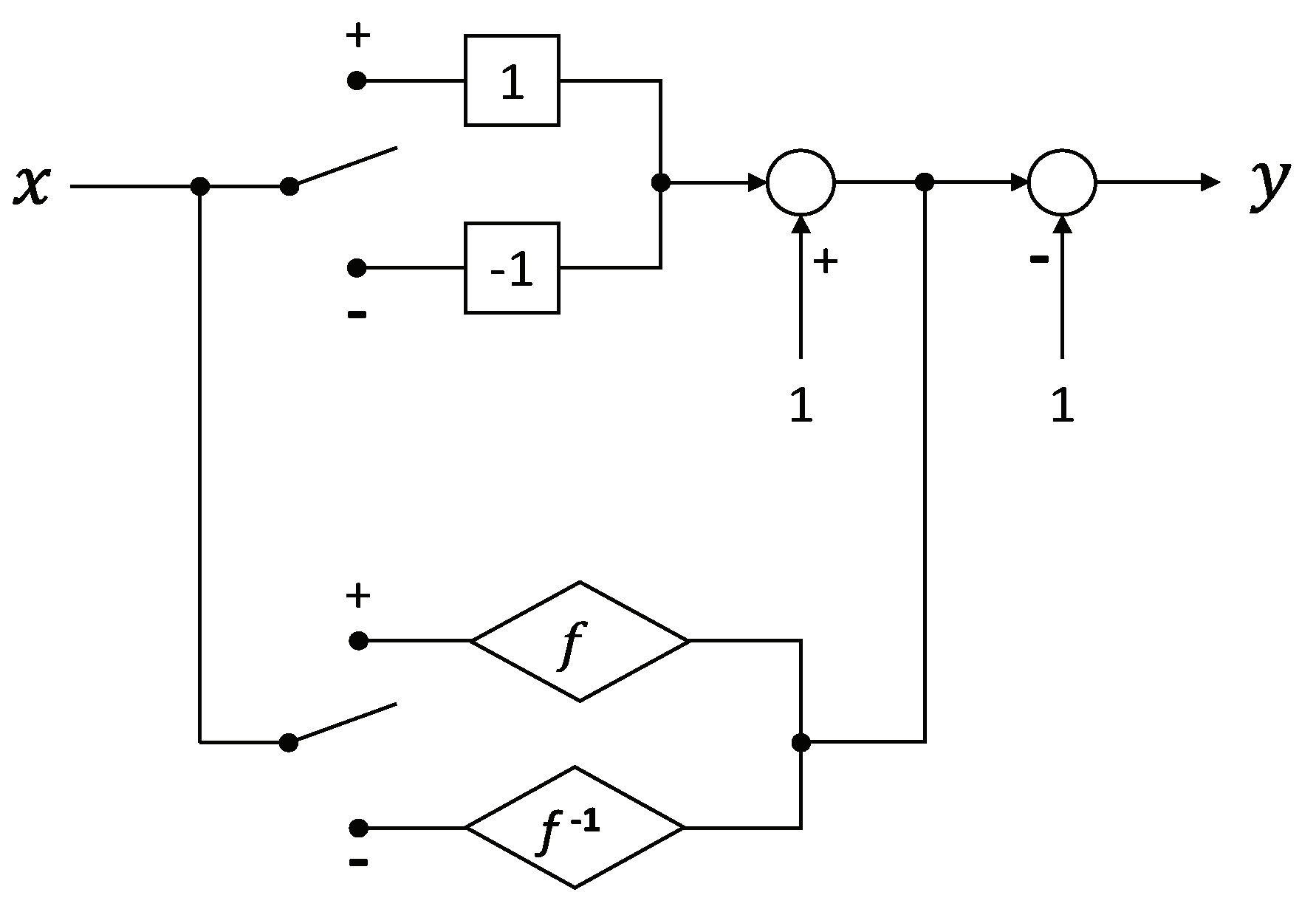
3.1. Source of Motivation
3.2. Derivation Process
- (I).
- Defined on the set of real numbers:
- (II).
- Through the origin of coordinate system:
- (III).
- Continuous at the demarcation point:
- (IV).
- Differentiable at the demarcation point:
- (V).
- Monotone increasing:
- (VI).
- Convex down:
- When , then subordinate condition (ii) is tenable.
- When , then subordinate condition (ii) is tenable.
4. Analysis of the Method
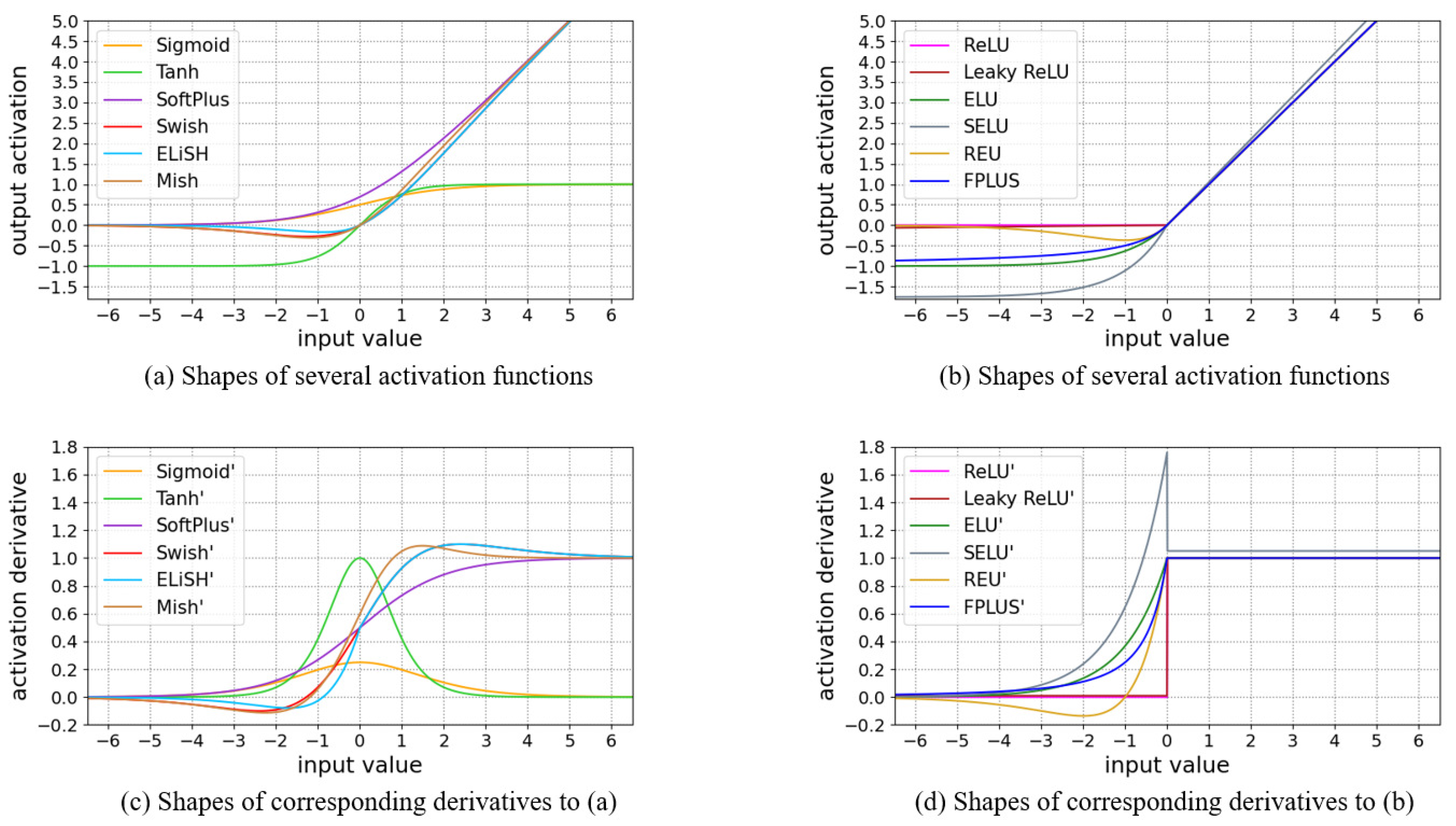
4.1. Characteristics and Attributes
- For positive zones, identity mapping is retained for the sake of avoiding the gradient vanishing problem.
- For negative zones, as the negative input deepens, the outcome will show a tendency to gradually reach saturation, which offers our method robustness to the noise.
- Entire outputs’ mean of the unit is close to zero, since the result yielded for negative input is not directly zero, but exists a relative minus response to neutralize the holistic activation, so that bias shift effect can be reduced.
- When bearing the corresponding formulation of the negative part processed in Taylor expansion, seen as Equation (43), the operation carried out in the negative domain is equivalent to dissociating each order component of the input signal received, and thus more abundant features might be attained up to a point.
- From an overall perspective, the shape of the function is unilateral inhibitive, and this kind of one-sided form could facilitate the introduction of sparsity to output nodes, making them similar to logical neurons.
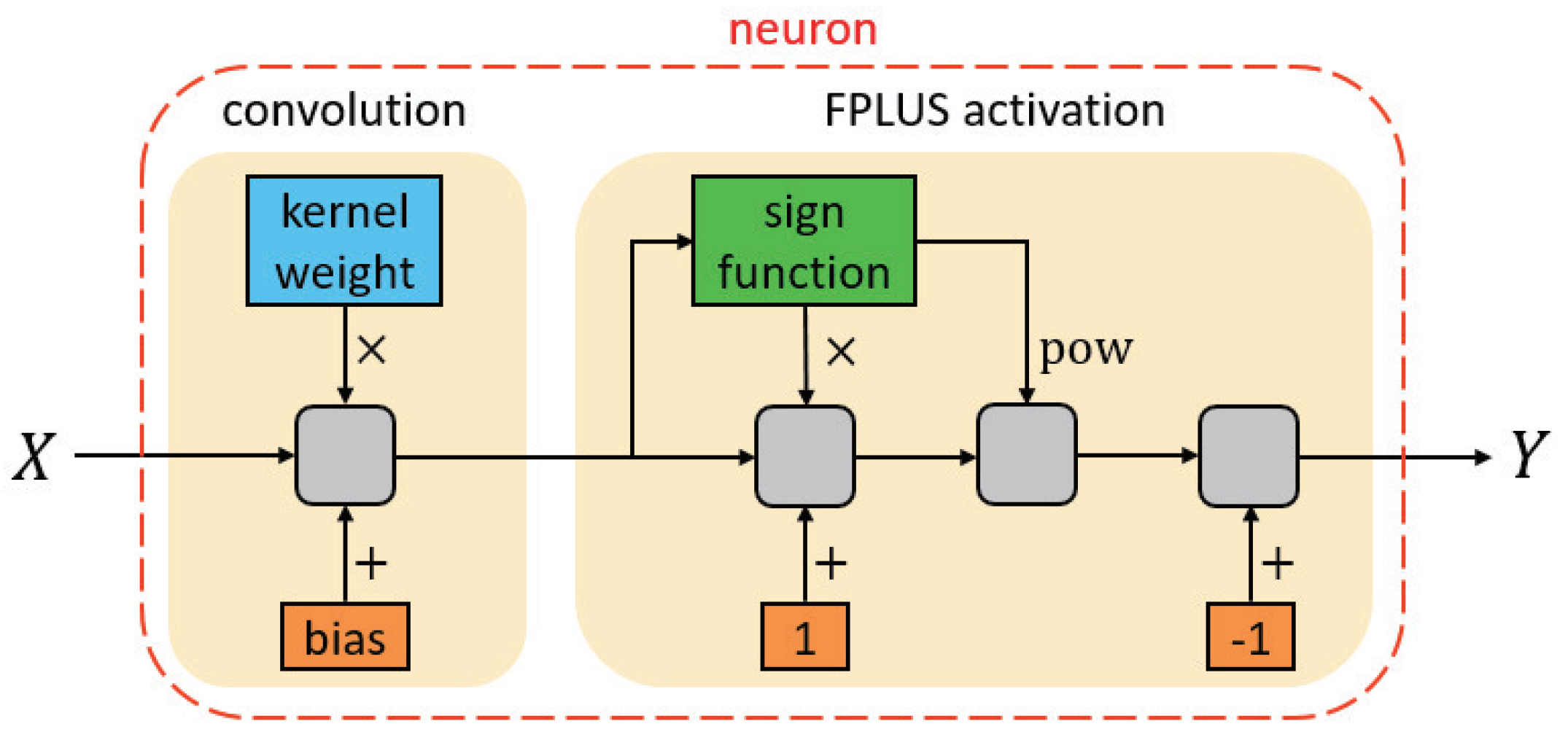
4.2. Implications and Examples
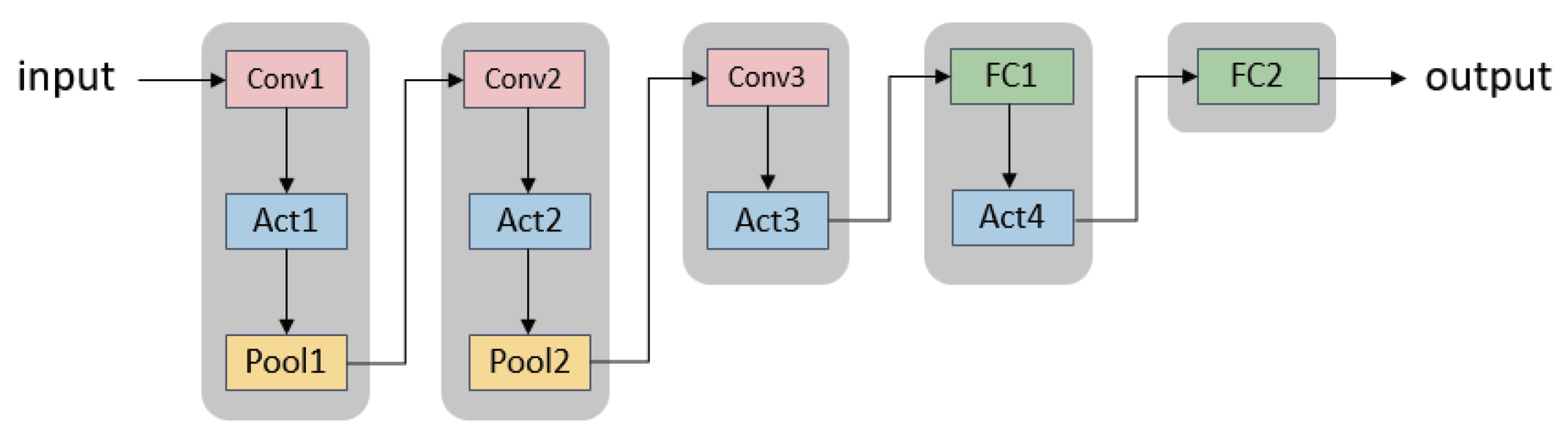
5. Experiments and Discussion
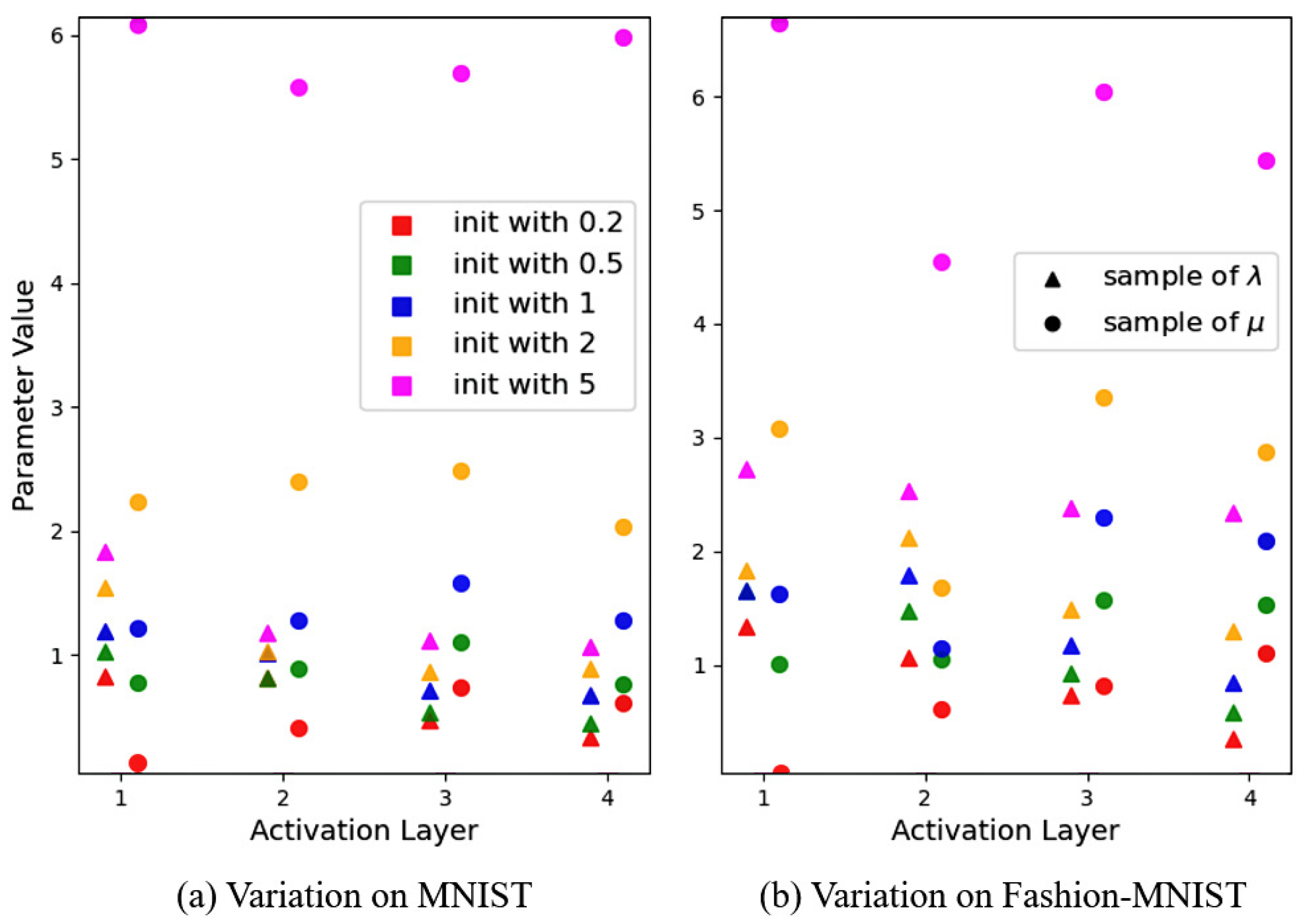
5.1. Influence of Two Alterable Factors and
5.2. Intuitive Features of Activation Effect
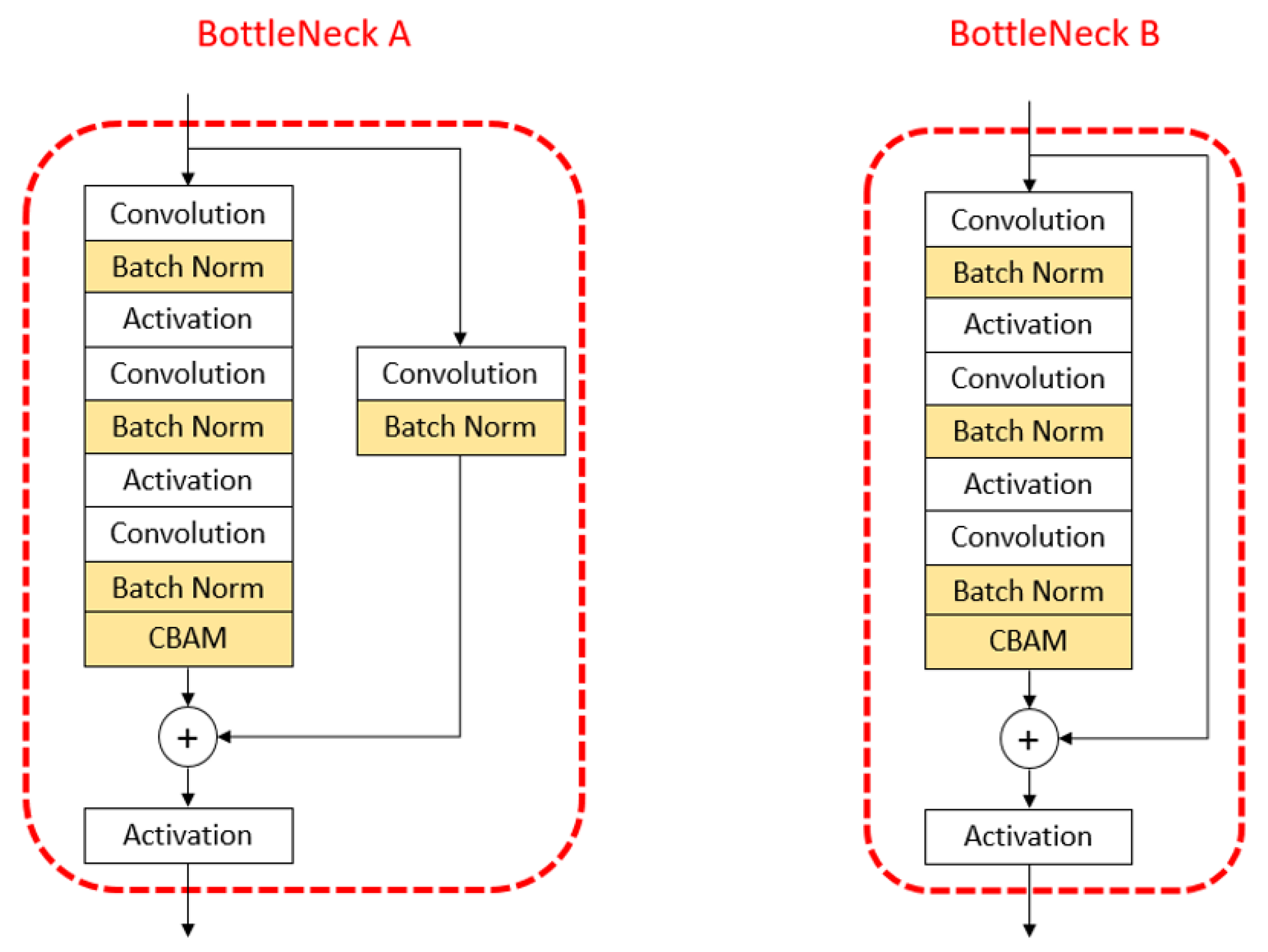
5.3. Explication of Robustness and Reliability
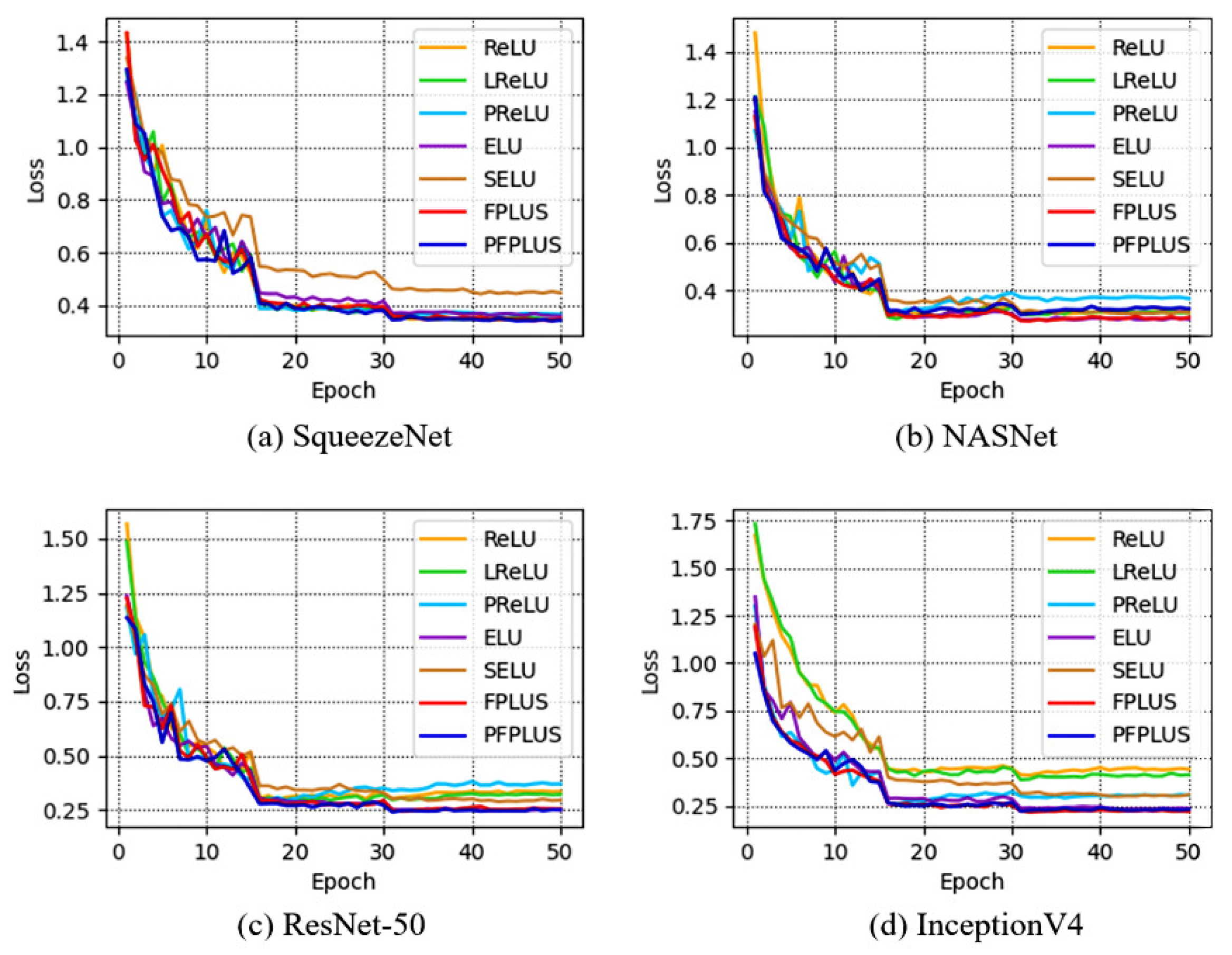
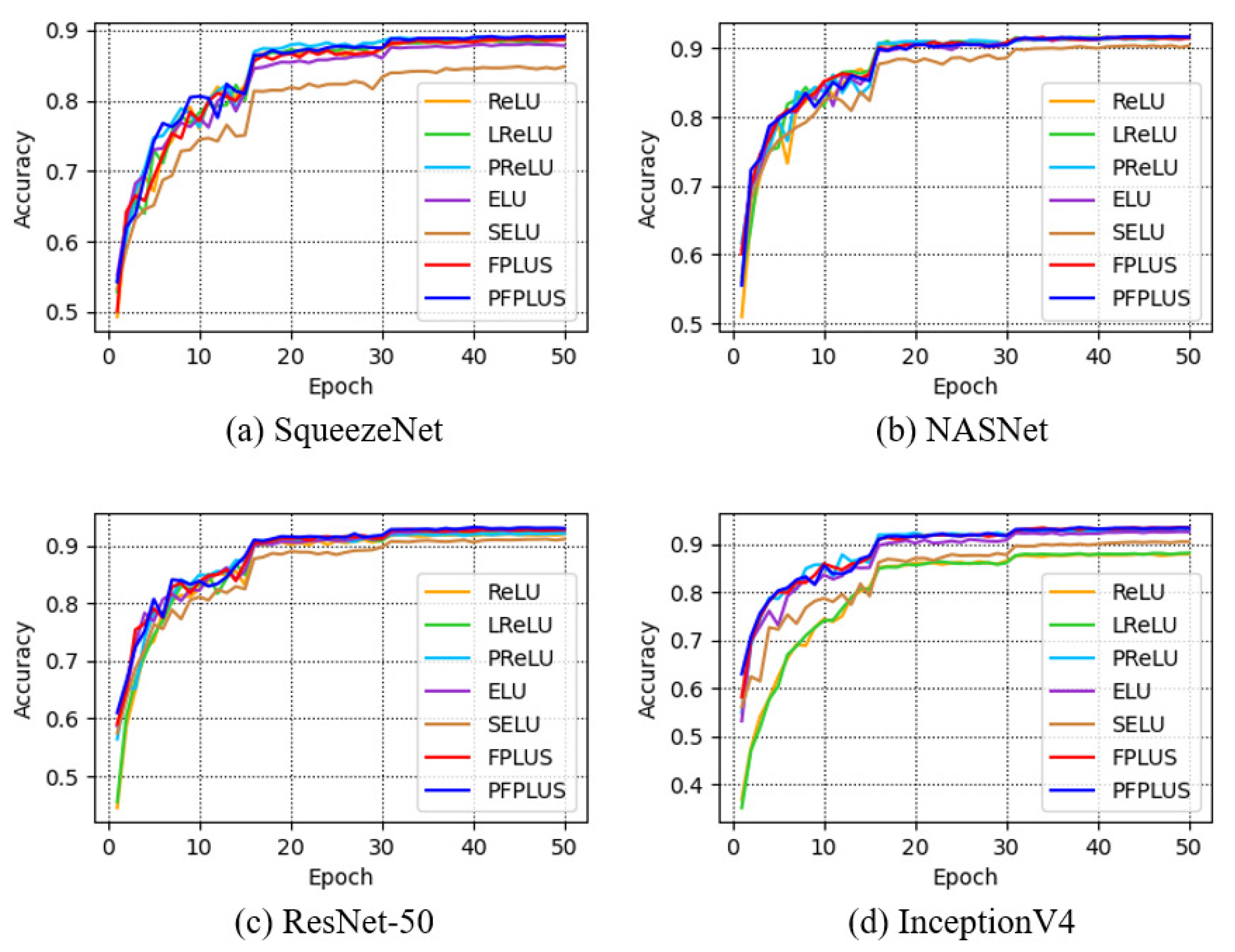
5.4. Comparison of Performance on CIFAR-10 & CIFAR-100
5.5. Experimental Results on ImageNet-ILSVRC2012
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1990, 52, 117. [Google Scholar] [CrossRef] [Green Version]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational & Mathematical Modeling of Neural Systems; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS), Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the 30 th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar] [CrossRef]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-Normalizing Neural Networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 972–981. [Google Scholar]
- Elfwing, S.; Uchibe, E.; Doya, K. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning. Neural Netw. 2018, 107, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Misra, D. Mish: A Self Regularized Non-Monotonic Neural Activation Function. arXiv 2019, arXiv:1908.08681v2. [Google Scholar]
- Goodfellow, I.; Warde-Farley, D.; Mirza, M.; Courville, A.; Bengio, Y. Maxout Networks. In Proceedings of the 30th International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Ma, N.; Zhang, X.; Liu, M.; Sun, J. Activate or Not: Learning Customized Activation. arXiv 2021, arXiv:2009.04759. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chen, B.; Wang, W.; Chen, L.C.; Tan, M.; Chu, G.; Vasudevan, V.; Zhu, Y.; Pang, R.; et al. Searching for MobileNetV3. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Courbariaux, M.; Bengio, Y.; David, J.P. BinaryConnect: Training Deep Neural Networks with Binary Weights during Propagations. arXiv 2015, arXiv:1511.00363. [Google Scholar] [CrossRef]
- Berradi, Y. Symmetric Power Activation Functions for Deep Neural Networks. In Proceedings of the International Conference on Learning and Optimization Algorithms: Theory and Applications, Rabat, Morocco, 2–5 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Gulcehre, C.; Moczulski, M.; Denil, M.; Bengio, Y. Noisy Activation Functions. arXiv 2016, arXiv:1603.00391. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef] [Green Version]
- Trottier, L.; Giguėre, P.; Chaib-draa, B. Parametric Exponential Linear Unit for Deep Convolutional Neural Networks. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 207–214. [Google Scholar] [CrossRef] [Green Version]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Lecun, Y.; Boser, B.; Denker, J.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Amari, S.I. Natural Gradient Works Efficiently in Learning. Neural Comput. 1999, 10, 251–276. [Google Scholar] [CrossRef]
- Attwell, D.; Laughlin, S.B. An Energy Budget for Signaling in the Grey Matter of the Brain. J. Cereb. Blood Flow Metab. 2001, 21, 1133–1145. [Google Scholar] [CrossRef] [PubMed]
- Lennie, P. The Cost of Cortical Computation. Curr. Biol. CB 2003, 13, 493–497. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar] [CrossRef]
- Shang, W.; Sohn, K.; Almeida, D.; Lee, H. Understanding and Improving Convolutional Neural Networks via Concatenated Rectified Linear Units. arXiv 2016, arXiv:1603.05201. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Sun, J. Funnel Activation for Visual Recognition. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, X.; Liu, M.; Chen, D.; Yuan, L.; Liu, Z. Dynamic ReLU. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020. [Google Scholar] [CrossRef]
- Barron, J.T. Continuously Differentiable Exponential Linear Units. arXiv 2017, arXiv:1704.07483. [Google Scholar]
- Zheng, Q.; Tan, D.; Wang, F. Improved Convolutional Neural Network Based on Fast Exponentially Linear Unit Activation Function. IEEE Access 2019, 7, 151359–151367. [Google Scholar]
- Basirat, M.; Roth, P.M. The Quest for the Golden Activation Function. arXiv 2018, arXiv:1808.00783. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Dugas, C.; Bengio, Y.; Bélisle, F.; Nadeau, C.; Garcia, R. Incorporating Second-Order Functional Knowledge for Better Option Pricing. In Proceedings of the 13th International Conference on Neural Information Processing Systems, Denver, CO, USA, 1 January 2000; pp. 451–457. [Google Scholar]
- Ying, Y.; Su, J.; Shan, P.; Miao, L.; Peng, S. Rectified Exponential Units for Convolutional Neural Networks. IEEE Access 2019, 7, 2169–3536. [Google Scholar] [CrossRef]
- Kiliarslan, S.; Celik, M. RSigELU: A nonlinear activation function for deep neural networks. Expert Syst. Appl. 2021, 174, 114805. [Google Scholar] [CrossRef]
- Pan, J.; Hu, Z.; Yin, S.; Li, M. GRU with Dual Attentions for Sensor-Based Human Activity Recognition. Electronics 2022, 11, 1797. [Google Scholar] [CrossRef]
- Tedesco, S.; Alfieri, D.; Perez-Valero, E.; Komaris, D.S.; Jordan, L.; Belcastro, M.; Barton, J.; Hennessy, L.; O’Flynn, B. A Wearable System for the Estimation of Performance-Related Metrics during Running and Jumping Tasks. Appl. Sci. 2021, 11, 5258. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive Fields of Single Neurons in the Cat’s Striate Cortex. J. Physiol. 1959, 148, 574–591. [Google Scholar] [CrossRef]
- Bhumbra, G.S. Deep learning improved by biological activation functions. arXiv 2018, arXiv:1804.11237. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q. Swish: A Self-Gated Activation Function. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Lecun, Y.; Bottou, L. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef] [Green Version]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar] [CrossRef]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning Transferable Architectures for Scalable Image Recognition. arXiv 2017, arXiv:1707.07012. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. arXiv 2016, arXiv:1602.07261. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef] [Green Version]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef] [Green Version]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer: Cham, Switzerland, 2018; Volume 11218. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]






| Dataset | Factor | Loss | Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.1 | 1 | 10 | 0.01 | 0.1 | 1 | 10 | |||
| MNIST | 0.01 | 1.573 | 1.485 | 1.441 | 1.534 | 39.93% | 43.85% | 44.89% | 41.20% | |
| 0.1 | 0.147 | 0.114 | 0.139 | 0.158 | 96.21% | 97.01% | 96.63% | 96.05% | ||
| 1 | 0.054 | 0.046 | 0.027 | 0.028 | 98.40% | 98.31% | 98.97% | 98.92% | ||
| 10 | 0.567 | 0.430 | 0.111 | 0.079 | 96.21% | 96.47% | 97.11% | 97.45% | ||
| Fashion-MNIST | 0.01 | 1.091 | 1.072 | 1.065 | 1.343 | 52.88% | 57.25% | 59.45% | 52.30% | |
| 0.1 | 0.630 | 0.568 | 0.534 | 0.579 | 76.49% | 78.84% | 79.87% | 77.97% | ||
| 1 | 0.309 | 0.307 | 0.253 | 0.267 | 87.75% | 88.18% | 89.62% | 88.98% | ||
| 10 | 0.496 | 0.636 | 0.371 | 0.341 | 83.49% | 84.99% | 86.53% | 86.71% | ||
| Architecture Configuration | Step Decay for lr | Exponential Decay for lr | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Loss | Testing Accuracy | Testing Loss | Testing Accuracy | |||||||
| BatchNorm | CBAM | Dropout | ReLU | FPLUS | ReLU | FPLUS | ReLU | FPLUS | ReLU | FPLUS |
| 0.674 | 0.484 | 75.24% | 83.18% | 1.098 | 0.822 | 55.39% | 66.95% | |||
| ✓ | 0.682 | 0.544 | 87.28% | 88.11% | 0.678 | 0.669 | 86.21% | 86.40% | ||
| ✓ | 0.802 | 0.551 | 69.98% | 80.19% | 1.335 | 1.133 | 44.25% | 55.75% | ||
| ✓ | 0.722 | 0.499 | 72.57% | 82.66% | 1.123 | 0.835 | 53.19% | 67.19% | ||
| ✓ | ✓ | 0.563 | 0.571 | 86.90% | 86.71% | 0.607 | 0.609 | 85.79% | 86.31% | |
| ✓ | ✓ | 0.846 | 0.490 | 87.08% | 87.44% | 0.683 | 0.684 | 86.03% | 86.51% | |
| ✓ | ✓ | 0.846 | 0.617 | 67.47% | 77.53% | 1.306 | 1.151 | 46.14% | 54.58% | |
| ✓ | ✓ | ✓ | 0.586 | 0.496 | 87.50% | 88.50% | 0.651 | 0.666 | 85.71% | 85.75% |
| Network | # Params | FLOPs |
|---|---|---|
| SqueezeNet [47] | 0.735 M | 0.054 G |
| NASNet [48] | 4.239 M | 0.673 G |
| ResNet-50 [43] | 23.521 M | 1.305 G |
| InceptionV4 [49] | 41.158 M | 7.521 G |
| Activation | SqueezeNet | NASNet | ResNet-50 | InceptionV4 |
|---|---|---|---|---|
| ReLU | 0.350 | 0.309 | 0.335 | 0.442 |
| LReLU | 0.345 | 0.307 | 0.322 | 0.412 |
| PReLU | 0.365 | 0.366 | 0.370 | 0.305 |
| ELU | 0.360 | 0.280 | 0.259 | 0.234 |
| SELU | 0.447 | 0.307 | 0.295 | 0.307 |
| FPLUS | 0.349 | 0.287 | 0.255 | 0.220 |
| PFPLUS | 0.344 | 0.323 | 0.251 | 0.230 |
| Activation | SqueezeNet | NASNet | ResNet-50 | InceptionV4 |
|---|---|---|---|---|
| ReLU | 88.67 | 91.55 | 91.94 | 87.95 |
| LReLU | 88.63 | 91.61 | 92.20 | 88.18 |
| PReLU | 88.91 | 91.52 | 92.09 | 92.95 |
| ELU | 87.82 | 91.70 | 92.71 | 92.59 |
| SELU | 84.83 | 90.35 | 91.10 | 90.53 |
| FPLUS | 88.70 | 91.46 | 92.75 | 93.47 |
| PFPLUS | 89.09 | 91.62 | 93.13 | 93.41 |
| Network | # Params | FLOPs |
|---|---|---|
| AlexNet [50] | 36.224 M | 201.056 M |
| GoogLeNet [51] | 6.403 M | 534.418 M |
| VGGNet-19 [52] | 39.328 M | 418.324 M |
| ResNet-101 [43] | 42.697 M | 2.520 G |
| DenseNet-121 [53] | 7.049 M | 898.225 M |
| Xception [54] | 21.014 M | 1.134 G |
| ShuffleNetV2 [55] | 1.361 M | 45.234 M |
| MobileNetV2 [56] | 2.369 M | 67.593 M |
| EfficientNetB0 [57] | 0.807 M | 2.432 M |
| Network | Top-1 Accuracy | Top-5 Accuracy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ReLU | ELU | Swish | Mish | FPLUS | PFPLUS | ReLU | ELU | Swish | Mish | FPLUS | PFPLUS | |
| AlexNet [50] | 59.73 | 65.84 | 51.99 | 61.30 | 66.28 | 66.08 | 85.19 | 89.14 | 79.21 | 86.19 | 89.14 | 89.07 |
| GoogLeNet [51] | 73.69 | 73.17 | 74.01 | 74.10 | 74.38 | 74.69 | 92.50 | 92.36 | 92.39 | 92.81 | 92.77 | 92.85 |
| VGGNet-19 [52] | 69.00 | 65.49 | 68.30 | 68.10 | 68.03 | 68.24 | 87.86 | 84.25 | 88.58 | 88.69 | 89.72 | 89.36 |
| ResNet-101 [43] | 74.42 | 74.99 | 74.48 | 74.97 | 75.20 | 75.51 | 93.06 | 93.18 | 92.57 | 93.13 | 93.29 | 93.26 |
| DenseNet-121 [53] | 74.74 | 72.77 | 75.36 | 75.16 | 73.72 | 74.63 | 92.59 | 93.20 | 93.30 | 93.28 | 93.32 | 93.30 |
| Xception [54] | 72.62 | 72.34 | 72.81 | 72.86 | 72.83 | 73.21 | 91.37 | 91.56 | 91.14 | 91.53 | 91.80 | 92.04 |
| ShuffleNetV2 [55] | 65.32 | 68.01 | 66.73 | 67.48 | 69.01 | 67.89 | 88.58 | 90.53 | 89.46 | 89.72 | 91.23 | 90.17 |
| MobileNetV2 [56] | 64.09 | 65.57 | 65.73 | 65.85 | 65.47 | 66.52 | 88.52 | 89.25 | 88.52 | 89.06 | 89.34 | 90.01 |
| EfficientNetB0 [57] | 62.33 | 63.62 | 63.20 | 63.45 | 64.40 | 64.31 | 86.72 | 88.20 | 85.97 | 86.81 | 88.61 | 89.02 |
| Activation Method | ReLU | ELU | FPLUS |
|---|---|---|---|
| Training Loss | 1.10 | 1.26 | 1.16 |
| Activation Method | Training Set | Validation Set | ||
|---|---|---|---|---|
| Top-1 Accuracy | Top-5 Accuracy | Top-1 Accuracy | Top-5 Accuracy | |
| ReLU | 73.98 | 90.76 | 73.55 | 91.37 |
| ELU | 70.23 | 88.01 | 72.15 | 90.36 |
| FPLUS | 72.20 | 89.23 | 73.64 | 91.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, B.; Yang, Y.; Dai, X. Feature Activation through First Power Linear Unit with Sign. Electronics 2022, 11, 1980. https://doi.org/10.3390/electronics11131980
Duan B, Yang Y, Dai X. Feature Activation through First Power Linear Unit with Sign. Electronics. 2022; 11(13):1980. https://doi.org/10.3390/electronics11131980
Chicago/Turabian StyleDuan, Boxi, Yufei Yang, and Xianhua Dai. 2022. "Feature Activation through First Power Linear Unit with Sign" Electronics 11, no. 13: 1980. https://doi.org/10.3390/electronics11131980
APA StyleDuan, B., Yang, Y., & Dai, X. (2022). Feature Activation through First Power Linear Unit with Sign. Electronics, 11(13), 1980. https://doi.org/10.3390/electronics11131980





