New Development in Quadratic
Abstract
:1. Introduction
| Notations | Descriptions |
| n-dimensional Euclidean space | |
| Identity matrix of size | |
| transpose of A | |
| trace of square matrix A | |
| W is symmetric and positive (negative) definite | |
| W is symmetric and non-negative (non-positive) definite | |
| expectation value of a random variable | |
| A is Hurwitz | all eigenvalues of A have negative real parts |
| SUSS | Switched uncertain stochastic systems |
| GQS-P (GAS-P) | globally quadratically (asymptotically) stable in probability |
| GQ-P | global quadratic performance in probability |
2. Preliminary Results and Problem Formulation
3. Convex Combination Based State-Dependent Switching Law
3.1. Design Condition and Switching Law
- Step 1
- Set the division number m of the interval as a moderate integer—for example, —and define .
- Step 2
- (1) choose from in ascending order; (2) fix and choose from in ascending order under the constraint ; (3) fix and choose from in ascending order under the constraint ; … (i) fix and choose from in ascending order under the constraint , and so on, until is chosen.
- Step 3
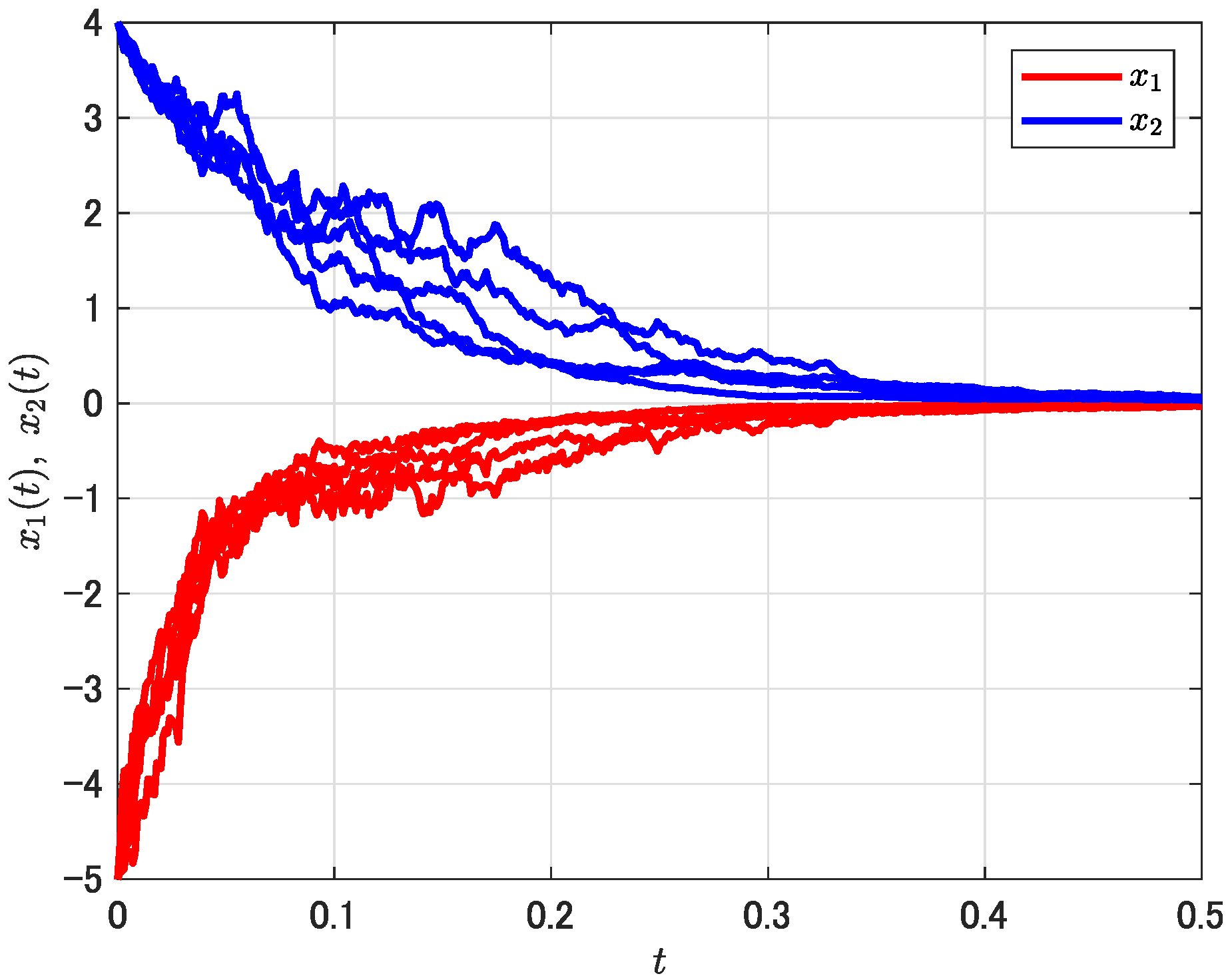
3.2. Numerical Example
4. State Feedback Controller Design
4.1. Controller Design
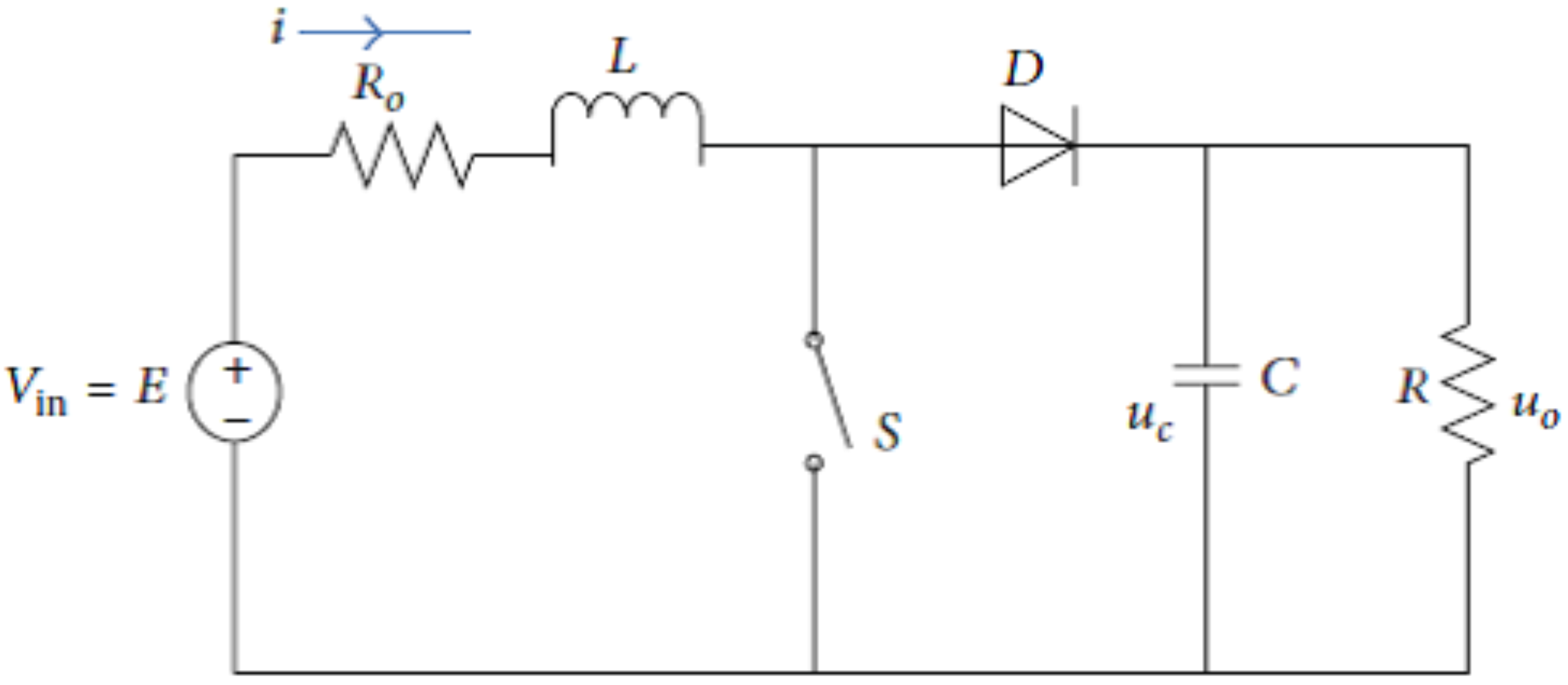
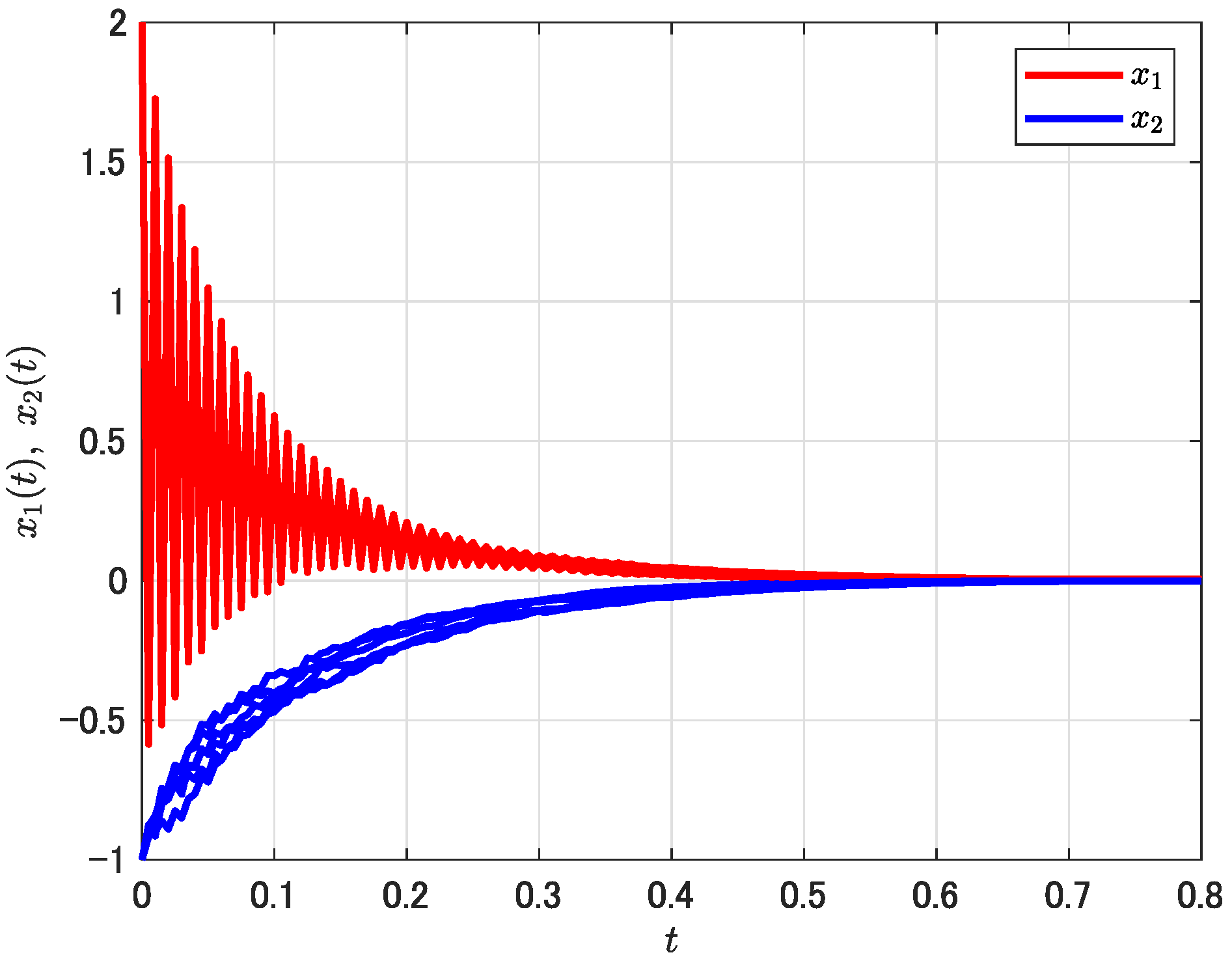
4.2. Application to Boost Converters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DeCarlo, R.; Branicky, M.S.; Pettersson, S.; Lennartson, B. Perspectives and results on the stability and stabilizability of hybrid systems. Proc. IEEE 2000, 88, 1069–1082. [Google Scholar] [CrossRef]
- Liberzon, D. Switching in Systems and Control; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Sun, Z.; Ge, S.S. Switched Linear Systems: Control and Design; Springer: London, UK, 2005. [Google Scholar]
- Zhai, G.; Hu, B.; Yasuda, K.; Michel, A.N. Disturbance attenuation properties of time-controlled switched systems. J. Frankl. Inst. 2001, 338, 765–779. [Google Scholar] [CrossRef]
- Chatterjee, D.; Liberzon, D. Stability analysis of deterministic and stochastic switched systems via a comparison principle and multiple Lyapunov functions. Siam J. Control. Optim. 2006, 45, 174–206. [Google Scholar] [CrossRef]
- Shorten, R.; Wirth, F.; Mason, O.; Wulff, K.; King, C. Stability criteria for switched and hybrid systems. Siam Rev. 2007, 49, 545–592. [Google Scholar] [CrossRef] [Green Version]
- Alwan, M.S.; Liu, X. Recent results on stochastic hybrid dynamical systems. J. Control. Decision 2016, 3, 68–103. [Google Scholar] [CrossRef]
- Wicks, M.A.; Peleties, P.; DeCarlo, R.A. Switched controller synthesis for the quadratic stabilization of a pair of unstable linear systems. Eur. J. Control. 1998, 4, 140–147. [Google Scholar] [CrossRef]
- Feron, E. Quadratic Stabilizability of Switched System via State and Output Feedback; MIT Technical Report CICS-P-468; Massachusetts Institute of Technology: Cambridge, MA, USA, 1996. [Google Scholar]
- Zhai, G.; Lin, H.; Antsaklis, P.J. Quadratic stabilizability of switched linear systems with polytopic uncertainties. Int. J. Control. 2003, 76, 747–753. [Google Scholar] [CrossRef]
- Zhao, J.; Dimirovski, G.M. Quadratic stability of a class of switched nonlinear systems. IEEE Trans. Autom. Control. 2004, 49, 574–578. [Google Scholar] [CrossRef] [Green Version]
- Ji, Z.; Wang, L.; Xie, G. Quadratic stabilization of switched systems. Int. J. Syst. Sci. 2005, 36, 395–404. [Google Scholar] [CrossRef]
- Chang, Y.; Zhai, G.; Fu, B.; Xiong, L. Quadratic stabilization of switched uncertain linear systems: A convex combination approach. IEEE/CAA J. Autom. Sin. 2019, 6, 1116–1126. [Google Scholar] [CrossRef]
- Huang, C.; Zhai, G.; Li, W. Quadratic performance analysis of switched affine time-varying systems. Int. J. Appl. Math. Comput. Sci. 2018, 28, 429–440. [Google Scholar]
- Chang, Y.; Zhai, G.; Fu, B.; Xiong, L. Stabilization of switched linear uncertain stochastic systems. In Proceedings of the 38th Chinese Control Conference (CCC2019), Guangzhou, China, 27–30 July 2019; pp. 1784–1788. [Google Scholar]
- Chang, Y.; Zhai, G.; Xiong, L.; Fu, B. Output-dependent switching laws for quadratic stabilization of switched linear stochastic systems. In Proceedings of the 32nd Chinese Control and Decision Conference (CCDC2020), Hefei, China, 22–24 August 2020; pp. 1796–1801. [Google Scholar]
- Åström, K.J. Introduction to Stochastic Control Theory; Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Chen, G.; Chen, G.; Hsu, S. Linear Stochastic Control Systems; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Petersen, I.R. A stabilization algorithm for a class of uncertain linear systems. Syst. Control. Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- Morse, A.S. Supervisory control of families of linear set-point controllers-Part 1: Exact matching. IEEE Trans. Autom. Control. 1996, 41, 1413–1431. [Google Scholar] [CrossRef]
- Hespanha, J.P.; Morse, A.S. Stability of switched systems with average dwell-time. In Proceedings of the 38th IEEE Conference on Decision & Control, Phoenix, AZ, USA, 7–10 December 1999; pp. 2655–2660. [Google Scholar]
- Zhai, G.; Hu, B.; Yasuda, K.; Michel, A.N. Stability analysis of switched systems with stable and unstable subsystems: An average dwell time approach. Int. J. Syst. Sci. 2001, 32, 1055–1061. [Google Scholar] [CrossRef]
- Branicky, M.S. Multiple Lyapunov functions and other analysis tools for switched and hybrid systems. IEEE Trans. Autom. Control. 1998, 43, 475–482. [Google Scholar] [CrossRef] [Green Version]
- Zhai, G.; Hu, B.; Yasuda, K.; Michel, A.N. Piecewise Lyapunov functions for switched systems with average dwell time. Asian J. Control. 2000, 2, 192–197. [Google Scholar] [CrossRef]
- Xiong, L.; Zhong, S.; Ye, M.; Wu, S. New stability and stabilization for switched neutral control systems. Chaos Solitons Fractals 2009, 42, 1800–1811. [Google Scholar] [CrossRef]
- Yang, Y.; Karimi, H.R.; Xiang, Z. Robust H∞ switching rule design for boost converters with uncertain parameters and disturbances. Abstr. Appl. Anal. 2013, 2013, 7. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Wang, J.; Zhao, J. Stability and robust stability of switched positive linear systems with all modes unstable. IEEE/CAA J. Autom. Sin. 2019, 6, 167–176. [Google Scholar] [CrossRef]
- Deaecto, G.S.; Geromel, J.C.; Garcia, F.S.; Pomilio, J.A. Switched affine systems control design with application to DC-DC converters. IET Control. Theory Appl. 2010, 4, 1201–1210. [Google Scholar] [CrossRef]
- Xiao, M.; Zhai, G.; Huang, C. Quadratic stabilisation of switched affine systems. J. Control. Decis. 2020, 7, 1–23. [Google Scholar] [CrossRef]
- Deaecto, G.S.; Geromel, J.C.; Daafouz, J. Dynamic output feedback H∞ control of switched linear systems. Automatica 2011, 47, 1713–1720. [Google Scholar] [CrossRef]
- Su, Q.; Fan, Z.; Li, J. Observer-based fault detection for switched systems with all unstable subsystems. J. Control. Decis. 2021, 8, 116–123. [Google Scholar] [CrossRef]
- Qi, Y.; Zeng, P.; Bao, W. Event-triggered and self-triggered H∞ control of uncertain switched linear systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1442–1454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Zhai, G.; Xiong, L.; Fu, B.
New Development in Quadratic
Chang Y, Zhai G, Xiong L, Fu B.
New Development in Quadratic
Chang, Yufang, Guisheng Zhai, Lianglin Xiong, and Bo Fu.
2022. "New Development in Quadratic
Chang, Y., Zhai, G., Xiong, L., & Fu, B.
(2022). New Development in Quadratic





