Investigation of Near-Field Source Localization Using Uniform Rectangular Array
Abstract
:1. Introduction
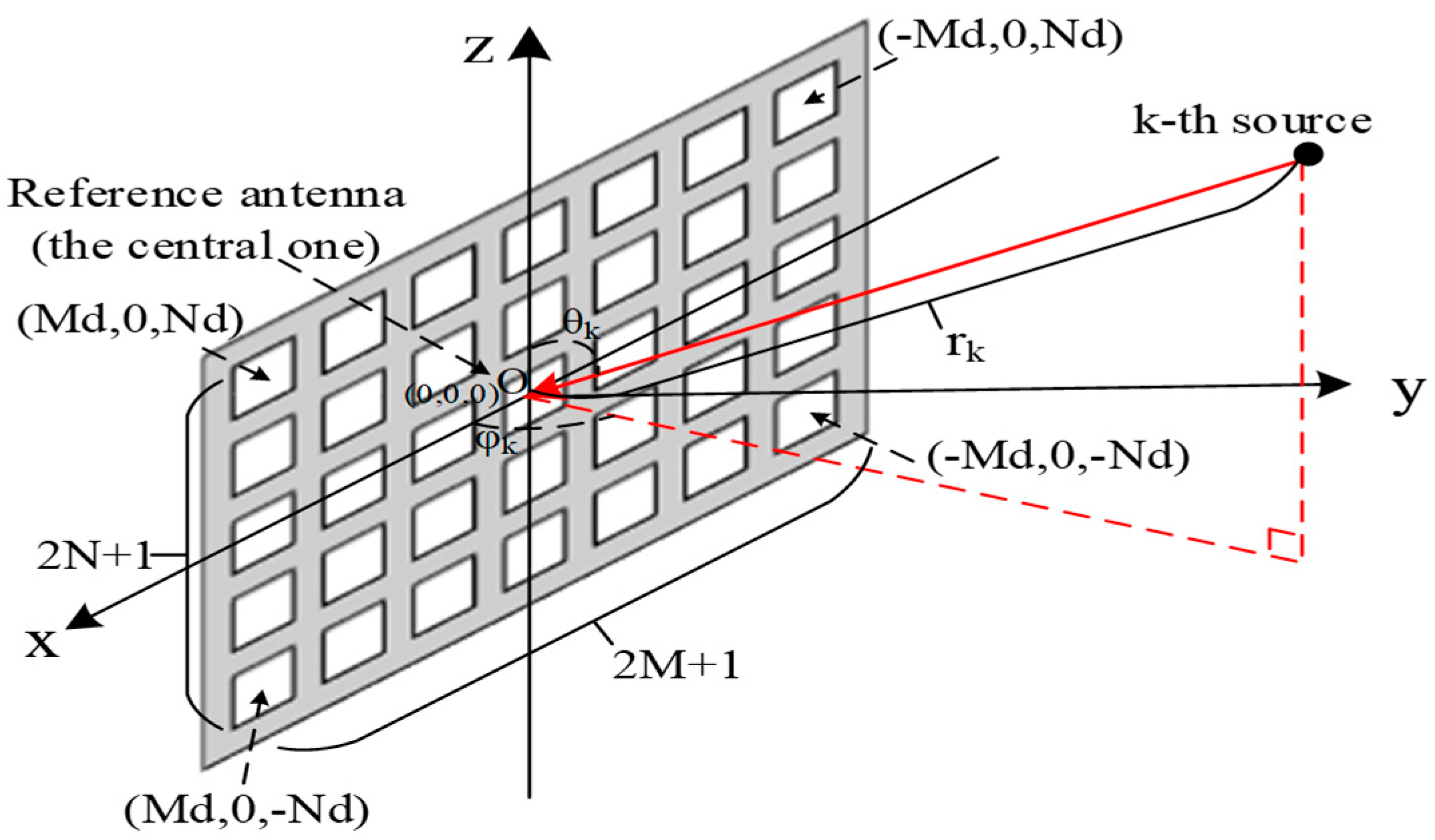
2. Near-Field Signal Model
3. Deterministic Maximum Likelihood Estimation
4. Parameter Sequential Updating Strategy Based on SAGE
5. Performance Analysis
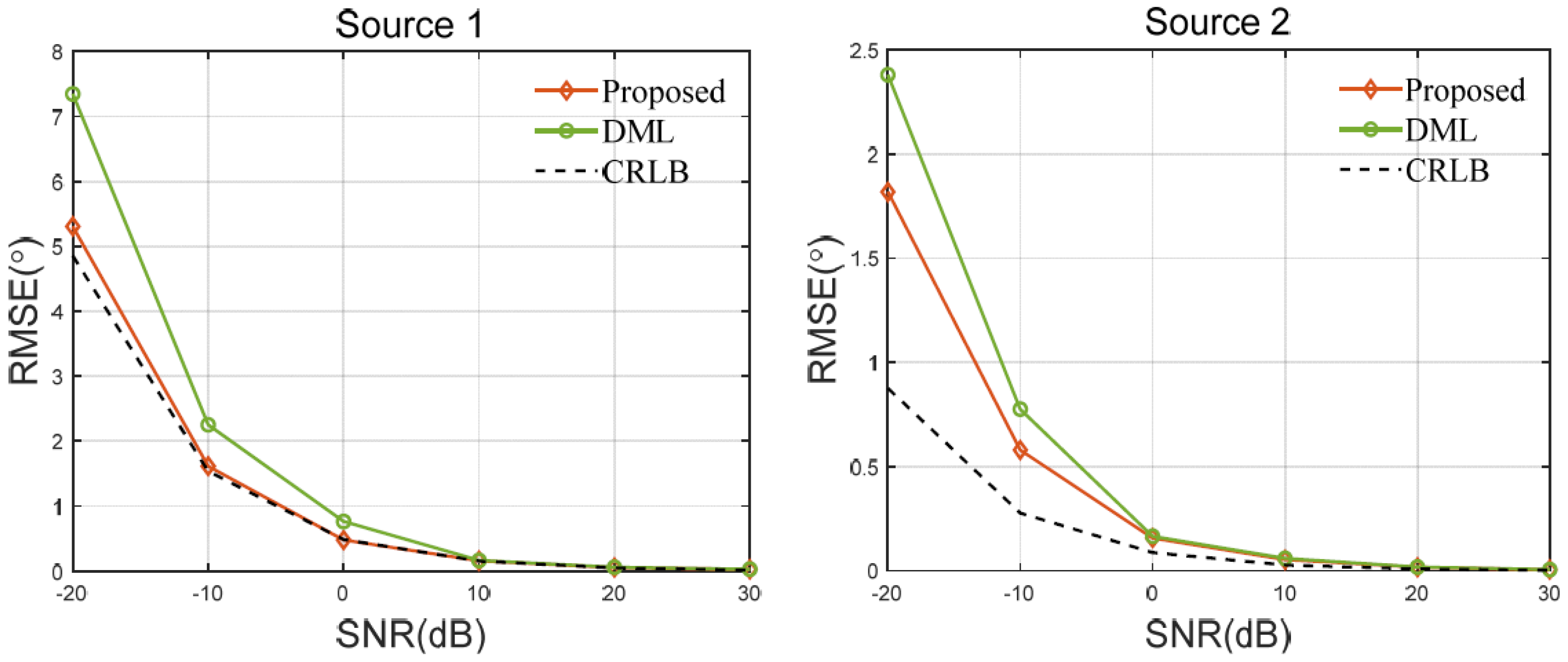
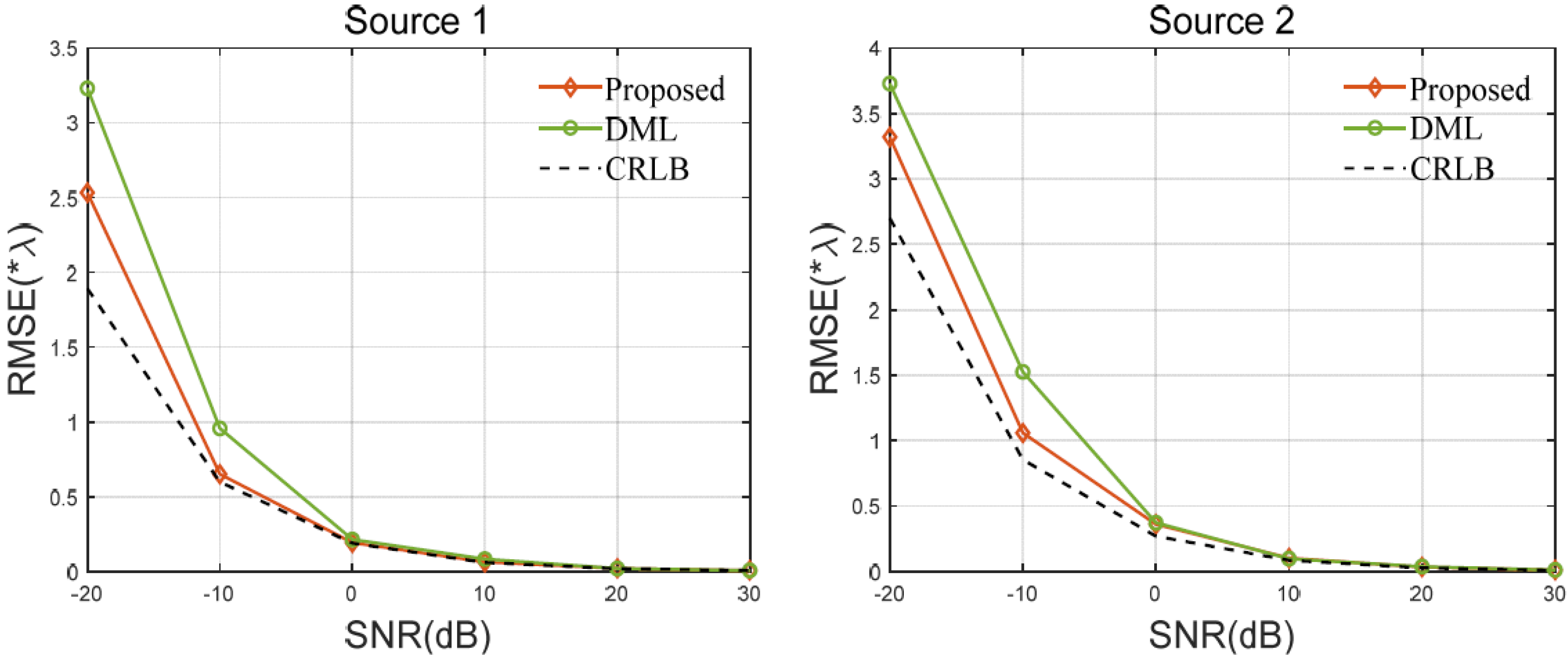
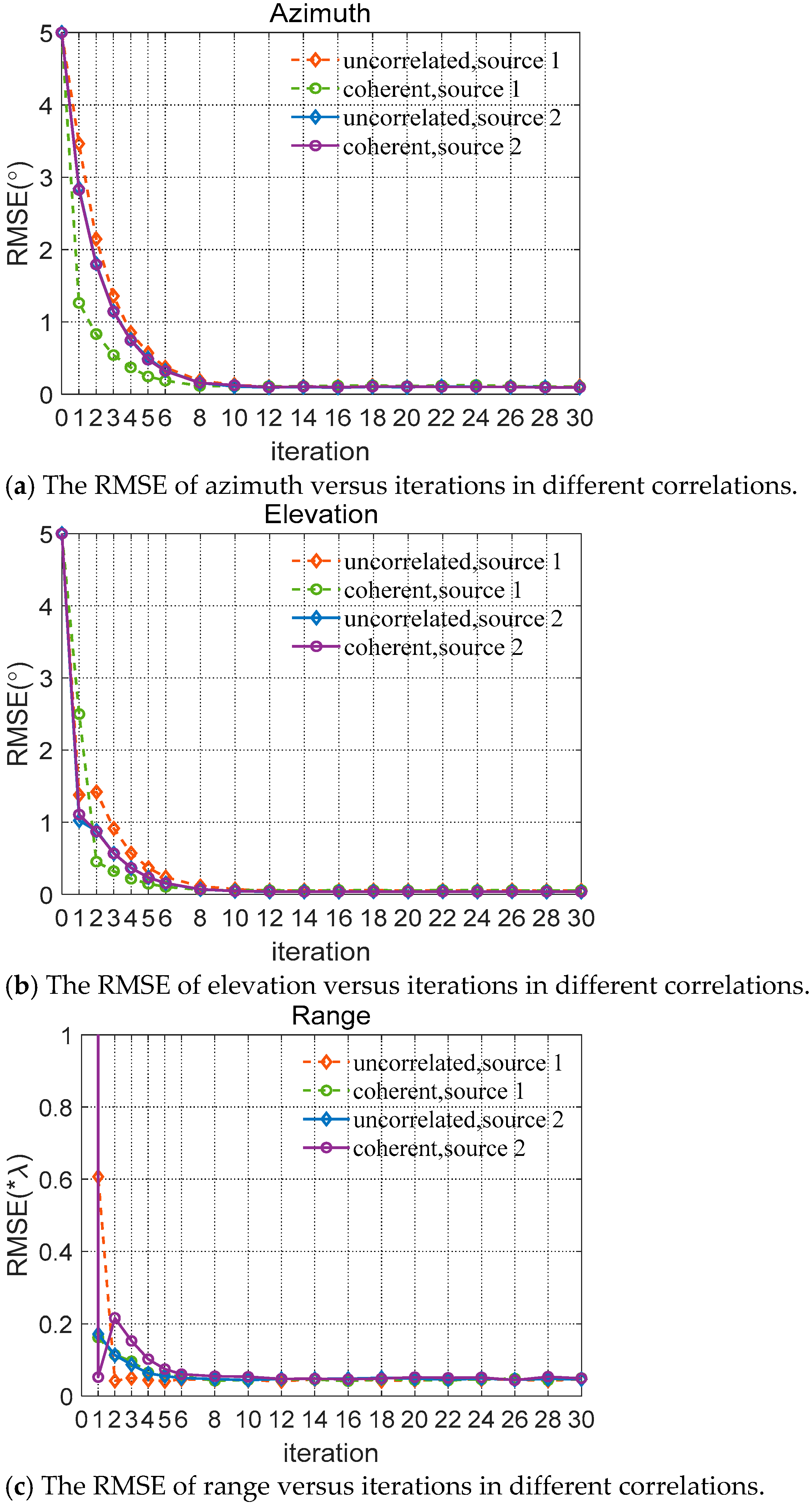
5.1. Simulation Results
5.2. Computational Complexity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, X.; Zhang, F.; Wang, B.; Liu, K.J.R. Massive MIMO for High-Accuracy Target Localization and Tracking. IEEE Internet Things J. 2021, 8, 10131–10145. [Google Scholar] [CrossRef]
- Wang, W.; Chen, H.; Jin, J.; Wang, X.; Wan, L.; Zhang, X. Quaternion-MUSIC for near-field strictly noncircular sources with large-scale polarization array. Digit. Signal Process. 2019, 94, 137–145. [Google Scholar] [CrossRef]
- Garcia, N.; Wymeersch, H.; Larsson, E.G.; Haimovich, A.M.; Coulon, M. Direct Localization for Massive MIMO. IEEE Trans. Signal Process. 2017, 65, 2475–2487. [Google Scholar] [CrossRef] [Green Version]
- Mestre, X.; Vallet, P. On the Resolution Probability of Conditional and Unconditional Maximum Likelihood DoA Estimation. IEEE Trans. Signal Process. 2020, 68, 4656–4671. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood and Cramer-Rao bound: Further results and comparisons. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 23–26 May 1989; pp. 2605–2608. [Google Scholar] [CrossRef]
- Miller, M.; Fuhrmann, D. Maximum-likelihood narrow-band direction finding and the EM algorithm. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1560–1577. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Wagner, M.; Park, Y.; Gerstoft, P. Gridless DOA Estimation and Root-MUSIC for Non-Uniform Linear Arrays. IEEE Trans. Signal Process. 2021, 69, 2144–2157. [Google Scholar] [CrossRef]
- Ziskind, M. Wax, ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xu, X.; Chen, Z.; Bao, M.; Zhang, X.-P.; Yang, J. High-Resolution DOA Estimation Algorithm for a Single Acoustic Vector Sensor at Low SNR. IEEE Trans. Signal Process. 2020, 68, 6142–6158. [Google Scholar] [CrossRef]
- Grosicki, E.; Abed-Meraim, K.; Hua, Y. A weighted linear prediction method for near-field source localization. IEEE Trans. Signal Process. 2005, 53, 3651–3660. [Google Scholar] [CrossRef]
- Weiss, A.J.; Amar, A. Direct Position Determination of Multiple Radio Signals. EURASIP J. Adv. Signal Process. 2005, 2005, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Han, Y.; Jin, M.; Li, X.-S. An Improved ESPRIT-Like Algorithm for Coherent Signals DOA Estimation. IEEE Commun. Lett. 2020, 24, 339–343. [Google Scholar] [CrossRef]
- Tirer, T.; Weiss, A.J. High Resolution Direct Position Determination of Radio Frequency Sources. IEEE Signal Process. Lett. 2015, 23, 192–196. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Shongwe, T. Direction-of-Arrival Estimation of Electromagnetic Wave Impinging on Spherical Antenna Array in the Presence of Mutual Coupling Using a Multiple Signal Classification Method. Electronics 2021, 10, 2651. [Google Scholar] [CrossRef]
- Satish, A.; Kashyap, R. Maximum likelihood estimation and Cramer-Rao bounds for direction of arrival parameters of a large sensor array. IEEE Trans. Antennas Propag. 1996, 44, 478–491. [Google Scholar] [CrossRef]
- Yan, F.; Jin, M.; Qiao, X. Low-Complexity DOA Estimation Based on Compressed MUSIC and Its Performance Analysis. IEEE Trans. Signal Process. 2013, 61, 1915–1930. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, X.; Li, Y.; Deng, Z.; Huang, Y. On Spatial Smoothing for DOA Estimation of 2D Coherently Distributed Sources with Double Parallel Linear Arrays. Electronics 2019, 8, 354. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.-S.; Jin, Y.; Lee, J.; Kim, S. Low-Complexity MUSIC-Based Direction-of-Arrival Detection Algorithm for Frequency-Modulated Continuous-Wave Vital Radar. Sensors 2020, 20, 4295. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Y.; He, L.; Wu, J. Low-Complexity Deep-Learning-Based DOA Estimation for Hybrid Massive MIMO Systems with Uniform Circular Arrays. IEEE Wirel. Commun. Lett. 2019, 9, 83–86. [Google Scholar] [CrossRef]
- Li, J.; Ai, B.; He, R.; Yang, M.; Zhong, Z.; Hao, Y.; Shi, G. On 3D Cluster-Based Channel Modeling for Large-Scale Array Communications. IEEE Trans. Wirel. Commun. 2019, 18, 4902–4914. [Google Scholar] [CrossRef]
- Huang, J.; Wang, C.-X.; Feng, R.; Sun, J.; Zhang, W.; Yang, Y. Multi-Frequency mmWave Massive MIMO Channel Measurements and Characterization for 5G Wireless Communication Systems. IEEE J. Sel. Areas Commun. 2017, 35, 1591–1605. [Google Scholar] [CrossRef]
- Hu, Z.; Ji, W.; Zhao, H.; Zhai, X.; Saleem, A.; Zheng, G. Channel Measurement for Multiple Frequency Bands in Subway Tunnel Scenario. Int. J. Antennas Propag. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Pu, X.; Shao, S.; Deng, K.; Tang, Y. Analysis of the Capacity Statistics for 2×2 3D MIMO Channels in Short-Range Communications. IEEE Commun. Lett. 2015, 19, 219–222. [Google Scholar] [CrossRef]
- Cirpan, H.A.; Cekli, E. Deterministic Maximum likelihood Approach for Localization of Near-field Sources. AEU Int. J. Electron. Commun. 2002, 56, 1–10. [Google Scholar] [CrossRef]
- Yang, D.-S.; Shi, J.; Liu, B.-S. A new near-field source localization algorithm based on generalized ESPRIT. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 1115–1120. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, W.; Zheng, W.; Xia, Z.; Wang, Y. Localization of Near-Field Sources: A Reduced-Dimension MUSIC Algorithm. IEEE Commun. Lett. 2018, 22, 1422–1425. [Google Scholar] [CrossRef]
- Cao, Y.; Lv, T.; Lin, Z.; Huang, P.; Lin, F. Complex ResNet Aided DoA Estimation for Near-Field MIMO Systems. IEEE Trans. Veh. Technol. 2020, 69, 11139–11151. [Google Scholar] [CrossRef]
- Pan, J.; Raj, S.P.; Men, S. A search-free near-field source localization method with exact signal model. J. Syst. Eng. Electron. 2021, 32, 756–763. [Google Scholar] [CrossRef]
- Chen, G.; Zeng, X.; Jiao, S.; Yu, Y.A.; Luo, Q. High Accuracy Near-Field Localization Algorithm at Low SNR Using Fourth-Order Cumulant. IEEE Commun. Lett. 2020, 24, 553–557. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Le Bastard, C.; Wu, Z.; Men, S. Low-Complexity High-Order Propagator Method for Near-Field Source Localization. Sensors 2018, 19, 54. [Google Scholar] [CrossRef] [Green Version]
- Fleury, B.; Tschudin, M.; Heddergott, R.; Dahlhaus, D.; Pedersen, K.I. Channel parameter estimation in mobile radio environments using the SAGE algorithm. IEEE J. Sel. Areas Commun. 1999, 17, 434–450. [Google Scholar] [CrossRef]
- Yau, S.F.; Bresler, Y. Maximum likelihood parameter estimation of superimposed signals by dynamic programming. IEEE Trans. Signal Process. 1993, 41, 804–820. [Google Scholar] [CrossRef]
- Friedlander, B. Localization of Signals in the Near-Field of an Antenna Array. IEEE Trans. Signal Process. 2019, 67, 3885–3893. [Google Scholar] [CrossRef]
- Shu, T.; Li, L.; He, J. Near-Field Source Localization with Two-Level Nested Arrays. IEEE Commun. Lett. 2020, 24, 2488–2492. [Google Scholar] [CrossRef]
- Yau, S.F.; Bresler, Y. A compact Cramer-Rao bound expression for parametric estimation of superimposed signals. IEEE Trans. Signal Process. 1992, 40, 1226–1230. [Google Scholar] [CrossRef]
- Key, S.M. Fundamentals of Statistical Processing, Volume I: Estimation Theory; PTR Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]



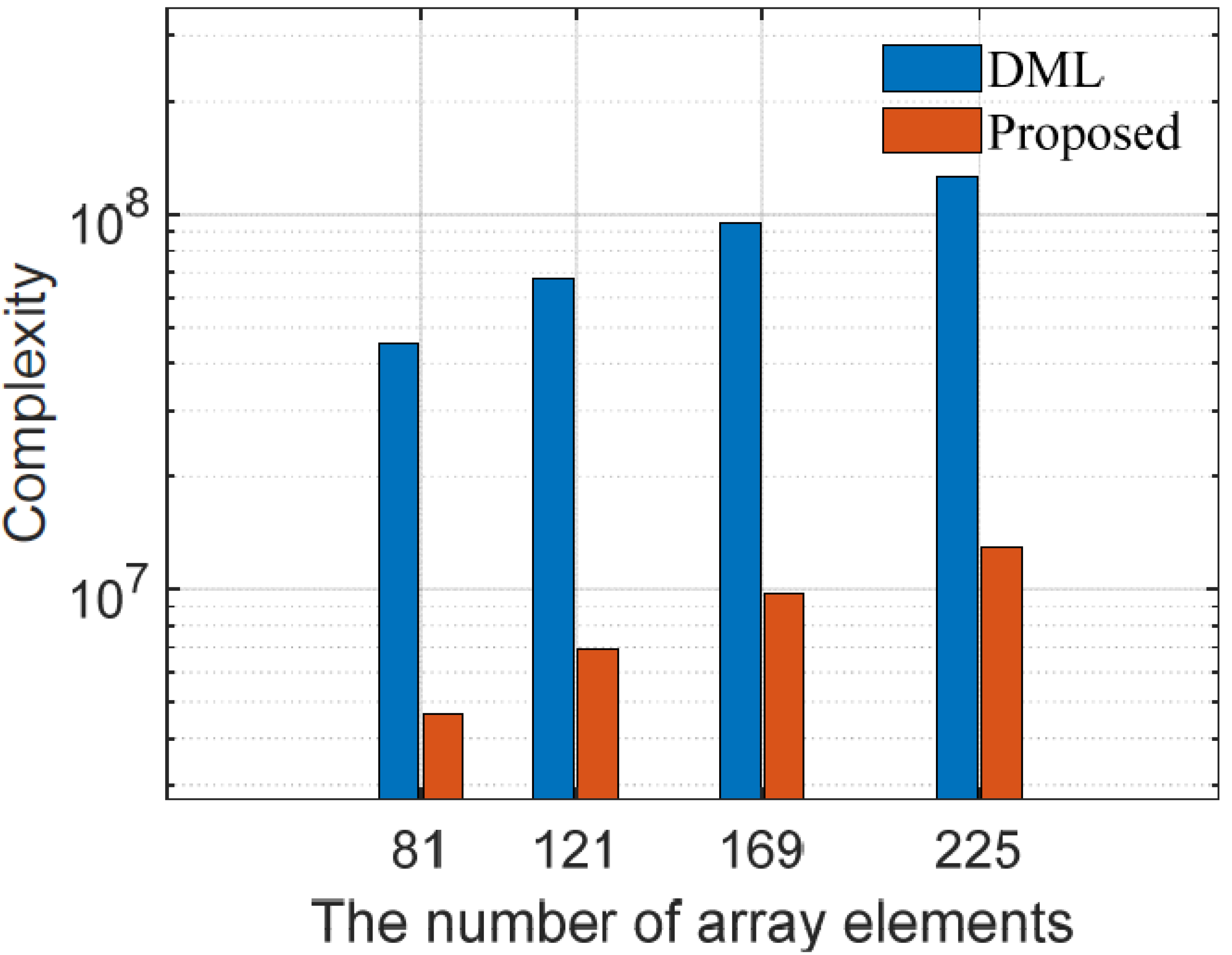
| Algorithm | Complexity |
|---|---|
| DML | |
| Proposed |
| Search Steep | Time Consumption (s) | |
|---|---|---|
| DML | Proposed | |
| 1478.2000 | 0.5362 | |
| 381.7101 | 0.4322 | |
| 1087.2000 | 0.3769 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, F.; Zhao, H.; Zhao, X.; Wang, X.; Saleem, A.; Zheng, G. Investigation of Near-Field Source Localization Using Uniform Rectangular Array. Electronics 2022, 11, 1916. https://doi.org/10.3390/electronics11121916
Lu F, Zhao H, Zhao X, Wang X, Saleem A, Zheng G. Investigation of Near-Field Source Localization Using Uniform Rectangular Array. Electronics. 2022; 11(12):1916. https://doi.org/10.3390/electronics11121916
Chicago/Turabian StyleLu, Fan, Hengkai Zhao, Xiaorong Zhao, Xiaoyong Wang, Asad Saleem, and Guoxin Zheng. 2022. "Investigation of Near-Field Source Localization Using Uniform Rectangular Array" Electronics 11, no. 12: 1916. https://doi.org/10.3390/electronics11121916
APA StyleLu, F., Zhao, H., Zhao, X., Wang, X., Saleem, A., & Zheng, G. (2022). Investigation of Near-Field Source Localization Using Uniform Rectangular Array. Electronics, 11(12), 1916. https://doi.org/10.3390/electronics11121916







