Numerical Study on Multiple Arcs in a Pyro-Breaker Based on the Black-Box Arc Model
Abstract
:1. Introduction
2. Numerical Analysis of the Driving Mechanism
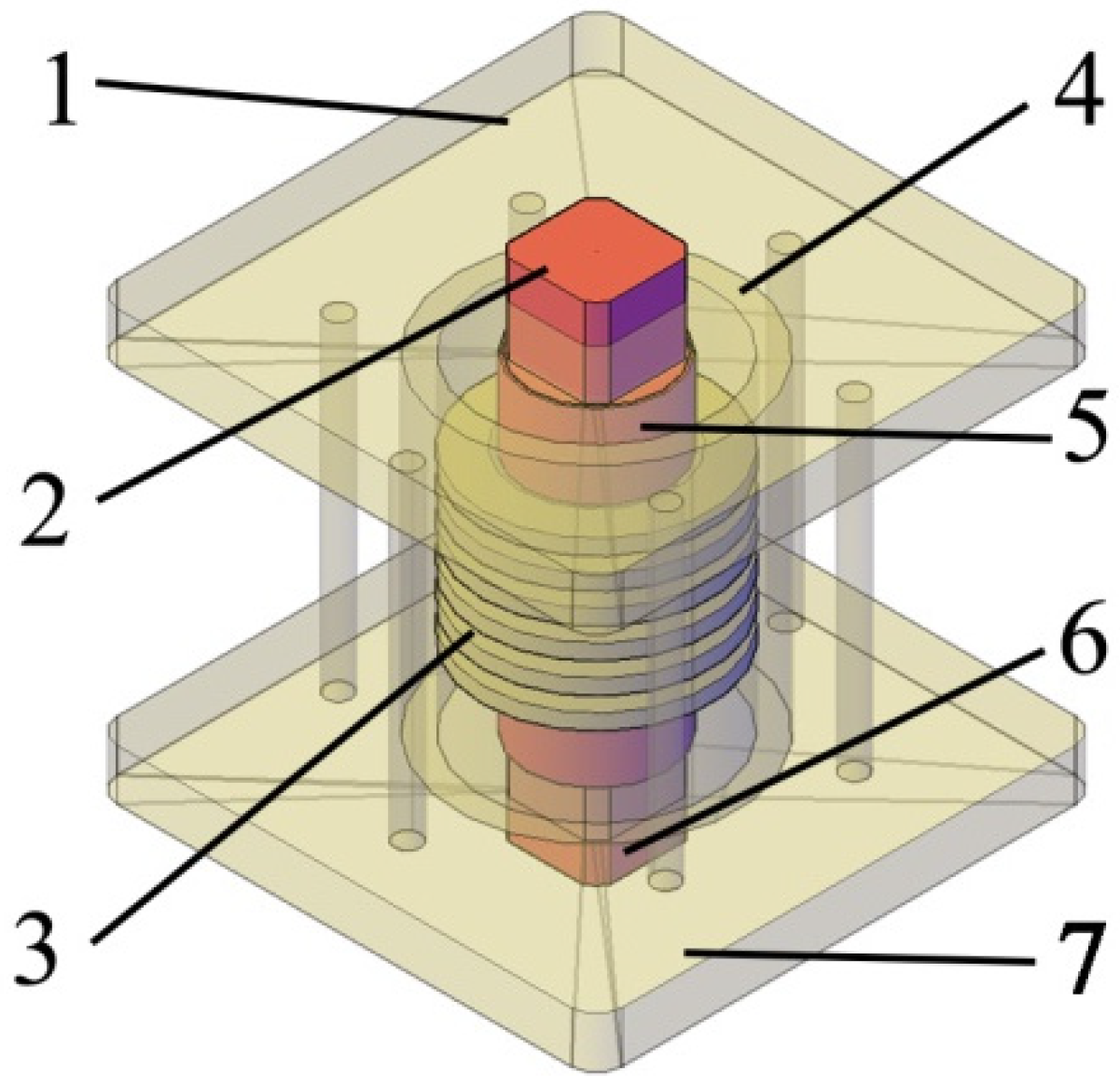
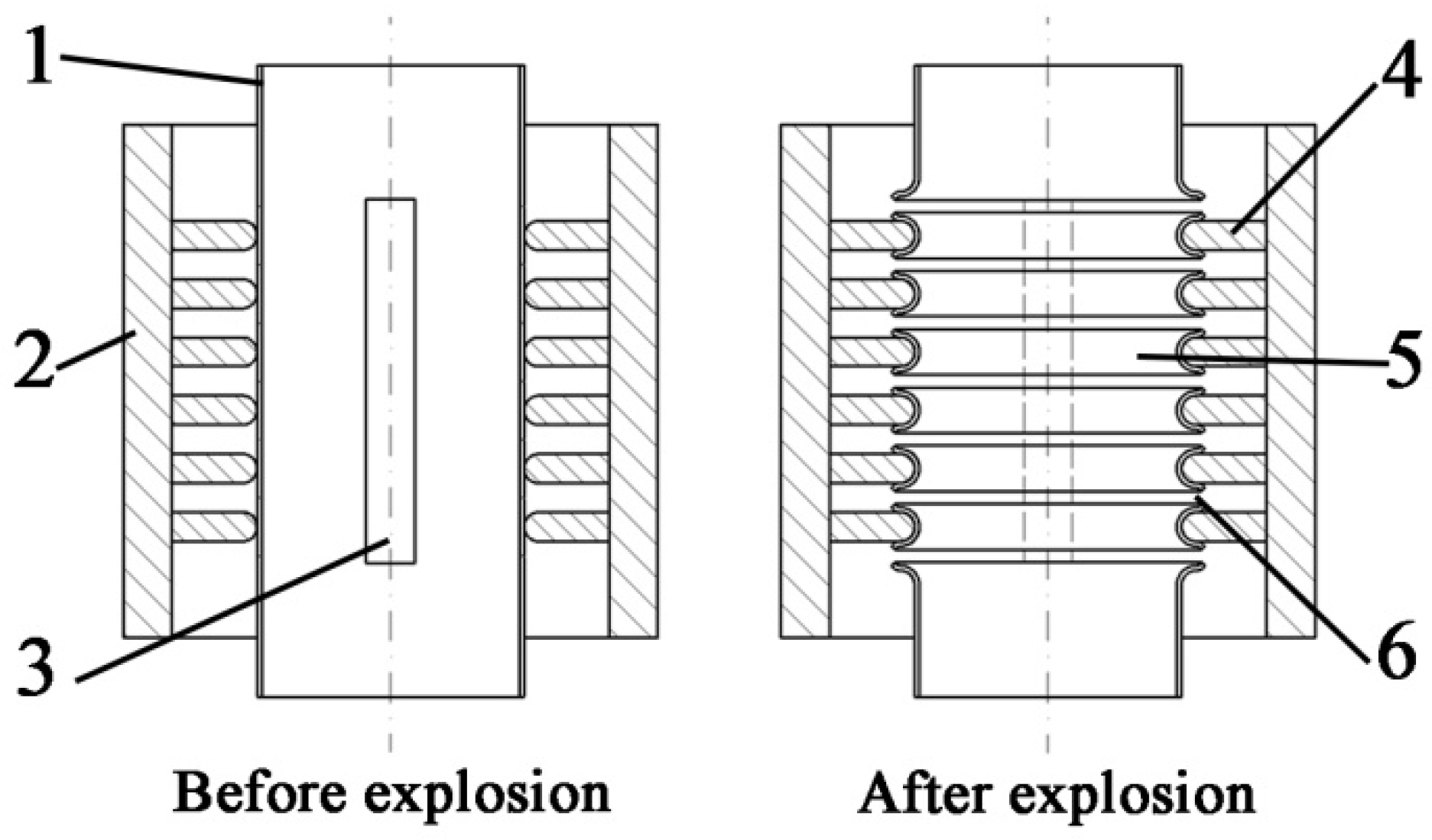
2.1. Model Description
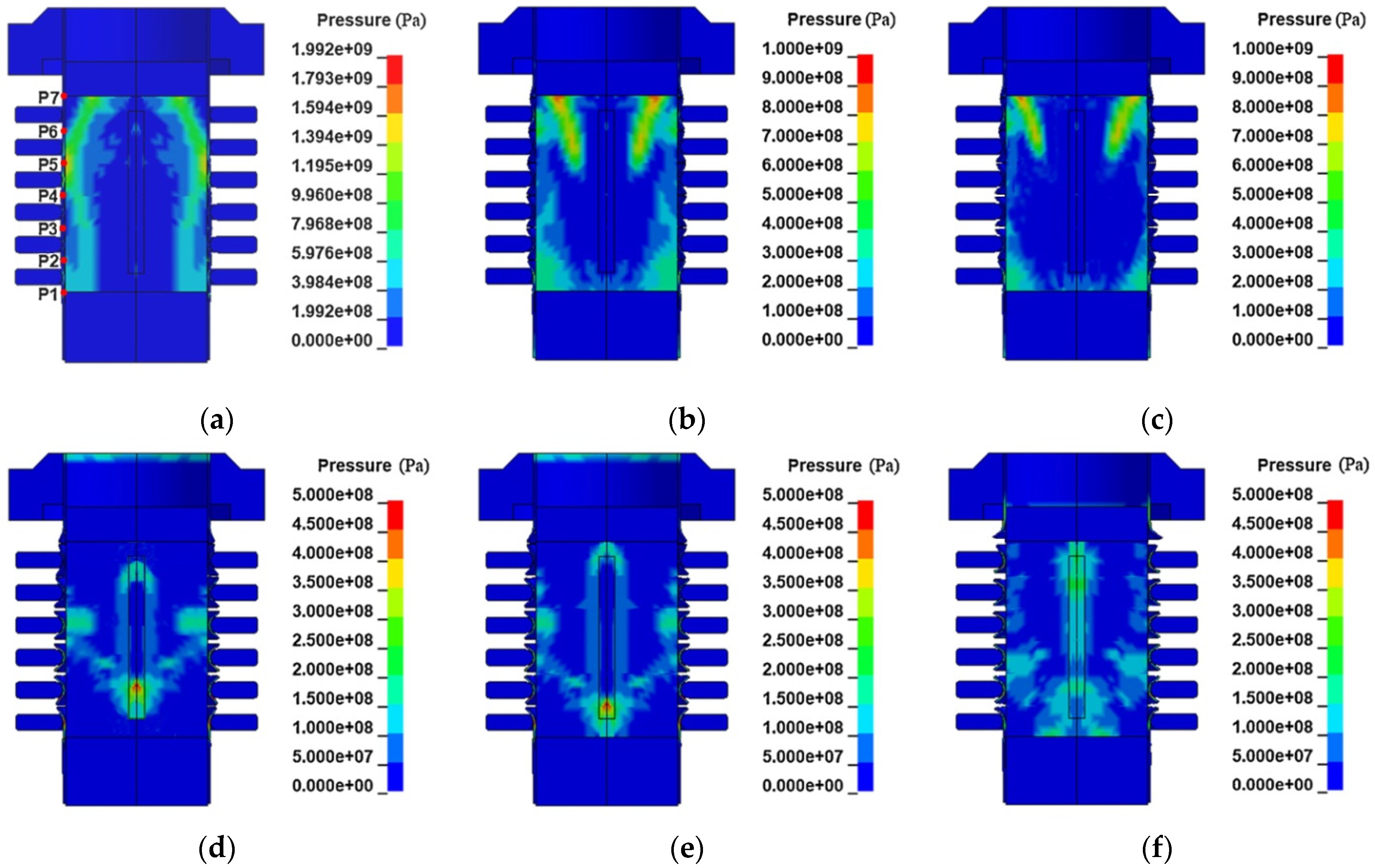
2.2. Numerical Analysis of the Driving Mechanism
3. Application of Schavemaker Arc Model on Multiple Arcs
3.1. Schavemaker Arc Model
- g—the arc conductance
- u—the arc voltage
- i—the arc current
- τ—the time constant
- P0—the cooling power
- E0—the reference arc voltage
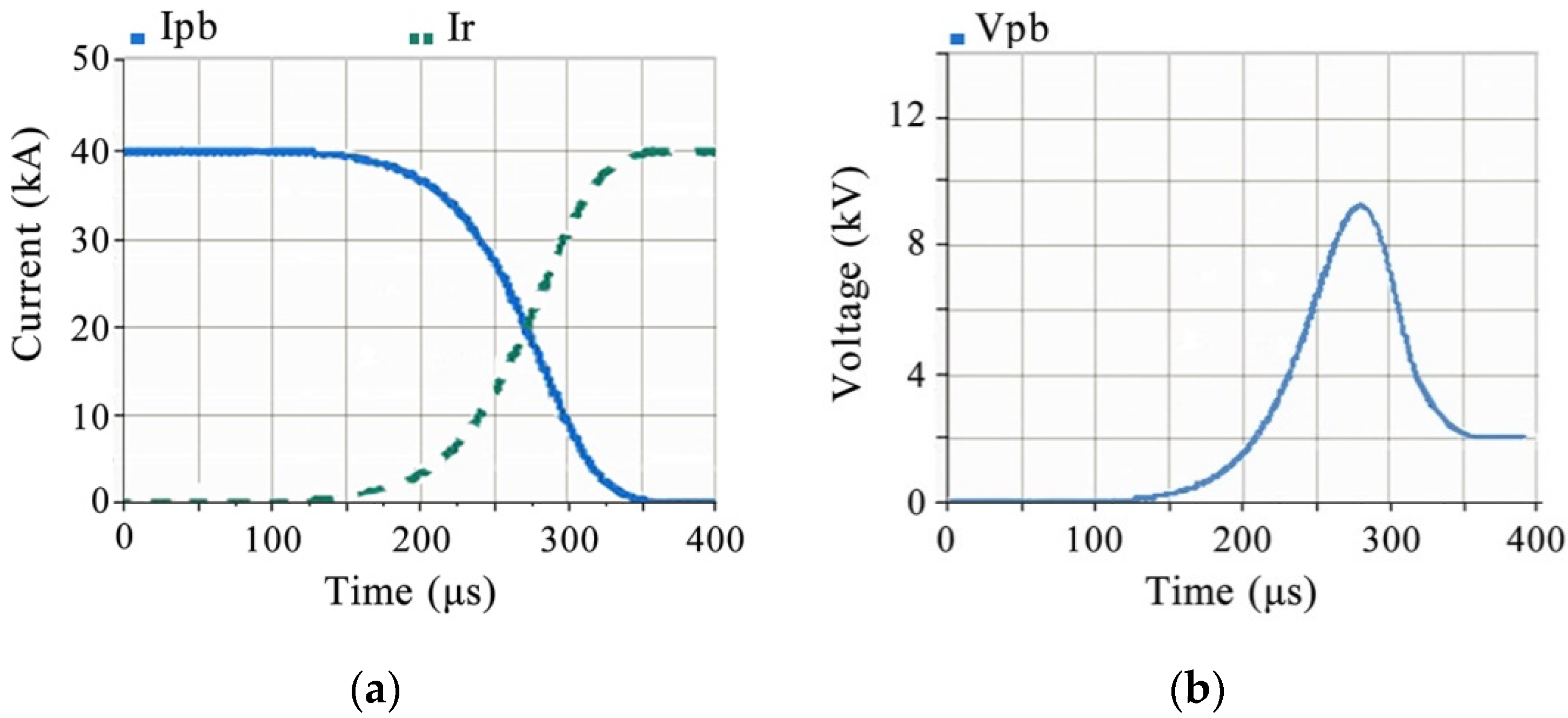
3.2. Parameter Fitting with the Experiment under 40 kA
4. Verification of the Arc Model under 60 kA
4.1. Simulation with the Mutiple-Arc Model
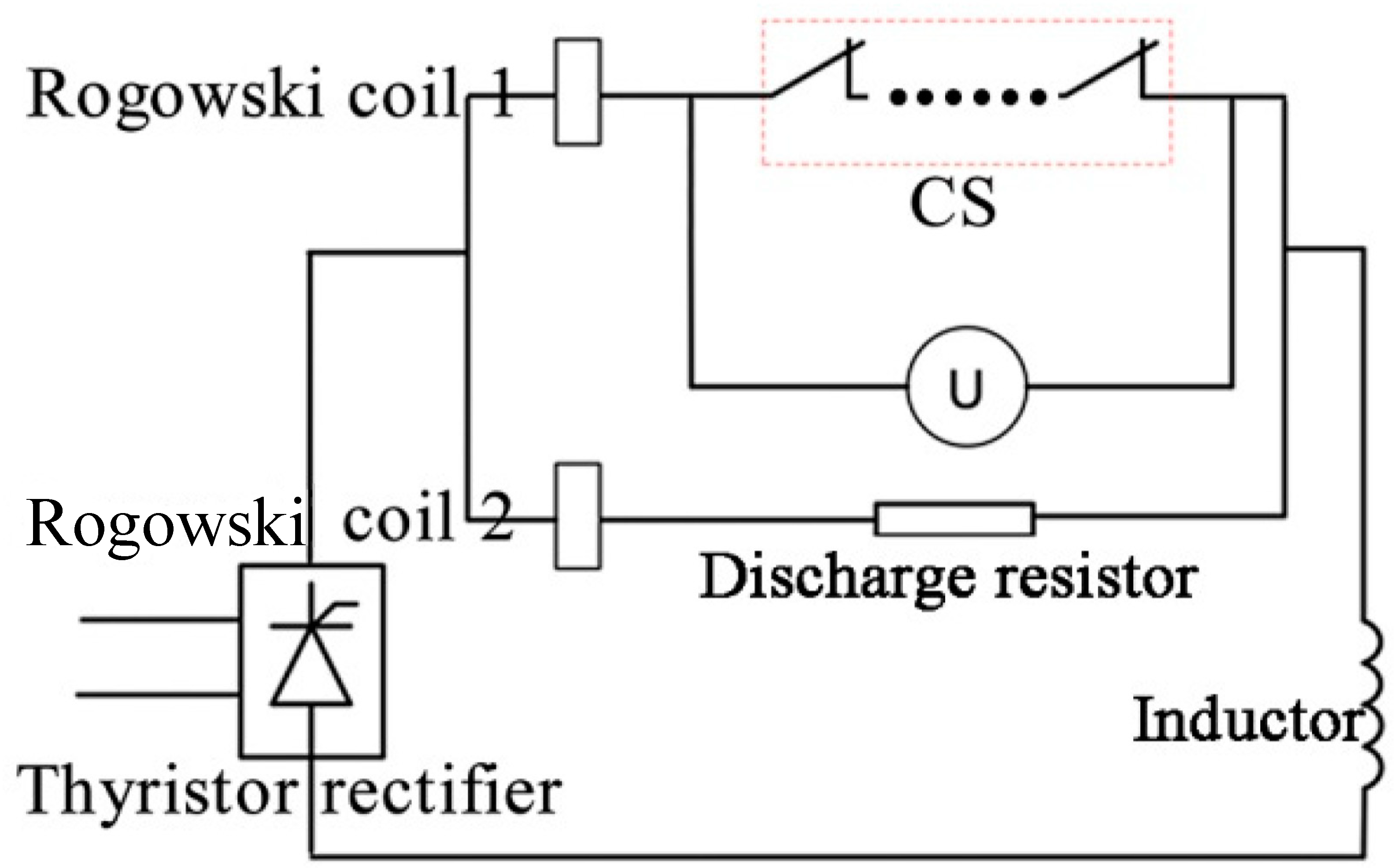
4.2. Experiment
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ludin, G.A.; Amin, M.A.; Matayoshi, H.; Rangarajan, S.S.; Hemeida, A.M.; Takahashi, H.; Senjyu, T. Solid-State DC circuit breakers and their comparison in modular multilevel converter Based-HVDC transmission system. Electronics 2021, 10, 1204. [Google Scholar] [CrossRef]
- Bhatta, S.; Fu, R.; Zhang, Y. A New method of detecting and interrupting high impedance faults by specifying the Z-Source breaker in DC power networks. Electronics 2020, 9, 1654. [Google Scholar] [CrossRef]
- Niewind, J.; Hemdan, N.G.A.; Klosinski, C.; Bösche, D.; Kurrat, M.; Gerdinand, F.; Meisner, J.; Passon, S. Operation and protection of 380V DC distribution systems. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Lee, K.A.; Cho, Y.M.; Lee, H.J. Circuit model and analysis of molded case circuit breaker interruption phenomenon. Electronics 2020, 9, 2047. [Google Scholar] [CrossRef]
- Pierri, R.; Moretta, R. An SVD approach for estimating the dimension of phaseless data on multiple arcs in fresnel zone. Electronics 2021, 10, 606. [Google Scholar] [CrossRef]
- Wang, D.; Liao, M.; Wang, R.; Li, T.; Qiu, J.; Li, J.; Duan, X.; Zou, J. Research on Vacuum arc commutation characteristics of a natural-commutate hybrid DC circuit breaker. Energies 2020, 13, 4823. [Google Scholar] [CrossRef]
- Mayr, O. Beitrage zur Theorie des Statischen und des Dynamischen Lichtbogens. Arch. Elektr. 1943, 37, 588–608. [Google Scholar] [CrossRef]
- Cassie, A.M. Arc rupture and circuit severity: A new theory. In Proceedings of the Conférence Internationale des Grands Réseaux Électriques à Haute Tension (CIGRE Report), Paris, France, 29 June–8 July 1939; Volume 102, pp. 1–14. [Google Scholar]
- Gammon, T.; Lee, W.; Zhang, Z.; Johnson, B.C. A review of commonly used DC arc models. IEEE Trans. Ind. Appl. 2015, 51, 1398. [Google Scholar] [CrossRef]
- Khakpour, A.; Franke, S.; Uhrlandt, D.; Gorchakov, S.; Methling, R. Electrical arc model based on physical parameters and power calculation. IEEE Trans. Plasma Sci. 2015, 43, 2721. [Google Scholar] [CrossRef]
- Rau, S.; Zhang, Z.; Lee, W. 3D magnetohydrodynamic modeling of DC arc in power system. IEEE Trans. Ind. Appl. 2016, 52, 4549–4555. [Google Scholar] [CrossRef]
- Fu, P.; Song, Z.Q.; Gao, G.; Tang, L.J.; Wu, Y.B.; Wang, L.S.; Liang, X.Y. Quench protection of the poloidal field superconducting coil system for the EAST tokamak. Nucl. Fusion. 2006, 46, S85. [Google Scholar] [CrossRef]
- Rummel, T.; Gaupp, O.; Lochner, G.; Sapper, J. Quench protection for the superconducting magnet system of WENDELSTEIN 7-X. IEEE Trans. Appl. Supercond. 2002, 12, 1382. [Google Scholar] [CrossRef]
- Barabaschi1, P.; Kamada, Y.; Shirai, H. Progress of the JT-60SA project. Nucl. Fusion. 2019, 59, 112005. [Google Scholar] [CrossRef]
- Song, I.; Choi, C.; Cho, M. Quench protection system for the superconducting coil of the KSTAR Tokamak. IEEE Trans. Appl. Supercond. 2007, 17, 1–6. [Google Scholar] [CrossRef]
- Manzuk, M.; Avanesov, S.; Roshal, A.; Bestuzhev, K.; Nesterenko, A.; Volkov, S. The 70 kA pyrobreaker for ITER magnet back-up protection. Fusion Eng. Des. 2013, 88, 1537–1540. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Y.; Dong, Y.; HL-2A Team. Characterization of plasma current quench during disruptions at HL-2A. Plasma Sci. Technol. 2017, 19, 055101. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Zhu, J.; Gao, X.; Shen, F.; Chen, S. Electromagnetic, mechanical and thermal performance analysis of the CFETR magnet system. Nucl. Fusion. 2015, 55, 093002. [Google Scholar] [CrossRef]
- Zheng, J.; Song, Y.; Liu, X.; Lu, K.; Qin, J. Overview of the Design Status of the Superconducting Magnet System of the CFETR. IEEE Trans. Appl. Supercond. 2018, 28, 4204305. [Google Scholar] [CrossRef]
- Song, Y.; Wu, S.; Li, J.; Wan, B.; Wan, Y.; Fu, P.; Ye, M.; Liu, S.; Gao, X. Concept design of CFETR Tokamak machine. IEEE Trans. Plasma Sci. 2013, 42, 503–509. [Google Scholar] [CrossRef]
- Schavemaker, P.H.; Slui, L. An improved Mayr-type arc model based on current-zero measurements [circuit breakers]. IEEE Trans. Power Deliv. 2000, 15, 580–584. [Google Scholar] [CrossRef]
- He, J.; Wang, K.; Li, J. Application of an Improved mayr-type arc model in pyro-breakers utilized in superconducting fusion facilities. Energies 2021, 14, 4383. [Google Scholar] [CrossRef]
- Tang, C.; Song, Z.; Li, C.; Wang, Z.; Ye, J.; Li, H.; Fu, P. Computational investigation on the explosively actuated switch utilized in quenching protection system. Fusion Eng. Des. 2021, 163, 112157. [Google Scholar] [CrossRef]
- He, J.; Wang, K.; Fu, P.; Song, Z.; Tang, C.; Ye, J. Numerical Analysis of a Pyro-breaker Utilized in Superconducting Fusion Facility. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Lim, S.; Khan, U.A.; Lee, J.; Lee, B.; Kim, K.; Gu, C. Simulation analysis of DC arc in circuit breaker applying with conventional black box arc model. In Proceedings of the 2015 3rd International Conference on Electric Power Equipment–Switching Technology (ICEPE-ST), Busan, Korea, 25–28 October 2015; pp. 332–336. [Google Scholar] [CrossRef]
- Park, K.; Lee, H.; Asif, M.; Lee, B.; Shin, T.; Gu, C. Assessment of various kinds of AC black-box arc models for DC circuit breaker. In Proceedings of the 2017 4th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017; pp. 465–469. [Google Scholar]



| Facilities | Nominal Voltage | Nominal Current | Commutation Time |
|---|---|---|---|
| EAST | 3 kV | 15 kA | <100 μs |
| W7-7 | 8 kV | 20 kA | 301 μs |
| JT60-SA | 5 kV | 25.7 kA | 350 μs |
| KSTAR | 8 kV | 40 kA | 200 μs |
| ITER | 10 kV | 70 kA | 350 μs |
| Number of Arc Modules | Commutation Time | Voltage Spike | Voltage Spike Time |
|---|---|---|---|
| 6 | 264 μs | 8.15 kV | 175 μs |
| 5 | 276 μs | 8.13 kV | 180 μs |
| 4 | 290 μs | 8.11 kV | 187 μs |
| Commutation Factors | Simulation Result | Experiment Results | Relative Error |
|---|---|---|---|
| Commutation time | 276 μs | 279 μs | 1.1% |
| Voltage spike | 8.13 kV | 8.07 kV | 7% |
| Voltage spike time | 180 μs | 184 μs | 2.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Wang, K.; Li, J. Numerical Study on Multiple Arcs in a Pyro-Breaker Based on the Black-Box Arc Model. Electronics 2022, 11, 1702. https://doi.org/10.3390/electronics11111702
He J, Wang K, Li J. Numerical Study on Multiple Arcs in a Pyro-Breaker Based on the Black-Box Arc Model. Electronics. 2022; 11(11):1702. https://doi.org/10.3390/electronics11111702
Chicago/Turabian StyleHe, Jun, Ke Wang, and Jiangang Li. 2022. "Numerical Study on Multiple Arcs in a Pyro-Breaker Based on the Black-Box Arc Model" Electronics 11, no. 11: 1702. https://doi.org/10.3390/electronics11111702
APA StyleHe, J., Wang, K., & Li, J. (2022). Numerical Study on Multiple Arcs in a Pyro-Breaker Based on the Black-Box Arc Model. Electronics, 11(11), 1702. https://doi.org/10.3390/electronics11111702






