Combining Event-Based Maneuver Selection and MPC Based Trajectory Generation in Autonomous Driving
Abstract
:1. Introduction
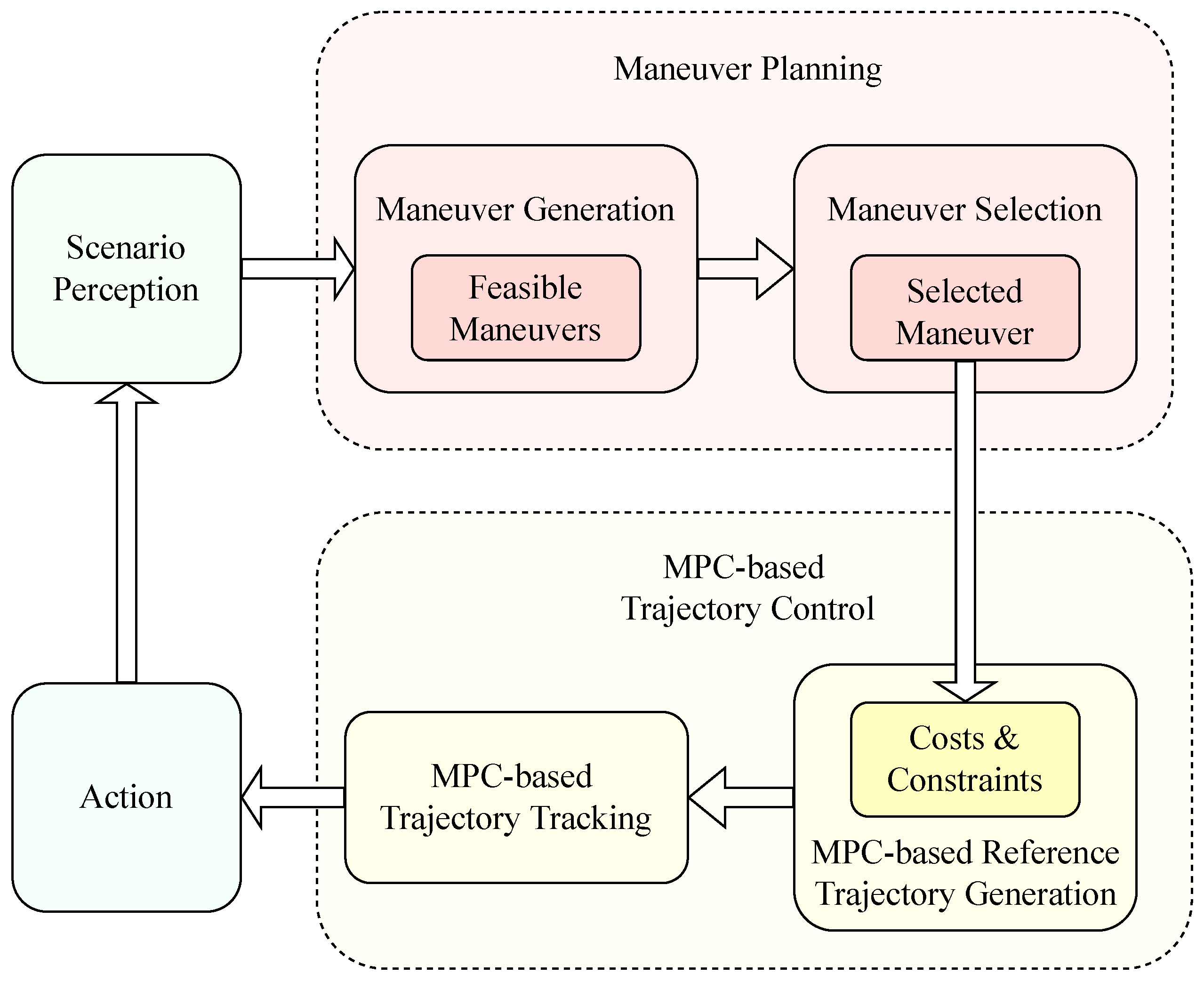
2. Maneuver Planning
2.1. Maneuver Generation
2.2. Safety Criteria
2.2.1. TTC
2.2.2. TIV
2.3. Maneuver Selection
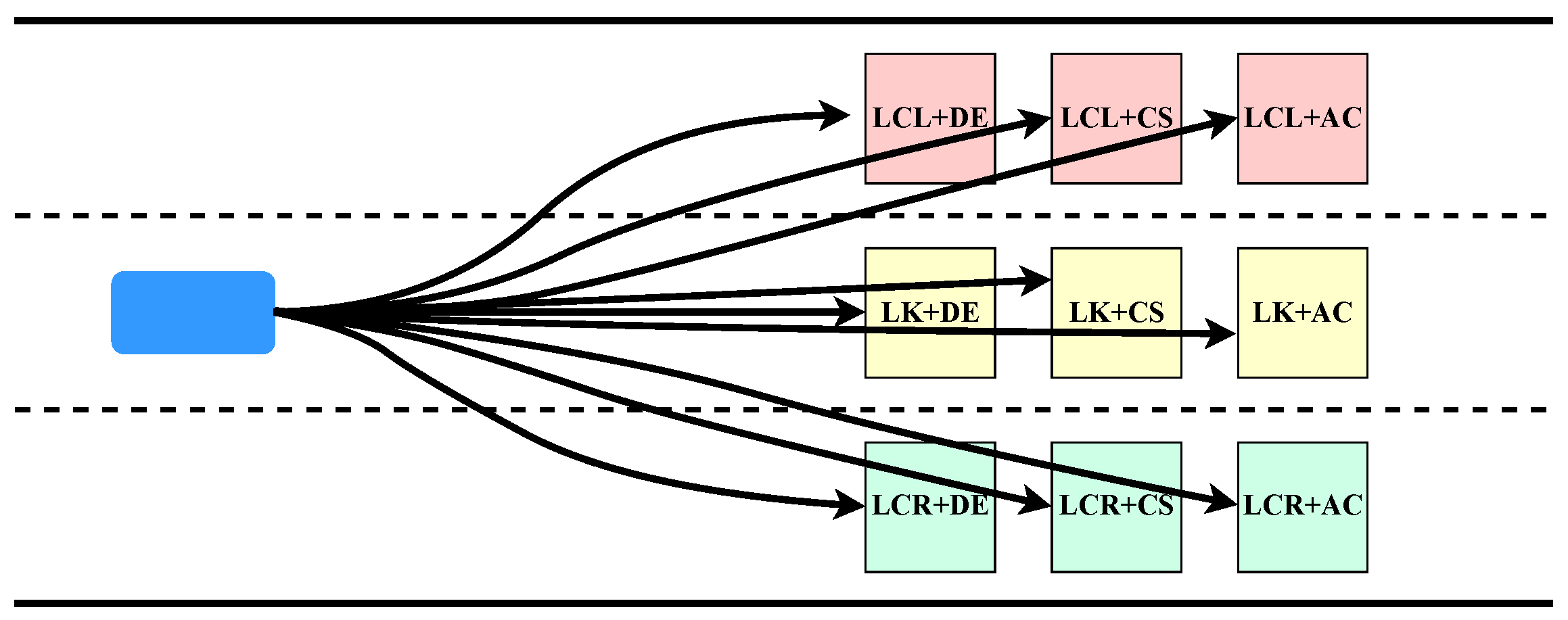
2.3.1. Lane-Choosing Maneuver in the Lateral Direction
- Remove the lateral maneuvers that will cause the road edge constraints to be violated. For instance, if the vehicle is in the rightmost lane of the road, the maneuver of changing to the right lane (LCR) is inadmissible.
- Exclude the lateral maneuvers with which the vehicle is not heading towards the goal lane. Here, we consider two cases: (a) the goal lane is the current lane; (b) the goal lane is a different lane. In case (a), we simply remove the lane-changing maneuvers, LCL and LCR. Case (b) is more complicated. If the goal lane is the lane at the left (right) side of the current lane, we first exclude the lateral maneuver with which the vehicle turns to the opposite/wrong direction, LCR (LCL) is therefore removed. Then, we consider whether the lane-changing maneuver is satisfied or not. If the conditions for changing lanes are satisfied, we exclude the LK maneuver; otherwise the lane-changing maneuver LCL (LCR) is removed.
2.3.2. Speed Generating Maneuver in the Longitudinal Direction
- The EV is behind the OV; .
- . The velocity of the EV is smaller than that of the OV:
- -
- When the EV maintains current longitudinal speed (CS), the distance between the two vehicles increases. Thus, both TTC and TIV increase as time goes on;
- -
- The EV’s choice of deceleration (DE) will cause the distance between the two vehicles () to increase, but also cause the relative velocity () to increase. Thus, the effect of deceleration (DE) on TTC is unknown;
- -
- Choosing acceleration (AC) will cause the TIV to decrease. Thus, we will not keep the AC.
Therefore, maintaining current longitudinal speed (CS) is the best choice. - . The velocity of the EV is greater than that of the OV, which is dangerous:
- -
- Both maintaining current speed (CS) and acceleration (AC) will definitely cause a decrease of the TTC and TIV;
- -
- However, by executing deceleration (DE), TTC and TIV will probably trend upward.
Consequently, deceleration (DE) is selected as the longitudinal maneuver performed in this situation. - . The two vehicles have the same longitudinal speed:
- -
- Under this circumstance, only TIV is used to estimate the risk;
- -
- Whether the distance between the two vehicles is small or not, decreasing the speed of the EV is a safe maneuver, which contributes to obtaining a greater TIV.
Thus, deceleration (DE) is selected for the EV in this situation.
- The EV is in front of the OV; .
- . The velocity of the EV is less than that of the OV:
- -
- Not only deceleration (DE), but also maintaining current speed (CS) will cause a decreasing trend of the TTC and TIV;
- -
- Additionally, when choosing acceleration (AC), TIV will experience a rapid drop, while TTC might show an upward trend.
This is not a safe situation, but increasing the speed of the EV will probably contribute to avoiding possible collisions, so AC is taken as the longitudinal maneuver. - . The velocity of the EV is greater than that of the OV:
- -
- Both decelerating (DE) and maintaining current speed (CS) are beneficial to increasing TTC and TIV, so they can be taken as candidate maneuvers;
- -
- Furthermore, DE has a negative effect on the efficiency and smoothness.
Therefore, we finally keep CS as the longitudinal maneuver in this situation. - . The EV and OV drive at same speed:
- -
- In this situation, TTC is not calculated and only TIV is considered as a safety criterion;
- -
- Increasing the speed (AC) will help obtain greater TIV;
- -
- Neither decreasing (DE), nor maintaining current speed (CS) will contribute to increasing TIV.
Therefore, acceleration (AC) is selected.
3. Model Predictive Control
3.1. Optimization Problem of the MPC Controller
3.2. Vehicle Model
3.3. Constraints
3.3.1. State Constraints
- Constraints for Traffic Rules:where is the width of vehicles, is the width of each lane, and m is the number of lanes. As shown in Equation (6), the vehicle can move forward freely in the longitudinal direction. Equation (7) is designed for keeping the vehicle within the road edges. Constraints (8) and (9) give the upper and lower limits to velocities in longitudinal and lateral directions, respectively.
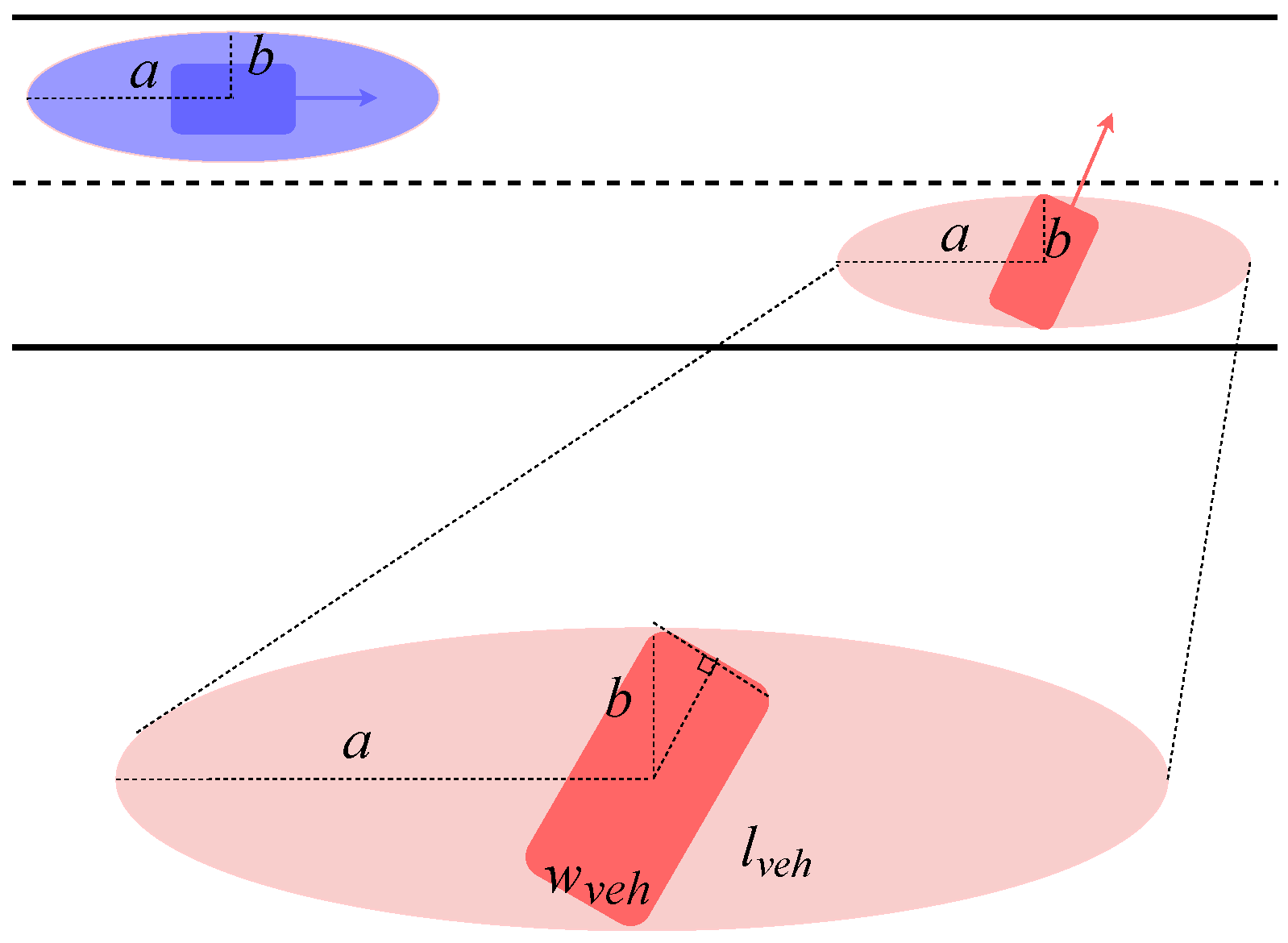
- Safety constraint:In order to avoid collisions, a region around each vehicle is defined that other vehicles are not allowed to enter [34,38]. The region can be any convex shape larger than the shape of the vehicle [38]. As in [34,39,40,41], an elliptic region is chosen for our implementation, as shown in Figure 4.This safety constraint is then realized by the following inequality:where a and b are the major and minor axes of the ellipse, respectively. The longitudinal distance between the EV and one OV is . The lateral distance between these two vehicles is . The center of the ellipse-shaped region is the same as the center of the vehicle. Since we use a point-mass model that does not provide information about the current orientation of the vehicle, the major axis of the ellipse is chosen to be aligned with the lanes.For safety, the ellipse-shaped region has to be large enough that the vehicle shape is covered by the ellipse for all possible vehicle orientations. In order to find appropriate a and b, we consider the vehicle turning left or right, see Figure 4. If the vehicle is covered by the ellipse here, it will also be covered for all other orientations. Let and denote the length and the width of a vehicle, respectively. Then it holds for a and b:where .
3.3.2. Input Constraints
3.4. Cost Function
3.5. MPC-Based Reference Trajectory Generation
4. Simulation Results
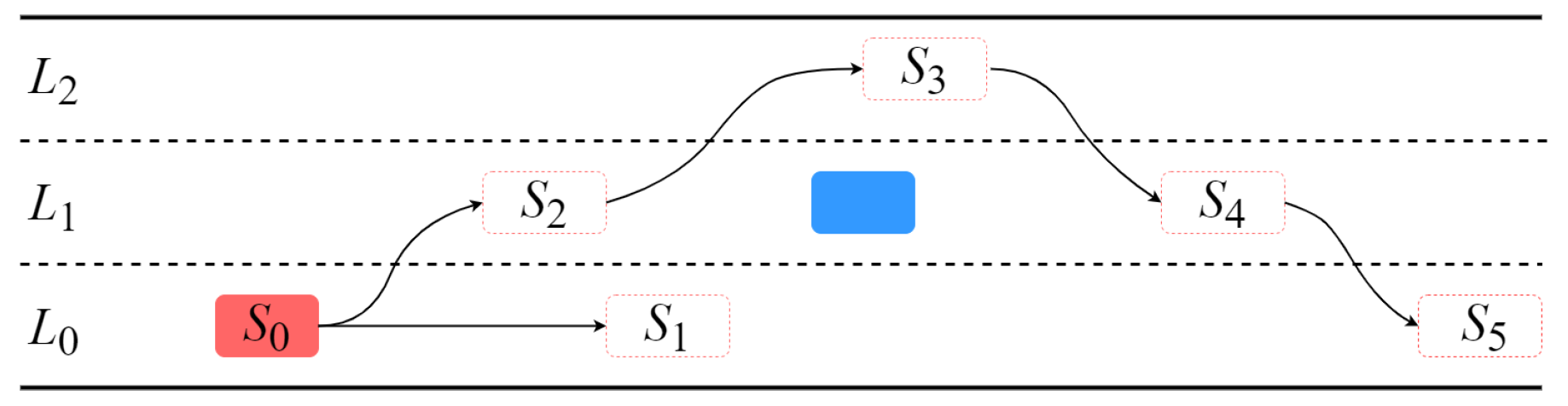
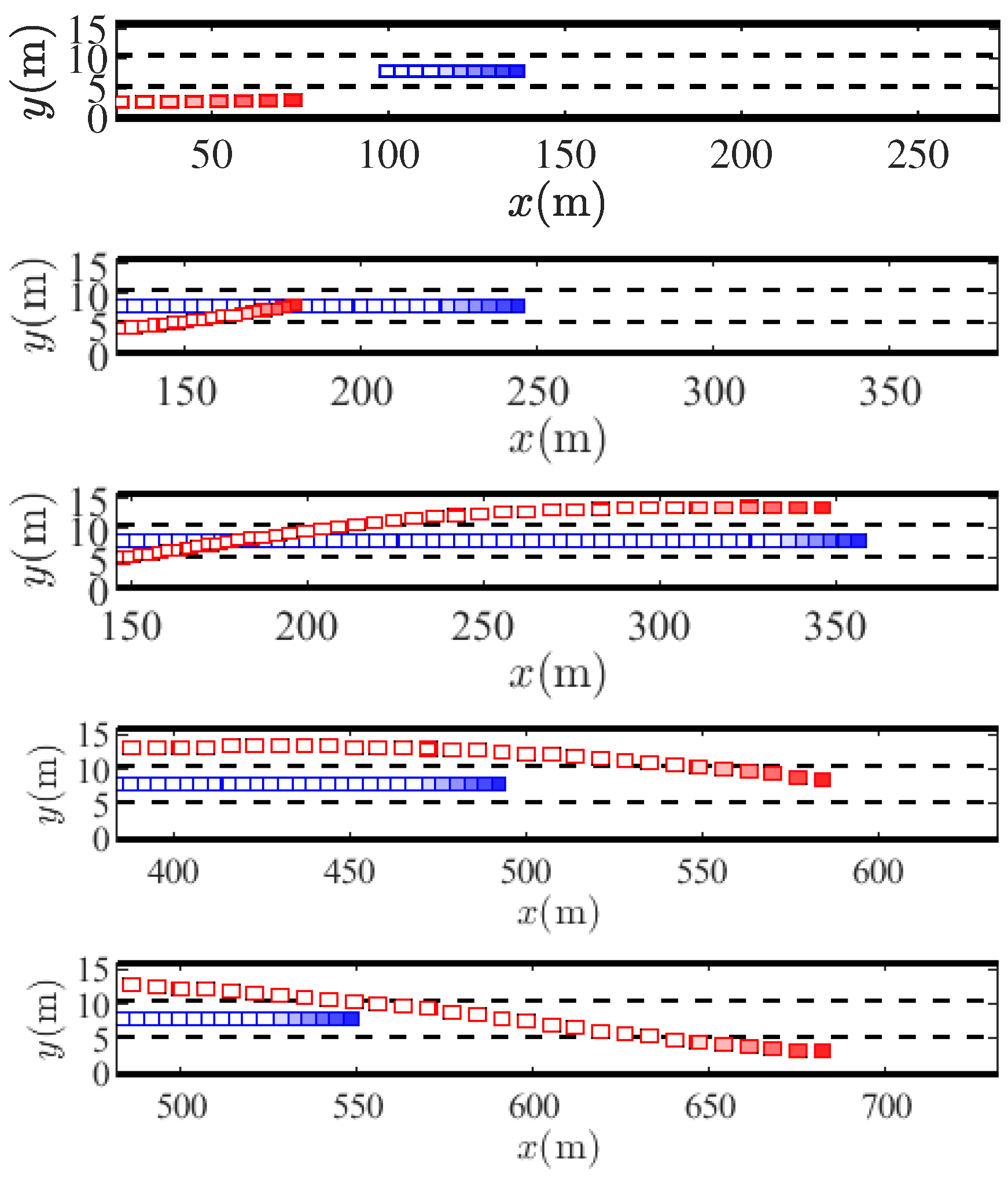
4.1. Scenario Description
- : The EV is driving behind the OV in with a greater longitudinal velocity.
- : The EV is following the OV in with a smaller longitudinal velocity.
- : The EV is driving in lane , waiting for a chance to change to . This is a transition stage.
- : The EV reaches lane and drives in before overtaking the OV from the left, looking for an opportunity to go back to lane . In this stage, lane keeping also occurs.
- : The EV reaches lane , and is preparing for moving to lane .
- : The EV drives in lane .
4.2. Maneuver Planning
- 1—The vehicle will reach the edge of the road if it turns left (or right).
- 2—The goal is to change lane but the the safety constraints for changing lane is not satisfied.
- 3—By conducting these maneuvers, the vehicle cannot move to the target lane even though the conditions for changing lane are fulfilled.
- 4—These maneuvers contribute less/nothing to increasing TTC and TIV.
- 5—These maneuvers contribute less to improving efficiency.
- 6—Selecting these maneuvers has a negative or no positive impact on smoothness of driving behaviors.
4.2.1. Maneuver Selection in Car-Following Scenario:
4.2.2. Maneuver Selection in Overtaking Scenario:
4.3. MPC-Based Trajectory Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPC | model predictive control |
| TTC | time to collision |
| TIV | intervehicular time |
| DE | decelerating |
| CS | maintaining current speed |
| AC | accelerating |
| LCL | changing to the left lane |
| LCR | changing to the right lane |
| LK | keeping moving in the current lane |
| EV | ego vehicle |
| OV | object vehicle |
References
- Menéndez-Romero, C.; Winkler, F.; Dornhege, C.; Burgard, W. Maneuver planning for highly automated vehicles. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1458–1464. [Google Scholar]
- Chen, C.; Gaschler, A.; Rickert, M.; Knoll, A. Task planning for highly automated driving. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 940–945. [Google Scholar]
- Ferguson, D.; Howard, T.M.; Likhachev, M. Motion planning in urban environments. J. Field Robot. 2008, 25, 939–960. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Glaser, S.; Vanholme, B.; Mammar, S.; Gruyer, D.; Nouvelière, L. Maneuver-Based Trajectory Planning for Highly Autonomous Vehicles on Real Road With Traffic and Driver Interaction. IEEE Trans. Intell. Transp. Syst. 2010, 11, 589–606. [Google Scholar] [CrossRef]
- Wang, D.; Qi, F. Trajectory planning for a four-wheel-steering vehicle. In Proceedings of the 2001 ICRA, IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Korea, 21–26 May 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 4, pp. 3320–3325. [Google Scholar]
- Frazzoli, E.; Dahleh, M.A.; Feron, E. Maneuver-based motion planning for nonlinear systems with symmetries. IEEE Trans. Robot. 2005, 21, 1077–1091. [Google Scholar] [CrossRef]
- Kushleyev, A.; Likhachev, M. Time-bounded lattice for efficient planning in dynamic environments. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1662–1668. [Google Scholar]
- Fraichard, T.; Scheuer, A. From Reeds and Shepp’s to continuous-curvature paths. IEEE Trans. Robot. 2004, 20, 1025–1035. [Google Scholar] [CrossRef] [Green Version]
- Petrov, P.; Nashashibi, F. Modeling and Nonlinear Adaptive Control for Autonomous Vehicle Overtaking. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1643–1656. [Google Scholar] [CrossRef] [Green Version]
- Piazzi, A.; Lo Bianco, C.G.; Bertozzi, M.; Fascioli, A.; Broggi, A. Quintic G/sup 2/-splines for the iterative steering of vision-based autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2002, 3, 27–36. [Google Scholar] [CrossRef]
- Rastelli, J.P.; Lattarulo, R.; Nashashibi, F. Dynamic trajectory generation using continuous-curvature algorithms for door to door assistance vehicles. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 510–515. [Google Scholar]
- Berglund, T.; Brodnik, A.; Jonsson, H.; Staffanson, M.; Soderkvist, I. Planning Smooth and Obstacle-Avoiding B-Spline Paths for Autonomous Mining Vehicles. IEEE Trans. Autom. Sci. Eng. 2010, 7, 167–172. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, E. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Bohren, J.; Foote, T.; Keller, J.; Kushleyev, A.; Lee, D.; Stewart, A.; Vernaza, P.; Derenick, J.; Spletzer, J.; Satterfield, B. Little Ben: The Ben Franklin Racing Team’s Entry in the 2007 DARPA Urban Challenge. In The DARPA Urban Challenge; Springer: Berlin/Heidelberg, Germany, 2009; pp. 231–255. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Wang, Q.; Ayalew, B.; Weiskircher, T. Predictive Maneuver Planning for an Autonomous Vehicle in Public Highway Traffic. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1303–1315. [Google Scholar] [CrossRef]
- Kogan, D.; Murray, R.M. Optimization-Based Navigation for the DARPA Grand Challenge. In Proceedings of the 45th Conference on Decision and Control (CDC), San Diego, CA, USA, 13–15 December 2006; p. 6. [Google Scholar]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Ziegler, J.; Bender, P.; Dang, T.; Stiller, C. Trajectory planning for Bertha—A local, continuous method. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 450–457. [Google Scholar]
- Elbanhawi, M.; Simic, M. Sampling-Based Robot Motion Planning: A Review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Kuwata, Y.; Teo, J.; Fiore, G.; Karaman, S.; Frazzoli, E.; How, J.P. Real-Time Motion Planning With Applications to Autonomous Urban Driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Yoon, J.; Crane, C.D. Path planning for Unmanned Ground Vehicle in urban parking area. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 26–29 October 2011; pp. 887–892. [Google Scholar]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1094–1099. [Google Scholar]
- Anderson, S.J.; Peters, S.C.; Pilutti, T.E.; Iagnemma, K. An optimal-control-based framework for trajectory planning, threat assessment, and semi-autonomous control of passenger vehicles in hazard avoidance scenarios. Int. J. Veh. Auton. Syst. 2010, 8, 190–216. [Google Scholar] [CrossRef]
- Bhargav, J.; Betz, J.; Zehng, H.; Mangharam, R. Deriving Spatial Policies for Overtaking Maneuvers with Autonomous Vehicles. In Proceedings of the 2022 14th International Conference on COMmunication Systems NETworkS (COMSNETS), Bengaluru, India, 4–8 January 2022; pp. 859–864. [Google Scholar] [CrossRef]
- Musa, A.; Pipicelli, M.; Spano, M.; Tufano, F.; De Nola, F.; Di Blasio, G.; Gimelli, A.; Misul, D.A.; Toscano, G. A Review of Model Predictive Controls Applied to Advanced Driver-Assistance Systems. Energies 2021, 14, 7974. [Google Scholar] [CrossRef]
- Hayward, J.C. Near-Miss Determination through Use of a Scale of Danger; University Park, Pa, Pennsylvania Transportation and Traffic Safety Center, The Pennsylvania State University: State College, PA, USA, 1972. [Google Scholar]
- Pendleton, S.D.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, Planning, Control, and Coordination for Autonomous Vehicles. Machines 2017, 5, 6. [Google Scholar] [CrossRef]
- Brüdigam, T.; Olbrich, M.; Wollherr, D.; Leibold, M. Stochastic Model Predictive Control with a Safety Guarantee for Automated Driving. IEEE Trans. Intell. Veh. 2021, 1. [Google Scholar] [CrossRef]
- Katrakazas, C.; Quddus, M.; Chen, W.H.; Deka, L. Real-time motion planning methods for autonomous on-road driving: State-of-the-art and future research directions. Transp. Res. Part C Emerg. Technol. 2015, 60, 416–442. [Google Scholar] [CrossRef]
- Rawlings, J.; Mayne, D.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Brüdigam, T.; Olbrich, M.; Leibold, M.; Wollherr, D. Combining Stochastic and Scenario Model Predictive Control to Handle Target Vehicle Uncertainty in an Autonomous Driving Highway Scenario. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1317–1324. [Google Scholar]
- Gao, Y.; Lin, T.; Borrelli, F.; Tseng, E.; Hrovat, D. Predictive Control of Autonomous Ground Vehicles with Obstacle Avoidance on Slippery Roads. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference, Cambridge, MA, USA, 12–15 September 2010; Volume 1. [Google Scholar] [CrossRef] [Green Version]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 163–168. [Google Scholar] [CrossRef]
- Carvalho, A.; Gao, Y.; Gray, A.; Tseng, H.E.; Borrelli, F. Predictive control of an autonomous ground vehicle using an iterative linearization approach. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 2335–2340. [Google Scholar] [CrossRef]
- Carvalho, A.; Gao, Y.; Lefevre, S.; Borrelli, F. Stochastic predictive control of autonomous vehicles in uncertain environments. In Proceedings of the 12th International Symposium on Advanced Vehicle Control, Tokyo, Japan, 22–26 September 2014; pp. 712–719. [Google Scholar]
- Brito, B.; Floor, B.; Ferranti, L.; Alonso-Mora, J. Model Predictive Contouring Control for Collision Avoidance in Unstructured Dynamic Environments. IEEE Robot. Autom. Lett. 2019, 4, 4459–4466. [Google Scholar] [CrossRef]
- Jewison, C.; Erwin, R.S.; Saenz-Otero, A. Model Predictive Control with Ellipsoid Obstacle Constraints for Spacecraft Rendezvous. IFAC-PapersOnLine 2015, 48, 257–262. [Google Scholar] [CrossRef]
- Schimpe, A.; Diermeyer, F. Steer with Me: A Predictive, Potential Field-Based Control Approach for Semi-Autonomous, Teleoperated Road Vehicles. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]


| Possible Maneuver | TTC | TIV | Result | |||||
|---|---|---|---|---|---|---|---|---|
| DE | ↑ | ↑ | ↓ | ? | ↑ | |||
| CS | ↑ | − | − | ↑ | ↑ | CS | ||
| AC | ↑ | ↓ | ↑ | ↑ | ↓ | |||
| DE | ↓ | ↓ | ↓ | ? | ? | |||
| CS | ↓ | − | − | ↓ | ↓ | DE | ||
| AC | ↓ | ↑ | ↑ | ↓ | ↓ | |||
| DE | ↑ | ↑ | ↓ | / | ↑ | |||
| CS | − | − | − | / | − | DE | ||
| AC | ↓ | ↑ | ↑ | / | ↓ | |||
| DE | ↓ | ↑ | − | ↓ | ↓ | |||
| CS | ↓ | − | − | ↓ | ↓ | AC | ||
| AC | ↓ | ↓ | − | ? | ↓ | |||
| DE | ↑ | ↓ | − | ↑ | ↑ | |||
| CS | ↑ | − | − | ↑ | ↑ | DE/CS | ||
| AC | ↑ | ↑ | − | ? | ↑ | |||
| DE | ↓ | ↑ | − | / | ↓ | |||
| CS | − | − | − | / | − | AC | ||
| AC | ↑ | ↑ | − | / | ↑ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, N.; Brüdigam, T.; Leibold, M.; Buss, M. Combining Event-Based Maneuver Selection and MPC Based Trajectory Generation in Autonomous Driving. Electronics 2022, 11, 1518. https://doi.org/10.3390/electronics11101518
Dang N, Brüdigam T, Leibold M, Buss M. Combining Event-Based Maneuver Selection and MPC Based Trajectory Generation in Autonomous Driving. Electronics. 2022; 11(10):1518. https://doi.org/10.3390/electronics11101518
Chicago/Turabian StyleDang, Ni, Tim Brüdigam, Marion Leibold, and Martin Buss. 2022. "Combining Event-Based Maneuver Selection and MPC Based Trajectory Generation in Autonomous Driving" Electronics 11, no. 10: 1518. https://doi.org/10.3390/electronics11101518
APA StyleDang, N., Brüdigam, T., Leibold, M., & Buss, M. (2022). Combining Event-Based Maneuver Selection and MPC Based Trajectory Generation in Autonomous Driving. Electronics, 11(10), 1518. https://doi.org/10.3390/electronics11101518







