An Approach to the Construction of a Recursive Argument of Polynomial Evaluation in the Discrete Log Setting

Abstract

Succinct Non-interactive Arguments of Knowledge (SNARks) are receiving a lot of attention as a core privacy-enhancing technology for blockchain applications. Polynomial commitment schemes are important building blocks for the construction of SNARks. Polynomial commitment schemes enable the prover to commit to a secret polynomial of the prover and convince the verifier that the evaluation of the committed polynomial is correct at a public point later. Bünz et al. recently presented a novel polynomial commitment scheme with no trusted setup in Eurocrypt’20. To provide a transparent setup, their scheme is built over an ideal class group of imaginary quadratic fields (or briefly, class group). However, cryptographic assumptions on a class group are relatively new and have, thus far, not been well-analyzed. In this paper, we study an approach to transpose Bünz et al.’s techniques in the discrete log setting because the discrete log setting brings a significant improvement in efficiency and security compared to class groups. We show that the transposition to the discrete log setting can be obtained by employing a proof system for the equality of discrete logarithms over multiple bases. Theoretical analysis shows that the transposition preserves security requirements for a polynomial commitment scheme.

1. Introduction

Zero-Knowledge Succinct Non-interactive Arguments of Knowledge (zk-SNARKs) are non-interactive proof systems between the prover and the verifier. They provide a way for the prover to convince the verifier that the statement claimed by the prover is true without disclosing any other information except the validity of the statement while maintaining a short proof size and an efficient verification by the verifier. Since their adoption to cryptocurrency systems, such as Zcash [1] and Ethereum [2], zk-SNARKs are regarded as an essential technique for solving data privacy issues in blockchain-based applications. There have been numerous SNARK proposals in the literature. Some constructions present very efficient proof systems with the help of a trusted setup [3,4,5]. Because the transparent property is desirable for applications, such as cryptocurrency, recent constructions [6,7,8] have focused on a proof system with a transparent setting, i.e., they have no trusted setup.

The construction of SNARKs with no trusted setup heavily relies on a transparent and efficient polynomial commitment scheme. At a high level, transparent zk-SNARKs can be constructed using the framework from polynomial interactive oracle proofs (IOP) [3,6] as follows: (1) The prover expresses the required computation for proving a statement as a set of low-degree polynomials over a finite field $\mathbb{F}$, which is a representation of its witness. (2) The prover sends commitments to low degree polynomials to the verifier, and the verifier then checks the proof by querying evaluations of polynomials for points chosen uniformly at random from $\mathbb{F}$, where we crucially require a polynomial commitment scheme. (3) Finally, one can obtain the non-interactive version of the previous proof systems by applying the Fiat–Shamir heuristic [9].

In this paper, we focus on polynomial commitment schemes. Let $f\left(X\right)$ be the prover’s secret polynomial over a field $\mathbb{F}$ with the degree at most d, i.e., $deg\left(f\right)\le d$. In polynomial commitment schemes, the prover sends the commitment to f to the verifier. Later, upon input of a public point $(x,y)\in \mathbb{F}\times \mathbb{F}$, the prover convinces the verifier that the committed polynomial f holds $y=f\left(X\right)$ with a proof. We call a polynomial commitment scheme transparent if it requires no trusted setup to generate public parameters for the scheme. Since the first construction was developed by Kate et al. [10], a variety of polynomial commitment schemes have been proposed in the literature.

For polynomial commitment schemes, the main factors of efficiency consist of the computation complexities of the prover (prover complexity) and verifier (verifier complexity), and the communication complexity between them. Usually, constructions with a trusted setup provide higher efficiency than those with a transparent setting. Recently, Bünz et al. [6] proposed an efficient polynomial commitment scheme with a transparent setting. Asymptotically, it achieves a logarithmic verifier complexity and proof size for evaluation (communication complexity). In brief, it improves efficiency by applying an evaluation protocol in a recursive manner. It reduces the degree of a polynomial f by half at each iteration; hence, $logdeg\left(f\right)$ iterations overall. Transparency in the scheme relies on the use of a group of unknown order whose concrete candidate is an ideal class group of imaginary quadratic fields.

The security of a group of unknown order stems from the infeasibility of computing the order of the group. Previous cryptographic constructions over a class group considered concrete group parameters, such as a 1665-bit negative fundamental discriminant for 128-bit security [11,12], which was used in Bünz et al.’s scheme [6]. However, recent works report that the above parameters for class groups provide less security than expected. Notably, Dobson and Galbraith estimate that class groups with a 1665-bit discriminant only offer 55-bit security [13]. They, therefore, claim that orders of a random class group should be at least $2^{3328}$ for a 128-bit security level. Those parameters correspond to approximately a 6656-bit discriminant. This leads to a decreased efficiency for the cryptographic primitives based on class groups.

In this paper, we put forward a study to overcome the efficiency degradation of Bünz et al.’s construction caused by the use of class groups. To do this, we focus on transposing their techniques in the discrete log setting, preserving a no-trust setup. This approach brings about two advantages. First, the (elliptic curve) discrete log problem is one of the standard cryptographic assumptions as opposed to the order assumption of class groups. To date, its security has been well-understood. Second, the group operation in the discrete log setting (e.g., elliptic curve groups) is much more efficient than that in the class groups, which significantly reduces the actual computation cost for both the prover and the verifier. In addition, a group element in the discrete log setting is shorter than that in class groups. This advantage cuts the cost of bandwidth spent by the prover and the verifier when applying the evaluation protocol of a polynomial commitment scheme.

Our approach is built on an information-theoretic abstraction given in [6] to construct a polynomial commitment scheme. The abstraction requires two properties, a linear homomorphism and a monomial homomorphism, which the underlying commitment scheme should provide. These two properties enable the verifier to apply the computations among polynomials over their committed forms, such as a linear combination (a linear homomorphism) and a degree-shift operation (a monomial homomorphism) of polynomials. The two properties are necessary for an evaluation protocol using a recursive call, which is critical in achieving a logarithmic verifier and communication complexities. To realize these properties in a discrete log setting, we utilize a polynomial encoding method devised by Bootle et al. [14]. This method uses a variant of the Pedersen commitment scheme [15], which naturally provides a linear homomorphism. Unfortunately, however, the Pedersen commitment scheme is not a monomial homomorphism, which is easily obtained in a class group-based scheme [6]. Thus, we focus our attention on the study of a discrete log-based proof system to prove that a monomial homomorphism is verifiably computed in the discrete log setting. The contribution of this work is as follows.

• We clarify a proof system that proves the correct computation of a monomorphism in the discrete log setting. Specifically, we show it suffices to have a proof system to check the equality of a discrete logarithm over multiple bases, say $Po{E}_{mDL}$. Given two subsets $\{g_1,\cdots ,g_d\}$ and $\{h_1,\cdots ,h_d\}$ of a group $\mathbb{G}$, $Po{E}_{mDL}$ allows the prover to convince the verifier that ${\prod }_{i=1}^d{g}_i^{a_i}$ and ${\prod }_{i=1}^d{h}_i^{b_i}$ have equal exponents, i.e., $a_i=b_i$ for $i=1,\cdots ,d$, without disclosing raw exponents. A number of studies on $Po{E}_{mDL}$ have been carried out independently of the construction of polynomial commitment schemes. This work bridges two rather independent proof systems and provides a blueprint to combine these proof systems for the construction of an efficient, transparent polynomial commitment scheme in the discrete log setting.
• We propose a recursive argument to show the correct polynomial evaluation by employing $Po{E}_{mDL}$. Our approach is to transpose a recursive argument from a class group in [6] to that from the discrete log setting. We present a security analysis to demonstrate the completeness and soundness of the proposed protocol. In addition, We present a zero-knowledge version of the obtained polynomial commitment scheme. A zero-knowledge version ensures that no information of the prover’s secret polynomial $f\left(X\right)$ is leaked while the prover convinces the verifier that $y=f\left(x\right)$ holds for a point $(x,y)$.

The remainder of this paper is organized as follows. In Section 2, we review related works. In Section 3, we provide the background on the hardness assumption and building blocks for polynomial commitment schemes. In Section 4, we present our approach to transpose Bünz et al.’s techniques in the discrete log setting and investigate a sub-routine protocol as a sufficient condition for our approach. In Section 5, we discuss the performance and security of our approach. In Section 6, we extend the polynomial commitment scheme in the previous section to the version with a zero-knowledge evaluation protocol. Finally, we provide some concluding remarks in Section 7.

2. Related Work

A lot of recent research on polynomial commitment schemes have been carried out in the context of Succinct Non-interactive ARguments of Knowledge (SNARKs). In particular, a polynomial commitment scheme provides a key tool to generate a zk-SNARK from a polynomial interactive oracle proof (IOP) [3,6].

Kate et al. first constructed efficient and succinct polynomial commitment schemes for univariate polynomials [10]. The construction is based on bilinear pairings over elliptic curves and requires a trusted setup. Its extension to multivariate polynomials has been proposed by Papamanthou et al. [16] and Zhang et al. [17]. Zhang et al. [18] also presented the zero-knowledge version of their work [17]. These schemes all use bilinear pairings and require a trusted setup.

Associated with transparent SNARKs, polynomial commitment schemes with a transparent setting have received significant attention and, along with the previously mentioned constructions, many schemes can be found in the literature. Bootle et al. [14] constructed a transparent polynomial commitment scheme in the discrete log setting. They represent a polynomial of degree d as a matrix with $\sqrt{d}$ rows and columns and then write a polynomial evaluation as matrix multiplications. This leads to a $O\left(\sqrt{d}\right)$ commitment size, verifier complexity, and communication complexity. Wahby et al. presented a transparent polynomial commitment scheme [7] for multilinear polynomials under the discrete log assumption. The scheme is built on the ideas of a matrix commitment of Bootle et al. [14] and the inner-product argument of Bünz et al. [19]. For a polynomial of degree d, the $O\left(\sqrt{d}\right)$ commitment size, verifier complexity, and communication complexity are required. Ben-Sasson et al. [20] introduced the Fast Reed Solomon IOP of Proximity (FRI), which implicitly yields a transparent polynomial commitment scheme. Kattis et al. [8] and Zhang et al. [21] independently presented a method for obtaining polynomial commitment schemes from FRI. Their construction has $O\left(\lambda \right)$ size commitments for the security parameter $\lambda$ and $O\left({log}^{2}d\right)$ communication complexity and supports quantum resistance. In addition, Lee [22] proposed a multivariate polynomial commitment scheme with a transparent setting using pairing-based commitments. The scheme builds on inner product arguments given in Bootle et al. [14] and Bünz et al. [6]. Recently, Boneh et al. [23] studied additive polynomial commitment schemes, where commitments form an additive group [6,10,14,19,22]. They showed that the additive property yields a batch evaluation of polynomial commitments, which can be used for the efficient construction of SNARKs.

Groups of unknown order provide a mathematical structure for interesting cryptographic applications, such as delay functions [24], accumulators [25], and polynomial commitment schemes [6]. Most cryptographic applications consider two candidate groups of unknown order, i.e., RSA groups [26] and ideal class groups of imaginary quadratic fields [27]. RSA groups assume a trusted setup in generating the RSA modulus and hence do not meet our current interest. By contrast, class groups do not require a trusted setup and thus have been used in recent constructions with a transparent setting [6,24,25]. Dobson and Galbraith [13] analyzed the security of the candidate parameters for class groups proposed in [11,12]. They argued that the parameters in [11,12] do not meet the desired security level and present much larger parameters, which lead to an extremely large size-up for commitments in previous constructions. In this line of research, Belabas et al. [28] recently reported that the order assumption in class groups of imaginary quadratic fields does not hold in certain special classes of prime numbers. Some studies have explored alternative source groups of unknown order with a transparent setting. As an example, Dobson and Galbraith [13] suggested the Jacobian of hyperelliptic curves of genus 3, whereas Lee [29] pointed out that the order of the Jacobian of a hyperelliptic curve can be efficiently computed.

3. Preliminaries

Throughout the paper, $\lambda$ denotes the security parameter written in unary. The function $\mathsf{negl}:\mathbb{N}\to [0,1]$ denotes a negligible function, i.e., $\mathsf{negl}\left(\lambda \right)=1-{\lambda }^{\omega \left(1\right)}$. For a set S, we use $e\stackrel{\$}{\leftarrow }S$ to denote that an element e is sampled uniformly at random from S. For a probabilistic algorithm A, we write $y\leftarrow A\left(x\right)$ to denote that y is returned as the result of A on input x together with a randomness r picked internally.

3.1. The Discrete Logarithm Assumptions

Let $\mathsf{Ggen}$ be an algorithm that takes on input $\lambda$ and returns a $\lambda$-bit prime number p, cyclic group $\mathbb{G}$ of order p, and a generator g of $\mathbb{G}$.

Definition 1

(Discrete Logarithm Assumption). The discrete logarithm assumption holds relative to $\mathsf{Ggen}$ if for any polynomial-time adversary $\mathcal{A}$,

$$Pr\left[g^a=h:\begin{array}{c}(\mathbb{G},p,g)\leftarrow \mathsf{Ggen}\left(1^{\lambda }\right),\\ h\stackrel{\$}{\leftarrow }\mathbb{G},\\ a\leftarrow \mathcal{A}(\mathbb{G},p,g,h)\end{array}\right]\le \mathsf{negl}\left(\lambda \right).$$

Definition 2

(Discrete Logarithm Relation Assumption). The discrete logarithm relation assumption holds relative to $\mathsf{Ggen}$ if for any polynomial-time adversary $\mathcal{A}$,

$$Pr\left[\exists a_i\ne 0\wedge \prod _{i=0}^n{g}_i^{a_i}=1:\begin{array}{c}(\mathbb{G},p,g_0)\leftarrow \mathsf{Ggen}\left(1^{\lambda }\right),\\ g_1,\cdots ,g_n\stackrel{\$}{\leftarrow }\mathbb{G},\\ a_0,\cdots ,a_n\leftarrow \mathcal{A}\left(\mathbb{G},p,g_0,\cdots g_n\right)\end{array}\right]\le \mathsf{negl}\left(\lambda \right).$$

In the above definition, ${\prod }_{i=0}^n{g}_i^{a_i}=1$ for some $a_i\ne 0$ is called a non-trivial discrete logarithm relation. It is well-known that the discrete logarithm relation assumption is equivalent to the discrete logarithm assumption [14].

3.2. Zero-Knowledge Arguments of Knowledge

Let $\mathcal{R}\subset \mathcal{S}\times \mathcal{W}$ be a polynomial-time-decidable binary relation. $s\in \mathcal{S}$ and $w\in \mathcal{W}$ are called a statement and a witness, respectively. We define $L_{\mathcal{R}}$ as the set $\{s\in {\{0,1\}}^{*}:\exists w\in {\{0,1\}}^{*}\mathrm{such} \mathrm{that}(s,w)\in \mathcal{R}\}$, which is called the language of $\mathcal{R}$. We consider an argument system for a relation $\mathcal{R}$ consisting of three probabilistic polynomial-time algorithms $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$. A non-interactive algorithm $\mathsf{Pgen}$ takes the security parameter $\lambda$ as an input and returns a common reference string (crs) $\mathsf{pp}$. $\mathcal{P}$ and $\mathcal{V}$ are called a prover and a verifier, respectively, and both are interactive algorithms. In addition, $\mathcal{P}$ takes as input a triple of $\mathsf{pp}$, a statement $s\in \mathcal{S}$, and a witness $w\in \mathcal{W}$. Moreover, $\mathcal{V}$ takes as input a pair of $\mathsf{pp}$ and a statement $s\in \mathcal{S}$ and outputs 0 or 1. We denote the transcript produced by $\mathcal{P}$ and $\mathcal{V}$ for an interaction by $\mathsf{tr}\leftarrow \mathcal{P}(\mathsf{pp},s,w),\mathcal{V}(\mathsf{pp},s)$ and write $\mathcal{P}(\mathsf{pp},s,w),\mathcal{V}(\mathsf{pp},s)=b$, where $b=1$ if $\mathcal{V}$ accepts and $b=0$ if $\mathcal{V}$ rejects.

Definition 3

(Argument of Knowledge). We call the triple $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ an argument of knowledge for relation $\mathcal{R}$ if it has completeness and witness-extended emulation, as defined below.

Definition 4

(Perfect Completeness). $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ has perfect completeness if for all non-uniform polynomial-time adversaries $\mathcal{A}$,

$$Pr\left[(s,w)\notin \mathcal{R}\vee \mathcal{P}(\mathsf{pp},s,w),\mathcal{V}(\mathsf{pp},s)=1:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Pgen}\left(1^{\lambda }\right),\\ (s,w)\leftarrow \mathcal{A}\left(\mathsf{pp}\right)\end{array}\right]=1.$$

Definition 5

(Witness-Extended Emulation [30,31]). $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ has witness-extended emulation if for every deterministic polynomial-time prover ${\mathcal{P}}^{*}$ there exists an expected polynomial-time emulator $\mathcal{E}$ such that for all non-uniform polynomial-time adversaries $\mathcal{A}$, the difference between the following two probabilities is less than or equal to $\mathsf{negl}\left(\lambda \right)$:

$$Pr\left[\mathcal{A}\left(\mathsf{tr}\right)=1:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Pgen}\left(1^{\lambda }\right),\\ (s,\mathsf{st})\in \mathcal{A}\left(\mathsf{pp}\right),\\ \mathsf{tr}\leftarrow {\mathcal{P}}^{*}(\mathsf{pp},s,\mathsf{st}),\mathcal{V}(\mathsf{pp},s)\end{array}\right]and$$

$$Pr\left[\mathcal{A}\left(\mathsf{tr}\right)=1\wedge if\mathsf{tr}is accepting, then (s,w)\in \mathcal{R}:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Pgen}\left(1^{\lambda }\right),\\ (s,\mathsf{st})\in \mathcal{A}\left(\mathsf{pp}\right),\\ \mathsf{tr}\leftarrow {\mathcal{P}}^{*}(\mathsf{pp},s,\mathsf{st}),\mathcal{V}(\mathsf{pp},s)\end{array}\right],$$

where the oracle called by ${\mathcal{E}}^{{\mathcal{P}}^{*}(\mathsf{pp},s,\mathsf{st}),\mathcal{V}(\mathsf{pp},s)}$ permits rewinding to any round and running again on fresh verifier randomness, and $\mathsf{st}$ is the initial state of ${\mathcal{P}}^{*}$.

Definition 6

(Public Coin). An argument system $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ is called public coin if the verifier chooses its messages uniformly at random, and independently of the messages sent by the prover, i.e., the challenges correspond to the verifier’s randomness.

We recall special honest verifier zero-knowledge, which states that the view of the verifier can be simulated if the verifier follows the protocol honestly and if challenges made by the verifier are known in advance.

Definition 7

(Perfect SHVZK). A public coin argument system $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ is called a perfect special honest verifier zero-knowledge (SHVZK) argument for relation $\mathcal{R}$ if there exists a probabilistic polynomial-time simulator $\mathsf{Sim}$ such that for all interactive non-uniform polynomial-time adversaries $\mathcal{A}$,

$$Pr\left[\mathcal{A}\left(tr\right)=1\wedge (s,w)\in \mathcal{R}:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Pgen}\left(1^{\lambda }\right),\\ (s,w,\rho )\leftarrow \mathcal{A}\left(\mathsf{pp}\right),\\ \mathsf{tr}\leftarrow \mathcal{P}(\mathsf{pp},s,w),\mathcal{V}(\mathsf{pp},s)\end{array}\right]$$

$$=Pr\left[\mathcal{A}\left(tr\right)=1\wedge (s,w)\in \mathcal{R}:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Pgen}\left(1^{\lambda }\right),\\ (s,w,\rho )\leftarrow \mathcal{A}\left(\mathsf{pp}\right),\\ \mathsf{tr}\leftarrow \mathsf{Sim}(s,\rho )\end{array}\right],$$

where ρ is the public coin randomness used by the verifier.

The general forking lemma [6,14] is useful for proving that an argument system has witness-extended emulation. Consider a public coin interactive argument system with r rounds. We view ${\prod }_{i=1}^r{n}_i$ distinct accepting transcripts as having a tree format with depth r and ${\prod }_{i=1}^r{n}_i$ leaves, which we call an $(n_1,\cdots ,n_r)$-tree. For $1\le i\le r$, let $c_i$ be the i-th round challenge chosen among exactly $n_i\ge 1$ values. The root node is labeled with a statement s and has exactly $n_1$ children labeled with a distinct value for $c_1$, where each edge from the root to a child is labeled with a message from the prover to the verifier on $c_1$. Similarly, each node in depth $1\le i\le r-1$ is labeled with a distinct value for $c_i$ and has $n_{i+1}$ children labeled with a distinct value for $c_{i+1}$, where each edge from $c_i$ to $c_{i+1}$ is labeled with a message from the prover to the verifier on $c_i$. Note that each path from the root to a leaf then corresponds to an accepting transcript.

Lemma 1

(General Forking Lemma [6,14]). Let $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ be a public coin argument system for relation $\mathcal{R}$ with r rounds. Let χ be a witness extraction algorithm that succeeds with overwhelming probability in extracting a witness from an $(n_1,\cdots ,n_r)$-tree of accepting transcripts in probabilistic polynomial time. If ${\prod }_{i=1}^r{n}_i$ is bounded above by a polynomial in the security parameter λ, $(\mathsf{Pgen},\mathcal{P},\mathcal{V})$ has witness-extended emulation.

3.3. Commitment Schemes

We review the definitions and security properties regarding the polynomial commitment schemes. In the following, we use a tuple $(a_0,\cdots ,a_n;b_0,\cdots ,b_{n^{\prime }})$ for arguments or a returned tuple of the prover $\mathcal{P}$ and the verifier $\mathcal{V}$. In a tuple, $(a_0,\cdots ,a_n)$ before the semicolon and $(b_0,\cdots ,b_{n^{\prime }})$ after it denotes public variables known to both $\mathcal{P}$ and $\mathcal{V}$, and secret variables known to only $\mathcal{P}$, respectively.

Definition 8

(Commitment Scheme). A commitment scheme is a triple $(\mathsf{Cgen},\mathsf{Commit},\mathsf{Open})$ of probabilistic polynomial-time algorithms defined as follows:

• $\mathsf{pp}\leftarrow \mathsf{Cgen}\left(1^{\lambda }\right)$takes the security parameter λ on input, and outputs the public parameter$\mathsf{pp}$, which specifies a message space, a randomness space, and a commitment space;
• $(c;r)\leftarrow \mathsf{Commit}(\mathsf{pp};m,r)$takes a secret message m and an optional random r chosen uniformly at random on input and returns a commitment c and (optionally) a secret opening hint r;
• $b\in \{0,1\}\leftarrow \mathsf{Open}(\mathsf{pp},c,m,r)$verifies the commitment c to the message m provided with the opening hint r. It outputs$b=1$if the commitment is valid and$b=0$otherwise.

A commitment scheme is binding if for all non-uniform polynomial-time adversaries$\mathcal{A}$,

$$Pr\left[b_0=b_1\ne 0\wedge m_0\ne m_1:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Cgen}\left(1^{\lambda }\right),\\ (c,m_0,m_1,r_0,r_1,\rho )\leftarrow \mathcal{A}\left(\mathsf{pp}\right),\\ b_0\leftarrow \mathsf{Open}(\mathsf{pp},c,x_0,r_0),\\ b_1\leftarrow \mathsf{Open}(\mathsf{pp},c,x_1,r_1)\end{array}\right]\le \mathsf{negl}\left(\lambda \right).$$

A commitment scheme is hiding if for all non-uniform polynomial-time adversaries$\mathcal{A}=({\mathcal{A}}_0,{\mathcal{A}}_1)$,

$$\left|\frac{1}{2}-Pr\left[b^{\prime }=b:\begin{array}{c}\mathsf{pp}\leftarrow \mathsf{Cgen}\left(1^{\lambda }\right),\\ (m_0,m_1,\mathsf{st})\leftarrow {\mathcal{A}}_0\left(\mathsf{pp}\right),\\ b\stackrel{\$}{\leftarrow }\{0,1\},\\ (c;r)\leftarrow \mathsf{Commit}(\mathsf{pp};m_b,r),\\ b^{\prime }\leftarrow {\mathcal{A}}_1(\mathsf{st},c)\end{array}\right]\right|\le \mathsf{negl}\left(\lambda \right).$$

In a polynomial commitment scheme, $\mathcal{V}$ additionally checks whether the evaluation at any point is correct with respect to the committed polynomial $f\left(X\right)$ given by $\mathcal{P}$. The below definition of polynomial commitment schemes is given by Bünz et al. [6], which extends that of Kate et al. [10].

Definition 9

(Polynomial Commitment Scheme [6,10]). Let $(\mathsf{Cgen},\mathsf{Commit},\mathsf{Open})$ be a commitment scheme for a message space $R\left[X\right]$ over a ring R. A polynomial commitment scheme additionally consists of a protocol $\mathsf{Eval}$ as follows:

• $b\in \{0,1\}\leftarrow \mathsf{Eval}(\mathsf{pp},c,x,y,d;f\left(X\right),r)$is an interactive public coin protocol between$\mathcal{P}$and$\mathcal{V}$. Both$\mathcal{P}$and$\mathcal{V}$have as input a commitment c, points$x,y\in R$, and a degree d. In addition, $\mathcal{P}$knows the opening of c to a secret polynomial$f\left(X\right)\in R\left[X\right]$with$deg\left(f\right(X\left)\right)\le d$and a secret opening hint r. $\mathcal{P}$convinces$\mathcal{V}$that$f\left(x\right)=y$by applying the protocol.

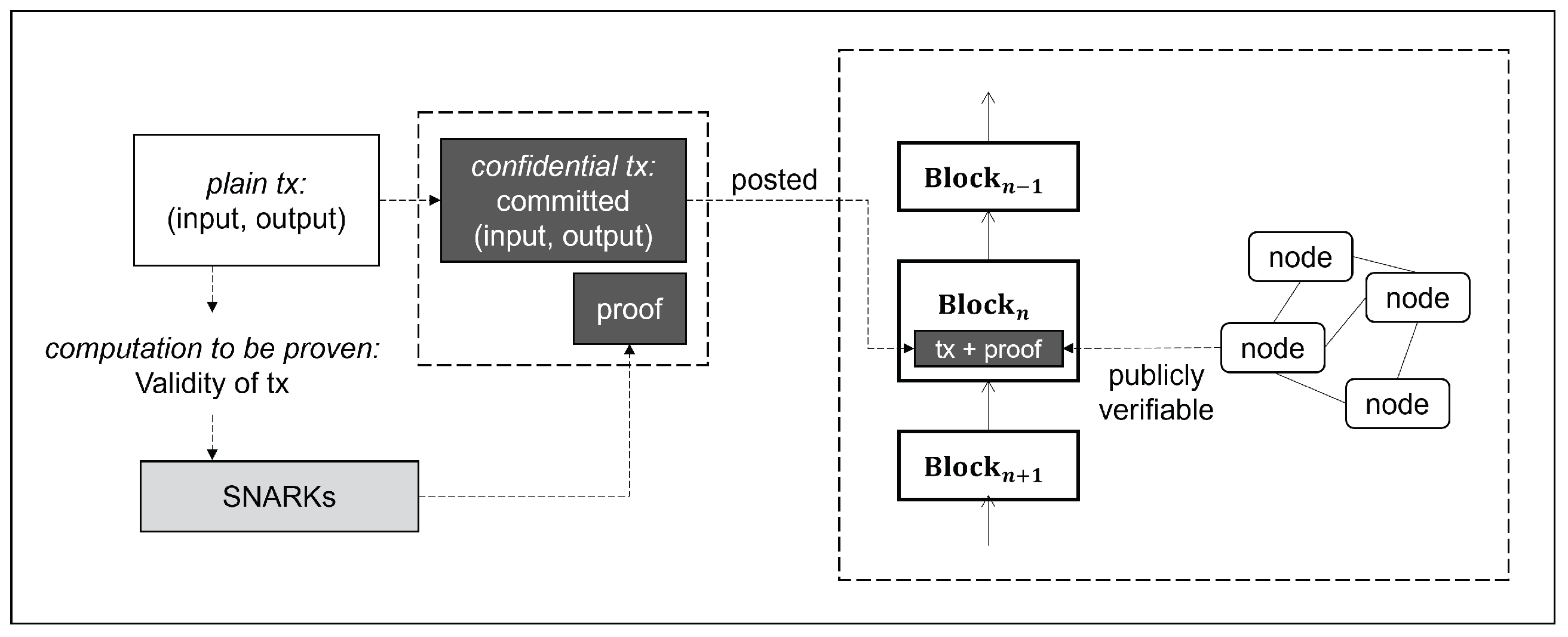
3.4. Privacy-Preserving Blockchain with SNARKs

Recently, SNARKs have been receiving a lot of attention from the blockchain industry as a solution for balancing privacy and publicly-verifiable integrity. For instance, Zcash employs SNARKs to provide Bitcoin with user anonymity and privacy of transaction data with anonymous coins [1]. SNARKs are also used to verify Ethereum smart contracts over private input [2].

Figure 1 presents a high-level architecture of privacy-preserving blockchains with SNARKs. A typical way that SNARKs are used in blockchains is as follows. The real data is stored in off-chain storage. The data posted to the on-chain blockchain (blockchain ledger) consist of the commitment to the transaction and its proof that the target transaction is valid. Cryptographic commitment schemes ensure that it is very difficult to obtain the original input value from the committed value, and the proof generated using SNARKs can be verifiable by any node in the blockchain network. Therefore, the privacy problem is solved because the data is hidden in the public on-chain blockchain. In addition, since zero-knowledge techniques provide fast verification, they are being used in various ways to improve the performance and minimize the size of the blockchain. It is worth noting that a polynomial commitment scheme is a key building block to compile a polynomial IOP system, which is a formal representation of a proving statement, into a SNARK [3,6].

4. Our Approach

In this section, we present our approach to transpose Bünz et al.’s techniques in the discrete log setting. We investigate and identify a sufficient condition for a transposition. Specifically, we show how to employ a proof system for the equality of discrete logarithms. For the rest of this paper, we encode a polynomial $f\left(X\right)={\sum }_{i=0}^{d-1}{f}_i{X}^i$ over a field $\mathbb{F}$ into a vector $\mathit{f}=(f_0,\cdots ,f_{d-1})\in {\mathbb{F}}^d$. For a group $\mathbb{G}$ let $\mathit{g}$ be a vector $(g_0,\cdots ,g_{\ell -1})\in {\mathbb{G}}^{\ell }$ for some positive integer ℓ. For $d\le \ell$ we denote the multi-exponentiation ${\prod }_{i=0}^{d-1}{g}_i^{f_i}$ by ${\mathit{g}}^{\mathit{f}}$. When it is clear from the context, we write the commitment to a polynomial $f\left(X\right)$ as $\mathsf{Commit}\left(f\right)$ instead of $\mathsf{Commit}(\mathsf{pp};f\left(X\right),r)$ for the sake of convenience. We also take a finite field $\mathbb{F}$ as ${\mathbb{Z}}_p$ for a prime p.

Table 1. Notations.

Notation	Definition
$\mathcal{P}$, $\mathcal{V}$	the prover and verifier of a proof system
$\mathbb{F}$	finite field (usually ${\mathbb{Z}}_p$ with a prime p)
$\mathbb{G}$	a group of a prime order p
$\left|\mathbb{G}\right|$	the size of an element of $\mathbb{G}$
$\left[\mathbb{G}\right]$	the computation cost for group operation in $\mathbb{G}$
$f\left(X\right)$, $deg\left(f\right(X\left)\right)$	a polynomial $f\left(X\right)\in \mathbb{F}\left[X\right]$ and its degree, respectively
$f_L\left(X\right)$, $f_R\left(X\right)$	the left and right half parts of a polynomial $f\left(X\right)$, respectively
$\mathit{f}$	the vector representation $(f_0,\cdots ,f_{d-1})$ of a polynomial $f\left(X\right)={\sum }_{i=0}^{d-1}{f}_i{X}^i\in \mathbb{F}\left[X\right]$
$\mathit{g}$	$(g_0,\cdots ,g_{\ell })\in {\mathbb{G}}^{\ell }$ for some positive integer ℓ
${\mathit{g}}^{\mathit{f}}$	${\prod }_{i=0}^{d-1}{g}_i^{f_i}$ for $\mathit{g}=(g_0,\cdots ,g_{\ell })\in {\mathbb{G}}^{\ell }$ and $\mathit{f}=(f_0,\cdots ,f_{d-1})$ where $d\le \ell$
$\mathsf{Commit}\left(f\right)$	the commitment to a polynomial $f\left(X\right)\in \mathbb{F}\left[X\right]$
${\mathsf{Commit}}_{\mathsf{H}}\left(f\right)$	the hiding commitment to a polynomial $f\left(X\right)\in \mathbb{F}\left[X\right]$
$Po{E}_{mDL}$	a proof system for equality of discrete logarithms over multiple bases
$|Po{E}_{mDL}|$	the communication complexity of $Po{E}_{mDL}$
${\left[Po{E}_{mDL}\right]}_{\mathcal{P}},{\left[Po{E}_{mDL}\right]}_{\mathcal{V}}$	the computation costs of $\mathcal{P}$ and $\mathcal{V}$ for $Po{E}_{mDL}$, respectively

presents frequently-used notations in the paper.

4.1. Bünz et al.’s Abstraction

Bünz et al. [6] presented a polynomial commitment scheme for their construction of SNARKs. The proposed scheme operates in a recursive way by reducing the degree of polynomial f by half during each iteration, and hence, there are $logdeg\left(f\right)$ iterations overall. More precisely, given an odd degree d polynomial $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i$, the prover splits it into two polynomials

$$f_L\left(X\right)=\sum _{i=0}^{\frac{d+1}{2}-1}{f}_i{X}^i \mathrm{and} f_R\left(X\right)=\sum _{i=0}^{\frac{d+1}{2}-1}{f}_{\frac{d+1}{2}+i}{X}^i,$$

which both polynomials have a degree of roughly $d/2$ satisfying

$$f\left(X\right)=f_L\left(X\right)+X^{d/2}{f}_R\left(X\right).$$

(1)

The prover then sends the verifier the commitments $\mathsf{Commit}\left(f_L\right)$ and $\mathsf{Commit}\left(f_R\right)$ to $f_L\left(X\right)$ and $f_R\left(X\right)$, respectively. At the end of each iteration, the prover takes the next input polynomial as

$$f\left(X\right)\leftarrow f_L\left(X\right)+\alpha f_R\left(X\right)$$

(2)

for a random $\alpha$ received from the verifier.

Because the verifier needs to check if $f\left(x\right)=y$ from committed polynomials, the verifier should be able to homomorphically compute a committed form of the current $f\left(X\right)$ and the next $f\left(X\right)$ from $\mathsf{Commit}\left(f_L\right)$ and $\mathsf{Commit}\left(f_R\right)$ to see whether (1) holds. The verifier also needs to compute a commitment to a polynomial in (2) for the next iteration from $\mathsf{Commit}\left(f_L\right)$ and $\mathsf{Commit}\left(f_R\right)$.

To support the computation of the committed form, Bünz et al. [6] define the following two abstract properties.

• linear homomorphism
  $\mathsf{Commit}{\left(f\right)}^a·\mathsf{Commit}{\left(g\right)}^b=\mathsf{Commit}(a·f+b·g)$ for polynomials f and g, and scalars a and b (a linear homomorphism);
• monomial homomorphism
  $\mathsf{Commit}{\left(f\right)}^{X^d}=\mathsf{Commit}(X^d·f)$ for some bounded positive integer d.

Figure 2 illustrates Bünz et al.’s abstraction for a polynomial commitment scheme with a recursive argument from the above two properties.

4.2. Base Commitment Scheme to Polynomial

We construct a polynomial commitment scheme based on a generalization of the Pedersen commitment scheme [32]. In the generalized Pedersen commitment, $\mathsf{pp}$ consists of a group $\mathbb{G}$ of a prime order p, and group elements $g,g_0,...,g_{n-1}\stackrel{\$}{\leftarrow }\mathbb{G}$. For a secret message vector $\mathit{m}=(m_0,\cdots ,m_{n-1})\in {\mathbb{Z}}_p^n$ the prover chooses $r\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ and computes

$$\left(g^r\prod _{i=0}^{n-1}{g}_i^{m_i};r\right)\leftarrow \mathsf{Commit}(\mathsf{pp};\mathit{m},r).$$

It is well-known that the generalized Pedersen commitment is perfectly hiding and computationally binding under the discrete logarithm relation assumption [32]. It is also important to note that the generalized Pedersen commitment scheme is homomorphic, i.e.,

$$\mathsf{Commit}(\mathsf{pp};\mathit{m},r)·\mathsf{Commit}(\mathsf{pp};{\mathit{m}}^{\prime },r^{\prime })=\mathsf{Commit}(\mathsf{pp};\mathit{m}+{\mathit{m}}^{\prime },r+r^{\prime }).$$

We consider a commitment scheme, which does not use the randomness in the generalized Pedersen commitment scheme, as follows:

• $\mathsf{Cgen}\left(1^{\lambda }\right)$: On input of the security parameter $\lambda$, it first samples $\mathbb{G}\leftarrow \mathsf{Ggen}\left(1^{\lambda }\right)$ of a prime order p of length $\lambda$. It then chooses $g_0,\cdots ,g_d\stackrel{\$}{\leftarrow }\mathbb{G}$ and returns $\mathsf{pp}=(\mathbb{G},p,\mathit{g})$ where $\mathit{g}=(g_0,\cdots ,g_d)$.
• $\mathsf{Commit}(\mathsf{pp};f\left(X\right))$: For a secret polynomial $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i\in {\mathbb{Z}}_p\left[X\right]$ with
  $deg\left(f\right(X\left)\right)\le d$, it computes and outputs $c\leftarrow {\mathbf{g}}^{\mathbf{f}}={\prod }_{i=0}^d{g}_i^{f_i}$.
• $\mathsf{Open}(\mathsf{pp},c,f\left(X\right))$: On input c and $f\left(X\right)$, the verifier computes $c^{\prime }\leftarrow {\prod }_{i=0}^d{g}_i^{f_i}$ and checks if $c=c^{\prime }$ in $\mathbb{G}$.

Because the generalized Pedersen commitment scheme is computationally binding under the discrete logarithm relation assumption, so is the commitment scheme above.

4.3. Evaluation Protocol

As presented in Section 4.1, Bünz et al.’s approach considers two properties (a linear homomorphism and a monomial homomorphism) for the underlying commitment schemes, which is crucial for the verifier to compute (1) from the commitments to the polynomials $f_L$ and $f_R$ on the right-hand side. However, our base commitment scheme does not provide monomial homomorphism, while it immediately holds the linear homomorphic property. A monomial homomorphic commitment scheme is not known thus far in the discrete log setting with no trusted setup. This is because a monomial homomorphic property may require some special structures for base elements in the group, which is impossible to generate without a trusted setup.

Thus, our approach focuses on providing a way to check the integrity of $f_L$ and $f_R$, i.e., $f=f_L+X^{d/2}·f_R$ using the linear homomorphic property only. The idea behind our approach is presented in Figure 3. To avoid monomial homomorphism, our approach simply lets the prover send one additional commitment to $X^{d/2}·f_R$ besides two commitments to $f_L$ and $f_R$ so that $f=f_L+X^{d/2}·f_R$ can be verified using the linear homomorphic property.

We present the evaluation protocol $\mathsf{Eval}$ in Algorithm 1, which is a transposition of Bünz et al.’s construction [6] in the discrete log setting. In Line 13 of the $\mathsf{Eval}$ protocol, the prover sends one additional commitment $c_{RR}\leftarrow \mathsf{Commit}(X^{d/2}·f_R)$. The verifier is then able to compute $\mathsf{Commit}\left(f\right)=\mathsf{Commit}\left(f_L\right)·\mathsf{Commit}(X^{d/2}·f_R)$ using a linear homomorphic property of the underlying commitment scheme (Line 13). However, because the polynomial $f_R\left(X\right)$ is committed to $c_R$ and $c_{RR}$ independently, it is required for the prover to prove that $c_R$ and $c_{RR}$ are generated from the same polynomial $f_R\left(X\right)$. More precisely, given public parameter $\mathsf{pp}\left(=\{g_0,\cdots ,g_d\}\right)$ and two target instances $c_R\left(={\prod }_{i=0}^{d^{\prime }}{g}_i^{f_{d^{\prime }+1+i}}\right)$ and $c_{RR}\left(={\prod }_{i=0}^{d^{\prime }}{g}_{d^{\prime }+1+i}^{f_{d^{\prime }+1+i}}\right)$, the prover needs to convince the verifier that $c_R$ and $c_{RR}$ have the same exponents. Thus, we require a proof for equality of discrete logarithms, which is invoked as a sub-protocol $Po{E}_{mDL}$ in the $\mathsf{Eval}$ protocol (Line 12). $Po{E}_{mDL}$ takes $\mathsf{pp}$, $c_R$, $c_{RR}$, and $deg\left(f_R\left(X\right)\right)=d^{\prime }$ on input and returns 1 if $c_R$ and $c_{RR}$ have the same exponents and 0 otherwise. If the returned value is 0, $\mathcal{V}$ aborts the $\mathsf{Eval}$ protocol because $\mathcal{P}$ is a cheating prover. We remark that several cryptographic protocols on $Po{E}_{mDL}$ have been proposed [33,34]. The works for $Po{E}_{mDL}$ have been developed independently from the construction of polynomial commitment schemes.

Algorithm 1$\mathsf{Eval}(\mathsf{pp},c\in \mathbb{G},x\in {\mathbb{Z}}_p,y\in {\mathbb{Z}}_p,d\in \mathbb{N};f\left(X\right)\in {\mathbb{Z}}_p\left[X\right])$
Common input: public parameter $\mathsf{pp}$, commitment $c={\prod }_{i=0}^d{g}_i^{f_i}$ to $f\left(X\right)$, point $(x,y=f(x\left)\right)$, degree bound d Prover’s witness: secret polynomial $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i$
1: if $d=0$ then
2:  $\mathcal{P}$ sends $f\left(X\right)=f_0\in {\mathbb{Z}}_p$ to $\mathcal{V}$	// $f\left(X\right)$ is a constant $f_0$
3:  $\mathcal{V}$ checks that $f_0=y$ in ${\mathbb{Z}}_p$
4:  $\mathcal{V}$ checks that $g_0^{f_0}=c$ in $\mathbb{G}$
5:  $\mathcal{V}$ returns 1 if all checks pass, 0 otherwise
6: else
7:  $\mathcal{P}$ and $\mathcal{V}$ compute $d^{\prime }\leftarrow \lfloor \frac{d}{2}\rfloor$
8:  $\mathcal{P}$ sets $f_L\left(X\right)\leftarrow {\sum }_{i=0}^{d^{\prime }}{f}_i{X}^i$ and $f_R\left(X\right)\leftarrow {\sum }_{i=0}^{d^{\prime }}{f}_{d^{\prime }+1+i}{X}^i$	//If d is even, then $f_{2d^{\prime }+1}=0$
9:  $\mathcal{P}$ computes $c_L\leftarrow {\prod }_{i=0}^{d^{\prime }}{g}_i^{f_i}$, $c_R\leftarrow {\prod }_{i=0}^{d^{\prime }}{g}_i^{f_{d^{\prime }+1+i}}$, and $c_{RR}\leftarrow {\prod }_{i=0}^{d^{\prime }}{g}_{d^{\prime }+1+i}^{f_{d^{\prime }+1+i}}$ in $\mathbb{G}$
10:  $\mathcal{P}$ computes $y_L\leftarrow f_L\left(x\right)$ and $y_R\leftarrow f_R\left(x\right)$ in ${\mathbb{Z}}_p$
11:  $\mathcal{P}$ sends $\{c_L,c_R,c_{RR},y_L,y_R\}$ to $\mathcal{V}$
12:  $\mathcal{P}$ and $\mathcal{V}$ run $Po{E}_{mDL}(pp,c_R,c_{RR},d^{\prime })$	//Checking that $mDL\left(c_R\right)=mDL\left(c_{RR}\right)$
13:  $\mathcal{V}$ checks that $c=c_L·c_{RR}$ in $\mathbb{G}$ and returns 0 if the equation does not hold
14:  $\mathcal{V}$ checks that $y=y_L+y_R·x^{d^{\prime }+1}$ in ${\mathbb{Z}}_p$ and returns 0 if the equation does not hold
15:  $\mathcal{V}$ chooses $\alpha \stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ and sends it to $\mathcal{P}$
16:  $\mathcal{P}$ and $\mathcal{V}$ compute $c^{\prime }\leftarrow {\left(c_L\right)}^{\alpha }·c_R$ in $\mathbb{G}$ and $y^{\prime }\leftarrow \alpha ·y_L+y_R$ in ${\mathbb{Z}}_p$
17:  $\mathcal{P}$ computes $f^{\prime }\left(X\right)\leftarrow \alpha ·f_L\left(X\right)+f_R\left(X\right)$ in ${\mathbb{Z}}_p\left[X\right]$	//$deg\left(f^{\prime }\left(X\right)\right)=d^{\prime }$
18:  $\mathcal{P}$ and $\mathcal{V}$ run $\mathsf{Eval}(\mathsf{pp},c^{\prime },x,y^{\prime },d^{\prime };f^{\prime }\left(X\right))$

5. Discussion: Performance & Security Analysis

Let $\Pi =(\mathsf{Cgen},\mathsf{Commit},\mathsf{Open},\mathsf{Eval})$ be the polynomial commitment scheme described in Section 4. In this section, we analyze the performance and security of the $\mathsf{Eval}$ protocol.

5.1. Performance

We analyze the efficiency of our approach in comparison with the recently proposed schemes with a transparent setting found in the literature. For a concrete performance analysis, we borrow the examples of groups and parameters at the 128-bit security level given by Lee [22], which is presented in

Table 2. Efficiency comparison between groups. The time is measured for operations to multiply a random point (element) of a group by a 256-bit scalar.

Group, Operation		Size (bytes)	Time (μs)
Elliptic curve (EC) group	$\mathbb{G}$	32	45
Class group	${\mathbb{G}}_U$	832	38,000
	${\mathbb{G}}_1$	48	220
EC group with pairing	${\mathbb{G}}_2$	96	490
	${\mathbb{G}}_T$	192	820
EC pairing operation	P	-	1600

. In Table 2, $\mathbb{G}$ denotes a cyclic group of known order, which is implemented by curve25519-dalek [35]. An imaginary class group ${\mathbb{G}}_U$ [36] is taken as an example group of unknown order. The discriminant of ${\mathbb{G}}_U$ is fixed as $\Delta =-(2^{6656}-26,745)$, which is estimated to offer the 128-bit security level [13]. This is implemented by ANTIC [37]. For a pairing-based construction, ${\mathbb{G}}_1$, ${\mathbb{G}}_2$, and ${\mathbb{G}}_T$ denote the two source groups and the target group of a pairing P. The groups of pairing are implemented by RELIC [38] over the curve BLS12-381 [39].

We analyze the efficiency of our approach. Let $\left|\mathbb{G}\right|$ and $|Po{E}_{mDL}|$ be the size of an element in G and the communication complexity of $Po{E}_{mDL}$, respectively. Let $\left[\mathbb{G}\right]$, ${\left[Po{E}_{mDL}\right]}_{\mathcal{P}}$, and ${\left[Po{E}_{mDL}\right]}_{\mathcal{V}}$ be the computation cost in $\mathbb{G}$, the prover’s computation cost for $Po{E}_{mDL}$, and the verifier’s computation cost for $Po{E}_{mDL}$, respectively. Below we focus on the dominated terms for each complexity comprising the transmission and operations of the group elements, i.e., we neglect operations over a field ${\mathbb{Z}}_p$. The $\mathsf{Eval}$ protocol makes recursive calls roughly $logd$ times. The messages between the prover and the verifier consist of $logd$ times of three elements in $\mathbb{G}$, and $|Po{E}_{mDL}|$, respectively. Thus, the communication complexity is equal to $3logd·\left|\mathbb{G}\right|·|Po{E}_{mDL}|$. The prover applies $logd$ times of three multi-exponentiations [40] of roughly $d/2$ size and one operation over $\mathbb{G}$, and $Po{E}_{mDL}$ on the prover’s side. This leads to $O\left(d\right)·\left[G\right]·{\left[Po{E}_{mDL}\right]}_{\mathcal{P}}$ computation complexity for the prover. The verifier applies $logd$ times of one exponentiation and two operations over $\mathbb{G}$, and $Po{E}_{mDL}$ on the verifier’s side, which leads to $O(logd)·\left[\mathbb{G}\right]·{\left[Po{E}_{mDL}\right]}_{\mathcal{V}}$ computation complexity overall. The size of public parameter $pp$ is $d·\left|\mathbb{G}\right|·|Po{E}_{mDL}|$.

We now provide a comparison for polynomial commitment schemes [6,22] with a transparent setting, which achieves a logarithmic verifier complexity in

Table 3. Comparison between polynomial commitment schemes with a transparent setting. $|·|$ and $[·]$ denote the size of an element and the computation cost of a group operation in the corresponding group, respectively. We express communication complexity in the number of group elements and computation complexity in a number of group operations.

Scheme	Bünz et al. [6]	Lee [22]	Our Approach
Communication	$3·|{\mathbb{G}}_U|·logd$	$6·|{\mathbb{G}}_T|·logd$	$3·\left|\mathbb{G}\right|·|Po{E}_{mDL}|·logd$
Prover Computation	$\left[{\mathbb{G}}_U\right]·O\left(d\right)$	$\left[{\mathbb{G}}_1\right]·O\left(d\right)$	$\left[\mathbb{G}\right]·{\left[Po{E}_{mDL}\right]}_{\mathcal{P}}·O\left(d\right)$
Verifier Computation	$\left[{\mathbb{G}}_U\right]·O(logd)$	$\left[{\mathbb{G}}_T\right]·O(logd)$	$\left[\mathbb{G}\right]·{\left[Po{E}_{mDL}\right]}_{\mathcal{V}}·O(logd)$
Size of $\mathsf{pp}$	$|{\mathbb{G}}_U|·d$	$\left(\right|{\mathbb{G}}_1|+|{\mathbb{G}}_2\left|\right)·d$	$\left|\mathbb{G}\right|·|Po{E}_{mDL}|·d$

. The table focuses on the dominated terms for each complexity comprising the transmission and operations of the group elements. As mentioned above, We apply multi-exponentiation techniques [40] to both our approach and Bünz et al.’s construction to reduce the prover complexity by a factor of $logd$. In the case of Bünz et al.’s construction, it is possible to reduce the size of public parameter $\mathsf{pp}$ to a single element of ${\mathbb{G}}_U$ when multi-exponentiation techniques are not applied. Table 3 summarizes the efficiency analysis on communication and computation complexities, and the size of the public parameter for recent polynomial commitment schemes with transparent setting and our approach.

Table 3 shows that the efficiency of our approach depends on that of $Po{E}_{mDL}$. If $Po{E}_{mDL}$ has a constant communication/computation complexity, we observe that each complexity is almost the same across the schemes, and the efficiency of a scheme depends highly on the underlying group. The benchmark result on base groups in Table 2 shows that the sizes of the element in ${\mathbb{G}}_U$ and ${\mathbb{G}}_T$ are approximately $25\times$ and $6\times$ larger than that of $\mathbb{G}$, respectively. For the operation time, ${\mathbb{G}}_U$ and ${\mathbb{G}}_T$ are approximately $844\times$ and $18\times$ slower than that of $\mathbb{G}$, respectively.

The above discussion shows that our scheme based on an elliptic curve group in the discrete log setting is very promising in the case that we have an efficient $Po{E}_{mDL}$. Unfortunately, currently known $Po{E}_{mDL}$ protocols have $O\left(d\right)$ communication complexity for the number of bases, i.e., degree of a polynomial in our setting, which is not desirable for our purpose of logarithmic complexity. However, we emphasize that it is meaningful to observe that two independent cryptographic primitives are closely connected and suggest a stepping stone for the construction of an efficient, transparent polynomial commitment scheme with a recursive argument in the discrete log setting.

5.2. Security

We analyze perfect completeness (Definition 4) and witness-extended emulation (Definition 5) of the proposed polynomial commitment scheme.

Theorem 1.

The$\mathsf{Eval}$protocol of the polynomial commitment scheme Π has perfect completeness.

Proof of Theorem 1.

First, we show that the case of $d=0$ satisfies the perfect completeness. When $d=0$, the valid input consists of the constant polynomial $f\left(X\right)=f_0$, $c=g_0^{f_0} \mathsf{Commit}(\mathsf{pp};f\left(X\right))$, and $y=f_0$. Thus, the verification equations checked by $\mathcal{V}$ immediately hold.

Next, we consider the case of $d>0$. For the polynomial $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i\in {\mathbb{Z}}_p\left[X\right]$, let $t_{in}\leftarrow (c,x,y,d;f\left(X\right))$ and $t_{out}\leftarrow (c^{\prime },x,y^{\prime },d^{\prime };f^{\prime }\left(X\right))$ be the input and output tuples for every recursive step in the $\mathsf{Eval}$ protocol. For the perfect completeness, it suffices to show that $t_{out}$ satisfies the relations $c^{\prime }={\mathit{g}}^{{\mathit{f}}^{\prime }}$, $y^{\prime }=f^{\prime }\left(x\right)$, and $deg\left(f^{\prime }\left(X\right)\right)\le d^{\prime }$ when the relations $c={\mathit{g}}^{\mathit{f}}$, $y=f\left(x\right)$, and $deg\left(f\right(X\left)\right)\le d$ hold for $t_{in}$.

When $d+1$ is odd, we can see that $(c^{\prime },y^{\prime },f^{\prime }\left(X\right))$ from $t_{out}$ is exactly equal to $(c,y,f(X\left)\right)$ from $t_{in}$ and $deg\left(f^{\prime }\left(X\right)\right)=deg\left(f\left(X\right)\right)\le d\le d^{\prime }=d+1.$ Thus, the relation holds for $t_{out}$. When $d+1$ is even, we have $f_L\left(X\right)$ and $f_R\left(X\right)$, such that $f\left(X\right)=f_L\left(X\right)+X^{\frac{d+1}{2}}{f}_R\left(X\right)$ and $f^{\prime }\left(X\right)=\alpha ·f_L\left(X\right)+f_R\left(X\right)$. Thus, we can see that the following equations hold:

$$\begin{array}{cc}\hfill c^{\prime }& ={\left(c_L\right)}^{\alpha }·c_R={\mathit{g}}^{\alpha {\mathit{f}}_{\mathit{L}}}·{\mathit{g}}^{{\mathit{f}}_{\mathit{R}}}={\mathit{g}}^{\alpha {\mathit{f}}_{\mathit{L}}+{\mathit{f}}_{\mathit{R}}}={\mathit{g}}^{{\mathit{f}}^{\prime }},\hfill \\ \hfill y^{\prime }& =\alpha ·y_L+y_R=\alpha ·f_L\left(x\right)+f_R\left(x\right)=f^{\prime }\left(x\right),\hfill \\ \hfill c& ={\mathit{g}}^{\mathit{f}}=\prod _{i=0}^d{g}_i^{f_i}=\prod _{i=0}^{\frac{d+1}{2}-1}{g}_i^{f_i}·\prod _{i=\frac{d+1}{2}}^d{g}_i^{f_i}=\prod _{i=0}^{\frac{d+1}{2}-1}{g}_i^{f_i}·\prod _{i=0}^{\frac{d+1}{2}-1}{g}_{\frac{d+1}{2}+i}^{f_{\frac{d+1}{2}+i}}=c_L·c_{RR},\hfill \\ \hfill y& =y_L+y_R·x^{d^{\prime }}=f_L\left(x\right)+x^{\frac{d+1}{2}}{f}_R\left(x\right)=f\left(x\right).\hfill \end{array}$$

Finally, we have,

$$deg{f}^{\prime }\left(X\right)\le max\{deg{f}_L\left(X\right),deg{f}_R\left(X\right)\}\le d^{\prime }=\frac{d+1}{2}-1.$$

This completes the proof of the perfect completeness. □

We now prove that the $\mathsf{Eval}$ protocol is sound, i.e., it has witness-extended emulation. In brief, we need to show that we can extract a witness polynomial $f\left(X\right)$ from a tree of accepting transcripts, where the number of transcripts is bounded in a polynomial in $\lambda$. This can be done by extracting an intermediate secret polynomial at each iteration of $Eval$, i.e., from Level $i+1$ to Level i in the tree. In Lemma 2, we first show that given two accepting transcripts, we can extract an intermediate witness polynomial at each iteration of the $\mathsf{Eval}$ protocol. We then prove the witness-extended emulation for the whole $\mathsf{Eval}$ protocol by using the lemma from leaf nodes to the root node sequentially in Theorem 2.

Lemma 2.

Let $\mathsf{pp}=(\mathbb{G},p,g_0,\cdots ,g_d)$ be the public parameter generated by $\mathsf{Ggen}$. Suppose we have two accepting transcripts $(x,c_L,c_R,c_{RR},y_L,y_R,\alpha ,f\left(X\right),y)$ and $(x,c_L,c_R,c_{RR},y_L,y_R,{\alpha }^{\prime },$$f^{\prime }\left(X\right),y^{\prime })$ for two distinct numbers α, ${\alpha }^{\prime }\in {\mathbb{Z}}_p$, such that ${\mathit{g}}^{\mathit{f}}=c_L^{\alpha }{c}_R$ and ${\mathit{g}}^{{\mathit{f}}^{\prime }}=c_L^{{\alpha }^{\prime }}{c}_R$. Furthermore, suppose $f\left(X\right)$ and $f^{\prime }\left(X\right)$ are polynomials in ${\mathbb{Z}}_p\left[X\right]$ with a degree of at most d and $y=f\left(x\right),y^{\prime }=f^{\prime }\left(x\right)\in {\mathbb{Z}}_p$. Then on the input of the above transcripts, there exists a probabilistic polynomial-time algorithm $\mathcal{E}$ that extracts either $f_L\left(X\right),f_R\left(X\right)\in {\mathbb{Z}}_p\left[X\right]$ with a degree of at most d such that $y_L=f_L\left(x\right)\in {\mathbb{Z}}_p$, $y_R=f_R\left(x\right)\in {\mathbb{Z}}_p$, or a breach of the binding property of the Pedersen commitment scheme relative to $\mathsf{Ggen}$.

Proof of Lemma 2.

Because the two transcripts are valid, it holds that

$${\mathit{g}}^{\mathit{f}}={\left(c_L\right)}^{\alpha }·c_R,{\mathit{g}}^{{\mathit{f}}^{\prime }}={\left(c_L\right)}^{{\alpha }^{\prime }}·c_R\in \mathbb{G}.$$

We then have

$$\begin{array}{c}{\mathit{g}}^{\mathit{f}-{\mathit{f}}^{\prime }}={\left(c_L\right)}^{\alpha -{\alpha }^{\prime }}={\mathit{g}}^{(\alpha -{\alpha }^{\prime }){\mathit{f}}_{\mathit{L}}},\\ {\mathit{g}}^{\alpha {\mathit{f}}^{\prime }-{\alpha }^{\prime }\mathit{f}}={\left(c_R\right)}^{\alpha -{\alpha }^{\prime }}={\mathit{g}}^{(\alpha -{\alpha }^{\prime }){\mathit{f}}_{\mathit{R}}}.\end{array}$$

Thus, $\mathcal{E}$ is able to compute

$$f_L\left(X\right)\leftarrow \frac{f\left(X\right)-f^{\prime }\left(X\right)}{\alpha -{\alpha }^{\prime }},f_R\left(X\right)\leftarrow \frac{\alpha f^{\prime }\left(X\right)-{\alpha }^{\prime }f\left(X\right)}{\alpha -{\alpha }^{\prime }}$$

from the binding property of the Pedersen commitment scheme. In addition, because it holds that

$$f\left(x\right)=y=\alpha ·y_L+y_R\mathrm{and}{y}^{\prime }=f^{\prime }\left(x\right)={\alpha }^{\prime }·y_L+y_R,$$

we let $y_L\leftarrow \frac{y-y^{\prime }}{\alpha -{\alpha }^{\prime }}$ and $y_R\leftarrow \frac{\alpha y^{\prime }-{\alpha }^{\prime }y}{\alpha -{\alpha }^{\prime }}$. Then, $y_L$ and $y_R$ are identical to the evaluations of the above $f_L\left(X\right)$ and $f_R\left(X\right)$ at $X=x$, respectively. □

Theorem 2.

The $\mathsf{Eval}$ protocol has witness-extended emulation for a relation

$${\mathcal{R}}_{\mathsf{Eval}}=\left\{((c,x,y,d),f\left(X\right)):deg\left(f\left(X\right)\right)\le d\wedge f\left(x\right)=y\wedge \mathsf{Open}(\mathsf{pp},c,f\left(X\right))=1\right\}$$

if the discrete logarithm relation assumption holds for$\mathsf{Ggen}$.

Proof of Theorem 2.

For witness-extended emulation, we call the general forking lemma (Lemma 1). Thus, we need to construct an expected polynomial-time extractor $\mathcal{E}$ that extracts a witness from a tree whose number of leaves is bounded above by a polynomial in $\lambda$.

For the statement $(c,x,y,d)\in L_{{\mathcal{R}}_{\mathsf{Eval}}}$, we consider the following tree of the accepting transcripts. The root node is labeled with the first input statement $(c,x,y,d)$ to $\mathsf{Eval}$. Including the root node, let N be a node labeled with the statement $(c,x,y,d)$. We denote the corresponding witness polynomial to $(c,x,y,d)$ by $f^{\left(d\right)}\left(X\right)\in {\mathbb{Z}}_p\left[X\right]$. N has two child nodes as follows. By rewinding the oracle $\langle {\mathcal{P}}^{*},\mathcal{V}\rangle$ two times with two different challenges ${\alpha }_1$ and ${\alpha }_2$ on the same input statement $(c,x,y,d)$, each child node for the given challenge is labeled with the update statement $(c^{\prime },x,y^{\prime },d^{\prime })$. Finally, nodes with $d=0$ are leaf nodes of the tree. Because the number of levels with a branching factor of 2 is bounded by $\lceil log(d+1)\rceil$, there are at most $2^{1+\lceil {log}_2(d+1)\rceil }\le 4(d+1)$ transcripts in total, which is a polynomial in $\lambda$.

We now prove that there exists an extractor $\mathcal{E}$ that extracts a witness $f\left(X\right)$ from the above tree, which we construct in a recursive way. That is, we construct an extractor ${\mathcal{E}}^{\left(d\right)}$ to extract $f^{\left(d\right)}\left(X\right)$ for a statement $(c,x,y,d)$ at each node starting from the leaf nodes in the tree. We note that ${\mathcal{E}}^{\left(d\right)}$ for the degree bound d in the root node is a desired extractor $\mathcal{E}$.

We fist consider ${\mathcal{E}}^{\left(0\right)}$ to extract a witness from the leaves of the tree, i.e., $d=0$. In this case, ${\mathcal{E}}^{\left(0\right)}$ directly obtains a witness $f\left(X\right)=f_0\in {\mathbb{Z}}_p$ from the transcript given by the prover, such that $f_0=y$ and $c=g_0^{f_0}$. We now move to the case of $d>0$. From the construction of the tree, the node has two child nodes, where each node is labeled with the update statement $\left(c^{\prime },x,y^{\prime },d^{\prime }=\lfloor \frac{d}{2}\rfloor \right)$ on the same input statement $\left(c,x,y,d\right)$ with two distinct challenges ${\alpha }_1$ and ${\alpha }_2$. We assume that we have the extractor ${\mathcal{E}}^{\left(d^{\prime }\right)}$ that returns the valid witness $f^{\left(d^{\prime }\right)}$ for each child node. We then construct the extractor ${\mathcal{E}}^{\left(d\right)}$. ${\mathcal{E}}^{\left(d\right)}$ extracts $f_L^{\left(d\right)}\left(X\right)$ and $f_R^{\left(d\right)}\left(X\right)$ with a degree of at most $d^{\prime }$ by applying Lemma 2. It then returns

$$f^{\left(d\right)}\left(X\right)=f_L^{\left(d\right)}\left(X\right)+f_R^{\left(d\right)}\left(X\right)X^{d^{\prime }+1}\in {\mathbb{Z}}_p\left[X\right],$$

whose degree is bounded by $2d^{\prime }=2\lfloor \frac{d}{2}\rfloor \le d$. Because the tree consists of the accepting transcripts, we have $c={\mathit{g}}^{{\mathit{f}}^{\left(\mathit{d}\right)}}$ and $f^{\left(d\right)}\left(x\right)=f_L^{\left(d\right)}\left(x\right)+f_R^{\left(d\right)}\left(x\right)x^{d^{\prime }+1}=y$. Then, by the general forking lemma, we conclude that Π has witness extended emulation. □

6. Extension to Zero-Knowledge Polynomial Evaluation

In this section, we extend the polynomial commitment scheme from Section 4 to a zero-knowledge version. The zero-knowledge protocol enables the prover to convince the verifier that the prover has a polynomial $f\left(X\right)$ with $deg\left(f\right)\le d$ such that $f\left(x\right)=y$ for a public point $(x,y)$ but does not leak any other information about f that is formally defined in the notion of perfect SHVZK (Definition 7). For this, we require a hiding commitment scheme to polynomials, such as the generalization of the Pedersen commitment scheme, which uses randomness when generating a commitment [32]. Below, we give a formal description of the generalization of the Pedersen commitment scheme $({\mathsf{Cgen}}_{\mathsf{H}},{\mathsf{Commit}}_{\mathsf{H}},{\mathsf{Open}}_{\mathsf{H}})$ over the polynomials in ${\mathbb{Z}}_p\left[X\right]$.

• ${\mathsf{Cgen}}_{\mathsf{H}}\left(1^{\lambda }\right)$: On input of the security parameter $\lambda$, it first samples $\mathbb{G}\leftarrow \mathsf{Ggen}\left(1^{\lambda }\right)$ of a prime order p of length $\lambda$. It then chooses $g,g_0,\cdots ,g_d\stackrel{\$}{\leftarrow }\mathbb{G}$ and returns ${\mathsf{pp}}_{\mathsf{H}}=(\mathbb{G},p,g,g_0,\cdots ,g_d)\leftarrow \mathsf{Cgen}\left(1^{\lambda }\right)$.
• ${\mathsf{Commit}}_{\mathsf{H}}({\mathsf{pp}}_{\mathsf{H}};f\left(X\right),d,r)$: For a secret polynomial $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i\in {\mathbb{Z}}_p\left[X\right]$ it selects $r\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ and outputs $c\leftarrow g^r{\prod }_{i=0}^d{g}_i^{f_i}$ with secret opening information $f\left(X\right),d,r$.
• ${\mathsf{Open}}_{\mathsf{H}}({\mathsf{pp}}_{\mathsf{H}},c,f\left(X\right),r)$: On input c and $f\left(X\right)$, a verifier $\mathcal{V}$ computes $c^{\prime }\leftarrow g^r{\prod }_{i=0}^d{g}_i^{f_i}$ and checks if $c=c^{\prime }$ in $\mathbb{G}$.

We present our zero-knowledge evaluation protocol $\mathsf{EvalZK}$ in Algorithm 2. The $\mathsf{EvalZK}$ protocol is also obtained by transposing the corresponding zero-knowledge evaluation protocol given by Bünz et al. under the discrete log setting [6]. The basic idea is to mask the prover’s secret polynomial with a random polynomial using the blinding technique introduced in [14,19,41] and then run the $\mathsf{Eval}$ protocol on it.

Algorithm 2$\mathsf{EvalZK}({\mathsf{pp}}_{\mathsf{H}},c_f\in \mathbb{G},x\in {\mathbb{Z}}_p,y_f\in {\mathbb{Z}}_p,d\in \mathbb{N};f\left(X\right)\in {\mathbb{Z}}_p\left[X\right],r_f\in {\mathbb{Z}}_p$)
Common input: public parameter ${\mathsf{pp}}_{\mathsf{H}}$, commitment $c_f=g^{r_f}{\prod }_{i=0}^d{g}_i^{f_i}$ to $f\left(X\right)$, point $(x,y_f=f\left(x\right))$, degree bound d Prover’s witness: secret polynomial $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i$, opening hint $r_f$ to $c_f$
1: $\mathcal{P}$ samples a random polynomial $h\left(X\right)={\sum }_{i=0}^d{h}_i{X}^i\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p\left[X\right]$ of degree d
2: $\mathcal{P}$ computes $c_h\leftarrow g^{r_h}{\prod }_{i=0}^d{g}_i^{h_i}$ in $\mathbb{G}$ for $r_h\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ and $y_h=h\left(x\right)$ in ${\mathbb{Z}}_p$	// $c_h\leftarrow {\mathsf{Commit}}_{\mathsf{H}}({\mathsf{pp}}_{\mathsf{H}};h\left(X\right),r_h)$
3: $\mathcal{P}$ sends $\{c_h,y_h\}$ to $\mathcal{V}$
4: $\mathcal{V}$ samples ${\alpha }_f\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ and sends it to $\mathcal{P}$
5: $\mathcal{P}$ computes $\tilde{f}\left(X\right)\leftarrow h\left(X\right)+{\alpha }_f·f\left(X\right)$ in ${\mathbb{Z}}_p\left[X\right]$ and $r_{\tilde{f}}\leftarrow r_h+{\alpha }_f·r_f$ in ${\mathbb{Z}}_p$
6: $\mathcal{P}$ sends $r_{\tilde{f}}$ to $\mathcal{V}$
7: $\mathcal{P}$ and $\mathcal{V}$ compute $c\leftarrow c_h·c_f^{{\alpha }_f}·g^{-r_{\tilde{f}}}$ in $\mathbb{G}$ and $y\leftarrow y_h+{\alpha }_f·y_f$ in ${\mathbb{Z}}_p$	//$c={\prod }_{i=0}^d{g}_i^{{\tilde{f}}_i}\leftarrow \mathsf{Commit}(\mathsf{pp};\tilde{f}\left(X\right))$ and $y=\tilde{f}\left(x\right)$
8: $\mathcal{P}$ and $\mathcal{V}$ run $\mathsf{Eval}(\mathsf{pp},c,x,y,d;\tilde{f}\left(X\right))$

The $\mathsf{EvalZK}$ protocol receives a hiding commitment to the prover’s secret polynomial $f\left(x\right)$ on input, i.e., $c_f\leftarrow {\mathsf{Commit}}_{\mathsf{H}}({\mathsf{pp}}_{\mathsf{H}};f\left(X\right),d,r_f)$, which is perfectly indistinguishable to a random element in $\mathbb{G}$. To hand it over to the $\mathsf{Eval}$ protocol, it is necessary to remove the randomization part $g^{r_f}$ from $c_f=g^{r_f}{\prod }_{i=0}^d{g}_i^{f_i}$, which is equal to $\mathsf{Commit}(\mathsf{pp},f\left(X\right))$. However, because this reveals information on $f\left(x\right)$, the protocol lets the prover and the verifier collaboratively blind $f\left(x\right)$ by $\tilde{f}\left(X\right)=h\left(X\right)+\alpha f\left(X\right)$ (Line 5). Here, $h\left(X\right)\in {\mathbb{Z}}_p\left[X\right]$ is a random polynomial selected by the prover (Line 1) and $\alpha \in {\mathbb{Z}}_p$ is a random number selected by the verifier (Line 4). Consequently, both the prover and the verifier succeed in generating a non-hiding commitment to $\tilde{f}\left(X\right)$ under Π and the point $(x,y=\tilde{f}\left(x\right))$, and then start the $\mathsf{Eval}$ protocol (Lines 7–8).

Theorem 3.

The $\mathsf{EvalZK}$ protocol has perfect completeness, witness-extended emulation, and perfect SHVZK for a relation

$${\mathcal{R}}_{\mathsf{EvalZK}}=\left\{((c,x,y,d),(f\left(X\right),r)):\begin{array}{c}deg\left(f\right(X\left)\right)\le d\wedge f\left(x\right)=y\\ \wedge {\mathsf{Open}}_{\mathsf{H}}(\mathsf{pp},c,f\left(X\right),r)=1\end{array}\right\}$$

if the discrete logarithm relation assumption holds for $\mathsf{Ggen}$.

Proof of Theorem 3.

(perfect completeness) We show that ${\Pi }_{\mathsf{H}}$ has perfect completeness. Because the $\mathsf{Eval}$ protocol has perfect completeness (Theorem 1), it suffices to show that c and y are a valid input to $\mathsf{Eval}$. That is, c is the correct commitment to $\tilde{f}\left(X\right)=h\left(X\right)+\alpha f\left(X\right)$ under $\Pi$ and y is the evaluation of $\tilde{f}\left(X\right)$ at $X=x$ in ${\mathbb{Z}}_p$. Given $f\left(X\right)={\sum }_{i=0}^d{f}_i{X}^i$ of a degree of at most d and $h\left(X\right)={\sum }_{i=0}^d{h}_i{X}^i$ of degree d, we have

$$\begin{array}{cc}\hfill c& =c_h·c_f^{{\alpha }_f}·g^{-r_{\tilde{f}}}\hfill \\ & =\left(g^{r_h}\prod _{i=0}^d{g}_i^{h_i}\right)·\left(g^{{\alpha }_f{r}_f}\prod _{i=0}^d{g}_i^{{\alpha }_f{f}_i}\right)·g^{-r_{\tilde{f}}}\hfill \\ \hfill & =g^{r_h+{\alpha }_f{r}_f}·g^{-r_{\tilde{f}}}·\prod _{i=0}^d{g}_i^{h_i+{\alpha }_f{f}_i}\hfill \\ \hfill & =\prod _{i=0}^d{g}_i^{h_i+{\alpha }_f{f}_i}=\prod _{i=0}^d{g}_i^{{\tilde{f}}_i}=\mathsf{Commit}(\mathsf{pp},\tilde{f}\left(X\right)))and\hfill \\ \hfill y& =y_h+{\alpha }_f{y}_f=y\left(x\right)+{\alpha }_{f}f\left(x\right)=\tilde{f}\left(x\right)modp.\hfill \end{array}$$

(witness-extended emulation) We show that ${\Pi }_{\mathsf{H}}$ has witness-extended emulation. From Theorem 2, we have an expected polynomial-time extractor $\mathcal{E}$ that extracts $\tilde{f}\left(X\right)$ for the $\mathsf{Eval}$ protocol. Using $\mathcal{E}$, we construct an extractor ${\mathcal{E}}_{\mathsf{H}}$ to extract a witness $f\left(X\right)$ from $\mathsf{EvalZK}$. The extractor ${\mathcal{E}}_{\mathsf{H}}$ runs the prover to obtain $\{c_h,y_h\}$. At this point, ${\mathcal{E}}_{\mathsf{H}}$ then rewinds the oracle $\langle {\mathcal{P}}^{*},\mathcal{V}\rangle$ twice with distinct challenges ${\alpha }_f$ and ${\alpha }_f^{\prime }$ and obtains the corresponding commitments $(c,y)$ and $(c^{\prime },y^{\prime })$ to the witnesses $\tilde{f}\left(X\right)$ and ${\tilde{f}}^{\prime }\left(X\right)$, respectively. Then, ${\mathcal{E}}_{\mathsf{H}}$ runs $\mathcal{E}$ on inputs $(\mathsf{pp},c,x,y,d)$ and $(\mathsf{pp},c^{\prime },x,y^{\prime },d)$ and receives the corresponding witnesses $\tilde{f}\left(X\right)$ and ${\tilde{f}}^{\prime }\left(X\right)$, respectively. Finally, ${\mathcal{E}}_{\mathsf{H}}$ is able to extract the witness $f\left(X\right)$ from $\tilde{f}\left(X\right)$ and ${\tilde{f}}^{\prime }\left(X\right)$, similarly to Lemma 2. This completes the proof of the witness-extended emulation. (perfect SHVZK) We construct the simulator $\mathsf{Sim}$. Given only the public input, the simulator $\mathsf{Sim}$ outputs a simulated transcript that is identical to the valid transcript produced by the prover and the verifier in the real interaction. The simulator $\mathsf{Sim}$ first samples a random polynomial $\tilde{f}\left(X\right)$ of degree d and $r_{\tilde{f}}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$. In addition, $\mathsf{Sim}$ samples a random challenge ${\alpha }_f\stackrel{\$}{\leftarrow }\mathbb{G}$ and computes $c_h=c·c_f^{-{\alpha }_f}·g^{r_{\tilde{f}}}$ and $y_h=y-{\alpha }_f·y_f.$ The simulator $\mathsf{Sim}$ then simply applies the $\mathsf{Eval}$ protocol honestly using $\tilde{f}\left(X\right)$ as the witness. Because in a real execution, the values ${\alpha }_f$ and $r_{\tilde{f}}$ are distributed uniformly at random over ${\mathbb{Z}}_p$, the simulated ${\alpha }_f$ and $r_{\tilde{f}}$ are identically distributed to real values. In addition, the real $c_f$ and $\tilde{f}\left(X\right)$) are distributed uniformly at random over $\mathbb{G}$ and ${\mathbb{Z}}_p\left[X\right]$ of degree d, respectively, and the same distributions hold for the simulated $c_f$ and $\tilde{f}\left(X\right)$, respectively. The simulated $c_h$ is also distributed uniformly at random over $\mathbb{G}$, and thus the real $c_h$ is, because of the perfect hiding property of the underlying commitment scheme. Clearly, the simulated $(c_h,y_h,{\alpha }_f,r_{\tilde{f}})$ holds the relations

$$c=c_h·c_f^{{\alpha }_f}·g^{-r_{\tilde{f}}}\in \mathbb{G},y=y_h+{\alpha }_f·y_f\in {\mathbb{Z}}_p.$$

Finally, the $\mathsf{Eval}$ protocol does not leak more than $\tilde{f}\left(X\right)$ itself, which contains no information about $f\left(X\right)$. Therefore, the views of the simulated and real transcripts are identically distributed. This completes the proof of the perfect SHVZK. □

7. Conclusions

In this paper, we presented how to transpose a recursive argument of polynomial evaluation over a class group proposed by Bünz et al. to the discrete log setting as a way to improve the efficiency. The transposition follows from their information-theoretic abstraction. We found that the challenge for a transposition is to provide a monomial homomorphism for an underlying commitment scheme. We observed that when we use a polynomial encoding method that presents coefficients of the polynomial to the power of random group elements, an essential sufficient condition is a proof system for the equality of discrete logarithms ($Po{E}_{mDL}$) over multiple bases. We believe that our approach suggests a stepping stone for the construction of an efficient, transparent polynomial commitment scheme with a recursive argument in the discrete log setting. Currently, the efficiency of known proof systems for $Po{E}_{mDL}$ is not sufficient to hava logarithmic communication and verifier complexities. Therefore, in future work, we will continue to research how to improve the efficiency of $Po{E}_{mDL}$, which leads to high-efficiency gains for the proposed construction in the discrete log setting.